1.E: Funciones (Ejercicios)

1.1: Funciones y notación de funciones

Un avión cambia de altitud a medida que aumenta su distancia desde el punto de partida de un vuelo. El peso de un niño en crecimiento aumenta con el tiempo. En cada caso, una cantidad depende de otra. Existe una relación entre las dos cantidades que podemos describir, analizar y usar para hacer predicciones. En esta sección, analizaremos dichas relaciones.

Verbal

1) ¿Cuál es la diferencia entre una relación y una función?

Contestar

Una relación es un conjunto de pares ordenados. Una función es un tipo especial de relación en la que no hay dos pares ordenados que tengan la misma primera coordenada.

2) ¿Cuál es la diferencia entre la entrada y la salida de una función?

3) ¿Por qué la prueba de línea vertical nos dice si la gráfica de una relación representa una función?

Contestar

Cuando una línea vertical cruza la gráfica de una relación más de una vez, eso indica que para esa entrada hay más de una salida. En cualquier valor de entrada en particular, solo puede haber una salida si la relación va a ser una función.

4) ¿Cómo se puede determinar si una relación es una función uno a uno?

5) ¿Por qué la prueba de línea horizontal nos dice si el gráfico de una función es uno a uno?

Contestar

Cuando una línea horizontal cruza la gráfica de una función más de una vez, eso indica que para esa salida hay más de una entrada. Una función es uno a uno si cada salida corresponde a una sola entrada.

Algebraico

Para los ejercicios 6-7, determinar si la relación representa una función.

6)$\{(a,b), (c,d), (a,c)\}$

7)$\{(a,b),(b,c),(c,c)\}$

Contestar

función

Para los ejercicios 8-26, determinar si la relación representa$y$ en función de$x$.

8)$5x+2y=10$

9)$y=x^2$

Contestar

función

10)$x=y^2$

11)$3x^2+y=14$

Contestar

función

12)$2x+y^2=6$

13)$y=−2x^2+40x$

Contestar

función

14)$y=\dfrac{1}{x}$

15)$x=\dfrac{3y+5}{7y−1}$

Contestar

función

16)$x=\sqrt{1−y^2}$

17)$y=\dfrac{3x+5}{7x−1}$

Contestar

función

18)$x^2+y^2=9$

19)$2xy=1$

Contestar

función

20)$x=y^3$

21)$y=x^3$

Contestar

función

22)$y=\sqrt{1−x^2}$

23)$x=\pm\sqrt{1-y}$

Contestar

función

24)$y=\pm\sqrt{1−x}$

25)$y^2=x^2$

Contestar

no es una función

26)$y^3=x^2$

Para los ejercicios 27-39, evaluar la función$f$ a los valores indicados$f(−3),f(2),f(−a),−f(a),f(a+h)$.

27)$f(x)=2x−5$

Contestar

$f(−3)=−11$;$f(2)=−1$;;$f(−a)=−2a−5$;$−f(a)=−2a+5$;$f(a+h)=2a+2h−5$

28)$f(x)=−5x^2+2x−1$

29)$f(x)=\sqrt{2−x}+5$

Contestar

$f(−3)=\sqrt{5+5}$;$f(2)=5$;;$f(−a)=\sqrt{2+a+5}$;$−f(a)=−\sqrt{2−a}−5$;$f(a+h)=\sqrt{2−a−h}+5$

30)$f(x)=\dfrac{6x−1}{5x+2}$

31)$f(x)=|x−1|−|x+1|$

Contestar

$f(−3)=2$;$f(2)=1−3=−2$;;$f(−a)=|−a−1|−|−a+1|$;$−f(a)=−|a−1| +|a+1|$;$f(a+h)= |a+h−1|−|a+h+1|$

32) Dada la función$g(x)=5−x^2$, evaluar$g(x+h)−g(x)h$,$h{\neq}0$.

33) Dada la función$g(x)=x^2+2x$, evaluar$\dfrac{g(x)−g(a)}{x−a}$,$x{\neq}a$.

Contestar

$\dfrac{g(x)−g(a)}{x−a}=x+a+2$,$x{\neq}a$

34) Dada la función$k(t)=2t−1$:

a. Evaluar$k(2)$.
b. Resolver$k(t)=7$.

35) Dada la función$f(x)=8−3x$:

a. Evaluar$f(−2)$.
b. Resolver$f(x)=−1$.

Contestar

a.$f(−2)=14$; b.$x=3$

36) Dada la función$p(c)=c^2+c$:

a. Evaluar$p(−3)$.
b. Resolver$p(c)=2$.

37) Dada la función$f(x)=x^2−3x$:

a. Evaluar$f(5)$.
b. Resolver$f(x)=4$.

Contestar

a.$f(5)=10$; b.$x=−1$ o$x=4$

38) Dada la función$f(x)=\sqrt{x+2}$:

a. Evaluar$f(7)$.
b. Resolver$f(x)=4$.

39) Considerar la relación$3r+2t=18$.

a. Escribir la relación como una función$r=f(t)$.
b. Evaluar$f(−3)$.
c. Resolver$f(t)=2$.

Contestar

a.$f(t)=6−\frac{2}{3}t$; b.$f(−3)=8$; c.$t=6$

Gráfica

Para los ejercicios 40-54, utilice la prueba de línea vertical para determinar qué gráficas muestran relaciones que son funciones.

40)

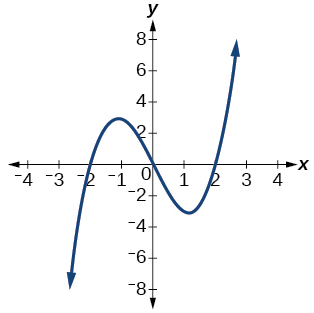
41)

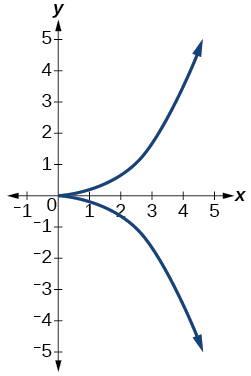
Contestar

no es una función

42)

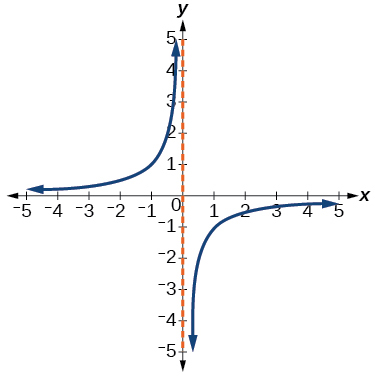
43)

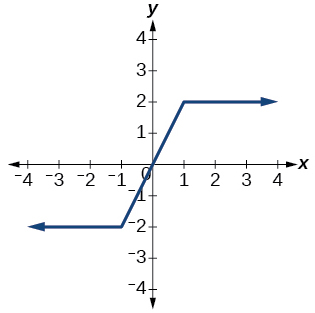
Contestar

función

44)

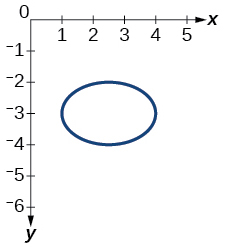
45)

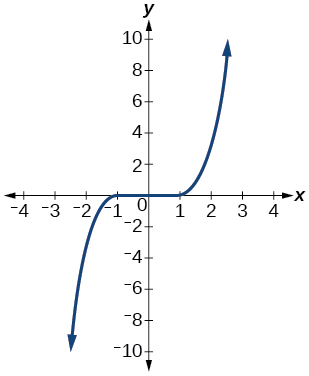
Contestar

función

46)

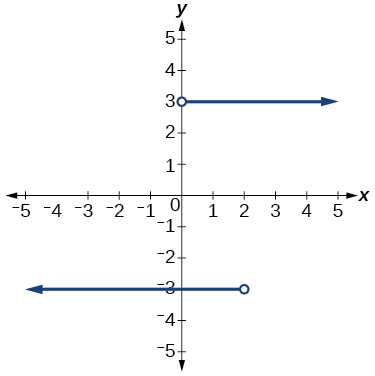
47)

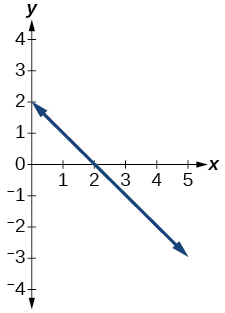
Contestar

función

48)

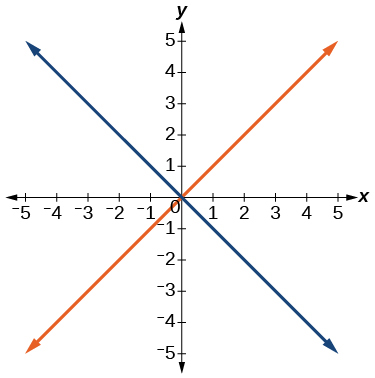
49)

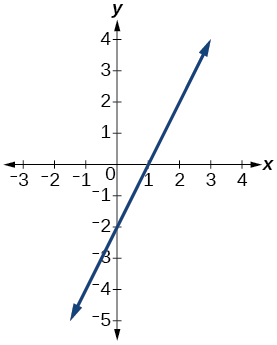
Contestar

función

50)

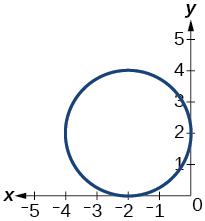
51)

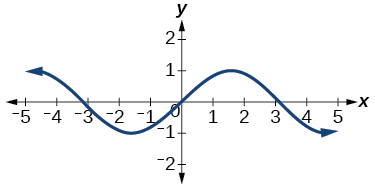
Contestar

función

52) Teniendo en cuenta la siguiente gráfica,

• Evaluar$f(−1)$.
• Resolver para$f(x)=3$.

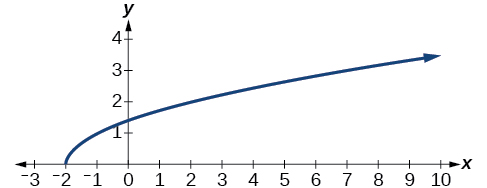
53) Teniendo en cuenta la siguiente gráfica,

• Evaluar$f(0)$.
• Resolver para$f(x)=−3$.

Contestar

a.$f(0)=1$; b.$f(x)=−3$,$x=−2$ o$x=2$

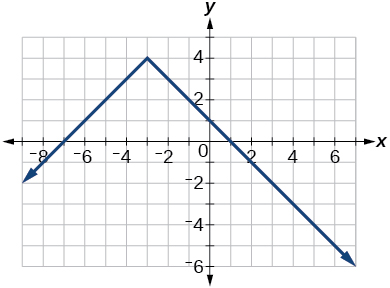
54) Teniendo en cuenta la siguiente gráfica,

• Evaluar$f(4)$.
• Resolver para$f(x)=1$.

Para los ejercicios 55-59, determine si la gráfica dada es una función uno a uno.

55)

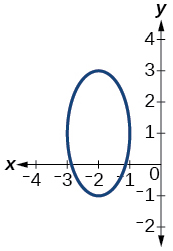
Contestar

no es una función así que tampoco es una función uno-a-uno

56)

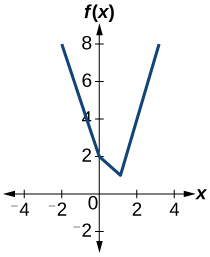
57)

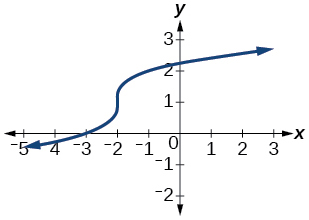
Contestar

función uno-a-uno

58)

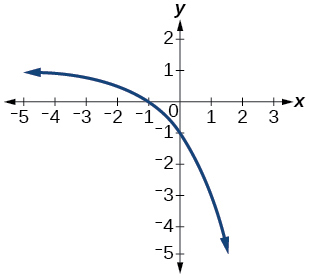
59)

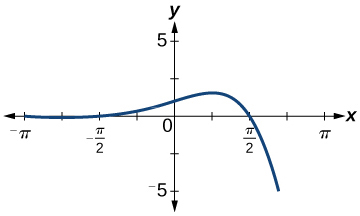
Contestar

función, pero no uno a uno

Numérico

Para los ejercicios 60-62, determinar si la relación representa una función.

60)$\{(−1,−1),(−2,−2),(−3,−3)\}$

61)$\{(3,4),(4,5),(5,6)\}$

Contestar

función

62)$(2,5),(7,11),(15,8),(7,9)\}$

Para los ejercicios 63-65, determinar si la relación representada en forma de tabla representa$y$ en función de$x$.

63)

$x$	5	10	15
$y$	3	8	14

Responder

función

64)

$x$	5	10	15
$y$	3	8	8

65)

$x$	5	10	10
$y$	3	8	14

Responder

no es una función

Para los ejercicios 66-67, utilice la función$f$ representada en la Tabla siguiente

$x$	$f(x)$
\ (x\) ">0	\ (f (x)\) ">74
\ (x\) ">1	\ (f (x)\) ">28
\ (x\) ">2	\ (f (x)\) ">1
\ (x\) ">3	\ (f (x)\) ">53
\ (x\) ">4	\ (f (x)\) ">56
\ (x\) ">5	\ (f (x)\) ">3
\ (x\) ">6	\ (f (x)\) ">36
\ (x\) ">7	\ (f (x)\) ">45
\ (x\) ">8	\ (f (x)\) ">14
\ (x\) ">9	\ (f (x)\) ">47

66) Evaluar$f(3)$.

67) Resolver$f(x)=1$.

Responder

$f(x)=1$,$x=2$

Para los ejercicios 68-73, evaluar la función$f$ en los valores$f(−2)$$f(−1)$,$f(0)$,$f(1)$, y$f(2)$.

68)$f(x)=4−2x$

69)$f(x)=8−3x$

Responder

$f(−2)=14$;$f(−1)=11$;;$f(0)=8$;$f(1)=5$;$f(2)=2$

70)$f(x)=8x^2−7x+3$

71)$f(x)=3+\sqrt{x+3}$

Responder

$f(−2)=4$;$f(−1)=4.414$;;$f(0)=4.732$;$f(1)=4.5$;$f(2)=5.236$

72)$f(x)=\dfrac{x-2}{x+3}$

73)$f(x)=3^x$

Responder

$f(−2)=\frac{1}{9}$;$f(−1)=\frac{1}{3}$;;$f(0)=1$;$f(1)=3$;$f(2)=9$

Para los ejercicios 74-75, evaluar las expresiones, funciones dadas$f$$g$, y$h$:

• $f(x)=3x−2$
• $g(x)=5−x^2$
• $h(x)=−2x^2+3x−1$

74)$3f(1)−4g(−2)$

75)$f \left (\dfrac{7}{3} \right )−h(−2)$

Responder

$20$

Tecnología

Para los ejercicios 76-78, grafica$y=x^2$ en la ventana de visualización dada. Determine el rango correspondiente para cada ventana de visualización. Mostrar cada gráfica.

76)$[−0.1, 0.1]$

77)$[−10, 10]$

Responder

$[0, 100]$

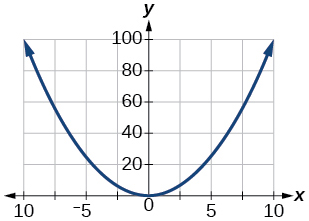
78)$[−100,100]$

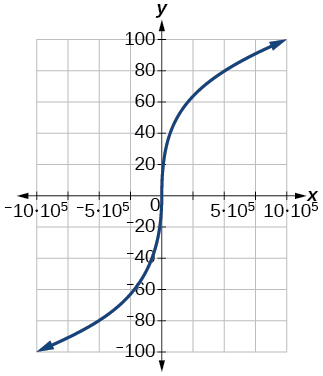
Para los ejercicios 79-81, grafica$y=x^3$ en la ventana de visualización dada. Determine el rango correspondiente para cada ventana de visualización. Mostrar cada gráfica.

79)$[−0.1, 0.1]$

Responder

$[−0.001, 0.001]$

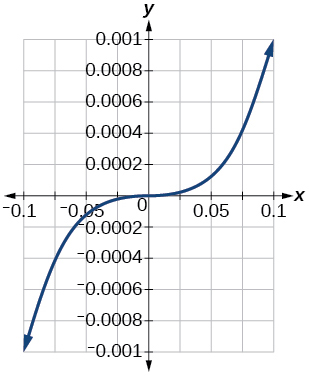
80)$[−10, 10]$

81)$[−100, 100]$

Responder

$[−1,000,000, 1,000,000]$

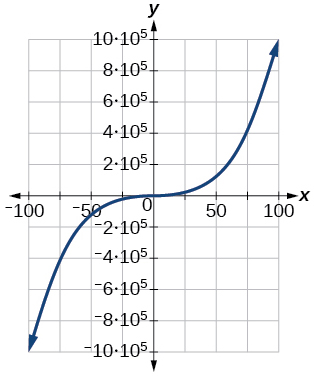
Para los ejercicios 82-84, grafica$y=\sqrt{x}$ en la ventana de visualización dada. Determine el rango correspondiente para cada ventana de visualización. Mostrar cada gráfica.

82)$[0, 0.01]$

83)$[0, 100]$

Responder

$[0, 10]$

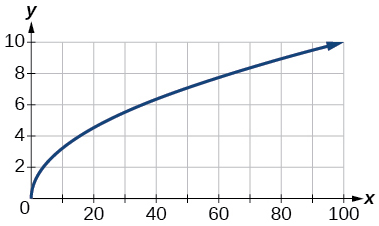
84)$[0, 10,000]$

Para los ejercicios 85-87, grafica$y=\sqrt[3]{x}$ en la ventana de visualización dada. Determine el rango correspondiente para cada ventana de visualización. Mostrar cada gráfica.

85)$[−0.001,0.001]$

Responder

$[−0.1,0.1]$

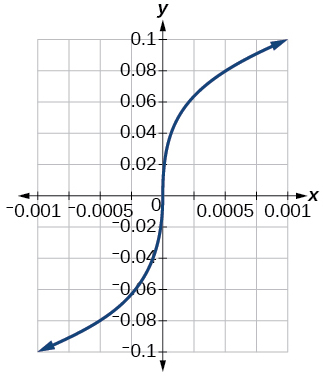
86)$[−1000,1000]$

87)$[−1,000,000,1,000,000]$

Responder

$[−100, 100]$

Aplicaciones del mundo real

88) La cantidad de basura,$G$, producida por una ciudad con población$p$ viene dada por$G=f(p)$. $G$se mide en toneladas por semana, y$p$ se mide en miles de personas.

El pueblo de Tola tiene una población de$40,000$ y produce$13$ toneladas de basura cada semana. Expresar esta información en términos de la función$f$ .Tola tiene una población de$40,000$ y produce$13$ toneladas de basura cada semana. Exprese esta información en términos de la función$f$.
Explique el significado de la declaración$f(5)=2$.

89) El número de yardas cúbicas de tierra$D$,, necesarias para cubrir un jardín con área de un pie cuadrado viene dado por$D=g(a)$.

a. Un jardín con área$5000$$ft^2$ requiere$50$$yd^3$ de tierra. Exprese esta información en términos de la función$g$.
b. Explique el significado de la declaración$g(100)=1$.

Responder

a.$g(5000)=50$; b. El número de yardas cúbicas de tierra requeridas para un jardín de pies$100$ cuadrados es$1$.

90)$f(t)$ Sea el número de patos en un lago$t$ años después de 1990. Explique el significado de cada enunciado:

a. f (5) =30
b. f (10) =40

91) Dejar$h(t)$ ser la altura sobre el suelo, en pies, de un cohete$t$ segundos después del lanzamiento. Explique el significado de cada enunciado:

a.$h(1)=200$
b.$h(2)=350$

Responder

a. La altura de un cohete sobre el suelo después del$1$ segundo es$200$ ft. b. la altura de un cohete sobre el suelo después de$2$ segundos es$350$ ft.

92) Demostrar que la función no$f(x)=3(x−5)^2+7$ es uno a uno.

1.2: Dominio y Rango

Al crear diversas funciones usando los datos, podemos identificar diferentes variables independientes y dependientes, y podemos analizar los datos y las funciones para determinar el dominio y el rango. En esta sección, investigaremos métodos para determinar el dominio y rango de funciones.

Verbal

1) ¿Por qué el dominio difiere para diferentes funciones?

Responder

El dominio de una función depende de qué valores de la variable independiente hacen que la función sea indefinida o imaginaria.

2) ¿Cómo determinamos el dominio de una función definida por una ecuación?

3) Explicar por qué el dominio de$f(x)=\sqrt[3]{x}$ es diferente del dominio de$f(x)=\sqrt{x}$.

Responder

No hay restricción en x$f(x)=\sqrt[3]{x}$ porque puedes tomar la raíz cubo de cualquier número real. Entonces el dominio es todo números reales,$(−∞,∞)$. Al tratar con el conjunto de números reales, no se puede tomar la raíz cuadrada de los números negativos. Entonces los valores x están restringidos$f(x)=\sqrt{x}$ para números no negativos y el dominio es$[0,∞)$.

4) Al describir conjuntos de números usando notación de intervalo, ¿cuándo se usa un paréntesis y cuándo se usa un corchete?

5) ¿Cómo graficas una función por tramos?

Responder

Grafique cada fórmula de la función por partes sobre su dominio correspondiente. Utilice la misma escala para el eje x y el eje y para cada gráfica. Indicar puntos finales inclusivos con un círculo sólido y extremos exclusivos con un círculo abierto. Usa una flecha para indicar$−∞$ o$∞$. Combine las gráficas para encontrar la gráfica de la función por partes.

Algebraico

Para los ejercicios 6-25, encuentra el dominio de cada función usando notación de intervalos.

6)$f(x)=−2x(x−1)(x−2)$

7)$f(x)=5−2x^2$

Responder

$(-\infty,\infty)$

8)$f(x)=3\sqrt{x-2}$

9)$f(x)=3-\sqrt{6-2x}$

Responder

$\left(-\infty,3\right]$

10)$f(x)=\sqrt{4-3x}$

11)$f(x)=\sqrt{x^2+4}$

Responder

$(-\infty,\infty)$

12)$f(x)=\sqrt[3]{1-2x}$

13)$f(x)=\sqrt[3]{x-1}$

Responder

$(-\infty,\infty)$

14)$f(x)=\dfrac{9}{x-6}$

15)$f(x)=\dfrac{3x+1}{4x+2}$

Responder

$\left (-\infty,-\dfrac{1}{2} \right )\cup \left (-\dfrac{1}{2},\infty \right )$

16)$f(x)=\dfrac{\sqrt{x+4}}{x-4}$

17)$f(x)=\dfrac{x-3}{x^2+9x-22}$

Responder

$(-\infty,-11)\cup(-11,2)\cup(2,\infty)$

18)$f(x)=\dfrac{1}{x^2-x-6}$

19)$f(x)=\dfrac{2x^3−250}{x^2−2x−15}$

Responder

$(-\infty,-3)\cup(-3,5)\cup(5,\infty)$

20)$\dfrac{5}{\sqrt{x-3}}$

21)$\dfrac{2x+1}{\sqrt{5-x}}$

Responder

$(-\infty,5)$

22)$\dfrac{\sqrt{x-4}}{\sqrt{x-6}}$

23)$\dfrac{\sqrt{x-6}}{\sqrt{x-4}}$

Responder

$\left[6,\infty\right)$

24)$f(x)=\dfrac{x}{x}$

25)$f(x)=\dfrac{x^2-9x}{x^2-81}$

Responder

$(-\infty,-9)\cup(-9,9)\cup(9,\infty)$

26) Encuentra el dominio de la función$f(x)=\sqrt{2x^3-50x}$ por:

a. usar álgebra

b. graficar la función en el radicando y determinando intervalos en el eje x para los cuales el radicando no es negativo.

Gráfica

Para los ejercicios 27-37, escriba el dominio y el rango de cada función usando notación de intervalo.

27)

\ (\ left (2, 8\ right]\).” style="background-color: transparente; border-bottom-color: rgb (0, 0, 0); border-bottom-style: none; border-bottom-width: 0px; border-image-principio: 0; border-image-repeat: stretch; border-image-slice: 100%; border-image-source: none; border-image-width: 1; border-left color: rgb ( 0, 0, 0); border-left style: none; border-left width: 0px; border-right color: rgb (0, 0, 0); border-right style: none; border-right width: 0px; border-top-color: rgb (0, 0, 0); border-top-style: none; border-top-width: 0px; color: rgb (0, 0, 0); cursor: default; font-family: lato, arial, helvética, sans-serif, & quot; arial unicode ms”; font-size: 16px; font-style: normal; font-variant: normal; font-weight: 400; height: 200px; leter-espaciado: normal; max-width: 1224px; opacidad: 0.8; huérfanos: 2; text-align: center; text-decoration: none; text-indent: 0px; text-transform: none; -webkit-text-ancho de trazo: 0px; blanco -espacio: normal; ancho: 200px; espaciado de palabras: 0px;” width="200px” height="200px” src=” https://math.libretexts.org/@api/dek..._01_02_202.jpg "/>

Responder

dominio:$\left(2,8\right]$, rango$\left[6,8\right)$

28)

\ (\ left [4, 8\ right)\).” style="background-color: transparente; border-bottom-color: rgb (0, 0, 0); border-bottom-style: none; border-bottom-width: 0px; border-image-principio: 0; border-image-repeat: stretch; border-image-slice: 100%; border-image-source: none; border-image-width: 1; border-left color: rgb ( 0, 0, 0); border-left style: none; border-left width: 0px; border-right color: rgb (0, 0, 0); border-right style: none; border-right width: 0px; border-top-color: rgb (0, 0, 0); border-top-style: none; border-top-width: 0px; color: rgb (0, 0, 0); cursor: default; font-family: lato, arial, helvética, sans-serif, & quot; arial unicode ms”; font-size: 16px; font-style: normal; font-variant: normal; font-weight: 400; height: 200px; leter-espaciado: normal; max-width: 1224px; opacidad: 0.8; huérfanos: 2; text-align: center; text-decoration: none; text-indent: 0px; text-transform: none; -webkit-text-ancho de trazo: 0px; blanco -espacio: normal; ancho: 200px; espaciado de palabras: 0px;” width="200px” height="200px” src=” https://math.libretexts.org/@api/dek..._01_02_203.jpg "/>

29)

Responder

dominio:$[−4, 4]$, rango:$[0, 2]$

30)

31)

Responder

dominio:$\left[−5, 3\right)$, rango:$[0,2]$

32)

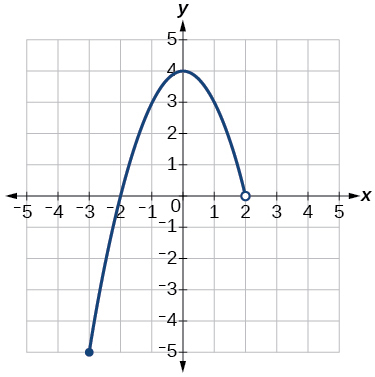
33)

Responder

dominio:$\left(−\infty,1\right]$, rango:$\left[0,\infty\right)$

34)

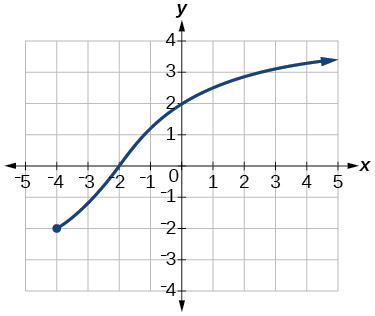
35)

Responder

dominio:$[−6,−16]\cup[16,6]$; rango:$[−6,−16]\cup[16,6]$

36)

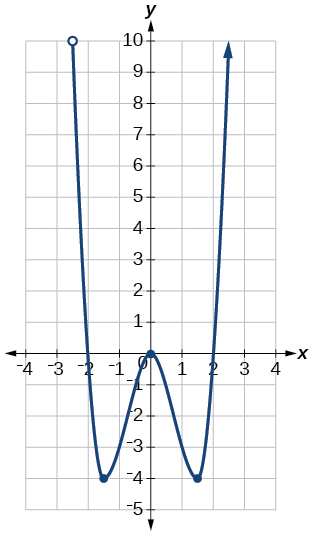
37)

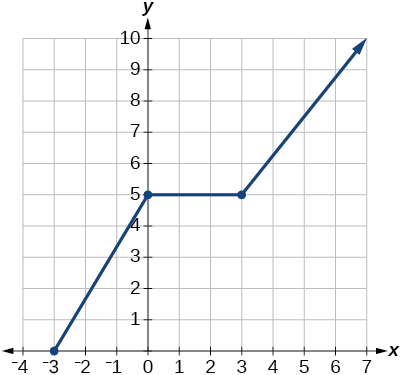
Responder

dominio:$\left[−3, \infty\right)$; rango:$\left[0,\infty\right)$

Para los ejercicios 38-45, esboce una gráfica de la función por partes. Escribe el dominio en notación de intervalos.

38)$f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}$

39)$f(x)= \begin{cases} 2x-1 & \text{if $x < 1$} \\ 1+x & \text{if $x {\geq} 1$} \end{cases}$

Responder

dominio:$(−\infty,\infty)$

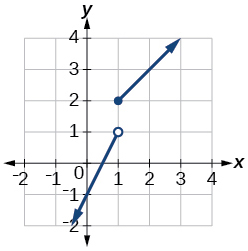
40)$f(x)= \begin{cases} x+1 & \text{if $x < 0$} \\ x-1 & \text{if $x > 0$} \end{cases}$

41)$f(x)= \begin{cases} 3 & \text{if $x < 0$} \\ \sqrt{x} & \text{if $x {\geq} 0$} \end{cases}$

Responder

dominio:$(−\infty,\infty)$

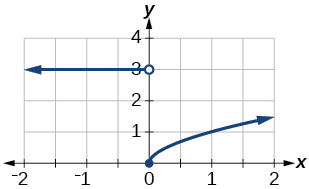
42)$f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ 1-x & \text{if $x > 0$} \end{cases}$

43)$f(x)= \begin{cases} x^2 & \text{if $x < 0$} \\ x+2 & \text{if $x {\geq} 0$} \end{cases}$

Responder

dominio:$(−\infty,\infty)$

44)$f(x)= \begin{cases} x+1 & \text{if $x < 1$} \\ x^3 & \text{if $x {\geq} 1$} \end{cases}$

45)$f(x)= \begin{cases} |x| & \text{if $x < 2$} \\ 1 & \text{if $x {\geq} 2$} \end{cases}$

Responder

dominio:$(−\infty,\infty)$

Numérico

Para los ejercicios 46-48, dada cada función$f$, evaluar$f(−3)$$f(−2)$,$f(−1)$, y$f(0)$.

46)$f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}$

47)$f(x)= \begin{cases} 1 & \text{if $x \leq -3$} \\ 0 & \text{if $x > -3$} \end{cases}$

Responder

$f(−3)=1$;$f(−2)=0$;$f(−1)=0$;$f(0)=0$

48)$f(x)= \begin{cases} -2x^2+3 & \text{if $x \leq -1$} \\ 5x-7 & \text{if $x > -1$} \end{cases}$

Para los ejercicios 49-51, dada cada función$f$, evaluar$f(−1)$$f(0)$,$f(2)$, y$f(4)$.

49)$f(x)= \begin{cases} 7x+3 & \text{if $x < 0$} \\ 7x+6 & \text{if $x {\geq} 0$} \end{cases}$

Responder

$f(−1)=−4$;$f(0)=6$;$f(2)=20$;$f(4)=34$

50)$f(x)= \begin{cases} x^2-2 & \text{if $x < 2$} \\ 4+|x-5| & \text{if $x {\geq} 2$} \end{cases}$

51)$f(x)= \begin{cases} 5x & \text{if $x < 0$} \\ 3 & \text{if $0 {\geq} x {\leq} 2$} \\ x^2 & \text{if $x > 3$} \end{cases}$

Responder

$f(−1)=−5$;$f(0)=3$;$f(2)=3$;$f(4)=16$

Para los ejercicios 52-54, escriba el dominio para la función por partes en notación de intervalos.

52)$f(x)= \begin{cases} x+1 & \text{if $x < -2$} \\ -2x-3 & \text{if $x {\geq} -2$} \end{cases}$

53)$f(x)= \begin{cases} x^2-2 & \text{if $x < 1$} \\ -x^2+2 & \text{if $x > 1$} \end{cases}$

Responder

dominio:$(−\infty,1)\cup(1,\infty)$

54)$f(x)= \begin{cases} x^2-3 & \text{if $x < 0$} \\ -3x^2 & \text{if $x {\geq} 2$} \end{cases}$

Tecnología

55) Gráfica$y=\dfrac{1}{x^2}$ en la ventana de visualización$[−0.5,−0.1]$ y$[0.1,0.5]$. Determinar el rango correspondiente para la ventana de visualización. Mostrar las gráficas.

Responder

ventana:$[−0.5,−0.1]$; rango:$[4, 100]$

ventana:$[0.1, 0.5]$; rango:$[4, 100]$

56) Gráfica$y=\dfrac{1}{x}$ en la ventana de visualización$[−0.5,−0.1]$ y$[0.1, 0.5]$. Determinar el rango correspondiente para la ventana de visualización. Mostrar las gráficas.

Extensión

57) Supongamos que el rango de una función$f$ es$[−5, 8]$. ¿Cuál es el rango de$|f(x)|$?

Responder

$[0, 8]$

58) Crear una función en la que el rango sea todos los números reales no negativos.

59) Crear una función en la que se encuentre el dominio$x>2$.

Responder

Muchas respuestas. Una función es$f(x)=\dfrac{1}{\sqrt{x-2}}$.

Aplicaciones del mundo real

60) La altura$h$ de un proyectil es función del tiempo$t$ que se encuentra en el aire. La altura en pies por$t$ segundos viene dada por la función$h(t)=−16t^2+96t$. ¿Cuál es el dominio de la función? ¿Qué significa el dominio en el contexto del problema?

Responder

El dominio es$[0, 6]$; tarda 6 segundos para que el proyectil salga del suelo y regrese al suelo

61) El costo en dólares de hacer$x$ artículos viene dado por la función$C(x)=10x+500$.

a. El costo fijo se determina cuando se producen cero artículos. Encuentra el costo fijo para este artículo.

b. ¿Cuál es el costo de hacer$25$ artículos?

c. Supongamos que el costo máximo permitido es$\$1500$. ¿Cuáles son el dominio y el rango de la función de costo,$C(x)$?

1.3: Tasas de Cambio y Comportamiento de las Gráficas

En esta sección, investigaremos los cambios en las funciones. Por ejemplo, una tasa de cambio relaciona un cambio en una cantidad de salida con un cambio en una cantidad de entrada. La tasa promedio de cambio se determina utilizando únicamente los datos de inicio y finalización. Identificar los puntos que marcan el intervalo en una gráfica se puede utilizar para encontrar la tasa promedio de cambio. La comparación de pares de valores de entrada y salida en una tabla también se puede utilizar para encontrar la tasa de cambio promedio.

Verbal

1) ¿La tasa promedio de cambio de una función puede ser constante?

Responder

Sí, la tasa promedio de cambio de todas las funciones lineales es constante.

2) Si una función$f$ está aumentando$(a,b)$ y disminuyendo en$(b,c)$, entonces ¿qué se puede decir sobre el extremo local de$f$ on$(a,c)$?

3) ¿En qué se asemejan y diferencian los máximos y mínimos absolutos a los extremos locales?

Responder

El máximo absoluto y el mínimo se relacionan con toda la gráfica, mientras que los extremos locales se relacionan solo con una región específica alrededor de un intervalo abierto.

4) ¿Cómo se compara la gráfica de la función de valor absoluto con la gráfica de la función cuadrática$y=x^2$, en términos de intervalos crecientes y decrecientes?

Algebraico

Para los ejercicios 5-15, encuentra la tasa promedio de cambio de cada función en el intervalo especificado para números reales$b$ o$h$.

5)$f(x)=4x^2−7$ en$[1, b]$

Responder

$4(b+1)$

6)$g(x)=2x^2−9$ en$[4, b]$

7)$p(x)=3x+4$ en$[2, 2+h]$

Responder

$3$

8)$k(x)=4x−2$ en$[3, 3+h]$

9)$f(x)=2x^2+1$ en$[x,x+h]$

Responder

$4x+2h$

10)$g(x)=3x^2−2$ en$[x,x+h]$

11)$a(t)=\dfrac{1}{t+4}$ en$[9,9+h]$

Responder

$\dfrac{−1}{13(13+h)}$

12)$b(x)=1x+3$ en$[1,1+h]$

13)$j(x)=3x^3$ en$[1,1+h]$

Responder

$3h^2+9h+9$

14)$r(t)=4t^3$ en$[2,2+h]$

15)$\dfrac{f(x+h)−f(x)}{h}$ dado$f(x)=2x^2−3x$ el$[x,x+h]$

Responder

$4x+2h−3$

Gráfica

Para los ejercicios 16-17, considere la gráfica de que$f$ se muestra en la Figura a continuación

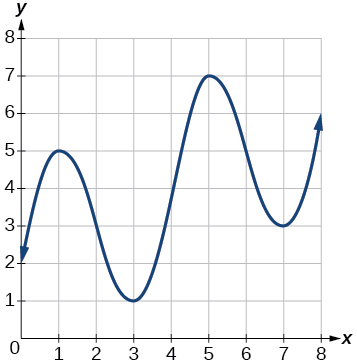
Gráfica de un polinomio.

16) Estimar la tasa promedio de cambio de$x=1$ a$x=4$.

17) Estimar la tasa promedio de cambio de$x=2$ a$x=5$.

Responder

$\dfrac{4}{3}$

Para los siguientes ejercicios, utilice la gráfica de cada función para estimar los intervalos en los que la función está aumentando o disminuyendo.

18)

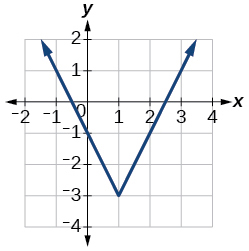
19)

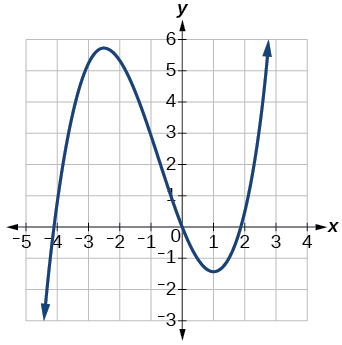
Responder

aumentando en$(−\infty,−2.5)\cup(1,\infty)$, disminuyendo en$(−2.5, 1)$

20)

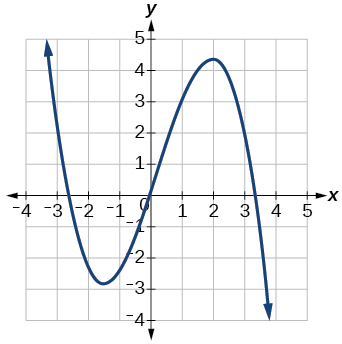
21)

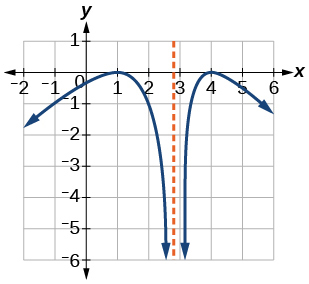
Responder

aumentando en$(−\infty,1)\cup(3,4)$, disminuyendo en$(1,3)\cup(4,\infty)$

Para los ejercicios 22-23, considere la gráfica que se muestra en la Figura a continuación.

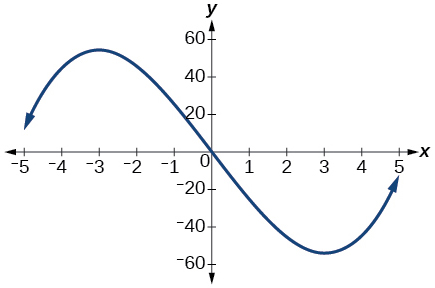
Gráfica de una función cúbica.

22) Estimar los intervalos donde la función está aumentando o disminuyendo.

23) Estimar el punto (s) en el que la gráfica de f tiene un máximo local o un mínimo local.

Responder

máximo local:$(−3, 60)$, mínimo local:$(3, −60)$

Para los ejercicios 24-25, considere la gráfica en la Figura a continuación.

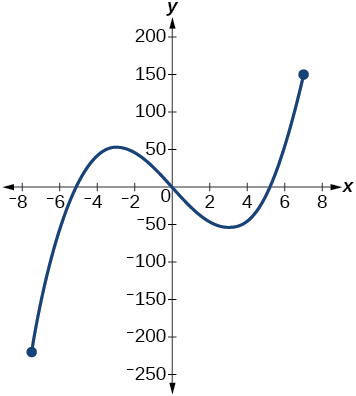
Gráfica de una función cúbica.

24) Si se muestra la gráfica completa de la función, estime los intervalos donde la función está aumentando o disminuyendo.

25) Si se muestra la gráfica completa de la función, estime el máximo absoluto y el mínimo absoluto.

Responder

máximo absoluto en aproximadamente$(7, 150)$, mínimo absoluto en aproximadamente$(−7.5, −220)$

Numérico

26) El cuadro siguiente da las ventas anuales (en millones de dólares) de un producto de 1998 a 2006. ¿Cuál fue la tasa promedio de variación de las ventas anuales (a) entre 2001 y 2002, y (b) entre 2001 y 2004?

Año	Ventas (millones de dólares)
1998	201
1999	219
2000	233
2001	243
2002	249
2003	251
2004	249
2005	243
2006	233

27) La siguiente Tabla da la población de una localidad (en miles) de 2000 a 2008. ¿Cuál fue la tasa promedio de cambio de la población a) entre 2002 y 2004, y b) entre 2002 y 2006?

Año	Población (miles)
2000	87
2001	84
2002	83
2003	80
2004	77
2005	76
2006	78
2007	81
2008	85

Responder

a.$-3000$; b.$-1250$

Para los ejercicios 28-34, encuentra la tasa promedio de cambio de cada función en el intervalo especificado.

28)$f(x)=x^2$ en$[1, 5]$

29)$h(x)=5−2x^2$ en$[−2,4]$

Responder

$-4$

30)$q(x)=x^3$ en$[−4,2]$

31)$g(x)=3x^3−1$ en$[−3,3]$

Responder

$27$

32)$y=\dfrac{1}{x}$ en$[1, 3]$

33)$p(t)=\dfrac{(t^2-4)(t+1)}{t^2+3}$ en$[-3,1]$

Responder

$-0.167$

34)$k(t)=6t^2+\dfrac{4}{t^3}$ en$[−1,3]$

Tecnología

Para los ejercicios 35-40, utilice una utilidad gráfica para estimar los extremos locales de cada función y estimar los intervalos en los que la función está aumentando y disminuyendo.

35)$f(x)=x^4−4x^3+5$

Responder

Mínimo local en$(3,−22)$, decreciente en$(−\infty, 3)$, aumentando el$(3, \infty)$

36)$h(x)=x^5+5x^4+10x^3+10x^2−1$

37)$g(t)=t\sqrt{t+3}$

Responder

Mínimo local en$(−2,−2)$, decreciente en$(−3,−2)$, aumentando el$(−2, \infty)$

38)$k(t)=3t^{\frac{2}{3}}−t$

39)$m(x)=x^4+2x^3−12x^2−10x+4$

Responder

Máximo local en$(−0.5, 6)$, mínimos locales en$(−3.25,−47)$ y$(2.1,−32)$, decreciente en$(−\infty,−3.25)$ y$(−0.5, 2.1)$, aumentando en$(−3.25, −0.5)$ y$(2.1,\infty)$

40)$n(x)=x^4−8x^3+18x^2−6x+2$

Extensión

41) La gráfica de la función$f$ se muestra en la siguiente figura:

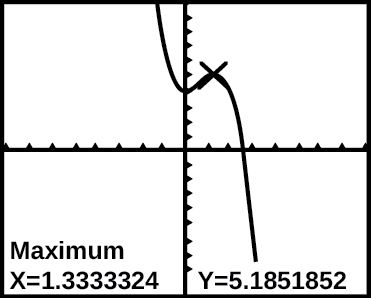
Gráfica de f (x) en una calculadora gráfica.

Con base en la captura de pantalla de la calculadora, el punto$(1.333, 5.185)$ es ¿cuál de las siguientes?

1. un máximo relativo (local) de la función
2. el vértice de la función
3. el máximo absoluto de la función
4. un cero de la función

Responder

a

42) Vamos$f(x)=\dfrac{1}{x}$. Encuentra un número$c$ tal que la tasa promedio de cambio de la función f en el intervalo$(1,c)$ sea$-\dfrac{1}{4}$.

43) Vamos$f(x)=\dfrac{1}{x}$. Encuentra el número$b$ tal que la tasa promedio de cambio de f en el intervalo$(2,b)$ sea$−\dfrac{1}{10}$.

Responder

$b=5$

Aplicaciones del mundo real

44) Al inicio de un viaje, leía el odómetro de un automóvil$21,395$. Al finalizar el viaje,$13.5$ horas después, leyó el odómetro$22,125$. Supongamos que la báscula en el odómetro está en millas. ¿Cuál es la velocidad promedio que recorrió el automóvil durante este viaje?

45) Un chofer de un automóvil se detuvo en una gasolinera para llenar su tanque de gasolina. Miró su reloj, y la hora leyó exactamente a las 3:40 de la tarde En este momento, comenzó a bombear gasolina en el tanque. A exactamente las 3:44, el tanque estaba lleno y notó que había bombeado$10.7$ galones. ¿Cuál es la tasa promedio de flujo de la gasolina hacia el tanque de gasolina?

Responder

$2.7$galones por minuto

46) Cerca de la superficie de la luna, la distancia que cae un objeto es función del tiempo. Se da por$d(t)=2.6667t^2$, donde$t$ está en segundos y$d(t)$ está en pies. Si un objeto se cae desde una cierta altura, encuentre la velocidad promedio del objeto de$t=1$ a$t=2$.

47) La gráfica de la siguiente figura ilustra la desintegración de una sustancia radiactiva a lo largo de$t$ días.

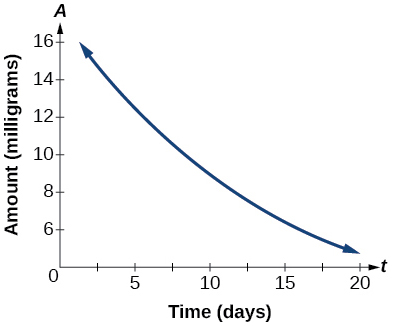
Gráfica de una función exponencial.

Utilice la gráfica para estimar la tasa de decaimiento promedio de$t=5$ a$t=15$.

Responder

aproximadamente$-0.6$ miligramos por día

1.4: Composición de las funciones

Supongamos que queremos calcular cuánto cuesta calentar una casa en un día determinado del año. El costo para calentar una casa dependerá de la temperatura media diaria, y a su vez, la temperatura media diaria depende del día particular del año. El costo depende de la temperatura, y la temperatura depende del día. Al combinar estas dos relaciones en una sola función, hemos realizado la composición de funciones, que es el foco de esta sección.

Verbal

1) ¿Cómo se encuentra el dominio del cociente de dos funciones,$\dfrac{f}{g}$?

Responder

Encuentra los números que hacen que la función en el denominador sea$g$ igual a cero, y verifica cualquier otra restricción de dominio sobre$f$ y$g$, como una raíz indexada par o ceros en el denominador.

2) ¿Cuál es la composición de dos funciones,$f{\circ}g$?

3) Si el orden se invierte al componer dos funciones, ¿puede el resultado ser el mismo que la respuesta en el orden original de la composición? En caso afirmativo, dar un ejemplo. Si no, explique por qué no.

Responder

Sí. Respuesta de muestra: Dejar$f(x)=x+1$ y$g(x)=x−1$. Entonces$f(g(x))=f(x−1)=(x−1)+1=x$ y$g(f(x))=g(x+1)=(x+1)−1=x$. Entonces$f{\circ}g=g{\circ}f$.

4) ¿Cómo encuentra el dominio para la composición de dos funciones,$f{\circ}g$?

Algebraico

5) Dado$f(x)=x^2+2x$ y$g(x)=6−x^2$, find$f+g$,,$f−g$$fg$, y$\dfrac{f}{g}$ .Determine el dominio para cada función en notación de intervalos.

Responder

$(f+g)(x)=2x+6$, dominio:$(−\infty,\infty)$

$(f−g)(x)=2x^2+2x−6$, dominio:$(−\infty,\infty)$

$(fg)(x)=−x^4−2x^3+6x^2+12x$, dominio:$(−\infty,\infty)$

$\left(\dfrac{f}{g}\right)(x)=\dfrac{x^2+2x}{6−x^2},$dominio:$(−\infty,−\sqrt{6})\cup(\sqrt{6},\sqrt{6})\cup(\sqrt{6},\infty)$

6) Dado$f(x)=−3x^2+x$ y$g(x)=5$, encontrar$f+g$,$f−g$,$fg$, y$\dfrac{f}{g}$. Determinar el dominio para cada función en notación de intervalos.

7) Dado$f(x)=2x^2+4x$ y$g(x)=\dfrac{1}{2x}$, encontrar$f+g$,$f−g$,$fg$, y$\dfrac{f}{g}$. Determinar el dominio para cada función en notación de intervalos.

Responder

$(f+g)(x)=\dfrac{4x^3+8x^2+1}{2x}$, dominio:$(−\infty,0)\cup(0,\infty)$

$(f−g)(x)=\dfrac{4x3+8x2−1}{2x}$, dominio:$(−\infty,0)\cup(0,\infty)$

$(fg)(x)=x+2$, dominio:$(−\infty,0)\cup(0,\infty)$

$(fg)(x)=4x^3+8x^2$, dominio:$(−\infty,0)\cup(0,\infty)$

8) Dado$f(x)=\dfrac{1}{x−4}$ y$g(x)=\dfrac{1}{6−x}$, encontrar$f+g$,$f−g$,$fg$, y$\dfrac{f}{g}$. Determinar el dominio para cada función en notación de intervalos.

9) Dado$f(x)=3x^2$ y$g(x)=\sqrt{x−5}$, encontrar$f+g$,$f−g$,$fg$, y$\dfrac{f}{g}$. Determinar el dominio para cada función en notación de intervalos.

Responder

$(f+g)(x)=3x^2+\sqrt{x−5}$, dominio:$\left[5,\infty\right)$

$(f−g)(x)=3x^2−\sqrt{x−5}$, dominio:$\left[5,\infty\right)$

$(fg)(x)=3x^2\sqrt{x−5}$, dominio:$\left[5,\infty\right)$

$\left(\dfrac{f}{g}\right)(x)=\dfrac{3x^2}{\sqrt{x−5}}$, dominio:$(5,\infty)$

10) Dado$f(x)=\sqrt{x}$ y$g(x)=|x−3|$, encontrar$\dfrac{g}{f}$. Determinar el dominio de la función en notación de intervalos.

11) Dado$f(x)=2x^2+1$ y$g(x)=3x−5$, encuentre lo siguiente:

1. $f(g(2))$
2. $f(g(x))$
3. $g(f(x))$
4. $(g{\circ}g)(x)$
5. $(f{\circ}f)(−2)$

Responder

1. $3$
2. $f(g(x))=2(3x−5)^2+1$
3. $f(g(x))=6x^2−2$
4. $(g{\circ}g)(x)=3(3x−5)−5=9x−20$
5. $(f{\circ}f)(−2)=163$

Para los ejercicios 12-17, usa cada par de funciones para encontrar$f(g(x))$ y$g(f(x))$. Simplifica tus respuestas.

12)$f(x)=x^2+1$,$g(x)=\sqrt{x+2}$

13)$f(x)=\sqrt{x}+2$,$g(x)=x^2+3$

Responder

$f(g(x))=\sqrt{x+3}$,$g(f(x))=x+4\sqrt{x}+7$

14)$f(x)=|x|$,$g(x)=5x+1$

15)$f(x)=\sqrt[3]{x}$,$g(x)=\dfrac{x+1}{x^3}$

Responder

$f(g(x))=\sqrt[3]{\dfrac{x+1}{x^3}}=\dfrac{\sqrt[3]{x+1}}{x}$,$g(f(x))=\dfrac{\sqrt[3]{x}+1}{x}$

16)$f(x)=\dfrac{1}{x−6}$,$g(x)=\dfrac{7}{x}+6$

17)$f(x)=\dfrac{1}{x−4}$,$g(x)=\dfrac{2}{x}+4$

Responder

$(f{\circ}g)(x)=\dfrac{1}{\frac{2}{x}+4-4}=\dfrac{x}{2}$,$(g{\circ}f)(x)=2x-4$

Para los ejercicios 18-25, usa cada conjunto de funciones para encontrar f (g (h (x))). Simplifica tus respuestas.

18)$f(x)=x^4+6$,$g(x)=x−6$, y$h(x)=\sqrt{x}$

19)$f(x)=x^2+1$,$g(x)=\dfrac{1}{x}$, y$h(x)=x+3$

Responder

$f(g(h(x)))=\left(\dfrac{1}{x+3}\right)^2+1$

20) Dado$f(x)=\dfrac{1}{x}$ y$g(x)=x−3$, encuentre lo siguiente:

1. $(f{\circ}g)(x)$
2. el dominio de$(f{\circ}g)(x)$ en notación de intervalos
3. $(g{\circ}f)(x)$
4. el dominio de$(g{\circ}f)(x)$
5. $\left(\dfrac{f}{g}\right)x$

21) Dado$f(x)=\sqrt{2−4x}$ y$g(x)=−\dfrac{3}{x}$, encuentre lo siguiente:

1. $(g{\circ}f)(x)$
2. el dominio de$(g{\circ}f)(x)$ en notación de intervalos

Responder

1. $(g{\circ}f)(x)=−\dfrac{3}{\sqrt{2−4x}}$
2. $\left(−\infty,\dfrac{1}{2}\right)$

22) Dadas las funciones$f(x)=\dfrac{1−x}{x}$ y$g(x)=\dfrac{1}{1+x^2}$, encuentre lo siguiente:

1. $(g{\circ}f)(x)$
2. $(g{\circ}f)(2)$

23) Dadas funciones$p(x)=\dfrac{1}{\sqrt{x}}$ y$m(x)=x^2−4$, indicar el dominio de cada una de las siguientes funciones usando notación de intervalo:

1. $\dfrac{p(x)}{m(x)}$
2. $p(m(x))$
3. $m(p(x))$

Responder

1. $(0,2)\cup(2,\infty)$
2. $(−\infty,−2)\cup(2,\infty)$
3. $(0,\infty)$

24) Dadas funciones$q(x)=\dfrac{1}{\sqrt{x}}$ y$h(x)=x^2−9$, declarar el dominio de cada una de las siguientes funciones usando notación de intervalo.

1. $\dfrac{q(x)}{h(x)}$
2. $q(h(x))$
3. $h(q(x))$

25) Para$f(x)=\dfrac{1}{x}$ y$g(x)=\sqrt{x−1}$, escribir el dominio de$(f{\circ}g)(x)$ en notación de intervalo.

Responder

$(1,\infty)$

Para los ejercicios 26-41, encontrar funciones$f(x)$ y$g(x)$ así la función dada se puede expresar como$h(x)=f(g(x))$.

26)$h(x)=(x+2)^2$

27)$h(x)=(x−5)^3$

Responder

muestra:$f(x)=x^3$

$g(x)=x−5$

28)$h(x)=\dfrac{3}{x−5}$

29)$h(x)=\dfrac{4}{(x+2)^2}$

Responder

muestra:$f(x)=\dfrac{4}{x}$

$g(x)=(x+2)^2$

30)$h(x)=4+\sqrt[3]{x}$

31)$h(x)=\sqrt[3]{\dfrac{1}{2x−3}}$

Responder

muestra:$f(x)=\sqrt[3]{x}$

$g(x)=\dfrac{1}{2x−3}$

32)$h(x)=\dfrac{1}{(3x^2−4)^{−3}}$

33)$h(x)=\sqrt[4]{\dfrac{3x−2}{x+5}}$

Responder

muestra:$f(x)=\sqrt[4]{x}$

$g(x)=\dfrac{3x−2}{x+5}$

34)$h(x)=(\dfrac{8+x^3}{8−x^3})^4$

35)$h(x)=\sqrt{2x+6}$

Responder

muestra:$f(x)=\sqrt{x}$

$g(x)=2x+6$

36)$h(x)=(5x−1)^3$

37)$h(x)=\sqrt[3]{x−1}$

Responder

muestra:$f(x)=\sqrt[3]{x}$
$g(x)=(x−1)$

38)$h(x)=|x^2+7|$

39)$h(x)=\dfrac{1}{(x−2)^3}$

Responder

muestra:$f(x)=x^3$
$g(x)=\dfrac{1}{x−2}$

40)$h(x)=\left(\dfrac{1}{2x−3}\right)^2$

41)$h(x)=\sqrt { \dfrac{2x−1}{3x+4}}$

Responder

muestra:$f(x)=\sqrt{x}$
$g(x)=\dfrac{2x−1}{3x+4}$

Gráfica

Para los ejercicios 42-49, utilice las gráficas de$f$, mostradas en la Figura 1, y$g$, mostradas en la Figura 2, para evaluar las expresiones.

Figura 1: Gráfica de una función.

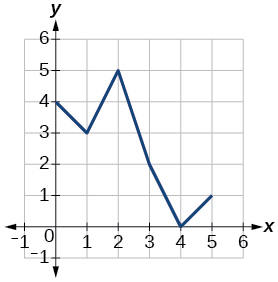
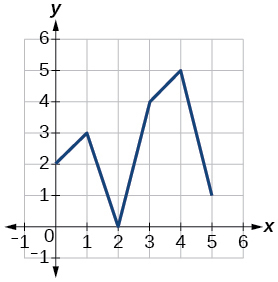
Figura 2: Gráfica de una función.

42)$f(g(3))$

43)$f(g(1))$

Responder

$2$

44)$g(f(1))$

45)$g(f(0))$

Responder

$5$

46)$f(f(5))$

47)$f(f(4))$

Responder

$4$

48)$g(g(2))$

49)$g(g(0))$

Responder

$0$

Para los ejercicios 50-57, utilice gráficas de$f(x)$, mostradas en la Figura 3,$g(x)$, mostradas en la Figura 4, y$h(x)$, mostradas en la Figura 5, para evaluar las expresiones.

Figura 3: Gráfica de una parábola.

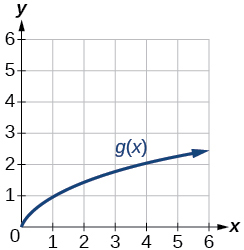
Figura 4: Gráfica de una función de raíz cuadrada.

Figura 5: Gráfica de una función de valor absoluto.

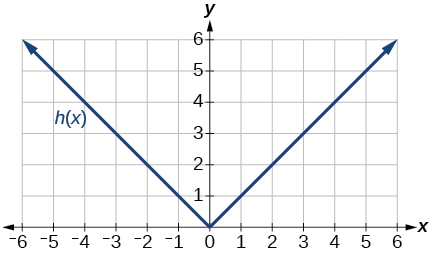
50)$g(f(1))$

51)$g(f(2))$

Responder

$2$

52)$f(g(4))$

53)$f(g(1))$

Responder

$1$

54)$f(h(2))$

55)$h(f(2))$

Responder

$4$

56)$f(g(h(4)))$

57)$f(g(f(−2)))$

Responder

$4$

Numérico

Para los ejercicios 58-65, utilice los valores de función para$f$ y$g$ mostrados en la Tabla siguiente para evaluar cada expresión.

$x$	$f(x)$	$g(x)$
\ (x\) ">0	\ (f (x)\) ">7	\ (g (x)\) ">9
\ (x\) ">1	\ (f (x)\) ">6	\ (g (x)\) ">5
\ (x\) ">2	\ (f (x)\) ">5	\ (g (x)\) ">6
\ (x\) ">3	\ (f (x)\) ">8	\ (g (x)\) ">2
\ (x\) ">4	\ (f (x)\) ">4	\ (g (x)\) ">1
\ (x\) ">5	\ (f (x)\) ">0	\ (g (x)\) ">8
\ (x\) ">6	\ (f (x)\) ">2	\ (g (x)\) ">7
\ (x\) ">7	\ (f (x)\) ">1	\ (g (x)\) ">3
\ (x\) ">8	\ (f (x)\) ">9	\ (g (x)\) ">4
\ (x\) ">9	\ (f (x)\) ">3	\ (g (x)\) ">0

58)$f(g(8))$

59)$f(g(5))$

Responder

$9$

60)$g(f(5))$

61)$g(f(3))$

Responder

$4$

62)$f(f(4))$

63)$f(f(1))$

Responder

$2$

64)$g(g(2))$

65)$g(g(6))$

Responder

$3$

Para los ejercicios 66-71, utilice los valores de función para$f$ y$g$ mostrados en la Tabla siguiente para evaluar las expresiones.

$x$	$f(x)$	$g(x)$
\ (x\) ">-3	\ (f (x)\) ">11	\ (g (x)\) ">-8
\ (x\) ">-2	\ (f (x)\) ">9	\ (g (x)\) ">-3
\ (x\) ">-1	\ (f (x)\) ">7	\ (g (x)\) ">0
\ (x\) ">0	\ (f (x)\) ">5	\ (g (x)\) ">1
\ (x\) ">1	\ (f (x)\) ">3	\ (g (x)\) ">0
\ (x\) ">2	\ (f (x)\) ">1	\ (g (x)\) ">-3
\ (x\) ">3	\ (f (x)\) ">-1	\ (g (x)\) ">-8

66)$(f{\circ}g)(1)$

67)$(f{\circ}g)(2)$

Responder

$11$

68)$(g{\circ}f)(2)$

69)$(g{\circ}f)(3)$

Responder

$0$

70)$(g{\circ}g)(1)$

71)$(f{\circ}f)(3)$

Responder

$7$

Para los ejercicios 72-75, utilice cada par de funciones para encontrar$f(g(0))$ y$g(f(0))$.

72)$f(x)=4x+8$,$g(x)=7−x^2$

73)$f(x)=5x+7$,$g(x)=4−2x^2$

Responder

$f(g(0))=27$,$g(f(0))=−94$

74)$f(x)=\sqrt{x+4}$,$g(x)=12−x^3$

75)$f(x)=\frac{1}{x+2}$,$g(x)=4x+3$

Responder

$f(g(0))=\frac{1}{5}$,$g(f(0))=5$

Para los ejercicios 76-79, utilice las funciones$f(x)=2x^2+1$ y$g(x)=3x+5$ para evaluar o encontrar la función compuesta como se indica.

76)$f(g(2))$

77)$f(g(x))$

Responder

$18x^2+60x+51$

78)$g(f(−3))$

79)$(g{\circ}g)(x)$

Responder

$g{\circ}g(x)=9x+20$

Extensiones

Para los ejercicios 80-84, use$f(x)=x^3+1$ y$g(x)=\sqrt[3]{x−1}$.

80) Encontrar$(f{\circ}g)(x)$ y$(g{\circ}f)(x)$. Compara las dos respuestas.

81) Encontrar$(f{\circ}g)(2)$ y$(g{\circ}f)(2)$.

Responder

$2$

82) ¿Cuál es el dominio$(g{\circ}f)(x)$?

83) ¿Cuál es el dominio$(f{\circ}g)(x)$?

Responder

$(−\infty,\infty)$

84) Vamos$f(x)=\frac{1}{x}$.

1. Encuentra$(f{\circ}f)(x)$.
2. ¿$(f{\circ}f)(x)$Para alguna función es$f$ el mismo resultado que la respuesta a la parte (a) para alguna función? Explique.

Para los ejercicios 85-87, let$F(x)=(x+1)^5$,$f(x)=x^5$, y$g(x)=x+1$.

85) Verdadero o Falso:$(g{\circ}f)(x)=F(x)$.

Responder

Falso

86) Verdadero o Falso:$(f{\circ}g)(x)=F(x)$.

Para los ejercicios 87-89, encuentra la composición cuando$f(x)=x^2+2$ para todos$x\geq0$ y$g(x)=\sqrt{x−2}$.

87)$(f{\circ}g)(6)$;$(g{\circ}f)(6)$

Responder

$(f{\circ}g)(6)=6$;$(g{\circ}f)(6)=6$

88)$(g{\circ}f)(a)$;$(f{\circ}g)(a)$

89)$(f{\circ}g)(11)$;$(g{\circ}f)(11)$

Responder

$(f{\circ}g)(11)=11$,$(g{\circ}f)(11)=11$

Aplicaciones del mundo real

90) La función$D(p)$ da el número de artículos que se demandarán cuando el precio sea$p$. El costo de producción$C(x)$ es el costo de producir$x$ artículos. Para determinar el costo de producción cuando es el precio$\$6$, ¿harías cuál de las siguientes?

1. Evaluar$D(C(6))$
2. Evaluar$C(D(6))$
3. Resolver$D(C(x))=6$
4. Resolver$C(D(p))=6$

91) La función$A(d)$ da el nivel de dolor en una escala de$0$ a$10$ experimentado por una paciente con$d$ miligramos de un fármaco reductor del dolor en su sistema. Los miligramos del medicamento en el sistema del paciente después de$t$ minutos están modelados por$m(t)$. ¿Cuál de las siguientes harías para determinar cuándo el paciente estará en un nivel de dolor de$4$?

1. Evaluar$A(m(4))$
2. Evaluar$m(A(4))$
3. Resolver$A(m(t))=4$
4. Resolver$m(A(d))=4$

Responder

c

92) Una tienda ofrece a los clientes un$30\%$ descuento en el precio$x$ de artículos seleccionados. Entonces, la tienda despega un adicional$15\%$ en la caja registradora. Escribir una función de precio$P(x)$ que compute el precio final del artículo en términos del precio original$x$. (Pista: Usa la composición de funciones para encontrar tu respuesta.)

93) Una gota de lluvia que golpea un lago hace una ondulación circular. Si el radio, en pulgadas, crece en función del tiempo en minutos según$r(t)=25\sqrt{t+2}$, encuentre el área de la ondulación en función del tiempo. Encuentra el área de la ondulación en$t=2$.

Responder

$A(t)=\pi(25\sqrt{t+2})^2$y pulgadas$A(2)=\pi(25\sqrt{4})^2=2500\pi$ cuadradas

94) Un incendio forestal deja atrás un área de pasto quemado en un patrón circular en expansión. Si el radio del círculo de pasto ardiente va aumentando con el tiempo según la fórmula$r(t)=2t+1$, exprese el área quemada en función del tiempo,$t$ (minutos).

95) Usa la función que encontraste en el ejercicio anterior para encontrar el área total quemada después de$5$ minutos.

Responder

$A(5)=\pi(2(5)+1)2=121\pi$unidades cuadradas

96) El radio$r$, en pulgadas, de un globo esférico está relacionado con el volumen,$V$, por$r(V)=\sqrt[3]{\frac{3V}{4\pi}}$. Se bombea aire al globo, por lo que el volumen después de$t$ segundos es dado por$V(t)=10+20t$.

1. Encuentra la función compuesta$r(V(t))$.
2. Encuentra la hora exacta en que el radio alcanza las 10 pulgadas.

97) El número de bacterias en un producto alimenticio refrigerado viene dado por$N(T)=23T^2−56T+1$$3<T<33$,, dónde$T$ está la temperatura del alimento. Cuando se retira la comida del refrigerador, la temperatura es dada por$T(t)=5t+1.5$, donde$t$ es el tiempo en horas.

1. Encuentra la función compuesta$N(T(t))$.
2. Encuentra el tiempo (redondo a dos decimales) cuando el recuento de bacterias alcanza 6752.

Responder

1. $N(T(t))=23(5t+1.5)^2−56(5t+1.5)+1$
2. $3.38$horas

1.5: Transformación de funciones

A menudo, cuando se nos da un problema, tratamos de modelar el escenario usando matemáticas en forma de palabras, tablas, gráficas y ecuaciones. Un método que podemos emplear es adaptar los gráficos básicos de las funciones del kit de herramientas para construir nuevos modelos para un escenario dado. Existen formas sistemáticas de alterar funciones para construir modelos adecuados a los problemas que estamos tratando de resolver.

Verbal

1) Al examinar la fórmula de una función que es el resultado de múltiples transformaciones, ¿cómo se puede distinguir un desplazamiento horizontal de un desplazamiento vertical?

Responder

Se produce un desplazamiento horizontal cuando se agrega o resta una constante de la entrada. Un desplazamiento vertical resulta cuando una constante se agrega o resta de la salida.

2) Al examinar la fórmula de una función que es el resultado de múltiples transformaciones, ¿cómo se puede distinguir un estiramiento horizontal de un estiramiento vertical?

3) Al examinar la fórmula de una función que es el resultado de múltiples transformaciones, ¿cómo se puede distinguir una compresión horizontal de una compresión vertical?

Responder

Una compresión horizontal resulta cuando una constante mayor que$1$ se multiplica por la entrada. Una compresión vertical resulta cuando una constante entre$0$ y$1$ se multiplica por la salida.

4) Al examinar la fórmula de una función que es el resultado de múltiples transformaciones, ¿cómo se puede distinguir una reflexión con respecto al$x$ eje a partir de una reflexión con respecto al$y$ eje -eje?

5) ¿Cómo se puede determinar si una función es impar o par a partir de la fórmula de la función?

Responder

Para una función$f$, sustituya (−x) por (x) pulg$f(x)$. Simplificar. Si la función resultante es la misma que la función original$f(−x)=f(x)$, entonces la función es par. Si la función resultante es la opuesta a la función original$f(−x)=−f(x)$, entonces la función original es impar. Si la función no es la misma o lo contrario, entonces la función no es ni impar ni par.

Algebraico

6) Escribir una fórmula para la función obtenida cuando la gráfica de$f(x)=\sqrt{x}$ se desplaza hacia arriba$1$ unidad y hacia las$2$ unidades de la izquierda.

7) Escribir una fórmula para la función obtenida cuando la gráfica de$f(x)=|x|$ se desplaza hacia abajo$3$ unidades y hacia la$1$ unidad derecha.

Responder

$g(x)=|x-1|−3$

8) Escribir una fórmula para la función obtenida cuando la gráfica de$f(x)=\dfrac{1}{x}$ se desplaza hacia abajo$4$ unidades y hacia las$3$ unidades correctas.

9) Escribir una fórmula para la función obtenida cuando la gráfica de$f(x)=\dfrac{1}{x^2}$ se desplaza hacia arriba$2$ unidades y hacia las$4$ unidades de la izquierda.

Responder

$g(x)=\dfrac{1}{(x+4)^2}+2$

Para los ejercicios 10-19, describa cómo la gráfica de la función es una transformación de la gráfica de la función original$f$.

10)$y=f(x−49)$

11)$y=f(x+43)$

Responder

La gráfica de$f(x+43)$ es un desplazamiento horizontal a las$43$ unidades izquierdas de la gráfica de$f$.

12)$y=f(x+3)$

13)$y=f(x−4)$

Responder

La gráfica de$f(x-4)$ es un desplazamiento horizontal a las$4$ unidades de la derecha de la gráfica de$f$.

14)$y=f(x)+5$

15)$y=f(x)+8$

Responder

La gráfica de$f(x)+8$ es un desplazamiento vertical hacia arriba$8$ unidades de la gráfica de$f$.

16)$y=f(x)−2$

17)$y=f(x)−7$

Responder

La gráfica de$f(x)−7$ es un desplazamiento vertical hacia abajo$7$ unidades de la gráfica de$f$.

18)$y=f(x−2)+3$

19)$y=f(x+4)−1$

Responder

La gráfica de$f(x+4)−1$ es un desplazamiento horizontal a las$4$ unidades de la izquierda y una$1$ unidad de desplazamiento vertical hacia abajo de la gráfica de$f$.

Para los ejercicios 20-23, determinar el (los) intervalo (s) en el que la función está aumentando y disminuyendo.

20)$f(x)=4(x+1)^2−5$

21)$g(x)=5(x+3)^2−2$

Responder

decreciente$(−\infty,−3)$ y aumentando en$(−3,\infty)$

22)$a(x)=\sqrt{−x+4}$

23)$k(x)=−3\sqrt{x}−1$

Responder

decreciente en$(0, \infty)$

Gráfica

Para los ejercicios 24-26, utilice la gráfica de que$f(x)=2^x$ se muestra en la Figura a continuación para bosquejar una gráfica de cada transformación de$f(x)$.

\ (f (x)\).” style="width: 301px; alto: 306px;” width="301px” height="306px” src=” https://math.libretexts.org/@api/dek..._01_05_201.jpg "/>

Gráfica de$f(x)$.

25)$h(x)=2^x−3$

24)$g(x)=2^x+1$

Responder

\ (k (x)\)” src=” https://math.libretexts.org/@api/dek..._01_05_202.jpg "/>

Gráfica de$k(x)$

26)$w(x)=2^x−1$

Para los ejercicios 27-30, esbozar una gráfica de la función como una transformación de la gráfica de una de las funciones del kit de herramientas.

27)$f(t)=(t+1)^2−3$

Responder

\ (f (t)\).” src=” https://math.libretexts.org/@api/dek..._01_05_206.jpg "/>

Gráfica de$f(t)$.

28)$h(x)=|x−1|+4$

29)$k(x)=(x−2)^3−1$

Responder

\ (k (x)\).” src=” https://math.libretexts.org/@api/dek..._01_05_208.jpg "/>

Gráfica de$k(x)$.

30)$m(t)=3+\sqrt{t+2}$

Numérico

31) Representaciones tabulares para las funciones$f$,$g$, y$h$ se dan a continuación. Escribir$g(x)$ y$h(x)$ como transformaciones de$f(x)$.

$x$	-2	-1	0	1	2
$f(x)$	-2	-1	-3	1	2

$x$	-1	0	1	2	3
$g(x)$	-2	-1	-3	1	2

$x$	-2	-1	0	1	2
$h(x)$	-1	0	-2	2	3

Responder

$g(x)=f(x-1)$,$h(x)=f(x)+1$

32) Representaciones tabulares para las funciones$f$,$g$, y$h$ se dan a continuación. Escribir$g(x)$ y$h(x)$ como transformaciones de$f(x)$.

$x$	-2	-1	0	1	2
$f(x)$	-1	-3	4	2	1

$x$	-3	-2	-1	0	1
$g(x)$	-1	-3	4	2	1

$x$	-2	-1	0	1	2
$h(x)$	-2	-4	3	1	0

Para los ejercicios 33-40, escriba una ecuación para cada función gráfica utilizando transformaciones de las gráficas de una de las funciones del kit de herramientas.

33)

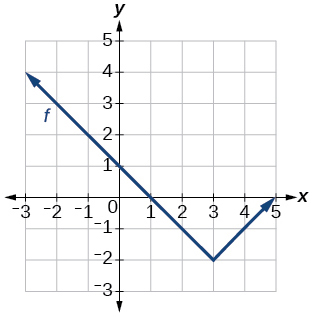
Gráfica de una función absoluta.

Responder

$f(x)=|x-3|−2$

34)

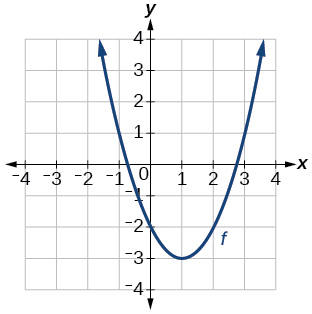
Gráfica de una parábola.

35)

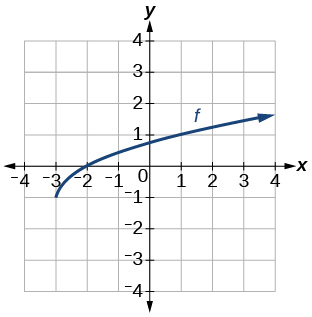
Gráfica de una función de raíz cuadrada.

Responder

$f(x)=\sqrt{x+3}−1$

36)

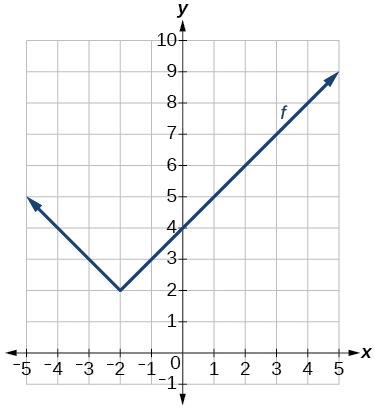
Gráfica de una función absoluta.

37)

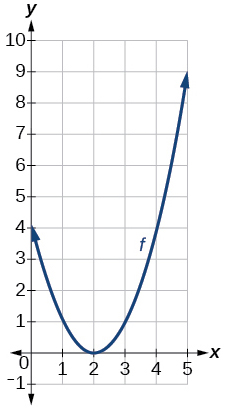
Gráfica de una parábola

Responder

$f(x)=(x-2)^2$

38)

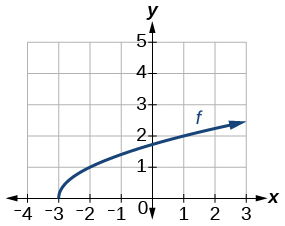
Gráfica de una función de raíz cuadrada.

39)

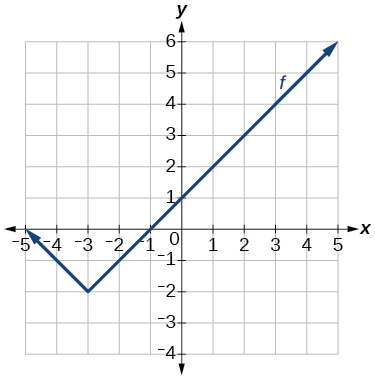
Gráfica de una función absoluta.

Responder

$f(x)=|x+3|−2$

40)

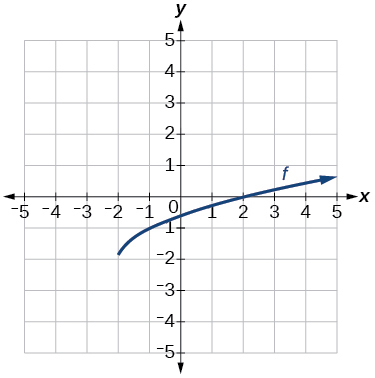
Gráfica de una función de raíz cuadrada.

Para los ejercicios 41-42, utilice las gráficas de transformaciones de la función raíz cuadrada para encontrar una fórmula para cada una de las funciones.

41)

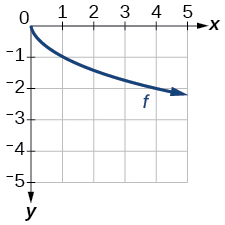
Gráfica de una función de raíz cuadrada.

Responder

$f(x)=−\sqrt{x}$

42)

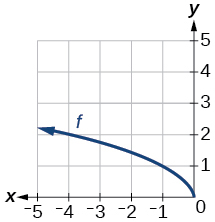
Gráfica de una función de raíz cuadrada.

Para los ejercicios 43-46, utilice las gráficas de las funciones transformadas del kit de herramientas para escribir una fórmula para cada una de las funciones resultantes.

43)

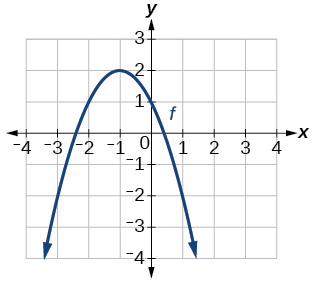
Gráfica de una parábola.

Responder

$f(x)=−(x+1)^2+2$

44)

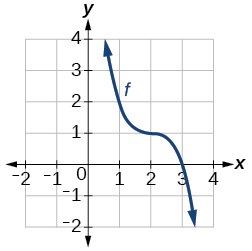
Gráfica de una función cúbica.

45)

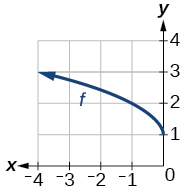
Gráfica de una función de raíz cuadrada.

Responder

$f(x)=\sqrt{−x}+1$

46)

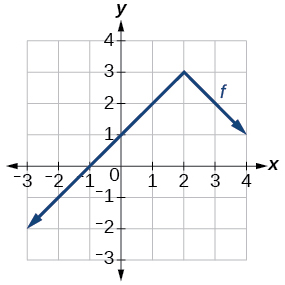
Gráfica de una función absoluta.

Para los ejercicios 47-52, determinar si la función es impar, par, o ninguno.

47)$f(x)=3x^4$

Responder

incluso

48)$g(x)=\sqrt{x}$

49)$h(x)=\dfrac{1}{x}+3x$

Responder

impar

50)$f(x)=(x−2)^2$

51)$g(x)=2x^4$

Responder

incluso

52)$h(x)=2x−x^3$

Para los ejercicios 53-62, describa cómo la gráfica de cada función es una transformación de la gráfica de la función original$f$.

53)$g(x)=−f(x)$

Responder

La gráfica de$g$ es una reflexión vertical (a través del eje x) de la gráfica de$f$.

54)$g(x)=f(−x)$

55)$g(x)=4f(x)$

Responder

La gráfica de$g$ es un estiramiento vertical por un factor de 4 de la gráfica de$f$.

56)$g(x)=6f(x)$

57)$g(x)=f(5x)$

Responder

La gráfica de$g$ es una compresión horizontal por un factor de$15$ de la gráfica de$f$.

58)$g(x)=f(2x)$

59)$g(x)=f \left(\dfrac{1}{3}x \right)$

Responder

La gráfica de$g$ es un estiramiento horizontal por un factor de 3 de la gráfica de$f$.

60)$g(x)=f \left(\dfrac{1}{5}x \right)$

61)$g(x)=3f(−x)$

Responder

La gráfica de$g$ es una reflexión horizontal a través del eje y y un estiramiento vertical por un factor de 3 de la gráfica de$f$.

62)$g(x)=−f(3x)$

Para los ejercicios 63-68, escriba una fórmula para la función$g$ que resulte cuando la gráfica de una función de kit de herramientas dada se transforme como se describe.

63) La gráfica de$f(x)=|x|$ se refleja sobre el$y$ eje y se comprime horizontalmente por un factor de$\dfrac{1}{4}$.

Responder

$g(x)=|−4x|$

64) La gráfica de$f(x)=\sqrt{x}$ se refleja sobre el$x$ eje y se estira horizontalmente por un factor de$2$.

65) La gráfica de$f(x)=\dfrac{1}{x^2}$ se comprime verticalmente por un factor de$\dfrac{1}{3}$, luego se desplaza a las$2$ unidades de la izquierda y a las$3$ unidades hacia abajo.

Responder

$g(x)=\dfrac{1}{3(x+2)^2}−3$

66) La gráfica de$f(x)=\dfrac{1}{x}$ se estira verticalmente por un factor de$8$, luego se desplaza a las$4$ unidades correctas y$2$ unidades hacia arriba.

67) La gráfica de$f(x)=x^2$ se comprime verticalmente por un factor de$\dfrac{1}{2}$, luego se desplaza a las$5$ unidades correctas y hacia arriba$1$ unidad.

Responder

$g(x)=\dfrac{1}{2}(x-5)^2+1$

68) La gráfica de$f(x)=x^2$ se estira horizontalmente por un factor de$3$, luego se desplaza a las$4$ unidades de la izquierda y a las$3$ unidades hacia abajo.

Para los ejercicios 69-77, describa cómo la fórmula es una transformación de una función de kit de herramientas. Después esbozar una gráfica de la transformación.

69)$g(x)=4(x+1)^2−5$

Responder

El gráfico de la función$f(x)=x^2$ se desplaza a la$1$ unidad izquierda, se estira verticalmente por un factor de$4$, y se desplaza hacia abajo$5$ unidades.

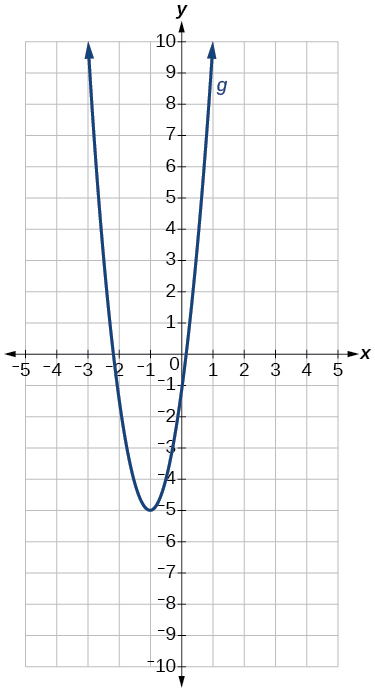
Gráfica de una parábola.

70)$g(x)=5(x+3)^2−2$

71)$h(x)=−2|x−4|+3$

Responder

La gráfica de$f(x)=|x|$ es estirada verticalmente por un factor de$2$, desplazada horizontalmente$4$ unidades hacia la derecha, reflejada a través del eje horizontal, y luego desplazada verticalmente$3$ unidades hacia arriba.

Gráfica de una función de valor absoluto.

72)$k(x)=−3\sqrt{x}−1$

73)$m(x)=\dfrac{1}{2}x^3$

Responder

La gráfica de la función$f(x)=x^3$ se comprime verticalmente por un factor de$\dfrac{1}{2}$.

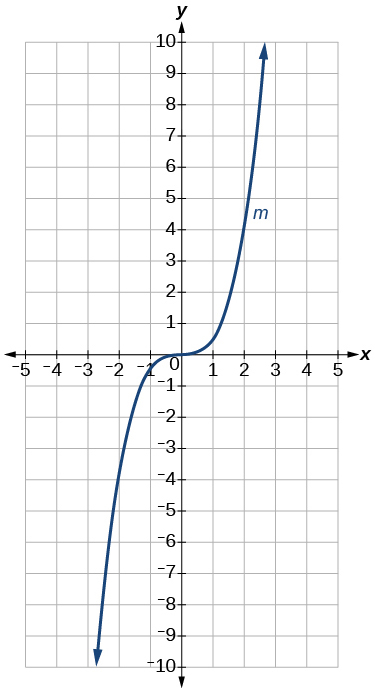
Gráfica de una función cúbica.

74)$n(x)=\dfrac{1}{3}|x−2|$

75)$p(x)=(\dfrac{1}{3}x)^3−3$

Responder

La gráfica de la función se estira horizontalmente por un factor de$3$ y luego se desplaza verticalmente hacia abajo por$3$ unidades.

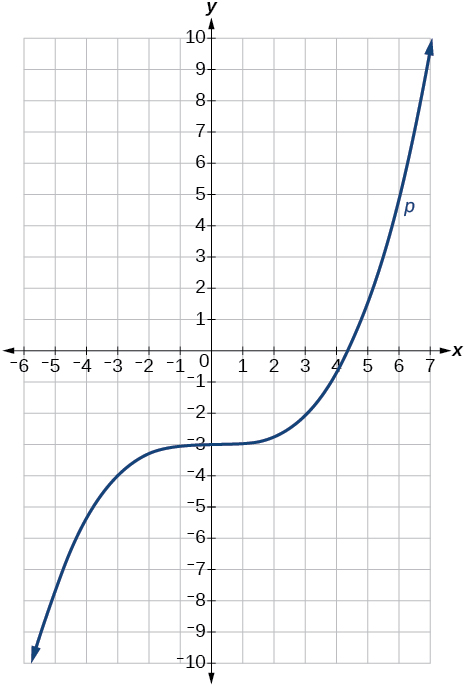
Gráfica de una función cúbica.

76)$q(x)=(\dfrac{1}{4}x)^3+1$

77)$a(x)=\sqrt{−x+4}$

Responder

El gráfico de$f(x)=\sqrt{x}$ se desplaza a la derecha$4$ unidades y luego se refleja a través de la línea vertical$x=4$.

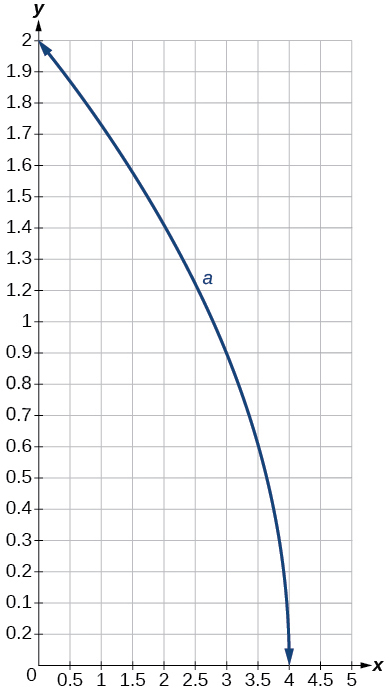
Gráfica de una función de raíz cuadrada.

Para los ejercicios 78-81, utilice la gráfica de la Figura a continuación para bosquejar las transformaciones dadas.

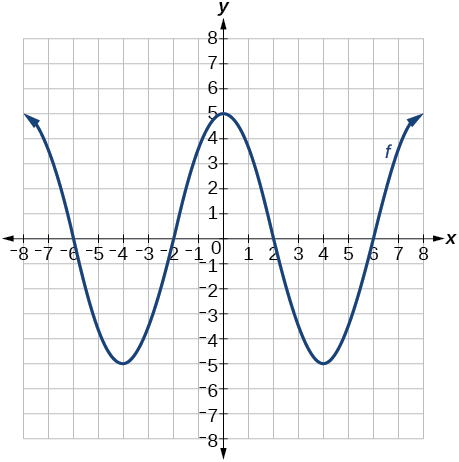
Gráfica de un polinomio.

78)$g(x)=f(x)−2$

79)$g(x)=−f(x)$

Responder

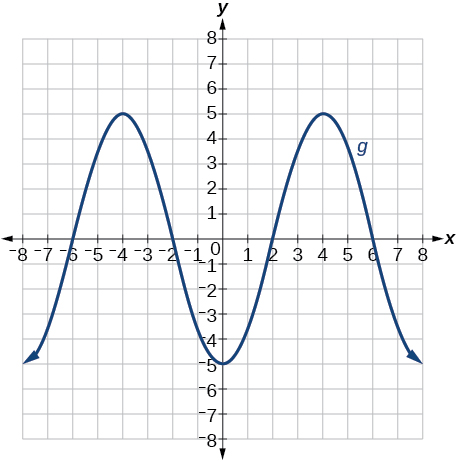
Gráfica de un polinomio.

80)$g(x)=f(x+1)$

81)$g(x)=f(x−2)$

Responder

Gráfica de un polinomio.

1.6: Funciones de Valor Absoluto

Las distancias en el universo se pueden medir en todas las direcciones. Como tal, es útil considerar la distancia como una función de valor absoluto. En esta sección, investigaremos las funciones de valor absoluto. La función de valor absoluto se piensa comúnmente como proporcionar la distancia que el número es de cero en una línea numérica. Álgebraicamente, para cualquiera que sea el valor de entrada, la salida es el valor sin tener en cuenta el signo.

Verbal

1) ¿Cómo se resuelve una ecuación de valor absoluto?

Responder

Aísle el término del valor absoluto para que la ecuación sea de la forma$|A|=B$. Formar una ecuación estableciendo la expresión dentro del símbolo de valor absoluto$A$,, igual a la expresión del otro lado de la ecuación,$B$. Formar una segunda ecuación estableciendo$A$ igual a lo opuesto de la expresión en el otro lado de la ecuación,$−B$. Resuelve cada ecuación para la variable.

2) ¿Cómo se puede saber si una función de valor absoluto tiene dos$x$ intercepciones sin graficar la función?

3) Al resolver una función de valor absoluto, el término de valor absoluto aislado es igual a un número negativo. ¿Qué te dice eso sobre la gráfica de la función de valor absoluto?

Responder

La gráfica de la función de valor absoluto no cruza el$x$ eje -eje, por lo que la gráfica está completamente por encima o completamente por debajo del$x$ eje -eje.

4) ¿Cómo se puede utilizar la gráfica de una función de valor absoluto para determinar los$x$ -valores para los cuales los valores de la función son negativos?

5) ¿Cómo se resuelve algebraicamente una desigualdad de valor absoluto?

Responder

Primero determine los puntos límite encontrando la (s) solución (s) de la ecuación. Utilice los puntos de límite para formar posibles intervalos de solución. Elija un valor de prueba en cada intervalo para determinar qué valores satisfacen la desigualdad.

Algebraico

6) Describir todos los números$x$ que están a una$4$ distancia del número$8$. Exprese esto usando notación de valor absoluto.

7) Describir todos los números$x$ que están a una$\dfrac{1}{2}$ distancia del número$-4$. Exprese esto usando notación de valor absoluto.

Responder

$|x+4|= \dfrac{1}{2}$

8) Describir la situación en la que la distancia a la que$x$ se encuentra ese punto$10$ es de al menos$15$ unidades. Exprese esto usando notación de valor absoluto.

9) Encuentra todos los valores de función de$f(x)$ tal manera que la distancia desde$f(x)$ hasta el valor$8$ sea menor que$0.03$ unidades. Exprese esto usando notación de valor absoluto.

Responder

$|f(x)−8|<0.03$

Para los ejercicios 10-24, resuelve las ecuaciones a continuación y expresa la respuesta usando la notación de conjunto.

10)$|x+3|=9$

11)$|6−x|=5$

Responder

${1,11}$

12)$|5x−2|=11$

13)$|4x−2|=11$

Responder

$\left \{\dfrac{9}{4}, \dfrac{13}{4} \right \}$

14)$2|4−x|=7$

15)$3|5−x|=5$

Responder

$\left \{\dfrac{10}{3},\dfrac{20}{3} \right \}$

16)$3|x+1|−4=5$

17)$5|x−4|−7=2$

Responder

$\left \{\dfrac{11}{5}, \dfrac{29}{5} \right \}$

18)$0=−|x−3|+2$

19)$2|x−3|+1=2$

Responder

$\left \{\dfrac{5}{2}, \dfrac{7}{2} \right \}$

20)$|3x−2|=7$

21)$|3x−2|=−7$

Responder

Sin solución

22)$\left |\dfrac{1}{2}x−5 \right |=11$

23)$\left |\dfrac{1}{3}x+5 \right |=14$

Responder

$\{−57,27\}$

24)$−\left |\dfrac{1}{3}x+5 \right |+14=0$

Para los ejercicios 25-28, encuentra las$x$ - y$y$ -intercepciones de las gráficas de cada función.

25)$f(x)=2|x+1|−10$

Responder

$(0,−8)$;$(−6,0)$,$(4,0)$

26)$f(x)=4|x−3|+4$

27)$f(x)=−3|x−2|−1$

Responder

$(0,−7)$; no$x$ -intercepta

28)$f(x)=−2|x+1|+6$

Para los ejercicios 29-36, resolver cada desigualdad y escribir la solución en notación de intervalos.

29)$| x−2 |>10$

Responder

$(−\infty,−8)\cup(12,\infty)$

30)$2|v−7|−4\geq42$

31)$|3x−4|\geq8$

Responder

$−\dfrac{4}{3}{\leq}x\leq4$

32)$|x−4|\geq8$

33)$|3x−5|\geq-13$

Responder

$\left (−\infty,− \dfrac{8}{3}\right ]\cup\left[6,\infty\right)$

34)$|3x−5|\geq−13$

35)$|\dfrac{3}{4}x−5|\geq7$

Responder

$\left (-\infty,-\dfrac{8}{3}\right ]\cup\left[16,\infty\right)$

36)$\left |\dfrac{3}{4}x−5 \right |+1\leq16$

Gráfica

Para los ejercicios 37-39, grafica la función de valor absoluto. Trazar al menos cinco puntos a mano para cada gráfica.

37)$y=|x−1|$

Responder

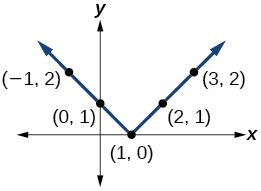
38)$y=|x+1|$

39)$y=|x|+1$

Responder

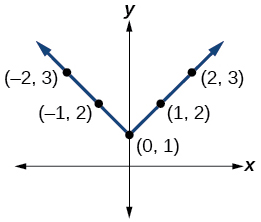
Para los ejercicios 40-52, grafica las funciones dadas a mano.

40)$y=|x|−2$

41)$y=−|x|$

Responder

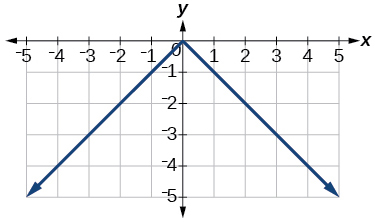
42)$y=−|x|−2$

43)$y=−|x−3|−2$

Responder

44)$f(x)=−|x−1|−2$

45)$f(x)=−|x+3|+4$

Responder

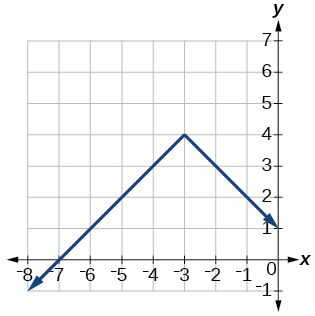
46)$f(x)=2|x+3|+1$

47)$f(x)=3|x−2|+3$

Responder

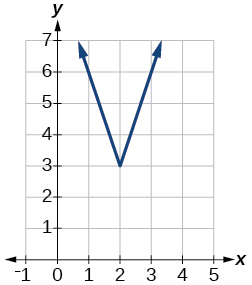
48)$f(x)=|2x−4|−3$

49)$f(x)=|3x+9|+2$

Responder

50)$f(x)=−|x−1|−3$

51)$f(x)=−|x+4|−3$

Responder

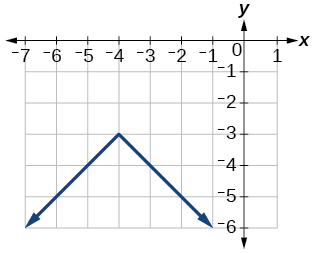
52)$f(x)=\dfrac{1}{2}|x+4|−3$

Tecnología

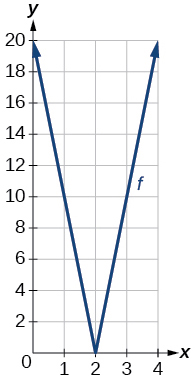
53) Utilice una utilidad gráfica para graficar$f(x)=10|x−2|$ en la ventana de visualización$[0,4]$. Identificar el rango correspondiente. Mostrar la gráfica.

Responder

Rango:$[0,20]$

54) Utilice una utilidad gráfica para graficar$f(x)=−100|x|+100$ en la ventana de visualización$[−5,5]$. Identificar el rango correspondiente. Mostrar la gráfica.

Para los ejercicios 55-56, grafica cada función usando una utilidad gráfica. Especifique la ventana de visualización.

55)$f(x)=−0.1|0.1(0.2−x)|+0.3$

Contestar

$x$-intercepta:

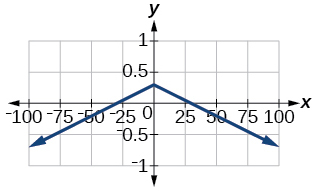
56)$f(x)=4 \times10^{9}|x−(5 \times 10^9)|+2 \times10^9$

Extensiones

Para los ejercicios 57-59, resolver la desigualdad.

57)$\left |−2x− \dfrac{2}{3}(x+1) \right |+3>−1$

Contestar

$(−\infty,\infty)$

58) Si es posible, encontrar todos los valores de un tal que no haya$x$ -intercepciones para$f(x)=2|x+1|+a$.

59) Si es posible, encontrar todos los valores de un tal que no haya$y$ -intercepciones para$f(x)=2|x+1|+a$.

Contestar

No hay solución para una que impediré que la función tenga una$y$ -intercepción. La función de valor absoluto siempre cruza la$y$ -intercepción cuando$x=0$.

Aplicaciones del mundo real

60) Las ciudades A y B están en la misma línea este-oeste. Supongamos que la ciudad A se encuentra en el origen. Si la distancia de la ciudad A a la ciudad B es de al menos$100$ millas y$x$ representa la distancia de la ciudad B a la ciudad A, exprese esto usando la notación de valor absoluto.

61) La verdadera proporción$p$ de personas que dan una calificación favorable al Congreso es$8\%$ con un margen de error de$1.5\%$. Describa esta afirmación usando una ecuación de valor absoluto.

Contestar

$|p−0.08|\leq0.015$

62) Los alumnos que anoten dentro de los$18$ puntos del número$82$ pasarán una prueba particular. Escribe esta declaración usando notación de valor absoluto y usa la variable$x$ para la puntuación.

63) Un maquinista debe producir un rodamiento que esté dentro de$0.01$ pulgadas del diámetro correcto de$5.0$ pulgadas. Usando$x$ como diámetro del rodamiento, escriba esta declaración usando notación de valor absoluto.

Contestar

$|x−5.0|\leq0.01$

64) La tolerancia para un rodamiento de bolas es$0.01$. Si el diámetro verdadero del rodamiento va a ser$2.0$ pulgadas y el valor medido del diámetro es$x$ pulgadas, exprese la tolerancia usando la notación de valor absoluto.

1.7: Funciones inversas

Si algunas máquinas físicas pueden funcionar en dos direcciones, podríamos preguntarnos si algunas de las funciones “máquinas” que hemos estado estudiando también pueden correr hacia atrás. En esta sección, consideraremos la naturaleza inversa de las funciones.

Verbal

1) Describir por qué la prueba de línea horizontal es una manera efectiva de determinar si una función es uno a uno?

Contestar

Cada salida de una función debe tener exactamente una salida para que la función sea uno a uno. Si alguna línea horizontal cruza la gráfica de una función más de una vez, eso significa que$y$ -valores se repiten y la función no es uno a uno. Si ninguna línea horizontal cruza la gráfica de la función más de una vez, entonces no se repiten$y$ valores y la función es uno a uno.

2) ¿Por qué restringimos el dominio de la función$f(x)=x^2$ para encontrar la inversa de la función?

3) ¿Puede una función ser su propia inversa? Explique.

Contestar

Sí. Por ejemplo,$f(x)=\dfrac{1}{x}$ es su propio inverso.

4) ¿Las funciones uno a uno son siempre crecientes o siempre decrecientes? ¿Por qué o por qué no?

5) ¿Cómo se encuentra la inversa de una función algebraicamente?

Contestar

Dada una función$y=f(x)$, resolver para$x$ en términos de$y$. Intercambiar el$x$ y$y$. Resuelve la nueva ecuación para$y$. La expresión for$y$ es la inversa,$y=f^{-1}(x)$.

Algebraico

6) Mostrar que la función$f(x)=a−x$ es su propia inversa para todos los números reales$a$.

Para los ejercicios 7-12, encuentra$f^{-1}(x)$ para cada función.

7)$f(x)=x+3$

Contestar

$f^{-1}(x)=x−3$

8)$f(x)=x+5$

9)$f(x)=2−x$

Contestar

$f^{-1}(x)=2−x$

10)$f(x)=3−x$

11)$f(x)=\dfrac{x}{x+2}$

Contestar

$f^{-1}(x)=\dfrac{−2x}{x−1}$

12)$f(x)=\dfrac{2x+3}{5x+4}$

Para los ejercicios 13-16, encuentra un dominio en el que cada función$f$ sea uno-a-uno y no decreciente. Escribe el dominio en notación de intervalos. Entonces encuentra la inversa de$f$ restringido a ese dominio.

13)$f(x)=(x+7)^2$

Contestar

dominio de$f(x)$:$\left[−7,\infty\right)$;$f^{-1}(x)=\sqrt{x}−7$

14)$f(x)=(x−6)^2$

15)$f(x)=x^2−5$

Contestar

dominio de$f(x)$:$\left[0,\infty\right)$;$f^{-1}(x)=\sqrt{x+5}$

16) Dado$f(x)=\dfrac{x}{2+x}$ y$g(x)=\dfrac{2x}{1-x}:$

1. Encontrar$f(g(x))$ y$g(f(x))$.
2. ¿Qué nos dice la respuesta sobre la relación entre$f(x)$ y$g(x)?$

Contestar

a.$f(g(x))=x$ y$g(f(x))=x$

b. Esto nos dice que$f$ y$g$ son funciones inversas

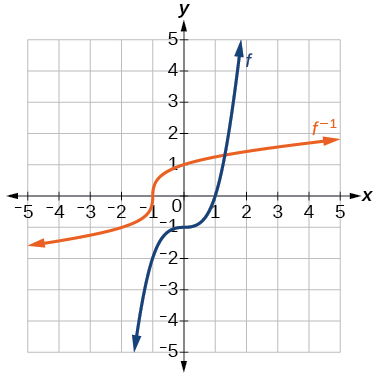
Para los ejercicios 17-18, utilizar la composición de funciones para verificar eso$f(x)$ y$g(x)$ son funciones inversas.

17)$f(x)=\sqrt[3]{x-1}$ y$g(x)=x^3+1$

Contestar

$f(g(x))=x$,$g(f(x))=x$

18)$f(x)=−3x+5$ y$g(x)=\dfrac{x-5}{-3}$

Gráfica

Para los ejercicios 19-22, utilice una utilidad gráfica para determinar si cada función es uno a uno.

19)$f(x)=\sqrt{x}$

Contestar

uno a uno

20)$f(x)=\sqrt[3]{3x+1}$

21)$f(x)=−5x+1$

Contestar

uno a uno

22)$f(x)=x^3−27$

Para los ejercicios 23-24, determine si la gráfica representa una función uno a uno.

23)

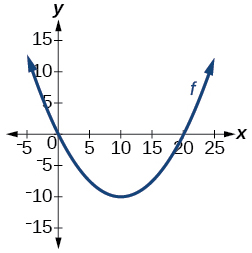
Contestar

no uno a uno

24)

Figura a continuación.

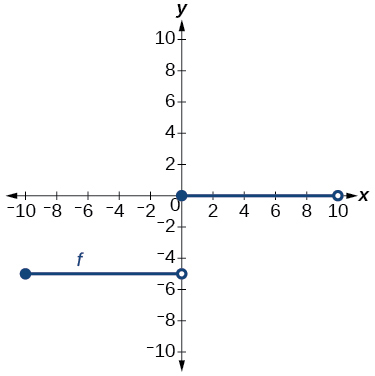
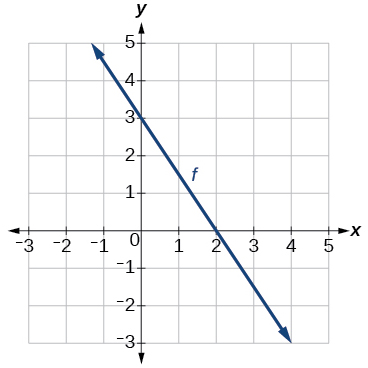
Gráfica de una línea

25) Encontrar$f(0)$.

Contestar

$3$

26) Resolver$f(x)=0$.

27) Encontrar$f^{-1}(0)$.

Contestar

$2$

28) Resolver$f^{-1}(x)=0$.

Para los ejercicios 29-32, use la gráfica de la función uno a uno que se muestra en la Figura siguiente

Gráfica de una función de raíz cuadrada.

29) Esbozar la gráfica de$f^{-1}$.

Contestar

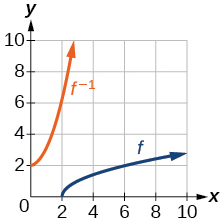
30) Encontrar$f(6)$ y$f^{-1}(2)$.

31) Si se muestra la gráfica completa de$f$, encuentra el dominio de$f$.

Contestar

$[2,10]$

32) Si$f$ se muestra la gráfica completa de, encuentre el rango de$f$

Numérico

Para los ejercicios 33-36, evaluar o resolver, asumiendo que la función$f$ es uno a uno.

33) Si$f(6)=7$, encuentra$f^{-1}(7)$.

Contestar

$6$

34) Si$f(3)=2$, encuentra$f^{-1}(2)$.

35) Si$f^{-1}(−4)=−8$, encuentra$f(−8)$.

Contestar

$-4$

36) Si$f^{-1}(−2)$ =−1, encuentra$f(−1)$.

Para los ejercicios 37-40, utilice los valores enumerados en la Tabla siguiente para evaluar o resolver.

$x$	$f(x)$
\ (x\) ">0	\ (f (x)\) ">8
\ (x\) ">1	\ (f (x)\) ">0
\ (x\) ">2	\ (f (x)\) ">7
\ (x\) ">3	\ (f (x)\) ">4
\ (x\) ">4	\ (f (x)\) ">2
\ (x\) ">5	\ (f (x)\) ">6
\ (x\) ">6	\ (f (x)\) ">5
\ (x\) ">7	\ (f (x)\) ">3
\ (x\) ">8	\ (f (x)\) ">9
\ (x\) ">9	\ (f (x)\) ">1

37) Encontrar$f(1)$.

Contestar

$0$

38) Resolver$f(x)=3$.

39) Encontrar$f^{-1}(0)$.

Contestar

$1$

40) Resolver$f^{-1}(x)=7$.

41) Utilice la representación tabular de$f$ en la Tabla siguiente para crear una tabla para$f^{-1}(x)$.

$x$	3	6	9	13	14
$f(x)$	1	4	7	12	16

Contestar

$x$	1	4	7	12	16
$f^{-1}(x)$	3	6	9	13	14

Tecnología

Para los ejercicios 42-44, encuentra la función inversa. Después, grafica la función y su inversa.

42)$f(x)=\dfrac{3}{x-2}$

43)$f(x)=x^3−1$

Contestar

$f^{-1}(x)=(1+x)^{1/3}$

44) Encuentra la función inversa de$f(x)=\dfrac{1}{x-1}$. Utilice una utilidad gráfica para encontrar su dominio y rango. Escribe el dominio y el rango en notación de intervalos.

Aplicaciones del mundo real

45) Para convertir de$x$ grados Celsius a$y$ grados Fahrenheit, utilizamos la fórmula$f(x)=\dfrac{9}{5}x+32$. Encuentra la función inversa, si existe, y explica su significado.

Contestar

$f^{-1}(x)=\dfrac{5}{9}(x−32)$. Dada la temperatura Fahrenheit$x$,, esta fórmula permite calcular la temperatura Celsius.

46) La circunferencia$C$ de un círculo es una función de su radio dado por$C(r)=2{\pi}r$. Expresar el radio de un círculo en función de su circunferencia. Llama a esta función$r(C)$. Encontrar$r(36\pi)$ e interpretar su significado.

47) Un automóvil viaja a una velocidad constante de$50$ millas por hora. La distancia que recorre el automóvil en millas es función del tiempo,$t$, en horas dadas por$d(t)=50t$. Encuentra la función inversa expresando el tiempo de viaje en términos de la distancia recorrida. Llama a esta función$t(d)$. Encontrar$t(180)$ e interpretar su significado.

Contestar

$t(d)=\dfrac{d}{50}$,$t(180)=\dfrac{180}{50}$. El tiempo para que el auto recorra$180$ millas es de$3.6$ horas.