1.2: Dominio y Rango
- Page ID
- 121357
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Encuentra el dominio de una función definida por una ecuación.
- Gráfica funciones definidas por partes.
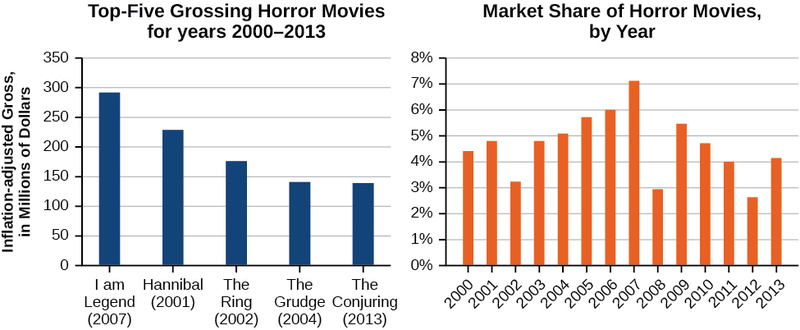
Si estás de humor para una película de terror, tal vez quieras ver una de las cinco películas de terror más populares de todos los tiempos: Soy Leyenda, Hannibal, El anillo, El rencor y El conjuramiento. La figura\(\PageIndex{1}\) muestra la cantidad, en dólares, de cada una de esas películas recaudadas cuando fueron estrenadas así como la venta de entradas para películas de terror en general por año. Observe que podemos usar los datos para crear una función de la cantidad ganada por cada película o la venta total de entradas para todas las películas de terror por año. Al crear diversas funciones usando los datos, podemos identificar diferentes variables independientes y dependientes, y podemos analizar los datos y las funciones para determinar el dominio y el rango. En esta sección, investigaremos métodos para determinar el dominio y rango de funciones como estas.
Encontrar el dominio de una función definida por una ecuación
En Funciones y Notación de Funciones, se introdujeron los conceptos de dominio y rango. En esta sección, vamos a practicar la determinación de dominios y rangos para funciones específicas. Tenga en cuenta que, al determinar dominios y rangos, debemos considerar lo que es físicamente posible o significativo en ejemplos del mundo real, como la venta de boletos y el año en el ejemplo de la película de terror anterior. También hay que considerar lo que se permite matemáticamente. Por ejemplo, no podemos incluir ningún valor de entrada que nos lleve a tomar una raíz par de un número negativo si el dominio y el rango consisten en números reales. O en una función expresada como fórmula, no podemos incluir ningún valor de entrada en el dominio que nos lleve a dividir por 0.
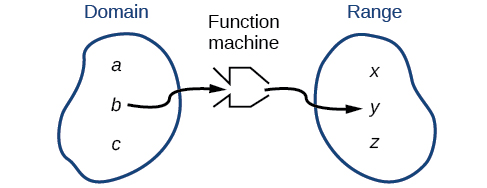
Podemos visualizar el dominio como un “área de retención” que contiene “materias primas” para una “máquina funcional” y el rango como otra “área de retención” para los productos de la máquina (Figura\(\PageIndex{2}\)).
Podemos escribir el dominio y el rango en notación de intervalos, que usa valores entre paréntesis para describir un conjunto de números. En la notación de intervalos, usamos un corchete [cuando el conjunto incluye el punto final y un paréntesis (para indicar que el punto final no está incluido o el intervalo no está limitado. Por ejemplo, si una persona tiene $100 para gastar, necesitaría expresar el intervalo que es más de 0 y menor o igual a 100 y escribir\(\left(0, 100\right]\). Discutiremos la notación de intervalos con mayor detalle más adelante.
Volvamos nuestra atención a encontrar el dominio de una función cuya ecuación se proporciona. A menudo, encontrar el dominio de tales funciones implica recordar tres formas diferentes. Primero, si la función no tiene denominador o una raíz par, considere si el dominio podría ser todo números reales. Segundo, si hay un denominador en la ecuación de la función, excluir valores en el dominio que fuerzan al denominador a ser cero. Tercero, si hay una raíz par, considera excluir valores que harían negativo al radicando.
Antes de comenzar, revisemos las convenciones de notación de intervalos:
- El término más pequeño del intervalo se escribe primero.
- El término más grande en el intervalo se escribe en segundo lugar, siguiendo una coma.
- Los paréntesis\()\),\((\) o, se utilizan para indicar que no se incluye un punto final, llamado exclusivo.
- Los corchetes\(]\),\([\) o, se utilizan para indicar que se incluye un punto final, llamado inclusivo.
Consulte la Figura\(\PageIndex{3}\) para un resumen de la notación de intervalos.
Ejemplo\(\PageIndex{1}\): Finding the Domain of a Function as a Set of Ordered Pairs
Encuentra el dominio de la siguiente función:\(\{(2, 10),(3, 10),(4, 20),(5, 30),(6, 40)\}\).
Solución
Primero identifique los valores de entrada. El valor de entrada es la primera coordenada en un par ordenado. No hay restricciones, ya que los pares ordenados simplemente se enumeran. El dominio es el conjunto de las primeras coordenadas de los pares ordenados.
\[\{2,3,4,5,6\} \nonumber\]
Exercse\(\PageIndex{1}\)
Encuentra el dominio de la función:
\[\{(−5,4),(0,0),(5,−4),(10,−8),(15,−12)\} \nonumber\]
- Contestar
-
\(\{−5, 0, 5, 10, 15\}\)
Cómo: Dada una función escrita en forma de ecuación, encontrar el dominio.
- Identificar los valores de entrada.
- Identificar cualquier restricción en la entrada y excluir esos valores del dominio.
- Escribe el dominio en forma de intervalo, si es posible.
Ejemplo\(\PageIndex{2}\): Finding the Domain of a Function
Encuentra el dominio de la función\(f(x)=x^2−1\).
Solución
El valor de entrada, mostrado por la variable x en la ecuación, es cuadrado y luego el resultado se baja en uno. Cualquier número real puede ser cuadrado y luego ser bajado en uno, por lo que no hay restricciones en el dominio de esta función. El dominio es el conjunto de números reales.
En forma de intervalo, el dominio de f es\((−\infty,\infty)\).
Exercse\(\PageIndex{2}\)
Encuentra el dominio de la función:
\[f(x)=5−x+x^3 \nonumber\]
- Contestar
-
\((−\infty,\infty)\)
Cómo: Dada una función escrita en una forma de ecuación que incluye una fracción, encuentra el dominio
- Identificar los valores de entrada.
- Identificar cualquier restricción en la entrada. Si hay un denominador en la fórmula de la función, establezca el denominador igual a cero y resuelva para x. Si la fórmula de la función contiene una raíz par, establezca el radicando mayor o igual a 0, y luego resuelva.
- Escriba el dominio en forma de intervalo, asegurándose de excluir cualquier valor restringido del dominio.
Ejemplo\(\PageIndex{3}\): Finding the Domain of a Function Involving a Denominator
Encuentra el dominio de la función\(f(x)=\dfrac{x+1}{2−x}\).
Solución
Cuando hay un denominador, queremos incluir únicamente valores de la entrada que no fuercen al denominador a ser cero. Entonces, pondremos el denominador igual a 0 y resolveremos para x.
\[ \begin{align*} 2−x=0 \\[4pt] −x &=−2 \\[4pt] x&=2 \end{align*}\]
Ahora, excluiremos 2 del dominio. Las respuestas son todas números reales donde\(x<2\) o\(x>2\). Podemos usar un símbolo conocido como la unión,\(\cup\), para combinar los dos conjuntos. En notación de intervalos, escribimos la solución:\((−\infty,2)∪(2,\infty)\).
![[Gráfico de líneas de f (x).]](https://math.libretexts.org/@api/deki/files/893/CNX_Precalc_Figure_01_02_028n.jpg)
En forma de intervalo, el dominio de f es\((−\infty,2)\cup(2,\infty)\).
Exercse\(\PageIndex{3}\)
Encuentra el dominio de la función:
\[f(x)=\dfrac{1+4x}{2x−1} \nonumber\]
- Contestar
-
\[(−\infty,\dfrac{1}{2})\cup(\dfrac{1}{2},\infty) \nonumber\]
Cómo: Dada una función escrita en forma de ecuación incluyendo una raíz par, encontrar el dominio.
- Identificar los valores de entrada.
- Como hay una raíz par, excluye cualquier número real que resulte en un número negativo en el radicando. Establezca el radical mayor o igual a cero y resuelva para x.
- La (s) solución (es) son el dominio de la función. Si es posible, escriba la respuesta en forma de intervalo.
Ejemplo\(\PageIndex{4}\): Finding the Domain of a Function with an Even Root
Encuentra el dominio de la función:
\[f(x)=\sqrt{7-x} \nonumber .\]
Solución
Cuando hay una raíz par en la fórmula, excluimos cualquier número real que resulte en un número negativo en el radicando.
Establezca el radical mayor o igual a cero y resuelva para x.
\[ \begin{align*} 7−x&≥0 \\[4pt] −x&≥−7\\[4pt] x&≤7 \end{align*}\]
Ahora, excluiremos del dominio cualquier número mayor que 7. Las respuestas son todas números reales menores o iguales a 7, o\(\left(−\infty,7\right]\).
Exercse\(\PageIndex{4}\)
Encuentra el dominio de la función
\[f(x)=\sqrt{5+2x}. \nonumber\]
- Contestar
-
\[\left[−2.5,\infty\right) \nonumber\]
Q&A: ¿Puede haber funciones en las que el dominio y el rango no se crucen en absoluto?
Sí. Por ejemplo, la función\(f(x)=-\dfrac{1}{\sqrt{x}}\) tiene el conjunto de todos los números reales positivos como su dominio pero el conjunto de todos los números reales negativos como su rango. Como ejemplo más extremo, las entradas y salidas de una función pueden ser categorías completamente diferentes (por ejemplo, nombres de días laborables como entradas y números como salidas, como en una tabla de asistencia), en tales casos el dominio y el rango no tienen elementos en común.
Uso de notaciones para especificar el dominio y el rango
En los ejemplos anteriores, se utilizaron desigualdades y listas para describir el dominio de las funciones. También podemos usar desigualdades, u otras declaraciones que puedan definir conjuntos de valores o datos, para describir el comportamiento de la variable en notación set-builder. Por ejemplo,\(\{x|10≤x<30\}\) describe el comportamiento de x en notación set-builder. \(\{\}\)Las llaves se leen como “el conjunto de”, y la barra vertical\(|\) se lee como “tal que”, por lo que leeríamos\( \{x|10≤x<30\}\) como “el conjunto de valores x tales que 10 es menor o igual a x, y x es menor que 30”.
La figura\(\PageIndex{4}\) compara la notación de desigualdad, la notación del constructor de conjuntos y la notación de intervalos
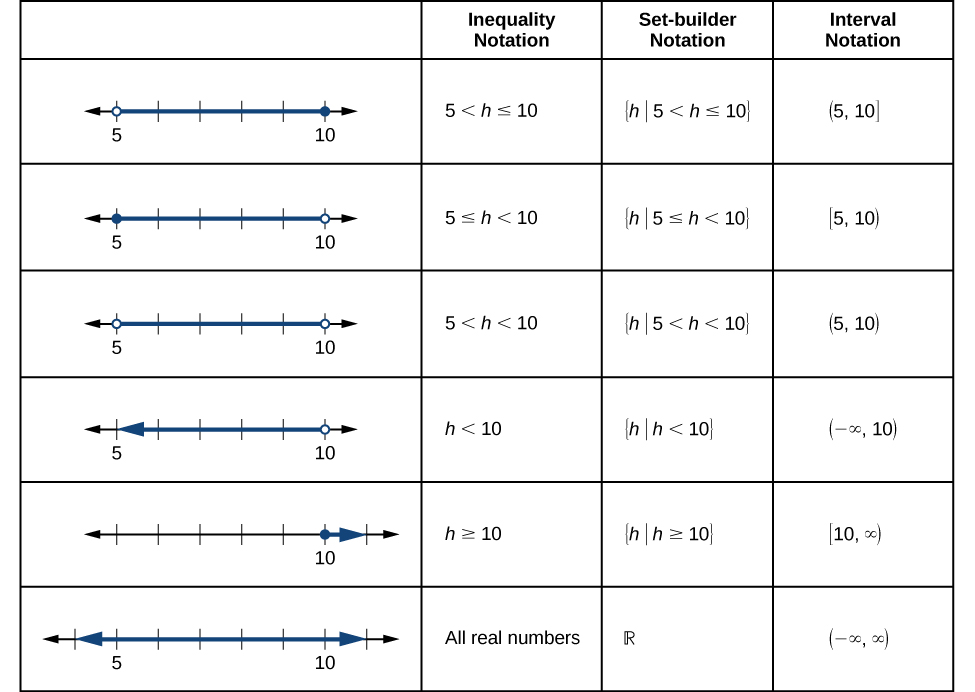
Para combinar dos intervalos usando notación de desigualdad o notación set-builder, usamos la palabra “o”. Como vimos en ejemplos anteriores, utilizamos el símbolo de unión,\(\cup\), para combinar dos intervalos desconectados. Por ejemplo, la unión de los conjuntos\(\{2,3,5\}\) y\(\{4,6\}\) es el conjunto\(\{2,3,4,5,6\}\). Es el conjunto de todos los elementos que pertenecen a uno u otro (o ambos) de los dos conjuntos originales. Para conjuntos con un número finito de elementos como estos, los elementos no tienen que ser listados en orden ascendente de valor numérico. Si los dos conjuntos originales tienen algunos elementos en común, esos elementos deben enumerarse solo una vez en el conjunto de unión. Para conjuntos de números reales en intervalos, otro ejemplo de unión es
\[\{x| |x|≥3\}=\left(−\infty,−3\right]\cup\left[3,\infty\right)\]
Notación de generador de conjuntos y notación de intervalos
La notación Set-Builder es un método para especificar un conjunto de elementos que satisfacen una determinada condición. Toma la forma\(\{x|\text{ statement about x}\}\) que se lee como, “el conjunto de todos x tal que la afirmación sobre x es verdadera”. Por ejemplo,
\[\{x|4<x≤12\} \nonumber\]
La notación de intervalos es una forma de describir conjuntos que incluyen todos los números reales entre un límite inferior que puede o no incluirse y un límite superior que puede o no incluirse. Los valores de punto final se enumeran entre paréntesis o paréntesis. Un corchete indica la inclusión en el conjunto y un paréntesis indica la exclusión del conjunto. Por ejemplo,
\[\left(4,12\right] \nonumber\]
![]() Dado un gráfico de líneas, describa el conjunto de valores usando notación de intervalos.
Dado un gráfico de líneas, describa el conjunto de valores usando notación de intervalos.
- Identificar los intervalos a incluir en el conjunto determinando donde la línea pesada se superpone a la línea real.
- En el extremo izquierdo de cada intervalo, use [con cada valor final a incluir en el conjunto (punto sólido) o (para cada valor final excluido (punto abierto).
- En el extremo derecho de cada intervalo, use] con cada valor final que se incluirá en el conjunto (punto relleno) o) para cada valor final excluido (punto abierto).
- Utilice el símbolo de unión\(\cup\) para combinar todos los intervalos en un solo conjunto.
Ejemplo\(\PageIndex{5}\): Describing Sets on the Real-Number Line
Describa los intervalos de valores mostrados en la Figura\(\PageIndex{5}\) usando notación de desigualdad, notación de constructor de conjuntos y notación de intervalos.
Solución
Para describir los valores\(x\), incluidos en los intervalos mostrados, diríamos, “\(x\)es un número real mayor o igual a 1 y menor o igual a 3, o un número real mayor que 5”.
Desigualdad
\[1≤x≤3 \text{ or }x>5 \nonumber\]
Notación de Set-Builder
\[\{x|1≤x≤3 \text{ or } x>5\}\nonumber\]
Notación de intervalos
\[[1,3]\cup(5,\infty)\nonumber\]
Recuerda que, al escribir o leer notación de intervalos, usar corchetes significa que el límite está incluido en el conjunto. Usar un paréntesis significa que el límite no está incluido en el conjunto.
Exercse\(\PageIndex{5}\)
Dada la figura\(\PageIndex{6}\), especifique el conjunto graficado en
- palabras
- notación set-builder
- notación de intervalos
![[Gráfico de líneas de -2<=x, -1<=x<3.]](https://math.libretexts.org/@api/deki/files/877/CNX_Precalc_Figure_01_02_005.jpg)
- Contestar a
-
Valores que son menores o iguales a —2, o valores que son mayores o iguales a —1 y menores que 3;
- Respuesta b
-
\(\{x|x≤−2 or −1≤x<3\}\)
- Contestar c
-
\(\left(−∞,−2\right]\cup\left[−1,3\right)\)
Búsqueda de dominio y rango a partir de gráficos
Otra forma de identificar el dominio y rango de funciones es mediante el uso de gráficos. Debido a que el dominio se refiere al conjunto de posibles valores de entrada, el dominio de una gráfica consiste en todos los valores de entrada mostrados en el eje x. El rango es el conjunto de posibles valores de salida, que se muestran en el eje y. Tenga en cuenta que si la gráfica continúa más allá de la porción de la gráfica que podemos ver, el dominio y el rango pueden ser mayores que los valores visibles. Ver Figura\(\PageIndex{7}\).
![[Gráfico de un polinomio que muestra que el eje x es el dominio y el eje y es el rango]](https://math.libretexts.org/@api/deki/files/878/CNX_Precalc_Figure_01_02_006.jpg)
Podemos observar que la gráfica se extiende horizontalmente de −5 a la derecha sin límite, por lo que el dominio es\(\left[−5,∞\right)\). La extensión vertical de la gráfica es todos los valores de rango 5 e inferiores, por lo que el rango es\(\left(−∞,5\right]\). Tenga en cuenta que el dominio y el rango siempre se escriben de valores más pequeños a mayores, o de izquierda a derecha para el dominio, y desde la parte inferior de la gráfica hasta la parte superior de la gráfica para el rango.
Ejemplo\(\PageIndex{6A}\): Finding Domain and Range from a Graph
Encuentra el dominio y rango de la función f cuya gráfica se muestra en la Figura 1.2.8.
![[Gráfica de una función de (-3, 1].]](https://math.libretexts.org/@api/deki/files/879/CNX_Precalc_Figure_01_02_007.jpg)
Solución
Podemos observar que la extensión horizontal de la gráfica es —3 a 1, por lo que el dominio de f es\(\left(−3,1\right]\).
La extensión vertical de la gráfica es de 0 a —4, por lo que el rango es\(\left[−4,0\right)\). Ver Figura\(\PageIndex{9}\).
![[El gráfico de la función anterior muestra el dominio y el rango.]](https://math.libretexts.org/@api/deki/files/880/CNX_Precalc_Figure_01_02_008.jpg)
Ejemplo\(\PageIndex{6B}\): Finding Domain and Range from a Graph of Oil Production
Encuentra el dominio y rango de la función f cuya gráfica se muestra en la Figura\(\PageIndex{10}\).
![[Gráfica de la Producción de Petróleo Crudo de Alaska donde el eje y es de mil barriles diarios y el eje -es los años.]](https://math.libretexts.org/@api/deki/files/881/CNX_Precalc_Figure_01_02_009.jpg)
Solución
La cantidad de entrada a lo largo del eje horizontal es “años”, que representamos con la variable t para el tiempo. La cantidad de salida es de “miles de barriles de petróleo por día”, que representamos con la variable b para barriles. La gráfica puede continuar hacia la izquierda y hacia la derecha más allá de lo que se ve, pero con base en la porción de la gráfica que es visible, podemos determinar el dominio como\(1973≤t≤2008\) y el rango como aproximadamente\(180≤b≤2010\).
En la notación de intervalos, el dominio es\([1973, 2008]\), y el rango es aproximadamente\([180, 2010]\). Para el dominio y el rango, aproximamos los valores más pequeños y mayores ya que no caen exactamente en las líneas de la cuadrícula.
Exercse\(\PageIndex{6}\)
Dada la Figura\(\PageIndex{11}\), identificar el dominio y el rango usando notación de intervalos.
![[Gráfica de Aumento de la Población Mundial donde el eje y representa a millones de personas y el eje x representa el año.]](https://math.libretexts.org/@api/deki/files/882/CNX_Precalc_Figure_01_02_010.jpg)
- Contestar
-
dominio =\([1950,2002]\)
rango =\([47,000,000,89,000,000]\)
![]() ¿El dominio y el rango de una función pueden ser los mismos?
¿El dominio y el rango de una función pueden ser los mismos?
Sí. Por ejemplo, el dominio y el rango de la función de raíz cúbica son ambos el conjunto de todos los números reales.
Búsqueda de dominios y rangos de las funciones del kit de herramientas
Ahora volveremos a nuestro conjunto de funciones del kit de herramientas para determinar el dominio y el rango de cada uno.
![[Función constante f (x) =c.]](https://math.libretexts.org/@api/deki/files/883/CNX_Precalc_Figure_01_02_011.jpg)
Para la función constante\( f(x)=c\), el dominio consiste en todos los números reales; no hay restricciones en la entrada. El único valor de salida es la constante\(c\), por lo que el rango es el conjunto\(\{c\}\) que contiene este único elemento. En la notación de intervalos, esto se escribe como\([c,c]\), el intervalo con el que ambos comienza y termina\(c\).
![[Función de identidad f (x) =x.]](https://math.libretexts.org/@api/deki/files/884/CNX_Precalc_Figure_01_02_012.jpg)
Figura\(\PageIndex{13}\): Función de identidad f (x) =x.
Para la función de identidad\(f(x)=x\), no hay restricción sobre\(x\). Tanto el dominio como el rango son el conjunto de todos los números reales.
![[Función absoluta f (x) =|x|.]](https://math.libretexts.org/@api/deki/files/885/CNX_Precalc_Figure_01_02_013.jpg)
Para la función de valor absoluto\(f(x)=|x|\), no hay restricción sobre\(x\). Sin embargo, debido a que el valor absoluto se define como una distancia desde 0, la salida solo puede ser mayor o igual a 0.
![[función cuadrática f (x) =x^2]](https://math.libretexts.org/@api/deki/files/886/CNX_Precalc_Figure_01_02_014.jpg)
Para la función cuadrática\(f(x)=x^2\), el dominio es todo números reales ya que la extensión horizontal de la gráfica es toda la línea numérica real. Debido a que la gráfica no incluye ningún valor negativo para el rango, el rango es solo números reales no negativos.
![[Función cúbica f (x) -x^3.]](https://math.libretexts.org/@api/deki/files/887/CNX_Precalc_Figure_01_02_015.jpg)
Para la función cúbica\(f(x)=x^3\), el dominio es todo números reales porque la extensión horizontal de la gráfica es toda la línea numérica real. Lo mismo se aplica a la extensión vertical de la gráfica, por lo que el dominio y el rango incluyen todos los números reales.
![[Función recíproca f (x) =1/x.]](https://math.libretexts.org/@api/deki/files/888/CNX_Precalc_Figure_01_02_016.jpg)
Para la función recíproca\(f(x)=\dfrac{1}{x}\), no podemos dividir por 0, por lo que debemos excluir 0 del dominio. Además, 1 dividido por cualquier valor nunca puede ser 0, por lo que el rango tampoco incluirá 0. En notación set-builder, también podríamos escribir\(\{x| x≠0\}\), el conjunto de todos los números reales que no son cero.
![[Función al cuadrado recíproco...]](https://math.libretexts.org/@api/deki/files/889/CNX_Precalc_Figure_01_02_017.jpg)
Para la función recíproca al cuadrado\(f(x)=\dfrac{1}{x^2}\), no podemos dividir por 0, por lo que debemos excluir 0 del dominio. Tampoco hay x que pueda dar una salida de 0, por lo que 0 también se excluye del rango. Tenga en cuenta que la salida de esta función siempre es positiva debido al cuadrado en el denominador, por lo que el rango incluye solo números positivos.
![[Función raíz cuadrada f (x) =sqrt (x).]](https://math.libretexts.org/@api/deki/files/890/CNX_Precalc_Figure_01_02_018.jpg)
Figura\(\PageIndex{19}\): Función raíz cuadrada\(f(x)=\sqrt{(x)}\).
Para la función raíz cuadrada\(f(x)=\sqrt{x}\), no podemos tomar la raíz cuadrada de un número real negativo, por lo que el dominio debe ser 0 o mayor. El rango también excluye números negativos porque la raíz cuadrada de un número positivo\(x\) se define como positiva, aunque el cuadrado del número negativo\(−\sqrt{x}\) también nos da\(x\).
![[Función de raíz cúbica f (x) =x^ (1/3).]](https://math.libretexts.org/@api/deki/files/891/CNX_Precalc_Figure_01_02_019.jpg)
Para la función de raíz cúbica\(f(x)=\sqrt[3]{x}\), el dominio y el rango incluyen todos los números reales. Tenga en cuenta que no hay problema en tomar una raíz cúbica, o cualquier raíz de entero impar, de un número negativo, y la salida resultante es negativa (es una función impar).
![]() Dada la fórmula para una función, determinar el dominio y el rango.
Dada la fórmula para una función, determinar el dominio y el rango.
- Excluir del dominio cualquier valor de entrada que resulte en división por cero.
- Excluir del dominio cualquier valor de entrada que tenga salidas numéricas no reales (o indefinidas).
- Utilice los valores de entrada válidos para determinar el rango de los valores de salida.
- Mire el gráfico de función y los valores de la tabla para confirmar el comportamiento real de la función.
Encontrar el dominio y el rango usando las funciones del kit de herramientas
Encuentra el dominio y la gama de\(f(x)=2x^3−x\).
Solución
No hay restricciones sobre el dominio, ya que cualquier número real puede ser cúbico y luego restado del resultado.
El dominio es\((−\infty,\infty)\) y el rango también lo es\((−\infty,\infty)\).
Ejemplo\(\PageIndex{7B}\): Finding the Domain and Range
Encuentra el dominio y la gama de\(f(x)=\frac{2}{x+1}\).
Solución
No podemos evaluar la función en −1 porque la división por cero no está definida. El dominio es\((−\infty,−1)\cup(−1,\infty)\). Debido a que la función nunca es cero, excluimos 0 del rango. El rango es\((−\infty,0)\cup(0,\infty)\).
Ejemplo\(\PageIndex{7C}\): Finding the Domain and Range
Encuentra el dominio y la gama de\(f(x)=2 \sqrt{x+4}\).
Solución
No podemos tomar la raíz cuadrada de un número negativo, por lo que el valor dentro del radical debe ser no negativo.
\(x+4≥0\)cuando\(x≥−4\)
El dominio de\(f(x)\) es\([−4,\infty)\).
Luego encontramos la gama. Eso lo sabemos\(f(−4)=0\), y el valor de la función aumenta a medida que\(x\) aumenta sin ningún límite superior. Se concluye que el rango de f es\(\left[0,\infty\right)\).
Análisis
La figura\(\PageIndex{19}\) representa la función\(f\).
 " src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">
" src="https://math.libretexts.org/@api/dek..._01_02_020.jpg">
Ejercicio\(\PageIndex{7}\)
Encuentra el dominio y la gama de
\(f(x)=\sqrt{−2−x}\).
- Contestar
-
dominio:\(\left(−\infty,-2\right]\)
Rango:\(\left[0,\infty\right)\)
Graficar funciones definidas por partes
A veces, nos encontramos con una función que requiere más de una fórmula para obtener la salida dada. Por ejemplo, en las funciones del kit de herramientas, introdujimos la función de valor absoluto\(f(x)=|x|\). Con un dominio de todos los números reales y un rango de valores mayor o igual a 0, el valor absoluto puede definirse como la magnitud, o módulo, de un valor de número real independientemente del signo. Es la distancia desde 0 en la recta numérica. Todas estas definiciones requieren que la salida sea mayor o igual a 0.
Si ingresamos 0, o un valor positivo, la salida es la misma que la entrada.
\[ f(x)=x \; \text{ if } \; x≥0 \nonumber \]
Si ingresamos un valor negativo, la salida es la opuesta a la entrada.
\[ f(x) = -x \; \text { if } \; x < 0 \nonumber \]
Debido a que esto requiere dos procesos o piezas diferentes, la función de valor absoluto es un ejemplo de una función por partes. Una función por partes es una función en la que se utiliza más de una fórmula para definir la salida sobre diferentes partes del dominio.
Usamos funciones por partes para describir situaciones en las que una regla o relación cambia a medida que el valor de entrada cruza ciertos “límites”. Por ejemplo, a menudo nos encontramos con situaciones en los negocios para las cuales el costo por pieza de un determinado artículo se descuenta una vez que el número pedido excede un cierto valor. Los tramos impositivos son otro ejemplo del mundo real de funciones por partes. Por ejemplo, consideremos un sistema tributario simple en el que los ingresos de hasta 10 mil dólares se graven al 10%, y cualquier ingreso adicional se imponga al 20%. El impuesto sobre un ingreso total S sería\(0.1S\) si\(S≤$10,000\) y\($1000+0.2(S−$10,000)\) si\(S>$10,000\).
Función por partes
Una función por partes es una función en la que se utiliza más de una fórmula para definir la salida. Cada fórmula tiene su propio dominio, y el dominio de la función es la unión de todos estos dominios más pequeños. Anotamos esta idea así:
\[f(x)= \begin{cases} \text{formula 1} & \text{if x is in domain 1} \\ \text{formula 2} &\text{if x is in domain 2} \\ \text{formula 3} &\text{if x is in domain 3}\end{cases} \nonumber \]
En notación por partes, la función de valor absoluto es
\[|x|= \begin{cases} x & \text{if $x \geq 0$} \\ -x &\text{if $x<0$} \end{cases} \nonumber \]
![]() Dada una función por partes, escriba la fórmula e identifique el dominio para cada intervalo.
Dada una función por partes, escriba la fórmula e identifique el dominio para cada intervalo.
- Identificar los intervalos para los que se aplican diferentes reglas.
- Determinar fórmulas que describen cómo calcular una salida a partir de una entrada en cada intervalo.
- Use llaves e instrucciones if para escribir la función.
Ejemplo\(\PageIndex{8A}\): Writing a Piecewise Function
Un museo cobra $5 por persona por una visita guiada con un grupo de 1 a 9 personas o una tarifa fija de $50 para un grupo de 10 o más personas. Escribir una función relacionando el número de personas,\(n\), con el costo,\(C\).
Solución
Se necesitarán dos fórmulas diferentes. Para\(n\) -valores menores de 10,\(C=5n\). Para valores de n que son 10 o mayores,\(C=50\).
\[C(n)= \begin{cases} 5n & \text{if $n < 10$} \\ 50 &\text{if $n\geq10$} \end{cases} \nonumber \]
Análisis
La función se representa en la Figura\(\PageIndex{20}\). La gráfica es una línea diagonal de\(n=0\) a\(n=10\) y una constante después de eso. En este ejemplo, las dos fórmulas coinciden en el punto de encuentro donde\(n=10\), pero no todas las funciones por partes tienen esta propiedad.
![[Gráfica de C (n).]](https://math.libretexts.org/@api/deki/files/894/CNX_Precalc_Figure_01_02_021.jpg)
Ejemplo\(\PageIndex{8B}\): Working with a Piecewise Function
Una compañía de telefonía celular utiliza la siguiente función para determinar el costo, C, en dólares por g gigabytes de transferencia de datos.
\[C(g)= \begin{cases} 25 & \text{if $0<g<2$} \\ 25+10(g-2) &\text{if $g\geq2$} \end{cases} \nonumber \]
Encuentre el costo de usar 1.5 gigabytes de datos y el costo de usar 4 gigabytes de datos.
Soltuion
Para encontrar el costo de usar 1.5 gigabytes de datos,\(C(1.5)\), primero miramos para ver en qué parte del dominio cae nuestra entrada. Debido a que 1.5 es menor que 2, usamos la primera fórmula.
\[C(1.5)=$25 \nonumber \]
Para encontrar el costo de usar 4 gigabytes de datos, C (4), vemos que nuestra entrada de 4 es mayor que 2, por lo que usamos la segunda fórmula.
\[C(4)=25+10(4−2)=$45 \nonumber \]
Análisis
La función se representa en la Figura\(\PageIndex{21}\). Podemos ver donde la función cambia de una constante a una identidad desplazada y estirada en\(g=2\). Trazamos las gráficas para las diferentes fórmulas en un conjunto común de ejes, asegurándonos de que cada fórmula se aplique en su dominio propio.
![[Gráfica de C (g)]](https://math.libretexts.org/@api/deki/files/895/CNX_Precalc_Figure_01_02_022.jpg)
![]() Dada una función por partes, esboce una gráfica.
Dada una función por partes, esboce una gráfica.
- Indicar en el eje x los límites definidos por los intervalos en cada parte del dominio.
- Para cada pieza del dominio, grafica en ese intervalo usando la ecuación correspondiente correspondiente a esa pieza. No graficar dos funciones en un intervalo porque violaría los criterios de una función.
Ejemplo\(\PageIndex{8C}\): Graphing a Piecewise Function
Haga un boceto de una gráfica de la función.
\[f(x)= \begin{cases} x^2 & \text{if $x \leq 1$} \\ 3 &\text{if $1<x\leq2$} \\ x &\text{if $x>2$} \end{cases} \nonumber \]
Solución
Cada una de las funciones componentes es de nuestra biblioteca de funciones del kit de herramientas, por lo que conocemos sus formas. Podemos imaginar graficar cada función y luego limitar la gráfica al dominio indicado. En los puntos finales del dominio, dibujamos círculos abiertos para indicar dónde no se incluye el punto final debido a una desigualdad menor que o mayor que; dibujamos un círculo cerrado donde el punto final se incluye debido a una desigualdad menor o igual a o mayor que o igual a.
La figura\(\PageIndex{20}\) muestra los tres componentes de la función por partes graficados en sistemas de coordenadas separados.
![[Gráfica de cada parte de la función por piezas f (x)]](https://math.libretexts.org/@api/deki/files/896/CNX_Precalc_Figure_01_02_023abc.jpg)
Figura\(\PageIndex{20}\): Gráfica de cada parte de la función por piezas f (x)
a)\( f(x)=x^2\) si\(x≤1\); b)\(f(x)=3\) si\(1< x≤2\); c)\(f(x)=x\) si\(x>2\)
Ahora que hemos esbozado cada pieza individualmente, las combinamos en el mismo plano de coordenadas. Ver Figura\(\PageIndex{21}\).
![[Gráfico de toda la función.]](https://math.libretexts.org/@api/deki/files/897/CNX_Precalc_Figure_01_02_026.jpg)
Análisis
Tenga en cuenta que la gráfica sí pasa la prueba de línea vertical incluso en\(x=1\) y\(x=2\) porque los puntos\((1,3)\) y no\((2,2)\) son parte de la gráfica de la función, aunque\((1,1)\) y\((2, 3)\) son.
Ejercicio\(\PageIndex{8}\)
Grafique la siguiente función por partes.
\[f(x)= \begin{cases} x^3 & \text{if $x < -1$} \\ -2 &\text{if $-1<x<4$} \\ \sqrt{x} &\text{if $x>4$} \end{cases} \nonumber \]
- Contestar
-
![[Gráfica de f (x).]](https://math.libretexts.org/@api/deki/files/898/CNX_Precalc_Figure_01_02_027.jpg)
Figura\(\PageIndex{22}\)
![]() ¿Se puede aplicar más de una fórmula de una función por partes a un valor en el dominio?
¿Se puede aplicar más de una fórmula de una función por partes a un valor en el dominio?
No. Cada valor corresponde a una ecuación en una fórmula por partes.
Conceptos clave
- El dominio de una función incluye todos los valores de entrada reales que no nos provocarían intentar una operación matemática indefinida, como dividir por cero o tomar la raíz cuadrada de un número negativo.
- El dominio de una función se puede determinar enumerando los valores de entrada de un conjunto de pares ordenados.
- El dominio de una función también se puede determinar identificando los valores de entrada de una función escrita como una ecuación.
- Los valores de intervalo representados en una recta numérica se pueden describir usando notación de desigualdad, notación de generador de conjuntos y notación de intervalos.
- Para muchas funciones, el dominio y el rango se pueden determinar a partir de una gráfica.
- Se puede usar una comprensión de las funciones del kit de herramientas para encontrar el dominio y la gama de funciones relacionadas.
- Una función por partes se describe mediante más de una fórmula.
- Una función por partes se puede graficar usando cada fórmula algebraica en su subdominio asignado.
Notas al pie
1 Los números: Dónde se encuentran los datos y el negocio del cine. “Historia de taquilla para películas de terror”. http://www.the-numbers.com/market/genre/Horror. Accedido 24/03/2014
2 www.EIA.gov/DNAV/PET/Hist/LEA... s=MCRFPAK2&f=A.
Glosario
- notación de intervalos
-
un método para describir un conjunto que incluye todos los números entre un límite inferior y un límite superior; los valores inferior y superior se enumeran entre corchetes o paréntesis, un corchete que indica la inclusión en el conjunto y un paréntesis que indica la exclusión
- función por partes
-
una función en la que se utiliza más de una fórmula para definir la salida
- notación set-builder
-
un método para describir un conjunto por una regla que todos sus miembros obedecen; toma la forma {x| declaración sobre x}


