3.3: Funciones de Potencia y Funciones Polinómicas
- Page ID
- 121421
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Objetivos de aprendizaje
- Identificar funciones de potencia.
- Identificar el comportamiento final de las funciones de potencia.
- Identificar funciones polinomiales.
- Identificar el grado y coeficiente principal de las funciones polinómicas.
Supongamos que cierta especie de ave prospera en una pequeña isla. Su población en los últimos años se muestra en la Tabla\(\PageIndex{1}\).
| Año | 2009 | 2010 | 2011 | 2012 | 2013 |
|---|---|---|---|---|---|
| Población de aves | 800 | 897 | 992 | 1,083 | 1,169 |
La población se puede estimar utilizando la función\(P(t)=−0.3t^3+97t+800\), donde\(P(t)\) representa la población de aves en la isla\(t\) años después de 2009. Podemos utilizar este modelo para estimar la población máxima de aves y cuándo ocurrirá. También podemos usar este modelo para predecir cuándo desaparecerá la población de aves de la isla. En esta sección, examinaremos las funciones que podemos utilizar para estimar y predecir este tipo de cambios.

Identificación de funciones de potencia
Para entender mejor el problema de las aves, necesitamos entender un tipo específico de función. Una función de potencia es una función con un solo término que es producto de un número real, un coeficiente y una variable elevada a un número real fijo. (Un número que multiplica una variable elevada a un exponente se conoce como coeficiente).
Como ejemplo, considere funciones para área o volumen. La función para el área de un círculo con radio\(r\) es
\[A(r)={\pi}r^2 \nonumber\]
y la función para el volumen de una esfera con radio\(r\) es
\[V(r)=\dfrac{4}{3}{\pi}r^3 \nonumber\]
Ambos son ejemplos de funciones de poder porque consisten en un coeficiente,\({\pi}\) o\(\dfrac{4}{3}{\pi}\), multiplicadas por una variable\(r\) elevada a una potencia.
Definición: Función de potencia
Una función de potencia es una función que se puede representar en la forma
\[f(x)=kx^p \label{power}\]
donde\(k\) y\(p\) son números reales, y\(k\) se conoce como el coeficiente.
Q&A: Es\(f(x)=2^x\) a power function?
No. Una función de potencia contiene una base variable elevada a una potencia fija (Ecuación\ ref {potencia}). Esta función tiene una base constante elevada a una potencia variable. A esto se le llama una función exponencial, no una función de potencia. Esta función se discutirá más adelante.
Ejemplo\(\PageIndex{1}\): Identifying Power Functions
¿Cuáles de las siguientes funciones son funciones de potencia?
\[\begin{align*} f(x)&=1 &\text{Constant function} \\f(x)&=x &\text{Identify function} \\f(x)&=x^2 &\text{Quadratic function} \\ f(x)&=x^3 &\text{Cubic function} \\ f(x)&=\dfrac{1}{x} &\text{Reciprocal function} \\f(x)&=\dfrac{1}{x^2} &\text{Reciprocal squared function} \\ f(x)&=\sqrt{x} &\text{Square root function} \\ f(x)&=\sqrt[3]{x} &\text{Cube root function} \end{align*}\]
Solución
Todas las funciones enumeradas son funciones de potencia.
Las funciones de constante e identidad son funciones de poder porque se pueden escribir como\(f(x)=x^0\) y\(f(x)=x^1\) respectivamente.
Las funciones cuadráticas y cúbicas son funciones de potencia con potencias de número entero\(f(x)=x^2\) y\(f(x)=x^3\).
Las funciones cuadradas recíprocas y recíprocas son funciones de poder con potencias negativas de número entero porque pueden escribirse como\(f(x)=x^{−1}\) y\(f(x)=x^{−2}\).
Las funciones de raíz cuadrada y cubo son funciones de potencia con potencias fraccionarias porque pueden escribirse como\(f(x)=x^{1/2}\) o\(f(x)=x^{1/3}\).
Ejercicio\(\PageIndex{1}\)
¿Qué funciones son las funciones de alimentación?
- \(f(x)=2x^2⋅4x^3\)
- \(g(x)=−x^5+5x^3−4x\)
- \(h(x)=\frac{2x^5−1}{3x^2+4}\)
- Contestar
-
\(f(x)\)es una función de poder porque se puede escribir como\(f(x)=8x^5\). Las otras funciones no son funciones de potencia.
Identificación del comportamiento final de las funciones de potencia
La figura\(\PageIndex{2}\) muestra los gráficos de\(f(x)=x^2\),\(g(x)=x^4\) y y\(h(x)=x^6\), que son todas las funciones de potencia con potencias pares de números enteros. Observe que estas gráficas tienen formas similares, muy parecidas a la de la función cuadrática en el kit de herramientas. Sin embargo, a medida que aumenta la potencia, las gráficas se aplanan un poco cerca del origen y se vuelven más pronunciadas lejos del origen.
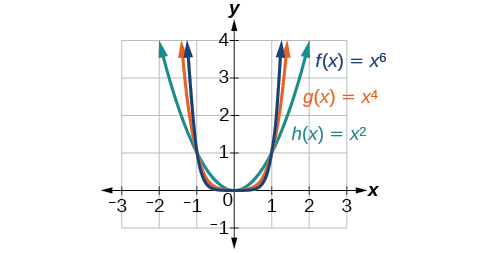
Para describir el comportamiento a medida que los números se hacen cada vez más grandes, usamos la idea de infinito. Usamos el símbolo\(\infty\) para infinito positivo y\(−\infty\) para infinito negativo. Cuando decimos que “x se acerca al infinito”, que puede escribirse simbólicamente como\(x{\rightarrow}\infty\), estamos describiendo un comportamiento; estamos diciendo que\(x\) está aumentando sin ataduras.
Con la función de potencia par, a medida que la entrada aumenta o disminuye sin límite, los valores de salida se convierten en números positivos muy grandes. Equivalentemente, podríamos describir este comportamiento diciendo que a medida que\(x\) se acerca al infinito positivo o negativo, los\(f(x)\) valores aumentan sin límite. En forma simbólica, podríamos escribir
\[\text{as } x{\rightarrow}{\pm}{\infty}, \;f(x){\rightarrow}{\infty} \nonumber\]
La figura\(\PageIndex{3}\) muestra los gráficos de\(f(x)=x^3\),\(g(x)=x^5\), y\(h(x)=x^7\), que son todas las funciones de potencia con potencias impares de números enteros. Observe que estas gráficas se parecen a la función cúbica en el kit de herramientas. Nuevamente, a medida que aumenta la potencia, las gráficas se aplanan cerca del origen y se vuelven más pronunciadas lejos del origen.
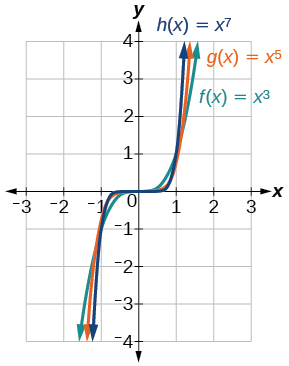
Estos ejemplos ilustran que las funciones de la forma\(f(x)=x^n\) revelan simetría de un tipo u otro. Primero, en Figura\(\PageIndex{2}\) vemos que incluso funciones de la forma\(f(x)=x^n\),\(n\) incluso, son simétricas alrededor del\(y\) eje -eje. En la Figura\(\PageIndex{3}\) vemos que las funciones impares de la forma\(f(x)=x^n\),\(n\) impar, son simétricas sobre el origen.
Para estas extrañas funciones de poder, a medida que\(x\) se acerca al infinito negativo,\(f(x)\) disminuye sin límite. A medida que\(x\) se acerca al infinito positivo,\(f(x)\) aumenta sin ataduras. En forma simbólica escribimos
\[\begin{align*} &\text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}-{\infty} \\ &\text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}{\infty} \end{align*}\]
El comportamiento de la gráfica de una función ya que los valores de entrada se vuelven muy pequeños\((x{\rightarrow}−{\infty})\) y\(x{\rightarrow}{\infty}\) se vuelven muy grandes se conoce como el comportamiento final de la función. Podemos usar palabras o símbolos para describir el comportamiento final.
La figura\(\PageIndex{4}\) muestra el comportamiento final de las funciones de potencia en la forma\(f(x)=kx^n\) donde\(n\) es un entero no negativo dependiendo de la potencia y la constante.
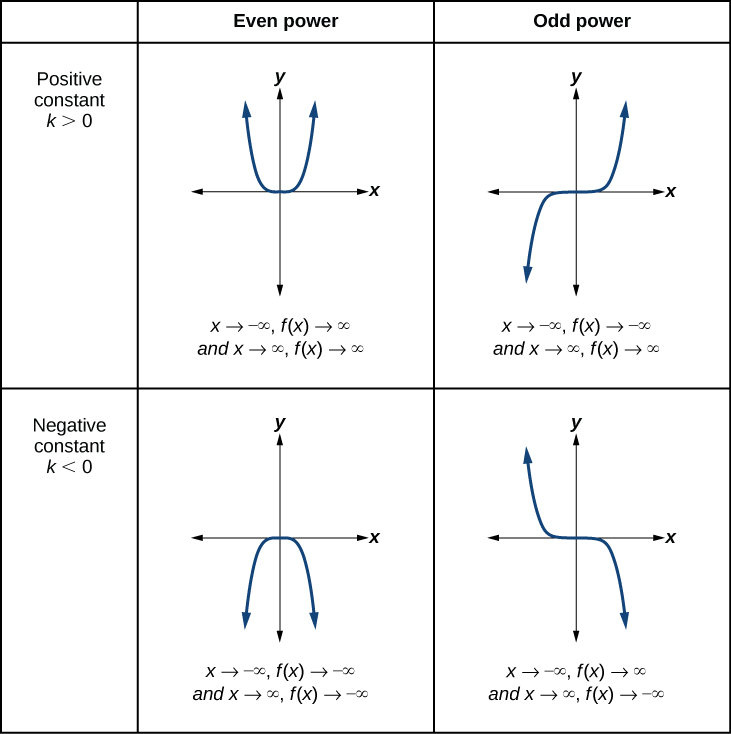
Cómo: Dada una función de potencia\(f(x)=kx^n\) where \(n\) is a non-negative integer, identify the end behavior.
- Determinar si la potencia es par o impar.
- Determinar si la constante es positiva o negativa.
- Utilice la Figura\(\PageIndex{4}\) para identificar el comportamiento final.
Ejemplo\(\PageIndex{2}\): Identifying the End Behavior of a Power Function
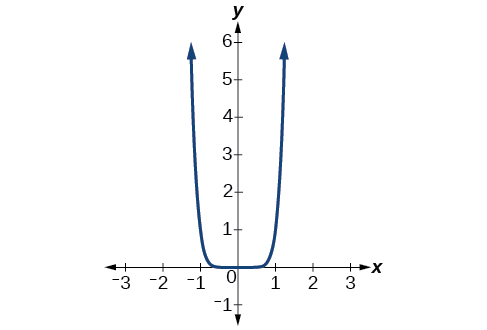
Describir el comportamiento final de la gráfica de\(f(x)=x^8\).
Solución
El coeficiente es 1 (positivo) y el exponente de la función de potencia es 8 (un número par). A medida que\(x\) se acerca al infinito, la salida (valor de\(f(x)\)) aumenta sin límite. Escribimos como A\(x→∞,\)\(f(x)→∞.\) medida que se\(x\) acerca al infinito negativo, la salida aumenta sin límite. En forma simbólica, como\(x→−∞,\)\(f(x)→∞.\) Podemos representar gráficamente la función como se muestra en la Figura\(\PageIndex{5}\).
Ejemplo\(\PageIndex{3}\): Identifying the End Behavior of a Power Function.
Describir el comportamiento final de la gráfica de\(f(x)=−x^9\).
Solución
El exponente de la función de potencia es 9 (un número impar). Debido a que el coeficiente es —1 (negativo), la gráfica es la reflexión alrededor del\(x\) eje -de la gráfica de\(f(x)=x^9\). La figura\(\PageIndex{6}\) muestra que a medida que\(x\) se acerca al infinito, la salida disminuye sin límite. A medida que\(x\) se acerca al infinito negativo, la salida aumenta sin límite. En forma simbólica, escribiríamos
\[\begin{align*} \text{as }x{\rightarrow}-{\infty},\;f(x){\rightarrow}{\infty} \\ \text{as }x{\rightarrow}{\infty},\;f(x){\rightarrow}-{\infty} \end{align*}\]
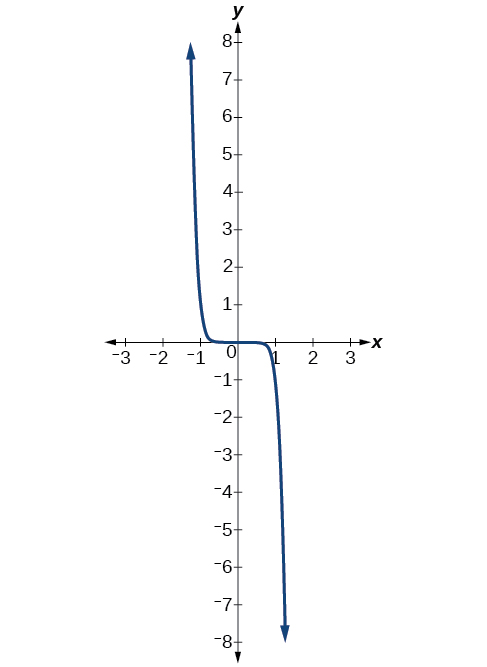
Análisis
Podemos verificar nuestro trabajo usando la función de tabla en una utilidad gráfica.
| \(x\) | \(f(x)\) |
|---|---|
| \ (x\)” style="vertical-align:middle; ">-10 | \ (f (x)\)” style="vertical-align:middle; ">1.000.000.000 |
| \ (x\)” style="vertical-align:middle; ">-5 | \ (f (x)\)” style="vertical-align:middle; ">1.953,125 |
| \ (x\)” style="vertical-align:middle; ">0 | \ (f (x)\)” style="vertical-align:middle; ">0 |
| \ (x\)” style="vertical-align:middle; ">5 | \ (f (x)\)” style="vertical-align:middle; ">-1.953,125 |
| \ (x\)” style="vertical-align:middle; ">10 | \ (f (x)\)” style="vertical-align:middle; ">-1.000.000.000 |
Podemos ver en Table\(\PageIndex{2}\) que, cuando sustituimos valores muy pequeños por\(x\), la salida es muy grande, y cuando sustituimos valores muy grandes por\(x\), la salida es muy pequeña (es decir, que es un valor negativo muy grande).
Ejercicio\(\PageIndex{2}\)
Describir en palabras y símbolos el comportamiento final de\(f(x)=−5x^4\).
- Contestar
-
A medida que\(x\) se acerca al infinito positivo o negativo,\(f(x)\) disminuye sin límite: as\(x{\rightarrow}{\pm}{\infty}\),\(f(x){\rightarrow}−{\infty}\) debido al coeficiente negativo.
Identificación de funciones polinomiales
Un oleoducto estalla en el Golfo de México, provocando una marea resbaladiza de forma aproximadamente circular. El resbaladizo tiene actualmente 24 millas de radio, pero ese radio está aumentando 8 millas cada semana. Queremos escribir una fórmula para el área cubierta por la marea negra combinando dos funciones. El radio\(r\) del derrame depende del número de semanas\(w\) que hayan pasado. Esta relación es lineal.
\[r(w)=24+8w \nonumber\]
Podemos combinar esto con la fórmula para el área A de un círculo.
\[A(r)={\pi}r^2 \nonumber\]
La composición de estas funciones da una fórmula para el área en términos de semanas.
\[ \begin{align*} A(w)&=A(r(w)) \\ &=A(24+8w) \\ & ={\pi}(24+8w)^2 \end{align*}\]
Multiplicar da la fórmula.
\[A(w)=576{\pi}+384{\pi}w+64{\pi}w^2 \nonumber\]
Esta fórmula es un ejemplo de una función polinómica. Una función polinómica consiste en cero o la suma de un número finito de términos distintos de cero, cada uno de los cuales es producto de un número, llamado coeficiente del término, y una variable elevada a una potencia entera no negativa.
Definición: Funciones polinómicas
Dejar\(n\) ser un entero no negativo. Una función polinómica es una función que se puede escribir en la forma
\[f(x)=a_nx^n+...+a_2x^2+a_1x+a_0 \label{poly}\]
A esto se le llama la forma general de una función polinómica. Cada uno\(a_i\) es un coeficiente y puede ser cualquier número real. Cada producto\(a_ix^i\) es un término de una función polinómica.
Ejemplo\(\PageIndex{4}\): Identifying Polynomial Functions
¿Cuáles de las siguientes son funciones polinómicas?
- \(f(x)=2x^3⋅3x+4\)
- \(g(x)=−x(x^2−4)\)
- \(h(x)=5\sqrt{x}+2\)
Solución
Las dos primeras funciones son ejemplos de funciones polinómicas porque pueden escribirse en forma de Ecuación\ ref {poly}, donde las potencias son números enteros no negativos y los coeficientes son números reales.
- \(f(x)\)se puede escribir como\(f(x)=6x^4+4\).
- \(g(x)\)se puede escribir como\(g(x)=−x^3+4x\).
- \(h(x)\)no se puede escribir en esta forma y por lo tanto no es una función polinómica.
Identificación del Grado y Coeficiente Líder de una Función Polinómica
Debido a la forma de una función polinómica, podemos ver una variedad infinita en el número de términos y la potencia de la variable. Aunque el orden de los términos en la función polinómica no es importante para realizar operaciones, normalmente los ordenamos en orden descendente de potencia, o en forma general. El grado del polinomio es la potencia más alta de la variable que ocurre en el polinomio; es la potencia de la primera variable si la función está en forma general. El término principal es el término que contiene la mayor potencia de la variable, o el término con el grado más alto. El coeficiente principal es el coeficiente del término principal.
Terminología de las funciones polinomiales
A menudo reorganizamos polinomios para que los poderes desciendan.
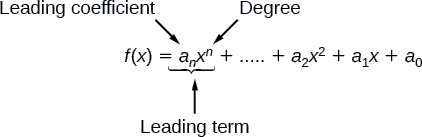
Cuando un polinomio se escribe de esta manera, decimos que es en forma general.
Cómo: Dada una función polinómica, identificar el grado y el coeficiente principal
- Encuentra el mayor poder de\(x\) para determinar la función de grado.
- Identificar el término que contiene el mayor poder de\(x\) para encontrar el término líder.
- Identificar el coeficiente del término principal.
Ejemplo\(\PageIndex{5}\): Identifying the Degree and Leading Coefficient of a Polynomial Function
Identificar el grado, término principal y coeficiente principal de las siguientes funciones polinómicas.
\(f(x)=3+2x^2−4x^3\)
\(g(t)=5t^5−2t^3+7t\)
\(h(p)=6p−p^3−2\)
Solución
Para la función\(f(x)\), la potencia más alta de\(x\) es 3, por lo que el grado es 3. El término principal es el término que contiene ese grado,\(−4x^3\). El coeficiente principal es el coeficiente de ese término, −4.
Para la función\(g(t)\), la potencia más alta de\(t\) es 5, por lo que el grado es 5. El término principal es el término que contiene ese grado,\(5t^5\). El coeficiente principal es el coeficiente de ese término, 5.
Para la función\(h(p)\), la potencia más alta de\(p\) es 3, por lo que el grado es 3. El término principal es el término que contiene ese grado,\(−p^3\); el coeficiente principal es el coeficiente de ese término, −1.
Ejercicio\(\PageIndex{3}\)
Identificar el grado, término principal y coeficiente principal del polinomio\(f(x)=4x^2−x^6+2x−6\).
- Contestar
-
El grado es\(6.\) El término principal es\(−x^6\). El coeficiente principal es\(−1.\)
Identificación del Comportamiento Final de Funciones Polinómicas
Conocer el grado de una función polinómica es útil para ayudarnos a predecir su comportamiento final. Para determinar su comportamiento final, observe el término principal de la función polinómica. Debido a que el poder del término líder es el más alto, ese término crecerá significativamente más rápido que los otros términos ya que\(x\) se vuelve muy grande o muy pequeño, por lo que su comportamiento dominará la gráfica. Para cualquier polinomio, el comportamiento final del polinomio coincidirá con el comportamiento final del término de grado más alto (Tabla\(\PageIndex{3}\)).
| Función polinomial | Término principal | Gráfica de Función Polinómica |
|---|---|---|
| \(f(x)=5x^4+2x^3−x−4\) | \(5x^4\) | 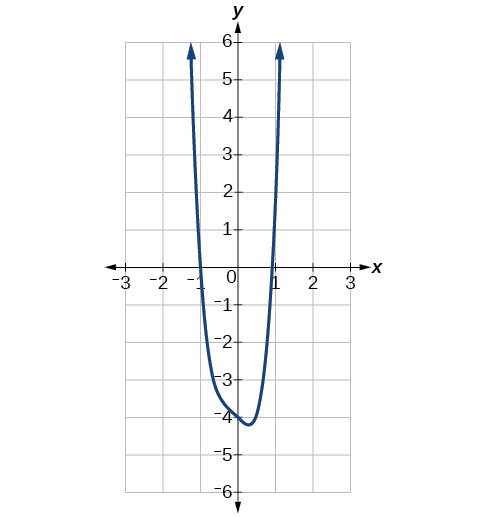 |
| \(f(x)=−2x^6−x^5+3x^4+x^3\) | \(−2x^6\) | 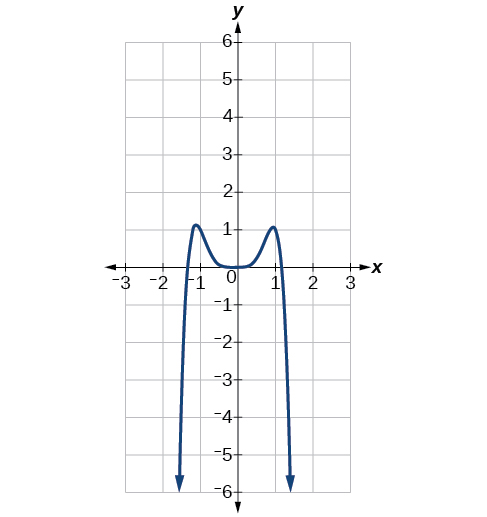 |
| \(f(x)=3x^5−4x^4+2x^2+1\) | \(3x^5\) | 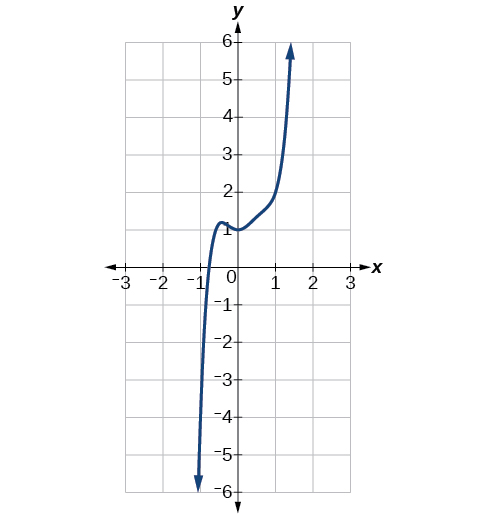 |
| \(f(x)=−6x^3+7x^2+3x+1\) | \(−6x^3\) | 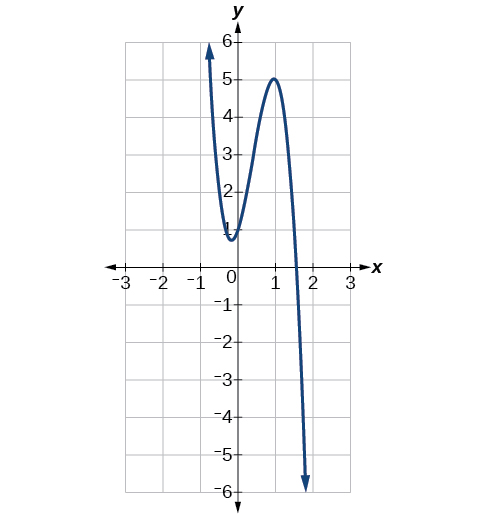 |
Ejemplo\(\PageIndex{6}\): Identifying End Behavior and Degree of a Polynomial Function
Describir el comportamiento final y determinar un posible grado de la función polinómica en la Figura\(\PageIndex{8}\).
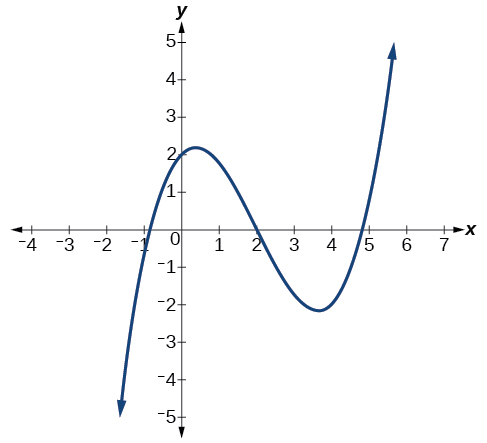
Solución
A medida que los valores de entrada se\(x\) vuelven muy grandes, los valores de salida\(f(x)\) aumentan sin límite. A medida que los valores de entrada se\(x\) vuelven muy pequeños, los valores de salida\(f(x)\) disminuyen sin límite. Podemos describir simbólicamente el comportamiento final escribiendo
\[\text{as } x{\rightarrow}{\infty}, \; f(x){\rightarrow}{\infty} \nonumber\]
\[\text{as } x{\rightarrow}-{\infty}, \; f(x){\rightarrow}-{\infty} \nonumber\]
En palabras, podríamos decir que a medida que\(x\) los valores se acercan al infinito, los valores de la función se acercan al infinito, y a medida que\(x\) los valores se acercan al infinito negativo, los valores de
Podemos decir que esta gráfica tiene la forma de una función de potencia de grado impar que no se ha reflejado, por lo que el grado del polinomio que crea esta gráfica debe ser impar y el coeficiente inicial debe ser positivo.
Ejercicio\(\PageIndex{1}\)
Describir el comportamiento final y determinar un posible grado de la función polinómica en la Figura\(\PageIndex{9}\).
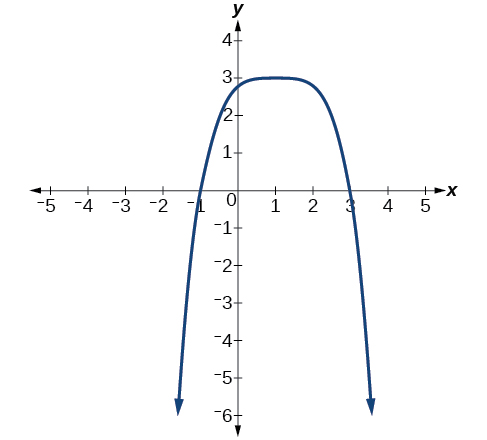
- Contestar
-
Como\(x{\rightarrow}{\infty}\),\(f(x){\rightarrow}−{\infty}\); como\(x{\rightarrow}−{\infty}\),\(f(x){\rightarrow}−{\infty}\). Tiene la forma de una función de potencia de grado par con un coeficiente negativo.
Ejemplo\(\PageIndex{7}\): Identifying End Behavior and Degree of a Polynomial Function
Dada la función\(f(x)=−3x^2(x−1)(x+4)\), expresar la función como polinomio en forma general, y determinar el término principal, grado y comportamiento final de la función.
Solución
Obtener la forma general expandiendo la expresión dada para\(f(x)\).
\[\begin{align*} f(x)&=−3x^2(x−1)(x+4) \\ &=−3x^2(x^2+3x−4) \\ &=−3x^4−9x^3+12x^2 \end{align*}\]
La forma general es\(f(x)=−3x^4−9x^3+12x^2\). El término principal es\(−3x^4\); por lo tanto, el grado del polinomio es 4. El grado es par (4) y el coeficiente principal es negativo (—3), por lo que el comportamiento final es
\[\text{as }x{\rightarrow}−{\infty}, \; f(x){\rightarrow}−{\infty} \nonumber\]
\[\text{as } x{\rightarrow}{\infty}, \; f(x){\rightarrow}−{\infty} \nonumber\]
Ejercicio\(\PageIndex{7}\)
Dada la función\(f(x)=0.2(x−2)(x+1)(x−5)\), expresar la función como polinomio en forma general y determinar el término principal, grado y comportamiento final de la función.
- Contestar
-
El término principal es\(0.2x^3\), por lo que es un polinomio grado 3. A medida que\(x\) se acerca al infinito positivo,\(f(x)\) aumenta sin límite; a medida que\(x\) se acerca al infinito negativo,\(f(x)\) disminuye sin límite.
Identificación del Comportamiento Local de Funciones Polinómicas
Además del comportamiento final de las funciones polinómicas, también nos interesa lo que sucede en el “medio” de la función. En particular, nos interesan las ubicaciones donde cambia el comportamiento de las gráficas. Un punto de inflexión es un punto en el que los valores de la función cambian de aumentar a disminuir o disminuir a aumentar.
También nos interesan los interceptos. Al igual que con todas las funciones, la\(y\) -intercepción es el punto en el que la gráfica se cruza con el eje vertical. El punto corresponde al par de coordenadas en el que el valor de entrada es cero. Debido a que un polinomio es una función, solo un valor de salida corresponde a cada valor de entrada por lo que solo puede haber una\(y\) -intercepción\((0,a_0)\). Las\(x\) -intercepciones ocurren en los valores de entrada que corresponden a un valor de salida de cero. Es posible tener más de una\(x\) -intercepción. Ver Figura\(\PageIndex{10}\).
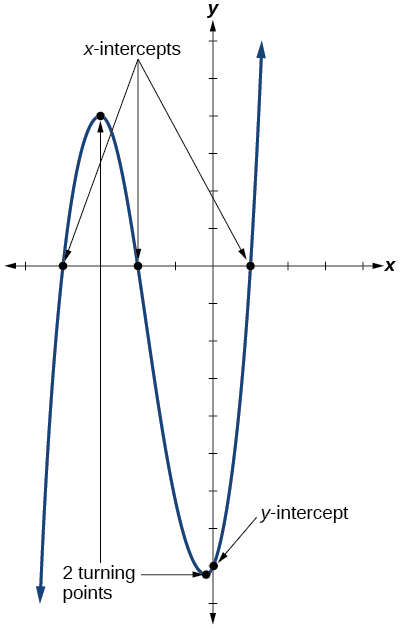
Definción: Intercepciones y Puntos de Inflexión de Funciones Polinómicas
Un punto de inflexión de una gráfica es un punto en el que la gráfica cambia de dirección de aumentar a disminuir o disminuir a aumentar. El\(y\) -intercept es el punto en el que la función tiene un valor de entrada de cero. Las\(x\) -intercepciones son los puntos en los que el valor de salida es cero.
![]() Dada una función polinómica, determinar las intercepciones.
Dada una función polinómica, determinar las intercepciones.
- Determine la\(y\) -intercepción estableciendo\(x=0\) y encontrando el valor de salida correspondiente.
- Determine las\(x\) -intercepciones resolviendo los valores de entrada que arrojan un valor de salida de cero.
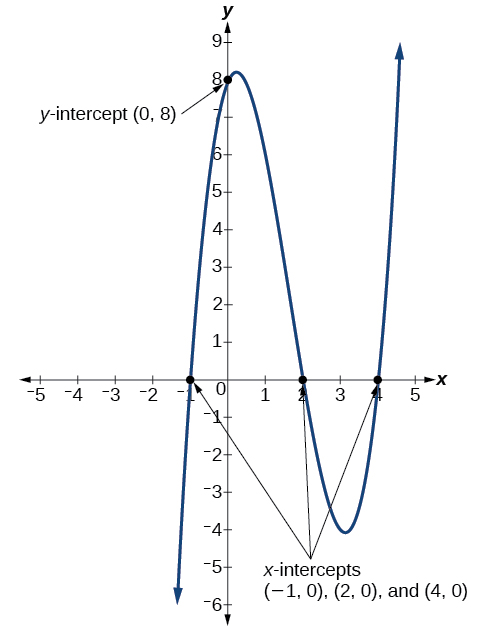
Ejemplo\(\PageIndex{8}\): Determining the Intercepts of a Polynomial Function
Dada la función polinomial\(f(x)=(x−2)(x+1)(x−4)\), escrita en forma factorizada para su conveniencia, determine las\(y\) - y\(x\) -intercepciones.
Solución
La\(y\) -intercepción ocurre cuando la entrada es cero, por lo que sustituya 0 por\(x\).
\[ \begin{align*}f(0)&=(0−2)(0+1)(0−4) \\ &=(−2)(1)(−4) \\ &=8 \end{align*}\]
El\(y\) -intercepto es\((0,8)\).
Las\(x\) -intercepciones ocurren cuando la salida es cero.
\[ 0=(x−2)(x+1)(x−4) \nonumber \]
\[\begin{align*} x−2&=0 & &\text{or} & x+1&=0 & &\text{or} & x−4&=0 \\ x&=2 & &\text{or} & x&=−1 & &\text{or} & x&=4 \end{align*}\]
Los\(x\) -interceptos son\((2,0)\),\((–1,0)\), y\((4,0)\).
Podemos ver estas intercepciones en la gráfica de la función mostrada en la Figura\(\PageIndex{11}\).
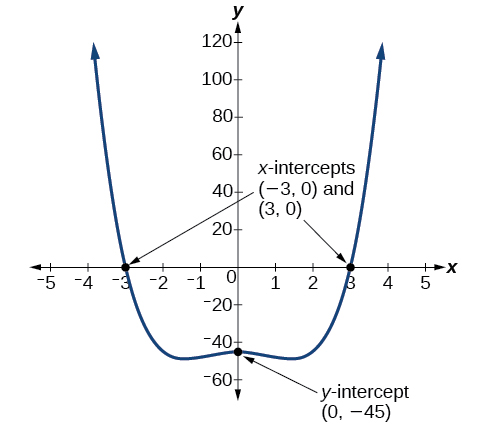
Ejemplo\(\PageIndex{9}\): Determining the Intercepts of a Polynomial Function with Factoring
Dada la función polinomial\(f(x)=x^4−4x^2−45\), determinar las\(y\) - y\(x\) -intercepciones.
Solución
La\(y\) -intercepción ocurre cuando la entrada es cero.
\[ \begin{align*} f(0) &=(0)^4−4(0)^2−45 \\[4pt] &=−45 \end{align*}\]
El\(y\) -intercepto es\((0,−45)\).
Las\(x\) -intercepciones ocurren cuando la salida es cero. Para determinar cuándo la salida es cero, necesitaremos factorial el polinomio.
\ [\ begin {alinear*} f (x) &=x^4−4x^2−45\\ &= (x^2−9) (x^2+5)\\ &= (x−3) (x+3) (x^2+5)
\ end {align*}\]
\[0=(x−3)(x+3)(x^2+5) \nonumber\]
\[\begin{align*} x−3&=0 & &\text{or} & x+3&=0 & &\text{or} & x^2+5&=0 \\ x&=3 & &\text{or} & x&=−3 & &\text{or} &\text{(no real solution)} \end{align*}\]
Los\(x\) -interceptos son\((3,0)\) y\((–3,0)\).
Podemos ver estas intercepciones en la gráfica de la función mostrada en la Figura\(\PageIndex{12}\). Podemos ver que la función es par porque\(f(x)=f(−x)\).
Ejercicio\(\PageIndex{5}\)
\(\PageIndex{5}\): Dada la función polinómica\(f(x)=2x^3−6x^2−20x\), determinar las\(y\) - y\(x\) -intercepciones.
- Solución
-
\(y\)-interceptar\((0,0)\);\(x\) -intercepta\((0,0)\)\((–2,0)\), y\((5,0)\)
Comparando Gráficas Lisas y Continuas
El grado de una función polinómica nos ayuda a determinar el número de\(x\) intercepciones y el número de puntos de inflexión. Una función polinómica de\(n^\text{th}\) grado es producto de\(n\) factores, por lo que tendrá como máximo\(n\) raíces o ceros, o\(x\) -intercepciones. La gráfica de la función polinómica de grado\(n\) debe tener como máximo puntos de\(n–1\) inflexión. Esto significa que la gráfica tiene como máximo un punto de inflexión menos que el grado del polinomio o uno menos que el número de factores.
Una función continua no tiene roturas en su gráfica: la gráfica se puede dibujar sin levantar la pluma del papel. Una curva suave es una gráfica que no tiene esquinas afiladas. Los puntos de inflexión de una gráfica suave siempre deben ocurrir en curvas redondeadas. Las gráficas de las funciones polinómicas son continuas y suaves.
Intercepciones y puntos de inflexión de polinomios
Un polinomio de grado\(n\) tendrá, a lo sumo,\(n\)\(x\) -intercepciones y puntos de\(n−1\) inflexión.
Ejemplo\(\PageIndex{10}\): Determining the Number of Intercepts and Turning Points of a Polynomial
Sin graficar la función, determinar el comportamiento local de la función mediante la búsqueda del número máximo de\(x\) -intercepciones y puntos de inflexión para\(f(x)=−3x^{10}+4x^7−x^4+2x^3\).
Solución
El polinomio tiene un grado de 10, por lo que hay a lo sumo\(n\)\(x\) -intercepciones y a lo sumo puntos de\(n−1\) inflexión.
Ejercicio\(\PageIndex{6}\)
Sin graficar la función, determine el número máximo\(x\) de intercepciones y puntos de inflexión para\(f(x)=108−13x^9−8x^4+14x^{12}+2x^3\)
- Contestar
-
Hay como máximo 12\(x\) intercepciones y como máximo 11 puntos de inflexión.
Ejemplo\(\PageIndex{11}\): Drawing Conclusions about a Polynomial Function from the Graph
¿Qué podemos concluir sobre el polinomio representado por la gráfica mostrada en la Figura a\(\PageIndex{12}\) partir de sus intercepciones y puntos de inflexión?
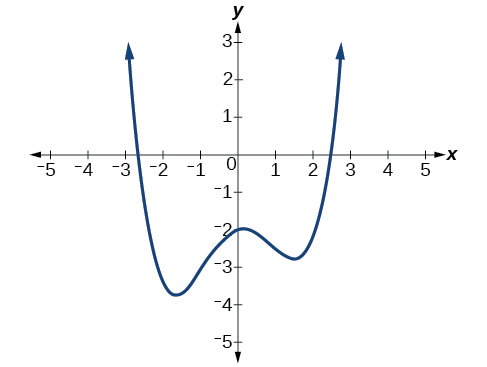
Solución
El comportamiento final de la gráfica nos dice que esta es la gráfica de un polinomio de grado par. Ver Figura\(\PageIndex{14}\).
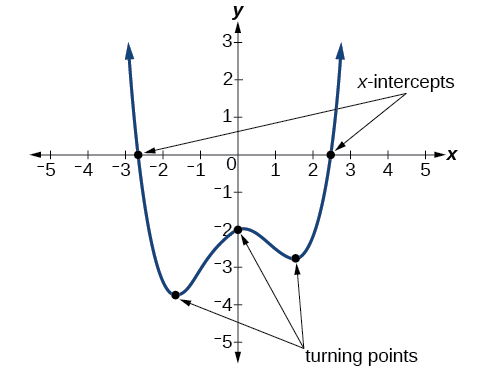
La gráfica tiene 2\(x\) intercepciones, lo que sugiere un grado de 2 o mayor, y 3 puntos de inflexión, lo que sugiere un grado de 4 o mayor. En base a esto, sería razonable concluir que el grado es parejo y al menos 4.
Ejercicio\(\PageIndex{7}\)
¿Qué podemos concluir sobre el polinomio representado por la gráfica mostrada en la Figura a\(\PageIndex{15}\) partir de sus intercepciones y puntos de inflexión?
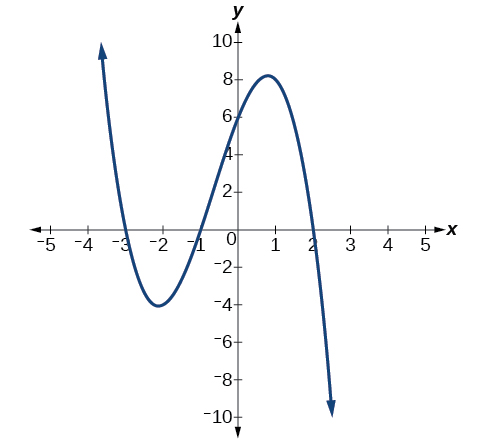
Figura\(\PageIndex{15}\).
- Contestar
-
Agrega textos aquí. No elimine primero este texto.
Solución
El comportamiento final indica una función polinómica de grado impar; hay 3\(x\) -intercepciones y 2 puntos de inflexión, por lo que el grado es impar y al menos 3. Por el comportamiento final, sabemos que el coeficiente de plomo debe ser negativo.
Ejemplo\(\PageIndex{12}\): Drawing Conclusions about a Polynomial Function from the Factors
Dada la función\(f(x)=−4x(x+3)(x−4)\), determinar el comportamiento local.
Solución
El\(y\) -intercepto se encuentra evaluando\(f(0)\).
\[\begin{align*} f(0)&=−4(0)(0+3)(0−4) \\ &=0 \end{align*}\]
El\(y\) -intercepto es\((0,0)\).
Las\(x\) -intercepciones se encuentran determinando los ceros de la función.
\[\begin{align*} 0&=-4x(x+3)(x-4) \\ x&=0 & &\text{or} & x+3&=0 & &\text{or} & x-4&=0 \\ x&=0 & &\text{or} & x&=−3 & &\text{or} & x&=4 \end{align*}\]
Los\(x\) -interceptos son\((0,0)\),\((–3,0)\), y\((4,0)\).
El grado es 3 por lo que la gráfica tiene como máximo 2 puntos de inflexión.
Ejercicio\(\PageIndex{8}\)
Dada la función\(f(x)=0.2(x−2)(x+1)(x−5)\), determinar el comportamiento local.
- Contestar
-
Las\(x\) -intercepciones son\((2,0)\), y\((−1,0)\)\((5,0)\), la\(y\) -intercepción es\((0,2)\), y la gráfica tiene como máximo 2 puntos de inflexión.
Ecuaciones Clave
- forma general de una función polinómica:\(f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0\)
Conceptos clave
- Una función de potencia es una base variable elevada a una potencia numérica.
- El comportamiento de una gráfica a medida que la entrada disminuye sin límite y aumenta sin límite se denomina comportamiento final.
- El comportamiento final depende de si el poder es par o impar.
- Una función polinómica es la suma de términos, cada uno de los cuales consiste en una función de potencia transformada con potencia positiva de número entero.
- El grado de una función polinómica es el mayor poder de la variable que ocurre en un polinomio. El término que contiene la mayor potencia de la variable se denomina término principal. El coeficiente del término principal se llama coeficiente principal.
- El comportamiento final de una función polinómica es el mismo que el comportamiento final de la función de potencia representada por el término principal de la función.
- Un polinomio de grado\(n\) tendrá a lo sumo\(n\)\(x\) -intercepciones y a lo sumo puntos de\(n−1\) inflexión.
Glosario
coeficiente
un número real distinto de cero que se multiplica por una variable elevada a un exponente (solo el factor numérico es el coeficiente)
función continua
una función cuya gráfica se puede dibujar sin levantar la pluma del papel porque no hay roturas en la gráfica
grado
la mayor potencia de la variable que ocurre en un polinomio
comportamiento final
el comportamiento de la gráfica de una función a medida que la entrada disminuye sin límite y aumenta sin límite
coeficiente principal
el coeficiente del término principal
término principal
el término que contiene la mayor potencia de la variable
función polinómica
una función que consiste en cero o la suma de un número finito de términos distintos de cero, cada uno de los cuales es un producto de un número, llamado coeficiente del término, y una variable elevada a una potencia entera no negativa.
función de potencia
una función que se puede representar en la forma\(f(x)=kx^p\) donde\(k\) es una constante, la base es una variable, y el exponente,\(p\), es una constante
curva suave
una gráfica sin esquinas afiladas
término de una función polinómica
cualquiera\(a_ix^i\) de una función polinómica en la forma\(f(x)=a_nx^n+a_{n-1}x^{n-1}...+a_2x^2+a_1x+a_0\)
punto de inflexión
la ubicación en la que la gráfica de una función cambia de dirección


