3.2: Funciones cuadráticas

Última actualización
Guardar como PDF

Page ID: 121461

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Reconocer las características de las parábolas.
Entender cómo se relaciona la gráfica de una parábola con su función cuadrática.
Determinar el valor mínimo o máximo de una función cuadrática.
Resolver problemas relacionados con el valor mínimo o máximo de una función cuadrática.

Las antenas curvas, como las que se muestran en la Figura$\PageIndex{1}$, se utilizan comúnmente para enfocar microondas y ondas de radio para transmitir señales de televisión y teléfono, así como la comunicación por satélite y naves espaciales. La sección transversal de la antena tiene la forma de una parábola, la cual puede describirse mediante una función cuadrática.

$Platos parabólicas.$

Figura$\PageIndex{1}$: Una serie de antenas parabólicas. (crédito: Matthew Colvin de Valle, Flickr)

En esta sección, investigaremos las funciones cuadráticas, que frecuentemente modelan problemas relacionados con el movimiento de área y proyectil. Trabajar con funciones cuadráticas puede ser menos complejo que trabajar con funciones de grado superior, por lo que brindan una buena oportunidad para un estudio detallado del comportamiento de la función.

Reconocer las características de las parábolas

La gráfica de una función cuadrática es una curva en forma de U llamada parábola. Una característica importante de la gráfica es que tiene un punto extremo, llamado vértice. Si la parábola se abre, el vértice representa el punto más bajo de la gráfica, o el valor mínimo de la función cuadrática. Si la parábola se abre hacia abajo, el vértice representa el punto más alto de la gráfica, o el valor máximo. En cualquier caso, el vértice es un punto de inflexión en la gráfica. La gráfica también es simétrica con una línea vertical dibujada a través del vértice, llamada eje de simetría. Estas características se ilustran en la Figura$\PageIndex{2}$.

alt — Figura$\PageIndex{2}$: Gráfico de una parábola que muestra dónde están las$y$ intercepciones$x$ e, vértice y eje de simetría.

La intercepción y es el punto en el que la parábola cruza el$y$ eje. Las intercepciones x son los puntos en los que la parábola cruza el$x$ eje. Si existen, las intercepciones x representan los ceros, o raíces, de la función cuadrática, los valores de$x$ a la cual$y=0$.

Ejemplo$\PageIndex{1}$: Identifying the Characteristics of a Parabola

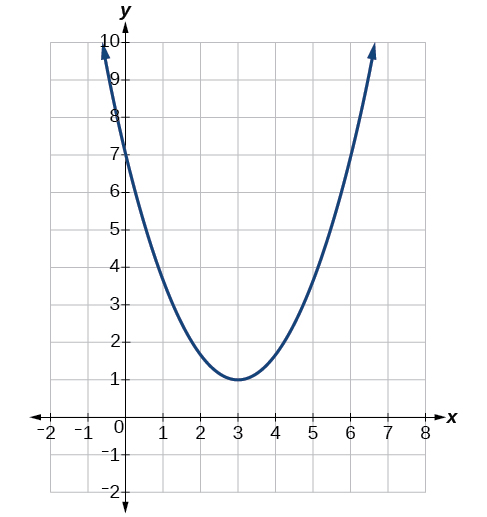
Determinar el vértice, eje de simetría, ceros e intersección y de la parábola mostrada en la Figura$\PageIndex{3}$.

Gráfico de una parábola con un vértice en (3, 1) y una intercepción y en (0, 7). — Figura$\PageIndex{3}$.

Solución

El vértice es el punto de inflexión de la gráfica. Podemos ver que el vértice está en$(3,1)$. Debido a que esta parábola se abre hacia arriba, el eje de simetría es la línea vertical que cruza la parábola en el vértice. Entonces el eje de simetría es$x=3$. Esta parábola no cruza el eje x, por lo que no tiene ceros. Cruza el$y$ eje en$(0,7)$ así que esta es la intercepción y.

Comprender cómo se relacionan las gráficas de las parábolas con sus funciones cuadráticas

La forma general de una función cuadrática presenta la función en la forma

\[f(x)=ax^2+bx+c\]

donde$a$,$b$, y$c$ son números reales y$a{\neq}0$. Si$a>0$, la parábola se abre hacia arriba. Si$a<0$, la parábola se abre hacia abajo. Podemos usar la forma general de una parábola para encontrar la ecuación para el eje de simetría.

El eje de simetría está definido por$x=−\frac{b}{2a}$. Si usamos la fórmula cuadrática,$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$, para resolver$ax^2+bx+c=0$ para las intercepciones x, o ceros, encontramos que el valor de$x$ a mitad de camino entre ellos es siempre$x=−\frac{b}{2a}$, la ecuación para el eje de simetría.

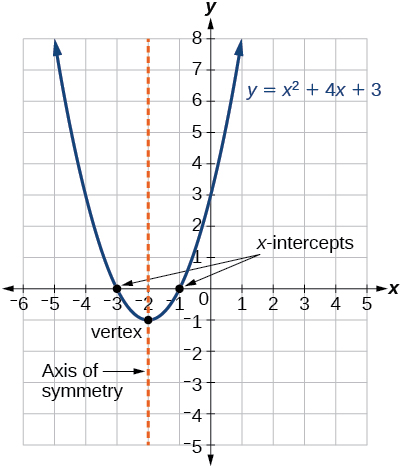
La figura$\PageIndex{4}$ representa la gráfica de la función cuadrática escrita en forma general como$y=x^2+4x+3$. En esta forma,$a=1$,$b=4$, y$c=3$. Porque$a>0$, la parábola se abre hacia arriba. El eje de simetría es$x=−\frac{4}{2(1)}=−2$. Esto también tiene sentido porque podemos ver en la gráfica que la línea vertical$x=−2$ divide la gráfica por la mitad. El vértice siempre ocurre a lo largo del eje de simetría. Para una parábola que se abre hacia arriba, el vértice se presenta en el punto más bajo de la gráfica, en esta instancia,$(−2,−1)$. Las intercepciones x, aquellos puntos donde la parábola cruza el eje x, ocurren en$(−3,0)$ y$(−1,0)$.

Gráfico de una parábola que muestra dónde están las interceptaciones x e y, vértice y eje de simetría para la función y=x^2+4x+3. — Figura$\PageIndex{4}$: Gráfico de una parábola que muestra dónde están las$y$ intercepciones$x$ e, vértice y eje de simetría para la función$y=x^2+4x+3$.

La forma estándar de una función cuadrática presenta la función en la forma

\[f(x)=a(x−h)^2+k\]

donde$(h, k)$ está el vértice. Debido a que el vértice aparece en la forma estándar de la función cuadrática, esta forma también se conoce como la forma de vértice de una función cuadrática.

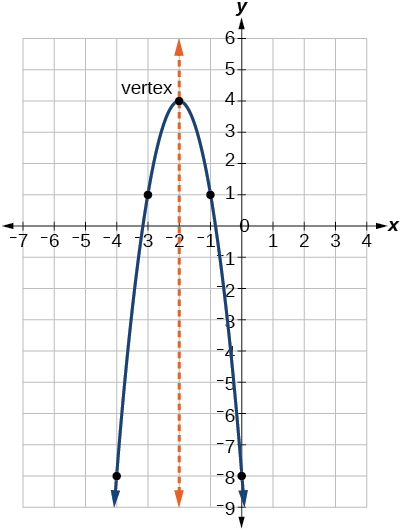
Al igual que con la forma general, si$a>0$, la parábola se abre hacia arriba y el vértice es mínimo. Si$a<0$, la parábola se abre hacia abajo, y el vértice es un máximo. La figura$\PageIndex{5}$ representa la gráfica de la función cuadrática escrita en forma estándar como$y=−3(x+2)^2+4$. Ya que$x–h=x+2$ en este ejemplo,$h=–2$. En esta forma,$a=−3$,$h=−2$, y$k=4$. Porque$a<0$, la parábola se abre hacia abajo. El vértice está en$(−2, 4)$.

Gráfico de una parábola que muestra dónde están las intercepciones x e y, vértice y eje de simetría, para la función y=-3 (x+2) ^2+4. — Figura$\PageIndex{5}$: Gráfico de una parábola que muestra dónde están las$y$ intercepciones$x$ e, vértice y eje de simetría para la función$y=-3(x+2)^2+4$.

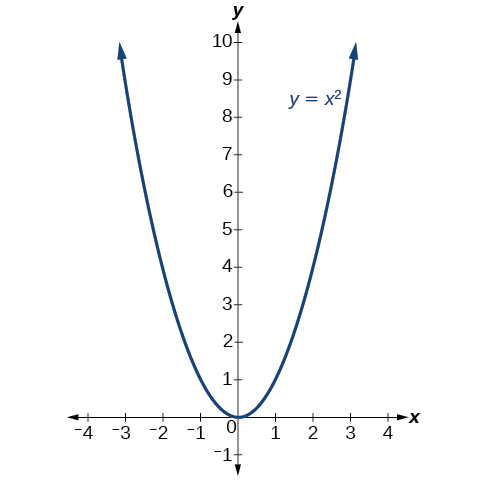
La forma estándar es útil para determinar cómo se transforma la gráfica a partir de la gráfica de$y=x^2$. La figura$\PageIndex{6}$ es la gráfica de esta función básica.

Si$k>0$, la gráfica se desplaza hacia arriba, mientras que si$k<0$, la gráfica se desplaza hacia abajo. En la Figura$\PageIndex{5}$,$k>0$, por lo que la gráfica se desplaza 4 unidades hacia arriba. Si$h>0$, la gráfica se desplaza hacia la derecha y si$h<0$, la gráfica se desplaza hacia la izquierda. En la Figura$\PageIndex{5}$,$h<0$, por lo que la gráfica se desplaza 2 unidades a la izquierda. La magnitud de$a$ indica el tramo de la gráfica. Si$|a|>1$, el punto asociado a un valor x particular se desplaza más lejos del eje x, por lo que la gráfica parece volverse más estrecha, y hay un estiramiento vertical. Pero si$|a|<1$, el punto asociado a un determinado valor x se desplaza más cerca del eje x, entonces la gráfica parece hacerse más amplia, pero de hecho hay una compresión vertical. En Figura$\PageIndex{5}$,$|a|>1$, así la gráfica se vuelve más estrecha.

La forma estándar y la forma general son métodos equivalentes para describir la misma función. Esto lo podemos ver expandiendo la forma general y configurándola igual a la forma estándar.

\[\begin{align*} a(x−h)^2+k &= ax^2+bx+c \\[4pt] ax^2−2ahx+(ah^2+k)&=ax^2+bx+c \end{align*} \]

Para que los términos lineales sean iguales, los coeficientes deben ser iguales.

\[–2ah=b \text{, so } h=−\dfrac{b}{2a}. \nonumber\]

Este es el eje de simetría que definimos anteriormente. Estableciendo los términos constantes iguales:

\[\begin{align*} ah^2+k&=c \\ k&=c−ah^2 \\ &=c−a\cdot\Big(-\dfrac{b}{2a}\Big)^2 \\ &=c−\dfrac{b^2}{4a} \end{align*}\]

En la práctica, sin embargo, suele ser más fácil recordar que$k$ es el valor de salida de la función cuando la entrada es$h$, entonces$f(h)=k$.

Definiciones: Formas de funciones cuadráticas

Una función cuadrática es una función del grado dos. La gráfica de una función cuadrática es una parábola.

La forma general de una función cuadrática es$f(x)=ax^2+bx+c$ donde$a$,$b$, y$c$ son números reales y$a{\neq}0$.
La forma estándar de una función cuadrática es$f(x)=a(x−h)^2+k$.
El vértice$(h,k)$ se encuentra en\[h=–\dfrac{b}{2a},\;k=f(h)=f(\dfrac{−b}{2a}).\]

CÓMO: Escribir una función cuadrática en forma general

Dada una gráfica de una función cuadrática, escribir la ecuación de la función en forma general.

Identificar el desplazamiento horizontal de la parábola; este valor es$h$. Identificar el desplazamiento vertical de la parábola; este valor es$k$.
Sustituir los valores del desplazamiento horizontal y vertical por$h$ y$k$. en la función$f(x)=a(x–h)^2+k$.
Sustituir los valores de cualquier punto, que no sea el vértice, en la gráfica de la parábola por$x$ y$f(x)$.
Resolver para el factor de estiramiento,$|a|$.
Si la parábola se abre,$a>0$. Si la parábola se abre hacia abajo,$a<0$ ya que esto significa que la gráfica se reflejó alrededor del eje x.
Ampliar y simplificar para escribir en forma general.

Ejemplo$\PageIndex{2}$: Writing the Equation of a Quadratic Function from the Graph

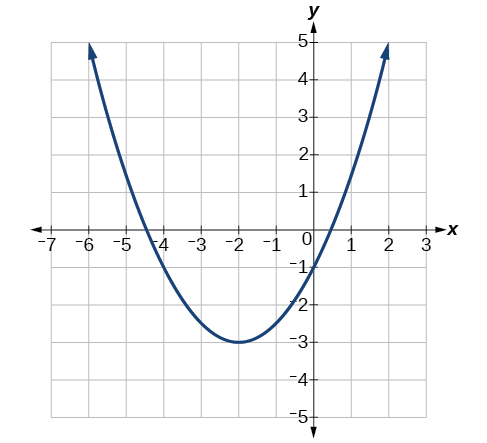
Escriba una ecuación para la función cuadrática$g$ en Figura$\PageIndex{7}$ como una transformación de$f(x)=x^2$, y luego expanda la fórmula, y simplifique los términos para escribir la ecuación en forma general.

alt — Figura$\PageIndex{7}$: Gráfico de una parábola con su vértice en$(-2, -3)$.

Solución

Podemos ver la gráfica de$g$ es la gráfica de$f(x)=x^2$ desplazada a la izquierda 2 y hacia abajo 3, dando una fórmula en la forma$g(x)=a(x+2)^2–3$.

Sustituyendo las coordenadas de un punto en la curva, como$(0,−1)$, podemos resolver por el factor de estiramiento.

\[\begin{align} −1&=a(0+2)^2−3 \\ 2&=4a \\ a&=\dfrac{1}{2} \end{align}\]

En forma estándar, el modelo algebraico para esta gráfica es$g(x)=\dfrac{1}{2}(x+2)^2–3$.

Para escribir esto en forma polinómica general, podemos ampliar la fórmula y simplificar términos.

\[\begin{align} g(x)&=\dfrac{1}{2}(x+2)^2−3 \\ &=\dfrac{1}{2}(x+2)(x+2)−3 \\ &=\dfrac{1}{2}(x^2+4x+4)−3 \\ &=\dfrac{1}{2}x^2+2x+2−3 \\ &=\dfrac{1}{2}x^2+2x−1 \end{align}\]

Observe que los desplazamientos horizontales y verticales de la gráfica básica de la función cuadrática determinan la ubicación del vértice de la parábola; el vértice no se ve afectado por estiramientos y compresiones.

Análisis

Podemos verificar nuestro trabajo usando la función de tabla en una utilidad gráfica. Primero entra$\mathrm{Y1=\dfrac{1}{2}(x+2)^2−3}$. A continuación, seleccione$\mathrm{TBLSET}$, luego use$\mathrm{TblStart=–6}$ y$\mathrm{ΔTbl = 2}$, y seleccione$\mathrm{TABLE}$. Ver Tabla$\PageIndex{1}$

Mesa$\PageIndex{1}$
$x$	-6	-4	-2	0	2
$y$	-5	-1	-3	-1	5

Los pares ordenados en la tabla corresponden a puntos en la gráfica.

Ejercicio$\PageIndex{2}$

Se ha superpuesto una cuadrícula de coordenadas sobre la trayectoria cuadrática de una básquetbol en la Figura$\PageIndex{8}$. Encuentra una ecuación para el camino de la pelota. ¿El tirador hace la canasta?

$alt$

Figura$\PageIndex{8}$: Detener la imagen moteada de un niño lanzando una básquetbol en un aro para mostrar la curva parabólica que realiza.
(crédito: modificación de obra por Dan Meyer)

Contestar: El camino pasa por el origen y tiene vértice en$(−4, 7)$, entonces$h(x)=–\frac{7}{16}(x+4)^2+7$. Para hacer el tiro,$h(−7.5)$ necesitaría ser alrededor de 4 pero$h(–7.5){\approx}1.64$; él no lo logra.

$alt$ Dada una función cuadrática en forma general, encuentra el vértice de la parábola.

Identificar$a$,$b$, y$c$.
Encontrar$h$, la coordenada x del vértice, sustituyendo$a$ y$b$ en$h=–\frac{b}{2a}$.
Encontrar$k$, la coordenada y del vértice, evaluando$k=f(h)=f\Big(−\frac{b}{2a}\Big)$.

Ejemplo$\PageIndex{3}$: Finding the Vertex of a Quadratic Function

Encuentra el vértice de la función cuadrática$f(x)=2x^2–6x+7$. Reescribir la cuadrática en forma estándar (forma de vértice).

Solución

La coordenada horizontal del vértice estará en

\[\begin{align} h&=–\dfrac{b}{2a} \\ &=-\dfrac{-6}{2(2)} \\ &=\dfrac{6}{4} \\ &=\dfrac{3}{2}\end{align}\]

La coordenada vertical del vértice estará en

\[\begin{align} k&=f(h) \\ &=f\Big(\dfrac{3}{2}\Big) \\ &=2\Big(\dfrac{3}{2}\Big)^2−6\Big(\dfrac{3}{2}\Big)+7 \\ &=\dfrac{5}{2} \end{align}\]

Reescribiendo en forma estándar, el factor de estiramiento será el mismo que$a$ en la cuadrática original.

\[f(x)=ax^2+bx+c \\ f(x)=2x^2−6x+7\]

Usando el vértice para determinar los desplazamientos,

\[f(x)=2\Big(x–\dfrac{3}{2}\Big)^2+\dfrac{5}{2}\]

Análisis

Una razón por la que quizás queramos identificar el vértice de la parábola es que este punto nos informará cuál es el valor máximo o mínimo de la función$(k)$,, y dónde ocurre,$(h)$.

Ejercicio$\PageIndex{3}$

Dada la ecuación$g(x)=13+x^2−6x$, escribir la ecuación en forma general y luego en forma estándar.

Contestar: $g(x)=x^2−6x+13$en forma general;$g(x)=(x−3)^2+4$ en forma estándar.

Encontrar el dominio y el rango de una función cuadrática

Cualquier número puede ser el valor de entrada de una función cuadrática. Por lo tanto, el dominio de cualquier función cuadrática es todo números reales. Debido a que las parábolas tienen un punto máximo o mínimo, el rango está restringido. Dado que el vértice de una parábola será un máximo o un mínimo, el rango consistirá en todos los valores y mayores o iguales a la coordenada y en el punto de inflexión o menores o iguales a la coordenada y en el punto de inflexión, dependiendo de si la parábola se abre hacia arriba o hacia abajo.

Definición: Dominio y rango de una función cuadrática

El dominio de cualquier función cuadrática es todo números reales.

El rango de una función cuadrática escrita en forma general$f(x)=ax^2+bx+c$ con un$a$ valor positivo es$f(x){\geq}f ( −\frac{b}{2a}\Big)$, o$[ f(−\frac{b}{2a}),∞ ) $; el rango de una función cuadrática escrita en forma general con un negativo a valor es$f(x) \leq f(−\frac{b}{2a})$, o$(−∞,f(−\frac{b}{2a})]$.

El rango de una función cuadrática escrita en forma estándar$f(x)=a(x−h)^2+k$ con un$a$ valor positivo es$f(x) \geq k;$ el rango de una función cuadrática escrita en forma estándar con un$a$ valor negativo es$f(x) \leq k$.

$alt$ Dada una función cuadrática, encuentra el dominio y el rango.

Identificar el dominio de cualquier función cuadrática como todos los números reales.
Determinar si$a$ es positivo o negativo. Si$a$ es positivo, la parábola tiene un mínimo. Si$a$ es negativo, la parábola tiene un máximo.
Determinar el valor máximo o mínimo de la parábola,$k$.
Si la parábola tiene un mínimo, el rango viene dado por$f(x){\geq}k$, o$\left[k,\infty\right)$. Si la parábola tiene un máximo, el rango viene dado por$f(x){\leq}k$, o$\left(−\infty,k\right]$.

Ejemplo$\PageIndex{4}$: Finding the Domain and Range of a Quadratic Function

Encuentra el dominio y la gama de$f(x)=−5x^2+9x−1$.

Solución

Como con cualquier función cuadrática, el dominio es todo números reales.

Porque$a$ es negativo, la parábola se abre hacia abajo y tiene un valor máximo. Tenemos que determinar el valor máximo. Podemos comenzar por encontrar el valor x del vértice.

\[\begin{align} h&=−\dfrac{b}{2a} \\ &=−\dfrac{9}{2(-5)} \\ &=\dfrac{9}{10} \end{align}\]

El valor máximo viene dado por$f(h)$.

\[\begin{align} f(\dfrac{9}{10})&=5(\dfrac{9}{10})^2+9(\dfrac{9}{10})-1 \\&= \dfrac{61}{20}\end{align}\]

El rango es$f(x){\leq}\frac{61}{20}$, o$\left(−\infty,\frac{61}{20}\right]$.

Ejercicio$\PageIndex{4}$

Encuentra el dominio y la gama de$f(x)=2\Big(x−\frac{4}{7}\Big)^2+\frac{8}{11}$.

Contestar: El dominio es todo números reales. El rango es$f(x){\geq}\frac{8}{11}$, o$\left[\frac{8}{11},\infty\right)$.

Determinación de los valores máximos y mínimos de las funciones cuadráticas

La salida de la función cuadrática en el vértice es el valor máximo o mínimo de la función, dependiendo de la orientación de la parábola. Podemos ver los valores máximo y mínimo en la Figura$\PageIndex{9}$.

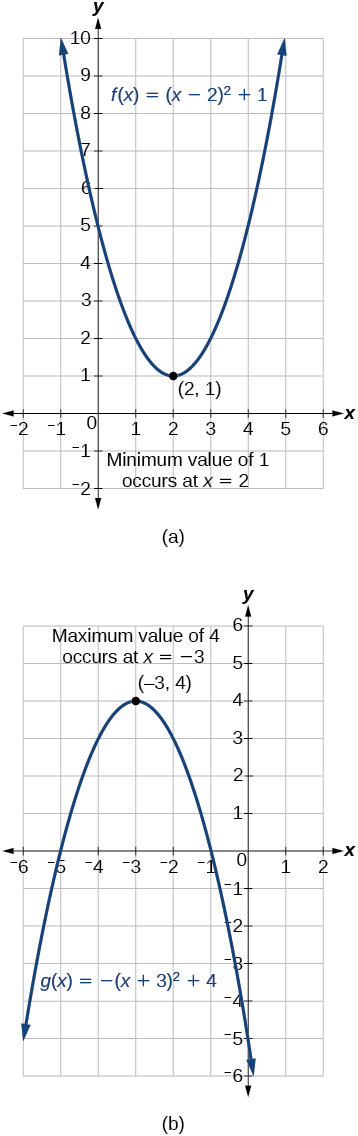
Dos gráficas donde la primera gráfica muestra el valor máximo para f (x) = (x-2) ^2+1 que ocurre en (2, 1) y la segunda gráfica muestra el valor mínimo para g (x) =- (x+3) ^2+4 que ocurre en (-3, 4). — Figura$\PageIndex{9}$: Mínimo y máximo de dos funciones cuadráticas.

Hay muchos escenarios del mundo real que implican encontrar el valor máximo o mínimo de una función cuadrática, como aplicaciones que involucran área e ingresos.

Ejemplo$\PageIndex{5}$: Finding the Maximum Value of a Quadratic Function

Un granjero de patio trasero quiere encerrar un espacio rectangular para un nuevo jardín dentro de su patio trasero cercado. Ella ha comprado 80 pies de cercado de alambre para encerrar tres lados, y utilizará una sección de la cerca del patio trasero como el cuarto lado.

Encuentre una fórmula para el área encerrada por la barda si los lados del cercado perpendiculares a la barda existente tienen longitud$L$.
¿Qué dimensiones debería hacer su jardín para maximizar el área cerrada?

Solución

Usemos un diagrama como Figura$\PageIndex{10}$ para registrar la información dada. También es útil introducir una variable temporal,$W$, para representar el ancho del jardín y la longitud de la sección de la cerca paralela a la cerca del patio trasero.

Figura$\PageIndex{10}$: Diagrama del jardín y el patio trasero.

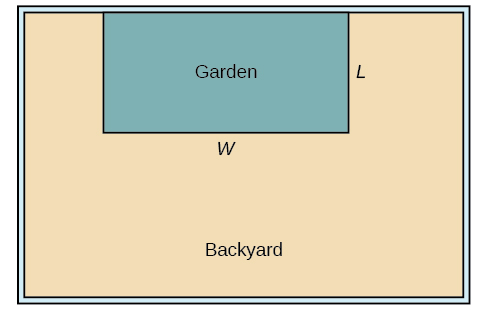
a. sabemos que solo tenemos 80 pies de barda disponibles, y$L+W+L=80$, o más simplemente,$2L+W=80$. Esto nos permite representar el ancho,$W$, en términos de$L$.

\[W=80−2L\]

Ahora estamos listos para escribir una ecuación para el área que encierra la barda. Sabemos que el área de un rectángulo es longitud multiplicada por ancho, entonces

\[\begin{align} A&=LW=L(80−2L) \\ A(L)&=80L−2L^2 \end{align}\]

Esta fórmula representa el área de la barda en términos de la longitud variable$L$. La función, escrita en forma general, es

\[A(L)=−2L^2+80L\].

El cuadrático tiene un coeficiente inicial negativo, por lo que la gráfica se abrirá hacia abajo, y el vértice será el valor máximo para el área. Al encontrar el vértice, debemos tener cuidado porque la ecuación no está escrita en forma polinómica estándar con potencias decrecientes. Es por ello que reescribimos la función en forma general arriba. Ya que$a$ es el coeficiente del término cuadrado,$a=−2$,$b=80$, y$c=0$.

Para encontrar el vértice:

\[\begin{align} h& =−\dfrac{80}{2(−2)} &k&=A(20) \\ &=20 & \text{and} \;\;\;\; &=80(20)−2(20)^2 \\ &&&=800 \end{align}\]

El valor máximo de la función es un área de 800 pies cuadrados, lo que ocurre cuando$L=20$ los pies. Cuando los lados más cortos son de 20 pies, quedan 40 pies de cercado para el lado más largo. Para maximizar el área, debe encerrar el jardín para que los dos lados más cortos tengan una longitud de 20 pies y el lado más largo paralelo a la cerca existente tenga una longitud de 40 pies.

Análisis

Este problema también podría resolverse graficando la función cuadrática. Podemos ver dónde ocurre el área máxima en una gráfica de la función cuadrática en la Figura$\PageIndex{11}$.

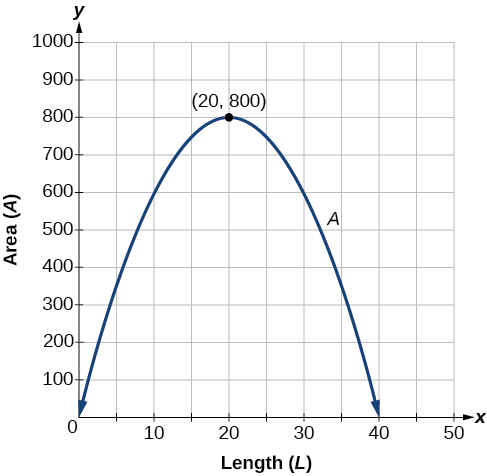
Gráfica de la función parabólica A (L) =-2L^2+80L, que el eje x se etiqueta Longitud (L) y el eje y se etiqueta Área (A). El vértice está en (20, 800). — Figura$\PageIndex{11}$: Gráfico de la función parabólica$A(L)=-2L^2+80L$

$alt$ Dada una aplicación que involucra ingresos, usa una ecuación cuadrática para encontrar el máximo.

Escribir una ecuación cuadrática para los ingresos.
Encuentra el vértice de la ecuación cuadrática.
Determinar el valor y del vértice.

Ejemplo$\PageIndex{6}$: Finding Maximum Revenue

El precio unitario de un artículo afecta su oferta y demanda. Es decir, si el precio unitario sube, la demanda del artículo generalmente disminuirá. Por ejemplo, un periódico local cuenta actualmente con 84 mil suscriptores a un cargo trimestral de 30 dólares. Estudios de mercado han sugerido que si los propietarios elevan el precio a 32 dólares, perderían 5 mil suscriptores. Suponiendo que las suscripciones están linealmente relacionadas con el precio, ¿qué precio debería cobrar el periódico por una suscripción trimestral para maximizar sus ingresos?

Solución

Los ingresos son la cantidad de dinero que aporta una empresa. En este caso, los ingresos se pueden encontrar multiplicando el precio por suscripción por el número de suscriptores, o cantidad. Podemos introducir variables,$p$ por precio por suscripción y$Q$ por cantidad, dándonos la ecuación$\text{Revenue}=pQ$.

Debido a que el número de suscriptores cambia con el precio, necesitamos encontrar una relación entre las variables. Sabemos que actualmente$p=30$ y$Q=84,000$. También sabemos que si el precio sube a 32 dólares, el periódico perdería 5 mil suscriptores, dando un segundo par de valores,$p=32$ y$Q=79,000$. De esto podemos encontrar una ecuación lineal que relaciona las dos cantidades. La pendiente será

\[\begin{align} m&=\dfrac{79,000−84,000}{32−30} \\ &=−\dfrac{5,000}{2} \\ &=−2,500 \end{align}\]

Esto nos dice que el periódico perderá 2,500 suscriptores por cada dólar que suban el precio. Entonces podemos resolver para la intercepción y.

\[\begin{align} Q&=−2500p+b &\text{Substitute in the point $Q=84,000$ and $p=30$} \\ 84,000&=−2500(30)+b &\text{Solve for $b$} \\ b&=159,000 \end{align}\]

Esto nos da la ecuación lineal que$Q=−2,500p+159,000$ relaciona costo y suscriptores. Ahora volvemos a nuestra ecuación de ingresos.

\[\begin{align} \text{Revenue}&=pQ \\ \text{Revenue}&=p(−2,500p+159,000) \\ \text{Revenue}&=−2,500p^2+159,000p \end{align}\]

Ahora tenemos una función cuadrática para los ingresos en función del cargo por suscripción. Para encontrar el precio que maximizará los ingresos para el periódico, podemos encontrar el vértice.

\[\begin{align} h&=−\dfrac{159,000}{2(−2,500)} \\ &=31.8 \end{align}\]

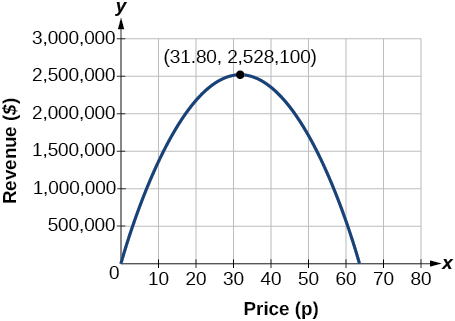
El modelo nos dice que los ingresos máximos se producirán si el periódico cobra 31.80 dólares por una suscripción. Para encontrar cuál es el ingreso máximo, evaluamos la función de ingresos.

\[\begin{align} \text{maximum revenue}&=−2,500(31.8)^2+159,000(31.8) \\ &=2,528,100 \end{align}\]

Análisis

Esto también podría resolverse graficando la cuadrática como en la Figura$\PageIndex{12}$. Podemos ver los ingresos máximos en una gráfica de la función cuadrática.

Gráfico de la función parabólica que el eje x está etiquetado Price (p) y el eje y está etiquetado Ingresos ($). El vértice está en (31.80, 258100). — Figura$\PageIndex{12}$: Gráfico de la función parabólica

Encontrar las intercepciones x e Y de una función cuadrática

Al igual que hicimos en los problemas de aplicación anteriores, también necesitamos encontrar intercepciones de ecuaciones cuadráticas para graficar parábolas. Recordemos que encontramos la intercepción y de una cuadrática evaluando la función en una entrada de cero, y encontramos las intercepciones x en ubicaciones donde la salida es cero. Observe en la Figura$\PageIndex{13}$ que el número de intercepciones x puede variar dependiendo de la ubicación de la gráfica.

<div data-mt-source="1" — Figura$\PageIndex{13}$: Número de intercepciones x de una parábola.

Figura$\PageIndex{13}$: Número de intercepciones x de una parábola.

$alt$ Dada una función cuadrática$f(x)$, encuentra las intercepciones y y x.

$f(0)$Evaluar para encontrar la intercepción y.
Resuelve la ecuación cuadrática$f(x)=0$ para encontrar las intercepciones x.

Ejemplo$\PageIndex{7}$: Finding the y- and x-Intercepts of a Parabola

Encuentra las intercepciones y y x de la cuadrática$f(x)=3x^2+5x−2$.

Solución

Encontramos la intercepción y evaluando$f(0)$.

\[\begin{align} f(0)&=3(0)^2+5(0)−2 \\ &=−2 \end{align}\]

Entonces la intercepción y está en$(0,−2)$.

Para las intercepciones x, encontramos todas las soluciones de$f(x)=0$.

\[0=3x^2+5x−2\]

En este caso, la cuadrática se puede factorizar fácilmente, proporcionando el método de solución más simple.

\[0=(3x−1)(x+2)\]

\[\begin{align} 0&=3x−1 & 0&=x+2 \\ x&= \frac{1}{3} &\text{or} \;\;\;\;\;\;\;\; x&=−2 \end{align}\]

Entonces las intercepciones x están en$(\frac{1}{3},0)$ y$(−2,0)$.

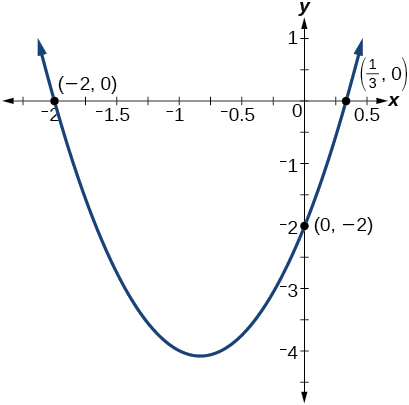
Análisis

Al graficar la función, podemos confirmar que la gráfica cruza el$y$ eje -en$(0,−2)$. También podemos confirmar que la gráfica cruza el eje x en$\Big(\frac{1}{3},0\Big)$ y$(−2,0)$. Ver Figura$\PageIndex{14}$.

Gráfica de una parábola que tiene las siguientes intercepciones (-2, 0), (1/3, 0) y (0, -2). — Figura$\PageIndex{14}$: Gráfica de una parábola.

Reescribir cuadráticas en forma estándar

En Ejemplo$\PageIndex{7}$, la cuadrática se resolvió fácilmente factorizando. No obstante, hay muchas cuadráticas que no se pueden factorizar. Podemos resolver estas cuadráticas reescribiéndolas primero en forma estándar.

$alt$ Dada una función cuadrática, encuentra las intercepciones x reescribiendo en forma estándar.

Sustituir a y$b$ en$h=−\frac{b}{2a}$.
Sustituir$x=h$ a la forma general de la función cuadrática a encontrar$k$.
Reescribir la cuadrática en forma estándar usando$h$ y$k$.
Resuelve para cuando la salida de la función será cero para encontrar las intercepciones x.

Ejemplo$\PageIndex{8}$: Finding the x-Intercepts of a Parabola

Encuentra las intercepciones x de la función cuadrática$f(x)=2x^2+4x−4$.

Solución

Comenzamos resolviendo para cuando la salida será cero.

\[0=2x^2+4x−4 \nonumber\]

Debido a que la cuadrática no es fácilmente factorizable en este caso, resolvemos para las intercepciones reescribiendo primero la cuadrática en forma estándar.

\[f(x)=a(x−h)^2+k\nonumber\]

Eso lo sabemos$a=2$. Entonces resolvemos para$h$ y$k$.

\[\begin{align*} h&=−\dfrac{b}{2a} & k&=f(−1) \\ &=−\dfrac{4}{2(2)} & &=2(−1)^2+4(−1)−4 \\ &=−1 & &=−6 \end{align*}\]

Entonces ahora podemos reescribir en forma estándar.

\[f(x)=2(x+1)^2−6\nonumber\]

Ahora podemos resolver para cuando la salida será cero.

\[\begin{align*} 0&=2(x+1)^2−6 \\ 6&=2(x+1)^2 \\ 3&=(x+1)^2 \\ x+1&={\pm}\sqrt{3} \\ x&=−1{\pm}\sqrt{3} \end{align*}\]

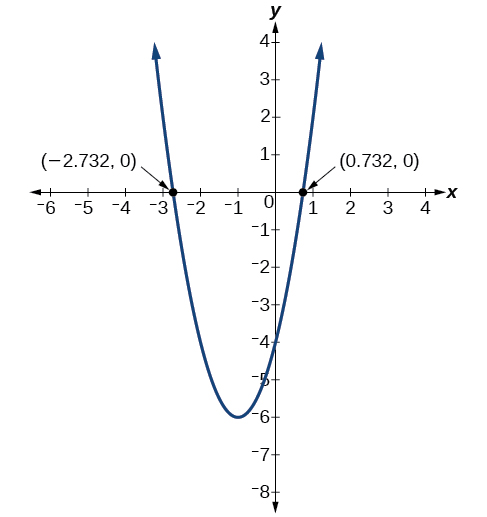
La gráfica tiene intercepciones x en$(−1−\sqrt{3},0)$ y$(−1+\sqrt{3},0)$.

Análisis

Podemos verificar nuestro trabajo graficando la función dada en una utilidad gráfica y observando las intercepciones x. Ver Figura$\PageIndex{15}$.

Gráfica de una parábola que tiene las siguientes intercepciones x (-2.732, 0) y (0.732, 0). — Figura$\PageIndex{15}$: Gráfica de una parábola que tiene las siguientes intercepciones x:$(-2.732, 0)$ y$(0.732, 0)$.

Ejercicio$\PageIndex{1}$

En Try It$\PageIndex{1}$, encontramos la forma estándar y general para la función$g(x)=13+x^2−6x$. Ahora encuentra las intercepciones y y x (si las hay).

Contestar: intercepción en y$(0, 13)$, Sin intercepciones x

Ejemplo$\PageIndex{9}$: Solving a Quadratic Equation with the Quadratic Formula

Resolver$x^2+x+2=0$.

Solución

Empecemos por escribir la fórmula cuadrática:$x=\frac{−b{\pm}\sqrt{b^2−4ac}}{2a}$.

Al aplicar la fórmula cuadrática, identificamos los coeficientes$a$,$b$ y$c$. Para la ecuación$x^2+x+2=0$, tenemos$a=1$,$b=1$, y$c=2$. Sustituyendo estos valores en la fórmula tenemos:

\[\begin{align*} x&=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a} \\ &=\dfrac{−1{\pm}\sqrt{1^2−4⋅1⋅(2)}}{2⋅1} \\ &=\dfrac{−1{\pm}\sqrt{1−8}}{2} \\ &=\dfrac{−1{\pm}\sqrt{−7}}{2} \\ &=\dfrac{−1{\pm}i\sqrt{7}}{2} \end{align*}\]

Las soluciones a la ecuación son$x=\frac{−1+i\sqrt{7}}{2}$ y$x=\frac{−1-i\sqrt{7}}{2}$ o$x=−\frac{1}{2}+\frac{i\sqrt{7}}{2}$ y$x=\frac{-1}{2}−\frac{i\sqrt{7}}{2}$.

Ejemplo$\PageIndex{10}$: Applying the Vertex and x-Intercepts of a Parabola

Se lanza una pelota hacia arriba desde lo alto de un edificio de 40 pies de altura a una velocidad de 80 pies por segundo. La altura de la pelota sobre el suelo puede ser modelada por la ecuación$H(t)=−16t^2+80t+40$.

¿Cuándo alcanza la bola la altura máxima?
¿Cuál es la altura máxima de la pelota?
¿Cuándo choca la pelota contra el suelo?

El balón alcanza la altura máxima en el vértice de la parábola.
\[\begin{align} h &= −\dfrac{80}{2(−16)} \\ &=\dfrac{80}{32} \\ &=\dfrac{5}{2} \\ & =2.5 \end{align}\]

El balón alcanza una altura máxima después de 2.5 segundos.

Para encontrar la altura máxima, encuentra la coordenada y del vértice de la parábola.
\[\begin{align} k &=H(−\dfrac{b}{2a}) \\ &=H(2.5) \\ &=−16(2.5)^2+80(2.5)+40 \\ &=140 \end{align}\]

El balón alcanza una altura máxima de 140 pies.

Para encontrar cuando la pelota golpea el suelo, necesitamos determinar cuando la altura es cero,$H(t)=0$.

Utilizamos la fórmula cuadrática.

\[\begin{align} t & =\dfrac{−80±\sqrt{80^2−4(−16)(40)}}{2(−16)} \\ & = \dfrac{−80±\sqrt{8960}}{−32} \end{align} \]

Debido a que la raíz cuadrada no simplifica muy bien, podemos usar una calculadora para aproximar los valores de las soluciones.

\[t=\dfrac{−80-\sqrt{8960}}{−32} ≈5.458 \text{ or }t=\dfrac{−80+\sqrt{8960}}{−32} ≈−0.458 \]

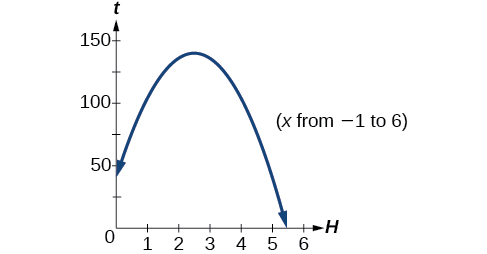
La segunda respuesta está fuera del dominio razonable de nuestro modelo, por lo que concluimos que la pelota golpeará el suelo después de aproximadamente 5.458 segundos. Ver Figura$\PageIndex{16}$.

$alt$ $\PageIndex{5}$: Una roca se lanza hacia arriba desde lo alto de un acantilado de 112 pies de altura con vista al océano a una velocidad de 96 pies por segundo. La altura de la roca sobre el océano puede ser modelada por la ecuación$H(t)=−16t^2+96t+112$.

¿Cuándo alcanza la roca la altura máxima?
¿Cuál es la altura máxima de la roca?
¿Cuándo golpea la roca al océano?

Solución

a. 3 segundos b. 256 pies c. 7 segundos

Ecuaciones Clave

forma general de una función cuadrática:$f(x)=ax^2+bx+c$
la fórmula cuadrática:$x=\dfrac{−b{\pm}\sqrt{b^2−4ac}}{2a}$
forma estándar de una función cuadrática:$f(x)=a(x−h)^2+k$

Conceptos clave

Una función polinómica de grado dos se denomina función cuadrática.
La gráfica de una función cuadrática es una parábola. Una parábola es una curva en forma de U que puede abrirse hacia arriba o hacia abajo.
El eje de simetría es la línea vertical que pasa por el vértice. Los ceros, o intercepciones x, son los puntos en los que la parábola cruza el eje x. La intercepción y es el punto en el que la parábola cruza el$y$ eje.
Las funciones cuadráticas a menudo se escriben en forma general. La forma estándar o vértice es útil para identificar fácilmente el vértice de una parábola. Cualquiera de las dos formas se puede escribir a partir de una gráfica.
El vértice se puede encontrar a partir de una ecuación que representa una función cuadrática.
El dominio de una función cuadrática es todo números reales. El rango varía con la función.
El valor mínimo o máximo de una función cuadrática viene dado por el valor y del vértice.
El valor mínimo o máximo de una función cuadrática se puede utilizar para determinar el rango de la función y para resolver muchos tipos de problemas del mundo real, incluidos problemas relacionados con el área y los ingresos.
Algunas ecuaciones cuadráticas deben resolverse usando la fórmula cuadrática.
El vértice y las intercepciones pueden ser identificados e interpretados para resolver problemas del mundo real.

Glosario

eje de simetría
una línea vertical dibujada a través del vértice de una parábola alrededor de la cual la parábola es simétrica; se define por$x=−\frac{b}{2a}$.

forma general de una función cuadrática
la función que describe una parábola, escrita en la forma$f(x)=ax^2+bx+c$, donde$a,b,$ y$c$ son números reales y a≠ 0.

forma estándar de una función cuadrática
la función que describe una parábola, escrita en la forma$f(x)=a(x−h)^2+k$, donde$(h, k)$ está el vértice.

vértice
el punto en el que una parábola cambia de dirección, correspondiente al valor mínimo o máximo de la función cuadrática

forma de vértice de una función cuadrática
otro nombre para la forma estándar de una función cuadrática

ceros
en una función dada, cuyos$x$ valores$y=0$, también llamados raíces

Search

Text Color

Text Size

Margin Size

Font Type

Mesa\(\PageIndex{1}\)
\(x\)	-6	-4	-2	0	2
\(y\)	-5	-1	-3	-1	5