3.8: Funciones inversas y radicales

Última actualización
Guardar como PDF

Page ID: 121439

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Objetivos de aprendizaje

En esta sección, usted:

Encuentra la inversa de una función polinómica invertible.
Restringir el dominio para encontrar la inversa de una función polinómica.

Un montículo de grava tiene la forma de un cono con la altura igual al doble del radio.

Grava en forma de cono. — Figura\(\PageIndex{1}\)

El volumen se encuentra usando una fórmula de geometría elemental.

\[ \begin{align*} V&=\dfrac{1}{3}\pi r^2h \\[4pt] &=\dfrac{1}{3}\pi r^2(2r)\\[4pt] &=\dfrac{2}{3}\pi r^3 \end{align*}\]

Hemos escrito el volumen\(V\) en términos del radio\(r\). Sin embargo, en algunos casos, podemos comenzar con el volumen y querer encontrar el radio. Por ejemplo: Un cliente compra 100 pies cúbicos de grava para construir un montículo en forma de cono con una altura del doble del radio. ¿Cuál es el radio y la altura del nuevo cono? Para responder a esta pregunta, utilizamos la fórmula

\[r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber\]

Esta función es la inversa de la fórmula para\(V\) en términos de\(r\).

En esta sección, exploraremos los inversos de las funciones polinomiales y racionales y en particular las funciones radicales que encontramos en el proceso.

Encontrar la inversa de una función polinómica

Dos funciones\(f\) y\(g\) son funciones inversas si por cada par de coordenadas en\(f\)\((a,b)\),, existe un par de coordenadas correspondiente en la función inversa,\(g\),\((b, a)\). En otras palabras, los pares de coordenadas de las funciones inversas tienen la entrada y la salida intercambiadas. Solo las funciones uno-a-uno tienen inversas. Recordemos que una función uno a uno tiene un valor de salida único para cada valor de entrada y pasa la prueba de línea horizontal.

Por ejemplo, supongamos que un colector de escorrentía de agua está construido en forma de un cilindroparabólico como se muestra en la Figura\(\PageIndex{2}\). Podemos usar la información de la figura para encontrar la superficie del agua en el abrevadero en función de la profundidad del agua.

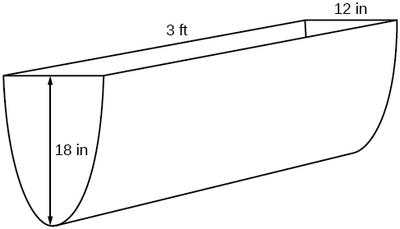
Diagrama de un cilindroparabólico que tiene 18” de altura, 3' de largo y 12” de ancho. — Figura\(\PageIndex{2}\)

Debido a que será útil tener una ecuación para la forma de la sección transversal parabólica, impondremos un sistema de coordenadas en la sección transversal, con\(x\) medidas horizontalmente y\(y\) medidas verticalmente, con el origen en el vértice de la parábola (Figura\(\PageIndex{3}\)).

Gráfica de una parábola. — Figura\(\PageIndex{3}\)

A partir de esto encontramos una ecuación para la forma parabólica. Colocamos el origen en el vértice de la parábola, así sabemos que la ecuación tendrá forma\(y(x)=ax^2\). Nuestra ecuación tendrá que pasar por el punto\((6, 18)\), a partir del cual podemos resolver para el factor de estiramiento\(a\).

\[ \begin{align*} 18&=a6^2 \\[4pt] a &=\dfrac{18}{36} \\[4pt] &=\dfrac{1}{2} \end{align*}\]

Nuestra sección transversal parabólica tiene la ecuación

\(y(x)=\dfrac{1}{2}x^2\)

Nos interesa la superficie del agua, por lo que debemos determinar el ancho en la parte superior del agua en función de la profundidad del agua. Para cualquier profundidad\(y\), el ancho estará dado por\(2x\), por lo que necesitamos resolver la ecuación anterior para\(x\) y encontrar la función inversa. Sin embargo, observe que la función original no es uno-a-uno, y de hecho, dada cualquier salida hay dos entradas que producen la misma salida, una positiva y otra negativa.

Para encontrar una inversa, podemos restringir nuestra función original a un dominio limitado en el que es uno a uno. En este caso, tiene sentido restringirnos a\(x\) valores positivos. En este dominio, podemos encontrar una inversa resolviendo para la variable de entrada:

\[ \begin{align*} y&=\dfrac{1}{2}x^2 \\[4pt] 2y&=x^2 \\[4pt] x&=\pm \sqrt{2y} \end{align*}\]

Esta no es una función como está escrita. Nos estamos limitando a\(x\) valores positivos, así que eliminamos la solución negativa, dándonos la función inversa que estamos buscando.

\(y=\dfrac{x^2}{2}\),\(x>0\)

Debido a que\(x\) es la distancia desde el centro de la parábola a cada lado, todo el ancho del agua en la parte superior será\(2x\). El canal tiene 3 pies (36 pulgadas) de largo, por lo que el área de superficie será entonces:

\[ \begin{align*} \text{Area} &=l⋅w \\[4pt] &=36⋅2x \\[4pt] &=72x \\[4pt] &=72\sqrt{2y} \end{align*}\]

Este ejemplo ilustra dos puntos importantes:

Al encontrar la inversa de una cuadrática, tenemos que limitarnos a un dominio en el que la función es uno a uno.
La inversa de una función cuadrática es una función de raíz cuadrada. Ambas son funciones de kit de herramientas y diferentes tipos de funciones de potencia.

Las funciones que involucran raíces a menudo se denominan funciones radicales. Si bien no es posible encontrar una inversa de la mayoría de las funciones polinómicas, algunos polinomios básicos sí tienen inversos. Tales funciones se llaman funciones invertibles, y usamos la notación\(f^{−1}(x)\).

Advertencia: no\(f^{−1}(x)\) es lo mismo que el recíproco de la función\(f(x)\). Este uso de “—1” está reservado para denotar funciones inversas. Para denotar el recíproco de una función\(f(x)\), necesitaríamos escribir:

\[ (f(x))^{−1}=\frac{1}{f(x)}.\]

Una relación importante entre las funciones inversas es que se “deshacen” entre sí. Si\(f^{−1}\) es la inversa de una función\(f\), entonces\(f\) es la inversa de la función\(f^{−1}\). En otras palabras, sea lo que sea que\(f\) le haga la función\(x\), la\(f^{−1}\) deshace y viceversa.

\(f^{−1}(f(x))=x\), para todos\(x\) en el dominio de\(f\)

\(f(f^{−1}(x))=x\), para todos\(x\) en el dominio de\(f^{−1}\)

Tenga en cuenta que la inversa cambia el dominio y el rango de la función original.

VERTICANDO QUE DOS FUNCIONES SON INVERSIONES ENTRE

Dos funciones,\(f\) y\(g\), son inversas la una de la otra si para todos\(x\) en el dominio de\(f\) y\(g\),

\(g(f(x))=f(g(x))=x\)

Cómo: Dada una función polinómica, encuentra la inversa de la función restringiendo el dominio de tal manera que la nueva función sea uno a uno

Reemplazar\(f(x)\) con\(y\).
Intercambio\(x\) y\(y\).
Resuelva y cambie el nombre de la función\(f^{−1}(x)\).\(y\)

Ejemplo\(\PageIndex{1}\): Verifying Inverse Functions

Demostrar eso\(f(x)=\frac{1}{x+1}\) y\(f^{−1}(x)=\frac{1}{x}−1\) son inversos, para\(x≠0,−1\).

Solución

Debemos demostrar eso\(f^{−1}(f(x))=x\) y\(f(f^{−1}(x))=x\).

\[ \begin{align*} f^{−1}(f(x)) &=f^{−1}\left(\dfrac{1}{x+1}\right)\\[4pt] &=\dfrac{1}{\dfrac{1}{x+1}}−1\\[4pt] &=(x+1)−1\\[4pt] &=x\end{align*}\]

\[ \begin{align*} f(f^{−1}(x)) &=f(\dfrac{1}{x−1})\\[4pt] &=\dfrac{1}{\left(\dfrac{1}{x−1}\right)+1}\\[4pt] &=\dfrac{1}{\dfrac{1}{x}}\\[4pt] &=x\end{align*}\]

Por lo tanto,\(f(x)=\dfrac{1}{x+1}\) y\(f^{−1}(x)=\dfrac{1}{x}−1\) son inversas.

Ejercicio\(\PageIndex{1}\)

\(f^{−1}(x)=3x−5\)Demuéstralo\(f(x)=\frac{x+5}{3}\) y son inversos.

Contestar a: \(f^{−1}(f(x))=f^{−1}(\frac{x+5}{3})=3(\frac{x+5}{3})−5=(x−5)+5=x\)
Respuesta b: \(f(f^{−1}(x))=f(3x−5)=\frac{(3x−5)+5}{3}=\frac{3x}{3}=x\)

Ejemplo\(\PageIndex{2}\): Finding the Inverse of a Cubic Function

Encuentra la inversa de la función\(f(x)=5x^3+1\).

Solución

Esta es una transformación de la función básica del kit de herramientas cúbicas, y en base a nuestro conocimiento de esa función, sabemos que es uno a uno. Resolviendo para lo inverso resolviendo para\(x\).

\(y=5x^3+1\)

\(x=5y^3+1\)

\(x−1=5y^3\)

\(\dfrac{x−1}{5}=y^3\)

\(f^{−1}(x)=\sqrt[3]{\dfrac{x−1}{5}}\)

Análisis

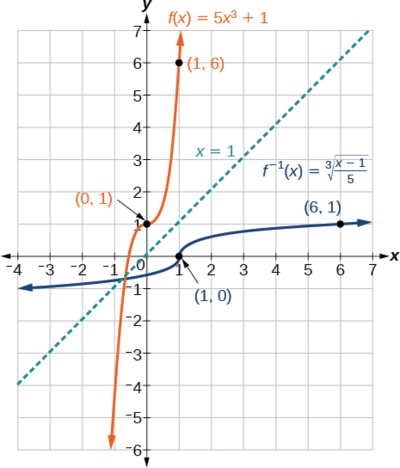
Mira la gráfica de\(f\) y\(f^{–1}\). Observe que una gráfica es el reflejo de la otra sobre la línea\(y=x\). Este es siempre el caso cuando se grafica una función y su función inversa.

También, ya que el método implicaba intercambiar\(x\) y\(y\), notar los puntos correspondientes. Si\((a,b)\) está en la gráfica de\(f\), entonces\((b,a)\) está en la gráfica de\(f^{–1}\). Ya que\((0,1)\) está en la gráfica de\(f\), entonces\((1,0)\) está en la gráfica de\(f^{–1}\). De igual manera, ya que\((1,6)\) está en la gráfica de\(f\), entonces\((6,1)\) está en la gráfica de\(f^{–1}\) (Figura\(\PageIndex{9}\)).

Gráfica de f (x) =5x^3+1 y su inversa, f^ (-1) (x) =3sqrt ((x-1)/(5)). — Figura\(\PageIndex{4}\)

Ejercicio\(\PageIndex{2}\)

Encuentra la función inversa de\(f(x)=\sqrt[3]{x+4}\).

Contestar: \(f^{−1}(x)=x^3−4\)

Restringir el dominio para encontrar la inversa de una función polinómica

Hasta el momento, hemos podido encontrar las funciones inversas de las funciones cúbicas sin tener que restringir sus dominios. Sin embargo, como sabemos, no todos los polinomios cúbicos son uno a uno. Algunas funciones que no son uno a uno pueden tener su dominio restringido para que sean uno a uno, sino solo sobre ese dominio. La función sobre el dominio restringido tendría entonces una función inversa. Dado que las funciones cuadráticas no son uno a uno, debemos restringir su dominio para encontrar sus inversos.

Restringir el dominio

Si una función no es uno a uno, no puede tener una inversa. Si restringimos el dominio de la función para que se convierta en uno a uno, creando así una nueva función, esta nueva función tendrá una inversa.

Cómo: Dada una función polinómica, restringir el dominio de una función que no es uno a uno y luego encontrar la inversa

Restringir el dominio determinando un dominio en el que la función original es uno a uno.
Reemplazar\(f(x)\) con\(y\).
Intercambio\(x\) y\(y\).
Resuelva y cambie el nombre de la función o par de funciones\(f^{−1}(x)\).\(y\)
Revisar la fórmula para\(f^{−1}(x)\) asegurando que las salidas de la función inversa corresponden al dominio restringido de la función original.

Ejemplo\(\PageIndex{3}\): Restricting the Domain to Find the Inverse of a Polynomial Function

Encuentra la función inversa de\(f\):

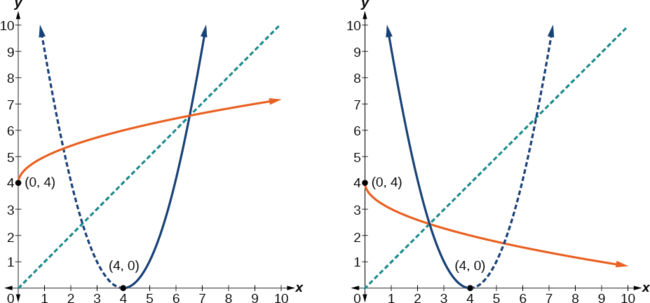
\(f(x)={(x−4)}^2\),\(x≥4\)
\(f(x)={(x−4)}^2\),\(x≤4\)

Solución

La función original no\(f(x)={(x−4)}^2\) es uno a uno, sino que la función está restringida a un dominio de\(x≥4\) o\(x≤4\) en el que es uno a uno (Figura\(\PageIndex{6}\)).

Dos gráficas de f (x) = (x-4) ^2 donde la primera es cuando x — Figura\(\PageIndex{5}\)

Para encontrar la inversa, comience\(f(x)\) reemplazando por la variable simple\(y\).

\(y={(x−4)}^2\)Intercambio\(x\) y\(y\).

\(x={(y−4)}^2\)Toma la raíz cuadrada.

\(\pm \sqrt{x}=y−4\)Añadir\(4\) a ambos lados.

\(4\pm \sqrt{x} =y\)

Esta no es una función como está escrita. Necesitamos examinar las restricciones sobre el dominio de la función original para determinar la inversa. Como invertimos los roles de\(x\) y\(y\) para el original\(f(x)\), miramos el dominio: los valores\(x\) podían asumir. Cuando invertimos los roles de\(x\) y\(y\), esto nos dio los valores que\(y\) podían asumir. Para esta función,\(x≥4\), entonces para la inversa, deberíamos tener\(y≥4\), que es lo que da nuestra función inversa.

El dominio de la función original estaba restringido a\(x≥4\), por lo que las salidas de la inversa deben ser las mismas\(f(x)≥4\),, y debemos usar el caso +:
\(f^{−1}(x)=4+\sqrt{x}\)
El dominio de la función original estaba restringido a\(x≤4\), por lo que las salidas de la inversa deben ser las mismas\(f(x)≤4\),, y debemos usar el caso —:
\(f^{−1}(x)=4−\sqrt{x}\)

Análisis

En las gráficas de la Figura\(\PageIndex{6}\), vemos la función original graficada en el mismo conjunto de ejes que su función inversa. Observe que juntas las gráficas muestran simetría sobre la línea\(y=x\). El par de coordenadas\((4,0)\) está en la gráfica de f y el par de coordenadas\((0, 4)\) está en la gráfica de\(f^{−1}\). Para cualquier par de coordenadas, si\((a, b)\) está en la gráfica de\(f\), entonces\((b, a)\) está en la gráfica de\(f^{−1}\). Por último, observar que la gráfica de\(f\) cruza la gráfica de\(f^{−1}\) en la línea\(y=x\). Puntos de intersección para las gráficas de\(f\) y siempre\(f^{−1}\) estarán en la línea\(y=x\).

Dos gráficas de una función parabólica con la mitad de su inversa. — Figura\(\PageIndex{6}\)

Ejemplo\(\PageIndex{4}\): Finding the Inverse of a Quadratic Function When the Restriction Is Not Specified

Restringir el dominio y luego encontrar la inversa de

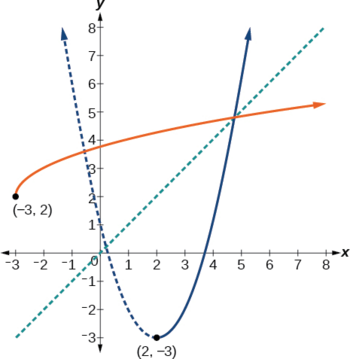
\(f(x)={(x−2)}^2−3\).

Solución

Podemos ver que esta es una parábola con vértice en la\((2,–3)\) que se abre hacia arriba. Debido a que la gráfica estará disminuyendo en un lado del vértice y aumentando en el otro lado, podemos restringir esta función a un dominio en el que será uno a uno limitando el dominio a\(x≥2\).

Para encontrar la inversa, usaremos la forma de vértice de la cuadrática. Comenzamos\(f(x)\) reemplazando por una variable simple,\(y\), luego resolvemos para\(x\).

\(y={(x−2)}^2−3\)Intercambio\(x\) y\(y\).

\(x={(y−2)}^2−3\)Agrega 3 a ambos lados.

\(x+3={(y−2)}^2\)Toma la raíz cuadrada.

\(\pm \sqrt{x+3}=y−2\)Agrega 2 a ambos lados.

\(2\pm \sqrt{x+3}=y\)Renombrar la función.

\(f^{−1}(x)=2\pm \sqrt{x+3}\)

Ahora tenemos que determinar qué caso usar. Debido a que restringimos nuestra función original a un dominio de\(x≥2\), las salidas de la inversa deberían ser las mismas, diciéndonos que utilicemos el caso +

\(f^{−1}(x)=2+\sqrt{x+3}\)

Si la cuadrática no se hubiera dado en forma de vértice, reescribirla en forma de vértice sería el primer paso. De esta manera podremos observar fácilmente las coordenadas del vértice para ayudarnos a restringir el dominio.

Análisis

Observe que arbitrariamente decidimos restringir el dominio en\(x≥2\). Con la misma facilidad podríamos haber optado por restringir el dominio a\(x≤2\), en cuyo caso\(f^{−1}(x)=2−\sqrt{x+3}\). Observe la función original graficada en el mismo conjunto de ejes que su función inversa en la Figura\(\PageIndex{7}\). Observe que ambas gráficas muestran simetría sobre la línea\(y=x\). El par de coordenadas\((2, −3)\) está en la gráfica de\(f\) y el par de coordenadas\((−3, 2)\) está en la gráfica de\(f^{−1}\). Observe desde la gráfica de ambas funciones en el mismo conjunto de ejes que

dominio de\(f=\) rango de\(f^{–1}=[2,\infty)\)

dominio de\(f^{–1}=\) rango de\(f=[–3,\infty)\).

Por último, observar que la gráfica de\(f\) cruza la gráfica de\(f^{−1}\) a lo largo de la línea\(y=x\).

Gráfica de una función parabólica con la mitad de su inversa. — Figura\(\PageIndex{7}\)

Ejercicio\(\PageIndex{4}\)

Encuentra la inversa de la función\(f(x)=x^2+1\), en el dominio\(x≥0\).

Contestar: \(f^{−1}(x)=\sqrt{x−1}\)

Encontrar inversos

Observe que las funciones de los ejemplos anteriores eran todas polinomios, y sus inversos fueron funciones radicales. Si queremos encontrar la inversa de una función radical, tendremos que restringir el dominio de la respuesta porque el rango de la función original es limitado.

Cómo: Dada una función radical, encontrar la inversa

Determinar el rango de la función original.
Reemplazar\(f(x)\) con\(y\), luego resolver para\(x\).
Si es necesario, restrinja el dominio de la función inversa al rango de la función original.

Ejemplo\(\PageIndex{5}\): Finding the Inverse of a Radical Function

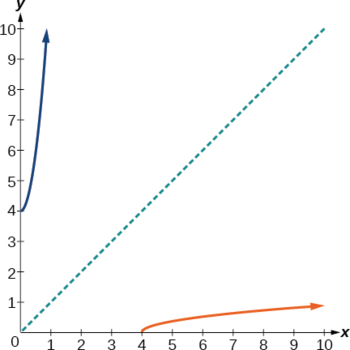
Restringir el dominio de la función\(f(x)=\sqrt{x−4}\) y luego encontrar el inverso.

Solución

Tenga en cuenta que la función original tiene rango\(f(x)≥0\). Reemplazar\(f(x)\) con\(y\), luego resolver para\(x\).

\(y=\sqrt{x−4}\)Reemplazar\(f(x)\) con\(y\).

\(x=\sqrt{y−4}\)Intercambio\(x\) y\(y\).

\(x=\sqrt{y−4}\)Cuadrado a cada lado.

\(x^2=y−4\)Agregar 4.

\(x^2+4=y\)Cambiar el nombre de la función\(f^{−1}(x)\).

\(f^{−1}(x)=x^2+4\)

Recordemos que el dominio de esta función debe limitarse al rango de la función original.

\(f^{−1}(x)=x^2+4\),\(x≥0\)

Análisis

Observe en la Figura\(\PageIndex{8}\) que la inversa es un reflejo de la función original sobre la línea\(y=x\). Debido a que la función original solo tiene salidas positivas, la función inversa solo tiene entradas no negativas.

Gráfica de f (x) =sqrt (x-4) y su inversa, f^ (-1) (x) =x^2+4. — Figura\(\PageIndex{8}\)

Ejercicio\(\PageIndex{5}\)

Restringir el dominio y luego encontrar la inversa de la función\(f(x)=\sqrt{2x+3}\).

Contestar: \(f^{−1}(x)=\frac{x^2−3}{2}\),\(x≥0\)

Resolver aplicaciones de funciones radicales

Las funciones radicales son comunes en los modelos físicos, como vimos en el abridor de sección. Ahora contamos con herramientas suficientes para poder resolver el problema planteado al inicio de la sección.

Ejemplo\(\PageIndex{6}\): Solving an Application with a Cubic Function

Un montículo de grava tiene la forma de un cono con la altura igual al doble del radio. El volumen del cono en términos del radio viene dado por

\[V=\dfrac{2}{3}\pi r^3 \nonumber\]

Encuentra la inversa de la función\(V=\frac{2}{3}\pi r^3\) que determina el volumen\(V\) de un cono y es una función del radio\(r\). Luego usa la función inversa para calcular el radio de tal montículo de grava que mide 100 pies cúbicos. Uso\(\pi=3.14\).

Solución

Comience con la función dada para\(V\). Observe que el dominio significativo para la función es\(r>0\) ya que los radios negativos no tendrían sentido en este contexto ni un radio de\(0\). También tenga en cuenta el rango de la función (de ahí, el dominio de la función inversa) es\(V>0\). Resolver para\(r\) en términos de\(V\), utilizando el método descrito anteriormente. Tenga en cuenta que en aplicaciones del mundo real, no intercambiamos las variables al encontrar inversas. En cambio, cambiamos qué variable se considera la variable independiente.

\[ V =\dfrac{2}{3}\pi r^3\nonumber \]

Resolver para\(r^3\).

\[r^3 =\dfrac{3V}{2\pi} \nonumber\]

Resolver para\(r\).

\[ r=\sqrt[3]{\dfrac{3V}{2\pi}} \nonumber \]

Este es el resultado que se afirma en el abridor de la sección. Ahora evalúe esto para\(V=100\) y\(\pi=3.14\).

\[ \begin{align*} r&=\sqrt[3]{\dfrac{3V}{2\pi}} \\[4pt] &=\sqrt[3]{\dfrac{3⋅100}{2⋅3.14}} \\[4pt] &≈\sqrt[3]{47.7707} \\[4pt] &≈3.63 \end{align*}\]

Por lo tanto, el radio es de aproximadamente 3.63 pies.

Determinar el dominio de una función radical compuesta con otras funciones

Cuando las funciones radicales se componen con otras funciones, determinar el dominio puede volverse más complicado.

Ejemplo\(\PageIndex{7}\): Finding the Domain of a Radical Function Composed with a Rational Function

Encuentra el dominio de la función:

\[f(x)=\sqrt{\frac{(x+2)(x−3)}{(x−1)}}. \nonumber\]

Solución

Debido a que una raíz cuadrada solo se define cuando la cantidad bajo el radical no es negativa, necesitamos determinar dónde

\[\frac{(x+2)(x−3)}{(x−1)}≥0. \nonumber\]

La salida de una función racional puede cambiar signos (cambiar de positivo a negativo o viceversa) en las intercepciones x y en las asíntotas verticales. Para esta ecuación, la gráfica podría cambiar signos en\(x=–2\),\(1\), y\(3\).

Para determinar los intervalos en los que la expresión racional es positiva, podríamos probar algunos valores en la expresión o esbozar una gráfica. Si bien ambos enfoques funcionan igual de bien, para este ejemplo utilizaremos una gráfica como se muestra en la Figura\(\PageIndex{9}\).

Gráfica de una función radical que muestra dónde las salidas son no negativas. — Figura\(\PageIndex{9}\)

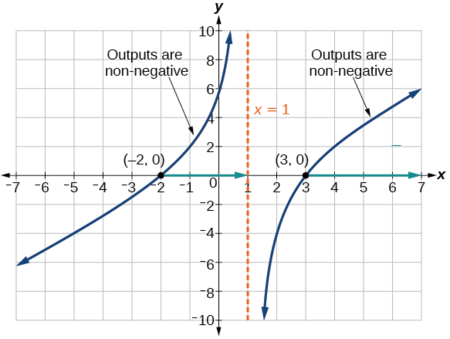
Esta función tiene dos intercepciones x, las cuales presentan un comportamiento lineal cerca de las intercepciones x. Hay una asíntota vertical, correspondiente a un factor lineal; este comportamiento es similar a la función básica del kit de herramientas recíprocas, y no hay asíntota horizontal porque el grado del numerador es mayor que el grado del denominador. Hay una intercepción y en\((0,\sqrt{6})\).

Desde la intersección y y la intersección x en\(x=−2\), podemos esbozar el lado izquierdo de la gráfica. A partir del comportamiento en la asíntota, podemos bosquejar el lado derecho de la gráfica.

A partir de la gráfica, ahora podemos decir en qué intervalos las salidas serán no negativas, para que podamos estar seguros de que se\(f(x)\) definirá la función original. \(f(x)\)tiene dominio\(−2≤x<1\) o\(x≥3\), o en notación de intervalo,\([−2,1)∪[3,\infty)\).

Encontrar inversos de funciones racionales

Al igual que con el hallazgo de inversos de funciones cuadráticas, a veces es deseable encontrar lo inverso de una función racional, particularmente de funciones racionales que son la relación de funciones lineales, como en aplicaciones de concentración.

Ejemplo\(\PageIndex{8}\): Finding the Inverse of a Rational Function

La función

\[\displaystyle C=\frac{20+0.4n}{100+n}\]

representa la concentración\(C\) de una solución ácida después de que se hayan agregado\(n\) mL de solución al 40% a 100 mL de una solución al 20%. Primero, encontrar la inversa de la función; es decir, encontrar una expresión para\(n\) en términos de\(C\). Entonces usa tu resultado para determinar cuánto de la solución al 40% se debe agregar para que la mezcla final sea una solución al 35%.

Solución

Primero queremos la inversa de la función para determinar cuántos mL necesitamos para una concentración dada. Vamos a resolver para\(n\) en términos de\(C\).

\[ \begin{align*} C&=\dfrac{20+0.4n}{100+n} \\[4pt] C(100+n)&=20+0.4n\\[4pt] 100C+Cn&=20+0.4n\\[4pt] 100C−20&=0.4n−Cn\\[4pt] 100C−20&=(0.4−C)n\\[4pt] n&=\dfrac{100C−20}{0.4−C}\end{align*}\]

Ahora evalúe esta función al 35%, que es\(C=0.35\).

\[ \begin{align*} n&=\dfrac{100(0.35)−20}{0.4−0.35}\\[4pt] &=\dfrac{15}{0.05}\\[4pt] &=300\end{align*}\]

Podemos concluir que se deben agregar 300 mL de la solución al 40%.

Ejercicio\(\PageIndex{8}\)

Encuentra la inversa de la función\(f(x)=\frac{x+3}{x−2}\).

Contestar: \(f^{−1}(x)=\frac{2x+3}{x−1}\)

Medios

Acceda a estos recursos en línea para una instrucción adicional y práctica con funciones inversas y radicales.

Conceptos clave

La inversa de una función cuadrática es una función de raíz cuadrada.
Si\(f^{−1}\) es la inversa de una función\(f\), entonces\(f\) es la inversa de la función\(f^{−1}\). Ver Ejemplo\(\PageIndex{1}\).
Si bien no es posible encontrar una inversa de la mayoría de las funciones polinómicas, algunos polinomios básicos son invertibles. Ver Ejemplo\(\PageIndex{2}\).
Para encontrar la inversa de ciertas funciones, debemos restringir la función a un dominio en el que será uno a uno. Ver ejemplos\(\PageIndex{3}\) y\(\PageIndex{4}\)
Al encontrar la inversa de una función radical, necesitamos una restricción en el dominio de la respuesta. Ver Ejemplo\(\PageIndex{5}\) y\(\PageIndex{7}\).
Las funciones inversas y radicales se pueden utilizar para resolver problemas de aplicación. Ver Ejemplos\(\PageIndex{6}\) y\(\PageIndex{8}\).