3.7: Funciones racionales

Última actualización
Guardar como PDF

Page ID: 121440

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Objetivos de aprendizaje

Utilice la notación de flecha.
Resolver problemas aplicados que involucran funciones racionales.
Encuentra los dominios de las funciones racionales.
Identificar asíntotas verticales.
Identificar asíntotas horizontales.
Graficar funciones racionales.

Supongamos que sabemos que el costo de hacer un producto depende del número de artículos,$x$, producidos. Esto viene dado por la ecuación$C (x)=15,000x−0.1x^2+1000.$ Si queremos conocer el costo promedio para producir$x$ artículos, dividiríamos la función de costo por el número de artículos,$x$. La función de costo promedio, que arroja el costo promedio por artículo para$x$ los artículos producidos, es

\[f(x)=\dfrac{15,000x−0.1x^2+1000}{x} \nonumber\]

Muchos otros problemas de aplicación requieren encontrar un valor promedio de manera similar, dándonos variables en el denominador. Escrita sin una variable en el denominador, esta función contendrá una potencia entera negativa.

En las últimas secciones, hemos trabajado con funciones polinómicas, que son funciones con enteros no negativos para exponentes. En esta sección, exploramos las funciones racionales, las cuales tienen variables en el denominador.

Uso de la notación de flecha

Hemos visto las gráficas de la función recíproca básica y la función recíproca cuadrada de nuestro estudio de las funciones del kit de herramientas. Examine estas gráficas, como se muestra en la Figura$\PageIndex{1}$, y observe algunas de sus características.

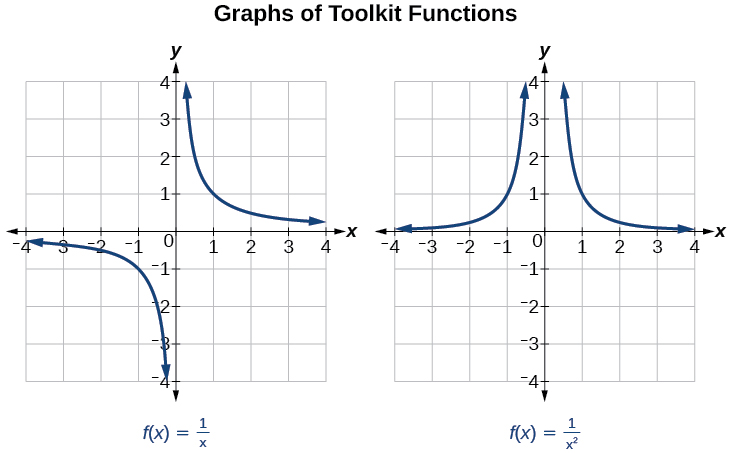
Gráficas de f (x) =1/x y f (x) =1/x^2 — Figura$\PageIndex{1}$

Varias cosas son evidentes si examinamos la gráfica de$f(x)=\frac{1}{x}$.

En la rama izquierda de la gráfica, la curva se acerca al$x$ eje$(y=0)$ -como$x\rightarrow -\infty$.
A medida que la gráfica se acerca$x = 0$ desde la izquierda, la curva cae, pero a medida que nos acercamos a cero desde la derecha, la curva sube.
Finalmente, en la rama derecha de la gráfica, las curvas se aproximan$x$ al eje$(y=0) $ como$x\rightarrow \infty$.

Para resumir, utilizamos la notación de flecha para mostrar que$x$ o$f (x)$ se acerca a un valor particular (Tabla$\PageIndex{1}$).

Mesa$\PageIndex{1}$
Símbolo	Significado
$x\rightarrow a^-$	$x$se acerca a una desde la izquierda ($x<a$pero cerca de$a$)
$x\rightarrow a^+$	$x$se acerca a una desde la derecha ($x>a$pero cerca de$a$)
$x\rightarrow \infty$	$x$se acerca al infinito ($x$aumenta sin límite)
$x\rightarrow −\infty$	$x$se acerca al infinito negativo ($x$disminuye sin límite)
$f(x)\rightarrow \infty$	la salida se acerca al infinito (la salida aumenta sin límite)
$f(x)\rightarrow −\infty$	la salida se acerca al infinito negativo (la salida disminuye sin límite)
$f(x)\rightarrow a$	los enfoques de salida$a$

Comportamiento Local de$f(x)=\frac{1}{x}$

Empecemos por mirar la función recíproca,$f(x)=\frac{1}{x}$. No podemos dividir por cero, lo que significa que la función está indefinida en$x=0$; entonces cero no está en el dominio. A medida que los valores de entrada se acercan a cero desde el lado izquierdo (volviéndose muy pequeños, valores negativos), los valores de la función disminuyen sin límite (en otras palabras, se acercan al infinito negativo). Podemos ver este comportamiento en la Tabla$\PageIndex{2}$.

Mesa$\PageIndex{2}$
$x$	—0.1	—0.01	—0.001	—0.0001
$f(x)=\frac{1}{x}$	—10	—100	—1000	—10,000

Escribimos en notación de flecha

como$x\rightarrow 0^−,f(x)\rightarrow −\infty$

A medida que los valores de entrada se acercan a cero desde el lado derecho (convirtiéndose en valores muy pequeños, positivos), los valores de la función aumentan sin límite (acercándose al infinito) Podemos ver este comportamiento en la Tabla$\PageIndex{3}$.

Mesa$\PageIndex{3}$
$x$	0.1	0.01	0.001	0.0001
$f(x)=\frac{1}{x}$	10	100	1000	10,000

Escribimos en notación de flecha

Como$x\rightarrow 0^+, f(x)\rightarrow \infty$.

Ver Figura$\PageIndex{2}$.

Gráfica de f (x) =1/x que denota el comportamiento final. A medida que x va al infinito negativo, f (x) va a 0, y como x va a 0^-, f (x) va al infinito negativo. A medida que x va al infinito positivo, f (x) va a 0, y como x va a 0^+, f (x) va al infinito positivo. — Figura$\PageIndex{2}$.

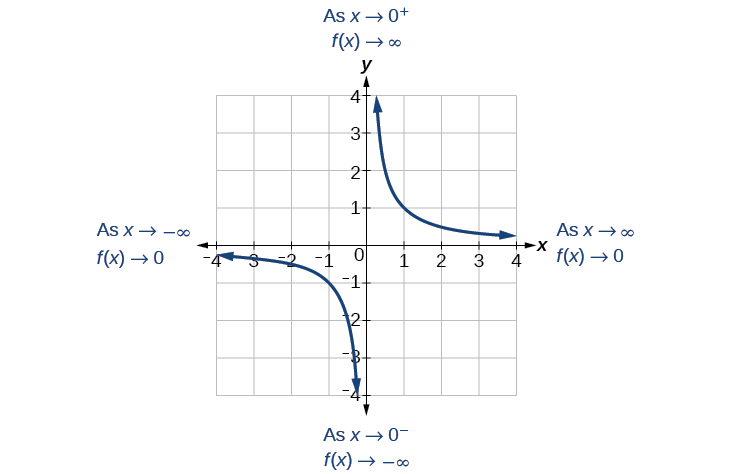
Este comportamiento crea una asíntota vertical, que es una línea vertical a la que se acerca la gráfica pero que nunca cruza. En este caso, la gráfica se acerca a la línea vertical a$x=0$ medida que la entrada se acerca a cero (Figura$\PageIndex{3}$).

Gráfica de f (x) =1/x con su asíntota vertical en x=0. — Figura$\PageIndex{3}$.

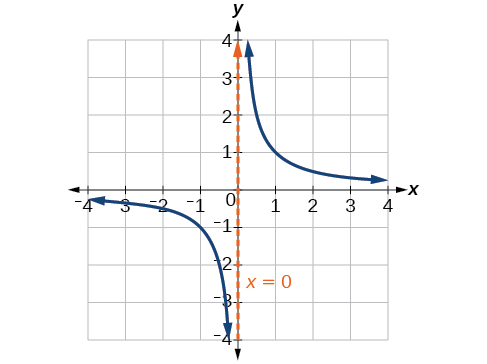
Definición: ASIMPTOTA VERTICAL

Una asíntota vertical de una gráfica es una línea vertical$x=a$ donde la gráfica tiende hacia el infinito positivo o negativo a medida que se acercan las entradas$a$. Escribimos

Como$x\rightarrow a$,$f(x)\rightarrow \infty$, o como$x\rightarrow a$,$f(x)\rightarrow −\infty$.

Comportamiento final de$f(x)=\frac{1}{x}$

A medida que los valores de$x$ aproximación al infinito, se acercan los valores de función$0$. A medida que los valores de$x$ aproximación al infinito negativo, los valores de función se acercan$0$ (Figura$\PageIndex{4}$). Simbólicamente, usando notación de flecha

Como$x\rightarrow \infty$,$f(x)\rightarrow 0$, y como$x\rightarrow −\infty$,$f(x)\rightarrow 0$.

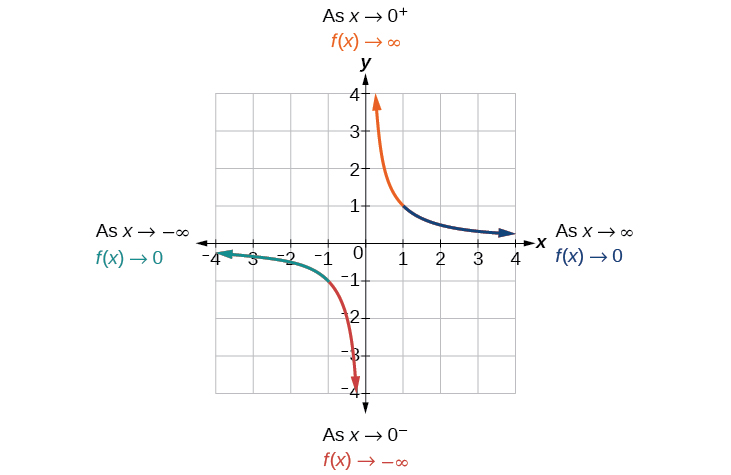
Gráfica de f (x) =1/x que resalta los segmentos de los puntos de inflexión para denotar su comportamiento final. — Figura$\PageIndex{4}$.

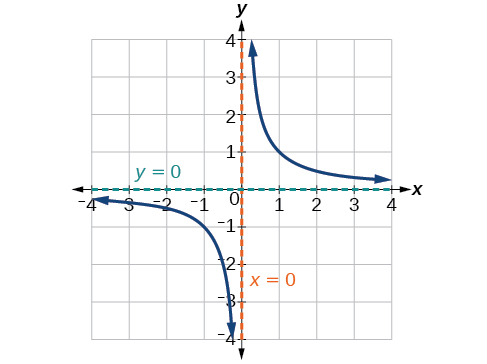
Con base en este comportamiento general y en la gráfica, podemos ver que la función se acerca a 0 pero nunca llega a 0; parece nivelarse a medida que las entradas se hacen grandes. Este comportamiento crea una asíntota horizontal, una línea horizontal a la que se acerca la gráfica a medida que la entrada aumenta o disminuye sin límite. En este caso, la gráfica se acerca a la línea horizontal$y=0$. Ver Figura$\PageIndex{5}$.

Gráfica de f (x) =1/x con su asíntota vertical en x=0 y su asíntota horizontal en y=0. — Figura$\PageIndex{5}$.

Definición: ASIMTOTA HORIZONTAL

Una asíntota horizontal de una gráfica es una línea horizontal$y=b$ donde la gráfica se acerca a la línea a medida que las entradas aumentan o disminuyen sin límite. Escribimos

Como$x\rightarrow \infty \text{ or } x\rightarrow −\infty$,$f(x)\rightarrow b$.

Ejemplo$\PageIndex{1}$: Using Arrow Notation.

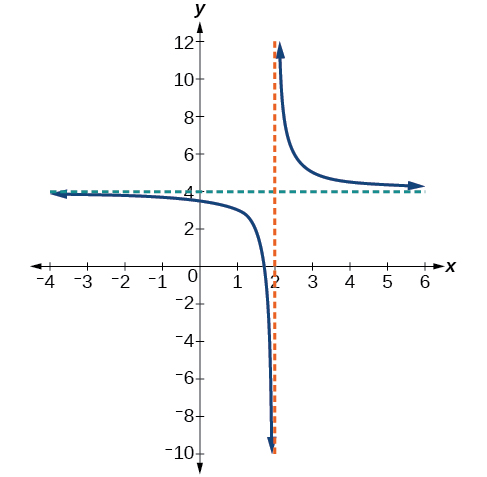
Utilice la notación de flecha para describir el comportamiento final y el comportamiento local de la función graficada en la Figura$\PageIndex{6}$.

Gráfica de f (x) =1/ (x-2) +4 con su asíntota vertical en x=2 y su asíntota horizontal en y=4. — Figura$\PageIndex{6}$.

Solución

Observe que la gráfica está mostrando una asíntota vertical en$x=2$, lo que nos dice que la función está indefinida en$x=2$.

Como$x\rightarrow 2^−$,$f(x)\rightarrow −\infty,$ y como$x\rightarrow 2^+$,$f(x)\rightarrow \infty$.

Y a medida que las entradas disminuyen sin límite, la gráfica parece estar nivelándose a los valores de salida de$4$, indicando una asíntota horizontal en$y=4$. A medida que las entradas aumentan sin límite, la gráfica se nivela en$4$.

Como$x\rightarrow \infty$,$f(x)\rightarrow 4$ y como$x\rightarrow −\infty$,$f(x)\rightarrow 4$.

Ejercicios$\PageIndex{1}$

Utilice la notación de flecha para describir el comportamiento final y el comportamiento local para la función cuadrada recíproca.

Contestar

Comportamiento final: as$x\rightarrow \pm \infty$,$f(x)\rightarrow 0$;

Comportamiento local: as$x\rightarrow 0$,$f(x)\rightarrow \infty$ (no hay intercepciones x o y)

Ejemplo$\PageIndex{2}$: Using Transformations to Graph a Rational Function.

Esboce una gráfica de la función recíproca desplazada dos unidades hacia la izquierda y tres unidades hacia arriba. Identificar las asíntotas horizontales y verticales de la gráfica, en su caso.

Solución

Desplazar la gráfica a la izquierda 2 y hacia arriba 3 resultaría en la función

\[f(x)=\dfrac{1}{x+2}+3\]

o equivalentemente, dando a los términos un denominador común,

\[f(x)=\dfrac{3x+7}{x+2}\]

El gráfico de la función desplazada se muestra en la Figura$\PageIndex{7}$.

Gráfica de f (x) =1/ (x+2) +3 con su asíntota vertical en x=-2 y su asíntota horizontal en y=3. — Figura$\PageIndex{7}$.

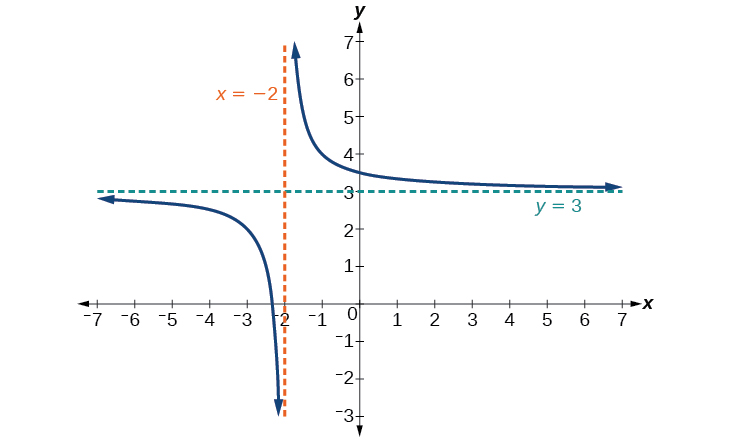
Observe que esta función no está definida en$x=−2$, y la gráfica también muestra una asíntota vertical en$x=−2$.

Como$x\rightarrow −2^−$,$f(x)\rightarrow −\infty$, y como$x\rightarrow −2^+$,$f(x)\rightarrow \infty$.

A medida que las entradas aumentan y disminuyen sin límite, la gráfica parece estar nivelándose a valores de salida de 3, indicando una asíntota horizontal en$y=3$.

Como$x\rightarrow \pm \infty$,$f(x)\rightarrow 3$.

Análisis

Observe que las asíntotas horizontales y verticales se desplazan hacia la izquierda 2 y hacia arriba 3 junto con la función.

Ejercicio$\PageIndex{2}$

Esboce la gráfica y encuentre las asíntotas horizontales y verticales de la función cuadrada recíproca que se ha desplazado hacia la derecha 3 unidades y hacia abajo 4 unidades.

Solución

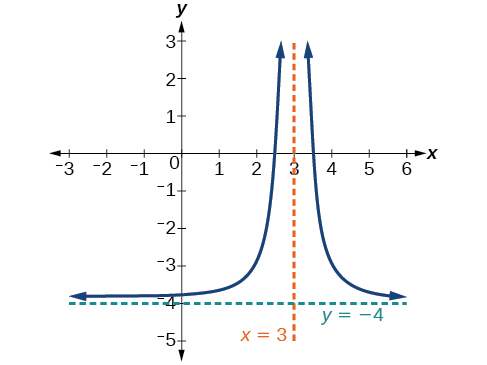
Gráfica de f (x) =1/ (x-3) ^2-4 con su asíntota vertical en x=3 y su asíntota horizontal en y=-4. — Figura$\PageIndex{8}$.

La función y las asíntotas se desplazan 3 unidades a la derecha y 4 unidades hacia abajo. Como$x\rightarrow 3$, $f(x)\rightarrow \infty$, and as $x\rightarrow \pm \infty$, $f(x)\rightarrow −4$.

La función es$f(x)=\frac{1}{{(x−3)}^2}−4$.

Resolución de problemas aplicados que involucran funciones racionales

En Ejemplo$\PageIndex{2}$, cambiamos una función de kit de herramientas de una manera que resultó en la función$f(x)=\frac{3x+7}{x+2}$. Este es un ejemplo de una función racional. Una función racional es una función que puede escribirse como el cociente de dos funciones polinómicas. Muchos problemas del mundo real nos obligan a encontrar la relación de dos funciones polinómicas. Los problemas que involucran tasas y concentraciones a menudo involucran funciones racionales.

Definición: FUNCIÓN RACIONAL

Una función racional es una función que se puede escribir como el cociente de dos funciones polinómicas$P(x)$ y$Q(x)$.

\[f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0\]

Ejemplo$\PageIndex{3}$: Solving an Applied Problem Involving a Rational Function

Un gran tanque de mezcla contiene actualmente 100 galones de agua en los que se han mezclado 5 libras de azúcar. Se abrirá un grifo vertiendo 10 galones por minuto de agua en el tanque al mismo tiempo que se vierte azúcar en el tanque a razón de 1 libra por minuto. Encuentra la concentración (libras por galón) de azúcar en el tanque después de 12 minutos. ¿Es esa una concentración mayor que al principio?

Solución

Que t sea el número de minutos desde que se abrió el grifo. Dado que el agua aumenta a 10 galones por minuto, y el azúcar aumenta a 1 libra por minuto, estas son tasas de cambio constantes. Esto nos dice que la cantidad de agua en el tanque está cambiando linealmente, al igual que la cantidad de azúcar en el tanque. Podemos escribir una ecuación independientemente para cada uno:

agua:$W(t)=100+10t$ en galones

azúcar:$S(t)=5+1t$ en libras

La concentración,$C$, será la proporción de libras de azúcar a galones de agua

\[C(t)=\dfrac{5+t}{100+10t}\]

La concentración después de 12 minutos se da evaluando$C(t)$ a$t= 12$.

\[\begin{align} C(12) & =\dfrac{5+12}{100+10(12)} \\ &= \dfrac{17}{220} \end{align} \]

Esto significa que la concentración es de 17 libras de azúcar a 220 galones de agua.

Al principio, la concentración es

\[\begin{align} C(0) & =\dfrac{5+0}{100+10(0)} \\ & =\dfrac{1}{20} \end{align} \]

Ya que$\frac{17}{220}≈0.08>\frac{1}{20}=0.05$, la concentración es mayor después de 12 minutos que al inicio.

Análisis

Para encontrar la asíntota horizontal, divida el coeficiente principal en el numerador por el coeficiente principal en el denominador:

\[\dfrac{1}{10}=0.1\]

Observe que la asíntota horizontal es$y= 0.1.$ Esto significa que$C,$ la concentración, la relación de libras de azúcar a galones de agua, se acercará a 0.1 a largo plazo.

Ejercicio$\PageIndex{3}$

Hay mil 200 estudiantes de primer año y mil 500 estudiantes de segundo año en un mitin de preparación al mediodía. Después de las 12 de la noche, 20 estudiantes de primer año llegan al mitin cada cinco minutos mientras 15 estudiantes de segundo año abandonan el mitin. Encuentra la proporción de estudiantes de primer año a estudiantes de segundo año a la 1 p.m.

Contestar: $\frac{12}{11}$

Encontrar los dominios de las funciones racionales

Una asíntota vertical representa un valor en el que una función racional es indefinida, por lo que ese valor no está en el dominio de la función. Una función recíproca no puede tener valores en su dominio que hagan que el denominador sea igual a cero. En general, para encontrar el dominio de una función racional, necesitamos determinar qué entradas provocarían división por cero.

Definición: Dominio de una función racional

El dominio de una función racional incluye todos los números reales excepto aquellos que hacen que el denominador sea igual a cero.

Cómo: Dada una función racional, encontrar el dominio.

Establece el denominador igual a cero.
Resuelve encontrar los valores x que hacen que el denominador sea igual a cero.
El dominio es todo números reales excepto los que se encuentran en el Paso 2.

Ejemplo$\PageIndex{4}$: Finding the Domain of a Rational Function

Encuentra el dominio de$f(x)=\dfrac{x+3}{x^2−9}$.

Solución

Comience estableciendo el denominador igual a cero y resolviendo.

\[x^2-9=0 \nonumber \]

\[x^2=9 \nonumber \]\[x=\pm 3 \nonumber \]

El denominador es igual a cero cuando$x=\pm 3$. El dominio de la función es todos los números reales excepto$x=\pm 3$.

Análisis

Una gráfica de esta función, como se muestra en la Figura$\PageIndex{9}$, confirma que la función no está definida cuando$x=\pm 3$.

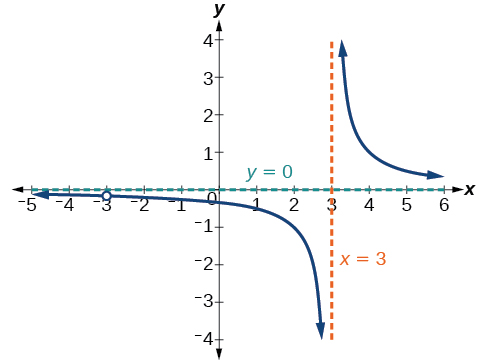
Gráfica de f (x) =1/ (x-3) con su asíntota vertical en x=3 y su asíntota horizontal en y=0. — Figura$\PageIndex{9}$.

Hay una asíntota vertical en$x=3$ y un agujero en la gráfica en$x=−3$. Discutiremos este tipo de agujeros con mayor detalle más adelante en esta sección.

Ejercicio$\PageIndex{4}$

Encuentra el dominio de$f(x)=\dfrac{4x}{5(x−1)(x−5)}$.

Contestar: El dominio es todo números reales excepto$x=1$ y$x=5$.

Identificación de asíntotas verticales de funciones racionales

Al mirar la gráfica de una función racional, podemos investigar su comportamiento local y ver fácilmente si hay asíntotas. Incluso podemos aproximar su ubicación. Aun sin la gráfica, sin embargo, todavía podemos determinar si una función racional dada tiene alguna asíntota, y calcular su ubicación.

Aíntotas Verticales

Las asíntotas verticales de una función racional se pueden encontrar examinando los factores del denominador que no son comunes a los factores en el numerador. Las asíntotas verticales ocurren en los ceros de tales factores.

Cómo: Dada una función racional, identificar cualquier asíntota vertical de su gráfica

Factorice el numerador y el denominador.
Anote cualquier restricción en el dominio de la función.
Reducir la expresión cancelando factores comunes en el numerador y el denominador.
Anote cualquier valor que haga que el denominador sea cero en esta versión simplificada. Aquí es donde ocurren las asíntotas verticales.
Anote cualquier restricción en el dominio donde no se presenten asíntotas. Estas son discontinuidades removibles, o “agujeros”.

Ejemplo$\PageIndex{5}$: Identifying Vertical Asymptotes

Encuentra las asíntotas verticales de la gráfica de$k(x)=\dfrac{5+2x^2}{2−x−x^2}$.

Solución

Primero, factifique el numerador y el denominador.

\[k(x)=\dfrac{5+2x^2}{2−x−x^2} \nonumber \]

\[=\dfrac{5+2x^2}{(2+x)(1-x)} \nonumber \]

Para encontrar las asíntotas verticales, determinamos dónde estará indefinida esta función estableciendo el denominador igual a cero:

\[(2+x)(1−x)=0 \nonumber \]

\[x=−2, \; x=1 \nonumber \]

Ni$x=–2$ tampoco$x=1$ son ceros del numerador, por lo que los dos valores indican dos asíntotas verticales. La gráfica de la Figura$\PageIndex{10}$ confirma la ubicación de las dos asíntotas verticales.

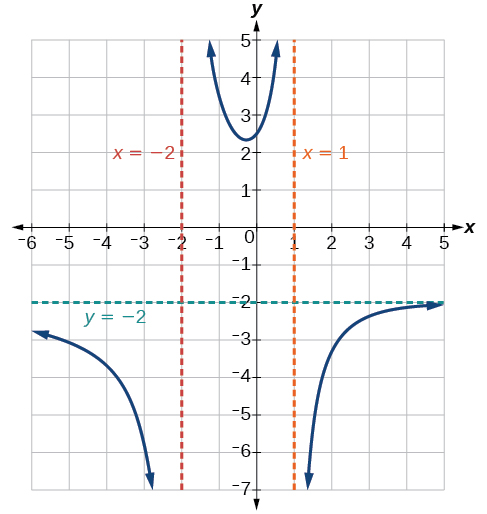
$Gráfica de k (x) = (5+2x) ^2/ (2-x-x^2) con sus asíntotas verticales en x=-2 y x=1 y su asíntota horizontal en y=-2.$

Figura$\PageIndex{10}$.

Discontinuidades removibles

Ocasionalmente, una gráfica contendrá un agujero: un solo punto donde la gráfica no está definida, indicada por un círculo abierto. Llamamos a tal agujero una discontinuidad removible. Por ejemplo, la función$f(x)=\dfrac{x^2−1}{x^2−2x−3}$ puede ser reescrita factorizando el numerador y el denominador.

\[f(x)=\dfrac{(x+1)(x−1)}{(x+1)(x−3)} \nonumber \]

Observe que$x+1$ es un factor común al numerador y al denominador. El cero de este factor,$x=−1$, es la ubicación de la discontinuidad removible. Observe también que no$ (x–3) $ es un factor tanto en el numerador como en el denominador. El cero de este factor,$x=3$, es la asíntota vertical. Ver Figura$\PageIndex{11}$. [Tenga en cuenta que las discontinuidades removibles pueden no ser visibles cuando usamos una calculadora gráfica, dependiendo de la ventana seleccionada.]

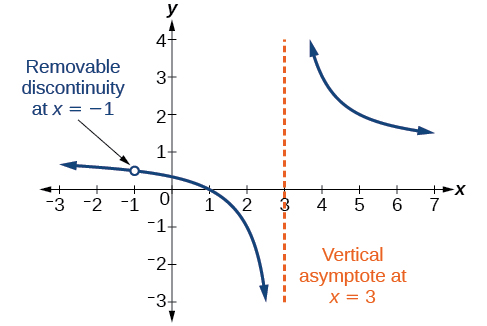
Gráfica de f (x) = (x^2-1)/(x^2-2x-3) con su asíntota vertical en x=3 y una discontinuidad removible en x=-1. — Figura$\PageIndex{11}$.

Discontinuidades removibles de funciones racionales

Una discontinuidad removible ocurre en la gráfica de una función racional en$x=a$ si$a$ es un cero para un factor en el denominador que es común con un factor en el numerador. Facturamos el numerador y denominador y verificamos los factores comunes. Si encontramos alguno, establecemos el factor común igual a 0 y resolvemos. Esta es la ubicación de la discontinuidad removible. Esto es cierto si la multiplicidad de este factor es mayor o igual a la del denominador. Si la multiplicidad de este factor es mayor en el denominador, entonces todavía hay una asíntota en ese valor.

Ejemplo$\PageIndex{6}$: Identifying Vertical Asymptotes and Removable Discontinuities for a Graph

Encuentra las asíntotas verticales y las discontinuidades removibles de la gráfica de$k(x)=\dfrac{x−2}{x^2−4}$.

Solución

Factorice el numerador y el denominador.

\[k(x)=\dfrac{x−2}{(x−2)(x+2)} \nonumber \]

Observe que hay un factor común en el numerador y el denominador,$x–2$. El cero para este factor es$x=2$. Esta es la ubicación de la discontinuidad removible.

Observe que hay un factor en el denominador que no está en el numerador,$x+2$. El cero para este factor es$x=−2$. La asíntota vertical es$x=−2$. Ver Figura$\PageIndex{12}$.

Gráfica de k (x) = (x-2)/(x-2) (x+2) con su asíntota vertical en x=-2 y una discontinuidad removible en x=2. — Figura$\PageIndex{12}$.

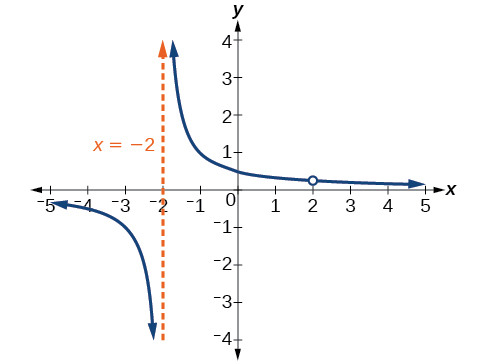
La gráfica de esta función tendrá la asíntota vertical en$x=−2$, pero en$x=2$ la gráfica tendrá un agujero.

Ejercicio$\PageIndex{5}$

Encuentra las asíntotas verticales y las discontinuidades removibles de la gráfica de$f(x)=\dfrac{x^2−25}{x^3−6x^2+5x}$.

Contestar

Discontinuidad removible en$x=5$.

Asintotas verticales:$x=0$,$x=1$.

Identificación de asíntotas horizontales de funciones racionales

Mientras que las asíntotas verticales describen el comportamiento de una gráfica ya que la salida se vuelve muy grande o muy pequeña, las asíntotas horizontales ayudan a describir el comportamiento de una gráfica ya que la entrada se vuelve muy grande o muy pequeña. Recordemos que el comportamiento final de un polinomio reflejará el del término principal. Asimismo, el comportamiento final de una función racional reflejará el del ratio de la función que es el ratio de los términos principales.

Hay tres resultados distintos al verificar las asíntotas horizontales:

Caso 1: Si el grado del denominador > grado del numerador, hay una asíntota horizontal en$y=0$.

Ejemplo:$f(x)=\dfrac{4x+2}{x^2+4x−5}$

En este caso, el comportamiento final es$f(x)≈\dfrac{4x}{x^2}=\dfrac{4}{x}$. Esto nos dice que, a medida que las entradas aumentan o disminuyen sin límite, esta función se comportará de manera similar a la función$g(x)=\dfrac{4}{x}$, y las salidas se acercarán a cero, resultando en una asíntota horizontal en$y=0$. Ver Figura$\PageIndex{13}$. Tenga en cuenta que esta gráfica cruza la asíntota horizontal.

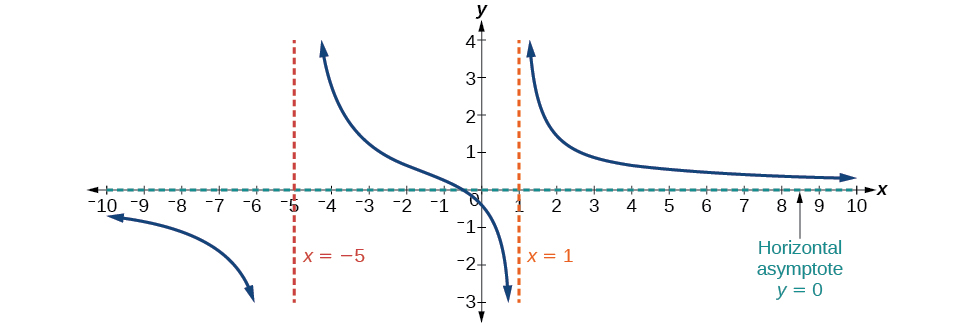
Gráfica de f (x) = (4x+2)/(x^2+4x-5) con sus asíntotas verticales en x=-5 y x=1 y su asíntota horizontal en y=0. — Figura$\PageIndex{13}$: Asintota horizontal$y=0$ cuando$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ donde grado de$p$ < grado de$q$.

Caso 2: Si el grado del denominador < grado del numerador por uno, obtenemos una asíntota inclinada.

Ejemplo:$f(x)=\dfrac{3x^2−2x+1}{x−1}$

En este caso, el comportamiento final es$f(x)≈\dfrac{3x^2}{x}=3x$. Esto nos dice que a medida que las entradas aumentan o disminuyen sin límite, esta función se comportará de manera similar a la función$g(x)=3x$. A medida que las entradas crecen grandes, las salidas crecerán y no se nivelarán, por lo que esta gráfica no tiene asíntota horizontal. No obstante, la gráfica de$g(x)=3x$ parece una línea diagonal, y dado que se$f$ comportará de manera similar a$g$, se acercará a una línea cercana a$y=3x$. Esta línea es una asíntota inclinada.

Para encontrar la ecuación de la asíntota inclinada, dividir$\dfrac{3x^2−2x+1}{x−1}$. El cociente es$3x+1$, y el resto es 2. La asíntota inclinada es la gráfica de la línea$g(x)=3x+1$. Ver Figura$\PageIndex{14}$.

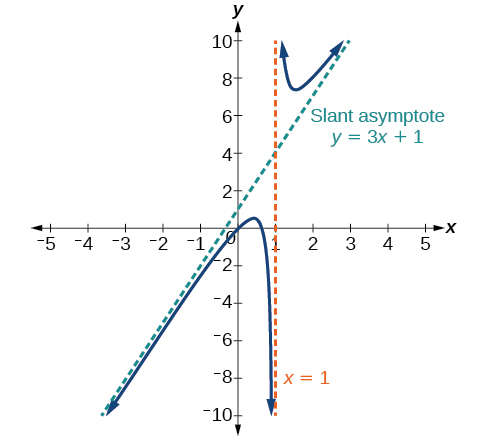
Gráfica de f (x) = (3x^2-2x+1)/(x-1) con su asíntota vertical en x=1 y una asíntota inclinada aty=3x+1. — Figura$\PageIndex{14}$: Asíntota inclinada cuando$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ donde grado de$p$ >grado de$q$ por 1.

Caso 3: Si el grado del denominador = grado del numerador, hay una asíntota horizontal en$y=\dfrac{a_n}{b_n}$, donde$a_n$ y$b_n$ son respectivamente los coeficientes principales de$p(x)$ y$q(x)$ para$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$.

Ejemplo:$f(x)=\dfrac{3x^2+2}{x^2+4x−5}$

En este caso, el comportamiento final es$f(x)≈\dfrac{3x^2}{x^2}=3$. Esto nos dice que a medida que las entradas crecen grandes, esta función se comportará como la función$g(x)=3$, que es una línea horizontal. Como$x\rightarrow \pm \infty$,$f(x)\rightarrow 3$, resultando en una asíntota horizontal en$y=3$. Ver Figura$\PageIndex{15}$. Tenga en cuenta que esta gráfica cruza la asíntota horizontal.

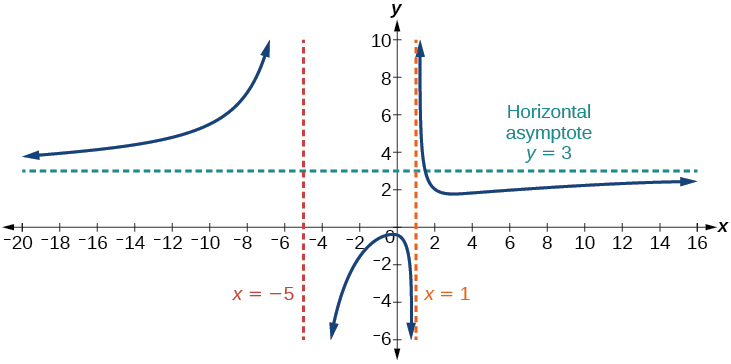
Gráfica de f (x) = (3x^2+2)/(x^2+4x-5) con sus asíntotas verticales en x=-5 y x=1 y su asíntota horizontal en y=3. — Figura$\PageIndex{15}$: Asintota horizontal cuando$f(x)=\dfrac{p(x)}{q(x)}$,$q(x)≠0$ donde grado de$p$ = grado de$q$.

Observe que, mientras que la gráfica de una función racional nunca cruzará una asíntota vertical, la gráfica puede o no cruzar una asíntota horizontal o inclinada. Además, aunque la gráfica de una función racional puede tener muchas asíntotas verticales, la gráfica tendrá como máximo una asíntota horizontal (o inclinada).

Cabe señalar que, si el grado del numerador es mayor que el grado del denominador en más de uno, el comportamiento final de la gráfica imitará el comportamiento de la fracción de comportamiento final reducido. Por ejemplo, si tuviéramos la función

\[f(x)=\dfrac{3x^5−x^2}{x+3} \nonumber \]

con comportamiento final

\[f(x)≈\dfrac{3x^5}{x}=3x^4 \nonumber \]

el comportamiento final de la gráfica se vería similar al de un polinomio par con un coeficiente inicial positivo.

$x\rightarrow \pm \infty, f(x)\rightarrow \infty$

ASÍNTOTAS HORIZONTALES DE FUNCIONES

La asíntota horizontal de una función racional se puede determinar observando los grados del numerador y denominador.

El grado de numerador es menor que el grado de denominador: asíntota horizontal en$y=0$.
El grado de numerador es mayor que el grado de denominador por uno: ninguna asíntota horizontal; asíntota inclinada.
El grado de numerador es igual al grado de denominador: asíntota horizontal en relación de coeficientes principales.

Ejemplo$\PageIndex{7}$: Identifying Horizontal and Slant Asymptotes

Para las funciones enumeradas, identifique la asíntota horizontal o inclinada.

$g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}$
$h(x)=\dfrac{x^2−4x+1}{x+2}$
$k(x)=\dfrac{x^2+4x}{x^3−8}$

Solución

Para estas soluciones, vamos a utilizar$f(x)=\dfrac{p(x)}{q(x)},\space q(x)≠0$.

$g(x)=\dfrac{6x^3−10x}{2x^3+5x^2}$: El grado de$p = $ grado de$q=3$, así podemos encontrar la asíntota horizontal tomando la proporción de los términos principales. Hay una asíntota horizontal en$y =\frac{6}{2}$ o$y=3$.
$h(x)=\dfrac{x^2−4x+1}{x+2}$: El grado de$p=2$ y grado de$q=1$. Ya que$p>q$ por 1, hay una asíntota inclinada encontrada en$\dfrac{x^2−4x+1}{x+2}$.
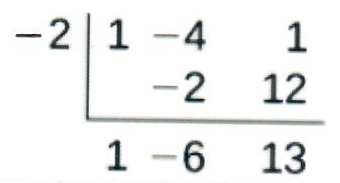
$clipboard_e5ff4f00a1466e92caa3ddac0dac32f5b.png$
$k(x)=\dfrac{x^2+4x}{x^3−8}$: El grado de$p=2$ < grado de$q=3$, por lo que hay una asíntota horizontal$y=0$.

Ejemplo$\PageIndex{8}$ Identifying Horizontal Asymptotes

En el problema de concentración de azúcar antes, creamos la ecuación$C(t)=\dfrac{5+t}{100+10t}$.

Encontrar la asíntota horizontal e interpretarla en contexto del problema.

Solución

Tanto el numerador como el denominador son lineales (grado 1). Debido a que los grados son iguales, habrá una asíntota horizontal en la relación de los coeficientes iniciales. En el numerador, el término principal es$t$, con coeficiente 1. En el denominador, el término principal es 10t, con coeficiente 10. La asíntota horizontal estará en la relación de estos valores:

$t\rightarrow \infty,\space C(t)\rightarrow \frac{1}{10}$

Esta función tendrá una asíntota horizontal en$y=\frac{1}{10}$.

Esto nos dice que a medida que los valores de$t$ incremento, los valores de$C$ voluntad se acercan$\frac{1}{10}$. En contexto, esto significa que, a medida que pasa más tiempo, la concentración de azúcar en el tanque se acercará a una décima parte de libra de azúcar por galón de agua o$\frac{1}{10}$ libras por galón.

Ejemplo$\PageIndex{9}$: Identifying Horizontal and Vertical Asymptotes

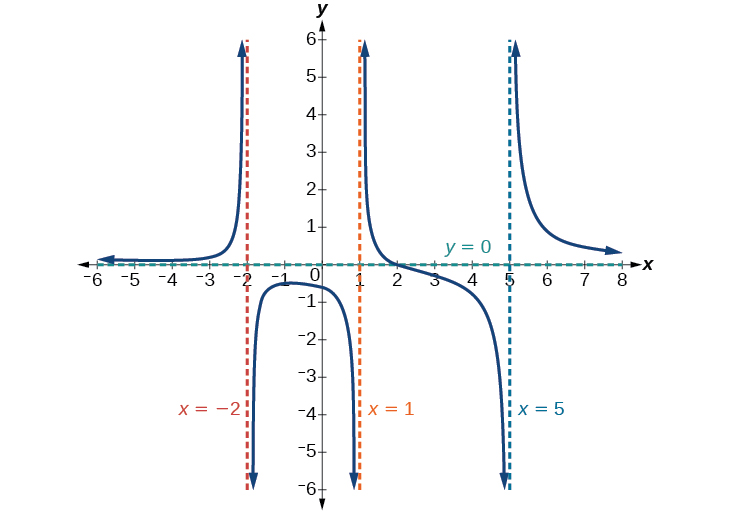
Encuentra las asíntotas horizontales y verticales de la función$f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}$

Solución

Primero, tenga en cuenta que esta función no tiene factores comunes, por lo que no hay discontinuidades removibles potenciales.

La función tendrá asíntotas verticales cuando el denominador sea cero, haciendo que la función esté indefinida. El denominador será cero en$x=1,–2,$ y$5$, indicando asíntotas verticales en estos valores.

El numerador tiene grado$2$, mientras que el denominador tiene grado 3. Dado que el grado del denominador es mayor que el grado del numerador, el denominador crecerá más rápido que el numerador, provocando que las salidas tiendan hacia cero a medida que las entradas se hacen grandes, y así como$x\rightarrow \pm \infty$,$f(x)\rightarrow 0$. Esta función tendrá una asíntota horizontal en$y =0.$ Ver Figura$\PageIndex{16}$.

Gráfica de f (x) = (x-2) (x+3)/(x-1) (x+2) (x-5) con sus asíntotas verticales en x=-2, x=1, y x=5 y su asíntota horizontal en y=0. — Figura$\PageIndex{16}$.

Ejercicio$\PageIndex{6}$

Encuentra las asíntotas verticales y horizontales de la función:

$f(x)=\dfrac{(2x−1)(2x+1)}{(x−2)(x+3)}$

Contestar

asíntotas verticales en$x=2$ y$x=–3$

asíntota horizontal en$y =4$.

INTERCEPCIONES DE FUNCIONES RACI

Una función racional tendrá una$y$ -intercepción en$f(0),$ si la función se define en cero. Una función racional no tendrá un$y$ -intercept si la función no está definida en cero.

De igual manera, una función racional tendrá$x$ -intercepciones en las entradas que hacen que la salida sea cero. Dado que una fracción solo es igual a cero cuando el numerador es cero, las intercepciones x solo pueden ocurrir cuando el numerador de la función racional es igual a cero.

Ejemplo$\PageIndex{10}$: Finding the Intercepts of a Rational Function

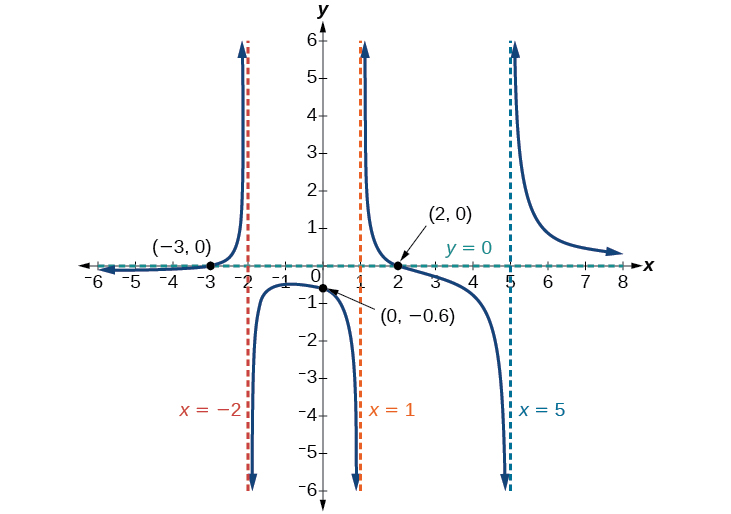
Encuentra las intercepciones de $f(x)=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)}$.

Solución

Podemos encontrar la intercepción y evaluando la función en cero

$f(0)=\dfrac{(0−2)(0+3)}{(0−1)(0+2)(0−5)}$

$=−\dfrac{6}{10}$

$=−\dfrac{3}{5}$

$=−0.6$

Las intercepciones x ocurrirán cuando la función sea igual a cero:

\[ 0=\dfrac{(x−2)(x+3)}{(x−1)(x+2)(x−5)} \text{ This is zero when the numerator is zero.} \nonumber \]

\[ 0=(x−2)(x+3) \qquad \qquad \qquad \qquad \qquad \nonumber \]

\[ x=2, x=−3 \qquad \qquad \qquad \qquad \qquad \nonumber \]

La intercepción y es$(0,–0.6)$, las intercepciones x son$(2,0)$ y$(–3,0)$. Ver Figura$\PageIndex{17}$.

Gráfica de f (x) = (x-2) (x+3)/(x-1) (x+2) (x-5) con sus asíntotas verticales en x=-2, x=1 y x=5, su asíntota horizontal en y=0, y sus intercepciones en (-3, 0), (0, -0.6) y (2, 0). — Figura$\PageIndex{17}$.

Ejercicio$\PageIndex{7}$

Dada la función cuadrada recíproca que se desplaza hacia la derecha 3 unidades y hacia abajo 4 unidades, escriba esto como una función racional. Luego, encuentra las intercepciones x e y y las asíntotas horizontales y verticales.

Contestar

Para la función cuadrada recíproca transformada, encontramos la forma racional.

$f(x)=\dfrac{1}{{(x−3)}^2}−4=\dfrac{1−4{(x−3)}^2}{{(x−3)}^2}=\dfrac{1−4(x^2−6x+9)}{(x−3)(x−3)}=\dfrac{−4x^2+24x−35}{x^2−6x+9}$

Debido a que el numerador es el mismo grado que el denominador sabemos que como$x\rightarrow \pm \infty$,$f(x)\rightarrow −4$; así$y=–4$ es la asíntota horizontal. A continuación, establecemos el denominador igual a cero, y encontramos que la asíntota vertical es$x=3$, porque as$x\rightarrow 3$,$f(x)\rightarrow \infty$. Luego establecemos el numerador igual a$0$ y encontramos que las intercepciones x están en$(2.5,0)$ y$(3.5,0)$. Finalmente, evaluamos la función en 0 y encontramos que la intercepción y está en$(0,−\frac{35}{9})$.

Graficar funciones racionales

En Ejemplo$\PageIndex{10}$, vemos que el numerador de una función racional revela las x -intercepciones de la gráfica, mientras que el denominador revela las asíntotas verticales de la gráfica. Al igual que con los polinomios, los factores del numerador pueden tener potencias enteras mayores a uno. Afortunadamente, el efecto sobre la forma de la gráfica en esas intercepciones es el mismo que vimos con polinomios.

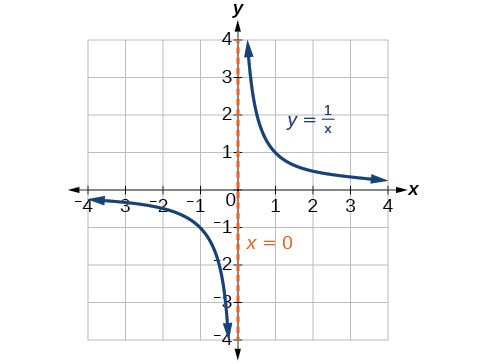
Las asíntotas verticales asociadas a los factores del denominador reflejarán una de las dos funciones recíprocas del kit de herramientas. Cuando el grado del factor en el denominador es impar, la característica distintiva es que en un lado de la asíntota vertical la gráfica se dirige hacia el infinito positivo, y en el otro lado la gráfica se dirige hacia el infinito negativo. Ver Figura$\PageIndex{18}$.

Gráfica de y=1/x con su asíntota vertical en x=0. — Figura$\PageIndex{18}$.

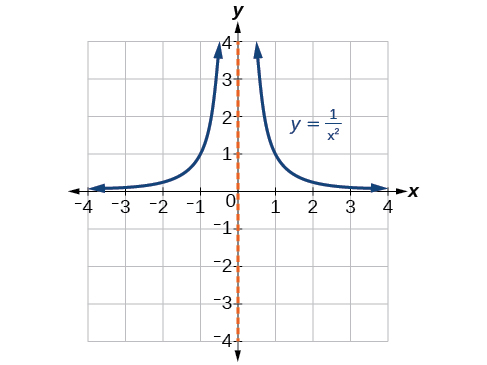
Cuando el grado del factor en el denominador es par, la característica distintiva es que la gráfica se dirige hacia el infinito positivo en ambos lados de la asíntota vertical o se dirige hacia el infinito negativo en ambos lados. Ver Figura$\PageIndex{19}$.

Gráfica de y=1/x^2 con su asíntota vertical en x=0. — Figura$\PageIndex{19}$.

Por ejemplo, la gráfica de $f(x)=\dfrac{{(x+1)}^2(x−3)}{{(x+3)}^2(x−2)}$se muestra en la Figura$\PageIndex{20}$.

Gráfica de f (x) = (x+1) ^2 (x-3)/(x+3) ^2 (x-2) con sus asíntotas verticales en x=-3 y x=2, su asíntota horizontal en y=1, y sus intercepciones en (-1, 0), (0, 1/6) y (3, 0). — Figura$\PageIndex{20}$.

En la intercepción x$x=−1$ correspondiente al${(x+1)}^2$ factor del numerador, la gráfica “rebota”, consistente con la naturaleza cuadrática del factor.
En la intercepción x$x=3$ correspondiente al$(x−3)$ factor del numerador, la gráfica pasa por el eje como cabría esperar de un factor lineal.
En la asíntota vertical$x=−3$ correspondiente al${(x+3)}^2$ factor del denominador, la gráfica se dirige hacia el infinito positivo en ambos lados de la asíntota, consistente con el comportamiento de la función$f(x)=\dfrac{1}{x^2}$.
En la asíntota vertical$x=2$, correspondiente al$(x−2)$ factor del denominador, la gráfica se dirige hacia el infinito positivo en el lado izquierdo de la asíntota y hacia el infinito negativo en el lado derecho, consistente con el comportamiento de la función$f(x)=\dfrac{1}{x}$.

Cómo: Dada una función racional, esbozar una gráfica.

Evalúe la función en 0 para encontrar la intersección y.
Factorice el numerador y el denominador.
Para factores en el numerador no comunes al denominador, determinar donde cada factor del numerador es cero para encontrar las intercepciones x.
Encuentra las multiplicidades de las intercepciones x para determinar el comportamiento de la gráfica en esos puntos.
Para los factores en el denominador, anotar las multiplicidades de los ceros para determinar el comportamiento local. Para aquellos factores no comunes al numerador, encuentre las asíntotas verticales estableciendo esos factores iguales a cero y luego resuelva.
Para factores en el denominador comunes a factores en el numerador, encuentre las discontinuidades removibles estableciendo esos factores iguales a 0 y luego resuelva.
Comparar los grados del numerador y el denominador para determinar las asíntotas horizontales o inclinadas.
Esbozar la gráfica.

Ejemplo$\PageIndex{11}$: Graphing a Rational Function

Esbozar una gráfica de$f(x)=\frac{(x+2)(x−3)}{{(x+1)}^2(x−2)}$.

Solución

Podemos comenzar por señalar que la función ya está factorizada, ahorrándonos un paso.

A continuación, encontraremos los interceptos. Evaluar la función en cero da la intersección y:

$f(0)=\dfrac{(0+2)(0−3)}{{(0+1)}^2(0−2)}=3$

Para encontrar las intercepciones x, determinamos cuándo el numerador de la función es cero. Al establecer cada factor igual a cero, encontramos intercepciones x en$x=–2$ y$x=3$. En cada uno, el comportamiento será lineal (multiplicidad 1), con la gráfica pasando por la intercepción.

Tenemos una intercepción$(0,3)$ y en e intercepta x en$(–2,0)$ y$(3,0)$.

Para encontrar las asíntotas verticales, determinamos cuándo el denominador es igual a cero. Esto ocurre cuando$x+1=0$ y cuando$x–2=0$, dándonos asíntotas verticales en$x=–1$ y$x=2$.

No hay factores comunes en el numerador y denominador. Esto significa que no hay discontinuidades removibles.

Por último, el grado de denominador es mayor que el grado del numerador, diciéndonos que esta gráfica tiene una asíntota horizontal en$y =0$.

Para bosquejar la gráfica, podríamos comenzar trazando las tres intercepciones. Dado que la gráfica no tiene intercepciones x entre las asíntotas verticales, y la intercepción y es positiva, sabemos que la función debe permanecer positiva entre las asíntotas, dejándonos rellenar la porción media de la gráfica como se muestra en la Figura$\PageIndex{21}$.

Gráfica de solo la porción media de f (x) = (x+2) (x-3)/(x+1) ^2 (x-2) con sus intercepciones en (-2, 0), (0, 3) y (3, 0). — Figura$\PageIndex{21}$.

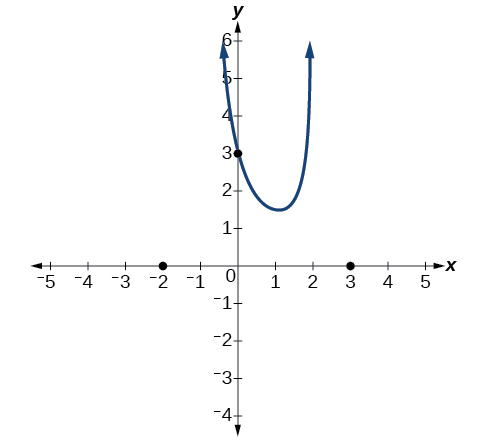
El factor asociado a la asíntota vertical$x=−1$ fue cuadrado, por lo que sabemos que el comportamiento será el mismo en ambos lados de la asíntota. La gráfica se dirige hacia el infinito positivo a medida que las entradas se acercan a la asíntota de la derecha, por lo que la gráfica también se dirigirá hacia el infinito positivo a la izquierda.

Para la asíntota vertical at$x=2$, el factor no fue cuadrado, por lo que la gráfica tendrá un comportamiento opuesto a cada lado de la asíntota. Ver Figura$\PageIndex{22}$. Después de pasar por las intercepciones x, la gráfica se nivelará hacia una salida de cero, como lo indica la asíntota horizontal.

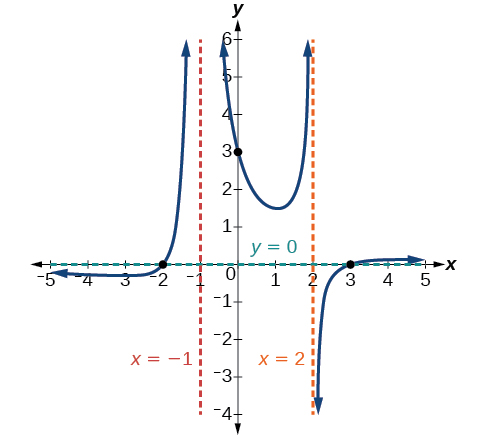
Gráfica de f (x) = (x+2) (x-3)/(x+1) ^2 (x-2) con sus asíntotas verticales en x=-1 y x=2, su asíntota horizontal en y=0, y sus intercepciones en (-2, 0), (0, 3) y (3, 0). — Figura$\PageIndex{22}$.

Ejercicio$\PageIndex{8}$

Dada la función$f(x)=\frac{{(x+2)}^2(x−2)}{2{(x−1)}^2(x−3)}$, utilizar las características de polinomios y funciones racionales para describir su comportamiento y esbozar la función.

Contestar

Asíntota horizontal en$y=\frac{1}{2}$. Asíntotas verticales en$x=1$ y$x=3$. y-interceptar en$(0,\frac{4}{3})$.

x-intercepta en$(2,0)$ y$(–2,0)$. $(–2,0)$es un cero con multiplicidad$2$, y la gráfica rebota en el eje x en este punto. $(2,0)$es un solo cero y la gráfica cruza el eje en este punto.

Gráfica de f (x) = (x+2) ^2 (x-2) /2 (x-1) ^2 (x-3) con sus asíntotas verticales y horizontales. — Figura$\PageIndex{23}$.

Escribir funciones racionales

Ahora que hemos analizado las ecuaciones para funciones racionales y cómo se relacionan con una gráfica de la función, podemos usar la información dada por una gráfica para escribir la función. Una función racional escrita en forma factorizada tendrá una intercepción x donde cada factor del numerador es igual a cero. (Se produce una excepción en el caso de una discontinuidad removible). Como resultado, podemos formar un numerador de una función cuya gráfica pasará por un conjunto de intercepciones x introduciendo un conjunto de factores correspondientes. Asimismo, debido a que la función tendrá una asíntota vertical donde cada factor del denominador es igual a cero, podemos formar un denominador que producirá las asíntotas verticales introduciendo un conjunto de factores correspondiente.

ESCRITURA FUNCIONES RACIONALES DESDE INTERCEPCIONES Y

Si una función racional tiene intercepciones x en$x=x_1,x_2,...,x_n$, asíntotas verticales en$x=v_1,v_2,…,v_m$, y$x_i=$ ninguna$v_j$, entonces la función se puede escribir en la forma:

$f(x)=a\dfrac{ {(x−x_1)}^{p_1} {(x−x_2)}^{p_2}⋯{(x−x_n)}^{p_n} }{ {(x−v_1)}^{q_1} {(x−v_2)}^{q_2}⋯{(x−v_m)}^{q_n}}$

donde las potencias$p_i$ o$q_i$ sobre cada factor pueden determinarse por el comportamiento de la gráfica en la intercepción o asíntota correspondiente, y el factor de estiramiento$a$ puede determinarse dado un valor de la función distinto de la intercepción x o por la asíntota horizontal si es distinto de cero.

Dada una gráfica de una función racional, escribe la función.

Determinar los factores del numerador. Examinar el comportamiento de la gráfica en las intercepciones x para determinar los ceros y sus multiplicidades. (Esto es fácil de hacer cuando se encuentra la función “más simple” con pequeñas multiplicidades, como 1 o 3, pero puede ser difícil para multiplicidades más grandes, como 5 o 7, por ejemplo).
Determinar los factores del denominador. Examinar el comportamiento en ambos lados de cada asíntota vertical para determinar los factores y sus poderes.
Usa cualquier punto claro en la gráfica para encontrar el factor de estiramiento.

Ejemplo$\PageIndex{12}$: Writing a Rational Function from Intercepts and Asymptotes

Escribe una ecuación para la función racional que se muestra en la Figura$\PageIndex{24}$.

Gráfica de una función racional. — Figura$\PageIndex{24}$.

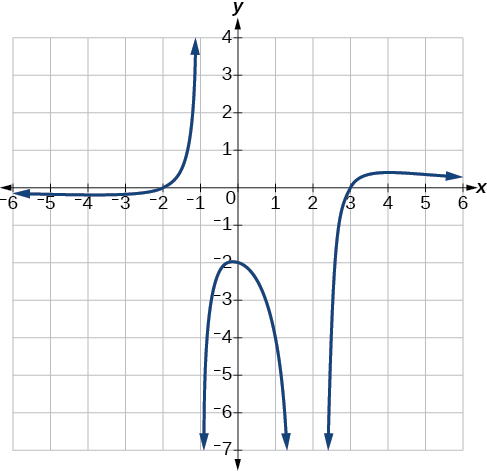
Solución

La gráfica parece tener intercepciones x en$x=–2$ y$x=3$. En ambos, la gráfica pasa por la intercepción, sugiriendo factores lineales. La gráfica tiene dos asíntotas verticales. El de$x=–1$ parece exhibir el comportamiento básico similar al de$\dfrac{1}{x}$, con la gráfica dirigiéndose hacia el infinito positivo en un lado y dirigiéndose hacia el infinito negativo en el otro. La asíntota en$x=2$ presenta un comportamiento similar al de$\dfrac{1}{x^2}$, con la gráfica dirigiéndose hacia el infinito negativo en ambos lados de la asíntota. Ver Figura$\PageIndex{25}$.

Gráfica de una función racional que denota sus asíntotas verticales e intercepciones x. — Figura$\PageIndex{25}$.

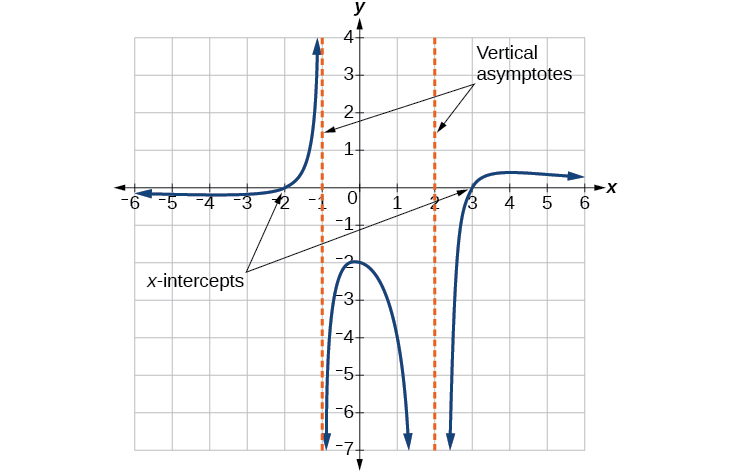
Podemos usar esta información para escribir una función del formulario

$f(x)=a\dfrac{(x+2)(x−3)}{(x+1){(x−2)}^2}$

Para encontrar el factor de estiramiento, podemos usar otro punto claro en la gráfica, como la intercepción y$(0,–2)$.

$−2=a\dfrac{(0+2)(0−3)}{(0+1){(0−2)}^2}$

$-2=a\dfrac{−6}{4}$

$a=\dfrac{−8}{−6}=\dfrac{4}{3}$

Esto nos da una función final de$f(x)=\dfrac{4(x+2)(x−3)}{3(x+1){(x−2)}^2}$.

Medios

Acceda a estos recursos en línea para obtener instrucción adicional y práctica con funciones racionales.

Ecuaciones Clave

Función Racional$ \qquad $$f(x)=\dfrac{P(x)}{Q(x)}=\dfrac{a_px^p+a_{p−1}x^{p−1}+...+a_1x+a_0}{b_qx^q+b_{q−1}x^{q−1}+...+b_1x+b_0},\space Q(x)≠0$

Conceptos clave

Podemos usar la notación de flecha para describir el comportamiento local y el comportamiento final de las funciones del kit de herramientas$f(x)=\frac{1}{x}$ y$f(x)=\frac{1}{x^2}$. Ver Ejemplo$\PageIndex{1}$.
Una función que se nivela en un valor horizontal tiene una asíntota horizontal. Una función puede tener más de una asíntota vertical. Ver Ejemplo.
Los problemas de aplicación que involucran tasas y concentraciones a menudo involucran funciones racionales. Ver Ejemplo.
El dominio de una función racional incluye todos los números reales excepto aquellos que hacen que el denominador sea igual a cero. Ver Ejemplo.
Las asíntotas verticales de una función racional ocurrirán donde el denominador de la función es igual a cero y el numerador no es cero. Ver Ejemplo.
Una discontinuidad removible podría ocurrir en la gráfica de una función racional si una entrada hace que tanto el numerador como el denominador sean cero. Ver Ejemplo.
El comportamiento final de una función racional reflejará el de la relación de los términos principales de las funciones numerador y denominador. Ver Ejemplo, Ejemplo, Ejemplo y Ejemplo.
Graficar las funciones racionales mediante la búsqueda de las intercepciones, el comportamiento en las intercepciones y asíntotas, y el comportamiento final. Ver Ejemplo.
Si una función racional tiene intercepciones x en$x=x_1,x_2,…,x_n$, asíntotas verticales en$x=v_1,v_2,…,v_m$, y$x_i=$ ninguna$v_j$, entonces la función se puede escribir en la forma

Símbolo	Significado
\(x\rightarrow a^-\)	\(x\)se acerca a una desde la izquierda (\(x<a\)pero cerca de\(a\))
\(x\rightarrow a^+\)	\(x\)se acerca a una desde la derecha (\(x>a\)pero cerca de\(a\))
\(x\rightarrow \infty\)	\(x\)se acerca al infinito (\(x\)aumenta sin límite)
\(x\rightarrow −\infty\)	\(x\)se acerca al infinito negativo (\(x\)disminuye sin límite)
\(f(x)\rightarrow \infty\)	la salida se acerca al infinito (la salida aumenta sin límite)
\(f(x)\rightarrow −\infty\)	la salida se acerca al infinito negativo (la salida disminuye sin límite)
\(f(x)\rightarrow a\)	los enfoques de salida\(a\)

Search

Text Color

Text Size

Margin Size

Font Type

Ecuaciones Clave

Conceptos clave

\(x\)	—0.1	—0.01	—0.001	—0.0001
\(f(x)=\frac{1}{x}\)	—10	—100	—1000	—10,000

Uso de la notación de flecha

Comportamiento Local de\(f(x)=\frac{1}{x}\)

Comportamiento final de\(f(x)=\frac{1}{x}\)

Resolución de problemas aplicados que involucran funciones racionales

Encontrar los dominios de las funciones racionales

Identificación de asíntotas verticales de funciones racionales

Aíntotas Verticales

Discontinuidades removibles

Identificación de asíntotas horizontales de funciones racionales

Graficar funciones racionales

Escribir funciones racionales

Ecuaciones Clave

Conceptos clave