4.4: Gráficas de funciones logarítmicas
- Page ID
- 121437
- Identificar el dominio de una función logarítmica.
- Gráfica funciones logarítmicas.
En la Sección de Gráficas de Funciones Exponenciales, vimos cómo crear una representación gráfica de un modelo exponencial nos da otra capa de conocimiento para predecir eventos futuros. ¿Cómo las gráficas logarítmicas nos dan una idea de las situaciones? Debido a que cada función logarítmica es la función inversa de una función exponencial, podemos pensar en cada salida en una gráfica logarítmica como la entrada para la ecuación exponencial inversa correspondiente. En otras palabras, los logaritmos dan la causa de un efecto.
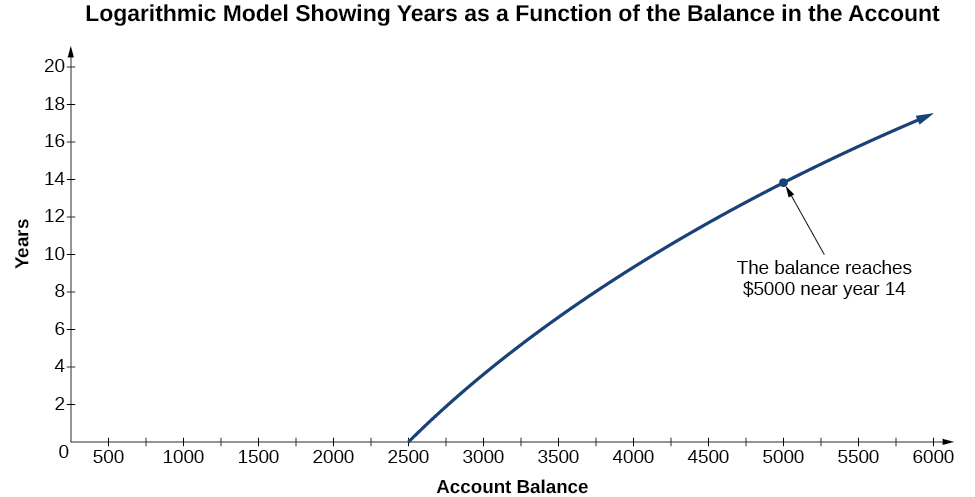
Para ilustrar, supongamos que invertimos\($2500\) en una cuenta que ofrezca una tasa de interés anual del 5%, compuesta continuamente. Ya sabemos que el saldo en nuestra cuenta para cualquier año se\(t\) puede encontrar con la ecuación\(A=2500e^{0.05t}\).
Pero, ¿y si quisiéramos saber el año para cualquier saldo? Tendríamos que crear una nueva función correspondiente intercambiando la entrada y la salida; así necesitaríamos crear un modelo logarítmico para esta situación. Al graficar el modelo, podemos ver la salida (año) para cualquier entrada (saldo de cuenta). Por ejemplo, ¿y si quisiéramos saber cuántos años tardaría en duplicarse nuestra inversión inicial? La figura\(\PageIndex{1}\) muestra este punto en la gráfica logarítmica.
En esta sección discutiremos los valores para los que se define una función logarítmica, y luego volveremos nuestra atención a graficar la familia de funciones logarítmicas.
Encontrar el dominio de una función logarítmica
Antes de trabajar con gráficas, echaremos un vistazo al dominio (el conjunto de valores de entrada) para el que se define la función logarítmica.
Recordemos que la función exponencial se define como\(y=b^x\) para cualquier número real\(x\) y constante\(b>0\),\(b≠1\), donde
- El dominio de\(y\) es\((−\infty,\infty)\).
- El rango de\(y\) es\((0,\infty)\).
En la última sección aprendimos que la función logarítmica\(y={\log}_b(x)\) es la inversa de la función exponencial\(y=b^x\). Entonces, como funciones inversas:
- El dominio de\(y={\log}_b(x)\) es el rango de\(y=b^x\):\((0,\infty)\).
- El rango de\(y={\log}_b(x)\) es el dominio de\(y=b^x\):\((−\infty,\infty)\).
Las transformaciones de la función padre\(y={\log}_b(x)\) se comportan de manera similar a las de otras funciones. Al igual que con otras funciones padre, podemos aplicar los cuatro tipos de transformaciones (desplazamientos, estiramientos, compresiones y reflexiones) a la función padre sin pérdida de forma.
En Gráficas de Funciones Exponenciales vimos que ciertas transformaciones pueden cambiar el rango de\(y=b^x\). Del mismo modo, aplicar transformaciones a la función padre\(y={\log}_b(x)\) puede cambiar el dominio. Al encontrar el dominio de una función logarítmica, por lo tanto, es importante recordar que el dominio consiste únicamente en números reales positivos. Es decir, el argumento de la función logarítmica debe ser mayor que cero.
Por ejemplo, considere\(f(x)={\log}_4(2x−3)\). Esta función se define para cualquier valor de\(x\) tal manera que el argumento, en este caso\(2x−3\), sea mayor que cero. Para encontrar el dominio, establecemos una desigualdad y resolvemos\(x\):
\[\begin{align*} 2x-3&> 0 \qquad \text {Show the argument greater than zero}\\ 2x&> 3 \qquad \text{Add 3} \\ x&> 1.5 \qquad \text{Divide by 2} \\ \end{align*}\]
En notación de intervalos, el dominio de\(f(x)={\log}_4(2x−3)\) is\((1.5,\infty)\).
- Establecer una desigualdad mostrando el argumento mayor que cero.
- Resolver para\(x\).
- Escribe el dominio en notación de intervalos.
¿De qué es el dominio\(f(x)={\log}_2(x+3)\)?
Solución
La función logarítmica se define solo cuando la entrada es positiva, por lo que esta función se define cuando\(x+3>0\). Resolviendo esta desigualdad,
\[\begin{align*} x+3&> 0 \qquad \text{The input must be positive}\\ x&> -3 \qquad \text{Subtract 3} \end{align*}\]
El dominio de\(f(x)={\log}_2(x+3)\) es\((−3,\infty)\).
¿De qué es el dominio\(f(x)={\log}_5(x−2)+1\)?
- Contestar
-
\((2,\infty)\)
¿De qué es el dominio\(f(x)=\log(5−2x)\)?
Solución
La función logarítmica se define solo cuando la entrada es positiva, por lo que esta función se define cuando\(5–2x>0\). Resolviendo esta desigualdad,
\[\begin{align*} 5-2x&> 0 \qquad \text{The input must be positive}\\ -2x&> -5 \qquad \text{Subtract 5}\\ x&< \dfrac{5}{2} \qquad \text{Divide by -2 and switch the inequality} \end{align*}\]
El dominio de\(f(x)=\log(5−2x)\) es\(\left(–\infty,\dfrac{5}{2}\right)\).
¿De qué es el dominio\(f(x)=\log(x−5)+2\)?
- Contestar
-
\((5,\infty)\)
Graficar funciones logarítmicas
Ahora que tenemos una idea del conjunto de valores para los que se define una función logarítmica, pasamos a graficar funciones logarítmicas. La familia de funciones logarítmicas incluye la función padre\(y={\log}_b(x)\) junto con todas sus transformaciones: desplazamientos, estiramientos, compresiones y reflexiones.
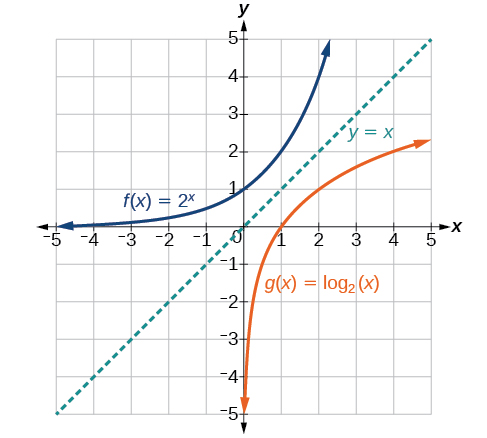
Comenzamos con la función padre\(y={\log}_b(x)\). Debido a que cada función logarítmica de esta forma es la inversa de una función exponencial con la forma\(y=b^x\), sus gráficas serán reflejos entre sí a través de la línea\(y=x\). Para ilustrar esto, podemos observar la relación entre los valores de entrada y salida de\(y=2^x\) y su equivalente\(x={\log}_2(y)\) en Table\(\PageIndex{1}\).
| \(x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
|---|---|---|---|---|---|---|---|
| \(2^x=y\) | \(\dfrac{1}{8}\) | \(\dfrac{1}{4}\) | \(\dfrac{1}{2}\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \({\log}_2(y)=x\) | \(−3\) | \(−2\) | \(−1\) | \(0\) | \(1\) | \(2\) | \(3\) |
Utilizando las entradas y salidas de Table\(\PageIndex{1}\), podemos construir otra tabla para observar la relación entre puntos en las gráficas de las funciones inversas\(f(x)=2^x\) y\(g(x)={\log}_2(x)\). Ver Tabla\(\PageIndex{2}\).
| \(f(x)=2^x\) | \(\left(−3,\dfrac{1}{8}\right)\) | \(\left(−2,\dfrac{1}{4}\right)\) | \(\left(−1,\dfrac{1}{2}\right)\) | \((0,1)\) | \((1,2)\) | \((2,4)\) | \((3,8)\) |
|---|---|---|---|---|---|---|---|
| \(g(x)={\log}_2(x)\) | \(\left(\dfrac{1}{8},−3\right)\) | \(\left(\dfrac{1}{4},−2\right)\) | \(\left(\dfrac{1}{2},−1\right)\) | \((1,0)\) | \((2,1)\) | \((4,2)\) | \((8,3)\) |
Como era de esperar, las\(y\) coordenadas\(x\) - y -se invierten para las funciones inversas. La figura\(\PageIndex{2}\) muestra la gráfica de\(f\) y\(g\).
Observe lo siguiente de la gráfica:
- \(f(x)=2^x\)tiene una\(y\) -intercepción en\((0,1)\) y\(g(x)={\log}_2(x)\) tiene una\(x\) - intercepción en\((1,0)\).
- El dominio de\(f(x)=2^x\),\((−\infty,\infty)\), es el mismo que el rango de\(g(x)={\log}_2(x)\).
- El rango de\(f(x)=2^x\),\((0,\infty)\), es el mismo que el dominio de\(g(x)={\log}_2(x)\).
Para cualquier número real\(x\) y constante\(b>0\),\(b≠1\), podemos ver las siguientes características en la gráfica de\(f(x)={\log}_b(x)\):
- función uno-a-uno
- asíntota vertical:\(x=0\)
- dominio:\((0,\infty)\)
- rango:\((−\infty,\infty)\)
- \(x\)- intercepción:\((1,0)\) y punto clave\((b,1)\)
- \(y\)-interceptar: ninguno
- aumentando si\(b>1\)
- decreciente si\(0<b<1\)
Ver Figura\(\PageIndex{3}\).
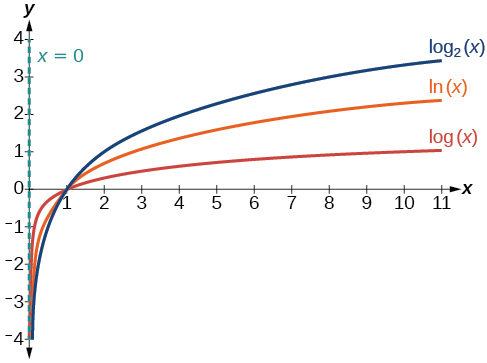
La figura\(\PageIndex{4}\) muestra cómo cambiar la base\(b\) en\(f(x)={\log}_b(x)\) puede afectar a las gráficas. Observe que las gráficas se comprimen verticalmente a medida que aumenta el valor de la base. (Nota: recuerde que la función\(\ln(x)\) tiene base\(e≈2.718\).)
- Dibujar y etiquetar la asíntota vertical,\(x=0\).
- Trazar la x- intercepción,\((1,0)\).
- Trazar el punto clave\((b,1)\).
- Dibuja una curva suave a través de los puntos.
- Indicar el dominio\((0,\infty)\),, el rango\((−\infty,\infty)\), y la asíntota vertical,\(x=0\).
Gráfica\(f(x)={\log}_5(x)\). Declarar el dominio, el rango y la asíntota.
Solución
Antes de graficar, identifique el comportamiento y los puntos clave para la gráfica.
- Ya que\(b=5\) es mayor que uno, sabemos que la función va en aumento. La cola izquierda de la gráfica se acercará a la asíntota vertical\(x=0\), y la cola derecha aumentará lentamente sin atarse.
- El\(x\) -intercepto es\((1,0)\).
- El punto clave\((5,1)\) está en la gráfica.
- Dibujamos y etiquetamos la asíntota, trazamos y etiquetamos los puntos, y dibujamos una curva suave a través de los puntos (ver Figura\(\PageIndex{5}\)).
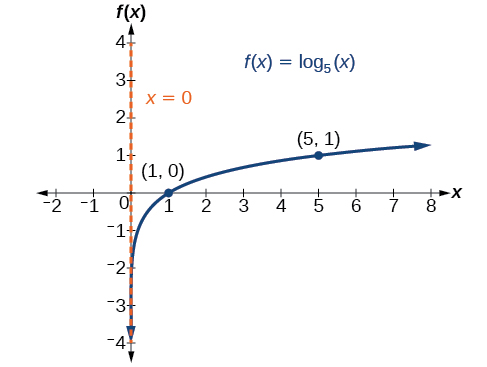
El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Gráfica\(f(x)={\log}_{\tfrac{1}{5}}(x)\). Declarar el dominio, el rango y la asíntota.
- Contestar
-
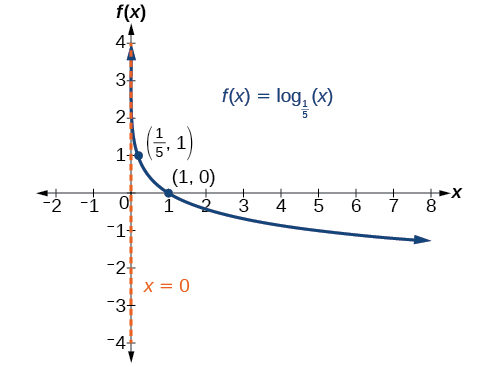
Figura\(\PageIndex{6}\) El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Graficando transformaciones de funciones logarítmicas
Como mencionamos al inicio de la sección, las transformaciones de las gráficas logarítmicas se comportan de manera similar a las de otras funciones padre. Podemos cambiar, estirar, comprimir y reflejar la función padre\(y={\log}_b(x)\) sin pérdida de forma.
Graficando un Desplazamiento Horizontal de\(f(x) = log_b(x)\)
Cuando\(c\) se agrega una constante a la entrada de la función padre\(f(x)={\log}_b(x)\), el resultado es un desplazamiento horizontal de\(c\) unidades en la dirección opuesta al signo encendido\(c\). Para visualizar los desplazamientos horizontales, podemos observar la gráfica general de la función padre\(f(x)={\log}_b(x)\) y para\(c>0\) junto al desplazamiento a la izquierda,\(g(x)={\log}_b(x+c)\), y el desplazamiento a la derecha,\(h(x)={\log}_b(x−c)\). Ver Figura\(\PageIndex{7}\).
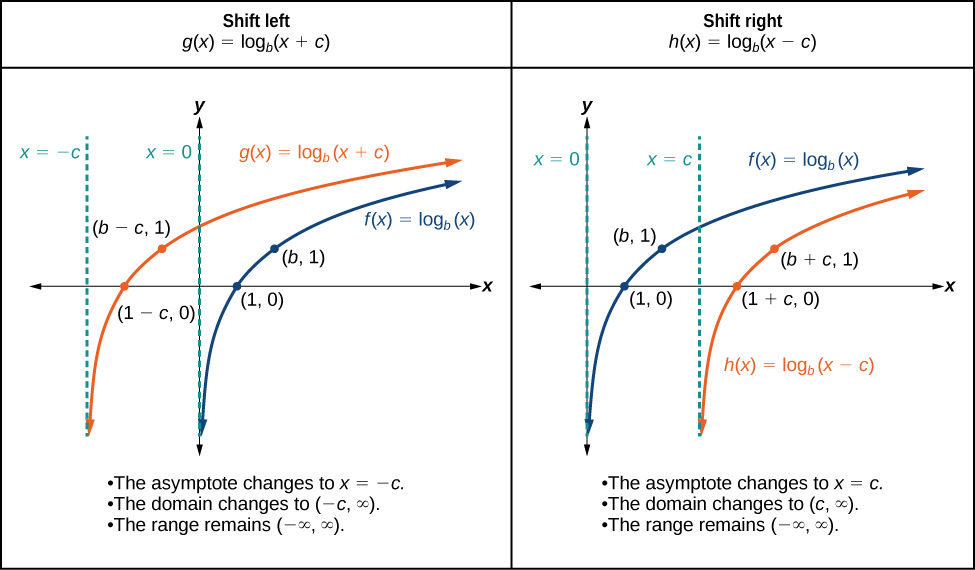
Para cualquier constante\(c\), la función\(f(x)={\log}_b(x+c)\)
- desplaza la función padre a\(y={\log}_b(x)\) la izquierda\(c\) unidades si\(c>0\).
- desplaza las\(c\) unidades de la\(y={\log}_b(x)\) derecha de la función padre si\(c<0\).
- tiene la asíntota vertical\(x=−c\).
- tiene dominio\((−c,\infty)\).
- tiene rango\((−\infty,\infty)\).
- Identificar el desplazamiento horizontal:
- Si\(c>0\), desplaza la gráfica de\(c\) unidades\(f(x)={\log}_b(x)\) izquierdas.
- Si\(c<0\), desplaza la gráfica de\(c\) unidades\(f(x)={\log}_b(x)\) derechas.
- Dibuja la asíntota vertical\(x=−c\).
- Identificar tres puntos clave de la función padre. Encuentra nuevas coordenadas para las funciones cambiadas restando\(c\) de la\(x\) coordenada.
- Etiquetar los tres puntos.
- El Dominio es\((−c,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=−c\).
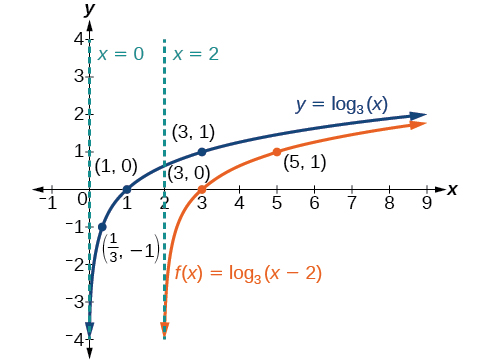
Esboce el desplazamiento horizontal\(f(x)={\log}_3(x−2)\) junto a su función padre. Incluir los puntos clave y asíntotas en la gráfica. Declarar el dominio, el rango y la asíntota.
Solución
Ya que la función es\(f(x)={\log}_3(x−2)\), nos damos cuenta\(x+(−2)=x–2\).
Así\(c=−2\), así\(c<0\). Esto significa que desplazaremos la función\(f(x)={\log}_3(x)\) a la derecha 2 unidades.
La asíntota vertical es\(x=−(−2)\) o\(x=2\).
Considere los tres puntos clave de la función padre,\(\left(\dfrac{1}{3},−1\right)\),\((1,0)\), y\((3,1)\).
Las nuevas coordenadas se encuentran sumando\(2\) a las\(x\) coordenadas.
Etiquetar los puntos\(\left(\dfrac{7}{3},−1\right)\),\((3,0)\), y\((5,1)\).
El dominio es\((2,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=2\).
Haga un boceto de una gráfica\(f(x)={\log}_3(x+4)\) junto a su función padre. Incluir los puntos clave y asíntotas en la gráfica. Declarar el dominio, el rango y la asíntota.
- Contestar
-
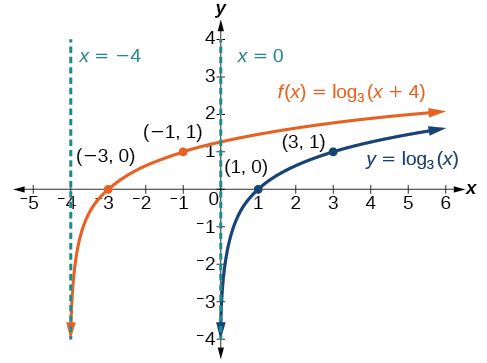
Figura\(\PageIndex{9}\) El dominio es\((−4,\infty)\), el rango\((−\infty,\infty)\) y la asíntota\(x=–4\).
Graficando un Desplazamiento Vertical de\(y = log_b(x)\)
Cuando\(d\) se agrega una constante a la función padre\(f(x)={\log}_b(x)\), el resultado es un desplazamiento vertical de\(d\) unidades en la dirección del signo encendido\(d\). Para visualizar los desplazamientos verticales, podemos observar la gráfica general de la función padre\(f(x)={\log}_b(x)\) junto con el shift up,\(g(x)={\log}_b(x)+d\) y el shift down,\(h(x)={\log}_b(x)−d\) .Ver Figura\(\PageIndex{10}\).
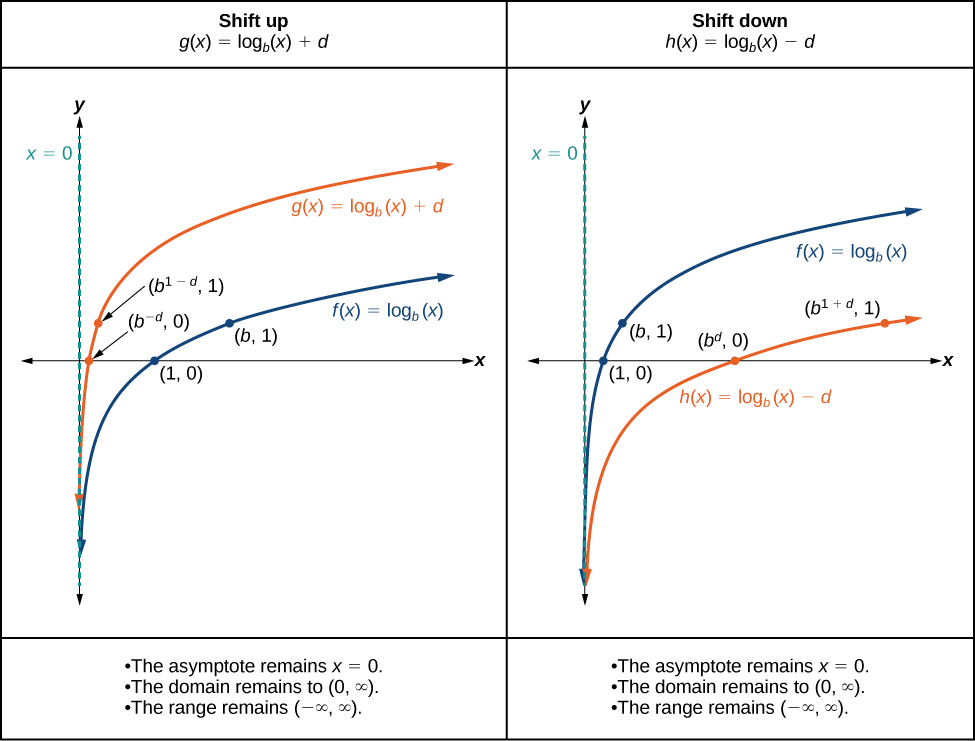
Para cualquier constante\(d\), la función\(f(x)={\log}_b(x)+d\)
- desplaza la función padre\(y={\log}_b(x)\) hacia arriba\(d\) unidades si\(d>0\).
- desplaza la función padre\(y={\log}_b(x)\) hacia abajo\(d\) unidades si\(d<0\).
- tiene la asíntota vertical\(x=0\).
- tiene dominio\((0,\infty)\).
- tiene rango\((−\infty,\infty)\).
- Identificar el desplazamiento vertical:
- Si\(d>0\), desplaza la gráfica de\(d\) unidades\(f(x)={\log}_b(x)\) hacia arriba.
- Si\(d<0\), desplaza la gráfica de\(d\) unidades\(f(x)={\log}_b(x)\) hacia abajo.
- Dibuja la asíntota vertical\(x=0\).
- Identificar tres puntos clave de la función padre. Encuentre nuevas coordenadas para las funciones cambiadas agregando\(d\) a la\(y\) coordenada.
- Etiquetar los tres puntos.
- El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Haga un boceto de una gráfica\(f(x)={\log}_3(x)−2\) junto a su función padre. Incluya los puntos clave y la asíntota en la gráfica. Declarar el dominio, el rango y la asíntota.
Solución
Ya que la función es\(f(x)={\log}_3(x)−2\), nos daremos cuenta\(d=–2\). Así\(d<0\).
Esto significa que cambiaremos la función\(f(x)={\log}_3(x)\) hacia abajo de\(2\) las unidades.
La asíntota vertical es\(x=0\).
Considere los tres puntos clave de la función padre,\(\left(\dfrac{1}{3},−1\right)\),\((1,0)\), y\((3,1)\).
Las nuevas coordenadas se encuentran restando\(2\) de las coordenadas y.
Etiquetar los puntos\(\left(\dfrac{1}{3},−3\right)\),\((1,−2)\), y\((3,−1)\).
El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
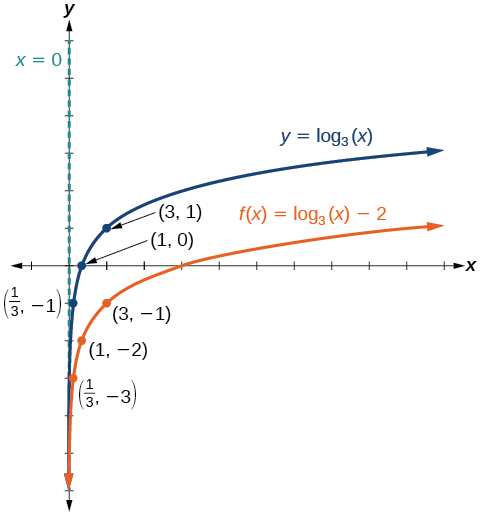
El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Haga un boceto de una gráfica\(f(x)={\log}_2(x)+2\) junto a su función padre. Incluya los puntos clave y la asíntota en la gráfica. Declarar el dominio, el rango y la asíntota.
- Contestar
-
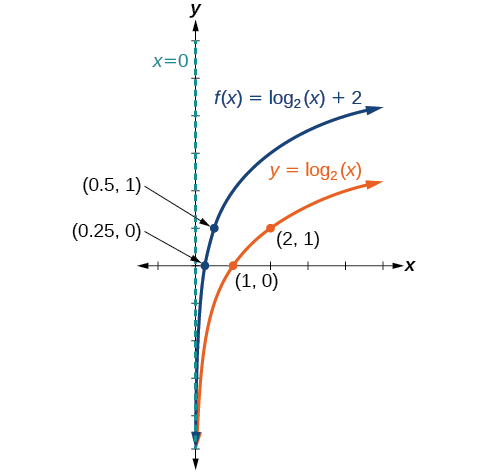
Figura\(\PageIndex{12}\) El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Graficando Estiramientos y Compresiones de\(y = log_b(x)\)
Cuando la función padre\(f(x)={\log}_b(x)\) se multiplica por una constante\(a>0\), el resultado es un estiramiento vertical o compresión de la gráfica original. Para visualizar estiramientos y compresiones, establecemos\(a>1\) y observamos la gráfica general de la función padre\(f(x)={\log}_b(x)\) junto al estiramiento vertical,\(g(x)=a{\log}_b(x)\) y la compresión vertical,\(h(x)=\dfrac{1}{a}{\log}_b(x)\) .Ver Figura\(\PageIndex{13}\).
Para cualquier constante\(a>1\), la función\(f(x)=a{\log}_b(x)\)
- estira la función padre\(y={\log}_b(x)\) verticalmente por un factor de\(a\) if\(a>1\).
- comprime la función padre\(y={\log}_b(x)\) verticalmente por un factor de\(a\) if\(0<a<1\).
- tiene la asíntota vertical\(x=0\).
- tiene la\(x\) -intercepción\((1,0)\).
- tiene dominio\((0,\infty)\).
- tiene rango\((−\infty,\infty)\).
- Identificar el estiramiento vertical o compresiones:
- Si\(|a|>1\), la gráfica de\(f(x)={\log}_b(x)\) se estira por un factor de\(a\) unidades.
- Si\(|a|<1\), la gráfica de\(f(x)={\log}_b(x)\) está comprimida por un factor de\(a\) unidades.
- Dibuja la asíntota vertical\(x=0\).
- Identificar tres puntos clave de la función padre. Encuentra nuevas coordenadas para las funciones cambiadas multiplicando las coordenadas y por\(a\).
- Etiquetar los tres puntos.
- El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Haga un boceto de una gráfica\(f(x)=2{\log}_4(x)\) junto a su función padre. Incluya los puntos clave y la asíntota en la gráfica. Declarar el dominio, el rango y la asíntota.
Solución
Ya que la función es\(f(x)=2{\log}_4(x)\), nos daremos cuenta\(a=2\).
Esto significa que estiraremos la función\(f(x)={\log}_4(x)\) por un factor de\(2\).
La asíntota vertical es\(x=0\).
Considere los tres puntos clave de la función padre,\(\left(\dfrac{1}{4},−1\right)\),\((1,0)\), y\((4,1)\).
Las nuevas coordenadas se encuentran multiplicando las\(y\) coordenadas por\(2\).
Etiquetar los puntos\(\left(\dfrac{1}{4},−2\right)\),\((1,0)\), y\((4,2)\).
El dominio es\((0, \infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\). Ver Figura\(\PageIndex{14}\).
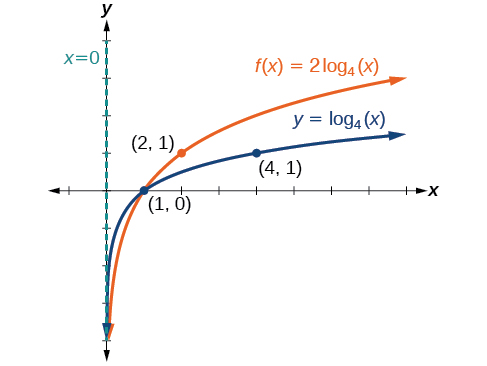
El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Haga un boceto de una gráfica\(f(x)=\dfrac{1}{2}{\log}_4(x)\) junto a su función padre. Incluya los puntos clave y la asíntota en la gráfica. Declarar el dominio, el rango y la asíntota.
- Contestar
-
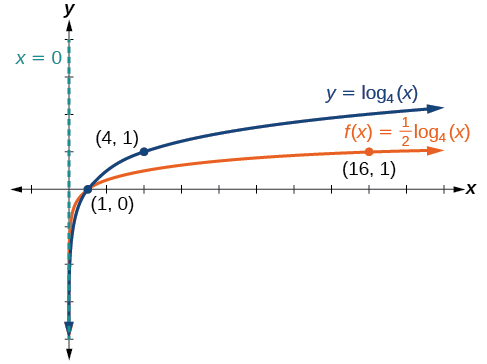
Figura\(\PageIndex{15}\) El dominio es\((0,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Esbozar una gráfica de\(f(x)=5{\log}(x+2)\). Declarar el dominio, el rango y la asíntota.
Solución
Recuerda: lo que sucede entre paréntesis pasa primero. Primero, movemos la gráfica a la izquierda\(2\) unidades, luego estiramos la función verticalmente por un factor de\(5\), como en la Figura\(\PageIndex{16}\). La asíntota vertical se desplazará a\(x=−2\). El\(x\) -intercepto será\((−1,0)\). El dominio será\((−2,\infty)\). Dos puntos ayudarán a dar la forma de la gráfica:\((−1,0)\) y\((8,5)\). Elegimos\(x=8\) como la coordenada x de un punto para graficar porque cuando\(x=8\),\(x+2=10\), la base del logaritmo común.
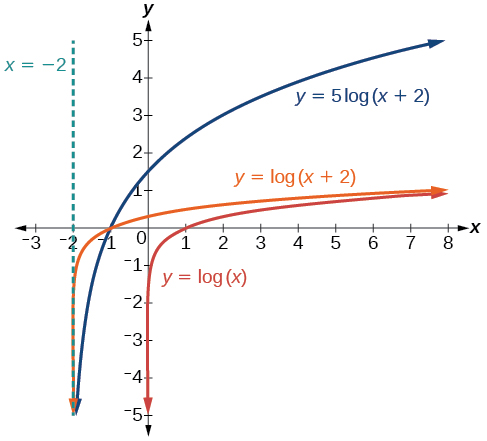
El dominio es\((−2,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=−2\).
Dibuje una gráfica de la función\(f(x)=3{\log}(x−2)+1\). Declarar el dominio, el rango y la asíntota.
- Contestar
-
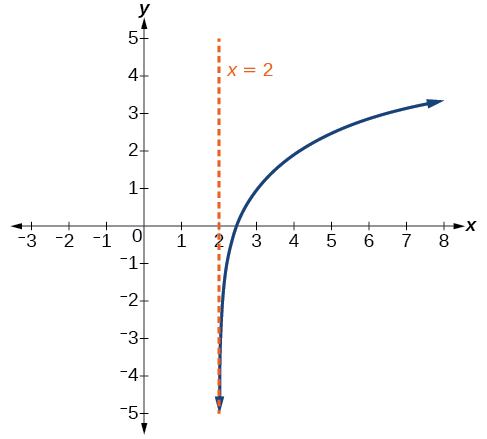
Figura\(\PageIndex{17}\) El dominio es\((2,\infty)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=2\).
Graficando Reflexiones de\(f(x) = log_b(x)\)
Cuando la función padre\(f(x)={\log}_b(x)\) se multiplica por\(−1\), el resultado es una reflexión sobre el\(x\) eje -axis. Cuando la entrada se multiplica por\(−1\), el resultado es una reflexión alrededor del\(y\) eje -axis. Para visualizar reflexiones\(b>1\), restringimos y observamos la gráfica general de la función padre\(f(x)={\log}_b(x)\) junto con la reflexión sobre el\(x\) eje\(g(x)=−{\log}_b(x)\) -y la reflexión sobre el\(y\) eje -eje,\(h(x)={\log}_b(−x)\).
La función\(f(x)=−{\log}_b(x)\)
- refleja la función padre\(y={\log}_b(x)\) sobre el\(x\) eje -.
- tiene dominio,\((0,\infty)\), rango\((−\infty,\infty)\), y asíntota vertical\(x=0\), que no cambian con respecto a la función padre.
La función\(f(x)={\log}_b(−x)\)
- refleja la función padre\(y={\log}_b(x)\) sobre el\(y\) eje -.
- tiene dominio\((−\infty,0)\).
- tiene rango,\((−\infty,\infty)\), y asíntota vertical,\(x=0\), que no cambian con respecto a la función padre.
| Si\(f(x)=−{\log}_b(x)\) | Si\(f(x)={\log}_b(−x)\) |
|---|---|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
\ (f (x) =− {\ log} _b (x)\) ">
|
\ (f (x) = {\ log} _b (−x)\) ">
|
Haga un boceto de una gráfica\(f(x)=\log(−x)\) junto a su función padre. Incluya los puntos clave y la asíntota en la gráfica. Declarar el dominio, el rango y la asíntota.
Solución
Antes de graficar\(f(x)=log(−x)\),\(f(x)=log(−x)\), identificar el comportamiento y los puntos clave para la gráfica.
- Ya que\(b=10\) es mayor que uno, sabemos que la función padre va en aumento. Dado que el valor de entrada se multiplica por\(−1\),\(f(x)\) es un reflejo de la gráfica padre alrededor del eje\(y\) -. Así,\(f(x)=\log(−x)\) irá disminuyendo a medida que\(x\) se mueve del infinito negativo a cero, y la cola derecha de la gráfica se acercará a la asíntota vertical\(x=0\).
- El\(x\) -intercepto es\((−1,0)\).
- Dibujamos y etiquetamos la asíntota, trazamos y etiquetamos los puntos, y dibujamos una curva suave a través de los puntos.
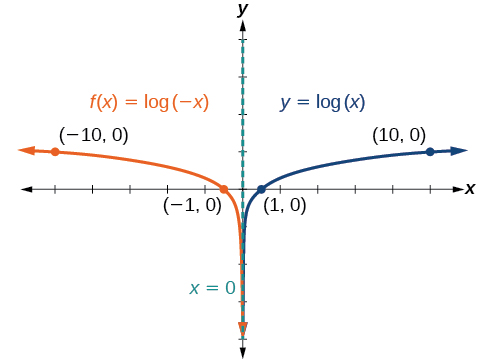
El dominio es\((−\infty,0)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
Gráfica\(f(x)=−\log(−x)\). Declarar el dominio, el rango y la asíntota.
- Contestar
-
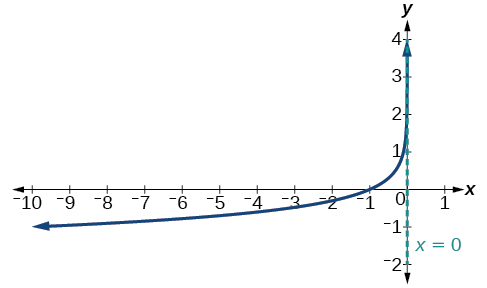
Figura\(\PageIndex{20}\) El dominio es\((−\infty,0)\), el rango es\((−\infty,\infty)\), y la asíntota vertical es\(x=0\).
- Presione [Y=]. Ingrese la ecuación o ecuaciones de logaritmo dadas como Y 1 = y, si es necesario, Y 2 =.
- Pulse [GRAPH] para observar las gráficas de las curvas y utilice [VENTANA] para encontrar una visión apropiada de las gráficas, incluyendo su punto (s) de intersección.
- Para encontrar el valor de\(x\), calculamos el punto de intersección. Presione [2ND] luego [CALC]. Seleccione “intersectar” y pulse [ENTRAR] tres veces. El punto de intersección da el valor de\(x\), para el punto (s) de intersección.
Resuelve\(4\ln(x)+1=−2\ln(x−1)\) gráficamente. Redondear a la milésima más cercana.
Solución
Presione [Y=] e ingrese\(4\ln(x)+1\) junto a Y 1 =. Después ingresa\(−2\ln(x−1)\) junto a Y 2 =. Para una ventana, use los valores\(0\) a\(5\) for\(x\0 and \(–10\) to\(10\) for\(y\). Pulse [GRÁFICO]. Los gráficos deben cruzarse en algún lugar un poco a la derecha de\(x=1\).
Para una mejor aproximación, presione [2ND] luego [CALC]. Seleccione [5: intersectar] y pulse [ENTRAR] tres veces. La coordenada x del punto de intersección se muestra como\(1.3385297\). (Tu respuesta puede ser diferente si usas una ventana diferente o usas un valor diferente para Guess? ) Entonces, a la milésima más cercana,\(x≈1.339\).
Resuelve\(5\log(x+2)=4−\log(x)\) gráficamente. Redondear a la milésima más cercana.
- Contestar
-
\(x≈3.049\)
Resumiendo traducciones de la función logarítmica
Ahora que hemos trabajado con cada tipo de traducción para la función logarítmica, podemos resumir cada una en Tabla para llegar\(\PageIndex{4}\) a la ecuación general para traducir funciones exponenciales.
| Traducciones de la Función Parent\(y={\log}_b(x)\) | |
|---|---|
| Traducción | Formulario |
| \ (y= {\ log} _b (x)\) Traducción">
Turno \(c\)Unidades horizontales a la izquierda \(d\)Unidades verticalmente hacia arriba |
\ (y= {\ log} _b (x)\) Formulario” style="vertical-align:middle; ">\(y={\log}_b(x+c)+d\) |
| \ (y= {\ log} _b (x)\) Traducción">
Estirar y comprimir Estirar si\(|a|>1\) Compresión si\(|a|<1\) |
\ (y= {\ log} _b (x)\) Formulario” style="vertical-align:middle; ">\(y=a{\log}_b(x)\) |
| \ (y= {\ log} _b (x)\) Traducción">Reflexionar sobre el eje x | \ (y= {\ log} _b (x)\) Formulario">\(y=−{\log}_b(x)\) |
| \ (y= {\ log} _b (x)\) Traducción">Reflexionar sobre el eje y | \ (y= {\ log} _b (x)\) Formulario">\(y={\log}_b(−x)\) |
| \ (y= {\ log} _b (x)\) Traducción">Ecuación general para todas las traducciones | \ (y= {\ log} _b (x)\) Formulario">\(y=a{\log}_b(x+c)+d\) |
Todas las traducciones de la función logarítmica padre\(y={\log}_b(x)\),, tienen la forma
\(f(x)=a{\log}_b(x+c)+d\)
donde la función padre,\(y={\log}_b(x)\),\(b>1\), es
- \(d\)unidades desplazadas verticalmente hacia arriba.
- desplazado horizontalmente a las\(c\) unidades de la izquierda.
- estirada verticalmente por un factor de\(|a|\) si\(|a|>0\).
- comprimido verticalmente por un factor de\(|a|\) if\(0<|a|<1\).
- reflejado alrededor del eje x cuando\(a<0\).
For\(f(x)=\log(−x)\), la gráfica de la función padre se refleja alrededor del eje y.
¿De qué es la asíntota vertical\(f(x)=−2{\log}_3(x+4)+5\)?
Solución
La asíntota vertical está en\(x=−4\).
Análisis
El coeficiente, la base y la traslación ascendente no afectan a la asíntota. El desplazamiento de las\(4\) unidades de curva hacia la izquierda desplaza la asíntota vertical a\(x=−4\).
¿De qué es la asíntota vertical\(f(x)=3+\ln(x−1)\)?
- Contestar
-
\(x=1\)
Encuentre una posible ecuación para la función logarítmica común graficada en la Figura\(\PageIndex{21}\).
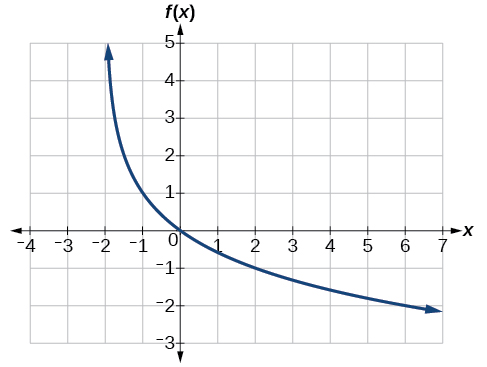
Solución
Esta gráfica tiene una asíntota vertical en\(x=–2\) y se ha reflejado verticalmente. Aún no conocemos el desplazamiento vertical o el estiramiento vertical. Sabemos hasta ahora que la ecuación tendrá forma:
\(f(x)=−a\log(x+2)+k\)
Aparece que la gráfica pasa por los puntos\((–1,1)\) y\((2,–1)\). Sustituyendo\((–1,1)\),
\[\begin{align*} 1&= -a\log(-1+2)+k \qquad \text{Substitute} (-1,1)\\ 1&= -a\log(1)+k \qquad \text{Arithmetic}\\ 1&= k\log(1)\\ &= 0 \end{align*}\]
A continuación, sustituyendo en\((2,–1)\),
\[\begin{align*} -1&= -a\log(2+2)+1 \qquad \text{Substitute} (2,-1)\\ -2&= -a\log(4) \qquad \text{Arithmetic}\\ a&= \dfrac{2}{\log(4)} \qquad \text{Solve for a} \end{align*}\]
Esto nos da la ecuación\(f(x)=–\dfrac{2}{\log(4)}\log(x+2)+1\).
Análisis
Podemos verificar esta respuesta comparando los valores de función en Tabla\(\PageIndex{5}\) con los puntos en la gráfica en la Figura\(\PageIndex{21}\).
| \(x\) | −1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|
| \(f(x)\) | 1 | 0 | −0.58496 | −1 | −1.3219 |
| \(x\) | 4 | 5 | 6 | 7 | 8 |
| \(f(x)\) | −1.5850 | −1.8074 | −2 | −2.1699 | −2.3219 |
Dar la ecuación del logaritmo natural graficado en la Figura\(\PageIndex{22}\).
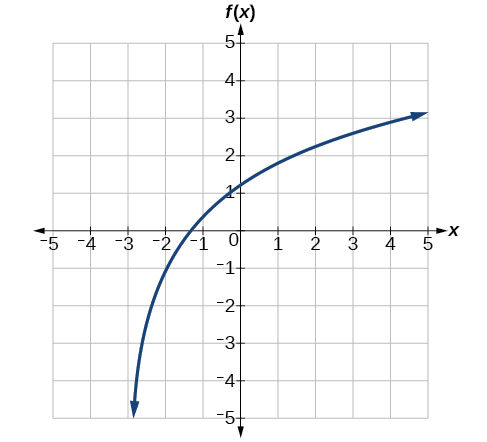
- Contestar
-
\(f(x)=2\ln(x+3)−1\)
Sí, si sabemos que la función es una función logarítmica general. Por ejemplo, mira la gráfica en la Figura\(\PageIndex{22}\). La gráfica se acerca\(x=−3\) (o por ahí) cada vez más de cerca, así\(x=−3\) es, o está muy cerca de, la asíntota vertical. Se acerca desde la derecha, por lo que el dominio es todo apunta a la derecha,\({x|x>−3}\). El rango, como con todas las funciones logarítmicas generales, es todo números reales. Y podemos ver el comportamiento final porque la gráfica baja a medida que va a la izquierda y sube como va a la derecha. El comportamiento final es que como\(x\rightarrow −3^+\),\(f(x)\rightarrow −\infty\) y como\(x\rightarrow \infty\),\(f(x)\rightarrow \infty\).
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con logaritmos gráficos.
- Graficar una función exponencial y una función logarítmica
- Coinciden gráficas con funciones exponenciales y logarítmicas
- Encontrar el dominio de las funciones logarítmicas
Ecuaciones Clave
| Formulario general para la traducción de la función logarítmica padre\(f(x)={\log}_b(x)\) | \(f(x)=a{\log}_b(x+c)+d\) |
Conceptos clave
- Para encontrar el dominio de una función logarítmica, establecer una desigualdad que muestre el argumento mayor que cero, y resolver para\(x\). Ver Ejemplo\(\PageIndex{1}\) y Ejemplo\(\PageIndex{2}\)
- La gráfica de la función padre\(f(x)={\log}_b(x)\) tiene una intersección x en\((1,0)\), dominio\((0,\infty)\), rango\((−\infty,\infty)\),\(x=0\) asíntota vertical y
-
- si\(b>1\), la función va en aumento.
- si\(0<b<1\), la función es decreciente.
- La ecuación\(f(x)={\log}_b(x+c)\) desplaza la función padre\(y={\log}_b(x)\) horizontalmente
- \(c\)unidades dejadas si\(c>0\).
- \(c\)unidades correctas si\(c<0\).
- La ecuación\(f(x)={\log}_b(x)+d\) desplaza la función padre\(y={\log}_b(x)\) verticalmente
- hasta\(d\) unidades si\(d>0\).
- abajo\(d\) unidades si\(d<0\).
- Para cualquier constante\(a>0\), la ecuación\(f(x)=a{\log}_b(x)\)
- estira la función padre\(y={\log}_b(x)\) verticalmente por un factor de\(a\) if\(|a|>1\).
- comprime la función padre\(y={\log}_b(x)\) verticalmente por un factor de\(a\) if\(|a|<\) 1.
- Cuando la función padre\(y={\log}_b(x)\) se multiplica por\(−1\), el resultado es una reflexión sobre el eje x. Cuando la entrada se multiplica por\(−1\), el resultado es una reflexión sobre el eje y.
- La ecuación\(f(x)=−{\log}_b(x)\) representa un reflejo de la función padre alrededor del eje x.
- La ecuación\(f(x)={\log}_b(−x)\) representa un reflejo de la función padre alrededor del eje y.
- Se puede utilizar una calculadora gráfica para aproximar soluciones a algunas ecuaciones logarítmicas Ver Ejemplo\(\PageIndex{9}\).
- Todas las traducciones de la función logarítmica se pueden resumir mediante la ecuación general\(f(x)=a{\log}_b(x+c)+d\). Ver Tabla\(\PageIndex{4}\).
- Dada una ecuación con la forma general\(f(x)=a{\log}_b(x+c)+d\), podemos identificar la asíntota vertical\(x=−c\) para la transformación. Ver Ejemplo\(\PageIndex{10}\).
- Usando la ecuación general\(f(x)=a{\log}_b(x+c)+d\), podemos escribir la ecuación de una función logarítmica dada su gráfica. Ver Ejemplo\(\PageIndex{11}\).


