4.7: Modelos Exponenciales y Logarítmicos
- Page ID
- 121429
- Modelar crecimiento exponencial y decaimiento.
- Utilice la Ley de Refrigeración de Newton.
- Utilizar modelos logístico-crecimiento.
- Elija un modelo apropiado para los datos.
- Expresar un modelo exponencial en base\(e\).
Ya hemos explorado algunas aplicaciones básicas de funciones exponenciales y logarítmicas. En esta sección, exploramos algunas aplicaciones importantes en mayor profundidad, incluyendo los isótopos radiactivos y la Ley de Enfriamiento de Newton.
Modelado del crecimiento exponencial y la decadencia
En aplicaciones del mundo real, necesitamos modelar el comportamiento de una función. En el modelado matemático, elegimos una función general familiar con propiedades que sugieren que modelará el fenómeno del mundo real que deseamos analizar. En el caso de crecimiento rápido, podemos elegir la función de crecimiento exponencial:
\[y=A_0e^{kt}\]
donde\(A_0\) es igual al valor en el tiempo cero,\(e\) es la constante de Euler, y\(k\) es una constante positiva que determina la tasa (porcentaje) de crecimiento. Podemos usar la función de crecimiento exponencial en aplicaciones que implican duplicar el tiempo, el tiempo que tarda una cantidad en duplicarse. Fenómenos como poblaciones de vida silvestre, inversiones financieras, muestras biológicas y recursos naturales pueden exhibir crecimiento basado en un tiempo de duplicación. En algunas aplicaciones, sin embargo, como veremos cuando discutamos la ecuación logística, el modelo logístico a veces se ajusta mejor a los datos que al modelo exponencial.
Por otro lado, si una cantidad está cayendo rápidamente hacia cero, sin llegar nunca a cero, entonces probablemente deberíamos elegir el modelo de decaimiento exponencial. Nuevamente, tenemos la forma\(y=A_0e^{kt}\) donde\(A_0\) está el valor inicial, y\(e\) es la constante de Euler. Ahora\(k\) es una constante negativa que determina la tasa de decaimiento. Podemos usar el modelo de decaimiento exponencial cuando calculamos la vida media, o el tiempo que tarda una sustancia en descomponerse exponencialmente a la mitad de su cantidad original. Utilizamos la vida media en aplicaciones que involucran isótopos radiactivos.
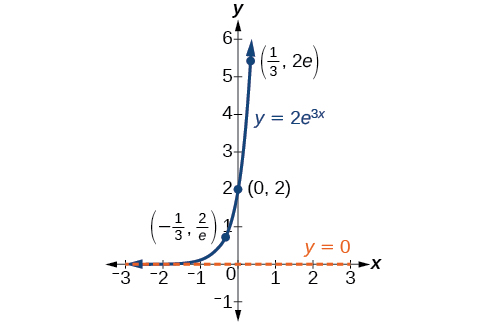
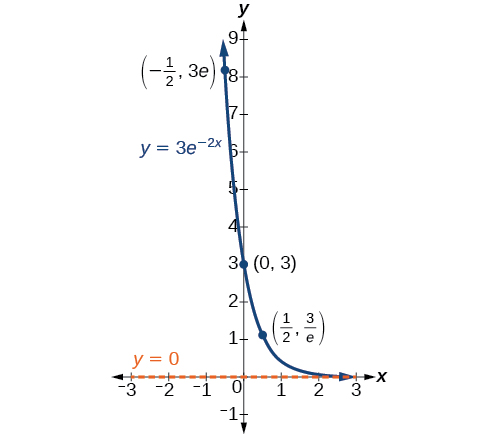
En nuestra elección de una función que sirva como modelo matemático, a menudo utilizamos puntos de datos recopilados por observación y medición cuidadosas para construir puntos en una gráfica y esperamos que podamos reconocer la forma de la gráfica. Las gráficas de crecimiento exponencial y decaimiento tienen una forma distintiva, como podemos ver en Figura\(\PageIndex{2}\) y Figura\(\PageIndex{3}\). Es importante recordar que, aunque partes de cada una de las dos gráficas parecen estar en el\(x\) eje -eje, realmente están a una distancia diminuta por encima del\(x\) eje -eje.
El crecimiento exponencial y la decadencia a menudo involucran números muy grandes o muy pequeños. Para describir estos números, a menudo usamos órdenes de magnitud. El orden de magnitud es la potencia de diez, cuando el número se expresa en notación científica, con un dígito a la izquierda del decimal. Por ejemplo, la distancia a la estrella más cercana, Próxima Centauri, medida en kilómetros, es de\(40,113,497,200,000\) kilómetros. Expresado en notación científica, esto es\(4.01134972 × 1013\). Entonces, podríamos describir este número como teniendo orden de magnitud\(1013\).
Una función exponencial con la forma\(y=A_0e^{kt}\) tiene las siguientes características:
- función uno-a-uno
- asíntota horizontal:\(y=0\)
- dominio:\((–\infty, \infty)\)
- Rango:\((0,\infty)\)
- \(x\)interceptar: ninguno
- \(y\)-interceptar:\((0,A_0)\)
- aumentando si\(k>0\) (ver Figura\(\PageIndex{4}\))
- decreciente si\(k<0\) (ver Figura\(\PageIndex{4}\))
Una población de bacterias se duplica cada hora. Si el cultivo comenzó con\(10\) bacterias, grafica la población en función del tiempo.
Solución
Cuando una cantidad crece a un porcentaje fijo por unidad de tiempo, el crecimiento es exponencial. Para encontrar\(A_0\) utilizamos el hecho de que\(A_0\) es la cantidad en el tiempo cero, entonces\(A_0=10\). Para encontrar\(k\), use el hecho de que después de una hora\((t=1)\) la población se duplica de\(10\) a\(20\) .La fórmula se deriva de la siguiente manera
\[\begin{align*} 20&= 10e^{k\cdot 1}\\ 2&= e^k \qquad \text{Divide by 10}\\ \ln2&= k \qquad \text{Take the natural logarithm} \end{align*}\]
así\(k=\ln(2)\). Así es la ecuación que queremos graficar\(y=10e^{(\ln2)t}=10{(e^{\ln2})}^t=10·2^t\). La gráfica se muestra en la Figura\(\PageIndex{5}\).
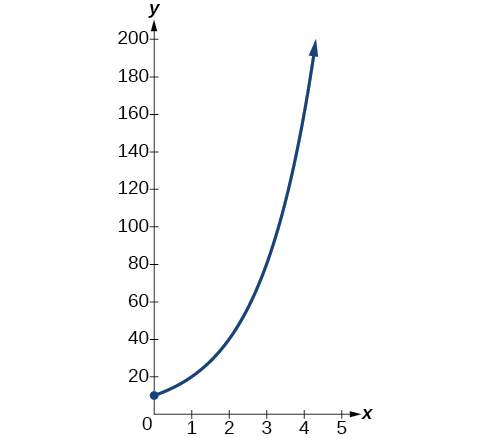
Análisis
La población de bacterias después de diez horas es\(10,240\). Podríamos describir que esta cantidad está siendo del orden de magnitud\(10^4\). La población de bacterias después de las veinte horas es la\(10,485,760\) que es del orden de magnitud\(10^7\), por lo que podríamos decir que la población ha aumentado en tres órdenes de magnitud en diez horas.
Vida media
Pasamos ahora a la decadencia exponencial. Uno de los términos comunes asociados a la decadencia exponencial, como se indicó anteriormente, es la vida media, el tiempo que tarda una cantidad exponencialmente en descomposición en disminuir a la mitad de su cantidad original. Cada isótopo radiactivo tiene una vida media, y el proceso que describe la desintegración exponencial de un isótopo se llama desintegración radiactiva.
Para encontrar la vida media de una función que describe la decadencia exponencial, resuelva la siguiente ecuación:
\(\dfrac{1}{2}A_0=A_0e^{kt}\)
Encontramos que la vida media depende únicamente de la constante\(k\) y no de la cantidad inicial\(A_0\).
La fórmula se deriva de la siguiente manera
\[\begin{align*} \dfrac{1}{2}A_0&= A_0e^{kt}\\ \dfrac{1}{2}&= e^{kt} \qquad \text{Divide by } A_0\\ \ln \left (\dfrac{1}{2} \right )&= ktv \qquad \text{Take the natural log}\\ -\ln(2)&= kt \qquad \text{Apply laws of logarithms}\\ -\ln(2)k&= t \qquad \text{Divide by k} \end{align*}\]
Ya que\(t\), el tiempo, es positivo,\(k\) debe, como se esperaba, ser negativo. Esto nos da la fórmula de vida media
\[t=−\dfrac{\ln(2)}{k}\]
- Escribir\(A=A_0e^{kt}\).
- Reemplazar\(A\) por\(\dfrac{1}{2}A_0\) y reemplazar\(t\) por la vida media dada.
- Resuelve encontrar\(k\). Expresar\(k\) como un valor exacto (no redondear).
Nota: También es posible encontrar la tasa de decaimiento usando\(k=−\ln(2)t\).
La vida media del carbono-14 es de\(5,730\) años. Expresar la cantidad de carbono-14 restante en función del tiempo,\(t\).
Solución
Esta fórmula se deriva de la siguiente manera.
\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for } f(t)\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{ \left (\tfrac{\ln(0.5)}{5730} \right ) t} \qquad \text{Substitute for r in the continuous growth formula} \end{align*}\]
La función que describe esta decadencia continua es\(f(t)=A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\). Observamos que el coeficiente de\(t\),\(\dfrac{\ln(0.5)}{5730}≈−1.2097×10^{−4}\) es negativo, como se esperaba en el caso de decaimiento exponencial.
La vida media del plutonio-244 es de\(80,000,000\) años. La función Find da la cantidad de carbono-14 restante en función del tiempo, medida en años.
- Contestar
-
\(f(t)=A_0e^{−0.0000000087t}\)
Datación por radiocarbono
La fórmula para la desintegración radiactiva es importante en la datación por radiocarbono, que se utiliza para calcular la fecha aproximada de muerte de una planta o animal. La datación por radiocarbono fue descubierta en 1949 por Willard Libby, quien ganó un Premio Nobel por su descubrimiento. Compara la diferencia entre la proporción de dos isótopos de carbono en un artefacto orgánico o fósil con la relación de esos dos isótopos en el aire. Se cree que es preciso dentro de aproximadamente el\(1\%\) error para las plantas o animales que murieron en los últimos\(60,000\) años.
El carbono-14 es un isótopo radiactivo de carbono que tiene una vida media de\(5,730\) años. Ocurre en pequeñas cantidades en el dióxido de carbono en el aire que respiramos. La mayor parte del carbono en la Tierra es carbono-12, que tiene un peso atómico de\(12\) y no es radiactivo. Los científicos han determinado la proporción de carbono-14 a carbono-12 en el aire durante los últimos\(60,000\) años, utilizando anillos de árboles y otras muestras orgánicas de fechas conocidas, aunque la proporción ha cambiado ligeramente a lo largo de los siglos.
Mientras una planta o un animal esté vivo, la proporción de los dos isótopos de carbono en su cuerpo es cercana a la proporción en la atmósfera. Cuando muere, el carbono-14 en su cuerpo se descompone y no es reemplazado. Al comparar la relación de carbono-14 a carbono-12 en una muestra en descomposición con la relación conocida en la atmósfera, se puede aproximar la fecha en que murió la planta o animal.
Dado que la vida media del carbono-14 es\(5,730\) años, la fórmula para la cantidad de carbono-14 restante después de\(t\) años es
\(A≈A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t}\)
donde
- \(A\)es la cantidad de carbono-14 restante
- \(A_0\)es la cantidad de carbono-14 cuando la planta o animal comenzó a desintegrarse.
Esta fórmula se deriva de la siguiente manera:
\[\begin{align*} A&= A_0e^{kt} \qquad \text{The continuous growth formula}\\ 0.5A_0&= A_0e^{k\cdot 5730} \qquad \text{Substitute the half-life for t and } 0.5A_0 \text{ for f(t)}\\ 0.5&= e^{5730k} \qquad \text{Divide by } A_0\\ \ln(0.5)&= 5730k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln(0.5)}{5730} \qquad \text{Divide by the coefficient of k}\\ A&= A_0e^{\left (\tfrac{\ln(0.5)}{5730} \right )t} \qquad \text{Substitute for r in the continuous growth formula}\\ \end{align*}\]
Para encontrar la edad de un objeto, resolvemos esta ecuación para\(t\):
\(t=\dfrac{\ln \left (\dfrac{A}{A_0} \right )}{−0.000121}\)
Por necesidad, descuidamos aquí los muchos detalles que un científico toma en consideración al hacer la datación por carbono-14, y solo miramos la fórmula básica. La relación de carbono-14 a carbono-12 en la atmósfera es aproximadamente\(0.0000000001%\). \(r\)Sea la proporción de carbono-14 a carbono-12 en el artefacto orgánico o fósil a fechar, determinada por un método llamado centelleo líquido. De la ecuación\(A≈A_0e^{−0.000121t}\) sabemos que la relación entre el porcentaje de carbono-14 en el objeto que estamos datando con el porcentaje de carbono-14 en la atmósfera es\(r=\dfrac{A}{A_0}≈e^{−0.000121t}\). Resolvemos esta ecuación para\(t\), para obtener
\(t=\dfrac{\ln(r)}{−0.000121}\)
- Expresar el porcentaje dado de carbono-14 como decimal equivalente,\(k\).
- Sustituir\(k\) en la ecuación\(t=\dfrac{\ln(r)}{−0.000121}\) y resolver por la edad,\(t\).
Se encuentra un fragmento óseo que contiene\(20\%\) de su carbono-14 original. Al año más cercano, ¿cuántos años tiene el hueso?
Solución
\(20\%=0.20\)Sustituimos\(k\) en la ecuación y resolvemos\(t\):
\[\begin{align*} t&= \dfrac{\ln(r)}{-0.000121} \qquad \text{Use the general form of the equation}\\ &= \dfrac{\ln(0.20)}{-0.000121} \qquad \text{Substitute for r}\\ &\approx 13301 \qquad \text{Round to the nearest year} \end{align*}\]
El fragmento de hueso tiene aproximadamente\(13,301\) años.
Análisis
Los instrumentos que miden el porcentaje de carbono-14 son extremadamente sensibles y, como mencionamos anteriormente, un científico necesitará hacer mucho más trabajo que nosotros para estar satisfecho. Aun así, la datación por carbono solo es precisa de aproximadamente\(1\%\), por lo que esta edad debe darse como\(13,301\) años\(\pm 1\%\) o\(13,301\) años\(\pm 133\) años.
El cesio-137 tiene una vida media de aproximadamente\(30\) años. Si comenzamos con\(200\) mg de cesio-137, ¿tardará más o menos de\(230\) años hasta que solo quede\(1\) miligramo?
- Contestar
-
menos de\(230\) años,\(229.3157\) para ser exactos
Cálculo del tiempo de duplicación
Para las cantidades en descomposición, determinamos cuánto tiempo tardó la mitad de una sustancia en desintegrarse. Para cantidades crecientes, es posible que queramos averiguar cuánto tiempo tarda una cantidad en duplicarse. Como mencionamos anteriormente, el tiempo que tarda una cantidad en duplicarse se denomina tiempo de duplicación.
Dada la ecuación básica de crecimiento exponencial\(A=A_0e^{kt}\), el tiempo de duplicación se puede encontrar resolviendo para cuando la cantidad original se haya duplicado, es decir, resolviendo\(2A_0=A_0e^{kt}\).
La fórmula se deriva de la siguiente manera:
\[\begin{align*} 2A_0&= A_0e^{kt}\\ 2&= e^{kt} \qquad \text{Divide by } A_0\\ \ln2&= kt \qquad \text{Take the natural logarithm}\\ t& =\dfrac{\ln2}{k} \qquad \text{Divide by the coefficient of t} \end{align*}\]
Así, el tiempo de duplicación es
\[t=\dfrac{\ln2}{k}\]
Según la Ley de Moore, el tiempo de duplicación para el número de transistores que se pueden poner en un chip de computadora es de aproximadamente dos años. Dar una función que describa este comportamiento.
Solución
La fórmula se deriva de la siguiente manera:
\[\begin{align*} t&= \dfrac{\ln2}{k} \qquad \text{The doubling time formula}\\ 2&= \dfrac{\ln2}{k} \qquad \text{Use a doubling time of two years}\\ k&= \dfrac{\ln2}{2} \qquad \text{Multiply by k and divide by 2}\\ A&= A_0e^{\tfrac{\ln2}{2}t} \qquad \text{Substitute k into the continuous growth formula} \end{align*}\]
La función es\(A=A_0e^{\dfrac{\ln2}{2}t}\).
Datos recientes sugieren que, a partir de 2013, la tasa de crecimiento pronosticada por la Ley de Moore ya no se mantiene. El crecimiento se ha ralentizado a un tiempo de duplicación de aproximadamente tres años. Encuentra la nueva función que toma en cuenta ese tiempo de duplicación más largo.
- Contestar
-
\(f(t)=A_0e^{\tfrac{\ln2}{3}t}\)
Uso de la Ley de Refrigeración de Newton
La descomposición exponencial también se puede aplicar a la temperatura. Cuando un objeto caliente se deja en el aire circundante que está a una temperatura más baja, la temperatura del objeto disminuirá exponencialmente, nivelándose a medida que se acerca a la temperatura del aire circundante. En una gráfica de la función de temperatura, la nivelación corresponderá a una asíntota horizontal a la temperatura del aire circundante. A menos que la temperatura ambiente sea cero, esto corresponderá a un desplazamiento vertical de la función genérica de decaimiento exponencial. Esta traducción lleva a la Ley de Enfriamiento de Newton, la fórmula científica para la temperatura en función del tiempo ya que la temperatura de un objeto se iguala con la temperatura ambiente
\(T(t)=ae^{kt}+T_s\)
Esta fórmula se deriva de la siguiente manera:
\[\begin{align*} T(t)&= Ab^{ct}+T_s\\ T(t)&= Ae^{\ln(b^{ct})}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{ct\ln b}+T_s \qquad \text{Laws of logarithms}\\ T(t)&= Ae^{kt}+T_s \qquad \text{Rename the constant c } ln b \text{, calling it } k\\ \end{align*}\]
La temperatura de un objeto,\(T\), en el aire circundante con la temperatura\(T_s\) se comportará de acuerdo con la fórmula
\[T(t)=Ae^{kt}+T_s\]
donde- \(t\)es tiempo
- \(A\)es la diferencia entre la temperatura inicial del objeto y el entorno
- \(k\)es una constante, la tasa continua de enfriamiento del objeto
- Establecer\(T_s\) igual a la\(y\) coordenada -de la asíntota horizontal (generalmente la temperatura ambiente).
- Sustituir los valores dados en la fórmula de crecimiento continuo\(T(t)=Ae^{kt}+T_s\) para encontrar los parámetros\(A\) y\(k\).
- Sustituir en el tiempo deseado para encontrar la temperatura o la temperatura deseada para encontrar el tiempo.
Una tarta de queso se saca del horno con una temperatura interna ideal de\(165°F\), y se coloca en un\(35°F\) refrigerador. Después de\(10\) minutos, la tarta de queso se ha enfriado a\(150°F\). Si debemos esperar hasta que la tarta de queso se haya enfriado hasta\(70°F\) antes de comerla, ¿cuánto tiempo tendremos que esperar?
Solución
Debido a que la temperatura del aire circundante en el refrigerador es de\(35\) grados, la temperatura de la tarta de queso disminuirá exponencialmente hacia\(35\), siguiendo la ecuación
\(T(t)=Ae^{kt}+35\)
Sabemos que la temperatura inicial era\(165\), entonces\(T(0)=165\).
\[\begin{align*} 165&= Ae^{k0}+35 \qquad \text{Substitute } (0,165)\\ A&= 130 \qquad \text{Solve for A} \end{align*}\]
Nos dieron otro punto de datos\(T(10)=150\),, que podemos usar para resolver\(k\).
\[\begin{align*} 150&= 130e^{k10}+35 \qquad \text{Substitute } (10, 150)\\ 115&= 130e^{k10} \qquad \text{Subtract 35}\\ \dfrac{115}{130}&= e^{10k} \qquad \text{Divide by 130}\\ \ln\left (\dfrac{115}{130} \right )&= 10k \qquad \text{Take the natural log of both sides}\\ k&= \dfrac{\ln \left (\dfrac{115}{130} \right )}{10}\\ &= -0.0123 \qquad \text{Divide by the coefficient of k} \end{align*}\]
Esto nos da la ecuación para el enfriamiento de la tarta de queso:\(T(t)=130e^{–0.0123t}+35\).
Ahora podemos resolver por el tiempo que tardará en que la temperatura se enfríe a\(70\) grados.
\[\begin{align*} 70&= 130e^{-0.0123t}+35 \qquad \text{Substitute in 70 for } T(t)\\ 35&= 130e^{-0.0123t} \qquad \text{Subtract 35}\\ \dfrac{35}{130}&= e^{-0.0123t} \qquad \text{Divide by 130}\\ \ln \left (\dfrac{35}{130} \right )&= -0.0123t \qquad \text{Take the natural log of both sides}\\ t&= \dfrac{\ln \left (\dfrac{35}{130} \right )}{-0.0123}\\ &\approx 106.68 \qquad \text{Divide by the coefficient of t} \end{align*}\]
Tomará unos\(107\) minutos, o una hora y\(47\) minutos, para que la tarta de queso se enfríe\(70°F\).
Una jarra de agua a\(40\) grados Fahrenheit se coloca en una sala de\(70\) grados. Una hora después, la temperatura ha subido a\(45\) grados. ¿Cuánto tiempo tardará en subir a\(60\) grados la temperatura?
- Contestar
-
\(6.026\)horas
Uso de modelos de crecimiento logístico
El crecimiento exponencial no puede continuar para siempre. Los modelos exponenciales, si bien pueden ser útiles a corto plazo, tienden a desmoronarse cuanto más tiempo continúen. Considera a una aspirante a escritora que escribe una sola línea el primer día y planea duplicar el número de líneas que escribe cada día durante un mes. Para fin de mes, debe escribir más de\(17\) mil millones de líneas, o medio billón de páginas. Es poco práctico, si no imposible, que alguien escriba tanto en tan poco tiempo. Eventualmente, un modelo exponencial debe comenzar a acercarse a algún valor limitante, y luego el crecimiento se ve obligado a desacelerarse. Por esta razón, muchas veces es mejor utilizar un modelo con un límite superior en lugar de un modelo de crecimiento exponencial, aunque el modelo de crecimiento exponencial sigue siendo útil a corto plazo, antes de acercarse al valor limitante.
El modelo de crecimiento logístico es aproximadamente exponencial al principio, pero tiene una tasa de crecimiento reducida a medida que la producción se acerca al límite superior del modelo, llamado capacidad de carga. Para constantes\(a\), y\(b\)\(c\), el crecimiento logístico de una población a lo largo del tiempo\(x\) está representado por el modelo
\(f(x)=\dfrac{c}{1+ae^{−bx}}\)
La gráfica de la Figura\(\PageIndex{6}\) muestra cómo cambia la tasa de crecimiento a lo largo del tiempo. El gráfico aumenta de izquierda a derecha, pero la tasa de crecimiento sólo aumenta hasta llegar a su punto de tasa máxima de crecimiento, momento en el que disminuye la tasa de incremento.
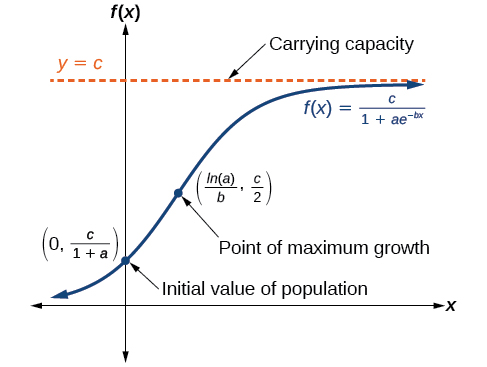
El modelo de crecimiento logístico es
\[f(x)=\dfrac{c}{1+ae^{−bx}}\]
donde
- \(\dfrac{c}{1+a}\)es el valor inicial
- \(c\)es la capacidad de carga, o valor limitante
- \(b\)es una constante determinada por la tasa de crecimiento.
Una epidemia de influenza se propaga a través de una población rápidamente, a un ritmo que depende de dos factores: Cuantas más personas tengan la gripe, más rápidamente se propaga, y también cuanto más personas no infectadas haya, más rápidamente se propaga. Estos dos factores hacen que el modelo logístico sea bueno para estudiar la propagación de enfermedades transmisibles. Y, claramente, hay un valor máximo para el número de personas infectadas: toda la población.
Por ejemplo, en el momento\(t=0\) hay una persona en una comunidad de\(1,000\) personas que tiene la gripe. Entonces, en esa comunidad, a lo sumo la\(1,000\) gente puede tener la gripe. Los investigadores encuentran que para esta cepa particular de la gripe, la constante de crecimiento logístico es\(b=0.6030\). Estimar el número de personas en esta comunidad que habrán tenido esta gripe después de diez días. Predecir cuántas personas en esta comunidad habrán tenido esta gripe después de que haya pasado un largo periodo de tiempo.
Solución
Sustituimos los datos dados en el modelo de crecimiento logístico
\(f(x)=\dfrac{c}{1+ae^{−bx}}\)
Porque a lo sumo la\(1,000\) gente, toda la población de la comunidad, puede contraer la gripe, sabemos que el valor limitante es\(c=1000\). Para encontrar\(a\), utilizamos la fórmula de que\(t=0\) es el número de casos en el momento\(\dfrac{c}{1+a}=1\), de la cual se deduce\(a=999\) que.Este modelo predice que, después de diez días, el número de personas que han tenido la gripe es\(f(x)=\dfrac{1000}{1+999e^{−0.6030x}}≈293.8\). Debido a que el número real debe ser un número entero (una persona ha tenido gripe o no) redondeamos a\(294\). A largo plazo, el número de personas que contraerán la gripe es el valor limitante,\(c=1000\).
Análisis
Recuerden que, debido a que estamos lidiando con un virus, no podemos predecir con certeza el número de personas infectadas. El modelo sólo se aproxima al número de personas infectadas y no nos dará valores exactos ni reales.
La gráfica de la Figura\(\PageIndex{7}\) da una buena imagen de cómo este modelo se ajusta a los datos.
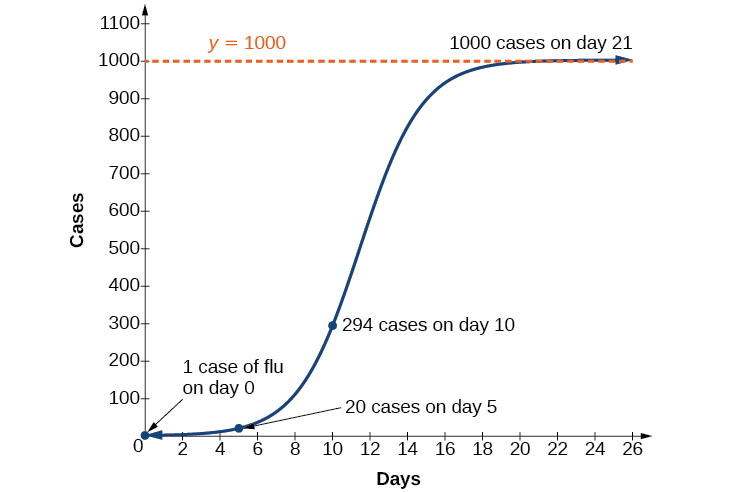
Utilizando el modelo del Ejemplo anterior, estime el número de casos de gripe en el día\(15\).
- Contestar
-
\(895\)casos en el día\(15\)
Elección de un modelo apropiado para los datos
Ahora que hemos discutido varios modelos matemáticos, necesitamos aprender a elegir el modelo apropiado para los datos brutos que tenemos. Muchos factores influyen en la elección de un modelo matemático, entre los que se encuentran la experiencia, las leyes científicas y los patrones en los propios datos. No todos los datos pueden ser descritos por funciones elementales. A veces, se elige una función que aproxima los datos a lo largo de un intervalo dado. Por ejemplo, supongamos que se recopilaron datos sobre el número de viviendas compradas en Estados Unidos desde los años 1960 hasta 2013. Después de trazar estos datos en un diagrama de dispersión, notamos que la forma de los datos de los años 2000 a 2013 sigue una curva logarítmica. Podríamos restringir el intervalo de 2000 a 2010, aplicar análisis de regresión utilizando un modelo logarítmico y utilizarlo para predecir el número de compradores de vivienda para el año 2015.
Tres tipos de funciones que suelen ser útiles en modelos matemáticos son las funciones lineales, las funciones exponenciales y las funciones logarítmicas. Si los datos se encuentran en una línea recta, o parecen estar aproximadamente a lo largo de una línea recta, un modelo lineal puede ser el mejor. Si los datos son no lineales, a menudo consideramos un modelo exponencial o logarítmico, aunque también se pueden considerar otros modelos, como los modelos cuadráticos.
Al elegir entre un modelo exponencial y un modelo logarítmico, observamos la forma en que se curvan los datos. A esto se le llama la concavidad. Si trazamos una línea entre dos puntos de datos, y todos (o la mayoría) de los datos entre esos dos puntos se encuentran por encima de esa línea, decimos que la curva es cóncava hacia abajo. Podemos pensarlo como un cuenco que se dobla hacia abajo y por lo tanto no puede retener el agua. Si todos (o la mayoría) de los datos entre esos dos puntos se encuentran por debajo de la línea, decimos que la curva es cóncava hacia arriba. En este caso, podemos pensar en un cuenco que se dobla hacia arriba y por lo tanto puede retener el agua. Una curva exponencial, ya sea ascendente o descendente, ya sea que represente crecimiento o decaimiento, siempre es cóncava hacia arriba lejos de su asíntota horizontal. Una curva logarítmica es siempre cóncava alejada de su asíntota vertical. En el caso de los datos positivos, que es el caso más común, una curva exponencial siempre es cóncava hacia arriba, y una curva logarítmica siempre cóncava hacia abajo.
Una curva logística cambia la concavidad. Comienza cóncavo hacia arriba y luego cambia a cóncavo hacia abajo más allá de cierto punto, llamado punto de inflexión.
Después de usar la gráfica para ayudarnos a elegir un tipo de función para usar como modelo, sustituimos puntos, y resolvemos para encontrar los parámetros. Reducimos el error de redondeo eligiendo puntos lo más separados posible.
¿Un modelo lineal, exponencial, logarítmico o logístico se ajusta mejor a los valores enumerados en la Tabla\(\PageIndex{1}\)? Encuentra el modelo y usa una gráfica para verificar tu elección.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 0 | 1.386 | 2.197 | 2.773 | 3.219 | 3.584 | 3.892 | 4.159 | 4.394 |
Solución
Primero, graficar los datos en una gráfica como en la Figura\(\PageIndex{8}\). Con el propósito de graficar, redondear los datos a dos dígitos significativos.
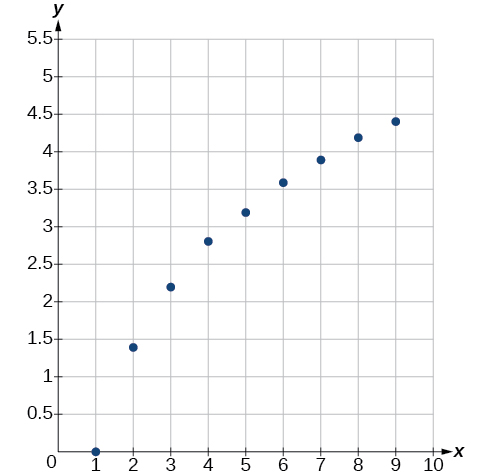
Claramente, los puntos no se encuentran en línea recta, por lo que rechazamos un modelo lineal. Si trazamos una línea entre cualquiera de los dos puntos, la mayoría o todos los puntos entre esos dos puntos se encuentran por encima de la línea, por lo que la gráfica es cóncava hacia abajo, sugiriendo un modelo logarítmico. Podemos intentarlo\(y=a\ln(bx)\). Tapando el primer punto,\((1,0)\), da\(0=a\ln b\). Rechazamos el caso de que\(a=0\) (si así fuera, todas las salidas serían\(0\)), así lo sabemos\(\ln(b)=0\). Así\(b=1\) y\(y=a\ln(x)\). A continuación podemos usar el punto\((9,4.394)\) para resolver para\(a\):
\[\begin{align*} y&= a\ln(x)\\ 4.394&= a\ln(9)\\ a&= \dfrac{4.394}{\ln(9)} \end{align*}\]
Porque\(a=\dfrac{4.394}{\ln(9)}≈2\), un modelo apropiado para los datos es\(y=2\ln(x)\).
Para verificar la precisión del modelo, graficamos la función junto con los puntos dados como en la Figura\(\PageIndex{9}\).
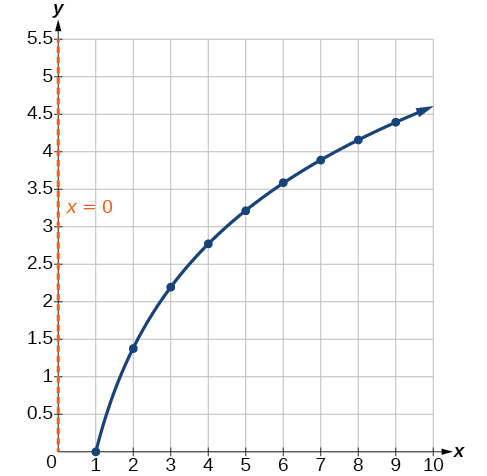
Podemos concluir que el modelo es un buen ajuste a los datos.
Compare la Figura\(\PageIndex{9}\) con la gráfica que\(y=\ln(x^2)\) se muestra en la Figura\(\PageIndex{10}\).
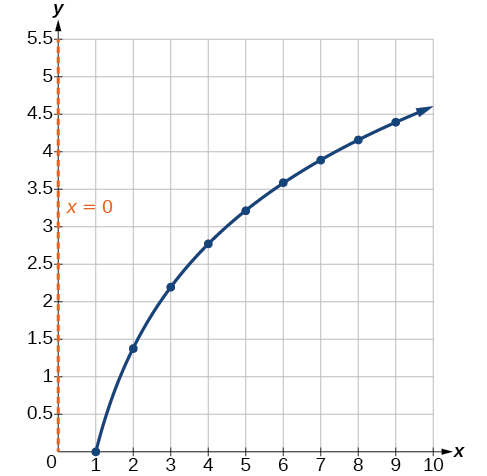
Las gráficas parecen ser idénticas cuando\(x>0\). Una comprobación rápida confirma esta conclusión:\(y=\ln(x^2)=2\ln(x)\) para\(x>0\).
Sin embargo, si\(x<0\), la gráfica de\(y=\ln(x^2)\) incluye una rama “extra”, como se muestra en la Figura\(\PageIndex{11}\). Esto ocurre porque, si bien\(y=2\ln(x)\) no puede tener valores negativos en el dominio (ya que tales valores obligarían al argumento a ser negativo), la función\(y=\ln(x^2)\) puede tener valores de dominio negativos.
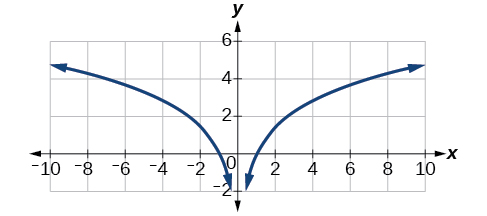
¿Un modelo lineal, exponencial o logarítmico se ajusta mejor a los datos de la Tabla\(\PageIndex{2}\)? Encuentra el modelo.
| \(x\) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| \(y\) | 3.297 | 5.437 | 8.963 | 14.778 | 24.365 | 40.172 | 66.231 | 109.196 | 180.034 |
- Contestar
-
Exponencial\(y=2e^{0.5x}\).
Expresar un Modelo Exponencial en Base\(e\)
Si bien los poderes y logaritmos de cualquier base pueden ser utilizados en el modelado, las dos bases más comunes son\(10\) y\(e\). En ciencias y matemáticas, a menudo\(e\) se prefiere la base. Podemos usar leyes de exponentes y leyes de logaritmos para cambiar cualquier base a base\(e\).
- Reescribir\(y=ab^x\) como\(y=ae^{\ln(b^x)}\).
- Utilice la regla de potencia de logaritmos para reescribir\(y\) como\(y=ae^{x\ln(b)}=ae^{\ln{(b)}^x}\).
- Obsérvese eso\(a=A_0\) y\(k=\ln(b)\) en la ecuación\(y=A_0e^{kx}\).
Cambia la función\(y=2.5{(3.1)}^x\) para que esta misma función quede escrita en la forma\(y=A_0e^{kx}\).
Solución
La fórmula se deriva de la siguiente manera
\[\begin{align*} y&= 2.5{(3.1)}^x\\ &= 2.5e^{\ln({3.1}^x)} \qquad \text{Insert exponential and its inverse}\\ &= 2.5e^{x\ln3.1} \qquad \text{Laws of logs}\\ &= 2.5e^{(\ln3.1)x} \qquad \text{Commutative law of multiplication} \end{align*}\]
Cambiar la función\(y=3{(0.5)}^x\) a una que tenga\(e\) como base.
- Contestar
-
\(y=3e^{(\ln0.5)x}\)
Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con modelos exponenciales y logarítmicos.
- Aplicación de logaritmo — pH
- Modelo exponencial: edad usando la vida media
- Ley del enfriamiento de Newton
- Crecimiento exponencial dado el tiempo de duplicación
- Crecimiento exponencial: encuentre la cantidad inicial dado el tiempo de duplicación
Ecuaciones Clave
| Fórmula de vida media | Si\(A=A_0e^{kt}\),\(k<0\), la vida media es\(t=−\dfrac{\ln(2)}{k}\). |
| Datación por carbono-14 | \(t=\dfrac{\ln(\dfrac{A}{A_0})}{−0.000121}\). \(A_0\)\(A\)es la cantidad de carbono-14 cuando la planta o animal murió \(t\) es la cantidad de carbono-14 restante hoy es la edad del fósil en años |
| Fórmula de tiempo de duplicación | Si\(A=A_0e^{kt}\),\(k>0\), el tiempo de duplicación es\(t=\dfrac{\ln2}{k}\) |
| Ley del enfriamiento de Newton | \(T(t)=Ae^{kt}+T_s\), donde\(T_s\) es la temperatura ambiente\(A=T(0)−T_s\), y\(k\) es la velocidad continua de enfriamiento. |
Conceptos clave
- La función exponencial básica es\(f(x)=ab^x\). Si\(b>1\), tenemos crecimiento exponencial; si\(0<b<1\), tenemos decaimiento exponencial.
- También podemos escribir esta fórmula en términos de crecimiento continuo como\(A=A_0e^{kx}\), donde\(A_0\) está el valor inicial. Si\(A_0\) es positivo, entonces tenemos crecimiento exponencial cuando\(k>0\) y decaimiento exponencial cuando\(k<0\). Ver Ejemplo\(\PageIndex{1}\).
- En general, resolvemos problemas que involucran crecimiento exponencial o decaimiento en dos pasos. Primero, configuramos un modelo y usamos el modelo para encontrar los parámetros. Luego usamos la fórmula con estos parámetros para predecir el crecimiento y la decadencia. Ver Ejemplo\(\PageIndex{2}\).
- Podemos encontrar la edad,\(t\), de un artefacto orgánico midiendo la cantidad,\(k\), de carbono-14 restante en el artefacto y usando la fórmula\(t=\dfrac{\ln(k)}{−0.000121}\) para resolver\(t\). Ver Ejemplo\(\PageIndex{3}\).
- Dado el tiempo de duplicación o medio tiempo de una sustancia, podemos encontrar una función que represente su crecimiento exponencial o decaimiento. Ver Ejemplo\(\PageIndex{4}\).
- Podemos usar la Ley de Enfriamiento de Newton para determinar cuánto tiempo tardará un objeto de enfriamiento en alcanzar una temperatura deseada, o para encontrar qué temperatura tendrá un objeto después de un tiempo determinado. Ver Ejemplo\(\PageIndex{5}\).
- Podemos usar funciones de crecimiento logístico para modelar situaciones del mundo real donde la tasa de crecimiento cambia con el tiempo, como el crecimiento de la población, la propagación de enfermedades y la propagación de rumores. Ver Ejemplo\(\PageIndex{6}\).
- Podemos usar datos del mundo real recopilados a lo largo del tiempo para observar tendencias. El conocimiento de gráficos lineales, exponenciales, logarítmicos y logísticos nos ayudan a desarrollar modelos que mejor se ajusten a nuestros datos. Ver Ejemplo\(\PageIndex{7}\).
- Cualquier función exponencial con la forma\(y=abx\) puede ser reescrita como una función exponencial equivalente con la forma\(y=A_0e^{kx}\) donde\(k=\ln b\). Ver Ejemplo\(\PageIndex{8}\).