7.1: Resolver ecuaciones trigonométricas con identidades
- Page ID
- 121587
- Verificar las identidades trigonométricas fundamentales.
- Simplifica las expresiones trigonométricas usando álgebra y las identidades.
En las películas de espionaje, vemos espías internacionales con múltiples pasaportes, cada uno reclamando una identidad diferente. No obstante, sabemos que cada uno de esos pasaportes representa a la misma persona. Las identidades trigonométricas actúan de manera similar a múltiples pasaportes; hay muchas formas de representar la misma expresión trigonométrica. Así como un espía elegirá un pasaporte italiano cuando viaje a Italia, elegimos la identidad que aplica al escenario dado al resolver una ecuación trigonométrica.

En esta sección, comenzaremos un examen de las identidades trigonométricas fundamentales, incluyendo cómo podemos verificarlas y cómo podemos utilizarlas para simplificar las expresiones trigonométricas.
Verificación de las Identidades Trigonométricas Fundamentales
Las identidades nos permiten simplificar expresiones complicadas. Son las herramientas básicas de la trigonometría utilizadas en la resolución de ecuaciones trigonométricas, así como factorizar, encontrar denominadores comunes y usar fórmulas especiales son las herramientas básicas para resolver ecuaciones algebraicas. De hecho, utilizamos constantemente técnicas algebraicas para simplificar las expresiones trigonométricas. Las propiedades básicas y fórmulas del álgebra, como la fórmula de diferencia de cuadrados y la fórmula de cuadrados perfectos, simplificarán el trabajo involucrado con expresiones y ecuaciones trigonométricas. Ya sabemos que todas las funciones trigonométricas están relacionadas porque todas están definidas en términos del círculo unitario. En consecuencia, cualquier identidad trigonométrica puede escribirse de muchas maneras.
Para verificar las identidades trigonométricas, generalmente comenzamos con el lado más complicado de la ecuación y esencialmente reescribimos la expresión hasta que se haya transformado en la misma expresión que el otro lado de la ecuación. A veces tenemos que factorizar expresiones, expandir expresiones, encontrar denominadores comunes o usar otras estrategias algebraicas para obtener el resultado deseado. En esta primera sección, trabajaremos con las identidades fundamentales: las identidades pitagóricas, las identidades pares-impares, las identidades recíprocas y las identidades cocientes.
Comenzaremos con las identidades pitagóricas (Tabla\(\PageIndex{1}\)), que son ecuaciones que involucran funciones trigonométricas basadas en las propiedades de un triángulo rectángulo. Ya hemos visto y utilizado la primera de estas identificaciones, pero ahora también usaremos identidades adicionales.
| \({\sin}^2 \theta+{\cos}^2 \theta=1\) | \(1+{\cot}^2 \theta={\csc}^2 \theta\) | \(1+{\tan}^2 \theta={\sec}^2 \theta\) |
La segunda y tercera identidades se pueden obtener manipulando la primera. La identidad\(1+{\cot}^2 \theta={\csc}^2 \theta\) se encuentra reescribiendo el lado izquierdo de la ecuación en términos de seno y coseno.
Demostrar:\(1+{\cot}^2 \theta={\csc}^2 \theta\)
\[\begin{align*} 1+{\cot}^2 \theta&= (1+\dfrac{{\cos}^2}{{\sin}^2})\qquad \text{Rewrite the left side}\\ &= \left(\dfrac{{\sin}^2}{{\sin}^2}\right)+\left (\dfrac{{\cos}^2}{{\sin}^2}\right)\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\sin}^2+{\cos}^2}{{\sin}^2}\\ &= \dfrac{1}{{\sin}^2}\\ &= {\csc}^2 \end{align*}\]
De igual manera, se\(1+{\tan}^2 \theta={\sec}^2 \theta\) puede obtener reescribiendo el lado izquierdo de esta identidad en términos de seno y coseno. Esto da
\[\begin{align*} 1+{\tan}^2 \theta&= 1+{\left(\dfrac{\sin \theta}{\cos \theta}\right )}^2\qquad \text{Rewrite left side}\\ &= {\left (\dfrac{\cos \theta}{\cos \theta}\right )}^2+{\left (\dfrac{\sin \theta}{\cos \theta}\right)}^2\qquad \text{Write both terms with the common denominator}\\ &= \dfrac{{\cos}^2 \theta+{\sin}^2 \theta}{{\cos}^2 \theta}\\ &= \dfrac{1}{{\cos}^2 \theta}\\ &= {\sec}^2 \theta \end{align*}\]
Recordemos que determinamos qué funciones trigonométricas son impares y cuáles son pares. El siguiente conjunto de identidades fundamentales es el conjunto de identidades pares e impares. Las identidades pares impares relacionan el valor de una función trigonométrica en un ángulo dado con el valor de la función en el ángulo opuesto (Tabla\(\PageIndex{2}\)).
| \(\tan(−\theta)=−\tan \theta\) | \(\sin(−\theta)=−\sin \theta\) | \(\cos(−\theta)=\cos \theta\) |
| \(\cot(−\theta)=−\cot \theta\) | \(\csc(−\theta)=−\csc \theta\) | \(\sec(−\theta)=\sec \theta\) |
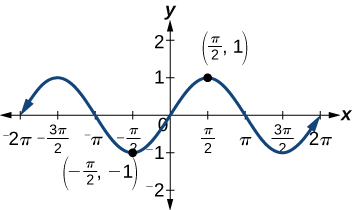
Recordemos que una función impar es aquella en la que\(f(−x)= −f(x)\) para todos\(x\) en el dominio off. f. La función seno es una función impar porque\(\sin(−\theta)=−\sin \theta\). La gráfica de una función impar es simétrica sobre el origen. Por ejemplo, considere las entradas correspondientes de\(\dfrac{\pi}{2}\) y\(−\dfrac{\pi}{2}\). La salida de\(\sin\left (\dfrac{\pi}{2}\right )\) es opuesta a la salida de\(\sin \left (−\dfrac{\pi}{2}\right )\). Por lo tanto,
\[\begin{align*} \sin\left (\dfrac{\pi}{2}\right)&=1 \\[4pt] \sin\left (-\dfrac{\pi}{2}\right) &=-\sin\left (\dfrac{\pi}{2}\right) \\[4pt] &=-1 \end{align*}\]
Esto se muestra en la Figura\(\PageIndex{2}\).
Recordemos que una función par es aquella en la que
\(f(−x)=f(x)\)para todos\(x\) en el dominio de\(f\)
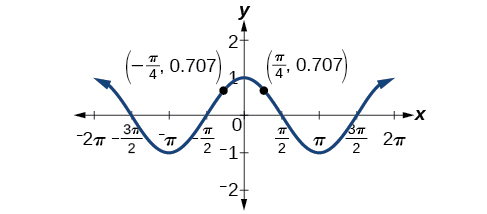
La gráfica de una función par es simétrica alrededor del eje y. La función coseno es una función par porque\(\cos(−\theta)=\cos \theta\). Por ejemplo, considere las entradas correspondientes\(\dfrac{\pi}{4}\) y\(−\dfrac{\pi}{4}\). La salida de\(\cos\left (\dfrac{\pi}{4}\right)\) es la misma que la salida de\(\cos\left (−\dfrac{\pi}{4}\right)\). Por lo tanto,
\[\begin{align*} \cos\left (−\dfrac{\pi}{4}\right ) &=\cos\left (\dfrac{\pi}{4}\right) \\[4pt] &≈0.707 \end{align*}\]
Ver Figura\(\PageIndex{3}\).
Para todos\(\theta\) en el dominio de las funciones seno y coseno, respectivamente, podemos afirmar lo siguiente:
- Ya que\(\sin(−\theta)=−\sin \theta\), seno es una función impar.
- Ya que\(\cos(−\theta)=\cos \theta\), el coseno es una función par.
Las otras identidades pares-impares se derivan de la naturaleza par e impar de las funciones seno y coseno. Por ejemplo, considere la identidad tangente,\(\tan(−\theta)=−\tan \theta\). Podemos interpretar la tangente de un ángulo negativo como
\[\tan (−\theta)=\dfrac{\sin (−\theta)}{\cos (−\theta)}=\dfrac{−\sin \theta}{\cos \theta}=−\tan \theta. \nonumber\]
Tangente es por lo tanto una función impar, lo que significa que\(\tan(−\theta)=−\tan(\theta)\) para todos\(\theta\) en el dominio de la función tangente.
La identidad cotangente,\(\cot(−\theta)=−\cot \theta\), también se desprende de las identidades seno y coseno. Podemos interpretar la cotangente de un ángulo negativo como
\[\cot(−\theta)=\dfrac{\cos(−\theta)}{\sin(−\theta)}=\dfrac{\cos \theta}{−\sin \theta}=−\cot \theta.\nonumber\]
Cotangente es por lo tanto una función impar, lo que significa que\(\cot(−\theta)=−\cot(\theta)\) para todos\(\theta\) en el dominio de la función cotangente.
La función cosecante es la recíproca de la función sinusoidal, lo que significa que la cosecante de un ángulo negativo se interpretará como
\[\csc(−\theta)=\dfrac{1}{\sin(−\theta)}=\dfrac{1}{−\sin \theta}=−\csc \theta. \nonumber\]
Por lo tanto, la función cosecante es impar.
Finalmente, la función secante es la recíproca de la función coseno, y la secante de un ángulo negativo se interpreta como
\[\sec(−\theta)=\dfrac{1}{\cos(−\theta)}=\dfrac{1}{\cos \theta}=\sec \theta. \nonumber\]
La función secante es, pues, parejo.
En resumen, sólo dos de las funciones trigonométricas, coseno y secante, son parejos. Las otras cuatro funciones son impares, verificando las identidades pares-impares.
El siguiente conjunto de identidades fundamentales es el conjunto de identidades recíprocas, que, como su nombre lo indica, relacionan funciones trigonométricas que son recíprocas entre sí. (Tabla\(\PageIndex{3}\)). Recordemos que por primera vez encontramos estas identidades al definir funciones trigonométricas desde ángulos rectos en trigonometría de ángulo recto.
| \(\sin \theta=\dfrac{1}{\csc \theta}\) | \(\csc \theta=\dfrac{1}{\sin \theta}\) |
| \(\cos \theta = \dfrac{1}{\sec \theta}\) | \(\sec \theta=\dfrac{1}{\cos \theta}\) |
| \(\tan \theta=\dfrac{1}{\cot \theta}\) | \(\cot \theta=\dfrac{1}{\tan \theta}\) |
El conjunto final de identidades es el conjunto de identidades de cocientes, que definen las relaciones entre ciertas funciones trigonométricas y pueden ser muy útiles para verificar otras identidades (Tabla\(\PageIndex{4}\)).
| \(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) | \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\) |
Las identidades recíprocas y cocientes se derivan de las definiciones de las funciones trigonométricas básicas.
Las identidades pitagóricas se basan en las propiedades de un triángulo rectángulo.
\[{\cos}^2 \theta+{\sin}^2 \theta=1\]
\[1+{\cot}^2 \theta={\csc}^2 \theta\]
\[1+{\tan}^2 \theta={\sec}^2 \theta\]
Las identidades pares impares relacionan el valor de una función trigonométrica en un ángulo dado con el valor de la función en el ángulo opuesto.
\[\tan(−\theta)=−\tan \theta\]
\[\cot(−\theta)=−\cot \theta\]
\[\sin(−\theta)=−\sin \theta\]
\[\csc(−\theta)=−\csc \theta\]
\[\cos(−\theta)=\cos \theta\]
\[\sec(−\theta)=\sec \theta\]
Las identidades recíprocas definen recíprocas de las funciones trigonométricas.
\[\sin \theta=\dfrac{1}{\csc \theta}\]
\[\cos \theta=\dfrac{1}{\sec \theta}\]
\[\tan \theta=\dfrac{1}{\cot \theta}\]
\[\csc \theta=\dfrac{1}{\sin \theta}\]
\[\sec \theta=\dfrac{1}{\cos \theta}\]
\[\cot \theta=\dfrac{1}{\tan \theta}\]
Las identidades del cociente definen la relación entre las funciones trigonométricas.
\[\tan \theta=\dfrac{\sin \theta}{\cos \theta}\]
\[\cot \theta=\dfrac{\cos \theta}{\sin \theta}\]
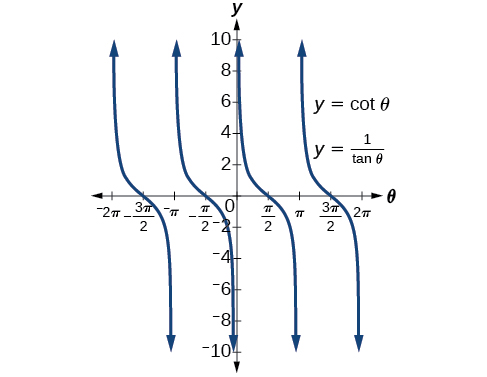
Grafica ambos lados de la identidad\(\cot \theta=\dfrac{1}{\tan \theta}\). En otras palabras, en la calculadora gráfica, gráfica\(y=\cot \theta\) y\(y=\dfrac{1}{\tan \theta}\).
Solución
Ver Figura\(\PageIndex{4}\).
Análisis
Solo vemos una gráfica porque ambas expresiones generan la misma imagen. Uno está encima del otro. Esta es una buena manera de probar cualquier identidad. Si ambas expresiones dan la misma gráfica, entonces deben ser identidades.
- Trabajar en un lado de la ecuación. Por lo general, es mejor comenzar por el lado más complejo, ya que es más fácil de simplificar que de construir.
- Busque oportunidades para factorizar expresiones, cuadrar un binomio o agregar fracciones.
- Observando qué funciones están en la expresión final, buscar oportunidades para usar las identidades y hacer las sustituciones adecuadas.
- Si estos pasos no dan el resultado deseado, intente convertir todos los términos en senos y cosenos.
Verificar\(\tan \theta \cos \theta=\sin \theta\).
Solución
Empezaremos por el lado izquierdo, ya que es el lado más complicado:
\[ \begin{align*} \tan \theta \cos \theta &=\left(\dfrac{\sin \theta}{\cos \theta}\right)\cos \theta \\[4pt] &=\sin \theta \end{align*}\]
Análisis
Esta identidad era bastante sencilla de verificar, ya que solo requería escribir\(\tan \theta\) en términos de\(\sin \theta\) y\(\cos \theta\).
Verificar la identidad\(\csc \theta \cos \theta \tan \theta=1\).
- Contestar
-
\[ \begin{align*} \csc \theta \cos \theta \tan \theta=\left(\dfrac{1}{\sin \theta}\right)\cos \theta\left(\dfrac{\sin \theta}{\cos \theta}\right) \\[4pt] & =\dfrac{\cos \theta}{\sin \theta}(\dfrac{\sin \theta}{\cos \theta}) \\[4pt] & =\dfrac{\sin \theta \cos \theta}{\sin \theta \cos \theta} \\[4pt] &=1 \end{align*}\]
Verifique la siguiente equivalencia usando las identidades pares-impares:
\((1+\sin x)[1+\sin(−x)]={\cos}^2 x\)
Solución
Trabajando en el lado izquierdo de la ecuación, tenemos
\( (1+\sin x)[1+\sin(−x)]=(1+\sin x)(1-\sin x)\)
Desde
\[\begin{align*} \sin(-x)&= -\sin x \\ [5pt] &=1-{\sin}^2 x\qquad \text{Difference of squares} \\ [5pt] &={\cos}^2 x \\ {\cos}^2 x&= 1-{\sin}^2 x \\ \end{align*}\]
Verificar la identidad\(\dfrac{{\sec}^2 \theta−1}{{\sec}^2 \theta}={\sin}^2 \theta\)
Solución
Como el lado izquierdo es más complicado, comencemos por ahí.
\ [\ begin {alinear*}
\ dfrac {{\ seg} ^2\ theta-1} {{\ seg} ^2\ theta} &=\ dfrac {({\ tan} ^2\ theta +1) -1} {{\ seg} ^2\ theta}\\
{\ seg} ^2\ theta&= {tan} ^2\ theta +1\\
=\ dfrac {{\ tan} ^2\ theta} {{\ seg} ^2\ theta}\\
&= {\ tan} ^2\ theta\ izquierda (\ dfrac {1} {{\ seg} ^2\ theta}\ derecha)\\
&= {\ tan} ^2\ theta\ izquierda ({\ cos} ^2\ theta\ derecha)\\
{\ cos} ^2\ theta&=\ dfrac {1} {{\ seg} ^2\ theta}\\
&=\ izquierda (\ dfrac {{\ sin} ^2\ theta} {{cos} ^2\ theta}\ derecha)\\
{\ tan} ^2\ theta&=\ dfrac {{\ sin} ^2\ theta} {{\ cos} ^2\ theta }\\
&= {\ sin} ^2\ theta
\ final {alinear*}\]
Hay más de una manera de verificar una identidad. Aquí hay otra posibilidad. Nuevamente, podemos comenzar por el lado izquierdo.
\[\begin{align*} \dfrac{{\sec}^2 \theta-1}{{\sec}^2 \theta}&= \dfrac{{\sec}^2 \theta}{{\sec}^2 \theta}-\dfrac{1}{{\sec}^2 \theta}\\ &= 1-{\cos}^2 \theta\\ &= {\sin}^2 \theta \end{align*}\]
Análisis
En el primer método, utilizamos la identidad\({\sec}^2 \theta={\tan}^2 \theta+1\) y seguimos simplificando. En el segundo método, dividimos la fracción, poniendo ambos términos en el numerador sobre el denominador común. Este problema ilustra que hay múltiples formas en las que podemos verificar una identidad. Emplear algo de creatividad a veces puede simplificar un procedimiento. Siempre y cuando las sustituciones sean correctas, la respuesta será la misma.
Demostrar eso\(\dfrac{\cot \theta}{\csc \theta}=\cos \theta\).
- Contestar
-
\[\begin{align*} \dfrac{\cot \theta}{\csc \theta}&= \dfrac{\tfrac{\cos \theta}{\sin \theta}}{\dfrac{1}{\sin \theta}}\\ &= \dfrac{\cos \theta}{\sin \theta}\cdot \dfrac{\sin \theta}{1}\\ &= \cos \theta \end{align*}\]
Crear una identidad para la expresión\(2 \tan \theta \sec \theta\) reescribiendo estrictamente en términos de seno.
Solución
Hay varias formas de comenzar, pero aquí usaremos el cociente y las identidades recíprocas para reescribir la expresión:
\[\begin{align*} 2 \tan \theta \sec \theta&= 2\left (\dfrac{\sin \theta}{\cos \theta}\right )\left(\dfrac{1}{\cos \theta}\right )\\ &= \dfrac{2\sin \theta}{{\cos}^2 \theta}\\ &= \dfrac{2\sin \theta}{1-{\sin}^2 \theta}\qquad \text{Substitute } 1-{\sin}^2 \theta \text{ for } {\cos}^2 \theta \end{align*}\]
Por lo tanto,
\(2 \tan \theta \sec \theta=\dfrac{2 \sin \theta}{1−{\sin}^2 \theta}\)
Verificar la identidad:
\(\dfrac{{\sin}^2(−\theta)−{\cos}^2(−\theta)}{\sin(−\theta)−\cos(−\theta)}=\cos \theta−\sin \theta\)
Solución
Empecemos por el lado izquierdo y simplifiquemos:
\[\begin{align*} \dfrac{{\sin}^2(-\theta)-{\cos}^2(-\theta)}{\sin(-\theta)-\cos(-\theta)}&= \dfrac{{[\sin(-\theta)]}^2-{[\cos(-\theta)]}^2}{\sin(-\theta)-\cos(-\theta)}\\ &= \dfrac{{(-\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta} \;\; \; , \sin(-x) = -\sin\space x\text { and } \cos(-x)=\cos \space x\\ &= \dfrac{{(\sin \theta)}^2-{(\cos \theta)}^2}{-\sin \theta -\cos \theta}\qquad \text{Difference of squares}\\ &= \dfrac{(\sin \theta-\cos \theta)(\sin \theta+\cos \theta)}{-(\sin \theta+\cos \theta)}\\ &= \cos \theta-\sin \theta \end{align*}\]
Verificar la identidad\(\dfrac{{\sin}^2 \theta−1}{\tan \theta \sin \theta−\tan \theta}=\dfrac{\sin \theta+1}{\tan \theta}\).
- Contestar
-
\[\begin{align*} \dfrac{{\sin}^2 \theta-1}{\tan \theta \sin \theta-\tan \theta}&= \dfrac{(\sin \theta +1)(\sin \theta -1)}{\tan \theta(\sin \theta -1)}\\ &= \dfrac{\sin \theta+1}{\tan \theta} \end{align*}\]
Verificar la identidad:\((1−{\cos}^2 x)(1+{\cot}^2 x)=1\).
Solución
\[\begin{align*} (1-{\cos}^2 x)(1+{\cot}^2 x)&= (1-{\cos}^2 x)\left(1+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right)\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x}{{\sin}^2 x}+\dfrac{{\cos}^2 x}{{\sin}^2 x}\right )\qquad \text{Find the common denominator}\\ &= (1-{\cos}^2 x)\left(\dfrac{{\sin}^2 x +{\cos}^2 x}{{\sin}^2 x}\right)\\ &= ({\sin}^2 x)\left (\dfrac{1}{{\sin}^2 x}\right )\\ &= 1 \end{align*}\]
Uso del álgebra para simplificar las expresiones trigonométricas
Hemos visto que el álgebra es muy importante en la verificación de identidades trigonométricas, pero es igual de crítico para simplificar las expresiones trigonométricas antes de resolverlo. Estar familiarizado con las propiedades y fórmulas básicas del álgebra, como la fórmula de diferencia de cuadrados, la fórmula cuadrada perfecta, o la sustitución, simplificará el trabajo involucrado con expresiones y ecuaciones trigonométricas.
Por ejemplo, la ecuación\((\sin x+1)(\sin x−1)=0\) se asemeja a la ecuación\((x+1)(x−1)=0\), que utiliza la forma factorizada de la diferencia de cuadrados. El uso del álgebra hace que encontrar una solución sea sencillo y familiar. Podemos establecer cada factor igual a cero y resolver. Este es un ejemplo de reconocimiento de patrones algebraicos en expresiones o ecuaciones trigonométricas.
Otro ejemplo es la fórmula de diferencia de cuadrados\(a^2−b^2=(a−b)(a+b)\), que es ampliamente utilizada en muchas áreas distintas a las matemáticas, como la ingeniería, la arquitectura y la física. También podemos crear nuestras propias identidades expandiendo continuamente una expresión y haciendo las sustituciones adecuadas. El uso de propiedades y fórmulas algebraicas hace que muchas ecuaciones trigonométricas sean más fáciles de entender y resolver.
Escribe la siguiente expresión trigonométrica como expresión algebraica:\(2{\cos}^2 \theta+\cos \theta−1\).
Solución
Observe que el patrón mostrado tiene la misma forma que una expresión cuadrática estándar,\(ax^2+bx+c\). Dejando\(\cos \theta=x\), podemos reescribir la expresión de la siguiente manera:
\(2x^2+x−1\)
Esta expresión se puede factorizar como\((2x+1)(x−1)\). Si se pusiera igual a cero y quisiéramos resolver la ecuación, usaríamos la propiedad del factor cero y resolveríamos cada factor para\(x\). En este punto, reemplazaríamos\(x\) con\(\cos \theta\) y resolveríamos para\(\theta\).
Reescribir la expresión trigonométrica usando la diferencia de cuadrados:\(4{cos}^2 \theta−1\).
Solución
Observe que tanto el coeficiente como la expresión trigonométrica en el primer término son cuadrados, y el cuadrado del número 1 es 1. Esta es la diferencia de cuadrados.
\[\begin{align*} 4{\cos}^2 \theta-1&= {(2\cos \theta)}^2-1\\ &= (2\cos \theta-1)(2\cos \theta+1) \end{align*}\]
Análisis
Si esta expresión se escribiera en forma de una ecuación establecida igual a cero, podríamos resolver cada factor usando la propiedad de factor cero. También podríamos usar la sustitución como hicimos en el problema anterior y dejar\(\cos \theta=x\), reescribir la expresión as\(4x^2−1\), y factor\((2x−1)(2x+1)\). Luego reemplace\(x\) con\(\cos \theta\) y resuelva para el ángulo.
Reescribir la expresión trigonométrica usando la diferencia de cuadrados:\(25−9{\sin}^2 \theta\).
- Contestar
-
Esta es una fórmula de diferencia de cuadrados:\(25−9{\sin}^2 \theta=(5−3\sin \theta)(5+3\sin \theta)\).
Simplifica la expresión reescribiendo y usando identidades:
\({\csc}^2 \theta−{\cot}^2 \theta\)
Solución
Podemos comenzar con la identidad pitagórica.
\[\begin{align*} 1+{\cot}^2 \theta&= {\csc}^2 \theta\\ \text{Now we can simplify by substituting } 1+{\cot}^2 \theta \text{ for } {\csc}^2 \theta\\ {\csc}^2 \theta-{\cot}^2 \theta&= 1+{\cot}^2 \theta-{\cot}^2 \theta\\ &= 1 \end{align*}\]
Utilizar técnicas algebraicas para verificar la identidad:\(\dfrac{\cos \theta}{1+\sin \theta}=\dfrac{1−\sin \theta}{\cos \theta}\).
(Pista: Multiplica el numerador y denominador del lado izquierdo por\(1−\sin \theta\).)
- Contestar
-
\[\begin{align*} \dfrac{\cos \theta}{1+\sin \theta}\left(\dfrac{1-\sin \theta}{1-\sin \theta}\right)&= \dfrac{\cos \theta (1-\sin \theta)}{1-{\sin}^2 \theta}\\ &= \dfrac{\cos \theta (1-\sin \theta)}{{\cos}^2 \theta}\\ &= \dfrac{1-\sin \theta}{\cos \theta} \end{align*}\]
Acceda a estos recursos en línea para una instrucción adicional y práctica con las identidades trigonométricas fundamentales.
- Identidades trigonométricas fundamentales
- Verificación de identidades trigonométricas
Ecuaciones Clave
| Identidades pitagóreas |
\({\cos}^2 \theta+{\sin}^2 \theta=1\) \(1+{\cot}^2 \theta={\csc}^2 \theta\) \(1+{\tan}^2 \theta={\sec}^2 \theta\) |
| Identidades pares e impares |
\(\tan(−\theta)=-\tan \theta\) \(\cot(-\theta)=-\cot \theta\) \(\sin(-\theta)=-\sin \theta\) \(\csc(-\theta)=-\csc \theta\) \(\cos(-\theta)=\cos \theta\) \(\sec(-\theta)=\sec \theta\) |
| Identidades recíprocas |
\(\sin \theta=\dfrac{1}{\csc \theta}\) \(\cos \theta=\dfrac{1}{\sec \theta}\) \(\tan \theta=\dfrac{1}{\cot \theta}\) \(\csc \theta=\dfrac{1}{\sin \theta}\) \(\sec \theta=\dfrac{1}{\cos \theta}\) \(\cot \theta=\dfrac{1}{\tan \theta}\) |
| Identidades de cocientes |
\(\tan \theta=\dfrac{\sin \theta}{\cos \theta}\) \(\cot \theta=\dfrac{\cos \theta}{\sin \theta}\) |
Conceptos clave
- Existen múltiples formas de representar una expresión trigonométrica. Verificar las identidades ilustra cómo se pueden reescribir las expresiones para simplificar un problema.
- Graficar ambos lados de una identidad la verificará. Ver Ejemplo\(\PageIndex{1}\).
- Simplificar un lado de la ecuación para igualar al otro lado es otro método para verificar una identidad. Ver Ejemplo\(\PageIndex{2}\) y Ejemplo\(\PageIndex{3}\).
- El enfoque para verificar una identidad depende de la naturaleza de la identidad. A menudo es útil comenzar en el lado más complejo de la ecuación. Ver Ejemplo\(\PageIndex{4}\).
- Podemos crear una identidad y luego verificarla. Ver Ejemplo\(\PageIndex{5}\).
- Verificar una identidad puede implicar álgebra con las identidades fundamentales. Ver Ejemplo\(\PageIndex{6}\) y Ejemplo\(\PageIndex{7}\).
- Las técnicas algebraicas se pueden utilizar para simplificar las expresiones trigonométricas. Utilizamos técnicas algebraicas a lo largo de este texto, ya que consisten en las reglas fundamentales de las matemáticas. Ver Ejemplo\(\PageIndex{8}\)\(\PageIndex{9}\), Ejemplo y Ejemplo\(\PageIndex{10}\).


