7.3: Fórmulas de doble ángulo, medio ángulo y reducción

Objetivos de aprendizaje

• Utilice fórmulas de doble ángulo para encontrar valores exactos
• Usar fórmulas de doble ángulo para verificar identidades
• Usar fórmulas de reducción para simplificar una expresión
• Utilice fórmulas de medio ángulo para encontrar valores exactos

Las rampas para bicicletas hechas para competición (ver Figura\(\PageIndex{1}\)) deben variar en altura dependiendo del nivel de habilidad de los competidores. Para los competidores avanzados, el ángulo formado por la rampa y el suelo debe ser\(\theta\) tal que\(\tan \theta=\dfrac{5}{3}\). El ángulo se divide por la mitad para los novatos. ¿Cuál es la pendiente de la rampa para principiantes? En esta sección, investigaremos tres categorías adicionales de identidades que podemos usar para responder preguntas como esta.

Figura\(\PageIndex{1}\): Las rampas para bicicletas para ciclistas avanzados tienen una inclinación más pronunciada que las diseñadas para principiantes.

Uso de fórmulas de doble ángulo para encontrar valores exactos

En la sección anterior, se utilizaron fórmulas de suma y resta para funciones trigonométricas. Ahora, echamos otro vistazo a esas mismas fórmulas. Las fórmulas de doble ángulo son un caso especial de las fórmulas de suma, donde\(\alpha=\beta\). Derivar la fórmula de doble ángulo para seno comienza con la fórmula de suma,

\[\sin(\alpha+\beta)=\sin \alpha \cos \beta+\cos \alpha \sin \beta\]

Si lo dejamos\(\alpha=\beta=\theta\), entonces tenemos

\[\begin{align*} \sin(\theta+\theta)&= \sin \theta \cos \theta+\cos \theta \sin \theta\\[4pt] \sin(2\theta)&= 2\sin \theta \cos \theta \end{align*}\]

Derivar el doble ángulo para coseno nos da tres opciones. Primero, partiendo de la fórmula de suma\(\cos(\alpha+\beta)=\cos \alpha \cos \beta−\sin \alpha \sin \beta\), y dejando\(\alpha=\beta=\theta\), tenemos

\[\begin{align*} \cos(\theta+\theta)&= \cos \theta \cos \theta-\sin \theta \sin \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \end{align*}\]

Usando las propiedades pitagóricas, podemos ampliar esta fórmula de doble ángulo para coseno y obtener dos variaciones más. La primera variación es:

\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta - {\sin}^2 \theta \\[4pt] &= (1-{\sin}^2 \theta)-{\sin}^2 \theta \end{align*}\]

La segunda variación es:

\[\begin{align*} \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta\\[4pt] &= {\cos}^2 \theta-(1-{\cos}^2 \theta)\\[4pt] &= 2 {\cos}^2 \theta-1 \end{align*}\]

Del mismo modo, para derivar la fórmula de doble ángulo para tangente, reemplazando\(\alpha=\beta=\theta\) en la fórmula suma da

\[\begin{align*} \tan(\alpha+\beta)&= \dfrac{\tan \alpha+\tan \beta}{1-\tan \alpha \tan \beta}\\[4pt] \tan(\theta+\theta)&= \dfrac{\tan \theta+\tan \theta}{1-\tan \theta \tan \theta}\\[4pt] \tan(2\theta)&= \dfrac{2\tan \theta}{1-{\tan}^2 \theta} \end{align*}\]

Fórmulas de doble ángulo

Las fórmulas de doble ángulo se resumen de la siguiente manera:

\[\begin{align} \sin(2\theta)&= 2 \sin \theta \cos \theta\\[4pt] \cos(2\theta)&= {\cos}^2 \theta-{\sin}^2 \theta =1-2 {\sin}^2 \theta = 2{\cos}^2 \theta-1\\[4pt] \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2\theta} \end{align}\]

Cómo: Dada la tangente de un ángulo y el cuadrante en el que se encuentra, utilice las fórmulas de doble ángulo para encontrar el valor exacto

1. Dibuja un triángulo para reflejar la información dada.
2. Determinar la fórmula correcta de doble ángulo.
3. Sustituye los valores en la fórmula basada en el triángulo.
4. Simplificar.

Ejemplo\(\PageIndex{1}\): Using a Double-Angle Formula to Find the Exact Value Involving Tangent

Dado que\(\tan \theta=−\dfrac{3}{4}\) y\(\theta\) está en el cuadrante II, encuentra lo siguiente:

1. \(\sin(2\theta)\)
2. \(\cos(2\theta)\)
3. \(\tan(2\theta)\)

Solución

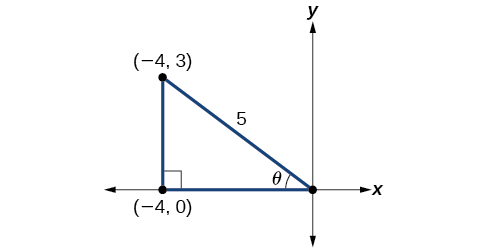
Si dibujamos un triángulo para reflejar la información dada, podemos encontrar los valores necesarios para resolver los problemas en la imagen. Se nos da\(\tan \theta=−\dfrac{3}{4}\), tal que\(\theta\) está en el cuadrante II. La tangente de un ángulo es igual al lado opuesto sobre el lado adyacente, y debido a que\(\theta\) está en el segundo cuadrante, el lado adyacente está en el eje x y es negativo. Usa el Teorema de Pitágoras para encontrar la longitud de la hipotenusa:

\[\begin{align*} {(-4)}^2+{(3)}^2&= c^2\\[4pt] 16+9&= c^2\\[4pt] 25&= c^2\\[4pt] c&= 5 \end{align*}\]

Ahora podemos dibujar un triángulo similar al que se muestra en la Figura\(\PageIndex{2}\).

Figura\(\PageIndex{2}\)

1. Empecemos por escribir la fórmula de doble ángulo para seno.

   \(\sin(2\theta)=2 \sin \theta \cos \theta\)

   Vemos que necesitamos encontrar\(\sin \theta\) y\(\cos \theta\). Con base en la Figura\(\PageIndex{2}\), vemos que la hipotenusa es igual a\(5\)\(\sin θ=35\), así\(\sin θ=35\), y\(\cos θ=−45\). Sustituir estos valores en la ecuación, y simplificar.

   Por lo tanto,

   \[\begin{align*} \sin(2\theta)&= 2\left(\dfrac{3}{5}\right)\left(-\dfrac{4}{5}\right)\\[4pt] &= -\dfrac{24}{25} \end{align*}\]

2. Escribe la fórmula de doble ángulo para coseno.

   \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\)

   Nuevamente, sustituya los valores del seno y del coseno en la ecuación, y simplifique.

   \[\begin{align*} \cos(2\theta)&= {\left(-\dfrac{4}{5}\right)}^2-{\left(\dfrac{3}{5}\right)}^2\\[4pt] &= \dfrac{16}{25}-\dfrac{9}{25}\\[4pt] &= \dfrac{7}{25} \end{align*}\]

3. Escribe la fórmula de doble ángulo para tangente.

   \(\tan(2\theta)=\dfrac{2 \tan \theta}{1−{\tan}^2\theta}\)

   En esta fórmula, necesitamos la tangente, que nos dieron como\(\tan \theta=−\dfrac{3}{4}\). Sustituir este valor en la ecuación, y simplificar.

   \ [\ begin {align*}\ tan (2\ theta) &=\ dfrac {2\ izquierda (-\ dfrac {3} {4}\ derecha)} {1- {\ izquierda (-\ dfrac {3} {4}\ derecha)} ^2}\\ [4pt]
   &=\ dfrac {-\ dfrac {3} {2}} {1-\ dfrac {9} {16}}\\ [4pt]
   &= -\ dfrac {3} {2}\ izquierda (\ dfrac {16} {7}\ derecha)\\ [4pt]
   &= -\ dfrac {24} {7}
   \ end {alinear*}\]

Ejercicio\(\PageIndex{1}\)

Dado\(\sin \alpha=\dfrac{5}{8}\), con\(\theta\) en el cuadrante I, encontrar\(\cos(2\alpha)\).

Contestar

\(\cos(2\alpha)=\dfrac{7}{32}\)

Ejemplo\(\PageIndex{2}\): Using the Double-Angle Formula for Cosine without Exact Values

Utilice la fórmula de doble ángulo para que el coseno escriba\(\cos(6x)\) en términos de\(cos(3x)\).

Solución

\[\begin{align*} \cos(6x)&= \cos(3x+3x)\\[4pt] &= \cos 3x \cos 3x-\sin 3x \sin 3x\\[4pt] &= {\cos}^2 3x-{\sin}^2 3x \end{align*}\]

Análisis

Este ejemplo ilustra que podemos usar la fórmula de doble ángulo sin tener valores exactos. Enfatiza que el patrón es lo que debemos recordar y que las identidades son verdaderas para todos los valores en el dominio de la función trigonométrica.

Uso de fórmulas de doble ángulo para verificar identidades

El establecimiento de identidades usando las fórmulas de doble ángulo se realiza usando los mismos pasos que usamos para derivar las fórmulas de suma y diferencia. Elige el lado más complicado de la ecuación y vuelve a escribirlo hasta que coincida con el otro lado.

Ejemplo\(\PageIndex{3}\): Using the Double-Angle Formulas to Verify an Identity

Verifique la siguiente identidad usando fórmulas de doble ángulo:

\[1+\sin(2\theta)={(\sin\theta+\cos\theta)}^2 \nonumber \]

Solución

Trabajaremos en el lado derecho del signo igual y reescribiremos la expresión hasta que coincida con el lado izquierdo.

\[\begin{align*} {(\sin \theta+\cos \theta)}^2&= {\sin}^2 \theta+2 \sin \theta \cos \theta+{\cos}^2 \theta\\[4pt] &= ({\sin}^2 \theta+{\cos}^2 \theta)+2 \sin \theta \cos \theta\\[4pt] &= 1+2 \sin \theta \cos \theta\\[4pt] &= 1+\sin(2\theta) \end{align*}\]

Análisis

Este proceso no es complicado, siempre y cuando recordemos la fórmula cuadrada perfecta del álgebra:

\[{(a\pm b)}^2=a^2\pm 2ab+b^2 \nonumber \]

dónde\(a=\sin \theta\) y\(b=\cos \theta\). Parte de tener éxito en matemáticas es la capacidad de reconocer patrones. Si bien los términos o símbolos pueden cambiar, el álgebra permanece consistente.

Ejercicio\(\PageIndex{2}\)

Verificar la identidad:\({\cos}^4 \theta−{\sin}^4 \theta=\cos(2\theta)\).

Contestar

\({\cos}^4 \theta−{\sin}^4 \theta=({\cos}^2 \theta+{\sin}^2 \theta)({\cos}^2 \theta−{\sin}^2 \theta)=\cos(2\theta)\)

Ejemplo\(\PageIndex{4}\): Verifying a Double-Angle Identity for Tangent

Verificar la identidad:\(\tan(2 \theta)=2\cot \theta−\tan \theta\)

Solución

En este caso, trabajaremos con el lado izquierdo de la ecuación y simplificaremos o reescribiremos hasta que iguale al lado derecho de la ecuación.

\[\begin{align*} \tan(2\theta)&= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \qquad \text{Double-angle formula}\\[4pt] &= \dfrac{2 \tan \theta\left (\dfrac{1}{\tan \theta}\right)}{(1-{\tan}^2 \theta)\left (\dfrac{1}{\tan \theta}\right )} \qquad \text{Multiply by a term that results in desired numerator}\\[4pt] &= \dfrac{2}{\dfrac{1}{\tan \theta}-\dfrac{ {\tan}^2 \theta}{\tan \theta}}\\[4pt] &= \dfrac{2}{\cot \theta-\tan \theta} \qquad \text {Use reciprocal identity for } \dfrac{1}{\tan \theta} \end{align*}\]

Análisis

Aquí hay un caso donde el lado más complicado de la ecuación inicial apareció a la derecha, pero optamos por trabajar el lado izquierdo. No obstante, si hubiéramos elegido el lado izquierdo para reescribir, habríamos estado trabajando hacia atrás para llegar a la equivalencia. Por ejemplo, supongamos que quisiéramos mostrar

\[\begin{align*} \dfrac{2\tan \theta}{1-{\tan}^2 \theta}&= \dfrac{2}{\cot \theta-\tan \theta} \\[4pt] \text{Lets work on the right side}\\[4pt] \dfrac{2}{\cot \theta-\tan \theta}&= \frac{2}{\frac{1}{\tan \theta }-\tan \theta }\left ( \frac{\tan \theta }{\tan \theta } \right )\\[4pt] &= \dfrac{2 \tan \theta}{\dfrac{1}{\tan \theta}(\tan \theta)-\tan \theta(\tan \theta)}\\[4pt] &= \dfrac{2 \tan \theta}{1-{\tan}^2 \theta} \end{align*}\]

Cuando se utilizan las identidades para simplificar una expresión trigonométrica o resolver una ecuación trigonométrica, generalmente hay varias rutas hacia un resultado deseado. No hay una regla establecida en cuanto a qué lado se debe manipular. No obstante, debemos comenzar con los lineamientos expuestos anteriormente.

Ejercicio\(\PageIndex{3}\)

Verificar la identidad:\(\cos(2\theta)\cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\).

Contestar

\(\cos(2 \theta)\cos \theta=({\cos}^2 \theta−{\sin}^2 \theta) \cos \theta={\cos}^3 \theta−\cos \theta {\sin}^2 \theta\)

Uso de fórmulas de reducción para simplificar una expresión

Las fórmulas de doble ángulo se pueden utilizar para derivar las fórmulas de reducción, que son fórmulas que podemos usar para reducir el poder de una expresión dada involucrando incluso potencias de seno o coseno. Nos permiten reescribir los poderes pares de seno o coseno en términos del primer poder del coseno. Estas fórmulas son especialmente importantes en los cursos de matemáticas de nivel superior, en particular el cálculo. También llamadas fórmulas reductoras de potencia, se incluyen tres identidades y se derivan fácilmente de las fórmulas de doble ángulo.

Podemos usar dos de las tres fórmulas de doble ángulo para coseno para derivar las fórmulas de reducción para seno y coseno. Empecemos con\(\cos(2\theta)=1−2 {\sin}^2 \theta\). Resolver para\({\sin}^2 \theta\):

\[\begin{align*} \cos(2\theta)&= 1-2 {\sin}^2 \theta\\[4pt] 2 {\sin}^2 \theta&= 1-\cos(2\theta)\\[4pt] {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2} \end{align*}\]

A continuación, usamos la fórmula\(\cos(2\theta)=2 {\cos}^2 \theta−1\). Resolver para\({\cos}^2 \theta\):

\[\begin{align*} \cos(2\theta)&= 2 {\cos}^2 \theta-1\\[4pt] 1+\cos(2\theta)&= 2 {\cos}^2 \theta\\[4pt] \dfrac{1+\cos(2\theta)}{2}&= {\cos}^2 \theta \end{align*}\]

La última fórmula de reducción se deriva escribiendo tangente en términos de seno y coseno:

\[\begin{align*} \tan^2 \theta &= \frac{\sin^2 \theta}{\cos^2 \theta} \\[4pt] &= \dfrac{\dfrac{1-\cos(2\theta)}{2}}{\dfrac{1+\cos(2\theta)}{2}} \qquad \tag{Substitute the reduction formulas} \\[4pt] &= \left(\dfrac{1-\cos(2 \theta)}{2}\right)\left(\dfrac{2}{1+\cos(2 \theta)}\right) \\[4pt] &= \dfrac{1-\cos(2 \theta)}{1+\cos(2 \theta)} \end{align*}\]

Fórmulas de reducción

Las fórmulas de reducción se resumen de la siguiente manera:

\[{\sin}^2 \theta=\dfrac{1−\cos(2 \theta)}{2}\]

\[{\cos}^2 \theta=\dfrac{1+\cos(2 \theta)}{2}\]

\[{\tan}^2 \theta=\dfrac{1−\cos(2 \theta)}{1+\cos(2 \theta)}\]

Ejemplo\(\PageIndex{5}\): Writing an Equivalent Expression Not Containing Powers Greater Than 1

Escribir una expresión equivalente para\({\cos}^4 x\) que no implique ningún poder de seno o coseno mayor que\(1\).

Solución

Aplicaremos la fórmula de reducción para coseno dos veces.

\ [\ begin {align*}
{\ cos} ^4 x&= {({\ cos} ^2 x)} ^2\\ [4pt]
&= {\ left (\ dfrac {1+\ cos (2x)} {2}\ derecha)} ^2\ qquad\ text {Fórmula de reducción sustituta}\\ [4pt]
&=\ dfrac {1} {4} (1+2\ cos (2x) + {\ cos} ^2 (2x))\\ [4pt]
&=\ dfrac {1} {4} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {4}\ left (\ dfrac {1+ {\ cos} ^2 (2x)} {2}\ derecha)\ qquad\ text {Sustituir fórmula de reducción para} {\ cos} ^2 x\\ [4pt]
&=\ dfrac {1} {4} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {8} +\ dfrac {1} {8}\ cos (4x)\\ [4pt]
&=\ dfrac {3} {8} +\ dfrac {1} {2}\ cos (2x) +\ dfrac {1} {8}\ cos (4x)
\ final {alinear*}\]

Análisis

La solución se encuentra usando la fórmula de reducción dos veces, como se señaló, y la fórmula cuadrada perfecta a partir del álgebra.

Ejemplo\(\PageIndex{6}\): Using the Power-Reducing Formulas to Prove an Identity

Utilice las fórmulas de reducción de energía para probar\({\sin}^3(2x)=\left[ \dfrac{1}{2} \sin(2x) \right] [ 1−\cos(4x) \)

Solución

Trabajaremos en simplificar el lado izquierdo de la ecuación:

\[\begin{align*} {\sin}^3(2x)&= [\sin(2x)][{\sin}^2(2x)]\\[4pt] &= \sin(2x)\left [\dfrac{1-\cos(4x)}{2}\right ]\qquad \text{Substitute the power-reduction formula.}\\[4pt] &= \sin(2x)\left(\dfrac{1}{2}\right)[1-\cos(4x)]\\[4pt] &= \dfrac{1}{2}[\sin(2x)][1-\cos(4x)] \end{align*}\]

Análisis

Tenga en cuenta que en este ejemplo, sustituimos\(\dfrac{1−\cos(4x)}{2}\) por\({\sin}^2(2x)\). La fórmula establece\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\)

Dejamos\(\theta=2x\), entonces\(2\theta=4x\).

Ejercicio\(\PageIndex{4}\)

Use las fórmulas de reducción de energía para probarlo\(10{\cos}^4 x=\dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x)\).

Contestar

\[\begin{align*} 10{\cos}^4 x&= 10{({\cos}^2x)}^2\\[4pt] &= 10{\left[\dfrac{ 1+\cos(2x)}{2} \right]}^2\qquad \text{Substitute reduction formula for } {\cos}^2x\\[4pt] &= \dfrac{10}{4}[1+2\cos(2x)+{\cos}^2(2x)]\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2}\cos(2x)+\dfrac{10}{4}\left(\dfrac{1+{\cos}^2(2x)}{2}\right)\qquad \text{ Substitute reduction formula for } {\cos}^2 x\\[4pt] &= \dfrac{10}{4}+\dfrac{10}{2} \cos(2x)+\dfrac{10}{8}+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{30}{8}+5\cos(2x)+\dfrac{10}{8}\cos(4x)\\[4pt] &= \dfrac{15}{4}+5\cos(2x)+\dfrac{5}{4}\cos(4x) \end{align*}\]

Uso de fórmulas de medio ángulo para encontrar valores exactos

El siguiente conjunto de identidades es el conjunto de fórmulas de medio ángulo, que se pueden derivar de las fórmulas de reducción y podemos usar cuando tenemos un ángulo que es la mitad del tamaño de un ángulo especial. Si\(\theta\) reemplazamos por\(\dfrac{\alpha}{2}\), la fórmula de medio ángulo para seno se encuentra simplificando la ecuación y resolviendo para\(\sin\left(\dfrac{\alpha}{2}\right)\). Tenga en cuenta que las fórmulas de medio ángulo están precedidas por un\(\pm\) signo. Esto no quiere decir que tanto las expresiones positivas como las negativas sean válidas. Más bien, depende del cuadrante en el que\(\dfrac{\alpha}{2}\) termina.

La fórmula de medio ángulo para seno se deriva de la siguiente manera:

\[\begin{align*} {\sin}^2 \theta&= \dfrac{1-\cos(2\theta)}{2}\\[4pt] {\sin}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\left(\cos 2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1-\cos \alpha}{2}\\[4pt] \sin \left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}} \end{align*}\]

Para derivar la fórmula de medio ángulo para el coseno, tenemos

\[\begin{align*} {\cos}^2 \theta&= \dfrac{1+\cos(2\theta)}{2}\\[4pt] {\cos}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{2}\\[4pt] &= \dfrac{1+\cos \alpha}{2}\\[4pt] \cos\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}} \end{align*}\]

Para la identidad tangente, tenemos

\[\begin{align*} {\tan}^2 \theta&= \dfrac{1-\cos(2\theta)}{1+\cos(2\theta)}\\[4pt] {\tan}^2\left(\dfrac{\alpha}{2}\right)&= \dfrac{1-\cos\left(2\cdot \dfrac{\alpha}{2}\right)}{1+\cos\left(2\cdot \dfrac{\alpha}{2}\right)}\\[4pt] \tan\left(\dfrac{\alpha}{2}\right)&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} \end{align*}\]

Fórmulas de medio ángulo

Las fórmulas de medio ángulo son las siguientes:

\[\begin{align} \sin\left(\dfrac{\alpha}{2}\right)&=\pm \sqrt{\dfrac{1-\cos \alpha}{2}} \label{halfsine} \\[4pt] \cos \left(\dfrac{\alpha}{2} \right) &=\pm \sqrt{\dfrac{1+\cos \alpha}{2}} \\[4pt] \tan\left(\dfrac{\alpha}{2}\right) &=\pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}} =\dfrac{\sin \alpha}{1+\cos \alpha} =\dfrac{1-\cos \alpha}{\sin \alpha}\end{align}\]

Ejemplo\(\PageIndex{7}\)

Usando una fórmula de medio ángulo para encontrar el valor exacto de una función sinusoidal. Encuentra\(\sin(15°)\) usando una fórmula de medio ángulo.

Solución

Ya que\(15°=\dfrac{30°}{2}\), usamos la fórmula de medio ángulo para seno (Ecuación\ ref {halfsine}):

\ [\ begin {alinear*}
\ sin\ dfrac {30^ {\ circ}} {2} &=\ sqrt {\ dfrac {1-\ cos 30^ {\ circ}} {2}}\\ [4pt]
&=\ sqrt {\ dfrac {1-\ dfrac {\ sqrt {3}} {2}} [4pt]
&=\ sqrt {\ dfrac {\ dfrac {2-\ sqrt {3}} {2}} {2}}\\ [4pt]
&=\ sqrt {\ dfrac {2-\ sqrt {3}} {4}}\\ [4pt]
&=\ dfrac {\ sqrt {2-\ sqrt {3}}} {2}
\ final {alinear*}\]

Recuerda que podemos verificar la respuesta con una calculadora gráfica.

Análisis

Observe que usamos solo la raíz positiva porque\(\sin(15°)\) es positiva.

Cómo: Dada la tangente de un ángulo y el cuadrante en el que se encuentra el ángulo, encontrar los valores exactos de las funciones trigonométricas de la mitad del ángulo.

1. Dibuja un triángulo para representar la información dada.
2. Determinar la fórmula correcta de medio ángulo.
3. Sustituye los valores en la fórmula basada en el triángulo.
4. Simplificar.

Ejemplo\(\PageIndex{8}\): Finding Exact Values Using Half-Angle Identities

Dado eso\(\tan \alpha=\dfrac{8}{15}\) y\(α\) se encuentra en el cuadrante III, encuentra el valor exacto de lo siguiente:

1. \(\sin\left(\dfrac{\alpha}{2}\right)\)
2. \(\cos\left(\dfrac{\alpha}{2}\right)\)
3. \(\tan\left(\dfrac{\alpha}{2}\right)\)

Solución

Usando la información dada, podemos dibujar el triángulo que se muestra en la Figura\(\PageIndex{3}\). Utilizando el Teorema de Pitágoras, encontramos que la hipotenusa es de 17. Por lo tanto, podemos calcular\(\sin \alpha=−\dfrac{8}{17}\) y\(\cos \alpha=−\dfrac{15}{17}\).

Figura\(\PageIndex{3}\)

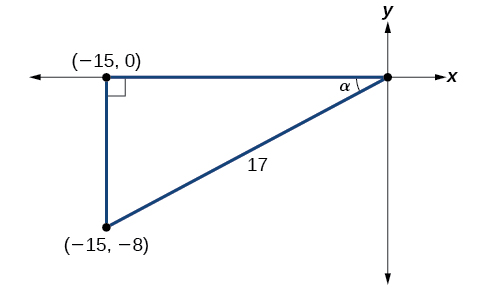
1. Antes de comenzar, debemos recordar que si\(α\) está en el cuadrante III, entonces\(180°<\alpha<270°\), así\(\dfrac{180°}{2}<\dfrac{\alpha}{2}<\dfrac{270°}{2}\). Esto quiere decir que el lado terminal de\(\dfrac{\alpha}{2}\) está en el cuadrante II, ya que\(90°<\dfrac{\alpha}{2}<135°\). Para encontrar\(\sin \dfrac{\alpha}{2}\), comenzamos por escribir la fórmula de medio ángulo para seno. Luego sustituimos el valor del coseno que encontramos del triángulo en Figura\(\PageIndex{3}\) y simplificamos. \[\begin{align*} \sin \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1-(-\dfrac{15}{17})}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{32}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{16}{17}}\\[4pt] &= \pm \dfrac{4}{\sqrt{17}}\\[4pt] &= \dfrac{4\sqrt{17}}{17} \end{align*}\]Elegimos el valor positivo de\(\sin \dfrac{\alpha}{2}\) porque el ángulo termina en el cuadrante II y el seno es positivo en el cuadrante II.
2. Para encontrar\(\cos \dfrac{\alpha}{2}\), escribiremos la fórmula de medio ángulo para coseno, sustituiremos el valor del coseno que encontramos del triángulo en la Figura\(\PageIndex{3}\), y simplificaremos. \[\begin{align*} \cos \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1+\cos \alpha}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1+\left(-\dfrac{15}{17}\right)}{2}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{2}{17}}{2}}\\[4pt] &= \pm \sqrt{\dfrac{2}{17}\cdot \dfrac{1}{2}}\\[4pt] &= \pm \sqrt{\dfrac{1}{17}}\\[4pt] &= -\dfrac{\sqrt{17}}{17} \end{align*}\]Elegimos el valor negativo de\(\cos \dfrac{\alpha}{2}\) porque el ángulo está en el cuadrante II porque el coseno es negativo en el cuadrante II.
3. Para encontrar\(\tan \dfrac{\alpha}{2}\), escribimos la fórmula de medio ángulo para tangente. Nuevamente, sustituimos el valor del coseno que encontramos del triángulo en Figura\(\PageIndex{3}\) y simplificamos. \[\begin{align*} \tan \dfrac{\alpha}{2}&= \pm \sqrt{\dfrac{1-\cos \alpha}{1+\cos \alpha}}\\[4pt] &= \pm \sqrt{\dfrac{1-\left(-\dfrac{15}{17}\right)}{1+\left(-\dfrac{15}{17}\right)}}\\[4pt] &= \pm \sqrt{\dfrac{\dfrac{32}{17}}{\dfrac{2}{17}}}\\[4pt] &= \pm \sqrt{\dfrac{32}{2}}\\[4pt] &= -\sqrt{16}\\[4pt] &= -4 \end{align*}\]Elegimos el valor negativo de\(\tan \dfrac{\alpha}{2}\) porque\(\dfrac{\alpha}{2}\) se encuentra en el cuadrante II, y la tangente es negativa en el cuadrante II.

Ejercicio\(\PageIndex{5}\)

Dado eso\(\sin \alpha=−\dfrac{4}{5}\) y\(\alpha\) se encuentra en el cuadrante IV, encontrar el valor exacto de\(\cos \left(\dfrac{\alpha}{2}\right)\).

Contestar

\(-\dfrac{2}{\sqrt{5}}\)

Ejemplo\(\PageIndex{9}\): Finding the Measurement of a Half Angle

Ahora, volveremos al problema planteado al inicio de la sección. Se construye una rampa para bicicletas para competencia de alto nivel con un ángulo de\(θ\) formado por la rampa y el suelo. Otra rampa se va a construir la mitad de empinada para la competencia de novatos. Si\(tan θ=53\) para la competencia de nivel superior, ¿cuál es la medida del ángulo para la competencia novata?

Solución

Dado que el ángulo para la competencia novato mide la mitad de la pendiente del ángulo para la competencia de alto nivel, y\(\tan \theta=\dfrac{5}{3}\) para la competencia alta, podemos encontrar\(\cos \theta\) desde el triángulo rectángulo y el teorema de Pitágoras para que podamos usar las identidades de medio ángulo. Ver Figura\(\PageIndex{4}\).

\[\begin{align*} 3^2+5^2&=34\\[4pt] c&=\sqrt{34} \end{align*}\]

Figura\(\PageIndex{4}\)

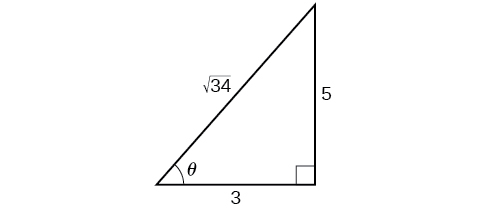
Eso lo vemos\(\cos \theta=\dfrac{3}{\sqrt{34}}=\dfrac{3\sqrt{34}}{34}\). Podemos usar la fórmula de medio ángulo para tangente:\(\tan \dfrac{\theta}{2}=\sqrt{\dfrac{1−\cos \theta}{1+\cos \theta}}\). Ya que\(\tan \theta\) está en el primer cuadrante, así es\(\tan \dfrac{\theta}{2}\).

\ [\ begin {align*}
\ tan\ dfrac {\ theta} {2} &=\ sqrt {\ dfrac {1-\ dfrac {3\ sqrt {34}} {34}} {1+\ dfrac {3\ sqrt {34}} {34}}\\ [4pt]
&=\ sqrt {\ dfrac {\ dfrac 34-3\ sqrt {34}} {34}} {\ dfrac {34+3\ sqrt {34}} {34}}}\\ [4pt]
&=\ sqrt {\ dfrac {34-3\ sqrt {34}} {34+3\ sqrt {34}}}\\ [4pt]
&\ aprox 0.57
\ final {alinear*}\]

Podemos tomar la tangente inversa para encontrar el ángulo:\({\tan}^{−1}(0.57)≈29.7°\). Por lo que el ángulo de la rampa para la competencia de novatos es\(≈29.7°\).

Medios

Acceda a estos recursos en línea para obtener instrucción y práctica adicionales con fórmulas de doble ángulo, medio ángulo y reducción.

• Identidades de doble ángulo
• Identidades de medio ángulo

Ecuaciones Clave

Fórmulas de doble ángulo	\(\sin(2\theta)=2\sin \theta \cos \theta\) \(\cos(2\theta)={\cos}^2 \theta−{\sin}^2 \theta\) \(=1−2{\sin}^2 \theta\) \(=2{\cos}^2 \theta−1\) \(\tan(2\theta)=\dfrac{2\tan \theta}{1−{\tan}^2 \theta}\)
Fórmulas de reducción	\({\sin}^2 \theta=\dfrac{1−\cos(2\theta)}{2}\) \({\cos}^2 \theta=\dfrac{1+\cos(2\theta)}{2}\) \({\tan}^2 \theta=\dfrac{1−\cos(2\theta)}{1+\cos(2\theta)}\)
Fórmulas de medio ángulo	\(\sin \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{2}}\) \(\cos \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1+\cos \alpha}{2}}\) \(\tan \dfrac{\alpha}{2}=\pm \sqrt{\dfrac{1−\cos \alpha}{1+\cos \alpha}}\) \(=\dfrac{\sin \alpha}{1+\cos \alpha}\) \(=\dfrac{1−\cos \alpha}{\sin \alpha}\)

Conceptos clave

• Las identidades de doble ángulo se derivan de las fórmulas de suma de las funciones trigonométricas fundamentales: seno, coseno y tangente. Ver Ejemplo\(\PageIndex{1}\), Ejemplo\(\PageIndex{2}\)\(\PageIndex{3}\), Ejemplo y Ejemplo\(\PageIndex{4}\).
• Las fórmulas de reducción son especialmente útiles en el cálculo, ya que nos permiten reducir la potencia del término trigonométrico. Ver Ejemplo\(\PageIndex{5}\) y Ejemplo\(\PageIndex{6}\).
• Las fórmulas de medio ángulo nos permiten encontrar el valor de las funciones trigonométricas que involucran semiángulos, ya sea que se conozca o no el ángulo original. Ver Ejemplo\(\PageIndex{7}\)\(\PageIndex{8}\), Ejemplo y Ejemplo\(\PageIndex{9}\).