7.6: Modelado con Ecuaciones Trigonométricas

Última actualización
Guardar como PDF

Page ID: 121564

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Supongamos que trazamos las temperaturas promedio diarias en la ciudad de Nueva York en el transcurso de un año. Esperaríamos encontrar las temperaturas más bajas en enero y febrero y las más altas en julio y agosto. Este ciclo familiar se repite año tras año, y si tuviéramos que extender la gráfica a lo largo de varios años, se parecería a una función periódica.

Figura$\PageIndex{1}$: Las manecillas de un reloj son periódicas: repiten posiciones cada doce horas. (crédito: “zoutedrop” /Flickr)

Muchos otros fenómenos naturales también son periódicos. Por ejemplo, las fases de la luna tienen un periodo de aproximadamente 28 días, y las aves saben volar hacia el sur aproximadamente a la misma hora cada año. Entonces, ¿cómo podemos modelar una ecuación para reflejar el comportamiento periódico? Primero, debemos recopilar y registrar datos. Luego encontramos una función que se asemeja a un patrón observado. Finalmente, realizamos las modificaciones necesarias a la función para obtener un modelo que sea confiable. En esta sección, analizaremos en profundidad tipos específicos de comportamiento periódico y ecuaciones de modelos para adaptarse a los datos.

Determinación de la amplitud y el período de una función sinusoidal

Cualquier movimiento que se repita en un periodo de tiempo fijo se considera movimiento periódico y puede ser modelado por una función sinusoidal. La amplitud de una función sinusoidal es la distancia desde la línea media hasta el valor máximo, o desde la línea media hasta el valor mínimo. La línea media es el valor promedio. Las funciones sinusoidales oscilan por encima y por debajo de la línea media, son periódicas y repiten valores en ciclos establecidos. Recordemos de Gráficas de las Funciones Seno y Cosino que es el periodo de la función sinusoidal y la función coseno$2π$. En otras palabras, por cualquier valor de$x$,

\[ \sin(x±2πk)=\sin x \; \text{and} \; \cos(x±2πk)=\cos x \]

donde$k$ es un entero.

Forma estándar de ecuaciones sinusoidales

Las formas generales de una ecuación sinusoidal se dan como

\[y=A \sin(Bt−C)+D\]

\[ y=A \cos(Bt−C)+D\]

donde$\text{amplitude}=|A|,B$ se relaciona con el periodo tal que el$\text{period}=\frac{2π}{B},C$ es el desplazamiento de fase tal que$\frac{C}{B}$ denota el desplazamiento horizontal, y$D$ representa el desplazamiento vertical de la gráfica padre de la gráfica.

Tenga en cuenta que los modelos a veces se escriben como

\[y=a \sin (ω t±C)+D\]

\[y=a \cos(ω t±C)+D,\]

con un periodo que se da como$\frac{2π}{ω}$.

La diferencia entre las gráficas de seno y coseno es que la gráfica sinusoidal comienza con el valor promedio de la función y la gráfica coseno comienza con el valor máximo o mínimo de la función.

Ejemplo$\PageIndex{1}$: Showing How the Properties of a Trigonometric Function Can Transform a Graph

Mostrar la transformación de la gráfica de$y=\sin x$ en la gráfica de$y=2 \sin(4x−\frac{π}{2})+2$.

Solución

Considera la serie de gráficas en la Figura$\PageIndex{1}$ y la forma en que cada cambio a la ecuación cambia la imagen.

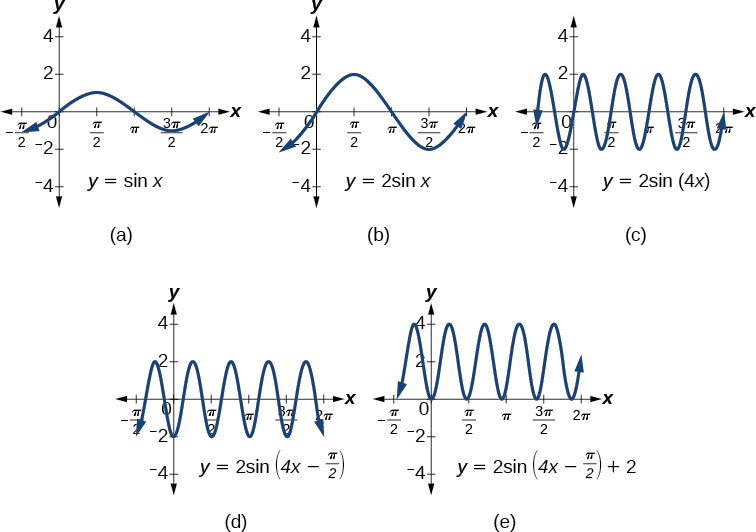
La gráfica básica de$y=\sin x$
Cambiar la amplitud de 1 a 2 genera la gráfica de$y=2 \sin x$.
El periodo de la función sinusoidal cambia con el valor de$B,$ tal que$\text{period}=\frac{2π}{B}.$ Aquí tenemos$B=4,$ lo que se traduce en un periodo de$\frac{π}{2}$. La gráfica completa un ciclo completo en$\frac{π}{2}$ unidades.
La gráfica muestra un desplazamiento horizontal igual a$\frac{C}{B}$, o$\frac{\frac{π}{2}}{4}=\frac{π}{8}$.
Finalmente, la gráfica se desplaza verticalmente por el valor de$D$. En este caso, la gráfica se desplaza hacia arriba en 2 unidades.

Ejemplo$\PageIndex{2}$: Finding the Amplitude and Period of a Function

Encuentra la amplitud y periodo de las siguientes funciones y grafica un ciclo.

$y=2 \sin (\frac{1}{4}x)$
$y=−3 \sin (2x+\frac{π}{2})$
$y= \cos x+3$

Solución

Resolveremos estos problemas de acuerdo a los modelos.

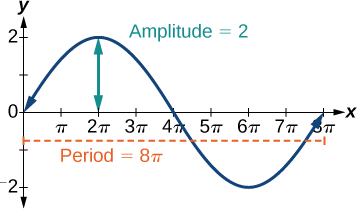
$y=2 \sin (\frac{1}{4}x)$implica seno, entonces usamos la forma\[y=A \sin (Bt+C)+D \nonumber\] Sabemos que$| A |$ es la amplitud, por lo que la amplitud es 2. Periodo es$\frac{2π}{B}$ así que el periodo es\[\begin{align*} \dfrac{2π}{B} &=\dfrac{2π}{\frac{1}{4}} \\ & =8π \end{align*}\] Ver la gráfica en la Figura$\PageIndex{3}$.

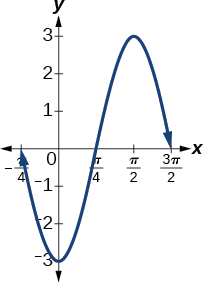
$y=−3 \sin(2x+ \frac{π}{2})$implica seno, por lo que usamos la forma\[y=A \sin (Bt−C)+D \nonumber\] Amplitud es$| A |$, por lo que la amplitud$A$ es$|−3|=3.$ Dado que es negativa, la gráfica se refleja sobre el eje x. Periodo es$\frac{2π}{B}$, por lo que el periodo es\[\dfrac{2π}{B}=\dfrac{2π}{2}=π \nonumber\] La gráfica se desplaza hacia la izquierda por$\frac{C}{B}=\frac{\frac{π}{2}}{2}=\frac{π}{4}$ unidades. Ver Figura$\PageIndex{4}$.

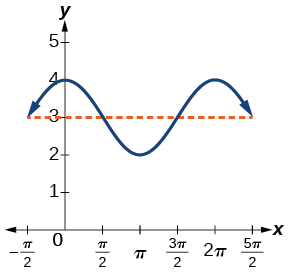
$y= \cos x+3$involucra coseno, por lo que usamos el formulario
\[y=A \cos (Bt±C)+D \nonumber\]La amplitud es$| A |$, por lo que la amplitud es 1 y el periodo es$2π$ (Figura$\PageIndex{5}$. Esta es la función coseno estándar desplazada hacia arriba tres unidades.

Ejercicio$\PageIndex{1}$:

¿Cuáles son la amplitud y el periodo de la función$y=3 \cos (3πx)$?

Responder: La amplitud es$3,$ y el periodo es$\frac{2}{3}$.

Búsqueda de ecuaciones y representación gráfica de funciones sinusoidales

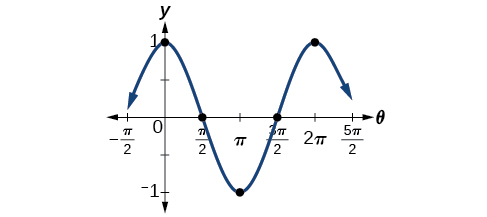
Un método para graficar funciones sinusoidales es encontrar cinco puntos clave. Estos puntos corresponderán a intervalos de igual longitud que representen$\frac{1}{4}$ del periodo. Los puntos clave indicarán la ubicación de los valores máximos y mínimos. Si no hay desplazamiento vertical, también indicarán x -intercepciones. Por ejemplo, supongamos que queremos graficar la función$y=cos θ.$ Sabemos que el periodo es$2π$, así encontramos el intervalo entre puntos clave de la siguiente manera.

\[\frac{2π}{4}=\frac{π}{2} \nonumber\]

Comenzando con$θ=0,$ calculamos el primer valor y-, sumamos la longitud del intervalo$\frac{π}{2}$ a$0$, y calculamos el segundo valor y. Luego agregamos$\frac{π}{2}$ repetidamente hasta que se determinen los cinco puntos clave. El último valor debe ser igual al primer valor, ya que los cálculos cubren un periodo completo. Haciendo una tabla similar a Tabla$\PageIndex{1}$, podemos ver estos puntos clave claramente en la gráfica que se muestra en la Figura$\PageIndex{6}$.

Mesa$\PageIndex{1}$
$θ$	$0$	$\frac{π}{2}$	$π$	$\frac{3π}{2}$	$2π$
$y=\cos θ$	$1$	$0$	−1−1	$0$	$1$

Ejemplo$\PageIndex{3}$: Graphing Sinusoidal Functions Using Key Points

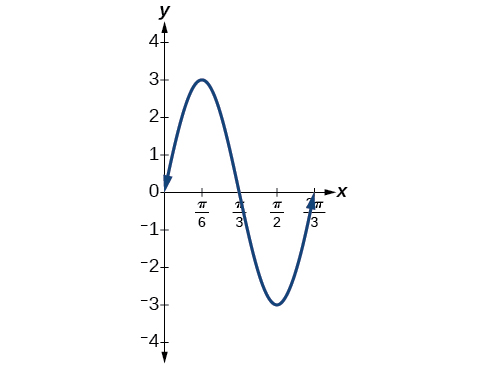
Grafique la función$y=−4 \cos (πx)$ usando amplitud, periodo y puntos clave.

Solución

La amplitud es$|−4|=4.$ El periodo es$\frac{2π}{ω}=\frac{2π}{π}=2.$ (Recordemos que a veces nos referimos$B$ como$ω.$) Un ciclo de la gráfica se puede dibujar sobre el intervalo$[ 0,2 ]$. Para encontrar los puntos clave, dividimos el periodo por 4. Hacer una tabla similar a la Figura$\PageIndex{1}$:, comenzando con$x=0$ y luego sumando$\frac{1}{2}$ sucesivamente a$x$ y calcular$y.$ Ver la gráfica en la Figura$\PageIndex{7}$.

Mesa$\PageIndex{1}$
$x$	$0$	$\frac{1}{2}$	$1$	$\frac{3}{2}$	$2$
$y=−4 \cos(πx)$	$−4$	$0$	$4$	$0$	$−4$

Ejercicio$\PageIndex{2}$:

Grafique la función$y=3 \sin(3x)$ usando la amplitud, el período y cinco puntos clave.

$x$	0	$\frac{π}{6}$	$\frac{π}{3}$	$\frac{π}{2}$	$\frac{2π}{3}$
$3 \sin (3x)$	0	3	0	-3	0


Responder: $CNX_Precalc_Figure_07_07_004.jpg$
Figura$\PageIndex{8}$

Modelado del Comportamiento Periódico

Ahora vamos a aplicar estas ideas a problemas que involucran comportamientos periódicos.

Ejemplo$\PageIndex{4}$: Modeling an Equation and Sketching a Sinusoidal Graph to Fit Criteria

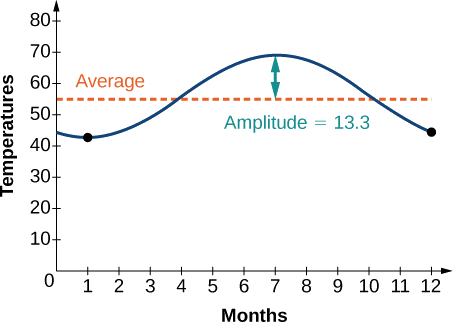
Las temperaturas promedio mensuales para un pueblo pequeño de Oregón se dan en la Tabla$\PageIndex{1}$. Encuentra una función sinusoidal de la forma$y=A \sin (Bt−C)+D$ que se ajuste a los datos (redondear a la décima más cercana) y esbozar la gráfica.

Mesa$\PageIndex{2}$
Mes	Temperatura,$^oF$
enero	\ (^de\) ">42.5
febrero	\ (^de\) ">44.5
marzo	\ (^de\) ">48,5
abril	\ (^de\) ">52.5
Mayo	\ (^de\) ">58
junio	\ (^de\) ">63
julio	\ (^de\) ">68,5
agosto	\ (^de\) ">69
septiembre	\ (^de\) ">64.5
Octubre	\ (^de\) ">55.5
noviembre	\ (^de\) ">46.5
diciembre	\ (^de\) ">43.5

Solución

Recordemos que la amplitud se encuentra usando la fórmula

\[A=\dfrac{\text{largest value −smallest value}}{2}\]

Así, la amplitud es

\[\begin{align*} |A| & = \dfrac{69−42.5}{2} \\ &=13.25 \end{align*}\]

El dato abarca un periodo de 12 meses, por lo$\frac{2π}{B}=12$ que da$B=\frac{2π}{12}=\frac{π}{6}$.

El desplazamiento vertical se encuentra usando la siguiente ecuación.

\[D=\dfrac{\text{highest value+lowest value}}{2}\]

Por lo tanto, el desplazamiento vertical es

\[\begin{align*} D &= \dfrac{69+42.5}{2} &=55.8 \end{align*}\]

Hasta el momento, tenemos la ecuación$y=13.3 \sin (\frac{π}{6}x−C)+55.8$.

Para encontrar el desplazamiento horizontal, ingresamos$y$ los valores$x$ y para el primer mes y resolvemos para$C$.

\[\begin{align*} 42.5 & =13.3 \sin (\frac{π}{6}(1)−C)+55.8 \\ −13.3 & =13.3 \sin (\frac{π}{6}−C) \\ −1 & =\sin (\frac{π}{6}−C) \;\;\;\;\;\;\;\; \sin θ=−1→ θ=−\frac{π}{2} \\ \frac{π}{6}−C=−\frac{π}{2} \\ \frac{π}{6}+\frac{π}{2} & =C \\ &=\frac{2π}{3} \end{align*}\]

Tenemos la ecuación$y=13.3 \sin (\frac{π}{6}x−\frac{2π}{3})+55.8$. Ver la gráfica en la Figura$\PageIndex{9}$.

Ejemplo$\PageIndex{5}$: Describing Periodic Motion

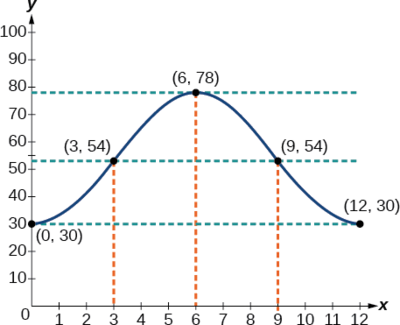
La manecilla horaria del reloj grande en la pared en Union Station mide 24 pulgadas de largo. Al mediodía, la punta de la manecilla de las horas está a 30 pulgadas del techo. A las 3 PM, la punta está a 54 pulgadas del techo, y a las 6 PM, 78 pulgadas. A las 9 de la tarde, está nuevamente a 54 pulgadas del techo, y a la medianoche, la punta de la manecilla de las horas vuelve a su posición original a 30 pulgadas del techo. Dejar$y$ igualar la distancia desde la punta de la manecilla de la hora hasta el techo$x$ horas después del mediodía. Encuentra la ecuación que modela el movimiento del reloj y dibuja el gráfico.

Solución

Comience haciendo una tabla de valores como se muestra en Tabla$\PageIndex{3}$.

Mesa$\PageIndex{3}$
$x$	$y$	Puntos a trazar
\ (x\) ">Mediodía	\ (y\) ">30 in	$(0,30)$
\ (x\) ">3 PM	\ (y\) ">54 in	$(3,54)$
\ (x\) ">6 PM	\ (y\) ">78 in	$(6,78)$
\ (x\) ">9 PM	\ (y\) ">54 in	$(9,54)$
\ (x\) ">Medianoche	\ (y\) ">30 in	$(12,30)$

Para modelar una ecuación, primero necesitamos encontrar la amplitud.

\[\begin{align*} | A | & =| \dfrac{78−30}{2} | \\ &=24 \end{align*}\]

El ciclo del reloj se repite cada 12 horas. Por lo tanto,

\[\begin{align*} B &=\dfrac{2π}{12} \\ &= \dfrac{π}{6} \end{align*}\]

El desplazamiento vertical es

\[\begin{align*} D & = \dfrac{78+30}{2} \\ &=54 \end{align*}\]

No hay desplazamiento horizontal, por lo$C=0.$ que Dado que la función comienza con el valor mínimo de$y$ when$x=0$ (a diferencia del valor máximo), usaremos la función coseno con el valor negativo para$A$. En la forma$y=A \cos (Bx±C)+D,$ la ecuación es

\[y=−24 \cos (\dfrac{π}{6}x)+54\]

Ver Figura$\PageIndex{10}$.

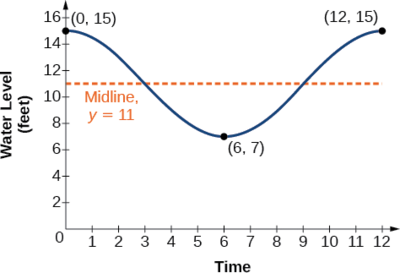
Ejemplo$\PageIndex{6}$: Determining a Model for Tides

La altura de la marea en un pequeño pueblo playero se mide a lo largo de un malecón. Los niveles de agua oscilan entre 7 pies en marea baja y 15 pies en marea alta. En un día determinado, la marea baja ocurrió a las 6 de la mañana y la marea alta ocurrió al mediodía. Aproximadamente cada 12 horas, el ciclo se repite. Encuentra una ecuación para modelar los niveles de agua.

Solución

Como el nivel del agua varía de 7 pies a 15 pies, podemos calcular la amplitud como

\[ \begin{align*} |A| &=| \frac{(15−7)}{2} | \\ & =4 \end{align*}\]

El ciclo se repite cada 12 horas; por lo tanto,$B$ es

\[\begin{align*} \dfrac{2π}{12}=\dfrac{π}{6} \end{align*}\]

Hay una traslación vertical de$\frac{(15+8)}{2}=11.5$. Dado que el valor de la función está en un máximo at$t=0$, usaremos la función coseno, con el valor positivo para$A$.

\[y=4 \cos (\dfrac{π}{6}) t+11 \nonumber\]

Ver Figura$\PageIndex{11}$.

Ejercicio$\PageIndex{3}$:

La temperatura diaria en el mes de marzo en una ciudad determinada varía de un mínimo de$24°F$ a un máximo de$40°F.$ Encuentra una función sinusoidal para modelar la temperatura diaria y bosquejar la gráfica. Aproximar el tiempo en que la temperatura alcanza el punto de congelación$32 °F.$ Dejar$t=0$ corresponder al mediodía.

Responder: \[y=8 \sin (\frac{π}{12}t)+32 \nonumber\]
La temperatura alcanza el punto de congelación al mediodía y a la medianoche.

Ejercicio$\PageIndex{4}$: Interpreting the Periodic Behavior Equation

La presión arterial promedio de la persona es modelada por la función$f(t)=20 \sin (160πt)+100$, donde$f(t)$ representa la presión arterial a la vez$t$, medida en minutos. Interpretar la función en términos de periodo y frecuencia. Esboza la gráfica y encuentra la lectura de la presión arterial.

Análisis

La presión arterial de$\frac{120}{80}$ se considera normal. El número superior es la lectura máxima o sistólica, que mide la presión en las arterias cuando el corazón se contrae. El número inferior es la lectura mínima o diastólica, que mide la presión en las arterias a medida que el corazón se relaja entre latidos, rellenándose con sangre. Así, la presión arterial normal puede modelarse mediante una función periódica con un máximo de 120 y un mínimo de 80.

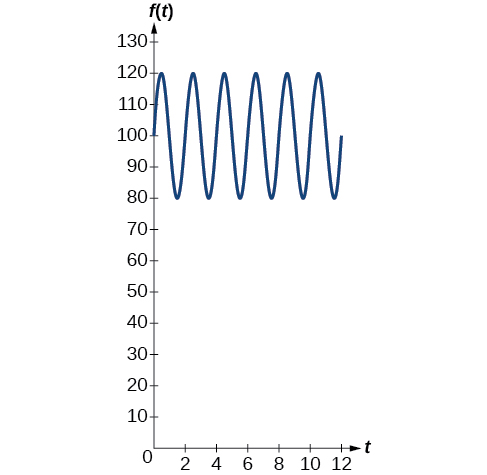
Ejemplo$\PageIndex{7}$: Interpreting the Periodic Behavior Equation

Solución

El periodo viene dado por

\[\begin{align*} \dfrac{2π}{ω} & = \dfrac{2π}{160π} \\ &=\dfrac{1}{80} \end{align*}\]

En una función de presión arterial, la frecuencia representa el número de latidos cardíacos por minuto. La frecuencia es el recíproco del período y viene dada por

\[\begin{align*} \dfrac{ω}{2π} & = \dfrac{160π}{2π} \\ & =80 \end{align*}\]

Figura$\PageIndex{12}$: La lectura de la presión arterial en la gráfica es$\frac{120}{80} (\frac{\text{maximum}}{\text{minimum}})$.

Análisis

Modelado de funciones armónicas de

El movimiento armónico es una forma de movimiento periódico, pero hay factores a considerar que diferencian los dos tipos. Mientras que las aplicaciones de movimiento periódico general recorren sus períodos sin interferencias externas, el movimiento armónico requiere una fuerza restauradora. Los ejemplos de movimiento armónico incluyen resortes, fuerza gravitacional y fuerza magnética.

Movimiento armónico simple

Un tipo de movimiento descrito como simple movimiento armónico implica una fuerza restauradora pero asume que el movimiento continuará para siempre. Imagínese un objeto ponderado colgando de un resorte, Cuando ese objeto no se perturba, decimos que el objeto está en reposo, o en equilibrio. Si el objeto es tirado hacia abajo y luego liberado, la fuerza del resorte tira del objeto hacia el equilibrio y comienza el movimiento armónico. La fuerza restauradora es directamente proporcional al desplazamiento del objeto desde su punto de equilibrio. Cuando$t=0,d=0.$

Movimiento armónico simple

Vemos que se dan ecuaciones simples de movimiento armónico en términos de desplazamiento:

\[d=a \cos (ωt) \; \text{or} \; d=a \sin (ωt) \]

donde$| a |$ es la amplitud,$\frac{2π}{ω}$ es el periodo, y$\frac{ω}{2π}$ es la frecuencia, o el número de ciclos por unidad de tiempo.

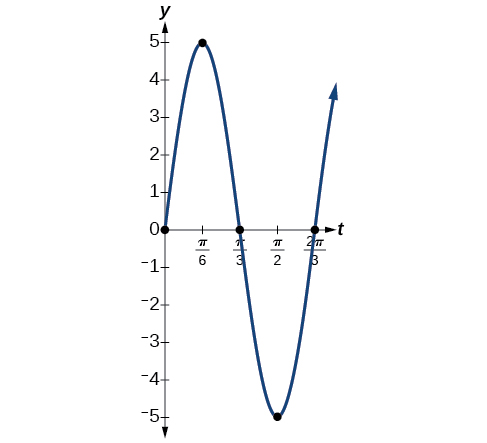
Ejercicio$\PageIndex{5}$: Finding the Displacement, Period, and Frequency, and Graphing a Function

Para cada una de las funciones dadas:

$y=5 \sin (3t)$
$y=6 \cos (πt)$
$y=5 \cos (\frac{π}{2}) t$

abordar las siguientes preguntas:

Encuentra el desplazamiento máximo de un objeto.
Encuentra el periodo o el tiempo requerido para una vibración.
Encuentra la frecuencia.
Esbozar la gráfica.

Gráfica de la función y=5sin (3t) de 0 a 2pi/3. Los cinco puntos clave son (0,0), (pi/6, 5), (pi/3, 0), (pi/2, -5), (2pi/3, 0). — Figura$\PageIndex{13}$

Contestar a

El desplazamiento máximo es igual a la amplitud,$ |a|$, que es 5.
El periodo es$\frac{2π}{ω}=\frac{2π}{3}$.
La frecuencia se da como$\frac{ω}{2π}=\frac{3}{2π}$.
Ver Figura$\PageIndex{13}$. La gráfica indica los cinco puntos clave.

Respuesta b

El desplazamiento máximo es$6$.
El periodo es$\frac{2π}{ω}=\frac{2π}{π}=2.$
La frecuencia es$\frac{ω}{2π}=\frac{π}{2π}=\frac{1}{2}.$
Ver Figura$\PageIndex{14}$.

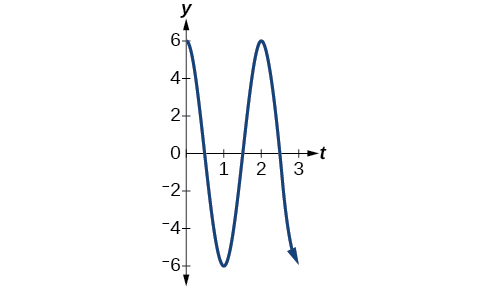
Gráfica de la función y=6cos (pi t) de 0 a 3. — Figura$\PageIndex{14}$

Respuesta c

El desplazamiento máximo es$5$.
El periodo es$\frac{2π}{ω}=\frac{2π}{\frac{π}{2}}=4$.
La frecuencia es$\frac{1}{4}.$
Ver Figura$\PageIndex{15}$.

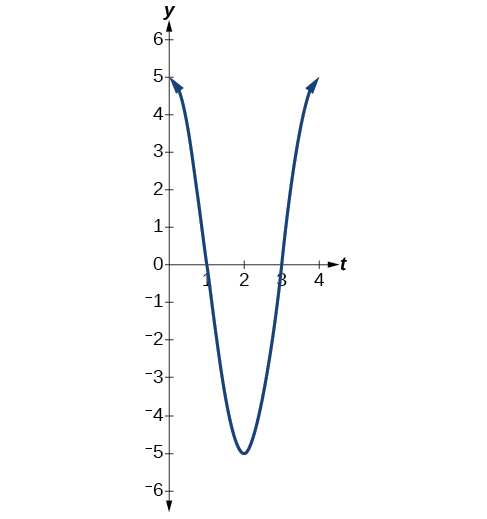
Gráfica de la función y=5cos (pi/2 t) de 0 a 4. — Figura$\PageIndex{15}$

Movimiento armónico amortiguado

En realidad, un péndulo no oscila de un lado a otro para siempre, ni un objeto en un resorte rebota arriba y abajo para siempre. Finalmente, el péndulo deja de balancearse y el objeto deja de rebotar y ambos regresan al equilibrio. El movimiento periódico en el que actúa una fuerza de disipación de energía, o factor de amortiguación, se conoce como movimiento armónico amortiguado. La fricción es típicamente el factor de amortiguación.

En física, se utilizan diversas fórmulas para dar cuenta del factor de amortiguación en el objeto en movimiento. Algunas de ellas son fórmulas basadas en cálculos que involucran derivados. Para nuestros propósitos, utilizaremos fórmulas para modelos básicos de movimiento armónico amortiguado.

Definición: MOVIMIENTO ARMÓNICO

En movimiento armónico amortiguado, el desplazamiento de un objeto oscilante desde su posición de reposo en el momento$t$ se da como

\[ f(t)=ae^{−ct} \sin (ωt) \; \text{ or} \; f(t)=ae^{−ct} \cos (ωt)\]

donde$c$ es un factor de amortiguamiento,$|a|$ es el desplazamiento inicial y$\frac{2π}{ω}$ es el periodo.

Ejemplo$\PageIndex{8}$: Modeling Damped Harmonic Motion

Modele las ecuaciones que se ajusten a los dos escenarios y utilice una utilidad gráfica para graficar las funciones: Dos sistemas de masa-resorte exhiben movimiento armónico amortiguado a una frecuencia de 0.5 ciclos por segundo. Ambos tienen un desplazamiento inicial de 10 cm. El primero tiene un factor de amortiguación de 0.5 y el segundo tiene un factor de amortiguación de 0.1.

Solución

En el momento$t=0$, el desplazamiento es el máximo de 10 cm, lo que requiere la función coseno. La función coseno se aplicará a ambos modelos.

Se nos da la frecuencia$f=\frac{ω}{2π}$ de 0.5 ciclos por segundo. Por lo tanto,

\[\begin{align*} \dfrac{ω}{2π} &=0.5 \\ ω&=(0.5)2π \\ &=π \end{align*}\]

El primer sistema de muelles tiene un factor de amortiguación de$c=0.5$. Siguiendo el modelo general para movimiento armónico amortiguado, tenemos

\[f(t)=10e^{−0.5t} \cos (πt) \nonumber\]

La figura$\PageIndex{16}$ modela el movimiento del primer sistema de muelles.

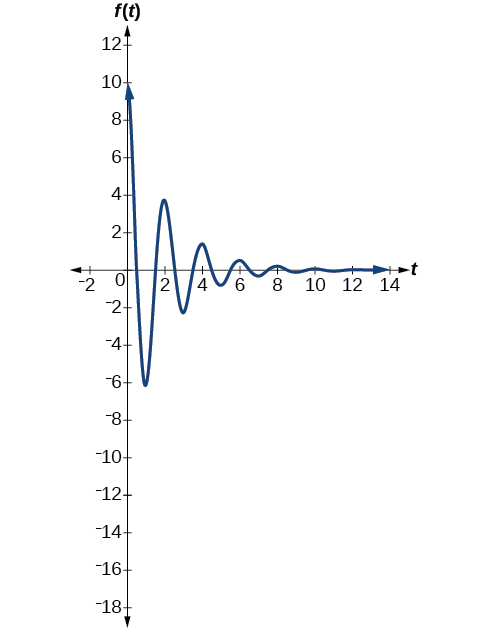
Gráfica del primer sistema de muelles, f (t) = 10 (e^ (-.5t)) cos (pi*t), que comienza con una amplitud alta y disminuye rápidamente. — Figura$\PageIndex{16}$

El segundo sistema de resorte tiene un factor de amortiguación$c=0.1$ y se puede modelar como

\[f(t)=10e^{−0.1t} \cos (πt)\]

La figura$\PageIndex{17}$ modela el movimiento del segundo sistema de muelles.

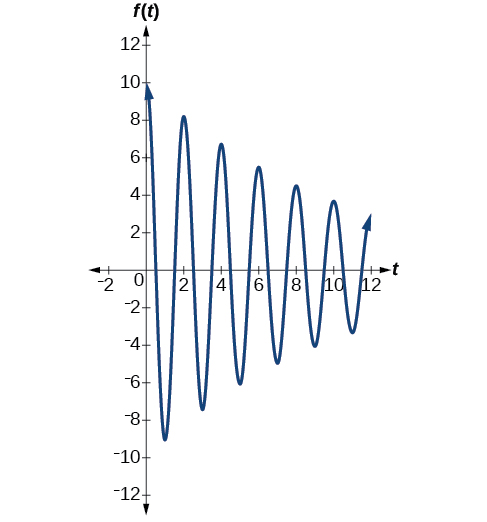
Gráfica de f (t) = 10 (e^ (-.1t)) cos (pi*t), que comienza con una amplitud alta y disminuye lentamente (pero tiene una frecuencia alta). — Figura$\PageIndex{17}$

Análisis

Observe los diferentes efectos de la constante de amortiguación. Los valores locales máximos y mínimos de la función con el factor de amortiguación$c=0.5$ disminuyen mucho más rápidamente que los de la función con$c=0.1$.

Ejercicio$\PageIndex{6}$: Finding a Cosine Function that Models Damped Harmonic Motion

Buscar y graficar una función de la forma$y=ae^{−ct} \cos (ωt)$ que modela la información dada.

$a=20,c=0.05,p=4$
$a=2,c=1.5,f=3$

Solución

Sustituir los valores dados en el modelo. Recordemos que el periodo es$\frac{2π}{ω}$ y la frecuencia es$\frac{ω}{2π}$.

$y=20e^{−0.05t} \cos (\frac{π}{2}t).$Ver Figura$\PageIndex{18}$.

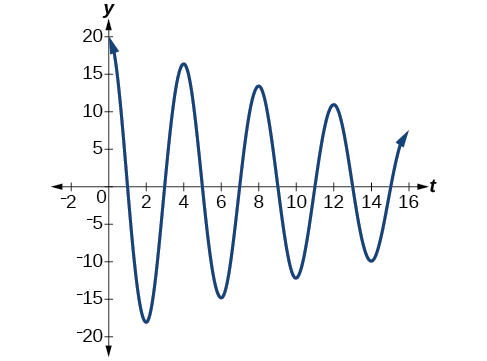
$Gráfica de f (t) = 20 (e^ (-.05t)) cos (pi/2 * t), que comienza con una amplitud alta y disminuye lentamente.$
Figura$\PageIndex{18}$
$y=2e^{−1.5t} \cos (6πt).$Ver Figura$\PageIndex{19}$.

$Gráfica de f (t) = 2 (e^ (-1.5t)) cos (6pi * t), que comienza con una pequeña amplitud y rápidamente disminuye a casi una línea recta.$
Figura$\PageIndex{19}$

Ejercicio$\PageIndex{7}$

La siguiente ecuación representa un modelo de movimiento armónico amortiguado:$f(t)=5e^{−6t} \cos (4t)$ Encuentra el desplazamiento inicial, la constante de amortiguación y la frecuencia.

Responder: desplazamiento inicial =6, constante de amortiguación = -6, frecuencia =$\frac{2}{π}$

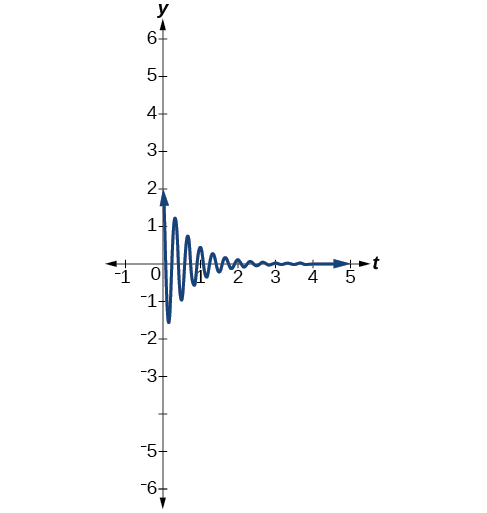
Ejemplo$\PageIndex{9}$: Finding a Sine Function that Models Damped Harmonic Motion

Buscar y graficar una función de la forma$y=ae^{−ct} \sin (ωt)$ que modela la información dada.

$a=7,c=10,p=\frac{π}{6}$
$a=0.3,c=0.2,f=20$

Solución

Calcular el valor de$ω$ y sustituir los valores conocidos en el modelo.

Como es el periodo$\frac{2π}{ω}$, tenemos
\[\begin{align*} \dfrac{π}{6} &=\dfrac{2π}{ω} \\ ωπ &=6(2π) \\ ω &=12 \end{align*}\]

El factor de amortiguación se da como 10 y la amplitud es 7. Así, el modelo es$y=7e^{−10t} \sin (12t)$. Ver Figura$\PageIndex{20}$.

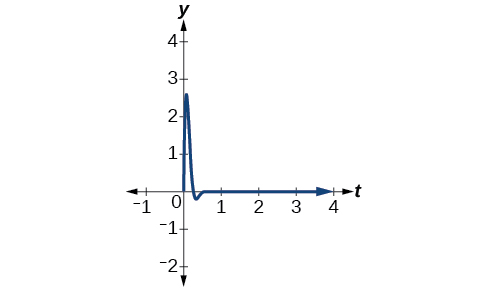
$Gráfica de f (t) = 7 (e^ (-10t)) sin (12t), que pincha cerca de t=0 y rápidamente se convierte casi en una línea recta.$
Figura$\PageIndex{20}$
Como es la frecuencia$\frac{ω}{2π}$, tenemos
\[\begin{align*} 20 &=\dfrac{ω}{2π} \\ 40π &=ω \end{align*}\]

El factor de amortiguación se da como$0.2$ y la amplitud es$0.3.$ El modelo es$y=0.3e^{−0.2t} \sin (40πt).$ Ver Figura$\PageIndex{21}$.

$Gráfica de f (t) = .3e^ (-.2t) sin (40pi*t), que tiene una amplitud pequeña pero disminuye rápidamente a la aparición de una línea recta. La frecuencia es tan alta que, en esta escala, la función parece una forma sólida. El recorte de zoom de la gráfica muestra la imagen sinusoidal real de la función.$
Figura$\PageIndex{21}$

Análisis

Una comparación de los dos últimos ejemplos ilustra cómo elegimos entre las funciones seno o coseno para modelar criterios sinusoidales. Vemos que la función coseno está en el desplazamiento máximo cuando$t=0$, y la función sinusoidal está en el punto de equilibrio cuando$t=0.$ Por ejemplo, considere la ecuación$y=20e^{−0.05t} \cos (\frac{π}{2}t)$ de Ejemplo. Podemos ver en la gráfica que cuando$t=0,y=20,$ cuál es la amplitud inicial. Compruebe esto configurando$t=0$ en la ecuación del coseno:

\[ \begin{align*} y &=20e^{−0.05(0)} \cos (\frac{π}{2})(0) \\ &=20(1)(1) \\ & =20 \end{align*}\]

El uso de la función sinusoidal rinde

\[\begin{align*} y &=20e^{−0.05(0)} \sin (\frac{π}{2})(0) \\ & =20(1)(0) \\ &=0 \end{align*}\]

Así, el coseno es la función correcta.

Ejercicio$\PageIndex{8}$:

Escriba la ecuación para el movimiento armónico amortiguado dado$a=10,c=0.5$, y$p=2.$

Responder: $y=10e^{−0.5t} \cos (πt)$

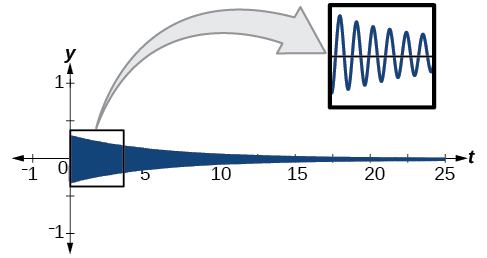
Ejemplo$\PageIndex{10}$: Modeling the Oscillation of a Spring

Un resorte que mide 10 pulgadas de longitud natural se comprime por 5 pulgadas y se libera. Oscila una vez cada 3 segundos, y su amplitud disminuye un 30% cada segundo. Encuentra una ecuación que modele la posición del resorte$t$ segundos después de ser liberado.

Solución

La amplitud comienza a las 5 pulg. y disminuye 30% cada segundo. Debido a que el resorte está inicialmente comprimido, escribiremos A como un valor negativo. Podemos escribir la porción de amplitud de la función como

\[A(t)=5(1−0.30)^t \nonumber\]

Ponemos$(1−0.30)^t$ en la forma de la$e^{ct}$ siguiente manera:

\[\begin{align*} 0.7 &=e^c \\ c &= \ln .7 \\ c & =−0.357 \end{align*}\]

Ahora abordemos el periodo. La primavera recorre sus posiciones cada 3 segundos, este es el periodo, y podemos usar la fórmula para encontrar omega.

\[\begin{align*} 3 &= \dfrac{2π}{ω} \\ ω &= \dfrac{2π}{3} \end{align*}\]

La longitud natural de 10 pulgadas es la línea media. Utilizaremos la función coseno, ya que el resorte inicia en su desplazamiento máximo. Esta parte de la ecuación se representa como

\[y=\cos (\dfrac{2π}{3}t)+10 \nonumber\]

Por último, juntamos ambas funciones. Nuestro el modelo para la posición del resorte en$t$ segundos se da como

\[y=−5e^{−0.357t} \cos (\dfrac{2π}{3}t)+10 \nonumber\]

Ver la gráfica en la Figura$\PageIndex{22}$.

Gráfica de la función y = -5e^ (-.35t) cos (2pi/3 t) + 10 de 0 a 24. Comienza como ondas con una gran amplitud y disminuye a casi una línea recta muy rápidamente. — Figura$\PageIndex{22}$

Ejercicio$\PageIndex{9}$

Una masa suspendida de un resorte se eleva a una distancia de 5 cm por encima de su posición de reposo. La masa se libera en el momento$t=0$ y se le permite oscilar. Después del$\frac{1}{3}$ segundo, se observa que la masa vuelve a su posición más alta. Encuentra una función para modelar este movimiento en relación con su posición inicial de reposo.

Responder: $y=5 \cos (6πt)$

De acuerdo con los Criterios dados

Una cuerda de guitarra es arrancada y vibra en movimiento armónico amortiguado. Se tira de la cuerda y se desplaza 2 cm de su posición de reposo. Después de 3 segundos, el desplazamiento de la cuerda mide 1 cm. Encuentra la constante de amortiguación.

Solución

El factor de desplazamiento representa la amplitud y está determinado por el coeficiente$ae^{−ct}$ en el modelo para el movimiento armónico amortiguado. La constante de amortiguación se incluye en el término$e^{−ct}$. Se sabe que después de 3 segundos, el máximo local mide la mitad de su valor original. Por lo tanto, tenemos la ecuación

\[ae^{−c(t+3)}=\dfrac{1}{2} ae^{−ct}\]

Utilizar el álgebra y las leyes de los exponentes para resolver$c$.

\[\begin{array}{cl} ae^{−c(t+3)}=\frac{1}{2}ae^{−ct} \\ e^{−ct}⋅e^{−3c}=\frac{1}{2}e^{−ct} & \text{Divide out } a. \\ e^{−3c}=\frac{1}{2} & \text{Divide out }e^{−ct}. \\ e^{3c}=2 & \text{Take reciprocals.} \end{array}\]

Entonces usa las leyes de los logaritmos.

\[\begin{align*} e^{3c} &=2 \\ 3c &=\ln 2 \\ c & =\frac{\ln 2}{3} \end{align*}\]

La constante de amortiguación es$\frac{\ln 2}{3}$.

Curvas delimitadoras en movimiento armónico

Los gráficos de movimiento armónicos pueden estar encerrados por curvas delimitadoras. Cuando una función tiene una amplitud variable, de tal manera que la amplitud sube y baja varias veces dentro de un periodo, podemos determinar las curvas delimitadoras a partir de parte de la función.

Ejemplo$\PageIndex{12}$: Graphing an Oscillating Cosine Curve

Grafica la función$f(x)=\cos (2πx) \cos (16πx)$.

Solución

La gráfica producida por esta función se mostrará en dos partes. La primera gráfica será la función exacta$f(x)$ (ver Figura$\PageIndex{23; top}$;), y la segunda gráfica es la función exacta$f(x)$ más una función delimitadora (ver Figura$\PageIndex{23; bottom}$). Los gráficos se ven bastante diferentes.

Gráfica de f (x) = cos (2pi*x) cos (16pi*x), una función sinusoidal que aumenta y disminuye su amplitud periódicamente. — Figure_07_07_016.jpg "/>

Figura$\PageIndex{23}$

Análisis

Las curvas$y=\cos (2πx)$ y$y=−\cos (2πx)$ son curvas delimitadoras: enlazan la función desde arriba y abajo, trazando los puntos altos y bajos. El gráfico de movimiento armónico se encuentra dentro de las curvas delimitadoras. Este es un ejemplo de una función cuya amplitud no sólo disminuye con el tiempo, sino que en realidad aumenta y disminuye varias veces dentro de un periodo.

Ecuaciones Clave


Forma estándar de la ecuación sinusoidal	$y=A \sin (Bt−C)+D \text{ or } y=A \cos (Bt−C)+D$
Movimiento armónico simple	$d=a \cos (ωt) \text{ or } d=a \sin (ωt) $
Movimiento armónico amortiguado	$f(t)=ae^{−ct} \sin (ωt) \text{ or } f(t)=ae^{−ct} \cos (ωt)$

Conceptos clave

Las funciones sinusoidales están representadas por las gráficas de seno y coseno. En forma estándar, podemos encontrar la amplitud, el período y los desplazamientos horizontales y verticales. Ver Ejemplo y Ejemplo.
Utilice puntos clave para graficar una función sinusoidal. Los cinco puntos clave incluyen los valores mínimo y máximo y los valores de la línea media. Ver Ejemplo.
Las funciones periódicas pueden modelar eventos que vuelven a ocurrir en ciclos establecidos, como las fases de la luna, las manecillas de un reloj y las estaciones en un año. Ver Ejemplo, Ejemplo, Ejemplo y Ejemplo.
Las funciones de movimiento armónico se modelan a partir de datos dados. Similar a las aplicaciones de movimiento periódico, el movimiento armónico requiere una fuerza restauradora. Los ejemplos incluyen la fuerza gravitacional y el movimiento de resorte activado por peso. Ver Ejemplo.
El movimiento armónico amortiguado es una forma de comportamiento periódico afectada por un factor de amortiguación. Los factores de disipación de energía, como la fricción, hacen que el desplazamiento del objeto se contraiga. Ver Ejemplo, Ejemplo, Ejemplo, Ejemplo y Ejemplo.
Las curvas delimitadoras delinean la gráfica de movimiento armónico con valores variables máximo y mínimo. Ver Ejemplo.

\(θ\)	\(0\)	\(\frac{π}{2}\)	\(π\)	\(\frac{3π}{2}\)	\(2π\)
\(y=\cos θ\)	\(1\)	\(0\)	−1−1	\(0\)	\(1\)

\(x\)	\(0\)	\(\frac{1}{2}\)	\(1\)	\(\frac{3}{2}\)	\(2\)
\(y=−4 \cos(πx)\)	\(−4\)	\(0\)	\(4\)	\(0\)	\(−4\)

\(x\)	0	\(\frac{π}{6}\)	\(\frac{π}{3}\)	\(\frac{π}{2}\)	\(\frac{2π}{3}\)
\(3 \sin (3x)\)	0	3	0	-3	0

\(x\)	\(y\)	Puntos a trazar
\ (x\) ">Mediodía	\ (y\) ">30 in	\((0,30)\)
\ (x\) ">3 PM	\ (y\) ">54 in	\((3,54)\)
\ (x\) ">6 PM	\ (y\) ">78 in	\((6,78)\)
\ (x\) ">9 PM	\ (y\) ">54 in	\((9,54)\)
\ (x\) ">Medianoche	\ (y\) ">30 in	\((12,30)\)

Forma estándar de la ecuación sinusoidal	\(y=A \sin (Bt−C)+D \text{ or } y=A \cos (Bt−C)+D\)
Movimiento armónico simple	\(d=a \cos (ωt) \text{ or } d=a \sin (ωt) \)
Movimiento armónico amortiguado	\(f(t)=ae^{−ct} \sin (ωt) \text{ or } f(t)=ae^{−ct} \cos (ωt)\)