7.E: Identidades y Ecuaciones Trigonométricas (Ejercicios)

7.1: Resolver ecuaciones trigonométricas con identidades

En esta sección, comenzaremos un examen de las identidades trigonométricas fundamentales, incluyendo cómo podemos verificarlas y cómo podemos utilizarlas para simplificar las expresiones trigonométricas.

Verbal

1) Sabemos que\(g(x)=\cos x\) es una función par,\(f(x)=\sin x\) y\(h(x)=\tan x\) son funciones impares. ¿Y qué pasa\(G(x)=\cos ^2 x\),\(F(x)=\sin ^2 x\) y\(H(x)=\tan ^2 x\)? ¿Son parejos, impares o ninguno? ¿Por qué?

Contestar

Las tres funciones,\(F,G,\) y\(H\),son parejos.

Esto se debe a que

\(F(-x)=\sin(-x)\sin(-x)=(-\sin x)(-\sin x)=\sin^2 x=F(x),G(-x)=\cos(-x)\cos(-x)=\cos x\cos x= cos^2 x=H(-x)=\tan(-x)\tan(-x)=(-\tan x)(-\tan x)=\tan2x=H(x)\)

2) Examinar la gráfica de\(f(x)=\sec x\) en el intervalo\([-\pi ,\pi ]\). ¿Cómo podemos saber si la función es par o impar solo observando la gráfica de\(f(x)=\sec x\)?

3) Después de examinar la identidad recíproca para\(\sec t\),explicar por qué la función está indefinida en ciertos puntos.

Contestar

Cuando\(\cos t = 0\),entonces\(\sec t = 10\),que no está definido.

4) Todas las identidades pitagóricas están relacionadas. Describir cómo manipular las ecuaciones para llegar de\(\sin^2t+\cos^2t=1\) a las otras formas.

Algebraico

Para los ejercicios 5-15, utilizar las identidades fundamentales para simplificar completamente la expresión.

5)\(\sin x \cos x \sec x\)

Contestar

\(\sin x\)

6)\(\sin(-x)\cos(-x)\csc(-x)\)

7)\(\tan x\sin x+\sec x\cos^2x\)

Contestar

\(\sec x\)

8)\(\csc x+\cos x\cot(-x)\)

9)\(\dfrac{\cot t+\tan t}{\sec (-t)}\)

Contestar

\(\csc x\)

10)\(3\sin^3 t\csc t+\cos^2 t+2\cos(-t)\cos t\)

11)\(-\tan(-x)\cot(-x)\)

Contestar

\(-1\)

12)\(\dfrac{-\sin (-x)\cos x\sec x\csc x\tan x}{\cot x}\)

13)\(\dfrac{1+\tan ^2\theta }{\csc ^2\theta }+\sin ^2\theta +\dfrac{1}{\sec ^2 \theta }\)

Contestar

\(\sec^2 x\)

14)\(\left (\dfrac{\tan x}{\csc ^2 x}+\dfrac{\tan x}{\sec ^2 x} \right )\left (\dfrac{1+\tan x}{1+\cot x} \right )-\dfrac{1}{\cos ^2 x}\)

15)\(\dfrac{1-\cos ^2 x}{\tan ^2 x}+2\sin ^2 x\)

Contestar

\(\sin^2 x+1\)

Para los ejercicios 16-28, simplificar la primera expresión trigonométrica escribiendo la forma simplificada en términos de la segunda expresión.

16)\(\dfrac{\tan x+\cot x}{\csc x}; \cos x\)

17)\(\dfrac{\sec x+\csc x}{1+\tan x}; \sin x\)

Contestar

\(\dfrac{1}{\sin x}\)

18)\(\dfrac{\cos x}{1+\sin x}+\tan x; \cos x\)

19)\(\dfrac{1}{\sin x\cos x}-\cot x; \cot x\)

Contestar

\(\dfrac{1}{\cot x}\)

20)\(\dfrac{1}{1-\cos x}-\dfrac{\cos x}{1+\cos x}; \csc x\)

21)\((\sec x+\csc x)(\sin x+\cos x)-2-\cot x; \tan x\)

Contestar

\(\tan x\)

22)\(\dfrac{1}{\csc x-\sin x}; \sec x\) y\(\tan x\)

23)\(\dfrac{1-\sin x}{1+\sin x}-\dfrac{1+\sin x}{1-\sin x}; \sec x\) y\(\tan x\)

Contestar

\(-4\sec x \tan x\)

24)\(\tan x; \sec x\)

25)\(\sec x; \cot x\)

Contestar

\(\pm \sqrt{\dfrac{1}{\cot ^2 x}+1}\)

26)\(\sec x; \sin x\)

27)\(\cot x; \sin x\)

Contestar

\(\dfrac{\pm \sqrt{1-\sin ^2 x}}{\sin x}\)

28)\(\cot x; \csc x\)

Para los ejercicios 29-33, verificar la identidad.

29)\(\cos x-\cos^3x=\cos x \sin^2 x\)

Contestar

Las respuestas variarán. Prueba de muestra:

\(\begin{align*} \cos x-\cos^3x &= \cos x (1-\cos^2 x)\\ &= \cos x\sin ^x \end{align*}\)

30)\(\cos x(\tan x-\sec(-x))=\sin x-1\)

31)\(\dfrac{1+\sin ^2x}{\cos ^2 x}=\dfrac{1}{\cos ^2 x}+\dfrac{\sin ^2x}{\cos ^2 x}=1+2\tan ^2x\)

Contestar

Las respuestas variarán. Prueba de muestra:

\(\begin{align*} \dfrac{1+\sin ^2x}{\cos ^2 x} &= \dfrac{1}{\cos ^2 x}+\dfrac{\sin ^2x}{\cos ^2 x}\\ &= \sec ^2x+\tan ^2x\\ &= \tan ^2x+1+\tan ^2x\\ &= 1+2\tan ^2x \end{align*}\)

32)\((\sin x+\cos x)^2=1+2 \sin x\cos x\)

33)\(\cos^2x-\tan^2x=2-\sin^2x-\sec^2x\)

Contestar

Las respuestas variarán. Prueba de muestra:

\(\begin{align*} \cos^2x-\tan^2x &= 1-\sin^2x-\left (\sec^2x -1 \right )\\ &= 1-\sin^2x-\sec^2x +1\\ &= 2-\sin^2x-\sec^2x \end{align*}\)

Extensiones

Para los ejercicios 34-39, acreditar o desacreditar la identidad.

34)\(\dfrac{1}{1+\cos x}-\dfrac{1}{1-\cos (-x)}=-2\cot x\csc x\)

35)\(\csc^2x(1+\sin^2x)=\cot^2x\)

Contestar

Falso

36)\(\left (\dfrac{\sec ^2(-x)-\tan ^2x}{\tan x} \right )\left (\dfrac{2+2\tan x}{2+2\cot x} \right )-2\sin ^2 x=\cos (2x) \)

37)\(\dfrac{\tan x}{\sec x}\sin (-x)=\cos ^2x\)

Contestar

Falso

38)\(\dfrac{\sec (-x)}{\tan x+\cot x}=-\sin (-x)\)

39)\(\dfrac{1+\sin x}{\cos x}=\dfrac{\cos x}{1+\sin (-x)}\)

Contestar

Demostrado con identidades negativas y pitagóricas

Para los ejercicios 40-, determinar si la identidad es verdadera o falsa. Si es falso, encuentra una expresión equivalente apropiada.

40)\(\dfrac{\cos ^2 \theta -\sin ^2 \theta }{1-\tan ^2 \theta }=\sin ^2 \theta\)

41)\(3\sin^2\theta + 4\cos^2\theta =3+\cos^2\theta\)

Contestar

Cierto

\(\begin{align*} 3\sin^2\theta + 4\cos^2\theta &= 3\sin ^2\theta +3\cos ^2\theta +\cos^2\theta \\ &= 3\left ( \sin ^2\theta +\cos ^2\theta \right )+\cos^2\theta \\ &= 3+\cos^2\theta \end{align*}\)

42)\(\dfrac{\sec \theta +\tan \theta }{\cot \theta+\cos ^\theta }=\sec ^2 \theta\)

7.2: Identidades de suma y diferencia

En esta sección aprenderemos técnicas que nos permitirán resolver problemas útiles. Las fórmulas que siguen simplificarán muchas expresiones y ecuaciones trigonométricas. Tenga en cuenta que, a lo largo de este apartado, el término fórmula se utiliza como sinónimo de la palabra identidad.

Verbal

1) Explicar las bases de las identidades de cofunción y cuándo aplican.

Contestar

Las identidades de cofunción se aplican a ángulos complementarios. Ver los dos ángulos agudos de un triángulo rectángulo, si uno de esos ángulos mide\(x\),el segundo ángulo mide\(\dfrac{\pi }{2}-x\). Entonces\(\sin x=\cos \left (\dfrac{\pi }{2}-x \right )\). Lo mismo vale para las otras identidades de cofunción. La clave es que los ángulos sean complementarios.

2) ¿Hay una sola manera de evaluar\(\cos \left (\dfrac{5\pi }{4} \right )\)? Explique cómo configurar la solución de dos maneras diferentes, y luego cómpule para asegurarse de que den la misma respuesta.

3) Explique a alguien que haya olvidado las propiedades pares-impares de las funciones sinusoidales cómo las fórmulas de suma y resta pueden determinar esta característica para\(f(x)=\sin (x)\) y\(g(x)=\cos (x)\). (Pista:\(0-x=-x\))

Contestar

\(\sin (-x)=-\sin x\), así\(\sin x\) es extraño. \(\cos (-x)=\cos (0-x)=\cos x\), así\(\cos x\) es parejo.

Algebraico

Para los ejercicios 4-9, encuentra el valor exacto.

4)\(\cos \left (\dfrac{7\pi }{12} \right)\)

5)\(\cos \left (\dfrac{\pi }{12} \right)\)

Contestar

\(\dfrac{\sqrt{2}+\sqrt{6}}{4}\)

6)\(\sin \left (\dfrac{5\pi }{12} \right)\)

7)\(\sin \left (\dfrac{11\pi }{12} \right)\)

Contestar

\(\dfrac{\sqrt{6}-\sqrt{2}}{4}\)

8)\(\tan \left (-\dfrac{\pi }{12} \right)\)

9)\(\tan \left (\dfrac{19\pi }{12} \right)\)

Contestar

\(-2-\sqrt{3}\)

Para los ejercicios 10-13, reescribir en términos de\(\sin x\) y\(\cos x\)

10)\(\sin \left (x+\dfrac{11\pi }{6} \right)\)

11)\(\sin \left (x-\dfrac{3\pi }{4} \right)\)

Contestar

\(-\dfrac{\sqrt{2}}{2}\sin x-\dfrac{\sqrt{2}}{2}\cos x\)

12)\(\cos \left (x-\dfrac{5\pi }{6} \right)\)

13)\(\cos \left (x+\dfrac{2\pi }{3} \right)\)

Contestar

\(-\dfrac{1}{2}\cos x-\dfrac{\sqrt{3}}{2}\sin x\)

Para los ejercicios 14-19, simplificar la expresión dada.

14)\(\csc \left (\dfrac{\pi }{2}-t \right)\)

15)\(\sec \left (\dfrac{\pi }{2}-\theta \right)\)

Contestar

\(\csc \theta\)

16)\(\cot \left (\dfrac{\pi }{2}-x \right)\)

17)\(\tan \left (\dfrac{\pi }{2}-x \right)\)

Contestar

\(\cot x\)

18)\(\sin(2x)\cos(5x)-\sin(5x)\cos(2x)\)

19)\(\dfrac{\tan \left (\dfrac{3}{2}x \right)-\tan \left (\dfrac{7}{5}x \right)}{1+\tan \left (\dfrac{3}{2}x \right)\tan \left (\dfrac{7}{5}x \right)}\)

Contestar

\(\tan \left (\dfrac{x}{10} \right)\)

Para los ejercicios 20-21, encuentra la información solicitada.

20) Dado que\(\sin a=\dfrac{2}{3}\) y\(\cos b=-\dfrac{1}{4}\),con\(a\) y\(b\) ambos en el intervalo\(\left [ \dfrac{\pi }{2}, \pi \right )\),encontrar\(\sin (a+b)\) y\(\cos (a-b)\).

21) Dado eso\(\sin a=\dfrac{4}{5}\) y\(\cos b=\dfrac{1}{3}\), con\(a\) y\(b\) ambos en el intervalo\(\left [ 0, \dfrac{\pi }{2} \right )\), encontrar\(\sin (a-b)\) y\(\cos (a+b)\).

Contestar

\(\sin (a-b)=\left ( \dfrac{4}{5} \right )\left ( \dfrac{1}{3} \right )-\left ( \dfrac{3}{5} \right )\left ( \dfrac{2\sqrt{2}}{3} \right )=\dfrac{4-6\sqrt{2}}{15}\)

\(\cos (a+b)=\left ( \dfrac{3}{5} \right )\left ( \dfrac{1}{3} \right )-\left ( \dfrac{4}{5} \right )\left ( \dfrac{2\sqrt{2}}{3} \right )=\dfrac{3-8\sqrt{2}}{15}\)

Para los ejercicios 22-24, encuentra el valor exacto de cada expresión.

22)\(\sin \left ( \cos^{-1}\left ( 0 \right )- \cos^{-1}\left ( \dfrac{1}{2} \right )\right )\)

23)\(\cos \left ( \cos^{-1}\left ( \dfrac{\sqrt{2}}{2} \right )+ \sin^{-1}\left ( \dfrac{\sqrt{3}}{2} \right )\right )\)

Contestar

\(\dfrac{\sqrt{2}-\sqrt{6}}{4}\)

24)\(\tan \left ( \sin^{-1}\left ( \dfrac{1}{2} \right )- \cos^{-1}\left ( \dfrac{1}{2} \right )\right )\)

Gráfica

Para los ejercicios 25-32, simplificar la expresión, y luego graficar ambas expresiones como funciones para verificar que las gráficas sean idénticas.

25)\(\cos \left ( \dfrac{\pi }{2}-x \right )\)

Contestar

\(\sin x\)

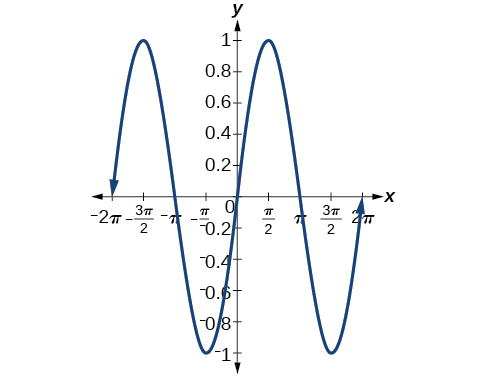
26)\(\sin (\pi -x)\)

27)\(\tan \left ( \dfrac{\pi }{3}+x \right )\)

Contestar

\(\cot \left ( \dfrac{\pi }{6}-x \right )\)

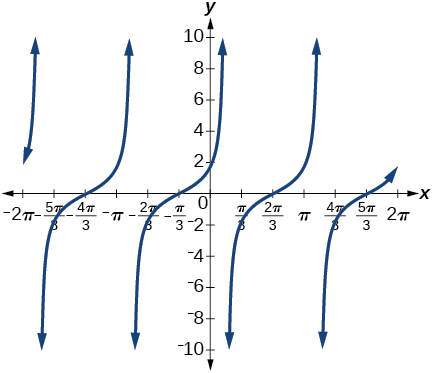
28)\(\sin \left ( \dfrac{\pi }{3}+x \right )\)

29)\(\tan \left ( \dfrac{\pi }{4}-x \right )\)

Contestar

\(\cot \left ( \dfrac{\pi }{4}+x \right )\)

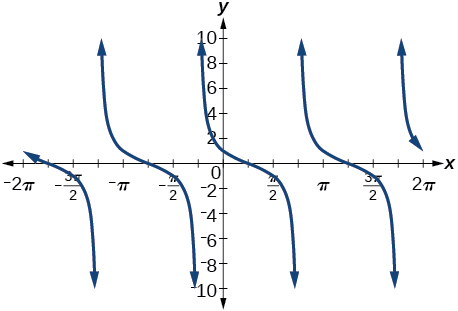
30)\(\cos \left ( \dfrac{7\pi }{6}+x \right )\)

31)\(\sin \left ( \dfrac{\pi }{4}+x \right )\)

Contestar

\(\dfrac{\sin x}{\sqrt{2}}+\dfrac{\cos x}{\sqrt{2}}\)

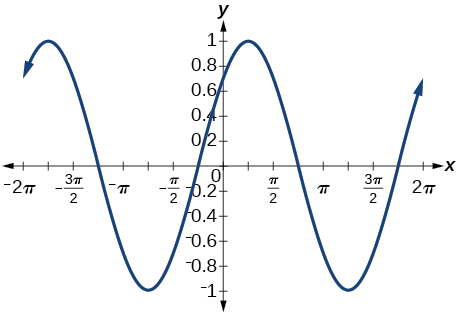
32)\(\cos \left ( \dfrac{5\pi }{4}+x \right )\)

Para los ejercicios 33-41, utilice una gráfica para determinar si las funciones son iguales o diferentes. Si son lo mismo, demuestre por qué. Si son diferentes, reemplace la segunda función por una que sea idéntica a la primera. (Pista: pensar\(2x=x+x\))

33)\(f(x)=\sin(4x)-\sin(3x)\cos x, g(x)=\sin x \cos(3x)\)

Contestar

Ellos son lo mismo.

34)\(f(x)=\cos(4x)+\sin x \sin(3x), g(x)=-\cos x \cos(3x)\)

35)\(f(x)=\sin(3x)\cos(6x), g(x)=-\sin(3x)\cos(6x)\)

Contestar

Ellos son diferentes, prueba\(g(x)=\sin(9x)-\cos(3x)\sin(6x)\)

36)\(f(x)=\sin(4x), g(x)=\sin(5x)\cos x-\cos(5x)\sin x\)

37)\(f(x)=\sin(2x), g(x)=2 \sin x \cos x\)

Contestar

Ellos son lo mismo.

38)\(f(\theta )=\cos(2\theta ), g(\theta )=\cos^2\theta -\sin^2\theta\)

39)\(f(\theta )=\tan(2\theta ), g(\theta )=\dfrac{\tan \theta }{1+\tan^2\theta }\)

Contestar

Ellos son diferentes, prueba\(g(\theta )=\dfrac{2\tan \theta }{1-\tan^2\theta }\)

40)\(f(x)=\sin(3x)\sin x, g(x)=\sin^2(2x)\cos^2x-\cos^2(2x)\sin2x\)

41)\(f(x)=\tan(-x), g(x)=\dfrac{\tan x-\tan(2x)}{1-\tan x \tan(2x)}\)

Contestar

Ellos son diferentes, prueba\(g(x)=\dfrac{\tan x-\tan(2x)}{1+\tan x \tan(2x)}\)

Tecnología

Para los ejercicios 42-46, encuentre el valor exacto algebraicamente, y luego confirme la respuesta con una calculadora al cuarto punto decimal.

42)\(\sin (75^{\circ})\)

43)\(\sin (195^{\circ})\)

Contestar

\(-\dfrac{\sqrt{3}-1}{2\sqrt{2}}\), o\(-0.2588\)

44)\(\cos (165^{\circ})\)

45)\(\cos (345^{\circ})\)

Contestar

\(\dfrac{1+\sqrt{3}}{2\sqrt{2}}\), o\(-0.9659\)

46)\(\tan (-15^{\circ})\)

Extensiones

Para los ejercicios 47-51, acreditar las identidades proporcionadas.

47)\(\tan \left ( x+\dfrac{\pi }{4} \right )=\dfrac{\tan x+1}{1-\tan x}\)

Contestar

\(\begin{align*} \tan \left ( x+\dfrac{\pi }{4} \right ) &= \\ \dfrac{\tan x + \tan\left (\tfrac{\pi}{4} \right )}{1-\tan x \tan\left (\tfrac{\pi}{4} \right )} &= \\ \dfrac{\tan x+1}{1-\tan x(1)} &= \dfrac{\tan x+1}{1-\tan x} \end{align*}\)

48)\(\dfrac{\tan (a+b)}{\tan (a-b)}=\dfrac{\sin a \cos a + \sin b \cos b}{\sin a \cos a - \sin b \cos b}\)

49)\(\dfrac{\cos (a+b)}{\cos a \cos b}=1-\tan a \tan b\)

Contestar

\(\begin{align*} \dfrac{\cos (a+b)}{\cos a \cos b} &= \\ \dfrac{\cos a \cos b}{\cos a \cos b}- \dfrac{\sin a \sin b}{\cos a \cos b} &= 1-\tan a \tan b \end{align*}\)

50)\(\cos(x+y)\cos(x-y)=\cos^2x-\sin^2y\)

51)\(\dfrac{\cos(x+h)-\cos(x)}{h}=\cos x\dfrac{\cos h-1}{h}-\sin x \dfrac{\sin h}{h}\)

Contestar

\(\begin{align*} \dfrac{\cos(x+h)-\cos(x)}{h} &= \\ \dfrac{\cos x\cosh - \sin x\sinh -\cos x}{h} &= \\ \dfrac{\cos x(\cosh-1) - \sin x(\sinh-1)}{h} &= \cos x\dfrac{\cos h-1}{h}-\sin x \dfrac{\sin h}{h} \end{align*}\)

Para los ejercicios 52-, acreditar o desacreditar las declaraciones.

52)\(\tan (u+v)=\dfrac{\tan u+\tan v}{1-\tan u \tan v}\)

53)\(\tan (u-v)=\dfrac{\tan u-\tan v}{1+\tan u \tan v}\)

Contestar

Cierto

54)\(\dfrac{\tan (x+y)}{1+\tan x \tan x}=\dfrac{\tan x + \tan y}{1-\tan^2 x \tan^2 y}\)

55) Si\(\alpha ,\beta\),y\(\gamma\) son ángulos en el mismo triángulo, luego probar o desmentir\(\sin(α+β)=\sin γ\).

Contestar

Cierto. Tenga en cuenta eso\(\sin (\alpha +\beta )=\sin (\pi -\gamma )\) y expanda el lado derecho.

56) Si\(\alpha ,\beta\), y\(\gamma\) son ángulos en un mismo triángulo, entonces probar o desmentir\(\tan \alpha +\tan \beta +\tan \gamma =\tan \alpha \tan \beta \tan \gamma\).

7.3: Fórmulas de doble ángulo, medio ángulo y reducción

En esta sección, investigaremos tres categorías adicionales de identidades. Las identidades de doble ángulo se derivan de las fórmulas de suma de las funciones trigonométricas fundamentales: seno, coseno y tangente. Las fórmulas de reducción son especialmente útiles en el cálculo, ya que nos permiten reducir la potencia del término trigonométrico. Las fórmulas de medio ángulo nos permiten encontrar el valor de las funciones trigonométricas que involucran semiángulos, ya sea que se conozca o no el ángulo original.

Verbal

1) Explicar cómo determinar las identidades de reducción a partir de la identidad de doble ángulo\(\cos(2x)=\cos^2x-\sin^2x\)

Contestar

Utilizar las identidades pitagóricas y aislar el término cuadrado.

2) Explicar cómo determinar la fórmula de doble ángulo para\(\tan(2x)\) usar las fórmulas de doble ángulo para\(\cos(2x)\) y\(\sin (2x)\).

3) Podemos determinar la fórmula de medio ángulo para\(\tan \left ( \dfrac{x}{2} \right )=\dfrac{\sqrt{1-\cos x}}{\sqrt{1+\cos x}}\) dividiendo la fórmula para\(\sin \left ( \dfrac{x}{2} \right )\) por\(\cos \left ( \dfrac{x}{2} \right )\). Explicar cómo determinar dos fórmulas para\(\tan \left ( \dfrac{x}{2} \right )\) que no involucren ninguna raíz cuadrada.

Contestar

\(\dfrac{1-\cos x}{\sin x}\),\(\dfrac{\sin x}{1+\cos x}\), multiplicando la parte superior e inferior por\(\sqrt{1-\cos x}\) y\(\sqrt{1+\cos x}\), respectivamente.

4) Para la fórmula de medio ángulo dada en el ejercicio anterior para\(\tan \left ( \dfrac{x}{2} \right )\),explicar por qué dividir por no\(0\) es una preocupación. (Pista: examinar los valores de\(\cos x\) necesario para que el denominador sea\(0\).)

Algebraico

Para los ejercicios 5-8, encuentra los valores exactos de a)\(\sin (2x)\), b)\(\cos(2x)\),y c)\(\tan(2x)\) sin resolver para\(x\).

5) Si\(\sin x =\dfrac{1}{8}\),y\(x\) está en cuadrante\(\mathrm{I}\).

Contestar

1. \(\dfrac{3\sqrt{7}}{32}\)
2. \(\dfrac{31}{32}\)
3. \(\dfrac{3\sqrt{7}}{31}\)

6) Si\(\cos x =\dfrac{2}{3}\), y\(x\) está en cuadrante\(\mathrm{I}\).

7) Si\(\cos x =-\dfrac{1}{2}\), y\(x\) está en cuadrante\(\mathrm{III}\).

Contestar

1. \(\dfrac{\sqrt{3}}{2}\)
2. \(-\dfrac{1}{2}\)
3. \(-\sqrt{3}\)

8) Si\(\tan x =-8\), y\(x\) está en cuadrante\(\mathrm{IV}\).

Para los ejercicios 9-10, encuentra los valores de las seis funciones trigonométricas si se mantienen las condiciones proporcionadas.

9)\(\cos(2\theta )=\dfrac{3}{5}\) y\(90^{\circ}\leq \theta \leq 180^{\circ}\)

Responder

\(\cos \theta =-\frac{2\sqrt{5}}{5},\sin \theta =\frac{\sqrt{5}}{5},\tan \theta =-\frac{1}{2},\csc \theta =\sqrt{5},\sec \theta =-\frac{\sqrt{5}}{2},\cot \theta =-2\)

10)\(\cos(2\theta )=\dfrac{1}{\sqrt{2}}\) y\(180^{\circ}\leq \theta \leq 270^{\circ}\)

Para los ejercicios 11-12, simplificar a una expresión trigonométrica.

11)\(2\sin \left ( \dfrac{\pi }{4} \right )2\cos \left ( \dfrac{\pi }{4} \right )\)

Responder

\(2\sin \left ( \dfrac{\pi }{2} \right )\)

12)\(4\sin \left ( \dfrac{\pi }{8} \right )\cos \left ( \dfrac{\pi }{8} \right )\)

Para los ejercicios 13-19, encuentra el valor exacto usando fórmulas de medio ángulo.

13)\(\sin \left ( \dfrac{\pi }{8} \right )\)

Responder

\(\dfrac{\sqrt{2-\sqrt{2}}}{2}\)

14)\(\cos \left ( -\dfrac{11\pi }{12} \right )\)

15)\(\sin \left ( \dfrac{11\pi }{12} \right )\)

Responder

\(\dfrac{\sqrt{2-\sqrt{3}}}{2}\)

16)\(\cos \left ( \dfrac{7\pi }{8} \right )\)

17)\(\tan \left ( \dfrac{5\pi }{12} \right )\)

Responder

\(2+\sqrt{3}\)

18)\(\tan \left ( -\dfrac{3\pi }{12} \right )\)

19)\(\tan \left ( -\dfrac{3\pi }{8} \right )\)

Responder

\(-1-\sqrt{2}\)

Para los ejercicios 20-23, encuentra los valores exactos de a)\(\sin \left ( \dfrac{x}{2} \right )\) b)\(\cos \left ( \dfrac{x}{2} \right )\),y c)\(\tan \left ( \dfrac{x}{2} \right )\) sin resolver para\(x\),cuando\(0^{\circ}\leq \theta \leq 360^{\circ}\)

20) Si\(\tan x =-\dfrac{4}{3}\), y\(x\) está en cuadrante\(\mathrm{IV}\).

21) Si\(\sin x =-\dfrac{12}{13}\), y\(x\) está en cuadrante\(\mathrm{III}\).

Responder

1. \(\dfrac{3\sqrt{13}}{13}\)
2. \(-\dfrac{2\sqrt{13}}{13}\)
3. \(-\dfrac{3}{2}\)

22) Si\(\csc x =7\), y\(x\) está en cuadrante\(\mathrm{II}\).

23) Si\(\sec x =-4\), y\(x\) está en cuadrante\(\mathrm{II}\).

Responder

1. \(\dfrac{\sqrt{10}}{4}\)
2. \(\dfrac{\sqrt{6}}{4}\)
3. \(\dfrac{\sqrt{15}}{3}\)

Para los ejercicios 24-27, use la Figura a continuación para encontrar los ángulos medio y doble solicitados.

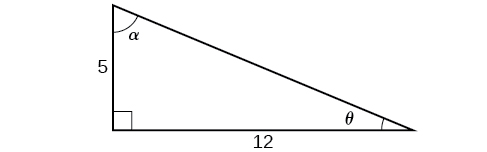
24) Encontrar\(\sin (2\theta )\),\(\cos (2\theta )\),y\(\tan (2\theta )\).

25) Encontrar\(\sin (2\alpha )\),\(\cos (2\alpha )\), y\(\tan (2\alpha )\).

Responder

\(\dfrac{120}{169}, -\dfrac{119}{169}, -\dfrac{120}{119}\)

26) Encontrar\(\sin \left (\dfrac{\theta }{2} \right )\),\(\cos \left (\dfrac{\theta }{2} \right )\), y\(\tan \left (\dfrac{\theta }{2} \right )\).

27) Encontrar\(\sin \left (\dfrac{\alpha }{2} \right )\),\(\cos \left (\dfrac{\alpha }{2} \right )\), y\(\tan \left (\dfrac{\alpha }{2} \right )\).

Responder

\(\dfrac{2\sqrt{13}}{13}, \dfrac{3\sqrt{13}}{13}, \dfrac{2}{3}\)

Para los ejercicios 28-33, simplificar cada expresión. No evaluar.

28)\(\cos ^2(28^{\circ})-\sin ^2(28^{\circ})\)

29)\(2\cos ^2(37^{\circ})-1\)

Responder

\(\cos (74^{\circ})\)

30)\(1-2\sin ^2(17^{\circ})\)

31)\(\cos ^2(9x)-\sin ^2(9x)\)

Responder

\(\cos (18x)\)

32)\(4\sin (8x)\cos (8x)\)

33)\(6\sin (5x)\cos (5x)\)

Responder

\(3\sin (10x)\)

Para los ejercicios 34-37, acreditar la identidad otorgada.

34)\((\sin t-\cos t)^2=1-\sin(2t)\)

35)\(\sin(2x)=-2 \sin(-x) \cos(-x)\)

Responder

\(-2 \sin(-x)\cos(-x)=-2(-\sin(x)\cos(x))=\sin(2x)\)

36)\(\cot x-\tan x=2 \cot(2x)\)

37)\(\dfrac{1+\cos (2\theta )}{\sin (2\theta )}\tan ^2\theta =\tan \theta\)

Responder

\(\dfrac{\sin (2\theta )}{1+\cos (2\theta )}\tan ^2\theta =\dfrac{2\sin (\theta )\cos (\theta )}{1+\cos ^2\theta -\sin ^2\theta }\tan ^2\theta=\)

\(\dfrac{2\sin (\theta )\cos (\theta )}{2\cos ^2\theta }\tan ^2\theta=\dfrac{\sin (\theta )}{\cos (\theta )}\tan ^2\theta=\)

\(\cot (\theta )\tan ^2\theta=\tan \theta\)

Para los ejercicios 38-44, reescribe la expresión con un exponente no superior a 1.

38)\(\cos ^2 (5x)\)

39)\(\cos ^2 (6x)\)

Responder

\(\dfrac{1+\cos (12x)}{2}\)

40)\(\sin ^4 (8x)\)

41)\(\sin ^4 (3x)\)

Responder

\(\dfrac{3+\cos(12x)-4\cos(6x)}{8}\)

42)\(\cos^2x \sin^4x\)

43)\(\cos^4x \sin^2x\)

Responder

\(\dfrac{2+\cos(2x)-2\cos(4x)-\cos(6x)}{32}\)

44)\(\tan^2x \sin^2x\)

Tecnología

Para los ejercicios 45-52, reducir las ecuaciones a potencias de uno, y luego verificar la respuesta gráficamente.

45)\(\tan^4x\)

Responder

\(\dfrac{3+\cos(4x)-4\cos(2x)}{3+\cos(4x)+4\cos(2x)}\)

46)\(\sin^2(2x)\)

47)\(\sin^2x \cos^2x\)

Responder

\(\dfrac{1-\cos(4x)}{8}\)

48)\(\tan^2x \sin x\)

49)\(\tan^4x \cos^2 x\)

Responder

\(\dfrac{3+\cos(4x)-4\cos(2x)}{4(\cos(2x)+1)}\)

50)\(\cos^2x \sin (2x)\)

51)\(\cos^2(2x) \sin x\)

Responder

\(\dfrac{(1+\cos(4x))\sin x}{2}\)

52)\(\tan ^2\left ( \dfrac{x}{2} \right )\sin x\)

Para los ejercicios 53-54, encontrar algebraicamente una función equivalente, solo en términos de\(\sin x\) y/o\(\cos x\),y luego verificar la respuesta graficando ambas ecuaciones.

53)\(\sin (4x)\)

Responder

\(4\sin x\cos x(\cos^2x-\sin^2x)\)

54)\(\cos (4x)\)

Extensiones

Para los ejercicios 55-63, acreditar las identidades.

55)\(\sin (2x)=\dfrac{2\tan x}{1+\tan ^2x}\)

Responder

\(\dfrac{2\tan x}{1+\tan ^2x}=\dfrac{\tfrac{2\sin x}{\cos x}}{1+\tfrac{\sin ^2x}{\cos ^2x}}=\dfrac{\tfrac{2\sin x}{\cos x}}{\tfrac{\cos ^2x+\sin ^2x}{\cos ^2x}}=\dfrac{2\sin x}{\cos x}\cdot \dfrac{\cos ^2x}{1}=2\sin x \cos x=\sin (2x)\)

56)\(\cos (2\alpha )=\dfrac{1-\tan ^2\alpha }{1+\tan ^2\alpha }\)

57)\(\tan (2x)=\dfrac{2\sin x \cos x }{2\cos ^2 x-1}\)

Responder

\(\dfrac{2\sin x \cos x }{2\cos ^2 x-1}=\dfrac{\sin (2x)}{ \cos (2x)}=\tan (2x)\)

58)\((\sin^2x-1)^2=\cos(2x)+\sin^4x\)

59)\(\sin(3x)=3\sin x \cos^2x-\sin^3x\)

Responder

\(\begin{align*} \sin (x+2x) &= \sin x \cos (2x)+\sin (2x) \cos x\\ &= \sin x(\cos ^2 x - \sin ^2 x)+2\sin x \cos x \cos x\\ &= \sin x \cos ^2 x-\sin ^3 x + 2\sin x\cos ^2 x\\ &= 3\sin x\cos ^2 x - \sin ^3 x \end{align*}\)

60)\(\cos(3x)=\cos^3x-3\sin^2x\cos x\)

61)\(\dfrac{1+\cos (2t)}{\sin (2t)-\cos t}=\dfrac{2\cos t}{2\sin t-1}\)

Responder

\(\begin{align*} \dfrac{1+\cos (2t)}{\sin (2t)-\cos t} &= \dfrac{1+2\cos ^2t-1}{2\sin t\cos t-\cos t}\\ &= \dfrac{2\cos ^2t}{\cos t(2\sin t-1)}\\ &= \dfrac{2\cos t}{2\sin t-1} \end{align*}\)

62)\(\sin(16x)=16 \sin x \cos x \cos(2x)\cos(4x)\cos(8x)\)

63)\(\cos(16x)=(\cos^2(4x)-\sin^2(4x)-\sin(8x))(\cos^2(4x)-\sin^2(4x)+\sin(8x))\)

Responder

\(\begin{align*} (\cos^2(4x)-\sin^2(4x)-\sin(8x))(\cos^2(4x)-\sin^2(4x)+\sin(8x)) &= (\cos(8x)-\sin(8x))(\cos(8x)+\sin(8x))\\ &= \cos ^2 (8x)-\sin ^2 (8x)\\ &= \cos(16x) \end{align*}\)

7.4: Fórmulas Suma a Producto y Producto a Suma

A partir de las identidades de suma y diferencia, podemos derivar las fórmulas de producto a suma y las fórmulas de suma a producto para seno y coseno. Las fórmulas de producto a suma pueden reescribir productos de senos, productos de cosenos y productos de seno y coseno como sumas o diferencias de senos y cosenos. También podemos derivar las identidades suma-a-producto a partir de las identidades de producto a suma usando la sustitución. Las fórmulas suma-a-producto se utilizan para reescribir suma o diferencia como productos de senos y cosenos.

Verbal

1) Comenzando con el producto para sumar la fórmula\(\sin \alpha \cos \beta =\dfrac{1}{2} \left[\sin(\alpha +\beta )+\sin(\alpha -\beta ) \right]\),explicar cómo determinar la fórmula para\(\cos \alpha \sin \beta\).

Responder

Sustituir\(\alpha \) en coseno y\(\beta \) en seno y evaluar.

2) Explicar dos métodos diferentes de cálculo\(\cos (195^{\circ}) \cos (105^{\circ})\),uno de los cuales utiliza el producto para sumar. ¿Qué método es más fácil?

3) Explicar una situación en la que convertiríamos una ecuación de una suma a un producto y pondríamos un ejemplo.

Responder

Las respuestas variarán. Hay algunas ecuaciones que involucran una suma de dos expresiones trigonométricas donde cuando se convierten a un producto son más fáciles de resolver. Por ejemplo:\(\dfrac{\sin (3x)+\sin x}{\cos x}=1\). Al convertir el numerador en un producto la ecuación se convierte en:\(\dfrac{2\sin (2x)\cos x}{\cos x}=1\)

4) Explicar una situación en la que convertiríamos una ecuación de un producto a una suma, y pondríamos un ejemplo.

Algebraico

Para los ejercicios 5-10, reescribe el producto como suma o diferencia.

5)\(16\sin(16x)\sin(11x)\)

Responder

\(8(\cos(5x)-\cos(27x))\)

6)\(2\cos(36t)\cos(6t)\)

7)\(2\sin(5x)\cos(3x)\)

Responder

\(\sin(2x)+\sin(8x)\)

8)\(10\cos(5x)\sin(10x)\)

9)\(\sin(-x)\sin(5x)\)

Responder

\(\dfrac{1}{2}(\cos(6x)-\cos(4x))\)

10)\(\sin(3x)\cos(5x)\)

Para los ejercicios 11-16, reescribe la suma o diferencia como producto.

11)\(\cos(6t)+\cos(4t)\)

Responder

\(2\cos(5t)\cos t\)

12)\(\sin(3x)+\sin(7x)\)

13)\(\cos(7x)+\cos(-7x)\)

Responder

\(2\cos(7x)\)

14)\(\sin(3x)-\sin(-3x)\)

15)\(\cos(3x)+\cos(9x)\)

Responder

\(2\cos(6x)\cos(3x)\)

16)\(\sin h-\sin(3h)\)

Para los ejercicios 17-21, evaluar el producto para lo siguiente utilizando una suma o diferencia de dos funciones.

17)\(\cos (45^{\circ}) \cos (15^{\circ})\)

Responder

\(\dfrac{1}{4}(1+\sqrt{3})\)

18)\(\cos (45^{\circ}) \sin (15^{\circ})\)

19)\(\sin (-345^{\circ}) \sin (-15^{\circ})\)

Responder

\(\dfrac{1}{4}(\sqrt{3}-2)\)

20)\(\sin (195^{\circ}) \cos (15^{\circ})\)

21)\(\sin (-45^{\circ}) \sin (-15^{\circ})\)

Responder

\(\dfrac{1}{4}(\sqrt{3}-1)\)

Para los ejercicios 22-26, evaluar el producto utilizando una suma o diferencia de dos funciones. Dejar en términos de seno y coseno.

22)\(\cos (23^{\circ}) \sin (17^{\circ})\)

23)\(2\sin (100^{\circ}) \sin (20^{\circ})\)

Responder

\(\cos (80^{\circ})-\cos (120^{\circ})\)

24)\(2\sin (-100^{\circ})\sin (-20^{\circ})\)

25)\(\sin (213^{\circ})\cos (8^{\circ})\)

Responder

\(\dfrac{1}{2}\left (\sin (221^{\circ})+\sin (205^{\circ}) \right )\)

26)\(2\cos (56^{\circ})\cos (47^{\circ})\)

Para los ejercicios 27-31, reescribir la suma como producto de dos funciones. Dejar en términos de seno y coseno.

27)\(\sin (76^{\circ})+\sin (14^{\circ})\)

Responder

\(\sqrt{3}\cos (31^{\circ})\)

28)\(\cos (58^{\circ})-\cos (12^{\circ})\)

29)\(\sin (101^{\circ})-\sin (32^{\circ})\)

Responder

\(2\cos (66.5^{\circ})\sin (34.5^{\circ})\)

30)\(\cos (100^{\circ})+\cos (200^{\circ})\)

31)\(\sin (-1^{\circ})+\sin (-2^{\circ})\)

Responder

\(2\sin (-1.5^{\circ})\cos (0.5^{\circ})\)

Para los ejercicios 32-38, acreditar la identidad.

32)\(\dfrac{\cos (a-b)}{\cos (a+b)}=\dfrac{1-\tan a \tan b}{1+\tan a \tan b}\)

33)\(4\sin(3x)\cos(4x)=2\sin(7x)-2\sin x\)

Responder

\(\begin{align*} 2\sin(7x)-2\sin x &= 2\sin(4x+3x)-2\sin(4x-3x)\\ &= 2(\sin(4x)\cos(3x)+\sin(3x)\cos(4x))-2(\sin(4x)\cos(3x)-\sin(3x)\cos(4x))\\ &= 2\sin(4x)\cos(3x)+2\sin(3x)\cos(4x))-2\sin(4x)\cos(3x)+2\sin(3x)\cos(4x))\\ &= 4\sin(3x)\cos(4x) \end{align*}\)

34)\(\dfrac{6\cos (8x)\sin (2x)}{\sin (-6x)}=-3\sin(10x)\csc(6x)+3\)

35)\(\sin x + \sin(3x)=4\sin x\cos^2 x\)

Responder

\(\begin{align*} \sin x + \sin(3x) &= 2\sin\left ( \dfrac{4x}{2} \right )\cos\left ( -\dfrac{2x}{2} \right )\\ &= 2\sin(2x)\cos x\\ &= 2(2\sin x \cos x)\cos x\\ &= 4\sin x\cos^2 x \end{align*}\)

36)\(2(\cos^3x-\cos x \sin^2x)=\cos(3x)+\cos x\)

37)\(2\tan x \cos(3x)=\sec x(\sin(4x)-\sin(2x))\)

Responder

\(\begin{align*} 2\tan x \cos(3x) &= \dfrac{2\sin x\cos (3x)}{\cos x}\\ &= \dfrac{2(.5(\sin (4x)-\sin (2x)))}{\cos x}\\ &= \dfrac{1}{\cos x}(\sin(4x)-\sin(2x))\\ &= \sec x(\sin(4x)-\sin(2x)) \end{align*}\)

38)\(\cos(a+b)+\cos(a-b)=2\cos a \cos b\)

Numérico

Para los ejercicios 39-43, reescribir la suma como producto de dos funciones o el producto como una suma de dos funciones. Da tu respuesta en términos de senos y cosenos. Después evaluar la respuesta final numéricamente, redondeada a cuatro decimales.

39)\(\cos (58^{\circ})+\cos (12^{\circ})\)

Responder

\(2\cos (35^{\circ})\cos (23^{\circ}),1.5081\)

40)\(\sin (2^{\circ})-\sin (3^{\circ})\)

41)\(\cos (44^{\circ})-\cos (22^{\circ})\)

Responder

\(-2\sin (33^{\circ})\sin (11^{\circ}),-0.2078\)

42)\(\cos (176^{\circ})\sin (9^{\circ})\)

43)\(\sin (-14^{\circ})\sin (85^{\circ})\)

Responder

\(\dfrac{1}{2}\left (\cos (99^{\circ})-\cos (71^{\circ}) \right ),-0.2410\)

Tecnología

Para los ejercicios 44-48, determinar algebraicamente si cada una de las expresiones dadas es una verdadera identidad. Si no es una identidad, sustituya el lado derecho por una expresión equivalente al lado izquierdo. Verifique los resultados graficando ambas expresiones en una calculadora.

44)\(2\sin(2x)\sin(3x)=\cos x-\cos(5x)\)

45)\(\dfrac{\cos(10\theta )+\cos(6\theta )}{\cos(6\theta )-\cos(10\theta )}=\cot(2\theta )\cot(\theta )\)

Responder

Es una identidad.

46)\(\dfrac{\sin(3x)-\sin(5x)}{\cos(3x)+\cos(5x)}=\tan x\)

47)\(2\cos(2x)\cos x+\sin(2x)\sin x=2\sin x\)

Responder

No es una identidad, sino\(2\cos ^3 x\) que sí.

48)\(\dfrac{\sin(2x)+\sin(4x)}{\sin(2x)-\sin(4x)}=-\tan (3x)\cot x\)

Para los ejercicios 49-53, simplifica la expresión a un término, luego grafica la función original y tu versión simplificada para verificar que sean idénticas.

49)\(\dfrac{\sin(9t)-\sin(3t)}{\cos(9t)+\cos(3t)}\)

Responder

\(\tan (3t)\)

50)\(2\sin(8x)\cos(6x)-\sin(2x)\)

51)\(\dfrac{\sin(3x)-\sin(x)}{\sin x}\)

Responder

\(2\cos (2x)\)

52)\(\dfrac{\cos(5x)+\cos(3x)}{\sin(5x)+\sin(3x)}\)

53)\(\sin x \cos(15x)-\cos x \sin(15x)\)

Responder

\(-\sin (14x)\)

Extensiones

Para los ejercicios 54-55, probar las siguientes fórmulas suma-a-producto.

54)\(\sin x - \sin y = 2\sin \left ( \dfrac{x-y}{2} \right )\cos \left ( \dfrac{x+y}{2} \right )\)

55)\(\cos x + \cos y = 2\cos \left ( \dfrac{x+y}{2} \right )\cos \left ( \dfrac{x-y}{2} \right )\)

Responder

Empezar con\(\cos x + \cos y\). Hacer una sustitución y dejar\(x=\alpha +\beta\) y dejar\(y=\alpha -\beta\),así\(\cos x + \cos y\) se convierte en:

\(\cos(\alpha +\beta )+\cos(\alpha -\beta )=\cos\alpha \cos\beta -\sin\alpha \sin\beta +\cos\alpha \cos\beta +\sin\alpha \sin\beta =2\cos\alpha \cos \beta\)

Desde\(x=\alpha +\beta\) y\(y=\alpha -\beta\),podemos resolver por\(\alpha \) y\(\beta \) en términos de\(x\)\(y\) y y sustituir\(2\cos\alpha \cos \beta\) y obtener

\(2\cos \left ( \dfrac{x+y}{2} \right )\cos \left ( \dfrac{x-y}{2} \right )\)

Para los ejercicios 56-63, acreditar la identidad.

56)\(\dfrac{\sin(6x)+\sin(4x)}{\sin(6x)-\sin(4x)}=\tan (5x)\cot x\)

57)\(\dfrac{\cos(3x)+\cos x}{\cos(3x)-\cos(4x)}=-\cot (2x)\cot x\)

Responder

\(\dfrac{\cos(3x)+\cos x}{\cos(3x)-\cos(4x)}=\dfrac{2\cos(2x)\cos x}{-2\sin(2x)\sin x}=-\cot (2x)\cot x\)

58)\(\dfrac{\cos(6y)+\cos(8y)}{\sin(6y)-\sin(4y)}=\cot y\cos(7y)\sec(5y)\)

59)\(\dfrac{\cos(2y)-\cos(4y)}{\sin(2y)+\sin(4y)}=\tan y\)

Responder

\(\begin{align*} \dfrac{\cos(2y)-\cos(4y)}{\sin(2y)+\sin(4y)} &= \dfrac{-2\sin(3y)\sin(-y)}{2\sin(3y)\cos y}\\ &= \dfrac{2\sin(3y)\sin(y)}{2\sin(3y)\cos y}\\ &= \tan y \end{align*}\)

60)\(\dfrac{\sin(10x)-\sin(2x)}{\cos(10x)+\cos(2x)}=\tan(4x)\)

61)\(\cos x-\cos(3x)=4\sin^2x \cos x\)

Responder

\(\begin{align*} \cos x-\cos(3x) &= -2\sin(2x)\sin(-x)\\ &= 2(2\sin x \cos x)\sin x\\ &= 4\sin^2x \cos x \end{align*}\)

62)\((\cos(2x)-\cos(4x))^2+(\sin(4x)+\sin(2x))^2=4\sin^2(3x)\)

63)\(\tan \left ( \dfrac{\pi }{4}-t \right )=\dfrac{1-\tan t}{1+\tan t}\)

Responder

\(\tan \left ( \dfrac{\pi }{4}-t \right )=\dfrac{\tan \left ( \dfrac{\pi }{4} \right )-\tan t}{1+\tan \left ( \dfrac{\pi }{4} \right )\tan t}=\dfrac{1-\tan t}{1+\tan t}\)

7.5: Resolver ecuaciones trigonométricas

En secciones anteriores de este capítulo, observamos identidades trigonométricas. Las identidades son verdaderas para todos los valores en el dominio de la variable. En esta sección, comenzamos nuestro estudio de ecuaciones trigonométricas para estudiar escenarios del mundo real como el hallazgo de las dimensiones de las pirámides.

Verbal

1) ¿Siempre habrá soluciones a las ecuaciones de funciones trigonométricas? De no ser así, describa una ecuación que no tendría solución. Explique por qué o por qué no.

Responder

No siempre habrá soluciones a las ecuaciones de funciones trigonométricas. Para un ejemplo básico,\(\cos(x)=-5\).

2) Al resolver una ecuación trigonométrica que involucra más de una función trigonométrica, ¿siempre queremos intentar reescribir la ecuación para que se exprese en términos de una función trigonométrica? ¿Por qué o por qué no?

3) Al resolver ecuaciones trigonométricas lineales en términos de solo seno o coseno, ¿cómo sabemos si habrá soluciones?

Responder

Si la función seno o coseno tiene un coeficiente de uno, aísle el término en un lado del signo igual. Si el número al que se establece igual tiene un valor absoluto menor o igual a uno, la ecuación tiene soluciones, de lo contrario no lo hace. Si el seno o coseno no tiene un coeficiente igual a uno, aún así aísla el término pero luego divide ambos lados de la ecuación por el coeficiente inicial. Entonces, si el número al que se establece igual tiene un valor absoluto mayor que uno, la ecuación no tiene solución.

Algebraico

Para los ejercicios 4-12, encuentra todas las soluciones exactamente en el intervalo \(0\leq \theta < 2\pi\)

4)\(2\sin \theta=-\sqrt{2}\)

5)\(2\sin \theta=\sqrt{3}\)

Responder

\(\dfrac{\pi }{3}, \dfrac{2\pi }{3}\)

6)\(2\cos \theta=1\)

7)\(2\cos \theta=-\sqrt{2}\)

Responder

\(\dfrac{3\pi }{4}, \dfrac{5\pi }{4}\)

8)\(\tan \theta=-1\)

9)\(\tan x=1\)

Responder

\(\dfrac{\pi }{4}, \dfrac{5\pi }{4}\)

10)\(\cot x+1=0\)

11)\(4\sin^2 x-2=0\)

Responder

\(\dfrac{\pi }{4}, \dfrac{3\pi }{4}, \dfrac{5\pi }{4}, \dfrac{7\pi }{4}\)

12)\(\csc^2 x-4=0\)

Para los ejercicios 13-22, resolver exactamente en\([0,2\pi )\)

13)\(2\cos \theta=\sqrt{2}\)

Responder

\(\dfrac{\pi }{4}, \dfrac{7\pi }{4}\)

14)\(2\cos \theta=-1\)

15)\(2\sin \theta=-1\)

Responder

\(\dfrac{7\pi }{6}, \dfrac{11\pi }{6}\)

16)\(2\sin \theta=-\sqrt{3}\)

17)\(2\sin (3\theta )=1\)

Responder

\(\dfrac{\pi }{18}, \dfrac{5\pi }{18}, \dfrac{13\pi }{18}, \dfrac{17\pi }{18}, \dfrac{25\pi }{18}, \dfrac{29\pi }{18}\)

18)\(2\sin (2\theta )=\sqrt{3}\)

19)\(2\cos (3\theta )=-\sqrt{2}\)

Responder

\(\dfrac{3\pi }{12}, \dfrac{5\pi }{12}, \dfrac{11\pi }{12}, \dfrac{13\pi }{12}, \dfrac{19\pi }{12}, \dfrac{21\pi }{12}\)

20)\(\cos (2\theta )=-\dfrac{\sqrt{3}}{2}\)

21)\(2\sin(\pi \theta )=1\)

Responder

\(\dfrac{1}{6}, \dfrac{5}{6}, \dfrac{13}{6}, \dfrac{17}{6}, \dfrac{25}{6}, \dfrac{29}{6}, \dfrac{37}{6}\)

22)\(2\cos \left(\dfrac{\pi }{5}\theta \right)=\sqrt{3}\)

Para los ejercicios 23-32, encuentre todas las soluciones exactas en\([0,2\pi )\)

23)\(\sec(x)\sin(x)-2\sin(x)=0\)

Responder

\(0, \dfrac{\pi }{3}, \pi , \dfrac{5\pi }{3}\)

24)\(\tan(x)-2\sin(x)\tan(x)=0\)

25)\(2\cos^2 t+\cos(t)=1\)

Responder

\(\dfrac{\pi }{3}, \pi , \dfrac{5\pi }{3}\)

26)\(2\tan^2(t)=3\sec(t)\)

27)\(2\sin(x)\cos(x)-\sin(x)+2\cos(x)-1=0\)

Responder

\(\dfrac{\pi }{3}, \dfrac{3\pi }{2}, \dfrac{5\pi }{3}\)

28)\(\cos^2\theta =\dfrac{1}{2}\)

29)\(\sec^2 x =1\)

Responder

\(0, \pi \)

30)\(\tan^2(x)=-1+2\tan(-x)\)

31)\(8\sin^2(x)+6\sin(x)+1=0\)

Responder

\(\pi -\sin^{-1}\left ( -\dfrac{1}{4} \right ), \dfrac{7\pi }{6}, \dfrac{11\pi }{6}, 2\pi +\sin^{-1}\left ( -\dfrac{1}{4} \right )\)

32)\(\tan^5(x)=\tan(x)\)

Para los ejercicios 33-40, resuelve con los métodos mostrados en esta sección exactamente en el intervalo\([0,2\pi )\)

33)\(\sin(3x)\cos(6x)-\cos(3x)\sin(6x)=-0.9\)

Responder

\(\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{\pi }{3}-\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{2\pi }{3}+\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \pi -\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{4\pi }{3}+\dfrac{1}{3}\left (\sin^{-1}\left ( \dfrac{9}{10} \right ) \right ), \dfrac{5\pi }{3}-\)

34)\(\sin(6x)\cos(11x)-\cos(6x)\sin(11x)=-0.1\)

35)\(\cos(2x)\cos x+\sin(2x)\sin x=1\)

Responder

\(0\)

36)\(6\sin(2t)+9\sin t=0\)

37)\(9\cos(2\theta )=9\cos^2\theta -4\)

Responder

\(\dfrac{\pi }{6}, \dfrac{5\pi }{6}, \dfrac{7\pi }{6}, \dfrac{11\pi }{6}\)

38)\(\sin(2t)=\cos t\)

39)\(\cos(2t)=\sin t\)

Responder

\(\dfrac{3\pi }{2}, \dfrac{\pi }{6}, \dfrac{5\pi }{6}\)

40)\(\cos(6x)-\cos(3x)=0\)

Para los ejercicios 41-49, resolver exactamente en el intervalo\([0,2\pi )\). Utilice la fórmula cuadrática si las ecuaciones no factoriales.

41)\(\tan^2 x-\sqrt{3}\tan x=0\)

Responder

\(0, \dfrac{\pi }{3}, \pi , \dfrac{4\pi }{3}\)

42)\(\sin^2 x+\sin x-2=0\)

43)\(\sin^2 x-2\sin x-4=0\)

Responder

No hay soluciones.

44)\(5\cos^2 x+3\cos x-1=0\)

45)\(3\cos^2 x-3\cos x-2=0\)

Responder

\(\cos^{-1}\left (\dfrac{1}{3}\left ( 1-\sqrt{7} \right ) \right ), 2\pi -\cos^{-1}\left (\dfrac{1}{3}\left ( 1-\sqrt{7} \right ) \right )\)

46)\(5\sin^2 x+2\sin x-1=0\)

47)\(\tan^2 x+5\tan x-1=0\)

Responder

\(\tan^{-1}\left (\dfrac{1}{2}\left ( \sqrt{29}-5 \right ) \right ), \pi +\tan^{-1}\left (\dfrac{1}{2}\left ( -\sqrt{29}-5 \right ) \right ), \pi +\tan^{-1}\left (\dfrac{1}{2}\left ( \sqrt{29}-5 \right ) \right ), 2\pi +\tan^{-1}\left (\dfrac{1}{2}\left ( -\sqrt{29}-5 \right ) \right )\)

48)\(\cot^2 x=-\cot x\)

49)\(-\tan^2 x-\tan x-2=0\)

Responder

No hay soluciones.

Para los ejercicios 50-65, encuentre soluciones exactas en el intervalo\([0,2\pi )\). Buscar oportunidades para usar identidades trigonométricas.

50)\(\sin^2 x-\cos^2 x-\sin x=0\)

51)\(\sin^2 x+\cos^2 x=0\)

Responder

No hay soluciones.

52)\(\sin(2x)-\sin x=0\)

53)\(\cos(2x)-\cos x=0\)

Responder

\(0, \dfrac{2\pi }{3}, \dfrac{4\pi }{3}\)

54)\(\dfrac{2\tan x}{2-\sec ^2 x}-\sin^2 x=\cos^2 x\)

55)\(1-\cos(2x)=1+\cos(2x)\)

Responder

\(\dfrac{\pi }{4}, \dfrac{3\pi }{4}, \dfrac{5\pi }{4}, \dfrac{7\pi }{4}\)

56)\(\sec^2 x=7\)

57)\(10\sin x \cos x=6 \cos x\)

Responder

\(\sin^{-1}\left ( \dfrac{3}{5} \right ), \dfrac{\pi }{2}, \pi -\sin^{-1}\left ( \dfrac{3}{5} \right ), \dfrac{3\pi }{2}\)

58)\(-3\sin t=15\cos t \sin t\)

59)\(4\cos^2x - 4 = 15\cos x\)

Responder

\(\cos^{-1}\left ( -\dfrac{1}{4} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{1}{4} \right )\)

60)\(8\sin^2 x+6\sin x+1=0\)

61)\(8\cos^2 \theta =3-2\cos \theta\)

Responder

\(\dfrac{\pi }{3}, \cos^{-1}\left ( -\dfrac{3}{4} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{3}{4} \right ), \dfrac{5\pi }{3}\)

62)\(6\cos^2 x+7\sin x-8=0\)

63)\(12\sin^2 t+\cos t-6=0\)

Responder

\(\cos^{-1}\left ( \dfrac{3}{4} \right ), \cos^{-1}\left ( -\dfrac{2}{3} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{2}{3} \right ), 2\pi -\cos^{-1}\left ( \dfrac{3}{4} \right )\)

64)\(\tan x=3\sin x\)

65)\(\cos^3 t=\cos t\)

Responder

\(0, \dfrac{\pi }{2}, \pi , \dfrac{3\pi }{2}\)

Gráfica

Para los ejercicios 66-72, determinar algebraicamente todas las soluciones de la ecuación trigonométrica exactamente, luego verificar los resultados graficando la ecuación y encontrando los ceros.

66)\(6\sin^2 x-5\sin x+1=0\)

67)\(8\cos^2 x-2\cos x-1=0\)

Responder

\(\dfrac{\pi }{3}, \cos^{-1}\left ( -\dfrac{1}{4} \right ), 2\pi -\cos^{-1}\left ( -\dfrac{1}{4} \right ), \dfrac{5\pi }{3}\)

68)\(100\tan^2x+20\tan x-3=0\)

69)\(2\cos^2 x-\cos x+15=0\)

Responder

No hay soluciones.

70)\(20\sin^2 x-27\sin x+7=0\)

71)\(2\tan^2 x+7\tan x+6=0\)

Responder

\(\pi +\tan^{-1}(-2), \pi +\tan^{-1}\left (-\dfrac{3}{2}\right ), 2\pi +\tan^{-1}(-2), 2\pi +\tan^{-1}\left (-\dfrac{3}{2} \right )\)

72)\(130\tan^2 x+69\tan x-130=0\)

Tecnología

Para los ejercicios 73-76, utilice una calculadora para encontrar todas las soluciones a cuatro decimales.

73)\(\sin x=0.27\)

Responder

\(2\pi k+0.2734, 2\pi k+2.8682\)

74)\(\sin x=-0.55\)

75)\(\tan x=-0.34\)

Responder

\(\pi k-0.3277\)

76)\(\cos x=0.71\)

77)\(\tan^2 x+3\tan x-3=0\)

Responder

\(0.6694,1.8287,3.8110,4.9703\)

78)\(6\tan^2 x+13\tan x=-6\)

79)\(\tan^2 x-\sec x=1\)

Responder

\(1.0472,3.1416,5.2360\)

80)\(\sin^2 x-2\cos^2 x=0\)

81)\(2\tan^2 x+9\tan x-6=0\)

Responder

\(0.5326,1.7648,3.6742,4.9064\)

82)\(4\sin^2 x+\sin(2x)\sec x-3=0\)

Extensiones

Para los ejercicios 83-92, encuentra todas las soluciones exactamente a las ecuaciones en el intervalo\([0,2\pi )\).

83)\(\csc^2 x-3\csc x-4=0\)

Responder

\(\sin^{-1}\left ( \dfrac{1}{4} \right ), \pi -\sin^{-1}\left ( \dfrac{1}{4} \right ), \dfrac{3\pi }{2}\)

84)\(\sin^2 x-\cos^2 x-1=0\)

85)\(\sin^2 x(1-\sin^2 x)+\cos^2 x(1-\sin^2 x)=0\)

Responder

\(\dfrac{\pi }{2}, \dfrac{3\pi }{2}\)

86)\(3\sec^2 x+2+\sin^2 x-\tan^2 x+\cos^2 x=0\)

87)\(\sin^2 x-1+2\cos(2x)-\cos^2 x=1\)

Responder

No hay soluciones.

88)\(\tan^2 x-1-\sec^3 x \cos x=0\)

89)\(\dfrac{\sin (2x)}{\sec ^2 x}=0\)

Responder

\(0, \dfrac{\pi }{2}, \pi , \dfrac{3\pi }{2}\)

90)\(\dfrac{\sin (2x)}{2\csc ^2 x}=0\)

91)\(2\cos^2 x-\sin^2 x-\cos x-5=0\)

Responder

No hay soluciones.

92)\(\dfrac{1}{\sec ^2 x}+2+\sin ^2 x+4\cos ^2 x=4\)

Aplicaciones del mundo real

93) Un avión solo tiene suficiente gasolina para volar a una ciudad\(200\) millas al noreste de su ubicación actual. Si el piloto sabe que la ciudad está\(25\) millas al norte, ¿cuántos grados al norte del este debería volar el avión?

Responder

\(7.2^{\circ}\)

94) Si se coloca una rampa de carga junto a un camión, a una altura de\(4\) pies, y la rampa mide\(15\) pies de largo, ¿qué ángulo hace la rampa con el suelo?

95) Si se coloca una rampa de carga junto a un camión, a una altura de\(2\) pies, y la rampa mide\(20\) pies de largo, ¿qué ángulo hace la rampa con el suelo?

Responder

\(5.7^{\circ}\)

96) Una mujer está observando un cohete lanzado actualmente\(11\) millas de altitud. Si está parada\(4\) a kilómetros de la plataforma de lanzamiento, ¿en qué ángulo está mirando hacia arriba desde la horizontal?

97) Un astronauta se encuentra en un cohete lanzado actualmente\(15\) millas de altitud. Si un hombre está parado\(2\) a kilómetros de la plataforma de lanzamiento, ¿en qué ángulo lo mira desde horizontal? (Pista: esto se llama el ángulo de depresión.)

Responder

\(82.4^{\circ}\)

98) Una mujer está de pie a\(8\) metros de un edificio de\(10\) -metros de altura. ¿En qué ángulo está mirando hacia lo alto del edificio?

99) Un hombre está parado a\(10\) metros de un edificio de\(6\) -metros de altura. Alguien en la parte superior del edificio lo está mirando hacia abajo. ¿En qué ángulo está la persona que lo mira?

Responder

\(31.0^{\circ}\)

100) Un edificio de\(20\) -pie de altura tiene una sombra de\(55\) pies de largo. ¿Cuál es el ángulo de elevación del sol?

101) Un edificio de\(90\) -pie de altura tiene una sombra de\(2\) pies de largo. ¿Cuál es el ángulo de elevación del sol?

Responder

\(88.7^{\circ}\)

102) Un foco en el suelo\(3\) a metros de un hombre de\(2\) -metro de altura proyecta una sombra de\(6\) metro en una pared\(6\) a metros del hombre. ¿En qué ángulo está la luz?

103) Un foco de luz en el suelo\(3\) pies de una mujer de\(5\) -pie de altura proyecta una sombra de\(15\) -pie de altura en una pared a\(6\) pies de la mujer. ¿En qué ángulo está la luz?

Responder

\(59.0^{\circ}\)

Para los ejercicios 104-106, encontrar una solución a la palabra problema algebraicamente. Después usa una calculadora para verificar el resultado. Redondear la respuesta al décimo de grado más cercano.

104) Una persona hace una parada de manos con los pies tocando una pared y las manos a\(1.5\) los pies lejos de la pared. Si la persona mide\(6\) pies de altura, ¿qué ángulo hacen sus pies con la pared?

105) Una persona hace una parada de manos con los pies tocando una pared y sus manos a\(3\) los pies lejos de la pared. Si la persona mide\(5\) pies de altura, ¿qué ángulo hacen sus pies con la pared?

Responder

\(36.9^{\circ}\)

106) Al lado\(23\) de una casa se coloca una escalera de pie. Si la escalera se desliza a\(7\) pies de la casa cuando no hay suficiente tracción, ¿qué ángulo debe hacer la escalera con el suelo para evitar resbalones?

7.6: Modelado con Ecuaciones Trigonométricas

Muchos fenómenos naturales también son periódicos. Por ejemplo, las fases de la luna tienen un periodo de aproximadamente\(28\) días, y las aves saben volar hacia el sur aproximadamente a la misma hora cada año. Entonces, ¿cómo podemos modelar una ecuación para reflejar el comportamiento periódico? Primero, debemos recopilar y registrar datos. Luego encontramos una función que se asemeja a un patrón observado y alteramos la función para obtener un modelo confiable. Aquí, analizaremos más a fondo tipos específicos de comportamiento periódico y ecuaciones de modelos para adaptarse a los datos.

Verbal

1) Explicar qué tipos de fenómenos físicos se modelan mejor mediante funciones sinusoidales. ¿Cuáles son las características necesarias?

Responder

El comportamiento físico debe ser periódico, o cíclico.

2) ¿Qué información es necesaria para construir un modelo trigonométrico de la temperatura diaria? Dar ejemplos de dos conjuntos diferentes de información que permitirían modelar con una ecuación.

3) Si queremos modelar la precipitación acumulada en el transcurso de un año, ¿sería un buen modelo una función sinusoidal? ¿Por qué o por qué no?

Responder

Dado que la precipitación acumulada siempre va en aumento, una función sinusoidal no sería ideal aquí.

4) Explicar el efecto de un factor de amortiguación en las gráficas de las funciones de movimiento armónico.

Algebraico

Para los ejercicios 5-13, encontrar una posible fórmula para la función trigonométrica representada por la tabla de valores dada.

5)

\(x\)	\(y\)
\ (x\) ">\(0\)	\ (y\) ">\(−4\)
\ (x\) ">\(3\)	\ (y\) ">\(−1\)
\ (x\) ">\(6\)	\ (y\) ">\(2\)
\ (x\) ">\(9\)	\ (y\) ">\(−1\)
\ (x\) ">\(12\)	\ (y\) ">\(−4\)
\ (x\) ">\(15\)	\ (y\) ">\(−1\)
\ (x\) ">\(18\)	\ (y\) ">\(2\)

 

Responder

\(y=−3 \cos \left(\dfrac{π}{6}x \right)−1\)

6)

\(x\)	\(y\)
\ (x\) ">\(0\)	\ (y\) ">\(5\)
\ (x\) ">\(2\)	\ (y\) ">\(1\)
\ (x\) ">\(4\)	\ (y\) ">\(−3\)
\ (x\) ">\(6\)	\ (y\) ">\(1\)
\ (x\) ">\(8\)	\ (y\) ">\(5\)
\ (x\) ">\(10\)	\ (y\) ">\(1\)
\ (x\) ">\(12\)	\ (y\) ">\(−3\)

7)

\(x\)	\(y\)
\ (x\) ">\(0\)	\ (y\) ">\(2\)
\ (x\) ">\(\frac{π}{4}\)	\ (y\) ">\(7\)
\ (x\) ">\(\frac{π}{2}\)	\ (y\) ">\(2\)
\ (x\) ">\(\frac{3π}{4}\)	\ (y\) ">\(−3\)
\ (x\) ">\(π\)	\ (y\) ">\(2\)
\ (x\) ">\(\frac{5π}{4}\)	\ (y\) ">\(7\)
\ (x\) ">\(\frac{3π}{2}\)	\ (y\) ">\(2\)

Responder

\(5 \sin (2x)+2\)

8)

\(x\)	\(y\)
\ (x\) ">\(0\)	\ (y\) ">\(2\)
\ (x\) ">\(\frac{π}{4}\)	\ (y\) ">\(7\)
\ (x\) ">\(\frac{π}{2}\)	\ (y\) ">\(2\)
\ (x\) ">\(\frac{3π}{4}\)	\ (y\) ">\(−3\)
\ (x\) ">\(π\)	\ (y\) ">\(2\)
\ (x\) ">\(\frac{5π}{4}\)	\ (y\) ">\(7\)
\ (x\) ">\(\frac{3π}{2}\)	\ (y\) ">\(2\)

9)

\(x\)	\(y\)
\ (x\) ">\(0\)	\ (y\) ">\(1\)
\ (x\) ">\(1\)	\ (y\) ">\(−3\)
\ (x\) ">\(2\)	\ (y\) ">\(−7\)
\ (x\) ">\(3\)	\ (y\) ">\(−3\)
\ (x\) ">\(4\)	\ (y\) ">\(1\)
\ (x\) ">\(5\)	\ (y\) ">\(−3\)
\ (x\) ">\(6\)	\ (y\) ">\(−7\)

Responder

\(4\cos \left(\dfrac{xπ}{2} \right)−3\)

10)

\(x\)	\(y\)
\ (x\) ">\(0\)	\ (y\) ">\(−2\)
\ (x\) ">\(1\)	\ (y\) ">\(4\)
\ (x\) ">\(2\)	\ (y\) ">\(10\)
\ (x\) ">\(3\)	\ (y\) ">\(4\)
\ (x\) ">\(4\)	\ (y\) ">\(−2\)
\ (x\) ">\(5\)	\ (y\) ">\(4\)
\ (x\) ">\(6\)	\ (y\) ">\(10\)

11)

\(x\)	\(y\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(0\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(5\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (243, 251, 255); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:rgb (204, 204); border-bottom--style: discontinua; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">\(1\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (243, 251, 255); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:rgb (204, 204); border-bottom--style: discontinua; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">\(-3\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(2\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(5\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom--style: discontinua; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">\(3\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom--style: discontinua; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">\(13\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(4\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(5\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom--style: discontinua; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">\(5\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom--style: discontinua; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">\(-3\)
\ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-ancho:1; border-izquierda-color:rgb (204, 204); border-izquierda-estilo:discontinua; border-izquierda-ancho:1px; border-derecho-color:rgb (204, 204); border-derecho-estilo:dashed; border-derecha-ancho:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(6\)	\ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-ancho:1; border-izquierda-color:rgb (204, 204); border-izquierda-estilo:discontinua; border-izquierda-ancho:1px; border-derecho-color:rgb (204, 204); border-derecho-estilo:dashed; border-derecha-ancho:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">\(5\)

Responder

\(5−8 \sin \left(\dfrac{xπ}{2} \right)\)

12)

\(x\)	\(y\)
\ (x\) ">\(−3\)	\ (y\) ">\(−1−\sqrt{2}\)
\ (x\) ">\(−2\)	\ (y\) ">\(−1\)
\ (x\) ">\(−1\)	\ (y\) ">\(1−\sqrt{2}\)
\ (x\) ">\(0\)	\ (y\) ">\(0\)
\ (x\) ">\(1\)	\ (y\) ">\(\sqrt{2}−1\)
\ (x\) ">\(2\)	\ (y\) ">\(1\)
\ (x\) ">\(3\)	\ (y\) ">\(\sqrt{2}+1\)

13)

\(x\)	\(y\)
\ (x\) ">\(−1\)	\ (y\) ">\(\sqrt{3}−2\)
\ (x\) ">\(0\)	\ (y\) ">\(0\)
\ (x\) ">\(1\)	\ (y\) ">\(2−\sqrt{3}\)
\ (x\) ">\(2\)	\ (y\) ">\(\frac{\sqrt{3}}{3}\)
\ (x\) ">\(3\)	\ (y\) ">\(1\)
\ (x\) ">\(4\)	\ (y\) ">\(\sqrt{3}\)
\ (x\) ">\(5\)	\ (y\) ">\(2+\sqrt{3}\)

Responder

\(\tan \left(\dfrac{xπ}{12} \right)\)

Gráfica

Para los ejercicios 14-16, graficar la función dada, y luego encontrar un posible proceso físico que la ecuación pudiera modelar.

14)\(f(x)=−30 \cos \left(\dfrac{xπ}{6} \right)−20 \cos ^2 \left(\dfrac{xπ}{6} \right)+80 \; [0,12]\)

15)\(f(x)=−18 \cos \left(\dfrac{xπ}{12} \right)−5 \sin \left(\dfrac{xπ}{12} \right)+100\) en el intervalo\([0,24]\)

Responder

Las respuestas variarán. Respuesta de muestra: Esta función podría modelar los cambios de temperatura en el transcurso de un día muy caluroso en Phoenix, Arizona.

16)\(f(x)=10−\sin \left(\dfrac{xπ}{6} \right)+24 \tan \left(\dfrac{xπ}{240} \right)\) en el intervalo\([0,80]\)

Tecnología

Para el ejercicio 17, construya un comportamiento de modelado de funciones y use una calculadora para encontrar los resultados deseados.

17) La precipitación promedio anual de una ciudad es actualmente\(20\) pulgadas y varía estacionalmente por\(5\) pulgadas. Debido a circunstancias imprevistas, las precipitaciones parecen estar disminuyendo\(15\%\) cada año. ¿Cuántos años a partir de ahora esperaríamos que las precipitaciones inicialmente alcanzaran\(0\) pulgadas? Tenga en cuenta que el modelo no es válido una vez que predice precipitaciones negativas, así que elija el primer punto en el que vaya por debajo\(0\).

Responder

\(9\)años a partir de ahora

Aplicaciones del mundo real

Para los ejercicios 18-29, construir una función sinusoidal con la información proporcionada, y luego resolver la ecuación para los valores solicitados.

18) Las temperaturas exteriores en el transcurso de un día se pueden modelar como una función sinusoidal. Supongamos que la temperatura alta de\(105°F\) ocurre a las 5PM y la temperatura promedio para el día es\(85°F\). Encuentra la temperatura, al grado más cercano, a las 9AM.

19) Las temperaturas exteriores en el transcurso de un día se pueden modelar como una función sinusoidal. Supongamos que la temperatura alta de\(84°F\) ocurre a las 6PM y la temperatura promedio para el día es\(70°F.\) Encontrar la temperatura, al grado más cercano, a las 7AM.

Responder

\(56 °F\)

20) Las temperaturas exteriores en el transcurso de un día se pueden modelar como una función sinusoidal. Supongamos que la temperatura varía entre\(47°F\) y\(63°F\) durante el día y la temperatura media diaria ocurre primero a las 10 AM. ¿Cuántas horas después de la medianoche alcanza primero la temperatura\(51°F\)?

21) Las temperaturas exteriores en el transcurso de un día se pueden modelar como una función sinusoidal. Supongamos que la temperatura varía entre\(64°F\) y\(86°F\) durante el día y la temperatura media diaria ocurre primero a las 12 AM. ¿Cuántas horas después de la medianoche alcanza primero la temperatura\(70°F\)?

Responder

\(1.8024\)horas

22) Una noria es de\(20\) metros de diámetro y abordada desde una plataforma que se encuentra\(2\) a metros sobre el suelo. La posición de las seis en punto en la noria está nivelada con la plataforma de carga. La rueda completa la revolución\(1\) completa en\(6\) minutos. ¿Cuánto del viaje, en minutos y segundos, se gasta\(13\) a más de metros sobre el suelo?

23) Una noria es de\(45\) metros de diámetro y abordada desde una plataforma que se encuentra\(1\) metros sobre el suelo. La posición de las seis en punto en la noria está nivelada con la plataforma de carga. La rueda completa la revolución\(1\) completa en\(10\) minutos. ¿Cuántos minutos del viaje se gastan\(27\) a más de metros sobre el suelo? Redondear al segundo más cercano.

Responder

\(4:30\)

24) La zona de hielo marino alrededor del Polo Norte fluctúa entre aproximadamente un\(6\) millón de kilómetros cuadrados el 1 de septiembre a\(14\) millones de kilómetros cuadrados el 1 de marzo. Asumiendo una fluctuación sinusoidal, ¿cuándo hay menos de 9 millones de kilómetros cuadrados de hielo marino? Da tu respuesta como un rango de fechas, al día más cercano.

25) La zona de hielo marino alrededor del Polo Sur fluctúa entre aproximadamente un\(18\) millón de kilómetros cuadrados en septiembre y\(3\) un millón de kilómetros cuadrados en marzo. Asumiendo una fluctuación sinusoidal, ¿cuándo hay más de 15 millones de kilómetros cuadrados de hielo marino? Da tu respuesta como un rango de fechas, al día más cercano.

Contestar

Del 8 de julio al 23 de octubre

26) Durante una temporada\(90\) monzónica de un día, las precipitaciones diarias pueden modelarse mediante funciones sinusoidales. Si la lluvia fluctúa entre un mínimo de\(2\) pulgadas en el día\(10\) y\(12\) pulgadas en el día\(55\), ¿durante qué periodo la precipitación diaria es superior a\(10\) pulgadas?

27) Durante una temporada\(90\) monzónica de un día, las precipitaciones diarias pueden modelarse mediante funciones sinusoidales. Se registró un mínimo de\(4\) pulgadas de lluvia el día\(30\), y en general la precipitación promedio diaria fue de\(8\) pulgadas. ¿Durante qué periodo la precipitación diaria fue inferior a\(5\) pulgadas?

Contestar

De día\(19\) a día\(40\)

28) En cierta región, la precipitación mensual alcanza su punto máximo en\(8\) pulgadas el 1 de junio y cae a un mínimo de\(1\) pulgada el 1 de diciembre. Identificar los períodos en los que la región se encuentra en condiciones de inundación (mayores a\(7\) pulgadas) y condiciones de sequía (menos de\(2\) pulgadas). Da tu respuesta en términos del día más cercano.

29) En cierta región, la precipitación mensual alcanza su punto máximo en\(24\) pulgadas en septiembre y cae a un mínimo de\(4\) pulgadas en marzo. Identificar los períodos en los que la región se encuentra en condiciones de inundación (mayores a\(22\) pulgadas) y condiciones de sequía (menos de\(5\) pulgadas). Da tu respuesta en términos del día más cercano.

Contestar

Inundaciones: del 24 de julio al 7 de octubre. Sequías: del 4 de febrero al 27 de marzo

Para los ejercicios 30-32, encuentre la amplitud, el periodo y la frecuencia de la función dada.

30) El desplazamiento\(h(t)\) en centímetros de una masa suspendida por un resorte es modelado por la función\(h(t)=8 \sin (6πt),\) donde\(t\) se mide en segundos. Encuentra la amplitud, periodo y frecuencia de este desplazamiento.

31) El desplazamiento\(h(t)\) en centímetros de una masa suspendida por un resorte es modelado por la función\(h(t)=11 \sin (12πt),\) donde\(t\) se mide en segundos. Encuentra la amplitud, periodo y frecuencia de este desplazamiento.

Contestar

Amplitud:\(11\), periodo:\(\dfrac{1}{6}\), frecuencia:\(6\) Hz

32) El desplazamiento\(h(t)\) en centímetros de una masa suspendida por un resorte es modelado por la función\(h(t)=4 \cos \left(\dfrac{π}{2}t \right)\), donde\(t\) se mide en segundos. Encuentra la amplitud, periodo y frecuencia de este desplazamiento.

Para el ejercicio 33, construir una ecuación que modele el comportamiento descrito.

33) El desplazamiento\(h(t)\), en centímetros, de una masa suspendida por un resorte es modelado por la función\(h(t)=−5 \cos (60πt)\), donde\(t\) se mide en segundos. Encuentra la amplitud, periodo y frecuencia de este desplazamiento.

Contestar

Amplitud:\(5\), periodo:\(\dfrac{1}{30}\), frecuencia:\(30\) Hz

Para los ejercicios 34-41, construir una ecuación que modele el comportamiento descrito.

34) Una población de ciervos oscila\(19\) por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en\(800\) venados y aumenta\(160\) cada año. Encontrar una función que modele la población,\(P\), en términos de meses desde enero,\(t\).

35) Una población de conejos oscila\(15\) por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en\(650\) conejos y aumenta\(110\) cada año. Encontrar una función que modele la población,\(P\), en términos de meses desde enero,\(t\).

Contestar

\(P(t)=−15 \cos \left(\dfrac{π}{6}t \right)+650+\dfrac{55}{6}t\)

36) Una población de crata almizclera oscila\(33\) por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en las\(900\) cratas almizcleras y aumenta\(7\%\) cada mes. Encontrar una función que modele la población,\(P\), en términos de meses desde enero,\(t\).

37) Una población de peces oscila\(40\) por encima y por debajo del promedio durante el año, alcanzando el valor más bajo en enero. La población promedio comienza en\(800\) peces y aumenta\(4\%\) cada mes. Encontrar una función que modele la población,\(P\), en términos de meses desde enero,\(t\).

Contestar

\(P(t)=−40 \cos \left(\dfrac{π}{6}t \right)+800(1.04)^t\)

38) Un resorte unido al techo se tira\(10\) cm hacia abajo del equilibrio y se libera. La amplitud disminuye por\(15\%\) cada segundo. El resorte oscila\(18\) veces cada segundo. Encuentra una función que modele la distancia,\(D\), el extremo del resorte es del equilibrio en términos de segundos,\(t\), desde que se liberó el resorte.

39) Un resorte unido al techo se tira\(7\) cm hacia abajo del equilibrio y se libera. La amplitud disminuye por\(11\%\) cada segundo. El resorte oscila\(20\) veces cada segundo. Encuentra una función que modele la distancia\(D\),, el extremo del resorte es del equilibrio en términos de segundos,\(t,\) ya que el resorte fue liberado.

Contestar

\(D(t)=7(0.89)^t \cos (40πt)\)

40) Un resorte unido al techo se tira\(17\) cm hacia abajo del equilibrio y se libera. Después de\(3\) segundos, la amplitud ha disminuido a\(13\) cm. El resorte oscila\(14\) veces cada segundo. Encuentra una función que modele la distancia,\(D,\) el extremo del resorte es del equilibrio en términos de segundos,\(t\), ya que el resorte fue liberado.

41) Un resorte unido al techo se tira\(19\) cm hacia abajo del equilibrio y se libera. Después de\(4\) segundos, la amplitud ha disminuido a\(14\) cm. El resorte oscila\(13\) veces cada segundo. Encuentra una función que modele la distancia,\(D\), el extremo del resorte es del equilibrio en términos de segundos,\(t\), desde que se liberó el resorte.

Contestar

\(D(t)=19(0.9265)^t \cos (26πt)\)

Para los ejercicios 42-47, crear una función modelando el comportamiento descrito. Después, calcula el resultado deseado usando una calculadora.

42) Cierto lago tiene actualmente una población promedio de truchas de\(20,000\). La población oscila naturalmente por encima y por debajo del promedio\(2,000\) cada año. Este año, el lago se abrió a los pescadores. Si los pescadores\(3,000\) pescan cada año, ¿cuánto tiempo tardará en que el lago no tenga más truchas?

43) Las poblaciones de peces blancos se encuentran actualmente\(500\) en un lago. La población oscila naturalmente por arriba y por debajo\(25\) cada año. Si los humanos pescan demasiado, tomando\(4\%\) de la población cada año, ¿en cuántos años el lago primero tendrá menos que el\(200\) pescado blanco?

Contestar

\(20.1\)años

44) Un resorte unido a un techo se tira hacia abajo\(11\) cm del equilibrio y se libera. Después de\(2\) segundos, la amplitud ha disminuido a\(6\) cm. El resorte oscila\(8\) veces cada segundo. Encuentra cuando la primavera viene por primera vez entre\(−0.1\) y\(0.1\) cm, efectivamente en reposo.

45) Un resorte unido a un techo se tira hacia abajo\(21\) cm del equilibrio y se libera. Después de\(6\) segundos, la amplitud ha disminuido a\(4\) cm. El resorte oscila\(20\) veces cada segundo. Encuentra cuando la primavera viene por primera vez entre\(−0.1\) y\(0.1\) cm, efectivamente en reposo.

Contestar

\(17.8\)segundos

46) Dos muelles se tiran hacia abajo del techo y se liberan al mismo tiempo. El primer resorte, que oscila\(8\) veces por segundo, fue inicialmente tirado hacia abajo\(32\) cm del equilibrio, y la amplitud disminuye en\(50\%\) cada segundo. El segundo resorte,\(18\) tiempos oscilantes por segundo, fue inicialmente tirado hacia abajo\(15\) cm del equilibrio y después de\(4\) segundos tiene una amplitud de\(2\) cm. ¿Qué primavera viene a descansar primero, y a qué hora? Considera el “descanso” como una amplitud menor a\(0.1\) cm.

47) Dos muelles son tirados hacia abajo del techo y liberados al mismo tiempo. El primer resorte, que oscila\(14\) veces por segundo, fue inicialmente tirado hacia abajo\(2\) cm del equilibrio, y la amplitud disminuye en\(8\%\) cada segundo. El segundo resorte,\(22\) tiempos oscilantes por segundo, fue inicialmente tirado hacia abajo\(10\) cm del equilibrio y después de\(3\) segundos tiene una amplitud de\(2\) cm. ¿Qué primavera viene a descansar primero, y a qué hora? Considera el “descanso” como una amplitud menor a\(0.1\) cm.

Contestar

La primavera 2 viene a descansar primero después de\(8.0\) segundos.

Extensiones

48) Un avión vuela\(1\) hora a\(150\) mph al\(22^∘\) este del norte, luego continúa volando durante\(1.5\) horas a\(120\) mph, esta vez a una dirección del\(112^∘\) este del norte. Encuentra la distancia total desde el punto de partida y el ángulo directo volado al norte del este.

49) Un avión vuela\(2\) horas a\(200\) mph a una dirección de\(60^∘\), luego continúa volando durante\(1.5\) horas a la misma velocidad, esta vez a un rumbo de\(150^∘\). Encuentra la distancia desde el punto de partida y el rumbo desde el punto de partida. (Pista: el rodamiento se mide en sentido antihorario desde el norte).

Contestar

\(500\)millas, a\(90^∘\)

Para los ejercicios 50-52, encuentra una función de la forma\(y=ab^x \sin \left(\dfrac{π}{2}x \right)+c\) que se ajuste a los datos dados.

50)

\(x\)	0	1	2	3
\(y\)	6	29	96	379

51)

\(x\)	0	1	2	3
\(y\)	6	34	150	746

Contestar

\(y=6(5)^x+4 \sin \left(\dfrac{π}{2}x \right)\)

52)

\(x\)	0	1	2	3
\(y\)	4	0	16	-40

Para los ejercicios 53-54, encuentra una función de la forma\(y=ab^x \cos \left(\dfrac{π}{2}x \right)+c\) que se ajuste a los datos dados.

53)

\(x\)	0	1	2	3
\(y\)	11	3	1	3

Contestar

\(y=8\left(\dfrac{1}{2} \right)^x \cos \left(\dfrac{π}{2}x \right)+3\)

54)

\(x\)	0	1	2	3
\(y\)	4	1	−11	1

Colaboradores y Atribuciones

• Template:OpenStaxPreCalc