8.R: Otras aplicaciones de la trigonometría (Revisión)

Última actualización
Guardar como PDF

Page ID: 121196

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

8.1: Triángulos no rectos: Ley de los senos

Para los ejercicios 1-5 suponemos que$\alpha $ es lado opuesto$a$,$\beta $ es lado opuesto$b$, y$\gamma $ es lado opuesto$c$. Resuelve cada triángulo, si es posible. Redondea cada respuesta a la décima más cercana.

1)$\beta =50^{\circ}, a=105, b=45$

Responder: No es posible

2)$\alpha =43.1^{\circ}, a=184.2, b=242.8$

3) Resuelve el triángulo.

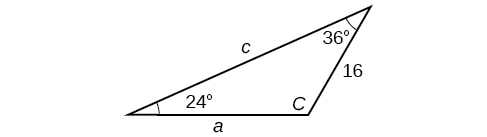
$Ex 8R 8.1.3.png$

Responder: $C=120^{\circ}, a=23.1, c=34.1$

4) Encuentra el área del triángulo.

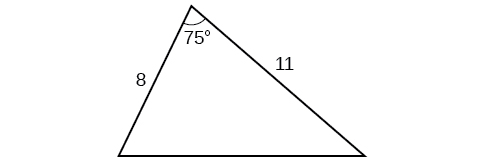
5) Un piloto sobrevuela una Autopista recta. Determina los ángulos de depresión a postes de dos millas a$2.1$ km de distancia para estar$25^{\circ}$ y$49^{\circ}$, como se muestra en la siguiente figura. Encuentra la distancia del plano desde el punto$A$ y la elevación del plano.

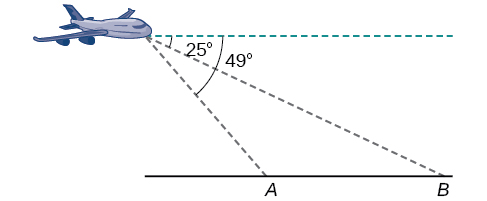
$Ex 8R 8.1.5.png$

Responder: distancia del avión desde el punto$A:2.2$ km, elevación del plano:$1.6$ km

8.2: Triángulos no rectos - Ley de Cosinos

1) Resolver el triángulo, redondeando a la décima más cercana, asumiendo$\alpha $ es lado opuesto$a$,$\beta $ es lado opuesto$b$, y$\gamma $ s lado opuesto$c: a=4, b=6,c=8$.

2) Resuelve el triángulo en la Figura siguiente, redondeando a la décima más cercana.

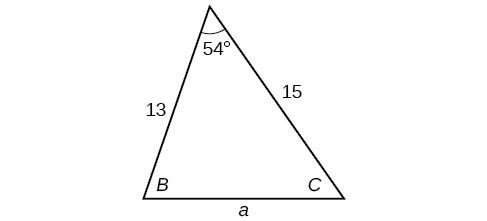
$Ex 8R 8.2.2.png$

Responder: $B=71.0^{\circ},C=55.0^{\circ},a=12.8$

3) Encontrar el área de un triángulo con lados de longitud$8.3$,$6.6$, y$9.1$.

4) Para encontrar la distancia entre dos ciudades, un satélite calcula las distancias y el ángulo que se muestran en la Figura a continuación (no a escala). Encuentra la distancia entre las ciudades. Respuestas redondas a la décima más cercana.

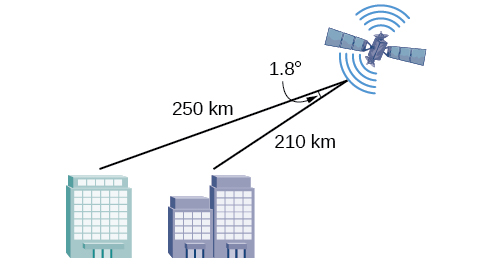
$Ex 8R 8.2.4.png$

Responder: $40.6$km

8.3: Coordenadas polares

1) Trazar el punto con coordenadas polares$\left ( 3,\dfrac{\pi }{6} \right )$.

2) Trazar el punto con coordenadas polares$\left ( 5,\dfrac{-2\pi }{3} \right )$.

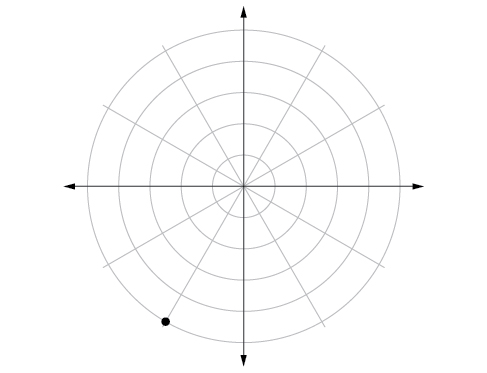
Responder: $Ex 8R 8.3.2.png$

3) Convertir$\left ( 6,\dfrac{-3\pi }{4} \right )$ a coordenadas rectangulares.

4) Convertir$\left ( -2,\dfrac{3\pi }{2} \right )$ a coordenadas rectangulares.

Responder: $(0,2)$

5) Convertir$(7,-2)$ a coordenadas polares.

6) Convertir$(-9,-4)$ a coordenadas polares.

Responder: $(9.8489,203.96^{\circ})$

Para los ejercicios 7-9, convertir la ecuación cartesiana dada en una ecuación polar.

7)$x=-2$

8)$x^2+y^2=64$

Responder: $r=8$

9)$x^2+y^2=-2y$

Para los ejercicios 10-11, convertir la ecuación polar dada en una ecuación cartesiana.

10)$r=7\cos \theta$

Responder: $x^2+y^2=7x$

11)$r=\dfrac{-2}{4\cos \theta +\sin \theta }$

Para los ejercicios 12-13, convertir a forma rectangular y graficar.

12)$\theta =\dfrac{3\pi }{4}$

Responder

$y=-x$

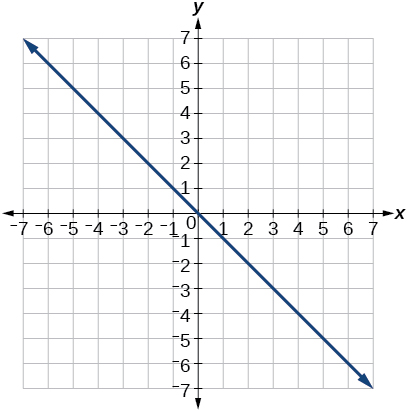
$Ex 8R 8.3.12.png$

13)$r=5\sec \theta$

8.4: Coordenadas polares - Gráficas

Para los ejercicios 1-5, pruebe cada ecuación para determinar la simetría.

1)$r=4+4\sin \theta$

Responder: simétrico con respecto a la línea$\theta =\dfrac{\pi }{2}$

2)$r=7$

3) Esbozar una gráfica de la ecuación polar$r=1-5\sin \theta$. Etiquete las intercepciones del eje.

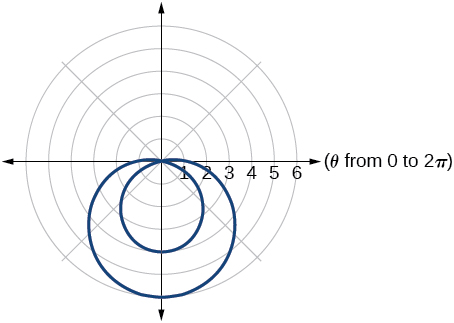
Responder: $Ex 8R 8.4.3.png$

4) Esbozar una gráfica de la ecuación polar$r=5\sin (7\theta )$.

5) Esbozar una gráfica de la ecuación polar$r=3-3\cos \theta$

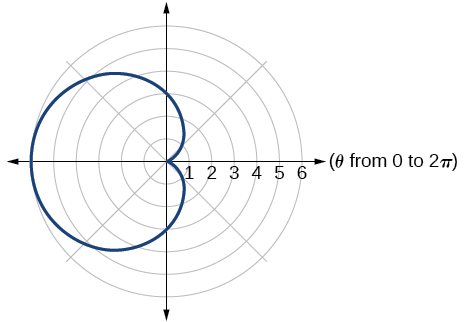
Responder: $Ex 8R 8.4.5.png$

8.5: Forma polar de números complejos

Para los ejercicios 1-2, encuentra el valor absoluto de cada número complejo.

1)$-2+6i$

2)$4-3i$

Responder: $5$

Escribe el número complejo en forma polar.

3)$5+9i$

4)$\dfrac{1}{2}-\dfrac{\sqrt{3}}{2}i$

Responder: $\mathrm{cis}\left (-\dfrac{\pi }{3} \right )$

Para los ejercicios 5-6, convierte el número complejo de forma polar a rectangular.

5)$z=5\mathrm{cis}\left (\dfrac{5\pi }{6} \right )$

6)$z=3\mathrm{cis}(40^{\circ})$

Responder: $2.3+1.9i$

Para los ejercicios 7-8, encuentra el producto$z_1 z_2$ en forma polar.

7)$\begin{align*} z_1 &= 2\mathrm{cis}(89^{\circ})\\ z_2 &= 5\mathrm{cis}(23^{\circ}) \end{align*}$

8)$\begin{align*} z_1 &= 10\mathrm{cis}\left ( \dfrac{\pi }{6} \right )\\ z_2 &= 6\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}$

Responder: $60\mathrm{cis}\left ( \dfrac{\pi }{2} \right )$

Para los ejercicios 9-10, encuentra el cociente$\dfrac{z_1}{z_2}$ en forma polar.

9)$\begin{align*} z_1 &= 12\mathrm{cis}(55^{\circ})\\ z_2 &= 3\mathrm{cis}(18^{\circ}) \end{align*}$

10)$\begin{align*} z_1 &= 27\mathrm{cis}\left ( \dfrac{5\pi }{3} \right )\\ z_2 &= 9\mathrm{cis}\left ( \dfrac{\pi }{3} \right ) \end{align*}$

Responder: $3\mathrm{cis}\left ( \dfrac{4\pi }{3} \right )$

Para los ejercicios 11-12, encuentra los poderes de cada número complejo en forma polar.

11) Encuentra$z^4$ cuándo$z=2\mathrm{cis}(70^{\circ})$

12) Encuentra$z^2$ cuándo$z=5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )$

Responder: $25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )$

Para los ejercicios 13-14, evalúe cada raíz.

13) Evaluar la raíz cubo de$z$ cuándo$z=64\mathrm{cis}(210^{\circ})$.

14) Evaluar la raíz cuadrada de$z$ cuándo$z=25\mathrm{cis}\left ( \dfrac{3\pi }{2} \right )$.

Responder: $5\mathrm{cis}\left ( \dfrac{3\pi }{4} \right )$,$5\mathrm{cis}\left ( \dfrac{7\pi }{4} \right )$

Para los ejercicios 15-16, trazar el número complejo en el plano complejo.

15)$6-2i$

16)$-1+3i$

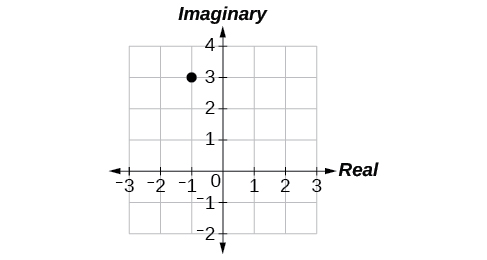
Responder: $Ex 8R 8.5.16.png$

8.6: Ecuaciones paramétricas

1)$\begin{cases} & x(t)= 3t-1\\ & y(t)= \sqrt{t} \end{cases}$

2)$\begin{cases} & x(t)= -\cos t\\ & y(t)= 2\sin ^2t \end{cases}$

Responder: $x^2+\dfrac{1}{2}y=1$

3) Parametrizar (escribir una ecuación paramétrica para) cada ecuación cartesiana usando$x(t)=a\cos t$ y$y(t)=b\sin t$ para$\dfrac{x^2}{25}+\dfrac{y^2}{16}=1$.

4) Parameterizar la línea de$(-2,3)$ a para$(4,7)$ que la línea esté$(-2,3)$ en$t=0$ y$(4,7)$ en$t=1$.

Responder: $\begin{cases} & x(t)= -2+6t\\ & y(t)= 3+4t \end{cases}$

8.7: Ecuaciones Paramétricas - Gráficas

Para los ejercicios 1-, haga una tabla de valores para cada conjunto de ecuaciones paramétricas, grafique las ecuaciones e incluya una orientación; luego escriba la ecuación cartesiana.

1)$\begin{cases} & x(t)= 3t^2\\ & y(t)= 2t-1 \end{cases}$

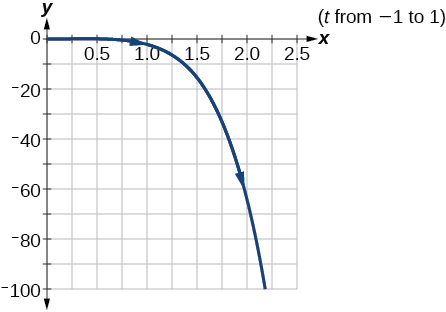
2)$\begin{cases} & x(t)= e^t\\ & y(t)= -2e^{5t} \end{cases}$

Responder

$y=-2x^5$

$Ex 8R 8.7.2.png$

3)$\begin{cases} & x(t)= 3\cos t\\ & y(t)= 2\sin t \end{cases}$

4) Se lanza una pelota con una velocidad inicial de$80$ pies por segundo en un ángulo con respecto$40^{\circ}$ a la horizontal. El balón se libera a una altura de$4$ pies sobre el suelo.

¿Dónde está el balón después de$3$ segundos?
¿Cuánto dura la pelota en el aire?

Responder

$\begin{cases} & x(t)= (80\cos (40^{\circ}))t\\ & y(t)= -16t^2+(80\sin (40^{\circ}))t+4 \end{cases}$
El balón mide 14 pies de altura y 184 pies de donde fue lanzado.
$3.3$segundos

8.8: Vectores

Para los ejercicios 1-2, determinar si los dos vectores,$\vecs u$ y$\vecs v$, son iguales, donde$\vecs u$ tiene un punto inicial$P_1$ y un punto terminal$P_2$, y$\vecs v$ tiene un punto inicial$P_3$ y un punto terminal$P_4$.

1)$P_1=(-1,4), P_2=(3,1), P_3=(5,5), P_4=(9,2)$

2)$P_1=(6,11), P_2=(-2,8), P_3=(0,-1), P_4=(-8,2)$

Responder: no es igual

Para los ejercicios 3-4, use los vectores$\vecs u=2\hat{\mathbf{i}}-\hat{\mathbf{j}}$,$\vecs v=4\hat{\mathbf{i}}-3\hat{\mathbf{j}}$, y$\vecs w=-2\hat{\mathbf{i}}+5\hat{\mathbf{j}}$ para evaluar la expresión.

3)$ \vecs u-\vecs v $

4)$ 2\vecs v-\vecs u+\vecs w $

Responder: $4\hat{\mathbf{i}}$

Para los ejercicios 5-6, encuentra un vector unitario en la misma dirección que el vector dado.

5)$\vecs a=8\hat{\mathbf{i}}-6\hat{\mathbf{j}}$

6)$\vecs b=-3\hat{\mathbf{i}}-\hat{\mathbf{j}}$

Responder: $-\dfrac{3\sqrt{10}}{10}\hat{\mathbf{i}}-\dfrac{\sqrt{10}}{10}\hat{\mathbf{j}}$

Para los ejercicios 7-11, calcule$\vecs u\cdot \vecs v$

7)$\vecs u=-2\hat{\mathbf{i}}+\hat{\mathbf{j}}$ y$\vecs v=3\hat{\mathbf{i}}+7\hat{\mathbf{j}}$

8)$\vecs u=\hat{\mathbf{i}}+4\hat{\mathbf{j}}$ y$\vecs v=4\hat{\mathbf{i}}+3\hat{\mathbf{j}}$

Responder: $16$

9) Dado$\vecs v=\left \langle -3,4 \right \rangle$ sorteo$\vecs v$,$2\vecs v$, y$\dfrac{1}{2}\vecs v$.

10) Dados los vectores que se muestran en la Figura a continuación, boceto$\vecs u + \vecs v$,$\vecs u − \vecs v$ y$3\vecs v$.

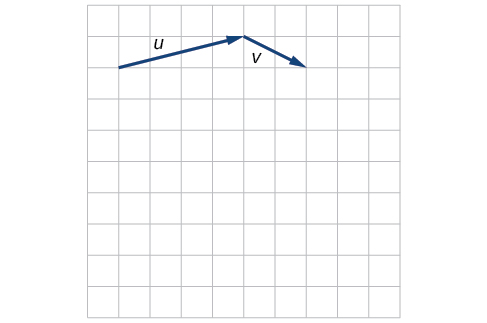
$Ex 8R 8.8.10.png$

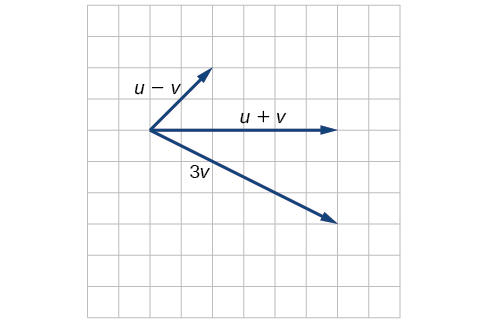
Responder: $Ex 8R 8.8.10 sol.png$

11) Dado punto inicial$P_1=(3,2)$ y punto terminal$P_2=(-5,-1)$, escribir el vector$\vecs v$ en términos de$\hat{\mathbf{i}}$ y$\hat{\mathbf{j}}$. Dibuja los puntos y el vector en la gráfica.

Prueba de práctica

1) Supongamos que$\alpha $ es lado opuesto$a$,$\beta $ es lado opuesto$b$, y$\gamma $ es lado opuesto$c$. Resuelve el triángulo, si es posible, y redondea cada respuesta a la décima más cercana, dada$\beta =68^{\circ},b=21,c=16$.

Responder: $\alpha =67.1^{\circ}, \gamma =44.9^{\circ}, a=20.9$

2) Encuentra el área del triángulo en la Figura a continuación. Redondea cada respuesta a la décima más cercana.

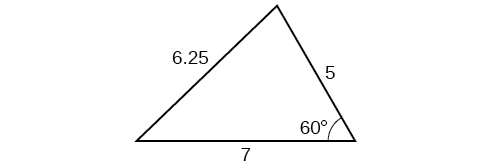
$Ex 8RP.2.png$

3) Un piloto vuela en camino recto durante$2$ horas. Luego hace una corrección de rumbo, dirigiéndose$15^{\circ}$ a la derecha de su curso original, y vuela$1$ hora en la nueva dirección. Si mantiene una velocidad constante de$575$ millas por hora, ¿a qué distancia está de su posición inicial?

Responder: $1712$millas

4) Convertir$(2,2)$ a coordenadas polares, y luego trazar el punto.

5) Convertir$\left ( 2,\dfrac{\pi }{3} \right )$ a coordenadas rectangulares.

Responder: $(1,\sqrt{3})$

6) Convertir la ecuación polar a una ecuación cartesiana:$x^2+y^2=5y$.

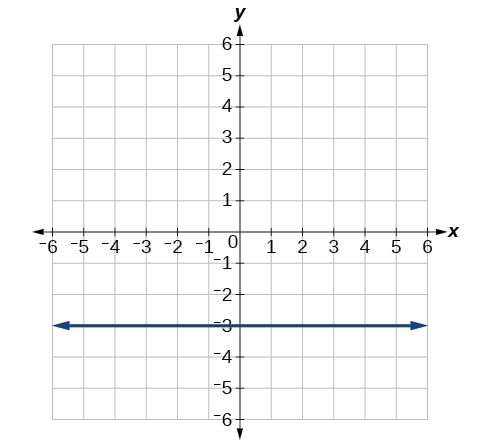
7) Convertir a forma rectangular y gráfica:$r=-3\csc θ$.

Responder

$y=-3$

$Ex 8rp.7.png$

8) Probar la ecuación para simetría:$r=-4\sin(2\theta )$.

9) Gráfica$r=3+3\cos \theta$.

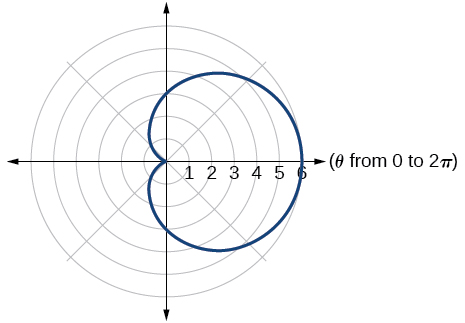
Responder: $Ex 8rp.9.png$

10) Gráfica$r=3-5\sin \theta$.

11) Encuentra el valor absoluto del número complejo$5-9i$.

Responder: $\sqrt{106}$

12) Escribe el número complejo en forma polar:$4+i$.

13) Convertir el número complejo de forma polar a rectangular:$z=5\mathrm{cis}\left ( \dfrac{2\pi }{3} \right )$

Responder: $\dfrac{-5}{2}+i\dfrac{5\sqrt{3}}{2}$

14)$z_1 z_2$

15)$\dfrac{z_1}{z_2}$

Responder: $4\mathrm{cis}(21^{\circ})$

16)$(z_2)^3$

17)$\sqrt{z_1}$

Contestar: $2\sqrt{2}\mathrm{cis}(18^{\circ}), 2\sqrt{2}\mathrm{cis}(198^{\circ})$

18) Trazar el número complejo$-5-i$ en el plano complejo.

19) Eliminar el parámetro$t$ para reescribir las siguientes ecuaciones paramétricas como una ecuación cartesiana:$\begin{cases} & x(t)= t+1\\ & y(t)= 2t^2 \end{cases}$

Contestar: $y=2(x-1)^2$

20) Parameterizar (escribir una ecuación paramétrica para) la siguiente ecuación cartesiana usando$x(t)=a\cos t$ y$y(t)=b\sin t : \dfrac{x^2}{36}+\dfrac{y^2}{100}=1$

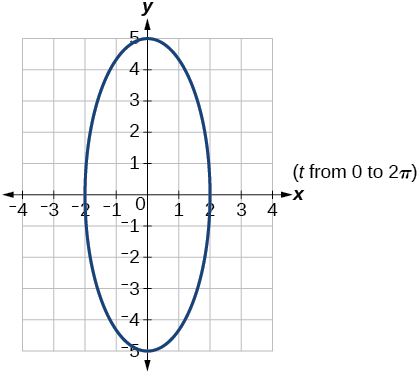
21) Grafica el conjunto de ecuaciones paramétricas y encuentra la ecuación cartesiana:$\begin{cases} & x(t)= -2\sin t\\ & y(t)= 5\cos t \end{cases}$

Contestar: $Ex 8rp.21.png$

22) Se lanza una pelota con una velocidad inicial de$95$ pies por segundo en un ángulo con respecto$52^{\circ}$ a la horizontal. El balón se libera a una altura de$3.5$ pies sobre el suelo.

¿Dónde está el balón después de$2$ segundos?
¿Cuánto dura la pelota en el aire?

Para los ejercicios 23-26, utilizar los vectores$\vecs u = \hat{\mathbf{i}} − 3\hat{\mathbf{j}}$ y$\vecs v = 2\hat{\mathbf{i}} + 3\hat{\mathbf{j}}$.

23) Encontrar$2\vecs u − 3\vecs v$.

Contestar: $-4\hat{\mathbf{i}}-15\hat{\mathbf{j}}$

24) Calcular$\vecs u\cdot \vecs v$.

25) Encuentra un vector unitario en la misma dirección que$\vecs v$.

Contestar: $\dfrac{2\sqrt{3}}{13}\hat{\mathbf{i}}+\dfrac{3\sqrt{3}}{13}\hat{\mathbf{j}}$

26) Dado vector$\vecs v$ tiene un punto inicial$P_1=(2,2)$ y un punto terminal$P_2=(-1,0)$, escribir el vector$\vecs u\cdot \vecs v$.

Colaboradores y Atribuciones

Template:OpenStaxPreCalc