8.E: Otras aplicaciones de la trigonometría (ejercicios)
- Page ID
- 121233
8.1: Triángulos no rectos: Ley de los senos
Verbal
1) Describir la altitud de un triángulo.
- Responder
-
La altitud se extiende desde cualquier vértice hasta el lado opuesto o hasta la línea que contiene el lado opuesto en\(90^{\circ}\) ángulo.
2) Comparar triángulos rectos y triángulos oblicuos.
3) ¿Cuándo se puede utilizar la Ley de los Sinos para encontrar un ángulo faltante?
- Responder
-
Cuando los valores conocidos son el lado opuesto al ángulo faltante y otro lado y su ángulo opuesto.
4) En la Ley de Sines, ¿cuál es la relación entre el ángulo en el numerador y el lado en el denominador?
5) ¿Qué tipo de triángulo resulta en un caso ambiguo?
- Responder
-
Un triángulo con dos lados dados y un ángulo no incluido.
Algebraico
Para los ejercicios 6-10, asumir\(\alpha\) es lado opuesto\(a\),\(\beta\) es lado opuesto\(b\), y\(\gamma\) es lado opuesto\(c\). Resuelve cada triángulo, si es posible. Redondea cada respuesta a la décima más cercana.
6)\(\alpha =43^{\circ}, \gamma =69^{\circ}, a=20\)
7)\(\alpha =35^{\circ}, \gamma =73^{\circ}, c=20\)
- Responder
-
\(\beta =72^{\circ}, a\approx 12.0, b\approx 19.9\)
8)\(\alpha =60^{\circ}, \beta =60^{\circ}, \gamma =60^{\circ}\)
9)\(a=4, \alpha =60^{\circ}, \beta =100^{\circ}\)
- Responder
-
\(\gamma =20^{\circ}, b\approx 4.5, c\approx 1.6\)
10)\(b=10, \beta =95^{\circ}, \gamma =30^{\circ}\)
11) Encontrar lado\(b\) cuando\(A=37^{\circ}, B=49^{\circ}, c=5\)
- Responder
-
\(b\approx 3.78\)
12) Encontrar lado\(a\) cuando\(A=132^{\circ}, C=23^{\circ}, b=10\)
13) Encontrar lado\(c\) cuando\(B=37^{\circ}, C=21^{\circ}, b=23\)
- Responder
-
\(c\approx 13.70\)
Para los ejercicios 14-23, asumir\(\alpha \) es lado opuesto\(a\),\(\beta\) es lado opuesto\(b\), y\(\gamma \) es lado opuesto\(c\). Determina si no hay triángulo, un triángulo o dos triángulos. Entonces resuelve cada triángulo, si es posible. Redondea cada respuesta a la décima más cercana.
14)\(\alpha =119^{\circ}, a=14, b=26\)
15)\(\gamma =113^{\circ}, b=10, c=32\)
- Responder
-
un triángulo,\(\alpha \approx 50.3^{\circ}, \beta \approx 16.7^{\circ}, a\approx 26.7\)
16)\(b=3.5, c=5.3, \gamma =80^{\circ}\)
17)\(a=12, c=17, \alpha =35^{\circ}\)
- Responder
-
dos triángulos,\(\gamma \approx 54.3^{\circ}, \beta \approx 90.7^{\circ}, b\approx 20.9\) o\(\gamma '\approx 125.7^{\circ}, \beta '\approx 19.3^{\circ}, b'\approx 6.9\)
18)\(a=20.5, b=35.0, \beta =25^{\circ}\)
19)\(a=7, c=9, \alpha =43^{\circ}\)
- Responder
-
dos triángulos,\(\beta \approx 75.7^{\circ}, \gamma \approx 61.3^{\circ}, b\approx 9.9\) o\(\beta '\approx 18.3^{\circ}, \gamma '\approx 118.7^{\circ}, b'\approx 3.2\)
20)\(a=7, b=3, \beta =24^{\circ}\)
21)\(b=13, c=5, \gamma =10^{\circ}\)
- Responder
-
dos triángulos,\(\alpha \approx 143.2^{\circ}, \beta \approx 26.8^{\circ}, a\approx 17.3\) o\(\alpha '\approx 16.8^{\circ}, \beta '\approx 153.2^{\circ}, a'\approx 8.3\)
22)\(a=2.3, c=1.8, \gamma =28^{\circ}\)
23)\(\beta =119^{\circ}, b=8.2, a=11.3\)
- Responder
-
ningún triángulo posible
Para los ejercicios 24-26, usa la Ley de Sines para resolver, si es posible, el lado o ángulo que falta para cada triángulo o triángulos en el caso ambiguo. Redondea cada respuesta a la décima más cercana.
24) Encontrar ángulo\(A\) cuando\(a=24, b=5, B=22^{\circ}\)
25) Encontrar ángulo\(A\) cuando\(a=13, b=6, B=20^{\circ}\)
- Responder
-
\(A\approx 47.8^{\circ}\)o\(A'\approx 132.2^{\circ}\)
26) Encontrar ángulo\(B\) cuando\(A=12^{\circ}, a=2, b=9\)
Para los ejercicios 27-30, encuentra el área del triángulo con las medidas dadas. Redondea cada respuesta a la décima más cercana.
27)\(a=5, c=6, \beta =35^{\circ}\)
- Responder
-
\(8.6\)
28)\(b=11, c=8, \alpha =28^{\circ}\)
29)\(a=32, b=24, \gamma =75^{\circ}\)
- Responder
-
\(370.9\)
30)\(a=7.2, b=4.5, \gamma =43^{\circ}\)
Gráfica
Para los ejercicios 31-36, encuentra la longitud del lado\(x\). Redondear a la décima más cercana.
31)
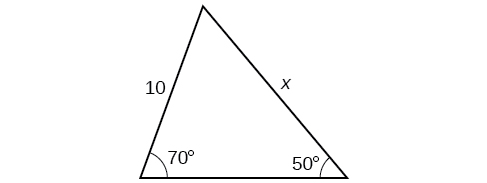
- Responder
-
\(12.3\)
32)
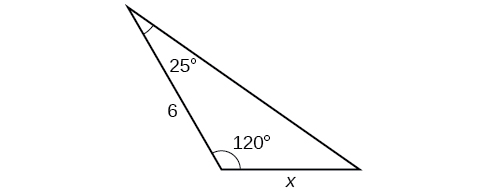
33)
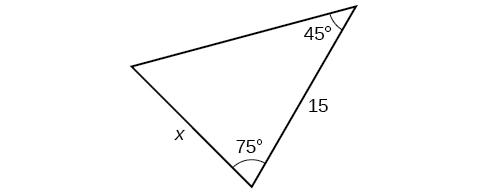
- Responder
-
\(12.2\)
34)
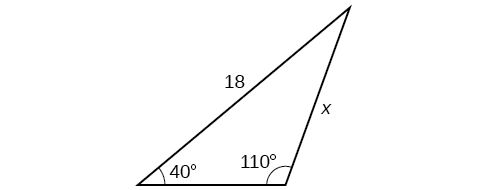
35)
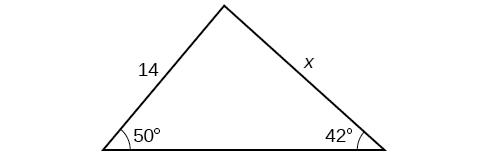
- Responder
-
\(16.0\)
36)
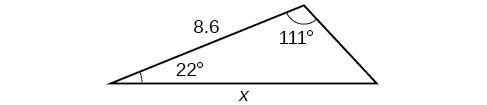
Para los ejercicios 37-,42 encuentra la medida del ángulo\(x\), si es posible. Redondear a la décima más cercana.
37)
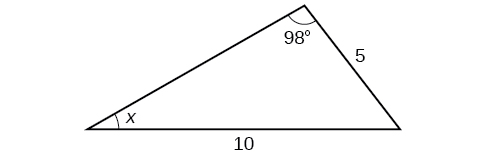
- Responder
-
\(29.7^{\circ}\)
38)

39)
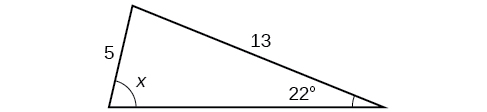
- Responder
-
\(x=76.9^{\circ}\)o\(x=103.1^{\circ}\)
40)
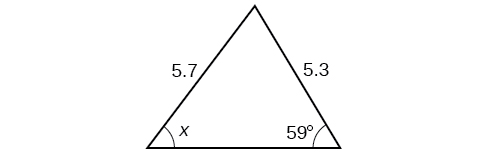
41) Observe que\(x\) es un ángulo obtuso.
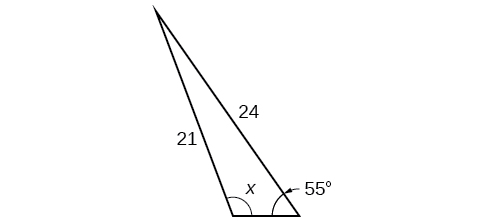
- Responder
-
\(110.6^{\circ}\)
42)
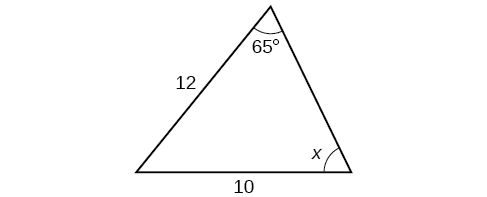
Para los ejercicios 43-49, encuentra el área de cada triángulo. Redondea cada respuesta a la décima más cercana.
43)
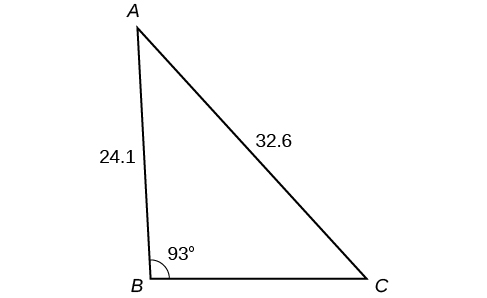
- Responder
-
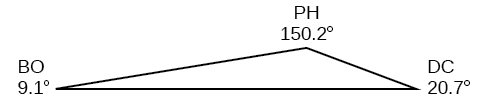
\(A\approx 39.4, C\approx 47.6, BC\approx 20.7\)
44)
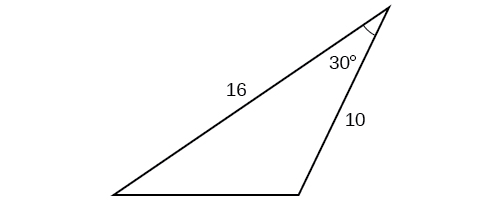
45)
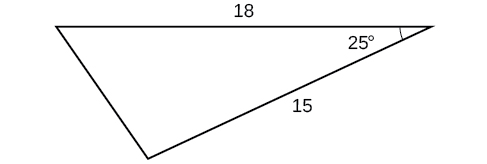
- Responder
-
\(57.1\)
46)
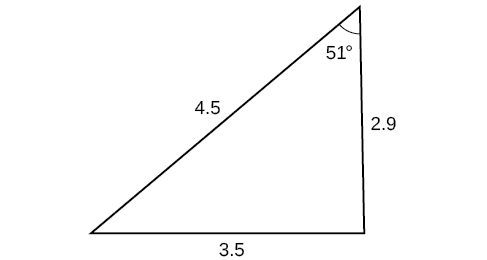
47)
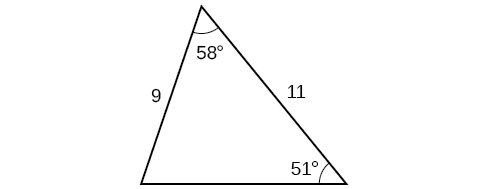
- Responder
-
\(42.0\)
48)
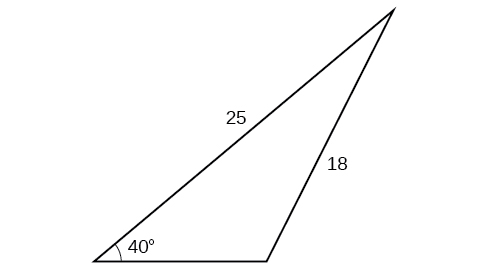
49)
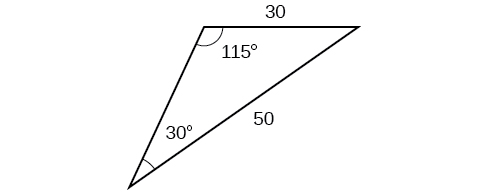
- Responder
-
\(430.2\)
Extensiones
50) Encuentra el radio del círculo en la figura a continuación. Redondear a la décima más cercana.
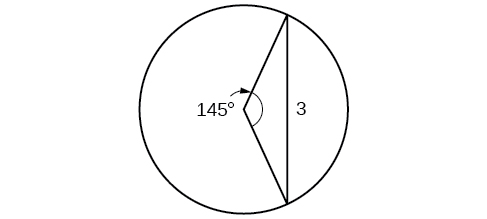
51) Encuentra el diámetro del círculo en la Figura a continuación. Redondear a la décima más cercana.
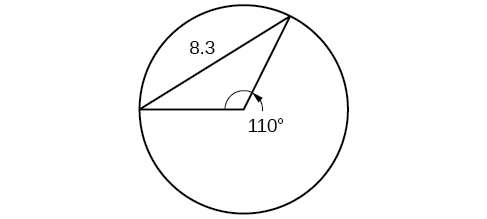
- Responder
-
\(10.1\)
52) Encuentre\(m\angle ADC\) en la Figura a continuación. Redondear a la décima más cercana.
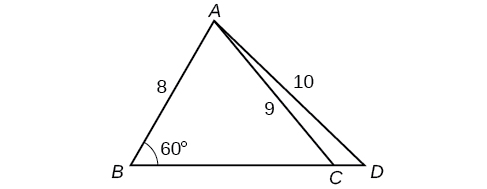
53) Encuentra lado\( AD\) en la Figura a continuación. Redondear a la décima más cercana.
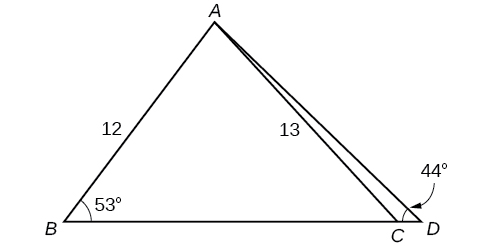
- Responder
-
\(AD\approx 13.8\)
54) Resuelve ambos triángulos en la Figura siguiente. Redondea cada respuesta a la décima más cercana.
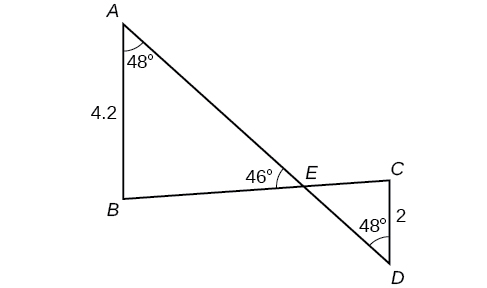
55) Encuentra lado\( AB\) en el paralelogramo que se muestra a continuación. Redondear a la décima más cercana.
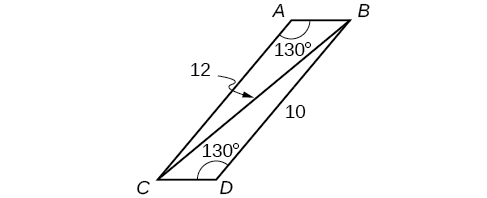
- Responder
-
\(AB\approx 2.8\)
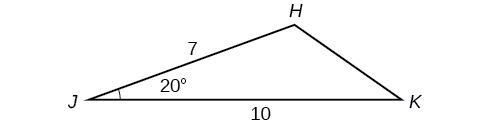
56) Resuelve el triángulo en la Figura a continuación. (Pista: Dibuja una perpendicular de\(H\) a\(JK\). Redondea cada respuesta a la décima más cercana.
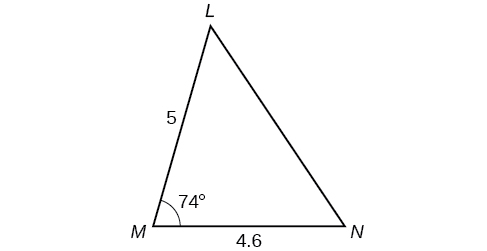
57) Resuelve el triángulo en la Figura a continuación. (Pista: Dibuja una perpendicular de\(N\) a\(LM\). Redondea cada respuesta a la décima más cercana.
- Responder
-
\(L\approx 49.7 ^{\circ} , N\approx 56.3 ^{\circ} , LN\approx 5.8\)
58) En la siguiente figura, no\(ABCD\) es un paralelogramo. \(\angle m\)es obtuso. Resuelve ambos triángulos. Redondea cada respuesta a la décima más cercana.
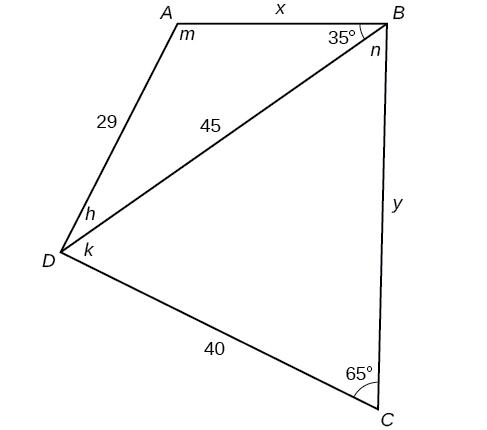
Aplicaciones del mundo real
59) Un poste se inclina alejándose del sol en ángulo con respecto\(7^{\circ}\) a la vertical, como se muestra en la Figura de abajo. Cuando la elevación del sol es\(55^{\circ}\), el poste proyecta una sombra de\(42\) pies de largo sobre el suelo llano. ¿Cuánto dura el poste? Redondear la respuesta a la décima más cercana.
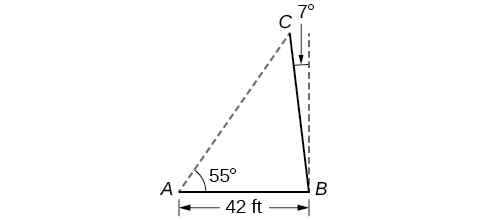
- Responder
-
\(51.4\)ft
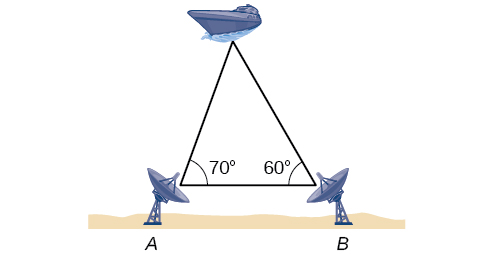
60) Para determinar qué tan lejos está una embarcación de la costa, dos estaciones de radar a\(500\) pies de distancia encuentran los ángulos hacia la embarcación, como se muestra en la Figura a continuación. Determinar la distancia del barco desde la estación\(A\) y la distancia del barco desde la costa. Redondea tus respuestas al pie entero más cercano.
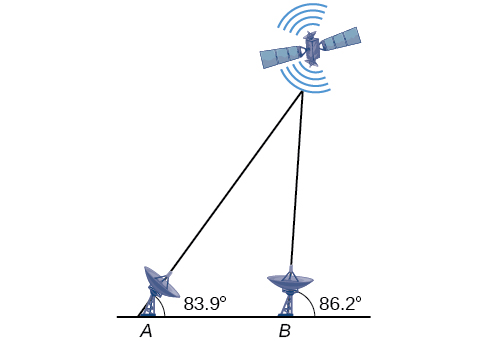
61) La siguiente figura muestra un satélite orbitando la Tierra. El satélite pasa directamente sobre dos estaciones de rastreo\(A\) y\(B\), que están\(69\) a millas de distancia. Cuando el satélite está en un lado de las dos estaciones, los ángulos de elevación en\(A\) y\(B\) se miden para ser\(86.2^{\circ}\) y\(83.9^{\circ}\) respectivamente. ¿A qué distancia está el satélite de la estación\(A\) y a qué altura está el satélite sobre el suelo? Respuestas redondas a la milla entera más cercana.
- Responder
-
La distancia del satélite a la estación\(A\) es de aproximadamente\(1716\) millas. El satélite se encuentra aproximadamente\(1706\) a millas sobre el suelo.
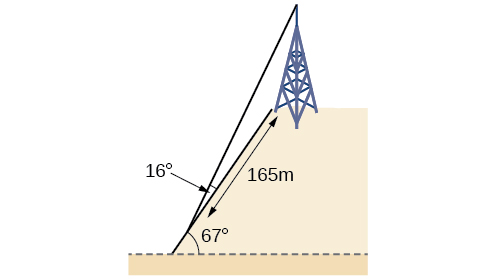
62) Una torre de comunicaciones se ubica en lo alto de un cerro empinado, como se muestra en la Figura a continuación. El ángulo de inclinación del cerro es\(67^{\circ}\). Un cable de sujeción se va a unir a la parte superior de la torre y al suelo,\(165\) metros cuesta abajo desde la base de la torre. El ángulo formado por el cable de sujeción y el cerro es\(16^{\circ}\). Encuentre la longitud del cable requerida para el cable de sujeción al medidor completo más cercano.
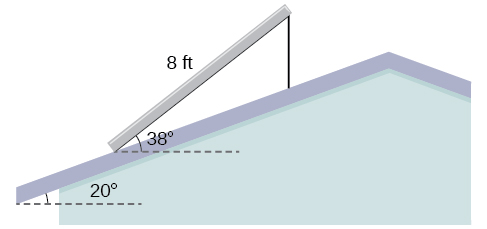
63) El techo de una casa está en\(20^{\circ}\) ángulo. Un panel solar\(8\) de pie debe montarse en el techo y debe estar en ángulo\(38^{\circ}\) con relación a la horizontal para obtener resultados óptimos. (Ver la Figura a continuación). ¿Cuánto tiempo necesita ser el soporte vertical que sostiene la parte posterior del panel? Redondear a la décima más cercana.
- Responder
-
\(2.6\)ft
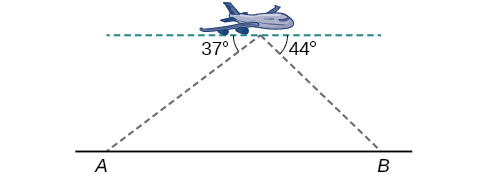
64) Similar a un ángulo de elevación, un ángulo de depresión es el ángulo agudo formado por una línea horizontal y una línea de visión del observador hacia un objeto debajo de la horizontal. Un piloto sobrevuela una carretera recta. Determina los ángulos de depresión a dos postes,\(6.6\) km de distancia, para ser\(37^{\circ}\) y\(44^{\circ}\) como se muestra en la Figura a continuación. Encuentra la distancia del avión de punto\(A\) a la décima de kilómetro más cercana.
65) Un piloto sobrevuela una carretera recta. Determina los ángulos de depresión a dos postes,\(4.3\) km de distancia, para ser\(32^{\circ}\) y\(56^{\circ}\), como se muestra en la Figura a continuación. Encuentra la distancia del avión de punto\(A\) a la décima de kilómetro más cercana.
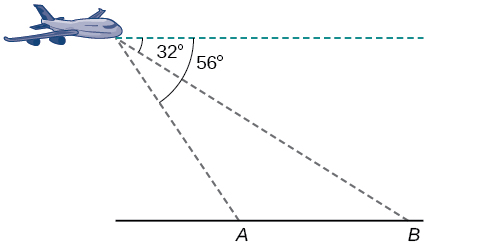
- Responder
-
\(5.6\)km
66) Para estimar la altura de un edificio, dos estudiantes se paran a cierta distancia del edificio a pie de calle. A partir de este punto, encuentran que el ángulo de elevación desde la calle hasta lo alto del edificio es ser\(39^{\circ}\). Luego se acercan\(300\) los pies al edificio y encuentran que el ángulo de elevación es\(50^{\circ}\). Suponiendo que la calle esté nivelada, estime la altura del edificio al pie más cercano.
67) Para estimar la altura de un edificio, dos estudiantes se paran a cierta distancia del edificio a pie de calle. A partir de este punto, encuentran que el ángulo de elevación desde la calle hasta lo alto del edificio es ser\(35^{\circ}\). Luego se acercan\(250\) los pies al edificio y encuentran que el ángulo de elevación es\(53^{\circ}\). Suponiendo que la calle esté nivelada, estime la altura del edificio al pie más cercano.
- Responder
-
\(371\)ft
68)\(A\) Puntas y\(B\) están en lados opuestos de un lago. \(C\)El punto está\(97\) a metros de\(A\). Se determina\(\angle BAC\) que la medida de es\(101^{\circ}\), y la medida de\(\angle ACB\) se determina que es\(53^{\circ}\). ¿Cuál es la distancia de\(A\) a\(B\)
69) Un hombre y una mujer parados\(3\dfrac{1}{2}\) a kilómetros de distancia ven un globo aerostático al mismo tiempo. Si el ángulo de elevación del hombre al globo es\(27^{\circ}\), y el ángulo de elevación de la mujer al globo es\(41^{\circ}\), encuentra la altitud del globo al pie más cercano.
- Responder
-
\(5936\)ft
70) Dos equipos de búsqueda localizan a un escalador varado en una montaña. El primer equipo de búsqueda está\(0.5\) a millas del segundo equipo de búsqueda, y ambos equipos están a una altitud de\(1\) milla. El ángulo de elevación desde el primer equipo de búsqueda hasta el escalador varado es\(15^{\circ}\). El ángulo de elevación desde el segundo equipo de búsqueda hasta el escalador es\(22^{\circ}\). ¿Cuál es la altitud del escalador? Redondear a la décima de milla más cercana.
71) Una luz de la calle está montada en un poste. Un hombre\(6\) de un pie de altura está parado en la calle a poca distancia del poste, proyectando una sombra. El ángulo de elevación desde la punta de la sombra del hombre hasta la parte superior de su cabeza de\(28^{\circ}\). Una mujer\(6\) de un pie de altura se encuentra parada en la misma calle en el lado opuesto del poste al hombre. El ángulo de elevación desde la punta de su sombra hasta la parte superior de su cabeza es\(28^{\circ}\). Si el hombre y la mujer están a\(20\) pies de distancia, ¿a qué distancia está la luz de la calle de la punta de la sombra de cada persona? Redondea la distancia hasta la décima de pie más cercana.
- Responder
-
\(24.1\)ft
72) Tres ciudades,,\(A\), y\(B\)\(C\), están ubicadas de manera que esa ciudad\(A\) se debe al este de la ciudad\(B\). Si la ciudad\(C\) se encuentra\(35^{\circ}\) al oeste del norte de la ciudad\(B\) y está\(100\) a millas de la ciudad\(A\) y\(70\) millas de la ciudad\(B\), ¿a qué distancia está la ciudad\(A\) de la ciudad\(B\)? Redondea la distancia hasta la décima de milla más cercana.
73) Dos calles se encuentran en\(80^{\circ}\) ángulo. En la esquina, se está construyendo un parque en forma de triángulo. Encuentra el área del parque si, a lo largo de una carretera, el parque mide\(180\) pies, y a lo largo de la otra carretera, el parque mide\(215\) pies.
- Responder
-
\(19,056\)ft 2
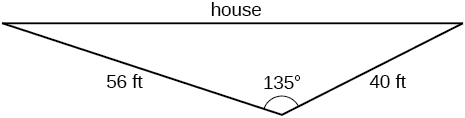
74) La casa de Brian está en un lote de esquina. Encuentre el área del patio delantero si los bordes miden\(40\) y\(56\) pies, como se muestra en la Figura a continuación.
75) El triángulo de las Bermudas es una región del Océano Atlántico que conecta Bermudas, Florida y Puerto Rico. Encuentra el área del triángulo de las Bermudas si la distancia de Florida a Bermudas es de\(1030\) millas, la distancia de Puerto Rico a Bermudas es de\(980\) millas, y el ángulo creado por las dos distancias es\(62^{\circ}\).
- Responder
-
\(445,624\)millas cuadradas
76) Un letrero de rendimiento mide\(30\) pulgadas en los tres lados. ¿Cuál es el área del letrero?
77) Naomi compró una mesa de comedor moderna cuya parte superior tiene forma de triángulo. Encuentre el área del tablero de la mesa si dos de los lados miden\(4\) pies y\(4.5\) pies, y los ángulos más pequeños miden\(32^{\circ}\) y\(42^{\circ}\), como se muestra en la Figura a continuación.
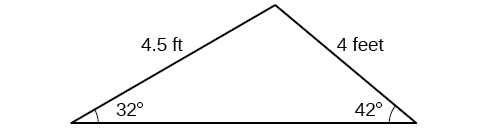
- Responder
-
\(8.65\)ft 2
8.2: Triángulos no rectos - Ley de Cosinos
Verbal
1) Si buscas un lado faltante de un triángulo, ¿qué necesitas saber al usar la Ley de Cosinos?
- Responder
-
dos lados y el ángulo opuesto al lado faltante.
2) Si buscas un ángulo faltante de un triángulo, ¿qué necesitas saber al usar la Ley de Cosinos?
3) Explicar lo que\(s\) representa en la fórmula de Heron.
- Responder
-
\(s\)es el semiperímetro, que es la mitad del perímetro del triángulo.
4) Explicar la relación entre el Teorema de Pitágoras y la Ley de los Cosinos.
5) ¿Cuándo se debe utilizar la Ley de Cosinos en lugar del Teorema de Pitágoras?
- Responder
-
La Ley de Cosinos debe ser utilizada para cualquier triángulo oblicuo (no derecho).
Algebraico
Para los ejercicios 6-15, asumir\(\alpha \) es lado opuesto\(a\),\(\beta \) es lado opuesto\(b\), y\(\gamma \) es lado opuesto\(c\). Si es posible, resuelve cada triángulo para el lado desconocido. Redondear a la décima más cercana.
6)\(\gamma =41.2^{\circ}, a=2.49, b=3.13\)
7)\(\alpha =120^{\circ}, b=6, c=7\)
- Responder
-
\(11.3\)
8)\(\beta =58.7^{\circ}, a=10.6, c=15.7\)
9)\(\alpha =115^{\circ}, a=18, b=23\)
- Responder
-
\(34.7\)
10)\(\alpha =119^{\circ}, a=26, b=14\)
11)\(\gamma =113^{\circ}, b=10, c=32\)
- Responder
-
\(26.7\)
12)\(\beta =67^{\circ}, a=49, b=38\)
13)\(\alpha =43.1^{\circ}, a=184.2, b=242.8\)
- Responder
-
\(257.4\)
14)\(\alpha =36.6^{\circ}, a=186.2, b=242.2\)
15)\(\beta =50^{\circ}, a=105, b=45\)
- Responder
-
no es posible
Para los ejercicios 16-20, usa la Ley de Cosinos para resolver el ángulo faltante del triángulo oblicuo. Redondear a la décima más cercana.
16)\(a=42, b=19, c=30\); encontrar ángulo\(A\).
17)\(a=14, b=13, c=20\); encontrar ángulo\(C\).
- Responder
-
\(95.5^{\circ}\)
18)\(a=16, b=31, c=20\); encontrar ángulo\(B\).
19)\(a=13, b=22, c=28\); encontrar ángulo\(A\).
- Responder
-
\(26.9^{\circ}\)
20)\(a=108, b=132, c=160\); encontrar ángulo\(C\).
Para los ejercicios 21-26, resolver el triángulo. Redondear a la décima más cercana.
21)\(A=35^{\circ}, b=8, c=11\)
- Responder
-
\(B\approx 45.9^{\circ}, C\approx 99.1^{\circ}, a\approx 6.4\)
22)\(B=88^{\circ}, a=4.4, c=5.2\)
23)\(C=121^{\circ}, a=21, b=37\)
- Responder
-
\(A\approx 20.6^{\circ}, B\approx 38.4^{\circ}, c\approx 51.1\)
24)\(a=13, b=11, c=15\)
25)\(a=3.1, b=3.5, c=5\)
- Responder
-
\(A\approx 37.8^{\circ}, B\approx 43.8^{\circ}, C\approx 98.4\)
26)\(a=51, b=25, c=29\)
Para los ejercicios 27-,31 usa la fórmula de Heron para encontrar el área del triángulo. Redondear a la centésima más cercana.
27) Encuentra el área de un triángulo con lados de longitud\(18\)\(21\) en, dentro y\(32\) en. Redondear a la décima más cercana.
- Responder
-
\(177.56\)en 2
28) Encuentra el área de un triángulo con lados de longitud\(20\)\(26\) cm,\(37\) cm y cm. Redondear a la décima más cercana.
29)\(a=\dfrac{1}{2}\)\(b=\dfrac{1}{3}\) m,\(c=\dfrac{1}{4}\) m
- Responder
-
\(0.04\)m 2
30)\(a=12.4\) pies,\(b=13.7\) pies,\(c=20.2\) pies
31)\(a=1.6\) yd,\(b=2.6\) yd,\(c=4.1\) yd
- Responder
-
\(0.91\)yd 2
Gráfica
Para los ejercicios 32-37, encuentra la longitud del lado\(x\). Redondear a la décima más cercana.
32)
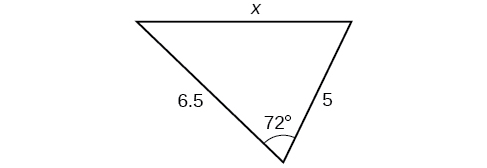
33)
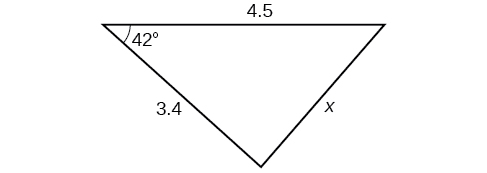
- Responder
-
\(3.0\)
34)
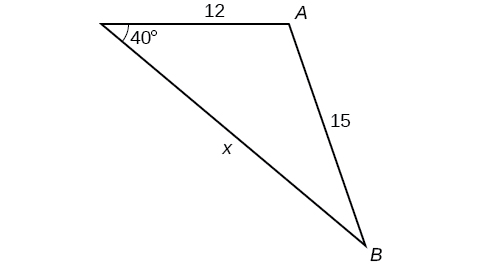
35)
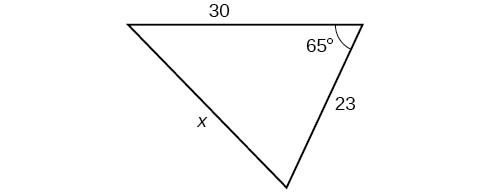
- Responder
-
\(29.1\)
36)
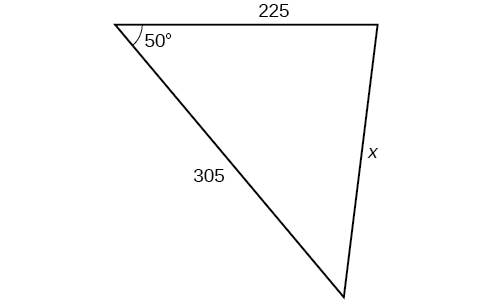
37)
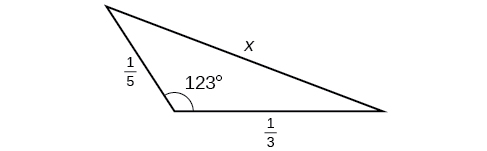
- Responder
-
\(0.5\)
Para los ejercicios 38-41, encuentra la medición del ángulo\(A\)
38)
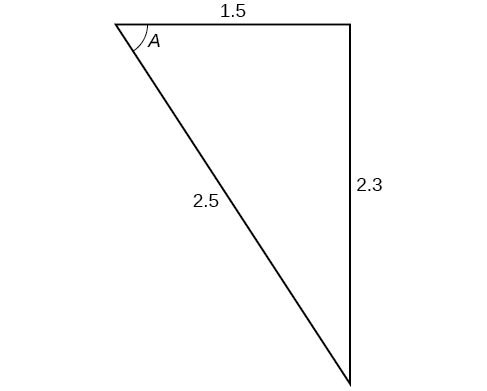
39)
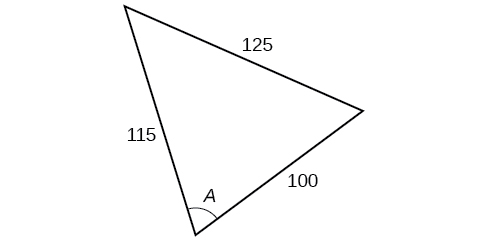
- Responder
-
\(70.7^{\circ}\)
40)
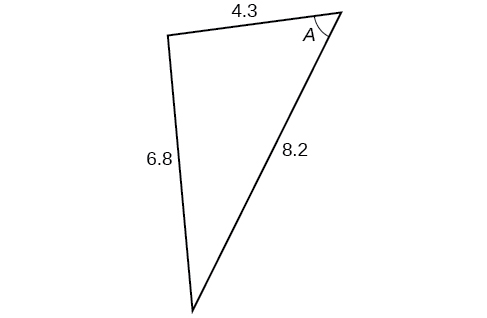
41)
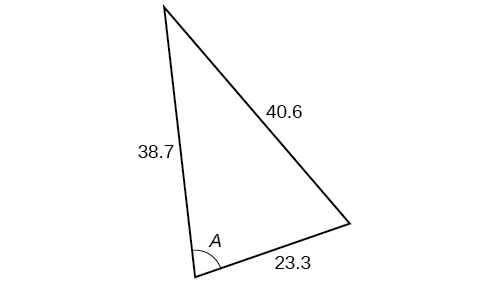
- Responder
-
\(77.4^{\circ}\)
42) Encuentra la medida de cada ángulo en el triángulo que se muestra en la Figura a continuación. Redondear a la décima más cercana.
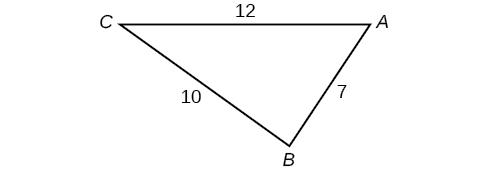
Para los ejercicios 43-46, resolver por el lado desconocido. Redondear a la décima más cercana.
43)
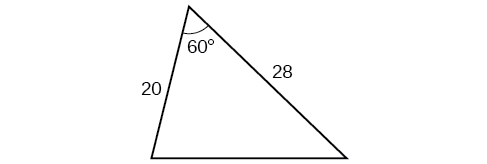
- Responder
-
\(25.0\)
44)
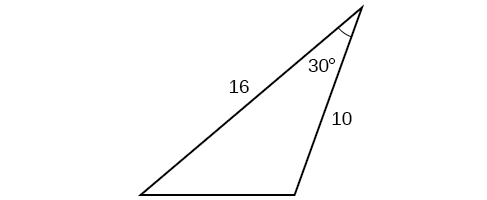
45)
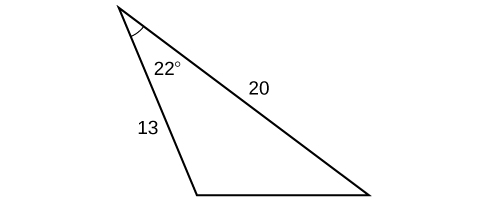
- Responder
-
\(9.3\)
46)

Para los ejercicios 47-51, encuentra el área del triángulo. Redondear a la centésima más cercana.
47)
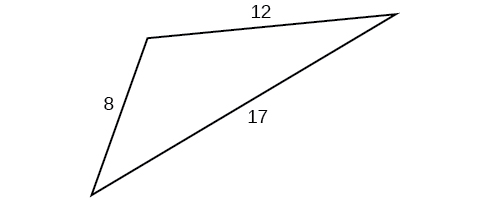
- Responder
-
\(43.52\)
48)
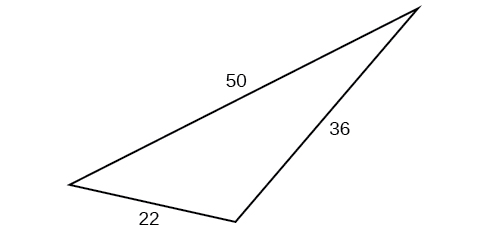
49)
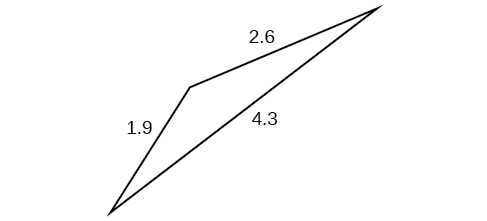
- Responder
-
\(1.41\)
50)
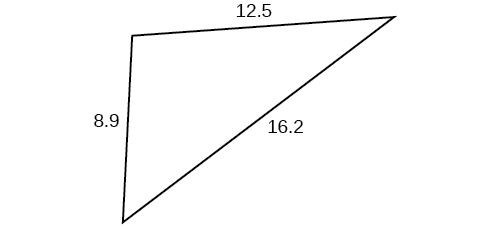
51)
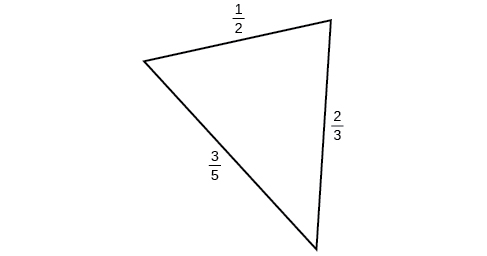
- Responder
-
\(0.14\)
Extensiones
52) Un paralelogramo tiene lados de\(16\) unidades de longitud y\(10\) unidades. La diagonal más corta son\(12\) las unidades. Encuentra la medida de la diagonal más larga.
53) Los lados de un paralelogramo son\(11\) pies y\(17\) pies. La diagonal más larga es\(22\) pies. Encuentra la longitud de la diagonal más corta.
- Responder
-
\(18.3\)
54) Los lados de un paralelogramo son\(28\) centímetros y\(40\) centímetros. La medida del ángulo más grande es\(100^{\circ}\). Encuentra la longitud de la diagonal más corta.
55) Un octágono regular se inscribe en un círculo con un radio de\(8\) pulgadas. (Vea la Figura a continuación.) Encuentra el perímetro del octágono.
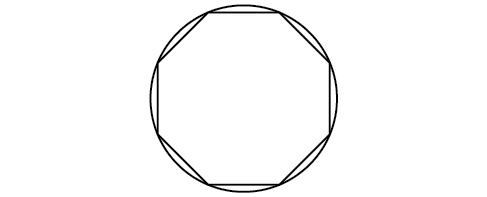
- Responder
-
\(48.98\)
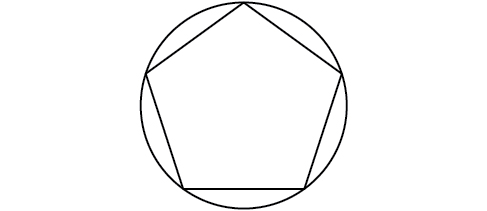
56) Un pentágono regular se inscribe en un círculo de radio\(12\) cm. (Vea la Figura a continuación.) Encuentra el perímetro del pentágono. Redondear a la décima de centímetro más cercana.
Para los ejercicios 57-58, supongamos que eso\(x^2=25+36-60\cos(52)\) representa la relación de tres lados de un triángulo y el coseno de un ángulo.
57) Dibuja el triángulo.
- Responder
-
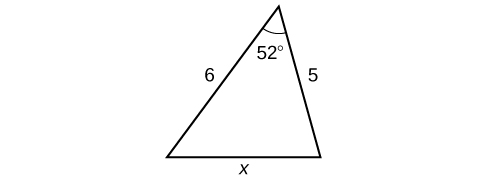
58) Encuentra la longitud del tercer lado.
Para los ejercicios 59-61, encuentra el área del triángulo.
59)

- Responder
-
\(7.62\)
60)
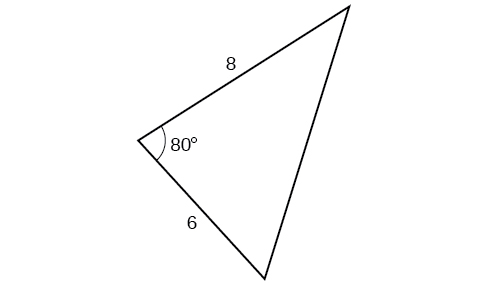
61)
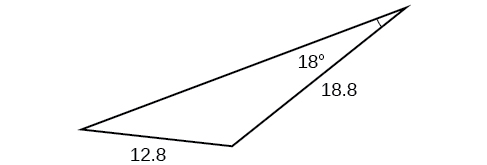
- Responder
-
\(85.1\)
Aplicaciones del mundo real
62) Un topógrafo ha tomado las medidas que se muestran en la Figura siguiente. Encuentra la distancia a través del lago. Respuestas redondas a la décima más cercana.
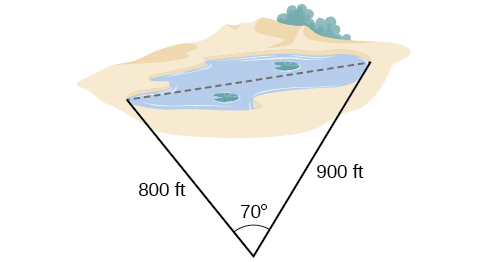
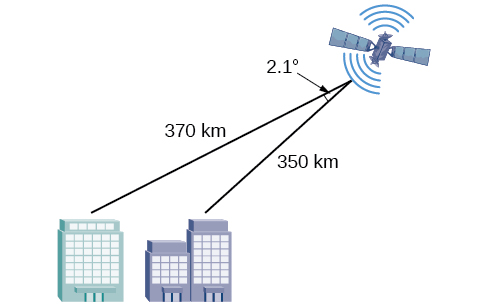
- Responder
-
\(24.0\)km
64) Un avión vuela\(220\) millas con rumbo de\(40^{\circ}\), y luego vuela\(180\) millas con un rumbo de\(170^{\circ}\). ¿A qué distancia está el avión de su punto de partida y en qué rumbo? Respuestas redondas a la décima más cercana.
65) Una torre\(113\) de pie se ubica sobre un cerro que se inclina\(34^{\circ}\) con respecto a la horizontal, como se muestra en la Figura a continuación. Un alambre tipo debe ser unido a la parte superior de la torre y anclado en un punto a\(98\) pies cuesta arriba desde la base de la torre. Encuentre la longitud de cable necesaria.
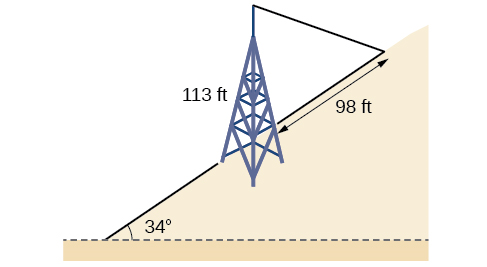
- Responder
-
\(99.9\)ft
66) Dos barcos salieron de un puerto al mismo tiempo. Un barco viajaba a una velocidad de\(18\) millas por hora a un rumbo de\(320^{\circ}\). El otro barco viajaba a una velocidad de\(22\) millas por hora a un rumbo de\(194^{\circ}\). Encuentra la distancia entre los dos barcos después de\(10\) horas de viaje.
67) La gráfica de la siguiente Figura representa dos embarcaciones que salen al mismo tiempo del mismo muelle. El primer barco viaja a\(18\) millas por hora en una dirección de\(327^{\circ}\) y el segundo barco viaja a\(4\) millas por hora en una dirección de\(60^{\circ}\). Encuentra la distancia entre las dos embarcaciones después de\(2\) horas.
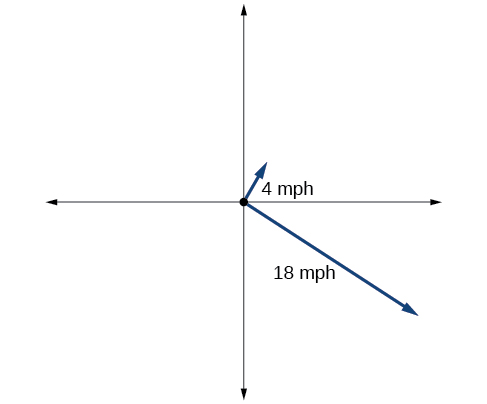
- Contestar
-
\(37.3\)millas
68) Una piscina triangular mide\(40\) pies en un lado y\(65\) pies en otro lado. Estos lados forman un ángulo que mide\(50^{\circ}\). ¿Cuánto dura el tercer lado (a la décima más cercana)?
69) Un piloto vuela en camino recto por\(1\) hora\(30\) min. Luego hace una corrección de rumbo, dirigiéndose\(10^{\circ}\) a la derecha de su curso original, y vuela\(2\) horas en la nueva dirección. Si mantiene una velocidad constante de\(680\) millas por hora, ¿a qué distancia está de su posición inicial?
- Contestar
-
\(2371\)millas
70) Los Ángeles se encuentra\(1,744\) a millas de Chicago, Chicago está a\(714\) millas de Nueva York y Nueva York\(2,451\) a millas de Los Ángeles. Dibuja un triángulo que conecte estas tres ciudades, y encuentre los ángulos en el triángulo.
71) Filadelfia se encuentra\(140\) a millas de Washington, D.C., Washington, D.C. está\(442\) a millas de Boston, y Boston está\(315\) a millas de Filadelfia. Dibuja un triángulo que conecte estas tres ciudades y encuentre los ángulos en el triángulo.
- Contestar
-
72) Dos aviones salen del mismo aeropuerto al mismo tiempo. Uno vuela al\(20^{\circ}\) este del norte a\(500\) millas por hora. El segundo vuela al\(30^{\circ}\) este del sur a\(600\) millas por hora. ¿Qué tan lejos están los aviones después de\(2\) las horas?
73) Dos aviones despegan en diferentes direcciones. Uno viaja\(300\) mph hacia el oeste y el otro viaja\(25^{\circ}\) al norte del oeste a\(420\) mph. Después de\(90\) minutos, ¿a qué distancia están, asumiendo que están volando a la misma altitud?
- Contestar
-
\(599.8\)millas
74) Un paralelogramo tiene lados de\(15.4\) unidades de longitud y\(9.8\) unidades. Su área es de unidades\(72.9\) cuadradas. Encuentra la medida de la diagonal más larga.
75) Los cuatro lados secuenciales de un cuadrilátero tienen longitudes\(4.5\)\(7.9\) cm,\(9.4\) cm,\(12.9\) cm y cm. El ángulo entre los dos lados más pequeños es\(117^{\circ}\). ¿Cuál es el área de este cuadrilátero?
- Contestar
-
\(65.4\)cm 2
76) Los cuatro lados secuenciales de un cuadrilátero tienen longitudes\(5.7\)\(7.2\) cm,\(9.4\) cm,\(12.8\) cm y cm. El ángulo entre los dos lados más pequeños es\(106^{\circ}\). ¿Cuál es el área de este cuadrilátero?
77) Encuentra el área de un terreno triangular que mide\(30\) pies en un lado y\(42\) pies en otro; el ángulo incluido mide\(132^{\circ}\). Redondear al pie cuadrado entero más cercano.
- Contestar
-
\(468\)ft 2
78) Encuentra el área de un terreno triangular que mide\(110\) pies en un lado y\(250\) pies en otro; el ángulo incluido mide\(85^{\circ}\). Redondear al pie cuadrado entero más cercano.
8.3: Coordenadas polares
Verbal
1) ¿En qué se diferencian las coordenadas polares de las coordenadas rectangulares?
- Contestar
-
Para las coordenadas polares, el punto en el plano depende del ángulo desde el\(x\) eje positivo y la distancia desde el origen, mientras que en las coordenadas cartesianas, el punto representa las distancias horizontal y vertical desde el origen. Para cada punto en el plano de coordenadas, hay una representación, pero para cada punto en el plano polar, hay representaciones infinitas
2) ¿En qué se diferencian los ejes polares de los\(y\) ejes\(x\) - y -del plano cartesiano?
3) Explicar cómo se grafican las coordenadas polares.
- Contestar
-
Determine\(\theta \) para el punto, luego mueva\(r\) las unidades del poste para trazar el punto. Si\(r\) es negativo, mueva\(r\) las unidades desde el polo en la dirección opuesta pero a lo largo del mismo ángulo. El punto es una\(r\) distancia de distancia del origen en un ángulo\(\theta \) del eje polar.
4) ¿Cómo están los puntos\(\left ( 3,\dfrac{\pi }{2} \right )\) y\(\left ( -3,\dfrac{\pi }{2} \right )\) relacionados?
5) Explique por qué los puntos\(\left ( -3,\dfrac{\pi }{2} \right )\) y\(\left ( 3,-\dfrac{\pi }{2} \right )\) son los mismos.
- Contestar
-
El punto\(\left ( -3,\dfrac{\pi }{2} \right )\) tiene un ángulo positivo pero un radio negativo y se traza moviéndose a un ángulo de\(\dfrac{\pi }{2}\) y luego moviendo\(3\) unidades en la dirección negativa. Esto coloca las\(3\) unidades de punto abajo del\(y\) eje negativo. El punto\(\left ( 3,-\dfrac{\pi }{2} \right )\) tiene un ángulo negativo y un radio positivo y se traza moviéndose primero a un ángulo de\(-\dfrac{\pi }{2}\) y luego moviendo\(3\) las unidades hacia abajo, que es la dirección positiva para un ángulo negativo. El punto es también\(3\) unidades abajo del\(y\) eje negativo.
Algebraico
6)\(\left ( 7,\dfrac{7\pi }{6} \right )\)
7)\((5,\pi )\)
- Contestar
-
\((-5,0)\)
8)\(\left ( 6,-\dfrac{\pi }{4} \right )\)
9)\(\left ( -3,\dfrac{\pi }{6} \right )\)
- Contestar
-
\(\left ( -\dfrac{3\sqrt{3}}{2},-\dfrac{3}{2} \right )\)
10)\(\left ( 4,\dfrac{7\pi }{4} \right )\)
Para los ejercicios 11-15, convertir las coordenadas cartesianas dadas a coordenadas polares con\(r>0\) y\(0\leq \theta \leq 2\pi\). Recuerde considerar el cuadrante en el que se encuentra el punto dado.
11)\((4,2)\)
- Contestar
-
\((2\sqrt{5},0.464)\)
12)\((-4,6)\)
13)\((3,-5)\)
- Contestar
-
\((\sqrt{34},5.253)\)
14)\((-10,-13)\)
15)\((8,8)\)
- Contestar
-
\(\left(8\sqrt{2},\dfrac{\pi }{4}\right)\)
Para los ejercicios 16-27, convertir la ecuación cartesiana dada en una ecuación polar.
16)\(x=3\)
17)\(y=4\)
- Contestar
-
\(r=4\csc \theta \)
18)\(y=4x^2\)
19)\(y=2x^4\)
- Contestar
-
\(r=\sqrt[3]{\dfrac{\sin \theta }{2\cos ^4\theta }}\)
20)\(x^2 + y^2 = 4y\)
21)\(x^2 + y^2 = 3x\)
- Contestar
-
\(r=3\cos \theta \)
22)\(x^2 - y^2 = x\)
23)\(x^2 - y^2 = 3y\)
- Contestar
-
\(r=\dfrac{3\sin \theta }{\cos (2\theta )}\)
24)\(x^2 + y^2 = 9\)
25)\(x^2 = 9y\)
- Contestar
-
\(r=\dfrac{9\sin \theta }{\cos ^2\theta }\)
26)\(y^2 = 9x\)
27)\(9xy = 1\)
- Contestar
-
\(r=\sqrt{\dfrac{1}{9\cos \theta \sin \theta }}\)
Para los ejercicios 28-39, convertir la ecuación polar dada en una ecuación cartesiana. Escriba en la forma estándar de una cónica si es posible, e identifique la sección cónica representada.
28)\(r=3\sin \theta\)
29)\(r=4\cos \theta\)
- Contestar
-
\(x^2 + y^2 =4x\)o\(\dfrac{(x-2)^2}{4} + \dfrac{y^2}{4} = 1\); círculo
30)\(r = \dfrac{4}{\sin \theta +7\cos \theta }\)
31)\(r = \dfrac{6}{\cos \theta +3\sin \theta }\)
- Contestar
-
\(3y+x=6\); línea
32)\(r=2\sec \theta\)
33)\(r=3\csc \theta\)
- Contestar
-
\(y=3\); línea
34)\(r = \sqrt{r\cos \theta +2}\)
35)\(r^2 = 4\sec \theta \csc \theta\)
- Contestar
-
\(xy=4\); hipérbola
36)\(r =4\)
37)\(r^2 = 4\)
- Contestar
-
\(x^2 + y^2 =4\); círculo
38)\(r = \dfrac{1}{4\cos \theta - 3\sin \theta }\)
39)\(r = \dfrac{3}{\cos \theta - 5\sin \theta }\)
- Contestar
-
\(x-5y=3\); línea
Gráfica
Para los ejercicios 40-44, encuentra las coordenadas polares del punto.
40)
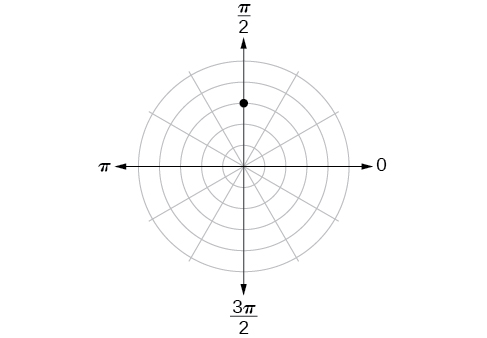
41)
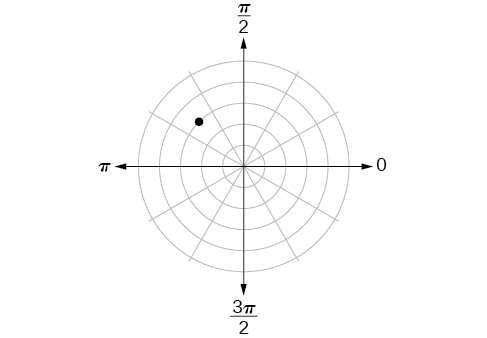
- Contestar
-
\(\left (3,\dfrac{3\pi }{4} \right )\)
42)
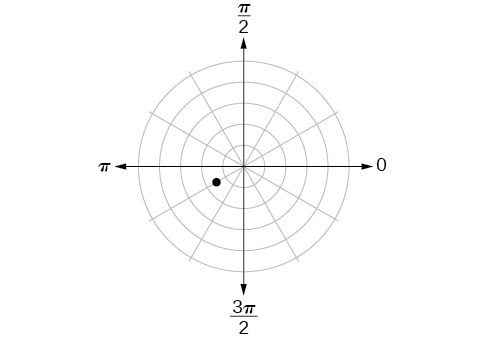
43)
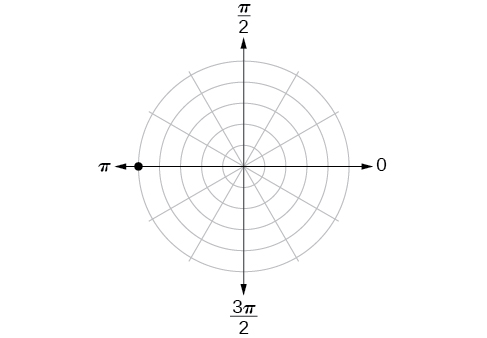
- Contestar
-
\((5,\pi )\)
44)
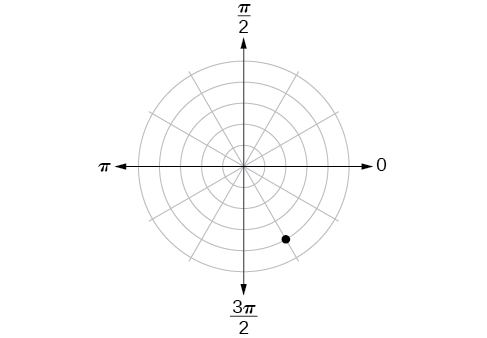
Para los ejercicios 45-54, trazar los puntos.
45)\(\left (-2,\dfrac{\pi }{3} \right )\)
- Contestar
-
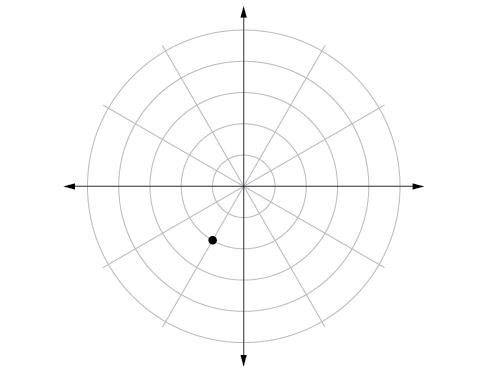
46)\(\left (-1,-\dfrac{\pi }{2} \right )\)
47)\(\left (3.5,\dfrac{7\pi }{4} \right )\)
- Contestar
-
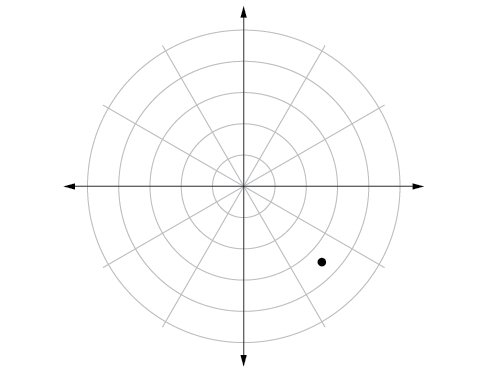
48)\(\left (-4,\dfrac{\pi }{3} \right )\)
49)\(\left (5,\dfrac{\pi }{2} \right )\)
- Contestar
-
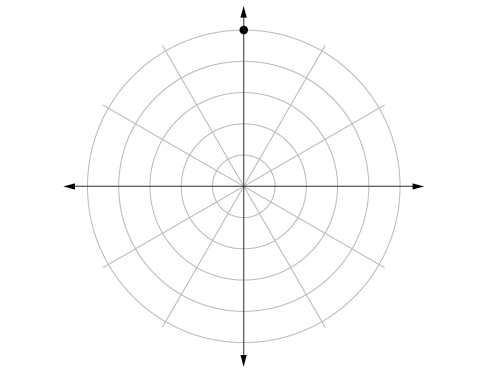
50)\(\left (4,\dfrac{-5\pi }{4} \right )\)
51)\(\left (3,\dfrac{5\pi }{6} \right )\)
- Contestar
-
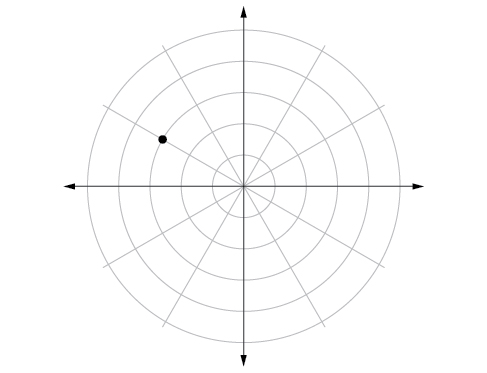
52)\(\left (-1.5,\dfrac{7\pi }{6} \right )\)
53)\(\left (-2,\dfrac{\pi }{4} \right )\)
- Contestar
-
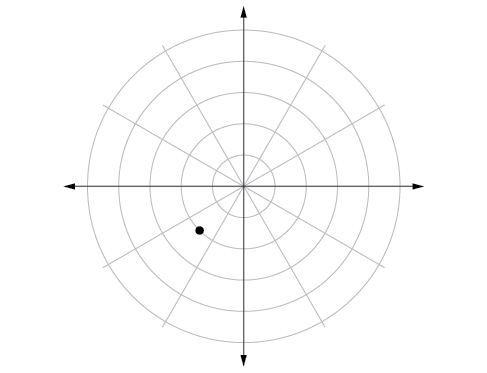
54)\(\left (1,\dfrac{3\pi }{2} \right )\)
Para los ejercicios 55-61, convertir la ecuación de forma rectangular a polar y graficar sobre el eje polar.
55)\(5x-y = 6\)
- Contestar
-
\(r = \dfrac{6}{5\cos \theta - \sin \theta }\)
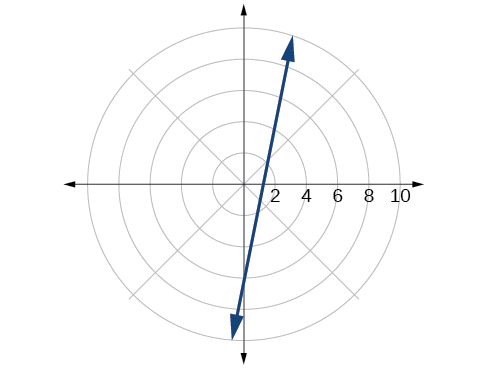
56)\(2x + 7y = -3\)
57)\(x^2 + (y-1)^2 = 1\)
- Contestar
-
\(r = 2\sin \theta \)
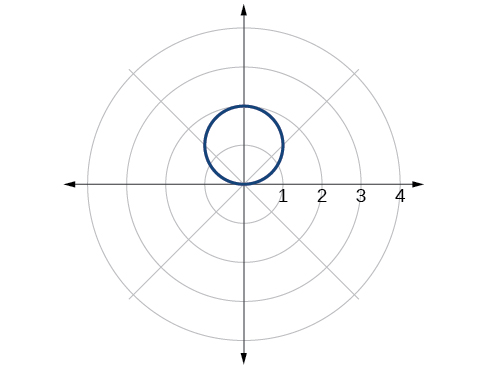
58)\((x+2)^2+(y+3)^2=13\)
59)\(x = 2\)
- Contestar
-
\(r = \dfrac{2}{\cos \theta }\)
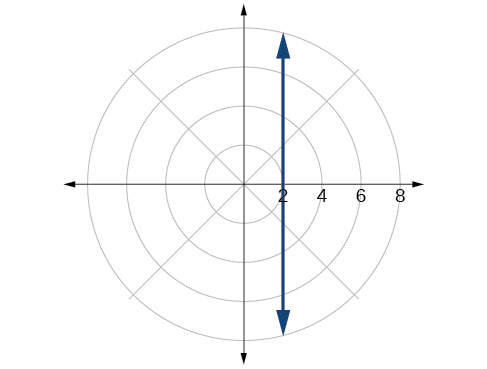
60)\(x^2 + y^2 =5y\)
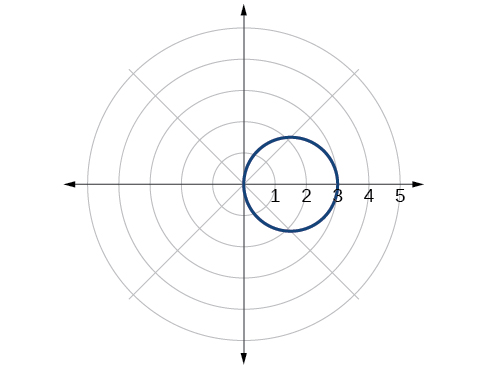
61)\(x^2 + y^2 =3x\)
- Contestar
-
\(r = 3\cos \theta \)
Para los ejercicios 62-68, convertir la ecuación de forma polar a rectangular y graficar en el plano rectangular.
62)\(r = 6\)
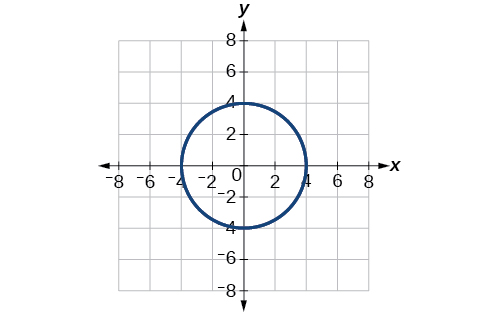
63)\(r = -4\)
- Contestar
-
\(x^2 + y^2 =16\)
64)\(\theta = -\dfrac{2\pi }{3}\)
65)\(\theta = \dfrac{\pi }{4}\)
- Contestar
-
\(y=x\)
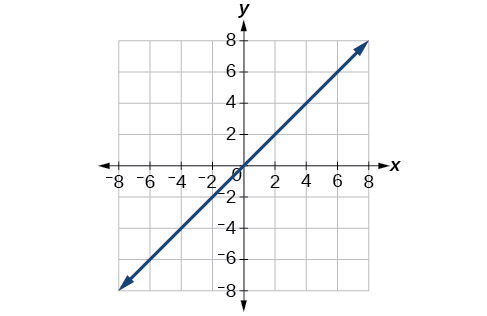
66)\(r = \sec \theta \)
67)\(r = -10\sin \theta \)
- Contestar
-
\(x^2 + (y+5)^2 = 25\)
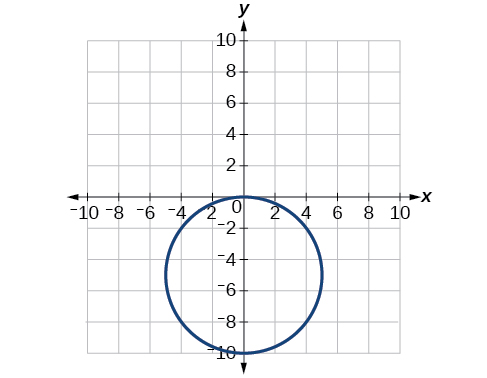
68)\(r = 3\cos \theta \)
Tecnología
69) Utilice una calculadora gráfica para encontrar las coordenadas rectangulares de\(\left (2,-\dfrac{\pi }{5} \right )\)
- Contestar
-
\((1.618,-1.176)\)
70) Utilice una calculadora gráfica para encontrar las coordenadas rectangulares de\(\left (-3,\dfrac{3\pi }{7} \right )\). Redondear a la milésima más cercana.
71) Utilice una calculadora gráfica para encontrar las coordenadas polares\((-7,8)\) en grados. Redondear a la milésima más cercana.
- Contestar
-
\((10.630,131.186^{\circ})\)
72) Utilice una calculadora gráfica para encontrar las coordenadas polares\((3,-4)\) en grados. Redondear a la centésima más cercana.
73) Utilice una calculadora gráfica para encontrar las coordenadas polares\((-2,0)\) en grados. Redondear a la centésima más cercana.
- Contestar
-
\((2,3.14)\)o\((2,\pi )\)
Extensiones
74) Describir la gráfica de\(r=a\sec \theta \);\(a>0\).
75) Describir la gráfica de\(r=a\sec \theta \);\(a<0\).
- Contestar
-
Una línea vertical con\(a\) unidades a la izquierda del\(y\) eje.
76) Describir la gráfica de\(r=a\csc \theta \);\(a>0\).
77) Describir la gráfica de\(r=a\csc \theta \);\(a<0\).
- Contestar
-
Una línea horizontal con\(a\) unidades por debajo del\(x\) eje.
78) ¿Qué ecuaciones polares darán una línea oblicua?
Para los ejercicios 79-84, graficar la desigualdad polar.
79)\(r<4\)
- Contestar
-
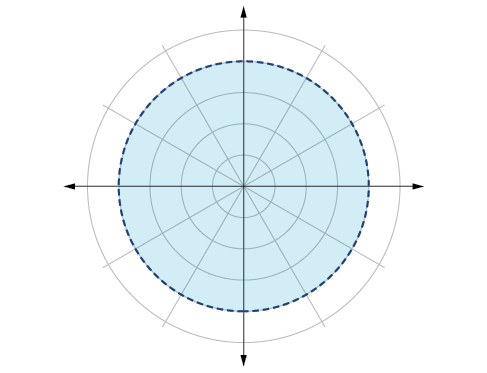
80)\(0\leq \theta \leq \dfrac{\pi }{4}\)
81)\(\theta = \dfrac{\pi }{4}, r\geq 2\)
- Contestar
-
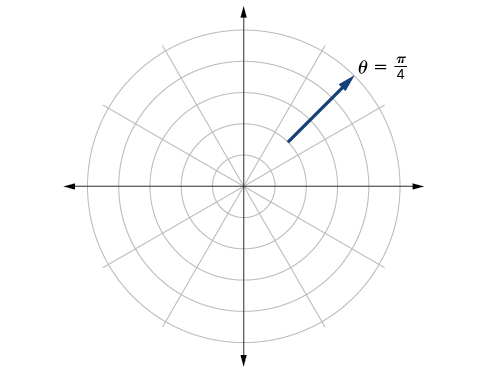
82)\(\theta = \dfrac{\pi }{4}, r\geq -3\)
83)\(0\leq \theta \leq \dfrac{\pi }{3}, r<2\)
- Contestar
-
84)\(\dfrac{-\pi }{6} < \theta \leq \dfrac{\pi }{3}, -3
8.4: Coordenadas polares - Gráficas
Verbal
1) Describir los tres tipos de simetría en las gráficas polares, y compararlos con la simetría del plano cartesiano.
- Contestar
-
La simetría con respecto al eje polar es similar a la simetría alrededor del\(x\) eje, la simetría con respecto al polo es similar a la simetría sobre el origen, y la simétrica con respecto a la línea\(\theta = \dfrac{\pi }{2}\) es similar a la simetría alrededor\(y\) del eje.
2) ¿Cuál de los tres tipos de simetrías para las gráficas polares corresponde a las\(x\) simetrías con respecto al\(y\) eje, eje y origen?
3) ¿Cuáles son los pasos a seguir a la hora de graficar ecuaciones polares?
- Contestar
-
Probar simetría; encontrar ceros, intercepciones y máximos; hacer una tabla de valores. Decidir el tipo general de gráfica, cardioide, limaçon, lemniscate, etc., luego trazar puntos en\(\theta = 0\),,\(\dfrac{\pi }{2}\)\(\pi \), y\(\dfrac{3\pi }{2}\) y bosquejar la gráfica.
4) Describir las formas de las gráficas de cardioides, limaçones y lemniscados.
5) ¿Qué parte de la ecuación determina la forma de la gráfica de una ecuación polar?
- Contestar
-
La forma de la gráfica polar está determinada por si incluye o no un seno, un coseno y constantes en la ecuación.
Gráfica
Para los ejercicios 6-15, pruebe la ecuación para la simetría.
6)\(r=5\cos 3\theta\)
7)\(r=3-3\cos \theta\)
- Contestar
-
simétrico con respecto al eje polar
8)\(r=3+2\sin \theta\)
9)\(r=3\sin 2\theta\)
- Contestar
-
simétrico con respecto al eje polar, simétrico con respecto a la línea\(\theta = \dfrac{\pi }{2}\)
,
10)\(r=4\)
11)\(r=2\theta \)
- Contestar
-
sin simetría
12)\(r=4\cos \dfrac{\theta }{2}\)
13)\(r=\dfrac{2}{\theta }\)
- Contestar
-
sin simetría
14)\(r=3\sqrt{1-\cos ^2\theta }\)
15)\(r=\sqrt{5\sin 2\theta }\)
- Contestar
-
simétrico con respecto al polo
Para los ejercicios 16-43, grafica la ecuación polar. Identificar el nombre de la forma.
16)\(r=3\cos \theta\)
17)\(r=4\sin \theta\)
- Contestar
-
círculo
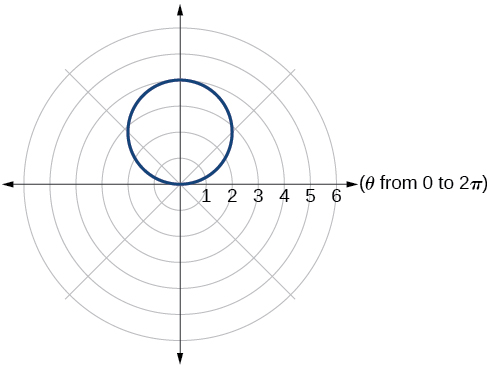
18)\(r=2+2\cos \theta\)
19)\(r=2-2\cos \theta\)
- Contestar
-
cardioide
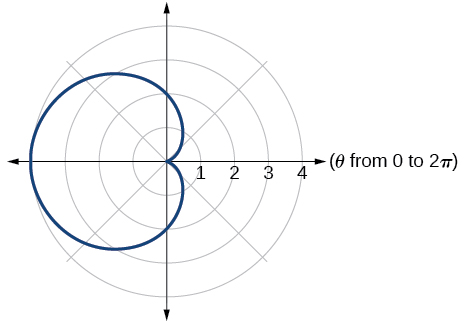
20)\(r=5-5\sin \theta\)
21)\(r=3+3\sin \theta\)
- Contestar
-
cardioide

22)\(r=3+2\sin \theta\)
23)\(r=7+4\sin \theta\)
- Contestar
-
limaçon uno-loop/hoyuelos
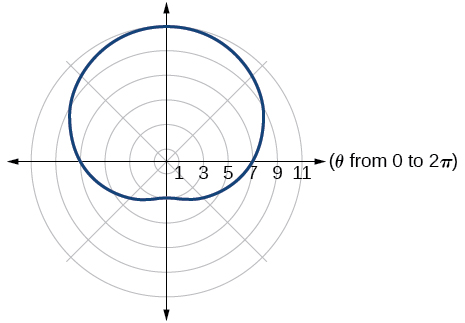
24)\(r=4+3\cos \theta\)
25)\(r=5+4cos \theta\)
- Contestar
-
limaçon uno-loop/hoyuelos
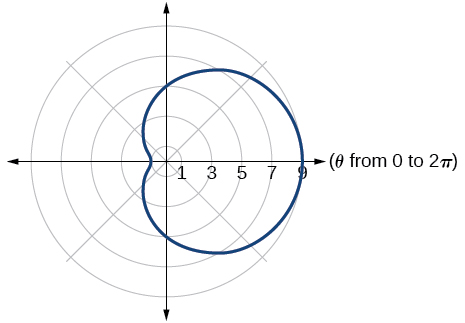
26)\(r=10+9\cos \theta\)
27)\(r=1+3\sin \theta\)
- Responder
-
lazo interior/ limaçon de dos bucles
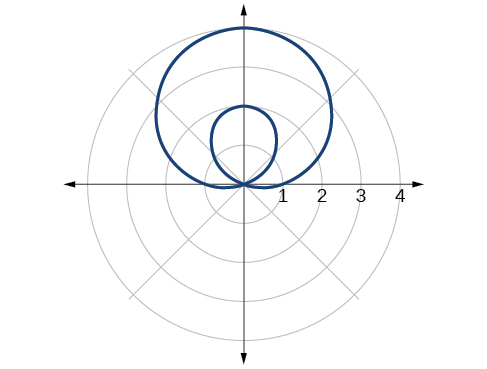
28)\(r=2+5\sin \theta\)
29)\(r=5+7\sin \theta\)
- Responder
-
lazo interior/ limaçon de dos bucles
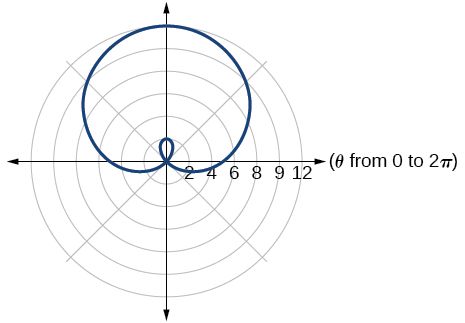
30)\(r=2+4\cos \theta\)
31)\(r=5+6\cos \theta\)
- Responder
-
lazo interior/ limaçon de dos bucles
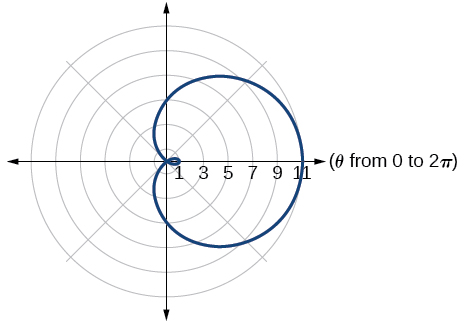
32)\(r^2=36\cos (2\theta )\)
33)\(r^2=10\cos (2\theta )\)
- Responder
-
lemniscado
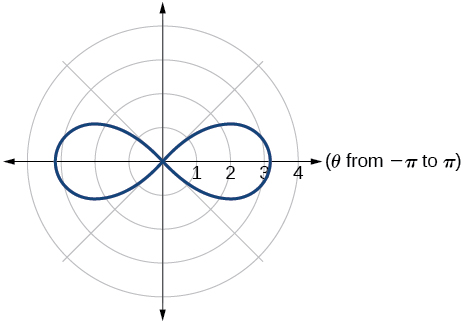
34)\(r^2=4\sin (2\theta )\)
35)\(r^2=10\sin (2\theta )\)
- Responder
-
lemniscado
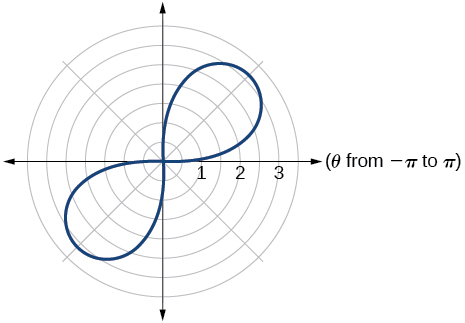
36)\(r=3\sin (2\theta )\)
37)\(r=3\cos (2\theta )\)
- Responder
-
curva rosa
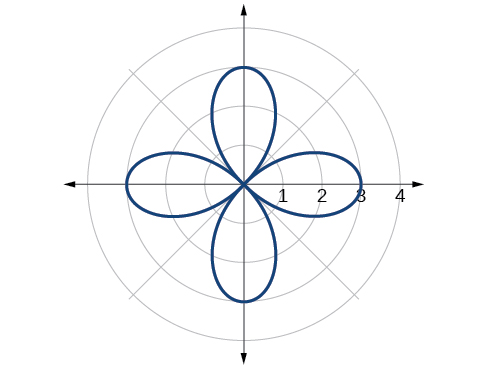
38)\(r=5\sin (3\theta )\)
39)\(r=4\sin (4\theta )\)
- Responder
-
curva rosa
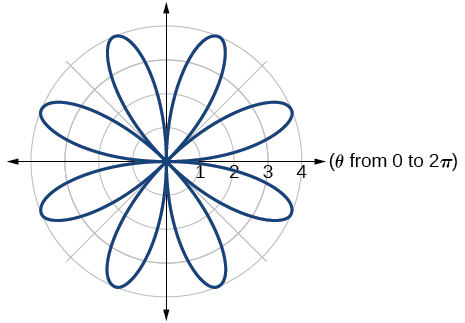
40)\(r=4\sin (5\theta )\)
41)\(r=-\theta\)
- Responder
-
Espiral de Arquímedes
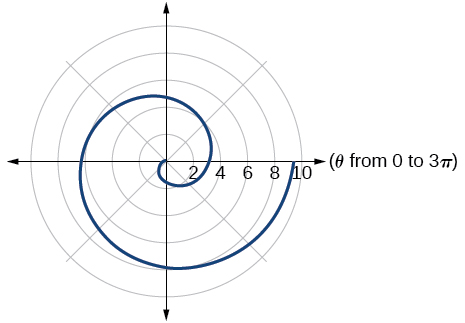
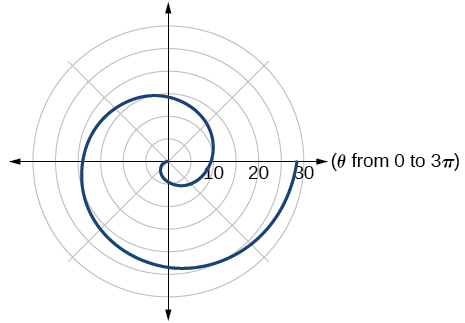
42)\(r=2\theta\)
43)\(r=-3\theta\)
- Responder
-
Espiral de Arquímedes
Tecnología
Para los ejercicios 44-53, utilice una calculadora gráfica para bosquejar la gráfica de la ecuación polar.
44)\(r=\dfrac{1}{\theta }\)
45)\(r=\dfrac{1}{\sqrt{\theta }}\)
- Responder
-
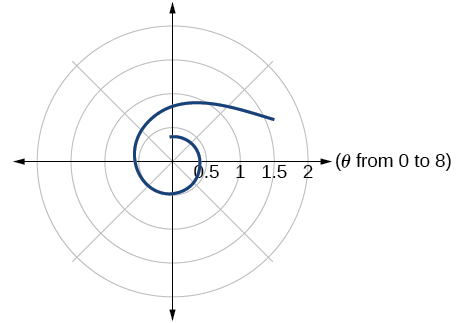
46)\(r=2\sin \theta \tan \theta\), un cissoide
47)\(r=2\sqrt{1-\sin ^2\theta }\), un hipopedo
- Responder
-
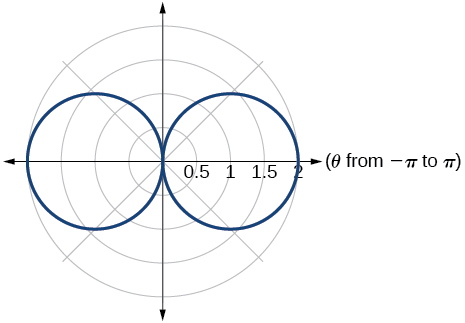
48)\(r=5+\cos (4\theta )\)
49)\(r=2-\sin (2\theta )\)
- Responder
-
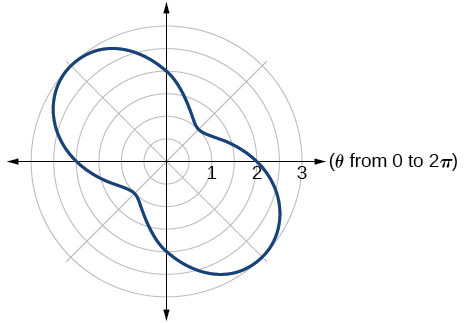
50)\(r=\theta ^2\)
51)\(r=\theta +1\)
- Responder
-
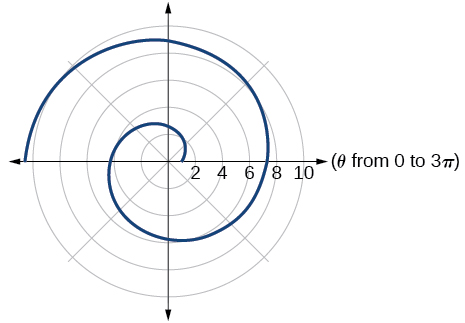
52)\(r=\theta \sin \theta\)
53)\(r=\theta \cos \theta\)
- Responder
-
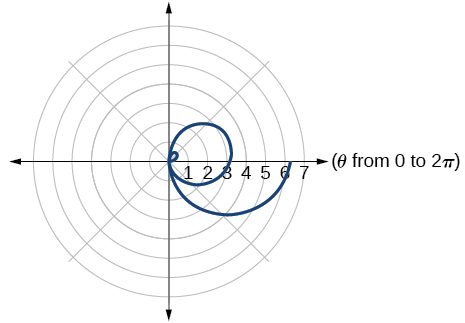
Para los ejercicios 54-63, utilice una utilidad gráfica para graficar cada par de ecuaciones polares en un dominio de\([0,4\pi ]\) y luego explicar las diferencias que se muestran en las gráficas.
54)\(r=\theta ,r=-\theta\)
55)\(r=\theta ,r=\theta +\sin \theta\)
- Responder
-
Ambas son espirales, pero no del todo lo mismo.
56)\(r=\sin \theta +\theta ,r=\sin \theta -\theta\)
57)\(r=2\sin \left (\dfrac{\theta }{2} \right ),r=\theta \sin \left (\dfrac{\theta }{2} \right )\)
- Responder
-
Ambas gráficas son curvas con\(2\) bucles. La ecuación con un coeficiente de\(\theta \) tiene dos bucles a la izquierda, la ecuación con un coeficiente de\(2\) tiene dos bucles uno al lado del otro. Grafica estos de\(0\)\(4\pi \) a para obtener una mejor imagen.
58)\(r=\sin (\cos (3\theta )),r=\sin (3\theta )\)
59) En una utilidad gráfica, grafica\(r=\sin \left (\dfrac{16}{5}\theta \right )\) sobre\([0,4\pi ]\)\([0,8\pi ]\),\([0,12\pi ]\) y\([0,16\pi ]\)
- Responder
-
Cuando se incrementa el ancho del dominio, se ven más pétalos de la flor.
60) Sobre una utilidad gráfica, gráfica y boceto\(r=\sin \theta + \left(\sin \left(\dfrac{5}{2}\theta \right) \right)^3\) sobre\([0,4\pi ]\).
61) En una utilidad gráfica, graficar cada ecuación polar. Explica las similitudes y diferencias que observas en las gráficas. \[\begin{align*} r_1 &= 3\sin(3\theta )\\ r_2 &= 2\sin(3\theta )\\ r_3 &= \sin(3\theta ) \end{align*}\]
- Responder
-
Las gráficas son curvas de tres pétalos, rosas. Cuanto mayor sea el coeficiente, mayor será la distancia de la curva desde el polo.
62) En una utilidad gráfica, graficar cada ecuación polar. Explica las similitudes y diferencias que observas en las gráficas. \[\begin{align*} r_1 &= 3+3\cos(\theta )\\ r_2 &= 2+2\cos(\theta )\\ r_3 &= 1+\cos(\theta ) \end{align*}\]
63) En una utilidad gráfica, graficar cada ecuación polar. Explica las similitudes y diferencias que observas en las gráficas. \[\begin{align*} r_1 &= 3\theta \\ r_2 &= 2\theta \\ r_3 &= \theta \end{align*}\]
- Responder
-
Las gráficas son espirales. Cuanto menor es el coeficiente, más apretada es la espiral.
Extensiones
Para los ejercicios 64-72, dibuja cada ecuación polar en el mismo conjunto de ejes polares, y encuentra los puntos de intersección.
64)\(r_1=3+2\sin \theta , r_2=2\)
65)\(r_1=6-4\cos \theta , r_2=4\)
- Responder
-
\(\left ( 4,\dfrac{\pi }{3} \right ), \left ( 4,\dfrac{5\pi }{3} \right )\)
66)\(r_1=1+\sin \theta , r_2=3\sin \theta\)
67)\(r_1=1+\cos \theta , r_2=3\cos \theta\)
- Responder
-
\(\left ( \dfrac{3}{2},\dfrac{\pi }{3} \right ), \left ( \dfrac{3}{2},\dfrac{5\pi }{3} \right )\)
68)\(r_1=\cos (2\theta ), r_2=\sin (2\theta )\)
69)\(r_1=\sin ^2(2\theta ), r_2=1-\cos (4\theta )\)
- Responder
-
\(\left ( 0,\dfrac{\pi }{2} \right ), (0,\pi ), \left ( 0,\dfrac{3\pi }{2} \right ), (0,2\pi )\)
70)\(r_1=\sqrt{3}, r_2=2\sin (\theta )\)
71)\(r_1^2=\sin \theta , r_2^2=\cos \theta\)
- Responder
-
\(\left ( \dfrac{\sqrt[4]{8}}{2},\dfrac{\pi }{4} \right )\),\(\left ( \dfrac{\sqrt[4]{8}}{2},\dfrac{5\pi }{4} \right )\), y en\(\theta =\dfrac{3\pi }{4}\),\(\dfrac{7\pi }{4}\) ya que\(r\) se cuadra
72)\(r_1=1+\cos \theta , r_2=1-\sin \theta\)
8.5: Forma polar de números complejos
Verbal
1) Un número complejo es\(a+bi\). Explique cada parte.
- Responder
-
\(a\)es la parte real,\(b\) es la parte imaginaria, y\(i=\sqrt{-1}\)
2) ¿Qué representa el valor absoluto de un número complejo?
3) ¿Cómo se convierte un número complejo a forma polar?
- Responder
-
La forma polar convierte la parte real e imaginaria del número complejo en forma polar usando\(x=r\cos \theta\) y\(y=r\sin \theta\).
4) ¿Cómo encontramos el producto de dos números complejos?
5) ¿Qué es el teorema de De Moivre y para qué se utiliza?
- Responder
-
\(z^n=r^n(\cos (n\theta )+i\sin (n\theta ))\)
Se utiliza para simplificar la forma polar cuando un número ha sido elevado a una potencia.
Algebraico
Para los ejercicios 6-11, encuentra el valor absoluto del número complejo dado.
6)\(5+3i\)
7)\(-7+i\)
- Responder
-
\(5\sqrt{2}\)
8)\(-3-3i\)
9)\(\sqrt{2}-6i\)
- Responder
-
\(\sqrt{38}\)
10)\(2i\)
11)\(2.2-3.1i\)
- Responder
-
\(\sqrt{14.45}\)
Para los ejercicios 12-16, escriba el número complejo en forma polar.
12)\(2+2i\)
13)\(8-4i\)
- Responder
-
\(4\sqrt{5}\mathbf{cis}(333.4^{\circ})\)
14)\(-\dfrac{1}{2}-\dfrac{1}{2}i\)
15)\(\sqrt{3}+i\)
- Responder
-
\(2\mathbf{cis}\left ( \dfrac{\pi }{6} \right )\)
16)\(3i\)
Para los ejercicios 17-22, convertir el número complejo de forma polar a rectangular.
17)\(z=7\mathbf{cis}\left ( \dfrac{\pi }{6} \right )\)
- Responder
-
\(\dfrac{7\sqrt{3}}{2}+i\dfrac{7}{2}\)
18)\(z=2\mathbf{cis}\left ( \dfrac{\pi }{3} \right )\)
19)\(z=4\mathbf{cis}\left ( \dfrac{7\pi }{6} \right )\)
- Responder
-
\(-2\sqrt{3}-2i\)
20)\(z=7\mathbf{cis}(25^{\circ})\)
21)\(z=3\mathbf{cis}(240^{\circ})\)
- Responder
-
\(-1.5-i\dfrac{3\sqrt{3}}{2}\)
22)\(z=\sqrt{2}\mathbf{cis}(100^{\circ})\)
Para los ejercicios 23-28, encuentra\(z_1 z_2\) en forma polar.
23)\(z_1=2\sqrt{3}\mathbf{cis}(116^{\circ}); z_2=2\mathbf{cis}(82^{\circ})\)
- Responder
-
\(4\sqrt{3}\mathbf{cis}(198^{\circ})\)
24)\(z_1=\sqrt{2}\mathbf{cis}(205^{\circ}); z_2=2\sqrt{2}\mathbf{cis}(118^{\circ})\)
25)\(z_1=3\mathbf{cis}(120^{\circ}); z_2=\dfrac{1}{4}\mathbf{cis}(60^{\circ})\)
- Responder
-
\(\dfrac{3}{4}\mathbf{cis}(180^{\circ})\)
26)\(z_1=3\mathbf{cis} \left(\dfrac{\pi }{4} \right); z_2=5\mathbf{cis}\left(\dfrac{\pi }{6} \right)\)
27)\(z_1=\sqrt{5}\mathbf{cis} \left(\dfrac{5\pi }{8} \right); z_2=\sqrt{15}\mathbf{cis}\left(\dfrac{\pi }{12} \right)\)
- Responder
-
\(5\sqrt{3}\mathbf{cis} \left(\dfrac{17\pi }{24} \right)\)
28)\(z_1=4\mathbf{cis} \left(\dfrac{\pi }{2} \right); z_2=2\mathbf{cis}\left(\dfrac{\pi }{4} \right)\)
Para los ejercicios 29-,34 encuentran\(\dfrac{z_1}{z_2}\) en forma polar.
29)\(z_1=21\mathbf{cis}(135^{\circ}); z_2=3\mathbf{cis}(65^{\circ})\)
- Responder
-
\(7\mathbf{cis}(70^{\circ})\)
30)\(z_1=\sqrt{2}\mathbf{cis}(90^{\circ}); z_2=2\mathbf{cis}(60^{\circ})\)
31)\(z_1=15\mathbf{cis}(120^{\circ}); z_2=3\mathbf{cis}(40^{\circ})\)
- Responder
-
\(5\mathbf{cis}(80^{\circ})\)
32)\(z_1=6\mathbf{cis} \left(\dfrac{\pi }{3} \right); z_2=2\mathbf{cis}\left(\dfrac{\pi }{4} \right)\)
33)\(z_1=5\sqrt{2}\mathbf{cis} (\pi ); z_2=\sqrt{2}\mathbf{cis}\left(\dfrac{2\pi }{3} \right)\)
- Responder
-
\(5\mathbf{cis} \left(\dfrac{\pi }{3} \right)\)
34)\(z_1=2\mathbf{cis} \left(\dfrac{3\pi }{5} \right); z_2=3\mathbf{cis}\left(\dfrac{\pi }{4} \right)\)
Para los ejercicios 35-40, encuentra los poderes de cada número complejo en forma polar.
35) Encuentra\(z^3\) cuándo\(z=5\mathbf{cis} (45^{\circ})\).
- Responder
-
\(125\mathbf{cis} (135^{\circ})\)
36) Encuentra\(z^4\) cuándo\(z=2\mathbf{cis} (70^{\circ})\).
37) Encuentra\(z^2\) cuándo\(z=3\mathbf{cis} (120^{\circ})\).
- Responder
-
\(9\mathbf{cis} (240^{\circ})\)
38) Encuentra\(z^2\) cuándo\(z=4\mathbf{cis}\left(\dfrac{\pi }{4} \right)\).
39) Encuentra\(z^4\) cuándo\(z=\mathbf{cis}\left(\dfrac{3\pi }{16} \right)\).
- Responder
-
\(\mathbf{cis}\left(\dfrac{3\pi }{4} \right) \)
40) Encuentra\(z^3\) cuándo\(z=3\mathbf{cis}\left(\dfrac{5\pi }{3} \right)\).
Para los ejercicios 41-45, evalúe cada raíz.
41) Evaluar la raíz cubo de\(z\) cuándo\(z=27\mathbf{cis} (240^{\circ})\).
- Responder
-
\(3\mathbf{cis}(80^{\circ}), 3\mathbf{cis}(200^{\circ}), 3\mathbf{cis}(320^{\circ})\)
42) Evaluar la raíz cuadrada de\(z\) cuándo\(z=16\mathbf{cis} (100^{\circ})\).
43) Evaluar la raíz cubo de\(z\) cuándo\(z=32\mathbf{cis} \left(\dfrac{2\pi }{3} \right)\).
- Responder
-
\(2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{2\pi }{9} \right), 2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{8\pi }{9} \right), 2\sqrt[3]{4}\mathbf{cis} \left(\dfrac{14\pi }{9} \right)\)
44) Evaluar la raíz cuadrada de\(z\) cuándo\(z=32\mathbf{cis} (\pi )\).
45) Evaluar la raíz cubo de\(z\) cuándo\(z=8\mathbf{cis} \left(\dfrac{7\pi }{4} \right)\).
- Responder
-
\(2\sqrt{2}\mathbf{cis} \left(\dfrac{7\pi }{8} \right), 2\sqrt{2}\mathbf{cis} \left(\dfrac{15\pi }{8} \right)\)
Gráfica
Para los ejercicios 46-55, trazar el número complejo en el plano complejo.
46)\(2+4i\)
47)\(-3-3i\)
- Responder
-
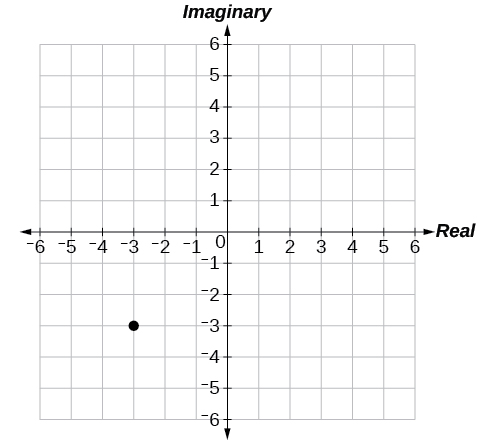
48)\(5-4i\)
49)\(-1-5i\)
- Responder
-
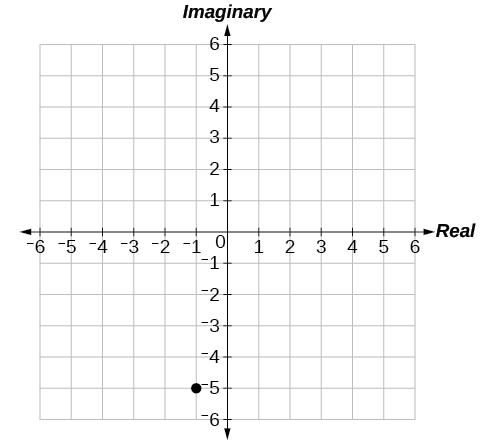
50)\(3+2i\)
51)\(2i\)
- Responder
-
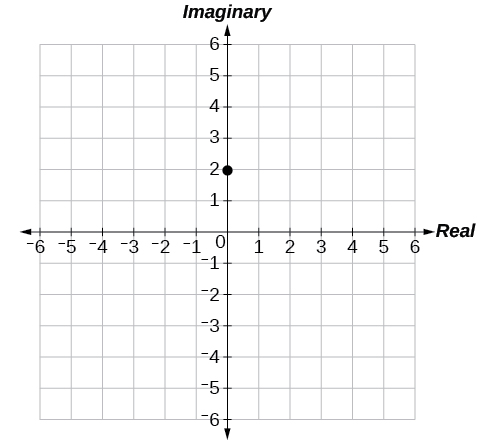
52)\(-4\)
53)\(6-2i\)
- Responder
-
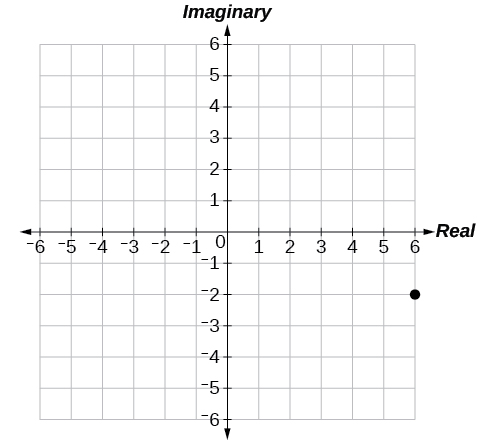
54)\(-2+i\)
55)\(1-4i\)
- Responder
-
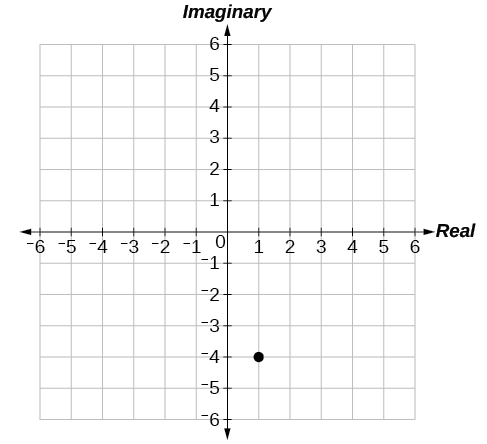
Tecnología
Para los ejercicios 56-, encuentra todas las respuestas redondeadas a la centésima más cercana.
56) Utilice la característica rectangular a polar en la calculadora gráfica para cambiar\(5+5i\) a la forma polar.
57) Utilice la característica rectangular a polar en la calculadora gráfica para cambiar\(3-2i\) a la forma polar.
- Responder
-
\(3.61e^{-0.59i}\)
58) Utilice la característica rectangular a polar en la calculadora gráfica para cambiar\(-3-8i\) a la forma polar.
59) Utilice la característica polar a rectangular en la calculadora gráfica para cambiar\(4\mathbf{cis} (120^{\circ})\) a forma rectangular.
- Responder
-
\(-2+3.46i\)
60) Utilice la característica polar a rectangular en la calculadora gráfica para cambiar\(2\mathbf{cis} (45^{\circ})\) a forma rectangular.
61) Utilice la característica polar a rectangular en la calculadora gráfica para cambiar\(5\mathbf{cis} (210^{\circ})\) a forma rectangular.
- Responder
-
\(-4.33-2.50i\)
8.6: Ecuaciones paramétricas
Verbal
1) ¿Qué es un sistema de ecuaciones paramétricas?
- Responder
-
Un par de funciones que depende de un factor externo. Las dos funciones están escritas en términos de un mismo parámetro. Por ejemplo,\(x=f(t)\) y\(y=f(t)\).
2) Algunos ejemplos de un tercer parámetro son el tiempo, la longitud, la velocidad y la escala. Explique cuándo se usa el tiempo como parámetro.
3) Explicar cómo eliminar un parámetro dado un conjunto de ecuaciones paramétricas.
- Responder
-
Elija una ecuación para resolver\(t\), sustituya en la otra ecuación y simplifique.
4) ¿Cuál es el beneficio de escribir un sistema de ecuaciones paramétricas como una ecuación cartesiana?
5) ¿Cuál es el beneficio de usar ecuaciones paramétricas?
- Responder
-
Algunas ecuaciones no pueden escribirse como funciones, como un círculo. Sin embargo, cuando se escriben como dos ecuaciones paramétricas, por separado las ecuaciones son funciones.
6) ¿Por qué hay muchos conjuntos de ecuaciones paramétricas para representar en la función cartesiana?
Algebraico
Para los ejercicios 7-25, eliminar el parámetro\(t\) para reescribir la ecuación paramétrica como una ecuación cartesiana.
7)\(\begin{cases} & x(t)= 5-t\\ & y(t)= 8-2t \end{cases}\)
- Responder
-
\(y=-2+2x\)
8)\(\begin{cases} & x(t)= 6-3t\\ & y(t)= 10-t \end{cases}\)
9)\(\begin{cases} & x(t)= 2t+1\\ & y(t)= 3\sqrt{t} \end{cases}\)
- Responder
-
\(y=3\sqrt{\dfrac{x-1}{2}}\)
10)\(\begin{cases} & x(t)= 3t-1\\ & y(t)= 2t^2 \end{cases}\)
11)\(\begin{cases} & x(t)= 2e^t\\ & y(t)= 1-5t \end{cases}\)
- Responder
-
\(x=2e^{\tfrac{1-y}{5}}\)o\(y=1-5\ln \left ( \dfrac{x}{2} \right )\)
12)\(\begin{cases} & x(t)= e^{-2t}\\ & y(t)= 2e^{-t} \end{cases}\)
13)\(\begin{cases} & x(t)= 4\log (t)\\ & y(t)= 3+2t \end{cases}\)
- Responder
-
\(x=4\log \left ( \dfrac{y-3}{2} \right )\)
14)\(\begin{cases} & x(t)= \log (2t)\\ & y(t)= \sqrt{t-1} \end{cases}\)
15)\(\begin{cases} & x(t)= t^3-t\\ & y(t)= 2t \end{cases}\)
- Responder
-
\(x=\left ( \dfrac{y}{2} \right )^3-\dfrac{y}{2}\)
16)\(\begin{cases} & x(t)= t-t^4\\ & y(t)= t+2 \end{cases}\)
17)\(\begin{cases} & x(t)= e^{2t}\\ & y(t)= e^{6t} \end{cases}\)
- Responder
-
\(y=x^3\)
18)\(\begin{cases} & x(t)= t^{5}\\ & y(t)= t^{10} \end{cases}\)
19)\(\begin{cases} & x(t)= 4\cos t\\ & y(t)= 5\sin t \end{cases}\)
- Responder
-
\(\left ( \dfrac{x}{4} \right )^2+\left ( \dfrac{y}{5} \right )^2=1\)
20)\(\begin{cases} & x(t)= 3\sin t\\ & y(t)= 6\cos t \end{cases}\)
21)\(\begin{cases} & x(t)= 2\cos ^2t\\ & y(t)= -\sin t \end{cases}\)
- Responder
-
\(y^2=1-\dfrac{1}{2}x\)
22)\(\begin{cases} & x(t)= \cos t+4\\ & y(t)= 2\sin ^2t \end{cases}\)
23)\(\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\)
- Responder
-
\(y=x^2+2x+1\)
24)\(\begin{cases} & x(t)= -t\\ & y(t)= t^3+1 \end{cases}\)
25)\(\begin{cases} & x(t)= 2t-1\\ & y(t)= t^3-2 \end{cases}\)
- Responder
-
\(y=\left ( \dfrac{x+1}{2} \right )^3 - 2\)
Para los ejercicios 26-29, reescribir la ecuación paramétrica como una ecuación cartesiana construyendo una\(x-y\) tabla.
26)\(\begin{cases} & x(t)= 2t-1\\ & y(t)= t+4 \end{cases}\)
27)\(\begin{cases} & x(t)= 4-t\\ & y(t)= 3t+2 \end{cases}\)
- Responder
-
\(y=-3x+14\)
28)\(\begin{cases} & x(t)= 2t-1\\ & y(t)= 5t \end{cases}\)
29)\(\begin{cases} & x(t)= 4t-1\\ & y(t)= 4t+2 \end{cases}\)
- Responder
-
\(y=x+3\)
Para los ejercicios 30-33, parametriza (escribe ecuaciones paramétricas para) cada ecuación cartesiana estableciendo\(x(t)=t\) o ajustando\(y(t)=t\).
30)\(y(x)=3x^2 + 3\)
31)\(y(x)=2\sin x + 1\)
- Responder
-
\(\begin{cases} & x(t)= t\\ & y(t)= 2\sin t + 1 \end{cases}\)
32)\(x(y)=3\log (y)+y\)
33)\(x(y)=\sqrt{y}+2y\)
- Responder
-
\(\begin{cases} & x(t)= \sqrt{t}+2t\\ & y(t)= t \end{cases}\)
Para los ejercicios 34-41, parametrizar (escribir ecuaciones paramétricas para) cada ecuación cartesiana usando\(x(t)=a\cos t\) y\(y(t)=b\sin t\). Identificar la curva.
34)\(\dfrac{x^2}{4}+\dfrac{x^2}{9}=1\)
35)\(\dfrac{x^2}{16}+\dfrac{x^2}{36}=1\)
- Responder
-
\(\begin{cases} & x(t)= 4\cos t\\ & y(t)= 6\sin t \end{cases}; \text{Ellipse}\)
36)\(x^2 + y^2 = 16\)
37)\(x^2 + y^2 = 10\)
- Responder
-
\(\begin{cases} & x(t)= \sqrt{10}\cos t\\ & y(t)= \sqrt{10}\sin t \end{cases}; \text{Circle}\)
38) Parameterizar la línea de\((3,0)\) a para\((-2,-5)\) que la línea esté\((3,0)\) en at\(t=0\), y\((-2,-5)\) at\(t=1\).
39) Parameterizar la línea de\((-1,0)\) a para\((3,-2)\) que la línea esté\((-1,0)\) en at\(t=0\), y\((3,-2)\) at\(t=1\).
- Responder
-
\(\begin{cases} & x(t)= -1+4t\\ & y(t)= -2t \end{cases}\)
40) Parameterizar la línea de\((-1,5)\) a para\((2,3)\) que la línea esté\((-1,5)\) en\(t=0\), y\((2,3)\) en\(t=1\).
41) Parameterizar la línea de\((4,1)\) a para\((6,-2)\) que la línea esté\((4,1)\) en\(t=0\), y\((6,-2)\) en\(t=1\).
- Responder
-
\(\begin{cases} & x(t)= 4+2t\\ & y(t)= 1-3t \end{cases}\)
Tecnología
Para los ejercicios 42-43, utilice la función de tabla en la calculadora gráfica para determinar si las gráficas se cruzan.
42)\(\begin{cases} & x_1(t)= 3t\\ & y_1(t)= 2t-1 \end{cases}\; \; \text{and}\; \; \begin{cases} & x_2(t)= t+3\\ & y_2(t)= 4t-4 \end{cases}\)
43)\(\begin{cases} & x_1(t)= t^2\\ & y_1(t)= 2t-1 \end{cases}\; \; \text{and}\; \; \begin{cases} & x_2(t)= -t+6\\ & y_2(t)= t+1 \end{cases}\)
- Responder
-
sí, a\(t=2\)
Para los ejercicios 44-46, utilice una calculadora gráfica para completar la tabla de valores para cada conjunto de ecuaciones paramétricas.
44)\(\begin{cases} & x_1(t)= 3t^2-3t+7\\ & y_1(t)= 2t+3 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| \ (t\) ">-1 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">0 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">1 | \ (x\) "> | \ (y\) "> |
45)\(\begin{cases} & x_1(t)= t^2-4\\ & y_1(t)= 2t^2-1 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">1 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style: discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-style:dashed; border-top-ancho:1px; tamaño-caja:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; padding-top:16px; text-align:center; vertical-align:top; palabra:break-word; ">2 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style: discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-estilo:discontinuo; border-top-ancho:1px; tamaño-caja:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style: discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-estilo:discontinuo; border-top-ancho:1px; tamaño-caja:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">3 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
- Responder
-
\(t\) \(x\) \(y\) \ (t\) ">1 \ (x\) ">-3 \ (y\) ">1 \ (t\) ">2 \ (x\) ">0 \ (y\) ">7 \ (t\) ">3 \ (x\) ">5 \ (y\) ">17
46)\(\begin{cases} & x_1(t)= t^4\\ & y_1(t)= t^3+4 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">-1 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style: discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-estilo:discontinuo; border-top-ancho:1px; tamaño-caja:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">0 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style: discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-estilo:discontinuo; border-top-ancho:1px; tamaño-caja:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-color:rgb (239, 239); background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style: discontinuo; border-bottom-width:1px; border-image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:none; border-image-width:1; border-left-color:rgb (204, 204); border-izquierda-estilo:dashed; border-izquierda-ancho:1px; border-derecha-color:rgb (204, 204); border-derecha-estilo:dashed ed; frontera-derecha ancho:1px; border-top-color:rgb (204, 204); border-top-estilo:discontinuo; border-top-ancho:1px; tamaño-caja:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">1 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
| \ (t\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; ">2 | \ (x\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> | \ (y\)” style="background-attachment:scroll; background-clip:border-box; background-image:none; background-origin:padding-box; background-position-x: 0%; background-position-y: 0%; background-repeat:repeat; background-size:auto; border-bottom-color:rgb (204, 204); border-bottom-style:dashed; border-bottom-width:1px; frontera -image-outset:0; border-image-repetir:stretch; border-image-slice: 100%; border-image-fuente:ninguno; border-image-width:1; border-left-color:rgb (204, 204); border-left-style:dashed; border-left-width:1px; border-rightcolor:rgb (204, 204); border-rightstyle:dashed; border-rightwidth:1px; border-top-top-color:rgb (204, 204 , 204); border-top-style:dashed; border-top-width:1px; box-sizing:border-box; padding-bottom:16px; padding-izquierda:16px; padding-derecha:16px; padding-top:16px; text-align:center; vertical-align:top; word-wrap:break-word; "> |
Extensiones
47) Encuentra dos conjuntos diferentes de ecuaciones paramétricas para\(y=(x+1)^2\).
- Responder
-
las respuestas pueden variar:\(\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\; \; \text{and}\; \; \begin{cases} & x(t)= t+1\\ & y(t)= (t+2)^2 \end{cases}\)
48) Encuentra dos conjuntos diferentes de ecuaciones paramétricas para\(y=3x-2\).
49) Encuentra dos conjuntos diferentes de ecuaciones paramétricas para\(y=x^2-4x+4\).
- Responder
-
las respuestas pueden variar:\(\begin{cases} & x(t)= t\\ & y(t)= t^2-4t+4 \end{cases}\; \; \text{and}\; \; \begin{cases} & x(t)= t+2\\ & y(t)= t^2 \end{cases}\)
8.7: Ecuaciones Paramétricas - Gráficas
Verbal
1) ¿Cuáles son los dos métodos utilizados para graficar ecuaciones paramétricas?
- Responder
-
trazar puntos con la flecha de orientación y una calculadora gráfica
2) ¿Cuál es una diferencia en las ecuaciones paramétricas de trazado de puntos en comparación con las ecuaciones cartesianas?
3) ¿Por qué algunas gráficas se dibujan con flechas?
- Responder
-
Las flechas muestran la orientación, la dirección del movimiento de acuerdo con valores crecientes de\(t\).
4) Nombrar algunos tipos comunes de gráficas de ecuaciones paramétricas.
5) ¿Por qué las gráficas paramétricas son importantes para entender el movimiento de los proyectiles
- Responder
-
Las ecuaciones paramétricas muestran los diferentes movimientos verticales y horizontales a lo largo del tiempo.
Gráfica
Para los ejercicios 6-11, grafica cada conjunto de ecuaciones paramétricas haciendo una tabla de valores. Incluya la orientación en la gráfica.
6)\(\begin{cases} & x(t)= t\\ & y(t)= t^2-1 \end{cases}\)
| \(t\) | \(x\) | \(y\) |
|---|---|---|
| \ (t\) ">-3 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">-2 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">-1 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">0 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">1 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">2 | \ (x\) "> | \ (y\) "> |
| \ (t\) ">3 |
7)\(\begin{cases} & x(t)= t-1\\ & y(t)= t^2 \end{cases}\)
| \(t\) | -3 | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|---|
| \(x\) | ||||||
| \(y\) |
- Responder
-
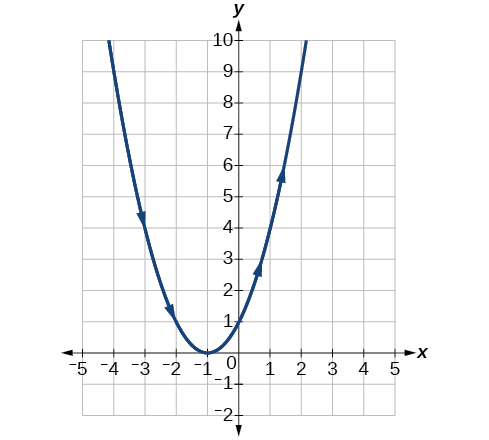
8)\(\begin{cases} & x(t)= 2+t\\ & y(t)= 3-2t \end{cases}\)
| \(t\) | -2 | -1 | 0 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| \(x\) | ||||||
| \(y\) |
9)\(\begin{cases} & x(t)= -2-2t\\ & y(t)= 3+t \end{cases}\)
| \(t\) | -3 | -2 | -1 | 0 | 1 |
|---|---|---|---|---|---|
| \(x\) | |||||
| \(y\) |
- Responder
-
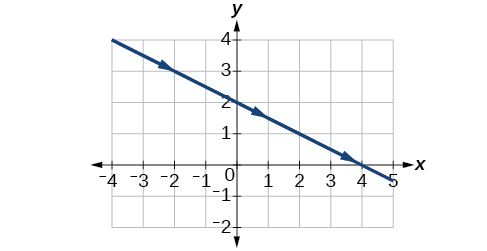
10)\(\begin{cases} & x(t)= t^3\\ & y(t)= t+2 \end{cases}\)
| \(t\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(x\) | |||||
| \(y\) |
11)\(\begin{cases} & x(t)= t^2\\ & y(t)= t+3 \end{cases}\)
| \(t\) | -2 | -1 | 0 | 1 | 2 |
|---|---|---|---|---|---|
| \(x\) | |||||
| \(y\) |
- Responder
-
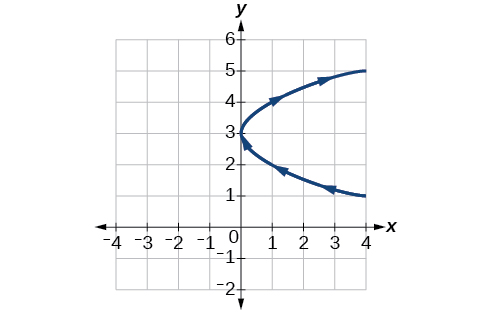
Para los ejercicios 12-22, esboza la curva e incluye la orientación.
12)\(\begin{cases} & x(t)= t\\ & y(t)= \sqrt{t} \end{cases}\)
13)\(\begin{cases} & x(t)= -\sqrt{t}\\ & y(t)= t \end{cases}\)
- Responder
-
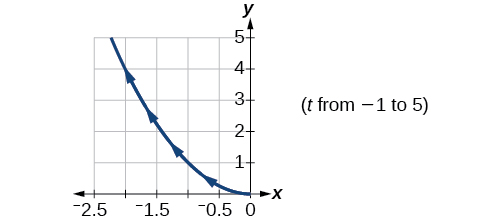
14)\(\begin{cases} & x(t)= 5-\left | t \right |\\ & y(t)= t+2 \end{cases}\)
15)\(\begin{cases} & x(t)= -t+2\\ & y(t)= 5-\left | t \right | \end{cases}\)
- Responder
-
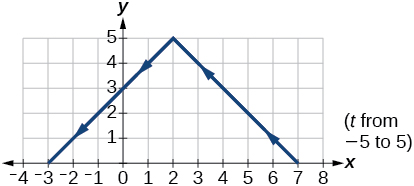
16)\(\begin{cases} & x(t)= 4\sin t\\ & y(t)= 2\cos t \end{cases}\)
17)\(\begin{cases} & x(t)= 2\sin t\\ & y(t)= 4\cos t \end{cases}\)
- Responder
-
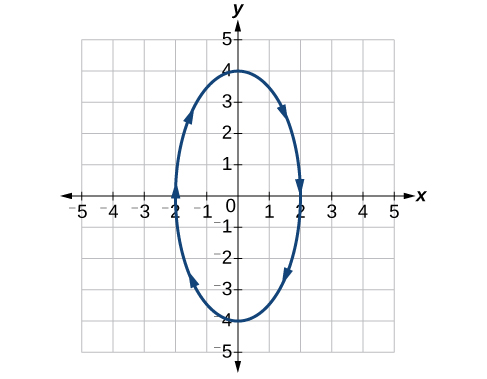
18)\(\begin{cases} & x(t)= 3\cos ^2t\\ & y(t)= -3\sin t \end{cases}\)
19)\(\begin{cases} & x(t)= 3\cos ^2t\\ & y(t)= -3\sin ^2t \end{cases}\)
- Responder
-
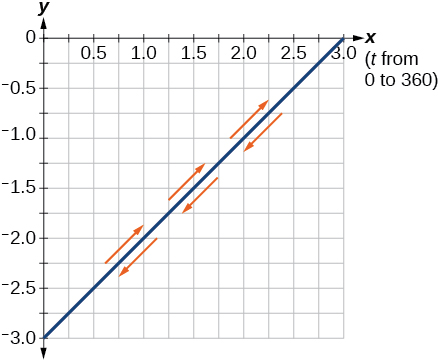
20)\(\begin{cases} & x(t)= \sec t\\ & y(t)= \tan t \end{cases}\)
21)\(\begin{cases} & x(t)= \sec t\\ & y(t)= \tan ^2t \end{cases}\)
- Responder
-
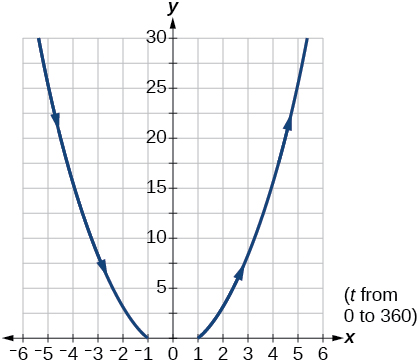
22)\(\begin{cases} & x(t)= \dfrac{1}{e^{2t}}\\ & y(t)= e^{-t} \end{cases}\)
Para los ejercicios 23-27, grafica la ecuación e incluye la orientación. Después, escribe la ecuación cartesiana.
23)\(\begin{cases} & x(t)= t-1\\ & y(t)= -t^2 \end{cases}\)
- Responder
-
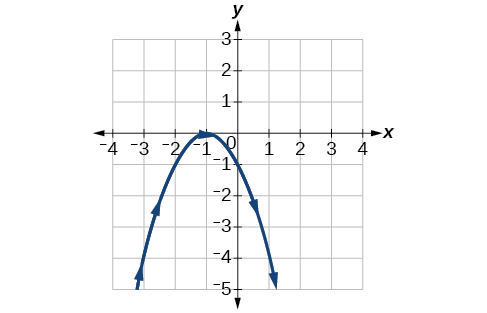
24)\(\begin{cases} & x(t)= t^3\\ & y(t)= t+3 \end{cases}\)
25)\(\begin{cases} & x(t)= 2\cos t\\ & y(t)= -\sin t \end{cases}\)
- Responder
-
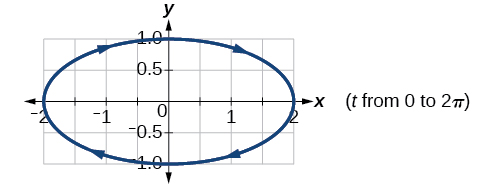
26)\(\begin{cases} & x(t)= 7\cos t\\ & y(t)= 7\sin t \end{cases}\)
27)\(\begin{cases} & x(t)= e^{2t}\\ & y(t)= -e^{t} \end{cases}\)
- Responder
-
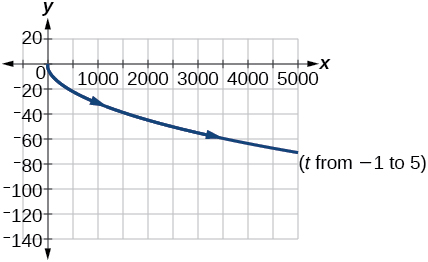
Para los ejercicios 28-33, grafica la ecuación e incluye la orientación.
28)\(x=t^2, y = 3t, 0\leq t\leq 5\)
29)\(x=2t, y = t^2, -5\leq t\leq 5\)
- Responder
-
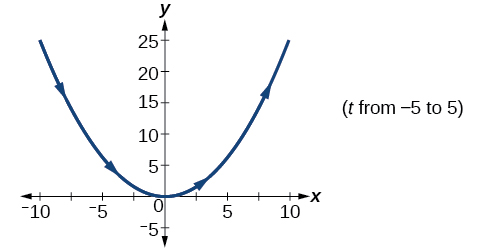
30)\(x=t, y=\sqrt{25-t^2}, 0<t\leq>
31)\(x(t)=-t,y(t)=\sqrt{t}, t\geq 0\)
- Responder
-
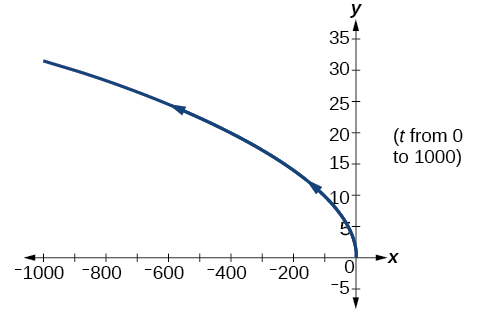
32)\(x=-2\cos t, y=6\sin t, 0\leq t\leq \pi\)
33)\(x=-\sec t, y=\tan t, -\dfrac{\pi }{2}< t< \dfrac{\pi }{2}\)
- Responder
-
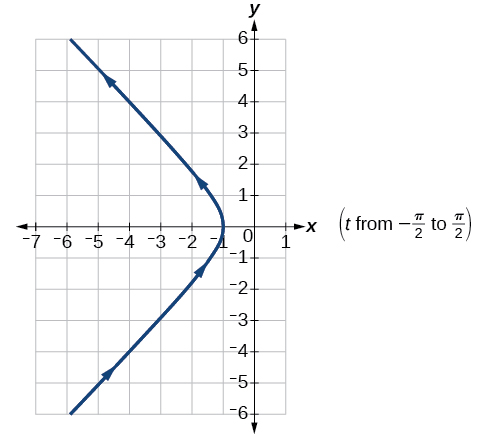
Para los ejercicios 34-41, utilice las ecuaciones paramétricas para números enteros\(a\) y\(b\):\[\begin{align*} x(t) &= a\cos ((a+b)t)\\ y(t) &= a\cos ((a-b)t) \end{align*} \nonumber\]
34) Gráfica sobre el dominio\([-\pi ,0]\), dónde\(a=2\) y\(b=1\), e incluye la orientación.
35) Gráfica sobre el dominio\([-\pi ,0]\), dónde\(a=3\) y\(b=2\), e incluye la orientación.
- Responder
-
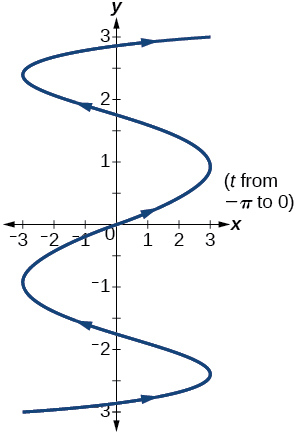
36) Gráfica sobre el dominio\([-\pi ,0]\), dónde\(a=4\) y\(b=3\), e incluye la orientación.
37) Gráfica sobre el dominio\([-\pi ,0]\), dónde\(a=5\) y\(b=4\), e incluye la orientación.
- Responder
-
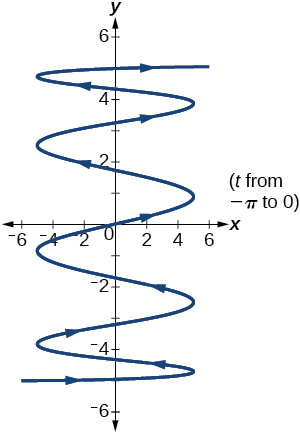
38) Si\(a\) es\(1\) mayor que\(b\), describa el efecto que tienen los valores de\(a\) y\(b\) tienen sobre la gráfica de las ecuaciones paramétricas.
39) Describir la gráfica si\(a=100\) y\(b=99\).
- Responder
-
Habrá movimientos\(100\) de ida y vuelta.
40) ¿Qué pasa si\(b\)
41) Si las ecuaciones paramétricas\(x(t)=t^2\) y\(y(t)=6-3t\) tienen la gráfica de una parábola horizontal que se abre a la derecha, ¿qué cambiaría la dirección de la curva?
- Responder
-
Toma lo contrario de la\(x(t)\) ecuación.
Para los ejercicios 42-46, describa la gráfica del conjunto de ecuaciones paramétricas.
42)\(x(t)=-t^2\) y\(y(t)\) es lineal
43)\(y(t)=t^2\) y\(x(t)\) es lineal
- Responder
-
Se abre la parábola.
44)\(y(t)=-t^2\) y\(x(t)\) es lineal
45) Escribir las ecuaciones paramétricas de un círculo con centro\((0,0)\)
- Responder
-
\(\begin{cases} & x(t)= 5\cos t\\ & y(t)= 5\sin t \end{cases}\)
46) Escribir las ecuaciones paramétricas de una elipse con centro\((0,0)\)
Para los ejercicios 47-52, utilice una utilidad gráfica para graficar en la ventana\([-3,3]\) por\([-3,3]\) en el dominio\([0,2\pi )\) para los siguientes valores de \(a\)e\(b\), e incluir la orientación. \[\begin{cases} & x(t)= \sin (at)\\ & y(t)= \sin (bt) \end{cases} \nonumber\]
47)\(a=1,b=2\)
- Responder
-
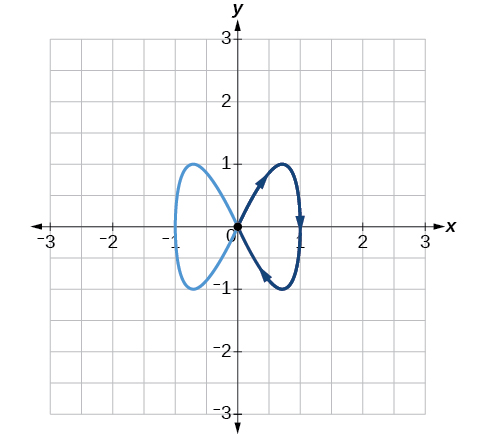
48)\(a=2, b=1\)
49)\(a=3, b=3\)
- Responder
-
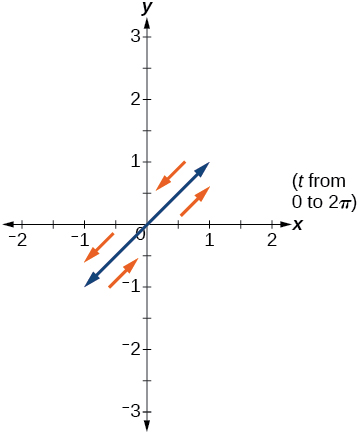
50)\(a=5, b=5\)
51)\(a=2, b=5\)
- Responder
-
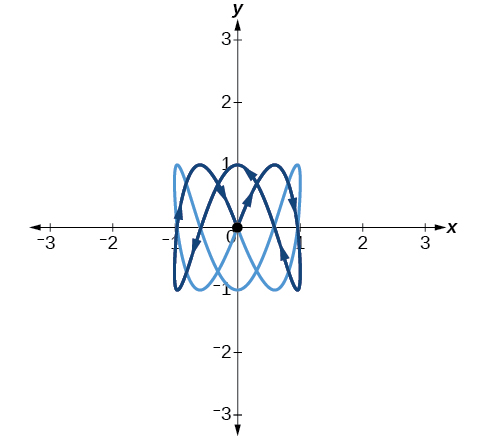
52)\(a=5, b=2\)
Tecnología
Para los ejercicios 53-56, mire las gráficas que fueron creadas por ecuaciones paramétricas de la forma\[\begin{cases} & x(t)= a\cos (bt)\\ & y(t)= c\sin (dt) \end{cases} \nonumber\] Utilice el modo paramétrico en la calculadora gráfica para encontrar los valores de\(a, b, c \), y\(d\) para lograr cada gráfica.
53)
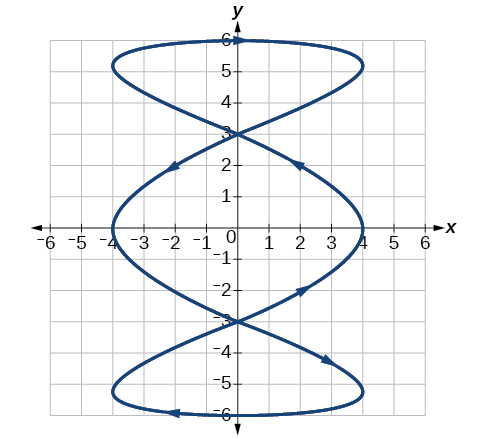
- Responder
-
\(a=4, b=3, c=6, d=1\)
54)
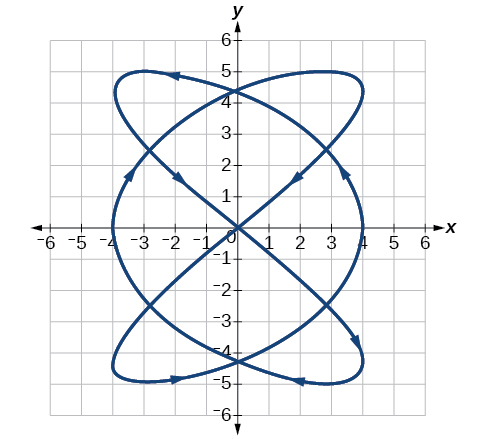
55)
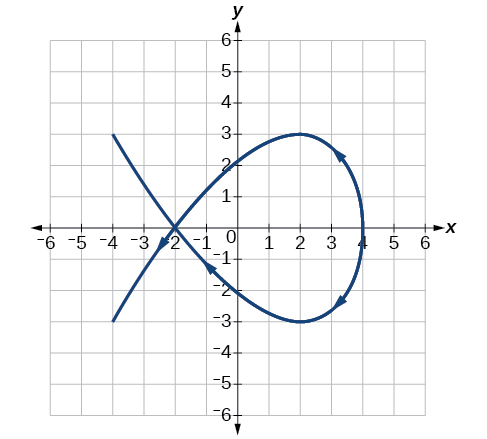
- Responder
-
\(a=4, b=2, c=3, d=3\)
56)
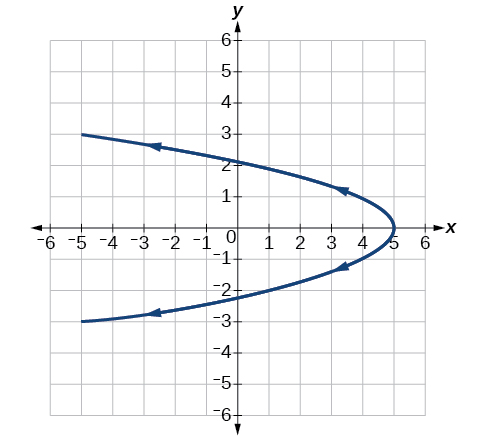
Para los ejercicios 57-62, utilice una utilidad gráfica para graficar las ecuaciones paramétricas dadas.
\[\begin{cases} & x(t)= \cos t-1\\ & y(t)= \sin t+t \end{cases} \nonumber\]
\[\begin{cases} & x(t)= \cos t+t\\ & y(t)= \sin t-1 \end{cases} \nonumber\]
\[\begin{cases} & x(t)= t-\sin t\\ & y(t)= \cos t-1 \end{cases} \nonumber\]
57) Grafica los tres conjuntos de ecuaciones paramétricas en el dominio\([0,2\pi ]\).
- Responder
-
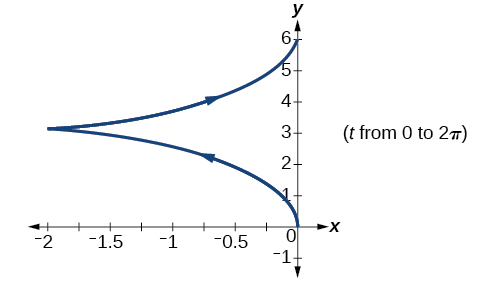
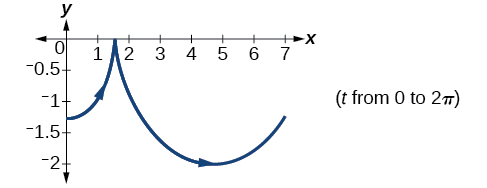
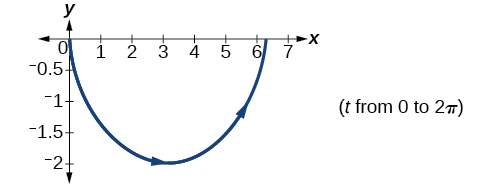
58) Grafica los tres conjuntos de ecuaciones paramétricas en el dominio\([0,4\pi]\).
59) Grafica los tres conjuntos de ecuaciones paramétricas en el dominio\([-4\pi ,6\pi]\).
- Responder
-
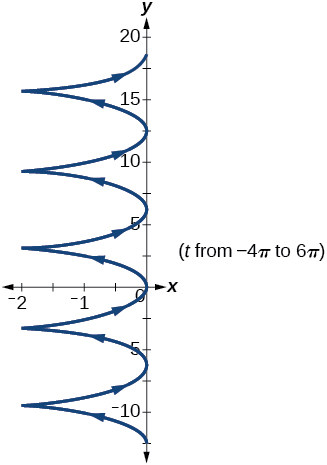
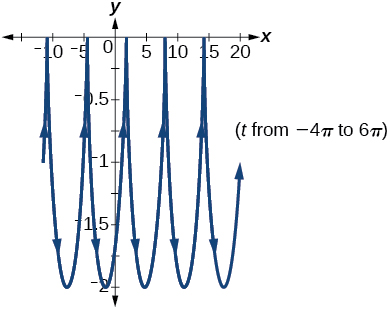
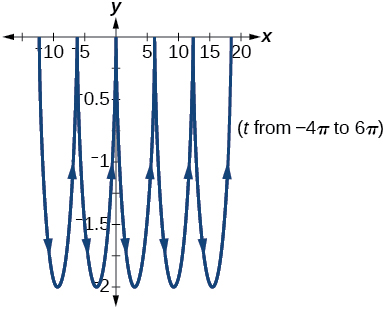
60) La gráfica de cada conjunto de ecuaciones paramétricas parece “arrastrarse” a lo largo de uno de los ejes. ¿Qué controla en qué eje se arrastra la gráfica?
61) Explicar el efecto en la gráfica de la ecuación paramétrica cuando cambiamos\(\sin t\) y\(\cos t\).
- Responder
-
La\(y\) -intercepción cambia.
62) Explicar el efecto en la gráfica de la ecuación paramétrica cuando cambiamos el dominio.
Extensiones
63) Un objeto es lanzado al aire con velocidad vertical de\(20\) ft/s y velocidad horizontal de\(15\) ft/s. La altura del objeto puede ser descrita por la ecuación\(y(t)=-16t^2+20t\), mientras que el objeto se mueve horizontalmente con velocidad constante\(15\) ft/s. Escribe ecuaciones paramétricas para el objeto. posición, y luego eliminar el tiempo para escribir la altura en función de la posición horizontal.
- Responder
-
\(y(x)=-16\left ( \dfrac{x}{15} \right )^2+20\left ( \dfrac{x}{15} \right )\)
64) Un skater que cabalga sobre una superficie nivelada a una velocidad constante de\(9\) pies/s lanza una pelota al aire, cuya altura puede ser descrita por la ecuación\(y(t)=-16t^2+10t+5\). Escribe ecuaciones paramétricas para la posición del balón, y luego elimina el tiempo para escribir la altura en función de la posición horizontal.
Para los ejercicios 65-69, usa este escenario: Se lanza un dardo hacia arriba con una velocidad inicial de\(65\) pies/s en un ángulo de elevación de\(52^{\circ}\). Considera la posición del dardo en cualquier momento\(t\). Negligencia de resistencia al aire.
65) Encontrar ecuaciones paramétricas que modelan la situación problemática.
- Responder
-
\(\begin{cases} & x(t)= 64t\cos (52^{\circ})\\ & y(t)= -16t^2+64t\sin (52^{\circ}) \end{cases}\)
66) Encontrar todos los valores posibles de\(x\) que representen la situación.
67) ¿Cuándo golpeará el dardo contra el suelo?
- Responder
-
\(3.2\)segundos aproximadamente
68) Encuentra la altura máxima del dardo.
69) ¿A qué hora alcanzará la altura máxima el dardo?
- Responder
-
\(1.6\)segundos
Para los ejercicios 70-73, mire las gráficas de cada una de las cuatro ecuaciones paramétricas. A pesar de que se ven inusuales y hermosos, son tan comunes que tienen nombres, como se indica en cada ejercicio. Utilice una utilidad gráfica para graficar cada uno en el dominio indicado.
70)\(\text{An epicycloid}\begin{cases} & x(t)= 14\cos t-\cos (14t)\\ & y(t)= 14\sin t+\sin (14t) \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
71)\(\text{An hypocycloid}\begin{cases} & x(t)= 6\sin t+2\sin (6t)\\ & y(t)= 6\cos t-2\cos (6t) \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
- Responder
-
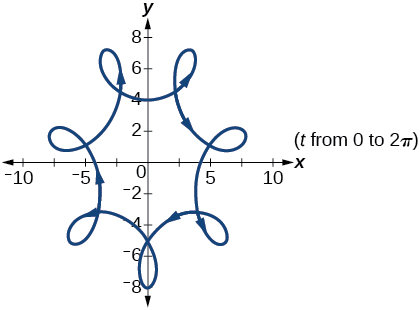
72)\(\text{An hypotrochoid}\begin{cases} & x(t)= 2\sin t+5\cos (6t)\\ & y(t)= 5\cos t-2\sin (6t) \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
73)\(\text{A rose}\begin{cases} & x(t)= 5\sin (2t)\sin t\\ & y(t)= 5\sin (2t)\cos t \end{cases}\; \; \text{on the domain }[0,2\pi ]\)
- Responder
-
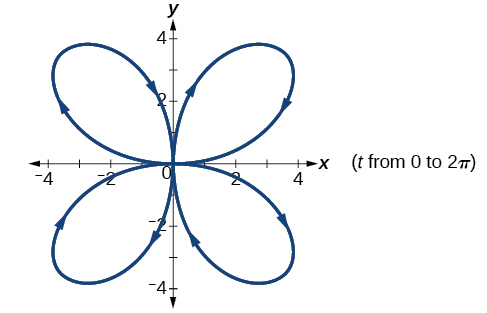
8.8: Vectores
Verbal
1) ¿Cuáles son las características de las letras que se utilizan comúnmente para representar vectores?
- Responder
-
minúscula, negrita, por lo general\(u, v, w\)
2) ¿Cómo es un vector más específico que un segmento de línea?
3) ¿Qué son\(i\) y\(j\), y qué representan?
- Responder
-
Son vectores unitarios. Se utilizan para representar los componentes horizontal y vertical de un vector. Cada uno tiene una magnitud de\(1\).
4) ¿Qué es la forma de componente?
5) Cuando un vector unitario se expresa como\(\left \langle a,b \right \rangle\) qué letra es el coeficiente de la\(i\) y cuál la\(j\)?
- Responder
-
El primer número siempre representa el coeficiente del\(i\) y el segundo representa el\(j\).
Algebraico
6) Dado un vector con punto inicial\((5,2)\) y punto terminal\((-1,-3)\), encontrar un vector equivalente cuyo punto inicial es\((0,0)\). Escribe el vector en forma de componente\(\left \langle a,b \right \rangle\).
7) Dado un vector con punto inicial\((-4,2)\) y punto terminal\((3,-3)\), encontrar un vector equivalente cuyo punto inicial es\((0,0)\). Escribir el vector en forma componente\(\left \langle a,b \right \rangle\).
- Responder
-
\(\left \langle 7,-5 \right \rangle\)
8) Dado un vector con punto inicial\((7,-1)\) y punto terminal\((-1,-7)\), encontrar un vector equivalente cuyo punto inicial es\((0,0)\). Escribir el vector en forma componente\(\left \langle a,b \right \rangle\).
Para los ejercicios 9-15, determinar si los dos vectores\(u\) y\(v\) son iguales, donde\(u\) tiene un punto inicial\(P_1\) y un punto terminal\(P_2\) y\(v\) tiene un punto inicial\(P_3\) y un punto terminal\(P_4\).
9)\(P_1=(5,1), P_2=(3,-2), P_3=(-1,3), P4=(9,−4)\)
- Responder
-
no es igual
10)\(P_1=(2,-3), P_2=(5,1), P_3=(6,-1), P_4=(9,3)\)
11)\(P_1=(-1,-1), P_2=(-4,5), P_3=(-10,6), P_4=(-13,12)\)
- Responder
-
igual
12)\(P_1=(3,7), P_2=(2,1), P_3=(1,2), P_4=(-1,-4)\)
13)\(P_1=(8,3), P_2=(6,5), P_3=(11,8), P4=(9,10)\)
- Responder
-
igual
14) Dado punto inicial\(P_1=(-3,1)\) y punto terminal\(P_2=(5,2)\), escribir el vector\(v\) en términos de\(i\) y\(j\).
15) Dado punto inicial\(P_1=(6,0)\) y punto terminal\(P_2=(-1,-3)\), escribir el vector\(v\) en términos de\(i\) y\(j\).
- Responder
-
\(7i-3j\)
Para los ejercicios 16-17, usa los vectores\(u = i+5j, v = -2i-3j, w = 4i-j\)
16) Buscar\(u+(v-w)\)
17) Buscar\(4v+2u\)
- Responder
-
\(-6i-2j\)
Para los ejercicios 18-21, utilice los vectores dados para calcular\(u + v, u - v, 2u - 3v\)
18)\(u=\left \langle 2,-3 \right \rangle, v=\left \langle 1,5 \right \rangle\)
1 9)\(u=\left \langle -3,4 \right \rangle, v=\left \langle -2,1 \right \rangle\)
- Responder
-
\(u+v=\left \langle -5,5 \right \rangle,u-v=\left \langle -1,3 \right \rangle,2u-3v=\left \langle 0,5 \right \rangle\)
20) Vamos\(v = -4i + 3j\). Encuentra un vector que tenga la mitad de la longitud y apunte en la misma dirección que\(v\).
21) Vamos\(v = 5i + 2j\). Encuentra un vector que tenga el doble de longitud y apunte en la dirección opuesta a como\(v\).
- Responder
-
\(-10i-4j\)
Para los ejercicios 22-27, encuentra un vector unitario en la misma dirección que el vector dado.
22)\(a = 3i + 4j\)
23)\(b = -2i + 5j\)
- Responder
-
\(-\dfrac{2\sqrt{29}}{29}i+\dfrac{5\sqrt{29}}{29}j\)
24)\(c = 10i - j\)
25)\(d=-\dfrac{1}{3}i+\dfrac{5}{2}j\)
- Responder
-
\(-\dfrac{2\sqrt{229}}{229}i+\dfrac{15\sqrt{229}}{229}j\)
26)\(u = 100i + 200j\)
27)\(u = -14i + 2j\)
- Responder
-
\(-\dfrac{7\sqrt{2}}{10}i+\dfrac{\sqrt{2}}{10}j\)
Para los ejercicios 28-35, encontrar la magnitud y dirección del vector,\(0\leq \theta < 2\pi\).
28)\(\left \langle 0,4 \right \rangle\)
29)\(\left \langle 6,5 \right \rangle\)
- Responder
-
\(\left | v \right |=7.810, \theta =39.806^{\circ}\)
30)\(\left \langle 2,-5 \right \rangle\)
31)\(\left \langle -4,-6 \right \rangle\)
- Responder
-
\(\left | v \right |=7.211, \theta =236.310^{\circ}\)
32) Dado\(u = 3i − 4j\) y\(v = −2i + 3j\), calcular\(u\cdot v\).
33) Dado\(u = −i − j\) y\(v = i + 5j\), calcular\(u\cdot v\).
- Responder
-
\(-6\)
34) Dado\(u=\left \langle -2,4 \right \rangle\) y\(v=\left \langle -3,1 \right \rangle\)
35) Dado\(u=\left \langle -1,6 \right \rangle\) y\(v=\left \langle 6,-1 \right \rangle\)
- Responder
-
\(-12\)
Gráfica
Para los ejercicios 36-,38 dados\(v\), sorteo\(v\),\(3v\), y\(\dfrac{1}{2}v\).
36)\(\left \langle 2,-1 \right \rangle\)
37)\(\left \langle -1,4 \right \rangle\)
- Responder
-

38)\(\left \langle -3,-2 \right \rangle\)
Para los ejercicios 39-41, utilice los vectores mostrados para bosquejar\(u + v\),\(u − v\), y\(2u\).
39)
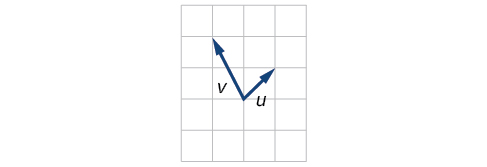
- Responder
-
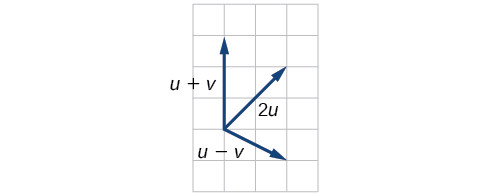
40)
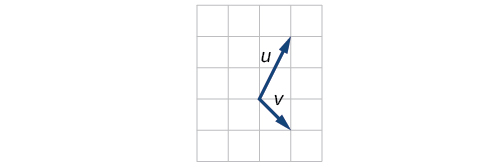
41)
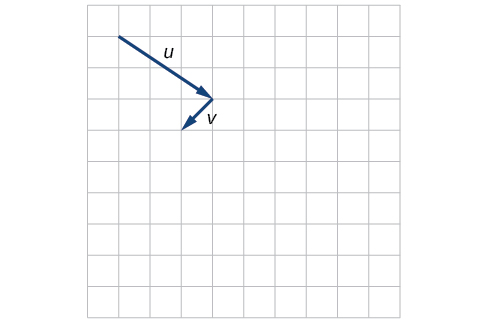
- Responder
-
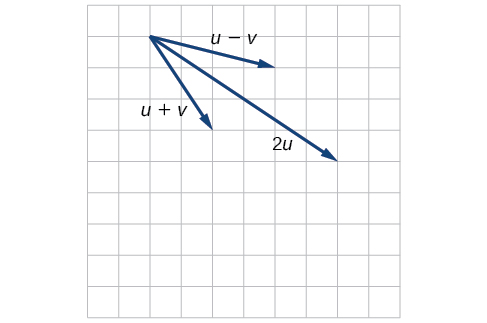
Para los ejercicios 42-43, utilice los vectores mostrados para bosquejar\(2u + v\).
42)
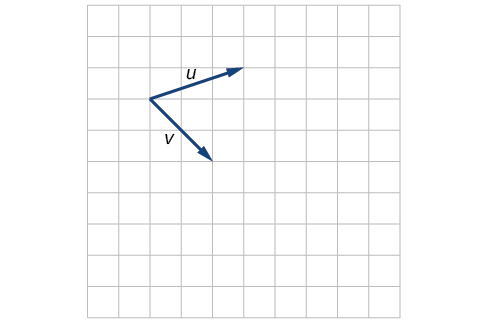
43)
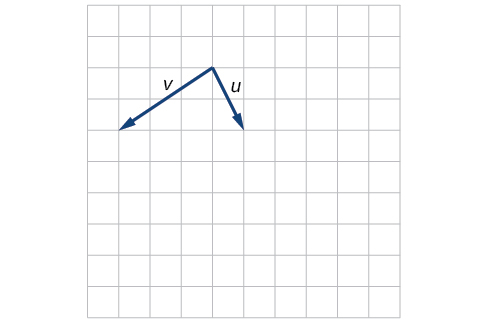
- Responder
-
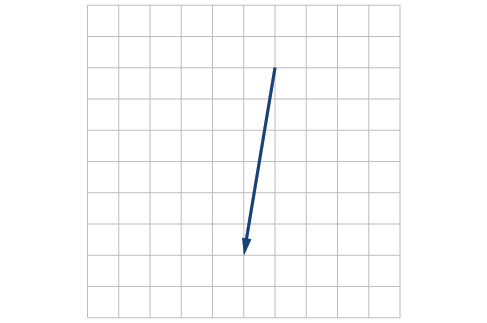
Para los ejercicios 44-45, utilice los vectores mostrados para bosquejar\(u − 3v\).
44)
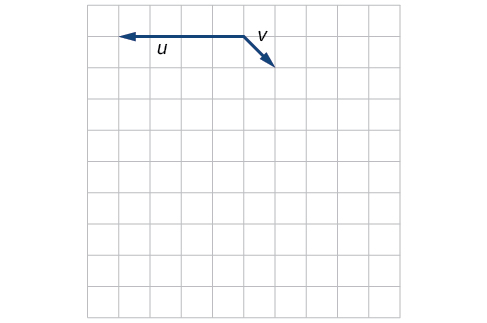
45)
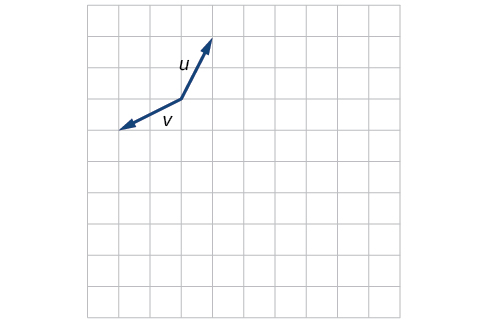
- Responder
-
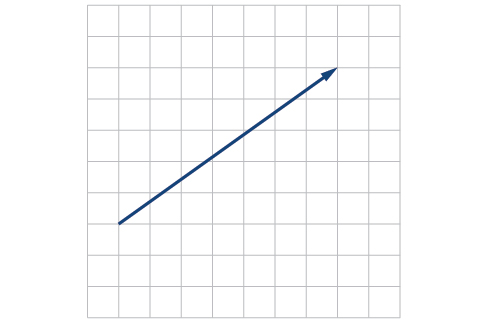
Para los ejercicios 46-47, escriba el vector mostrado en forma de componente.
46)
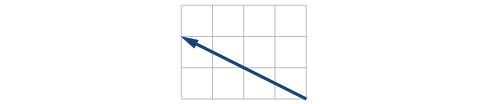
47)
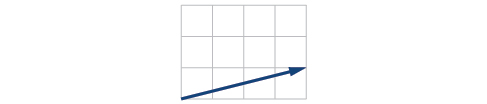
- Responder
-
\(\left \langle 4,1 \right \rangle\)
48) Dado punto inicial\(P_1=(2,1\) y punto terminal\(P_2=(-1,2)\)
49) Dado punto inicial\(P_1=(4,-1\) y punto terminal\(P_2=(-3,2)\), escribir el vector\(v\) en términos de\(i\) y\(j\). Dibuja los puntos y el vector en la gráfica.
- Responder
-
\(v=-7i+3j\)
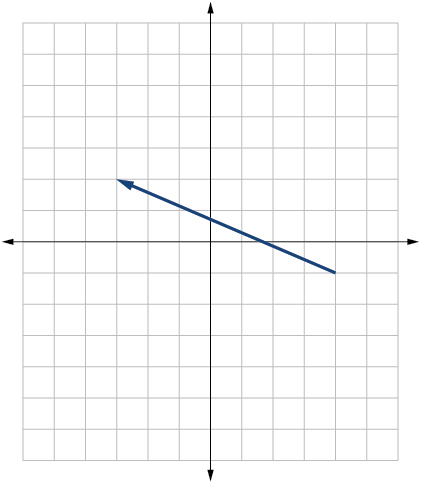
50) Dado punto inicial\(P_1=(3,3\) y punto terminal\(P_2=(-3,3)\), escribir el vector\(v\) en términos de\(i\) y\(j\). Dibuja los puntos y el vector en la gráfica.
Extensiones
Para los ejercicios 51-54, use la magnitud y dirección dadas en posición estándar, escriba el vector en forma de componente.
51)\(\left | v \right |=6, \theta =45^{\circ}\)
- Responder
-
\(3\sqrt{2}i+3\sqrt{2}j\)
52)\(\left | v \right |=8, \theta =220^{\circ}\)
53)\(\left | v \right |=2, \theta =300^{\circ}\)
- Responder
-
\(i-\sqrt{3}j\)
54)\(\left | v \right |=5, \theta =135^{\circ}\)
55) Una caja de\(60\) libras descansa sobre una rampa inclinada\(12^{\circ}\). Redondeo a la décima más cercana,
- Encuentra la magnitud de la componente normal (perpendicular) de la fuerza.
- Encuentra la magnitud de la componente de la fuerza que es paralela a la rampa.
- Responder
-
- \(58.7\)
- \(12.5\)
56) Una caja de\(25\) libras descansa sobre una rampa inclinada\(8^{\circ}\). Redondeo a la décima más cercana,
- Encuentra la magnitud de la componente normal (perpendicular) de la fuerza.
- Encuentra la magnitud de la componente de la fuerza que es paralela a la rampa.
57) Encontrar la magnitud de los componentes horizontal y vertical de un vector con magnitud\(8\) libras apuntando en una dirección\(27^{\circ}\) por encima de la horizontal. Redondear a la centésima más cercana.
- Responder
-
\(x=7.13\)libras,\(y=3.63\) libras
58) Encontrar la magnitud de los componentes horizontal y vertical del vector con\(4\) libras de magnitud apuntando en una dirección\(127^{\circ}\) por encima de la horizontal. Redondear a la centésima más cercana.
59) Encontrar la magnitud de los componentes horizontal y vertical de un vector con magnitud\(5\) libras apuntando en una dirección\(55^{\circ}\) por encima de la horizontal. Redondear a la centésima más cercana.
- Responder
-
\(x=2.87\)libras,\(y=4.10\) libras
60) Encontrar la magnitud de los componentes horizontal y vertical del vector con magnitud\(1\) libra apuntando en una dirección\(8^{\circ}\) por encima de la horizontal. Redondear a la centésima más cercana.
Aplicaciones del mundo real
61) Una mujer sale de casa y camina\(3\) millas al oeste, luego\(2\) millas al suroeste. ¿Qué tan lejos de casa está, y en qué dirección debe caminar para dirigirse directamente a casa?
- Responder
-
\(4.635\)millas,\(17.764^{\circ}\) N de E
62) Un barco sale del puerto deportivo y navega\(6\) millas al norte, luego\(2\) millas al noreste. ¿A qué distancia del puerto deportivo está el barco, y en qué dirección debe navegar para regresar directamente al puerto deportivo?
63) Un hombre comienza a caminar desde su casa y camina\(4\) millas al este,\(2\) millas al sureste,\(5\) millas al sur,\(4\) millas al suroeste y\(2\) millas al este. ¿Hasta dónde ha caminado? Si caminaba directo a casa, ¿hasta dónde tendría que caminar?
- Responder
-
\(17\)millas,\(10.318\) millas
64) Una mujer comienza a caminar desde casa y camina\(4\) millas al este,\(7\) millas al sureste,\(6\) millas al sur,\(5\) millas al suroeste y\(3\) millas al este. ¿Hasta dónde ha caminado? Si caminaba directo a casa, ¿hasta dónde tendría que caminar?
65) Un hombre comienza a caminar desde su casa y camina\(3\) millas al\(20^{\circ}\) norte del oeste, luego\(5\) millas al\(10^{\circ}\) oeste del sur, luego\(4\) millas al\(15^{\circ}\) norte del este. Si caminaba directo a casa, ¿qué tan lejos tendría que andar y en qué dirección?
- Responder
-
Distancia:\(2.868\), Dirección:\(86.474^{\circ}\) Norte de Oeste, o\(3.526^{\circ}\) Oeste de Norte
66) Una mujer comienza a caminar desde su casa y camina\(6\) millas al\(40^{\circ}\) norte del este, luego\(2\) millas al\(15^{\circ}\) este del sur, luego\(5\) millas al\(30^{\circ}\) sur del oeste. Si caminaba directo a casa, ¿hasta dónde tendría que caminar y en qué dirección?
67) Un avión se dirige hacia el norte a una velocidad aérea de\(600\) km/hr, pero hay un viento que sopla del suroeste a\(80\) km/hr. ¿Cuántos grados de rumbo terminará volando el avión y cuál es la velocidad del avión con respecto al suelo?
- Responder
-
\(4.924^{\circ}\), 659 km/hr
68) Un avión se dirige hacia el norte a una velocidad aérea de\(500\) km/hr, pero hay un viento que sopla del noroeste a\(50\) km/hr. ¿Cuántos grados de rumbo terminará volando el avión y cuál es la velocidad del avión con respecto al suelo?
69) Un avión necesita dirigirse hacia el norte, pero hay un viento que sopla del suroeste a\(60\) km/hr. El avión vuela con una velocidad aérea de\(550\) km/hr. Para terminar volando hacia el norte, ¿cuántos grados al oeste de norte necesitará el piloto para volar el avión?
- Responder
-
\(4.424^{\circ}\)
70) Un avión necesita dirigirse hacia el norte, pero hay un viento que sopla del noroeste a\(80\) km/hr. El avión vuela con una velocidad aérea de\(500\) km/hr. Para terminar volando hacia el norte, ¿cuántos grados al oeste de norte necesitará el piloto para volar el avión?
71) Como parte de un videojuego, el punto\((5,7)\) se gira en sentido antihorario sobre el origen a través de un ángulo de\(35^{\circ}\). Encuentra las nuevas coordenadas de este punto.
- Responder
-
\((0.081,8.602)\)
72) Como parte de un videojuego, el punto\((7,3)\) se gira en sentido antihorario sobre el origen a través de un ángulo de\(40^{\circ}\). Encuentra las nuevas coordenadas de este punto.
73) Dos niños están lanzando una pelota de ida y vuelta recta por el asiento trasero de un automóvil. La pelota está siendo lanzada\(10\) mph en relación con el auto, y el auto viaja\(25\) mph por la carretera. Si un niño no atrapa la pelota y vuela por la ventana, ¿en qué dirección vuela la pelota (ignorando la resistencia al viento)?
- Responder
-
\(21.801^{\circ}\), relativo a la dirección de avance del automóvil
74) Dos niños están lanzando una pelota de ida y vuelta recta por el asiento trasero de un automóvil. La pelota está siendo lanzada\(8\) mph en relación con el auto, y el auto viaja\(45\) mph por la carretera. Si un niño no atrapa la pelota y vuela por la ventana, ¿en qué dirección vuela la pelota (ignorando la resistencia al viento)?
75) Un objeto\(50\) -libra descansa sobre una rampa inclinada\(19^{\circ}\). Encuentra la magnitud de los componentes de la fuerza paralela y perpendicular a (normal) la rampa a la décima de libra más cercana.
- Responder
-
paralelo:\(16.28\), perpendicular:\(47.28\) libras
76) Supongamos que un cuerpo tiene una fuerza de\(10\) libras que actúan sobre él a la derecha,\(25\) libras que actúan sobre él hacia arriba, y\(5\) libras que actúan sobre él\(45^{\circ}\) desde la horizontal. ¿Qué fuerza única es la fuerza resultante que actúa sobre el cuerpo?
77) Supongamos que un cuerpo tiene una fuerza de\(10\) libras actuando sobre él a la derecha,\(25\) libras que actúan sobre él ─\(135^{\circ}\) desde la horizontal, y\(5\) libras que actúan sobre él dirigidas\(150^{\circ}\) desde la horizontal. ¿Qué fuerza única es la fuerza resultante que actúa sobre el cuerpo?
- Responder
-
\(19.35\)libras,\(231.54^{\circ}\) desde la horizontal
78) La condición de equilibrio es cuando la suma de las fuerzas que actúan sobre un cuerpo es el vector cero. Supongamos que un cuerpo tiene una fuerza de\(2\) libras actuando sobre él a la derecha,\(5\) libras que actúan sobre él hacia arriba, y\(3\) libras que actúan sobre él\(45^{\circ}\) desde la horizontal. ¿Qué fuerza única se necesita para producir un estado de equilibrio en el cuerpo?
79) Supongamos que un cuerpo tiene una fuerza de\(3\) libras que actúan sobre él a la izquierda,\(4\) libras que actúan sobre él hacia arriba, y\(2\) libras que actúan sobre él\(30^{\circ}\) desde la horizontal. ¿Qué fuerza única se necesita para producir un estado de equilibrio en el cuerpo? Dibuja el vector.
- Responder
-
\(5.1583\)libras,\(75.8^{\circ}\) desde la horizontal


