11.3: Secuencias geométricas
- Page ID
- 121377
- Encuentra la relación común para una secuencia geométrica.
- Enumere los términos de una secuencia geométrica.
- Utilice una fórmula recursiva para una secuencia geométrica.
- Utilice una fórmula explícita para una secuencia geométrica.
Muchos empleos ofrecen un aumento anual del costo de vida para mantener los salarios consistentes con la inflación. Supongamos, por ejemplo, que un recién graduado universitario encuentra un puesto como gerente de ventas ganando un salario anual de\($26,000\). Se le promete un aumento del\(2\%\) costo de vida cada año. Su salario anual en un año determinado se puede encontrar multiplicando su salario del año anterior por\(102\%\). Su salario será\($26,520\) después de un año;\($27,050.40\) después de dos años;\($27,591.41\) después de tres años; y así sucesivamente. Cuando un salario aumenta en una tasa constante cada año, el salario crece por un factor constante. En esta sección, revisaremos secuencias que crecen de esta manera.
Encontrar Ratios Comunes
Los valores salariales anuales descritos forman una secuencia geométrica porque cambian por un factor constante cada año. Cada término de una secuencia geométrica aumenta o disminuye por un factor constante llamado la relación común. La siguiente secuencia es un ejemplo de una secuencia geométrica porque cada término aumenta en un factor constante de 6. Multiplicar cualquier término de la secuencia por la relación común 6 genera el término posterior.

Una secuencia geométrica es aquella en la que cualquier término dividido por el término anterior es una constante. Esta constante se llama la relación común de la secuencia. La relación común se puede encontrar dividiendo cualquier término en la secuencia por el término anterior. Si\(a_1\) es el término inicial de una secuencia geométrica y\(r\) es la relación común, la secuencia será
\[\{a_1, a_1r,a_1r^2,a_1r^3,...\} .\]
- Dividir cada término por el término anterior.
- Compara los cocientes. Si son iguales, existe una proporción común y la secuencia es geométrica.
¿La secuencia es geométrica? Si es así, encuentra la proporción común.
- \(1\),\(2\),\(4\),\(8\),\(16\),...
- \(48\),\(12\),\(4\),\(2\),...
Solución
Dividir cada término por el término anterior para determinar si existe una relación común.
- \(\dfrac{2}{1}=2\)\(\dfrac{4}{2}=2\)\(\dfrac{8}{4}=2\)\(\dfrac{16}{8}=2\)
La secuencia es geométrica porque hay una relación común. El cociente común es\(2\).
- \(\dfrac{12}{48}=\dfrac{1}{4}\)\(\dfrac{4}{12}=\dfrac{1}{3}\)\(\dfrac{2}{4}=\dfrac{1}{2}\)
La secuencia no es geométrica porque no hay una relación común.
Análisis
La gráfica de cada secuencia se muestra en la Figura\(\PageIndex{1}\). Parece a partir de las gráficas que aparecen tanto (a) como (b) tienen la forma de la gráfica de una función exponencial en esta ventana de visualización. No obstante, sabemos que (a) es geométrica y así se sostiene esta interpretación, pero (b) no lo es.
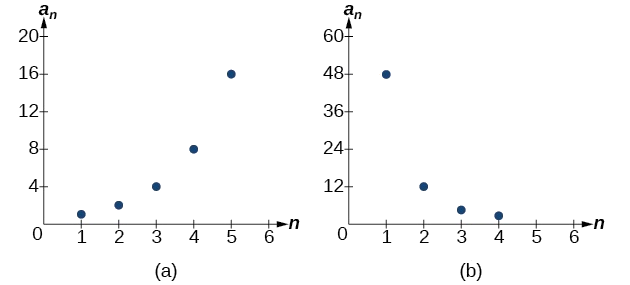
Figura\(\PageIndex{1}\)
Si te dicen que una secuencia es geométrica, ¿tienes que dividir cada término por el término anterior para encontrar la proporción común?
No. Si sabes que la secuencia es geométrica, puedes elegir cualquier término en la secuencia y dividirlo por el término anterior para encontrar la proporción común.
¿La secuencia es geométrica? Si es así, encuentra la proporción común.
\(5\),\(10\),\(15\),\(20\),...
- Contestar
-
La secuencia no es geométrica porque\(\dfrac{10}{5}≠\dfrac{15}{10}\)
¿La secuencia es geométrica? Si es así, encuentra la proporción común.
\(100\),\(20\),\(4\),\(\dfrac{4}{5}\),...
- Contestar
-
La secuencia es geométrica. La relación común es\(\dfrac{1}{5}\)
Términos de escritura de secuencias geométricas
Ahora que podemos identificar una secuencia geométrica, aprenderemos a encontrar los términos de una secuencia geométrica si se nos da el primer término y la relación común. Los términos de una secuencia geométrica se pueden encontrar comenzando con el primer término y multiplicando por la proporción común repetidamente. Por ejemplo, si el primer término de una secuencia geométrica es\(a_1=−2\) y la proporción común es\(r=4\), podemos encontrar términos subsiguientes multiplicando\(−2⋅4\) para obtener\(−8\) luego multiplicando el resultado\(−8⋅4\) para obtener\(−32\) y así sucesivamente.
\[\begin{align*} a_1 &= −2 \\ a_2 &= (−2⋅4)=−8 \\ a_3 &= (−8⋅4)=−32 \\ a_4 &= (−32⋅4)=128 \end{align*}\]
Los primeros cuatro términos son\(\{–2, –8, –32, –128\}\).
- Multiplique el término inicial\(a_1\),, por la proporción común para encontrar el siguiente término,\(a_2\).
- Repita el proceso, usando\(a_n=a_2\) para buscar\(a_3\) y luego usar\(a_3\) para encontrar\(a_4\), hasta que se hayan identificado los cuatro términos.
- Escribir entre paréntesis los términos separados por comunes.
Enumere los primeros cuatro términos de la secuencia geométrica con\(a_1=5\) y\(r=–2\).
Solución
Multiplicar\(a_1\) por\(−2\) para encontrar\(a_2\). Repita el proceso, usando\(a_2\) para encontrar\(a_3\), y así sucesivamente.
\[\begin{align*} a_1 &= 5 \\ a_2 &= −2a_1=−10 \\ a_3 &= −2a_2=20 \\ a_4 &= −2a_3=−40 \end{align*}\]
Los primeros cuatro términos son\(\{5,–10,20,–40\}\).
Enumere los primeros cinco términos de la secuencia geométrica con\(a_1=18\) y\(r=\dfrac{1}{3}\).
- Contestar
-
\(\left \{18, 6, 2, \dfrac{2}{3}, \dfrac{2}{9} \right \} \)
Uso de fórmulas recursivas para secuencias geométricas
Una fórmula recursiva nos permite encontrar cualquier término de una secuencia geométrica utilizando el término anterior. Cada término es producto de la proporción común y del término anterior. Por ejemplo, supongamos que la proporción común es\(9\). Entonces cada término es nueve veces el término anterior. Al igual que con cualquier fórmula recursiva, se debe dar el término inicial.
La fórmula recursiva para una secuencia geométrica con relación común r y primer término\(a_1\) es
\[a_n=ra_{n−1},\;\;\; n≥2\]
- Anotar el término inicial.
- Encuentra la relación común dividiendo cualquier término por el término anterior.
- Sustituir la proporción común en la fórmula recursiva por una secuencia geométrica.
Escribe una fórmula recursiva para la siguiente secuencia geométrica.
\(\{6, 9, 13.5, 20.25, ...\} \nonumber\)
Solución
El primer término se da como\(6\). La relación común se puede encontrar dividiendo el segundo término por el primer término.
\(r=\dfrac{9}{6}=1.5 \nonumber\)
Sustituir la relación común en la fórmula recursiva para secuencias geométricas y definir\(a_1\).
\[\begin{align*} a_n &= ra_{n−1} \\ a_n &= 1.5a_{n−1} \text{ for }n≥2 \\ a_1 &= 6 \end{align*}\]
Análisis
La secuencia de puntos de datos sigue un patrón exponencial. La relación común es también la base de una función exponencial como se muestra en la Figura\(\PageIndex{2}\).
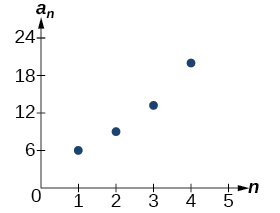
Figura\(\PageIndex{2}\)
¿Tenemos que dividir el segundo término por el primer término para encontrar la proporción común?
No. Podemos dividir cualquier término en la secuencia por el término anterior. Sin embargo, es más común dividir el segundo término por el primer término porque suele ser el método más fácil de encontrar la proporción común.
Escribe una fórmula recursiva para la siguiente secuencia geométrica.
\(\{2, 43, 89, 1627, ...\}\)
- Contestar
-
\(\begin{align*}a_1 &= 2 \\ a_n &= \dfrac{2}{3}a_{n−1} \text{ for }n≥2 \end{align*}\)
Uso de fórmulas explícitas para secuencias geométricas
Debido a que una secuencia geométrica es una función exponencial cuyo dominio es el conjunto de enteros positivos, y la razón común es la base de la función, podemos escribir fórmulas explícitas que nos permitan encontrar términos particulares.
\[a_n=a_1r^{n−1}\]
Echemos un vistazo a la secuencia\(\{18, 36, 72, 144, 288, ...\}\). Esta es una secuencia geométrica con una relación común de\(2\) y una función exponencial con una base de\(2\). Una fórmula explícita para esta secuencia es
\(a_n=18·2^{n−1}\)
El gráfico de la secuencia se muestra en la Figura\(\PageIndex{3}\).
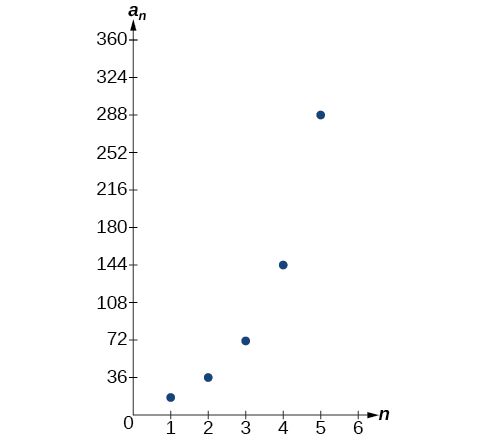
Figura\(\PageIndex{3}\)
El\(n^{th}\) término de una secuencia geométrica viene dado por la fórmula explícita:
\[a_n=a_1r^{n−1}\]
Dada una secuencia geométrica con\(a_1=3\) y\(a_4=24\), encontrar\(a_2\).
Solución
La secuencia se puede escribir en términos del término inicial y la relación común\(r\).
\(3\),\(3r\),\(3r^2\),\(3r^3\),...
Encuentra la proporción común usando el cuarto término dado.
\[\begin{align*} a_n&=a_1r^{n-1} \\ a_4&=3r^3 \qquad \text{Write the fourth term of sequence in terms of }\alpha_1 \text{ and } r \\ 24&=3r^3 \qquad \text{Substitute }24 \text{ for }a_4 \\ 8&=r^3 \qquad \text{Divide} \\ r&=2 \qquad \text{Solve for the common ratio} \end{align*}\]
Encuentra el segundo término multiplicando el primer término por la proporción común.
\[\begin{align*} a_2 &= 2 \\ a_1 &= 2(3) \\ & = 6 \end{align*}\]
Análisis
La proporción común se multiplica por el primer término una vez para encontrar el segundo término, dos veces para encontrar el tercer término, tres veces para encontrar el cuarto término, y así sucesivamente. El décimo término podría encontrarse multiplicando el primer término por la proporción común nueve veces o multiplicando por la relación común elevada a la novena potencia.
Dada una secuencia geométrica con\(a_2=4\) y\(2a_3=32\), encontrar\(a_6\).
- Contestar
-
\(a_6=16,384\)
Escribe una fórmula explícita para el enésimo término de la siguiente secuencia geométrica.
\(\{2, 10, 50, 250, ...\}\)
Solución
El primer término es\(2\). La relación común se puede encontrar dividiendo el segundo término por el primer término.
\(\dfrac{10}{2}=5\)
El cociente común es\(5\). Sustituir la relación común y el primer término de la secuencia en la fórmula.
\[\begin{align*}a_n &= a_1r^{(n−1)} \\ a_n &= 2⋅5^{n−1} \end{align*}\]
La gráfica de esta secuencia en la Figura\(\PageIndex{4}\) muestra un patrón exponencial.
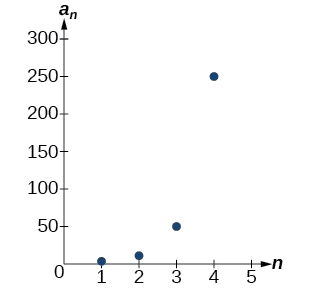
Figura\(\PageIndex{4}\)
Escribe una fórmula explícita para la siguiente secuencia geométrica.
\(\{–1, 3, –9, 27, ...\}\)
- Contestar
-
\(a_n=−{(−3)}^{n−1}\)
Resolución de problemas de aplicación con secuencias geométricas
En escenarios del mundo real que involucran secuencias aritméticas, es posible que necesitemos usar un término inicial de\(a_0\) en lugar de\(a_1\). En estos problemas, podemos alterar ligeramente la fórmula explícita usando la siguiente fórmula:
\(a_n=a_0r^n\)
En 2013, el número de alumnos en una escuela pequeña es\(284\). Se estima que la población estudiantil aumentará\(4\%\) cada año.
- Escribir una fórmula para la población estudiantil.
- Estimar la población estudiantil en 2020.
Solución
- La situación puede ser modelada por una secuencia geométrica con un término inicial de\(284\). La población estudiantil será\(104\%\) del año anterior, por lo que la proporción común es\(1.04\).
Dejar\(P\) ser la población estudiantil y\(n\) ser el número de años después de 2013. Usando la fórmula explícita para una secuencia geométrica obtenemos
\(P_n =284⋅{1.04}^n\)
- Podemos encontrar el número de años desde 2013 restando.
\(2020−2013=7\)
Buscamos a la población después de\(7\) años. Podemos sustituir\(7\) para\(n\) estimar la población en 2020.
\(P_7=284⋅{1.04}^7≈374\)
La población estudiantil estará aproximadamente\(374\) en 2020.
Un negocio inicia un nuevo sitio web. Inicialmente el número de aciertos se\(293\) debe al factor curiosidad. El negocio estima que el número de aciertos aumentará\(2.6%\) por semana.
- Escribe una fórmula para el número de aciertos.
- Estimar el número de aciertos en\(5\) semanas.
- Contestar a
-
\(P_n = 293⋅1.026a^n\)
- Respuesta b
-
El número de aciertos será sobre\(333\).
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con secuencias geométricas.
Ecuaciones Clave
| fórmula recursiva para el enésimo término de una secuencia geométrica | \(a_n=ra_{n−1}\),\(n≥2\) |
| fórmula explícita para el enésimo término de una secuencia geométrica | \(a_n=a_1r^{n−1}\) |
Conceptos clave
- Una secuencia geométrica es una secuencia en la que la relación entre dos términos consecutivos cualesquiera es una constante.
- La relación constante entre dos términos consecutivos se llama la relación común.
- La relación común se puede encontrar dividiendo cualquier término en la secuencia por el término anterior. Ver Ejemplo\(\PageIndex{1}\).
- Los términos de una secuencia geométrica se pueden encontrar comenzando con el primer término y multiplicando por la proporción común repetidamente. Ver Ejemplo\(\PageIndex{2}\) y Ejemplo\(\PageIndex{4}\).
- Una fórmula recursiva para una secuencia geométrica con relación común\(r\) viene dada por\(a_n=ra_{n–1}\) for\(n≥2\).
- Al igual que con cualquier fórmula recursiva, se debe dar el término inicial de la secuencia. Ver Ejemplo\(\PageIndex{3}\).
- Una fórmula explícita para una secuencia geométrica con relación común\(r\) viene dada por\(a_n=a_1r^{n–1}\). Ver Ejemplo\(\PageIndex{5}\).
- En problemas de aplicación, a veces alteramos ligeramente la fórmula explícita para\(a_n=a_0r^n\). Ver Ejemplo\(\PageIndex{6}\).


