11.4: Las series y sus anotaciones
- Page ID
- 121342
- Utilice notación de suma.
- Utilice la fórmula para la suma de los primeros\(n\) términos de una serie aritmética.
- Usa la fórmula para la suma de los primeros\(n\) términos de una serie geométrica.
- Usa la fórmula para la suma de una serie geométrica infinita.
- Resolver problemas de anualidad.
Una pareja decide iniciar un fondo universitario para su hija. Planean invertir\($50\) en el fondo cada mes. El fondo paga intereses\(6\%\) anuales, compuestos mensualmente. ¿Cuánto dinero habrán ahorrado cuando su hija esté lista para comenzar la universidad en\(6\) años? En esta sección, aprenderemos a responder a esta pregunta. Para ello, debemos considerar la cantidad de dinero invertido y la cantidad de intereses ganados.
Uso de la notación de suma
Para encontrar la cantidad total de dinero en el fondo universitario y la suma de los montos depositados, necesitamos sumar los montos depositados cada mes y los montos ganados mensualmente. La suma de los términos de una secuencia se llama serie. Consideremos, por ejemplo, las siguientes series.
\(3+7+11+15+19+ \ldots \nonumber \)
La suma\(n^{th}\) parcial de una serie es la suma de un número finito de términos consecutivos que comienzan con el primer término. La notación\(S_n\) representa la suma parcial.
\[\begin{align} S_1 &= 3 \nonumber \\ S_2 &= 3+7=10 \nonumber \\ S_3 &= 3+7+11=21 \nonumber \\ S_4 &= 3+7+11+15 =36 \nonumber \end{align} \nonumber\]
La notación de suma se utiliza para representar series. La notación de suma a menudo se conoce como notación sigma porque usa la letra mayúscula griega sigma\(\sum\),, para representar la suma. La notación de suma incluye una fórmula explícita y especifica el primer y último término de la serie. Se da una fórmula explícita para cada término de la serie a la derecha de la sigma. Una variable llamada índice de suma se escribe debajo de la sigma. El índice de suma se establece igual al límite inferior de suma, que es el número utilizado para generar el primer término en la serie. El número por encima de la sigma, denominado límite superior de suma, es el número utilizado para generar el último término en una serie.
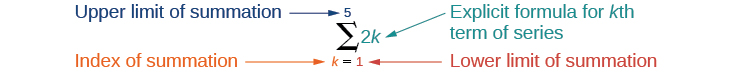
Si interpretamos la notación dada, vemos que nos pide encontrar la suma de los términos en la serie\(a_k=2k\) para\(k=1\) a través\(k=5\). Podemos comenzar sustituyendo los términos\(k\) y enumerando los términos de esta serie.
\[\begin{align}a_1 &=2(1)=2 \nonumber \\ a_2 &=2(2)=4 \nonumber \\ a_3 &= 2(3)=6 \nonumber \\ a_4 &= 2(4)=8 \nonumber \\ a_5 &= 2(5)=10 \nonumber \end{align} \nonumber\]
Podemos encontrar la suma de la serie agregando los términos:
\[\sum_{k=1}^{5}2k=2+4+6+8+10=30 \nonumber\]
La suma de los primeros\(n\) términos de una serie se puede expresar en notación de suma de la siguiente manera:
\[\sum_{k=1}^{n}a_k\]
Esta notación nos dice encontrar la suma de\(a_k\) de\(k=1\) a\(k=n\).
\(k\)se llama el índice de suma,\(1\) es el límite inferior de la suma, y\(n\) es el límite superior de la suma.
No. El límite inferior de suma puede ser cualquier número, pero\(1\) se usa frecuentemente. Veremos ejemplos con menores límites de suma distintos a\(1\).
- Identificar el límite inferior de suma.
- Identificar el límite superior de suma.
- Sustituir cada valor\(k\) del límite inferior al límite superior en la fórmula.
- Agregar para encontrar la suma.
Evaluar
\(\sum_{k=3}^{7}k^2\)
Solución
Según la notación, el límite inferior de suma es\(3\) y el límite superior es\(7\). Entonces necesitamos encontrar la suma de\(k^2\) de\(k=3\) a\(k=7\). Encontramos los términos de la serie sustituyendo\(k=3, 4, 5, 6,\) y\(7\) en la función\(k^2\). Agregamos los términos para encontrar la suma.
\[\begin{align}\sum_{k=3}^{7}k^2 &= 3^2+4^2+5^2+6^2+7^2 \nonumber \\[4pt] &= 9+16+25+36+49 \nonumber \\[4pt] &= 135 \nonumber \end{align} \nonumber\]
Evaluar
\(\sum_{k=2}^{5}(3k–1)\)
- Contestar
-
\(38\)
Uso de la fórmula para series aritméticas
Así como estudiamos tipos especiales de secuencias, veremos tipos especiales de series. Recordemos que una secuencia aritmética es una secuencia en la que la diferencia entre dos términos consecutivos cualesquiera es la diferencia común,\(d\). La suma de los términos de una secuencia aritmética se denomina serie aritmética. Podemos escribir la suma de los primeros\(n\) términos de una serie aritmética como:
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n. \nonumber \]
También podemos invertir el orden de los términos y escribir la suma como
\[S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1. \nonumber\]
Si agregamos estas dos expresiones para la suma de los primeros\(n\) términos de una serie aritmética, podemos derivar una fórmula para la suma de los primeros\(n\) términos de cualquier serie aritmética.
\[S_n=a_1+(a_1+d)+(a_1+2d)+...+(a_n–d)+a_n \nonumber\]
\[\underline{+S_n=a_n+(a_n–d)+(a_n–2d)+...+(a_1+d)+a_1} \nonumber\]
\[2S_n=(a_1+a_n)+(a_1+a_n)+...+(a_1+a_n) \nonumber\]
Debido a que hay\(n\) términos en la serie, podemos simplificar esta suma para
\[2S_n=n(a_1+a_n). \nonumber \]
Dividimos por\(2\) para encontrar la fórmula para la suma de los primeros\(n\) términos de una serie aritmética.
\[S_n=\dfrac{n(a_1+a_n)}{2} \nonumber \]
Una serie aritmética es la suma de los términos de una secuencia aritmética. La fórmula para la suma de los primeros\(n\) términos de una secuencia aritmética es
\[S_n=\dfrac{n(a_1+a_n)}{2}\]
- Identificar\(a_1\) y\(a_n\).
- Determinar\(n\).
- Sustituir valores por\(a_1\),\(a_n\), y\(n\) en la fórmula\(S_n=\dfrac{n(a_1+a_n)}{2}\).
- Simplificar para encontrar\(S_n\).
Encuentra la suma de cada serie aritmética.
- \(5 + 8 + 11 + 14 + 17 + 20 + 23 + 26 + 29 + 32\)
- \(20 + 15 + 10 +…+ −50\)
- \(\sum_{k=1}^{12}3k−8\)
Solución
- Nos dan\(a_1=5\) y\(a_n=32\).
Contar el número de términos en la secuencia a encontrar\(n=10\).
Sustituir valores por\(a_1\)\(a_n\),, y\(n\) en la fórmula y simplificar.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{10}&=\dfrac{10(5+32)}{2}\\ &=185 \end{align*}\]
- Nos dan\(a_1=20\) y\(a_n=−50\).
Utilice la fórmula para el término general de una secuencia aritmética para encontrar\(n\).
\[\begin{align*} a_n&=a_1+(n-1)d\\ -50&=20+(n-1)(-5)\\ -70&=(n-1)(-5)\\ 14&=n-1\\ 15&=n \end{align*}\]
Sustituir valores por\(a_1\)\(a_n\),,\(n\) en la fórmula y simplificar.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{15}&=\dfrac{15(20-50)}{2}\\ &=-225 \end{align*}\]
- Para encontrar\(a_1\), sustituir\(k=1\) en la fórmula explícita dada.
\[\begin{align*} a_k&=3k-8\\ a_1&=3(1)-8\\ &=-5 \end{align*}\]
Se nos da eso\(n=12\). Para encontrar\(a_12\), sustituir\(k=12\) en la fórmula explícita dada.
\[\begin{align*} a_k&=3k-8\\ a_{12}&=3(12)-8\\ &=28 \end{align*}\]
Sustituir valores por\(a_1\)\(a_n\),, y\(n\) en la fórmula y simplificar.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_{12}&=\dfrac{12(-5+28)}{2}\\ &=138 \end{align*}\]
Usa la fórmula para encontrar la suma de cada serie aritmética.
\(1.4 + 1.6 + 1.8 + 2.0 + 2.2 + 2.4 + 2.6 + 2.8 + 3.0 + 3.2 + 3.4\)
- Contestar
-
\(26.4\)
\(13 + 21 + 29 + …+ 69\)
- Contestar
-
\(328\)
\(\sum_{k=1}{10}5−6k\)
- Contestar
-
\(−280\)
El domingo después de una cirugía menor, una mujer es capaz de caminar media milla. Cada domingo, camina un cuarto de milla adicional. Después de\(8\) semanas, ¿cuál será el número total de millas que ha recorrido?
Solución
Este problema puede ser modelado por una serie aritmética con\(a_1=\dfrac{1}{2}\) y\(d=\dfrac{1}{4}\). Estamos buscando el número total de millas recorridas después de\(8\) semanas, así que lo sabemos\(n=8\), y estamos buscando\(S_8\). Para encontrar\(a_8\), podemos usar la fórmula explícita para una secuencia aritmética.
\[\begin{align*} a_n&=a_1+d(n-1)\\ a_8&=\dfrac{1}{2}+\dfrac{1}{4}(8-1)\\ &=\dfrac{9}{4} \end{align*}\]
Ahora podemos usar la fórmula para series aritméticas.
\[\begin{align*} S_n&=\dfrac{n(a_1+a_n)}{2}\\ S_8&=\dfrac{8\left(\dfrac{1}{2}+\dfrac{9}{4}\right)}{2}\\ &=11 \end{align*}\]
Ella habrá caminado un total de\(11\) kilómetros.
Un hombre gana\($100\) en la primera semana de junio. Cada semana, gana\($12.50\) más que la semana anterior. Después de\(12\) semanas, ¿cuánto ha ganado?
- Contestar
-
\($2,025\)
Uso de la fórmula para series geométricas
Así como la suma de los términos de una secuencia aritmética se llama serie aritmética, la suma de los términos en una secuencia geométrica se denomina serie geométrica. Recordemos que una secuencia geométrica es una secuencia en la que la relación de dos términos consecutivos cualesquiera es la relación común,\(r\). Podemos escribir la suma de los primeros\(n\) términos de una serie geométrica como
\(S_n=a_1+ra_1+r^2a_1+...+r^{n–1}a_1\).
Al igual que con las series aritméticas, podemos hacer alguna manipulación algebraica para derivar una fórmula para la suma de los primeros\(n\) términos de una serie geométrica. Comenzaremos multiplicando ambos lados de la ecuación por\(r\).
\(rS_n=ra_1+r^2a_1+r^3a_1+...+r^na_1\)
A continuación, restamos esta ecuación de la ecuación original.
\[\begin{align*} S_n&=a_1+ra_1+r^2a_1+...+r^{n-1}a_1\\ \underline{-rS_n}&=\underline{-(ra_1+r^2a_1+r^3a_1+...+r^na_1)}\\ (1-r)S_n&=a_1-r^na_1 \end{align*}\]
Observe que cuando restamos, todos menos el primer término de la ecuación superior y el último término de la ecuación inferior se cancelan. Para obtener una fórmula para\(S_n\), dividir ambos lados por\((1−r)\).
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\)\(r≠1\)
Una serie geométrica es la suma de los términos en una secuencia geométrica. La fórmula para la suma de los primeros\(n\) términos de una secuencia geométrica se representa como
\(S_n=\dfrac{a_1(1−r^n)}{1−r}\)\(r≠1\)
- Identificar\(a_1\),\(r\), y\(n\).
- Sustituir valores por\(a_1\),\(r\), y\(n\) en la fórmula\(S_n=\dfrac{a_1(1−r^n)}{1−r}\).
- Simplificar para encontrar\(S_n\).
Usa la fórmula para encontrar la suma parcial indicada de cada serie geométrica.
- \(S_{11}\)para la serie\(8 + -4 + 2 + …\)
- \(\sum_{ 6}^{k=1}3⋅2k\)
Solución
- \(a_1=8\), y se nos da eso\(n=11\).
Podemos encontrar\(r\) dividiendo el segundo término de la serie por el primero.
\(r=\dfrac{−4}{8}=−\dfrac{1}{2}\)
Sustituir valores por\(a_1\)\(r\),, y\(n\) en la fórmula y simplificar.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_{11}&=\dfrac{8\left(1-{\left(-\dfrac{1}{2}\right)}^{11}\right)}{1-\left(-\dfrac{1}{2}\right)}\\ &\approx 5.336 \end{align*}\]
- Encuentra\(a_1\) sustituyendo\(k=1\) en la fórmula explícita dada.
\(a_1=3⋅2^1=6\)
Podemos ver por la fórmula explícita dada que\(r=2\). El límite superior de suma es\(6\), así\(n=6\).
Sustituir valores por\(a_1\)\(r\),, y\(n\) en la fórmula, y simplificar.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_6&=\dfrac{6(1-2^6)}{1-2}\\ &=378 \end{align*}\]
Usa la fórmula para encontrar la suma parcial indicada de cada serie geométrica.
\(S_{20}\)para la serie\(1,000 + 500 + 250 + …\)
- Contestar
-
\(≈2,000.00\)
\(\sum_{k=1}^{8}3^k\)
- Contestar
-
\(9,840\)
En un nuevo empleo, el salario inicial de un empleado es\($26,750\). Recibe un aumento\(1.6\%\) anual. Encuentra sus ganancias totales al final de los\(5\) años.
Solución
El problema puede ser representado por una serie geométrica con\(a_1=26,750\);\(n=5\); y\(r=1.016\). Sustituir valores por\(a_1\)\(r\),, y\(n\) en la fórmula y simplificar para encontrar la cantidad total ganada al final de los\(5\) años.
\[\begin{align*} S_n&=\dfrac{a_1(1-r^n)}{1-r}\\ S_5&=\dfrac{26,750(1-{1.016}^5)}{1-1.016}\\ &\approx 138,099.03 \end{align*}\]
Habrá ganado un total de\($138,099.03\) al final de los\(5\) años.
En un nuevo empleo, el salario inicial de un empleado es\($32,100\). Ella recibe un aumento\(2\%\) anual. ¿Cuánto habrá ganado al final de los\(8\) años?
- Contestar
-
\($275,513.31\)
Uso de la fórmula para la suma de una serie geométrica infinita
Hasta el momento, sólo hemos mirado las series finitas. A veces, sin embargo, nos interesa la suma de los términos de una secuencia infinita más que la suma de sólo los primeros\(n\) términos. Una serie infinita es la suma de los términos de una secuencia infinita. Un ejemplo de una serie infinita es\(2+4+6+8+...\)
Esta serie también se puede escribir en notación sumatoria como\(\sum_{k=1}^{\infty}2k\), donde el límite superior de la suma es infinito. Debido a que los términos no tienden a cero, la suma de la serie aumenta sin límite a medida que agregamos más términos. Por lo tanto, no se define la suma de esta serie infinita. Cuando la suma no es un número real, decimos que la serie diverge.
Determinar si se define la suma de una serie geométrica infinita
Si se acercan los términos de una serie geométrica infinita\(0\), se puede definir la suma de una serie geométrica infinita. Los términos de esta serie se acercan a\(0\):
\(1+0.2+0.04+0.008+0.0016+...\)
El cociente común\(r = 0.2\). Como\(n\) se pone muy grande, los valores de\(r^n\) consiguen muy pequeños y se acercan\(0\). Cada término sucesivo afecta la suma menor que el término anterior. A medida que cada término siguiente se acerca\(0\), la suma de los términos se acerca a un valor finito. Los términos de cualquier serie geométrica infinita con\(−1<r<1\) aproximación\(0\); la suma de una serie geométrica se define cuando\(−1<r<1\).
La suma de una serie infinita se define si la serie es geométrica y\(−1<r<1\).
- Encuentra la relación entre el segundo término y el primer término.
- Encuentra la relación entre el tercer término y el segundo término.
- Continuar con este proceso para asegurar que la relación entre un término y el término anterior sea constante a lo largo de todo. Si es así, la serie es geométrica.
- Si se encontró una relación común\(r\),, en el paso 3, verifique para ver si\(−1<r<1\). Si es así, se define la suma. De no ser así, no se define la suma.
Determinar si se define la suma de cada serie infinita.
- \(12 + 8 + 4 + …\)
- \(\dfrac{3}{4}+\dfrac{1}{2}+\dfrac{1}{3}+...\)
- \(\sum_{k=1}^{\infty}27⋅{(\dfrac{1}{3})}^k\)
- \(\sum_{k=1}^{\infty}5k\)
Solución
- La relación entre el segundo término y el primero es\(\dfrac{2}{3}\), que no es lo mismo que la relación del tercer término al segundo,\(\dfrac{1}{2}\) .La serie no es geométrica.
- La relación del segundo término al primero es la misma que la relación del tercer término al segundo. La serie es geométrica con una proporción común de\(\dfrac{2}{3}\). Se define la suma de la serie infinita.
- La fórmula dada es exponencial con una base de\(\dfrac{1}{3}\); la serie es geométrica con una proporción común de\(\dfrac{1}{3}\). Se define la suma de la serie infinita.
- La fórmula dada no es exponencial; la serie no es geométrica porque los términos van en aumento, por lo que no puede dar una suma finita.
Determinar si se define la suma de la serie infinita.
\(\dfrac{1}{3}+\dfrac{1}{2}+\dfrac{3}{4}+\dfrac{9}{8}+...\)
- Contestar
-
Se define la suma. Es geométrico.
\(24+(−12)+6+(−3)+...\)
- Contestar
-
Se define la suma de la serie infinita.
\(\sum_{k=1}^{\infty}15⋅{(–0.3)}^k\)
- Contestar
-
Se define la suma de la serie infinita.
Encontrar sumas de series infinitas
Cuando existe la suma de una serie geométrica infinita, podemos calcular la suma. La fórmula para la suma de una serie infinita está relacionada con la fórmula para la suma de los primeros\(n\) términos de una serie geométrica.
\[S_n=\dfrac{a_1(1−r^n)}{1−r}\]
Examinaremos una serie infinita con\(r=\dfrac{1}{2}\). ¿Qué pasa a\(r^n\) medida que\(n\) aumenta?
\[\begin{align*} \left(\dfrac{1}{2}\right)^2&=\dfrac{1}{4}\\ \left(\dfrac{1}{2}\right)^3&=\dfrac{1}{8}\\ \left(\dfrac{1}{2}\right)^4&=\dfrac{1}{16} \end{align*}\]
El valor de\(r^n\) disminuye rápidamente. ¿Qué pasa para mayores valores de\(n\)?
\[\begin{align*} {\left(\dfrac{1}{2}\right)}^{10} &= \dfrac{1}{1,024} \\ {\left(\dfrac{1}{2}\right)}^{20} &= \dfrac{1}{1,048,576} \\ {\left(\dfrac{1}{2}\right)}^{30} &= \dfrac{1}{1,073,741,824} \end{align*}\]
Como\(n\) se pone muy grande,\(r^n\) se pone muy pequeño. Decimos que, a medida que\(n\) aumenta sin ataduras,\(r^n\) se acerca a 0. Como\(r^n\) enfoques\(0\),\(1\),\(−r^n\) enfoques\(1\). Cuando esto sucede, el numerador se acerca\(a_1\). Esto nos da una fórmula para la suma de una serie geométrica infinita.
La fórmula para la suma de una serie geométrica infinita con\(−1<r<1\) es
\[S=\dfrac{a_1}{1−r}\]
- Identificar\(a_1\) y\(r\).
- Confirme eso\(–1<r<1\).
- Sustituir valores para\(a_1\) y\(r\) en la fórmula,\(S=\dfrac{a_1}{1−r}\).
- Simplificar para encontrar\(S\).
Encuentra la suma, si existe, para lo siguiente:
- \(10+9+8+7+…\)
- \(248.6+99.44+39.776 + …\)
- \(\sum_{k=1}^{\infty}4,374⋅{(–\dfrac{1}{3})}^{k–1}\)
- \(\sum_{k=1}^{\infty}\dfrac{1}{9}⋅{(\dfrac{4}{3})}^k\)
Solución
- No hay una relación constante; la serie no es geométrica.
- Hay una relación constante; la serie es geométrica. \(a_1=248.6\)y\(r=\dfrac{99.44}{248.6}=0.4\), así existe la suma. Sustituir\(a_1=248.6\) y\(r=0.4\) en la fórmula y simplificar para encontrar la suma:
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &=\dfrac{248.6}{1−0.4} \\[4pt] &=414.\overline{3} \end{align*}\]
- La fórmula es exponencial, por lo que la serie es geométrica con\(r=–\dfrac{1}{3}\). Encuentra\(a_1\) sustituyendo\(k=1\) en la fórmula explícita dada:
\(a_1=4,374⋅{(–\dfrac{1}{3})}^{1–1}=4,374\)
Sustituir\(a_1=4,374\) y\(r=−\dfrac{1}{3}\) en la fórmula, y simplificar para encontrar la suma:
\[ \begin{align*} S&=\dfrac{a_1}{1−r} \\[4pt] &= \dfrac{4,374}{1−\left(−\dfrac{1}{3}\right)} \\[4pt] &= 3,280.5 \end{align*}\]
- La fórmula es exponencial, por lo que la serie es geométrica, pero\(r>1\). La suma no existe.
Encuentra una fracción equivalente para el decimal repetido\(0.\overline{3}\)
Solución
Observamos el decimal repetido\(0.\overline{3}=0.333...\) para que podamos reescribir el decimal repetido como una suma de términos.
\(0.\overline{3}=0.3+0.03+0.003+...\)
Buscando un patrón, reescribimos la suma, notando que vemos el primer término multiplicado a\(0.1\) en el segundo término, y el segundo término multiplicado por\(0.1\) en el tercer término.

Observe el patrón; multiplicamos cada término consecutivo por una proporción común de\(0.1\) comenzar con el primer término de\(0.3\). Entonces, sustituyendo en nuestra fórmula por una suma geométrica infinita, tenemos
\(S_n=\dfrac{a_1}{1−r}=\dfrac{0.3}{1−0.1}=\dfrac{0.3}{0.9}=\dfrac{1}{3}\).
Encuentra la suma, si existe.
\(2+23+29+...\)
- Contestar
-
\(3\)
\(\sum_{k=1}^{\infty}0.76k+1\)
- Contestar
-
La serie no es geométrica.
\(\sum_{k=1}^{\infty}{\left(−\dfrac{3}{8}\right)}^k\)
- Contestar
-
\(−\dfrac{3}{11}\)
Resolviendo problemas de anualidades
Al inicio de la sección, analizamos un problema en el que una pareja invirtió una cantidad fija de dinero cada mes en un fondo universitario durante seis años. Una anualidad es una inversión en la que el comprador realiza una secuencia de pagos periódicos e iguales. Para encontrar el monto de una anualidad, necesitamos encontrar la suma de todos los pagos y los intereses devengados. En el ejemplo, la pareja invierte\($50\) cada mes. Este es el valor del depósito inicial. La cuenta pagó intereses\(6\%\) anuales, compuestos mensualmente. Para encontrar la tasa de interés por periodo de pago, necesitamos dividir la tasa de interés porcentual\(6\%\) anual (TAE) por\(12\). Entonces la tasa de interés mensual es\(0.5\%\). Podemos multiplicar el monto en la cuenta cada mes por\(100.5\%\) para encontrar el valor de la cuenta después de que se hayan agregado intereses.
Podemos encontrar el valor de la anualidad justo después del último depósito mediante el uso de una serie geométrica con\(a_1=50\) y\(r=100.5%=1.005\). Después del primer depósito, el valor de la anualidad será\($50\). Veamos si podemos determinar el monto en el fondo universitario y los intereses devengados.
Podemos encontrar el valor de la anualidad después de nn depósitos usando la fórmula para la suma de los primeros nn términos de una serie geométrica. En\(6\) años, hay\(72\) meses, entonces\(n=72\). Podemos sustituir\(a_1=50\),\(r=1.005\), y\(n=72\) en la fórmula, y simplificar para encontrar el valor de la anualidad después de 6 años.
\(S_{72}=\dfrac{50(1−{1.005}^{72})}{1−1.005}≈4,320.44\)
Después del último depósito, la pareja tendrá un total de\($4,320.44\) en la cuenta. Aviso, la pareja realizó\(72\) pagos de\($50\) cada uno por un total de\(72(50) = $3,600\). Esto quiere decir que por la anualidad, la pareja ganó\($720.44\) intereses en su fondo universitario.
- Determinar\(a_1\), el valor del depósito inicial.
- Determinar\(n\), el número de depósitos.
- Determinar\(r\).
- Dividir la tasa de interés anual por el número de veces al año en que se compone el interés.
- Agrega 1 a esta cantidad para encontrar\(r\).
- Sustituir valores para\(a_1\)\(r\),, y\(n\) en la fórmula para la suma de los primeros nn términos de una serie geométrica,\(S_n=\dfrac{a_1(1–r^n)}{1–r}\).
- Simplificar para encontrar\(S_n\), el valor de la anualidad después de\(n\) los depósitos.
Un depósito de\($100\) se coloca en un fondo universitario al comienzo de cada mes durante\(10\) años. El fondo gana intereses\(9\%\) anuales, compuestos mensuales y pagados al final del mes. ¿Cuánto hay en la cuenta justo después del último depósito?
Solución
El valor del depósito inicial es\($100\), entonces\(a_1=100\). Un total de depósitos\(120\) mensuales se realizan en los\(10\) años, así\(n=120\). Para encontrar\(r\), divida la tasa de interés anual entre\(12\) para encontrar la tasa de interés mensual y agregar\(1\) para representar el nuevo depósito mensual.
\(r=1+\dfrac{0.09}{12}=1.0075\)
Sustituir\(a_1=100\)\(r=1.0075\),, y\(n=120\) en la fórmula para la suma de los primeros\(n\) términos de una serie geométrica, y simplificar para encontrar el valor de la anualidad.
\(S_{120}=\dfrac{100(1−{1.0075}^{120})}{1−1.0075}≈19,351.43\)
Por lo que la cuenta tiene $19,351.43 después de que se realice el último depósito.
Al inicio de cada mes,\($200\) se deposita en un fondo de retiro. El fondo gana intereses\(6\%\) anuales, compuestos mensuales, y ingresados en la cuenta al final del mes. ¿Cuánto hay en la cuenta si los depósitos se hacen por\(10\) años?
- Contestar
-
\($92,408.18\)
Acceda a estos recursos en línea para obtener instrucción adicional y práctica con series.
Ecuaciones Clave
| suma de los primeros\(n\) términos de una serie aritmética | \(S_n=\dfrac{n(a_1+a_n)}{2}\) |
| suma de los primeros\(n\) términos de una serie geométrica | \(S_n=\dfrac{a_1(1−r^n)}{1−r}\)⋅\(r≠1\) |
| suma de una serie geométrica infinita con\(–1<r< 1\) | \(S_n=\dfrac{a_1}{1−r}\)⋅\(r≠1\) |
Conceptos clave
- La suma de los términos en una secuencia se llama serie.
- Una notación común para series se llama notación de suma, que utiliza la letra griega sigma para representar la suma. Ver Ejemplo\(\PageIndex{1}\).
- La suma de los términos en una secuencia aritmética se denomina serie aritmética.
- La suma de los primeros\(n\) términos de una serie aritmética se puede encontrar usando una fórmula. Ver Ejemplo\(\PageIndex{2}\) y Ejemplo\(\PageIndex{3}\).
- La suma de los términos en una secuencia geométrica se denomina serie geométrica.
- La suma de los primeros\(n\) términos de una serie geométrica se puede encontrar usando una fórmula. Ver Ejemplo\(\PageIndex{4}\) y Ejemplo\(\PageIndex{5}\).
- La suma de una serie infinita existe si la serie es geométrica con\(–1<r<1\).
- Si existe la suma de una serie infinita, se puede encontrar usando una fórmula. Ver Ejemplo\(\PageIndex{6}\)\(\PageIndex{7}\), Ejemplo y Ejemplo\(\PageIndex{8}\).
- Una anualidad es una cuenta en la que el inversionista realiza una serie de pagos programados regularmente. El valor de una anualidad se puede encontrar usando series geométricas. Ver Ejemplo\(\PageIndex{9}\).


