2.1: Líneas, pendiente e intercepciones
- Page ID
- 117645
En este capítulo vamos a introducir la noción de una función. Antes de dar la definición general, recordamos un tipo especial de función que ya es familiar para el estudiante. Más precisamente, comenzamos recordando funciones que vienen dadas por líneas rectas.
Hemos visto en la última sección que cada punto de la recta numérica está representado por un número real\(x\) en\(\mathbb{R}\). De igual manera, cada punto en el plano de coordenadas está representado por un par de números reales\((x,y)\). El plano de coordenadas se denota por\(\mathbb{R}^{2}\). Aquí hay una imagen del plano de coordenadas:
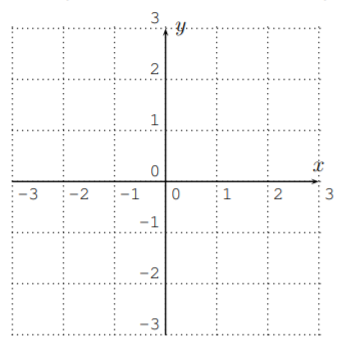
En esta sección, discutiremos la línea recta en el plano de coordenadas. Discutiremos su pendiente e intercepciones. También discutiremos las formas algebraicas correspondientes a la línea: la forma punto-pendiente y la forma pendiente-intercepción.
Al dibujar una línea en un plano de coordenadas asociamos cada punto de la línea con un par de números\((a,b)\), donde\(a\) se llama la\(x-\) coordenada y\(b\) se llama la\(y-\) coordenada. Considere, por ejemplo, la imagen
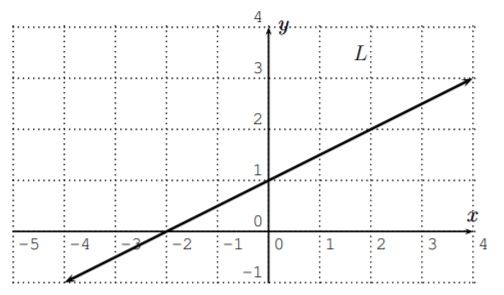
Vemos que\((-2,0)\) yace en la línea y también lo hace\((2,2)\). Por supuesto, hay un número infinito de puntos en la línea. Este conjunto de puntos también se puede describir mediante una ecuación que relaciona las\(y-\) coordenadas\(x-\) y de los puntos en la línea. Por ejemplo\(2y-x=2\) es la ecuación de la línea anterior. Observe que\((-2,0)\) satisface la ecuación desde\(2(0)-(-2)=2\) y\((2,2)\) satisface la ecuación desde\(2(2)-(2)=2\). Es un hecho que cada línea tiene una ecuación de la forma\(px+qy=r\), es decir, dada una línea, hay números\(p, q\) y\(r\) para que un punto\((a,b)\) esté en la gráfica de la línea si y solo si\(pa+qb=r\).
Observe que, en el ejemplo, si ponemos nuestro dedo\((-2,0)\) y lo movemos hacia arriba y hacia arriba hasta el punto\((2,2)\) hemos movido\(2\) unidades hacia arriba y\(4\) unidades a la derecha. Si de ahí (\((2,2)\)) movemos otras\(2\) unidades hacia arriba y\(4\) unidades a la derecha entonces volvemos a aterrizar en la línea (at\((6,4)\)). De hecho no importa donde empecemos en la línea si de ahí movemos\(2\) unidades hacia arriba y\(4\) unidades a la derecha siempre volvemos a aterrizar en la línea. A la relación\(\dfrac{\text{rise}}{\text{run}}=\dfrac24\) se le llama pendiente de esta línea. La palabra 'subida' indica movimiento vertical (siendo negativo hacia abajo) y 'correr' indica movimiento horizontal (siendo negativo a la izquierda). Observe eso\(\dfrac24=\dfrac12=\dfrac{-1}{-2}\) y así sucesivamente. Entonces también podríamos ver que si empezamos en\((-2,0)\) y subimos\(1\) y\(2\) corremos aterrizamos en\((0,1)\) lo que está en la línea y si empezamos en\((2,2)\) y subimos\(-1\) (bajamos\(1\)) y correr\(-2\) (mover a la izquierda\(2\)) terminamos en\((0,1)\), que vuelve a estar en la línea.
Generalmente, la pendiente describe qué tan rápido crece la línea hacia la derecha. Para dos puntos cualesquiera\(P_1(x_1,y_1)\) y\(P_2(x_2,y_2)\) en la línea\(L\), la pendiente\(m\) viene dada por la siguiente fórmula\(\left (\text {which is } \dfrac{\text{rise}}{\text{run}} \right )\):
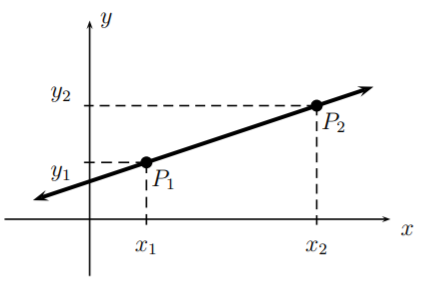
\[\label{slope} \text{Slope: } \quad\quad \boxed{m=\dfrac{y_2-y_1}{x_2-x_1}}\quad\quad\]
La pendiente determina qué tan rápido crece una línea. Cuando la pendiente\(m\) es negativa la línea desciende hacia la derecha.
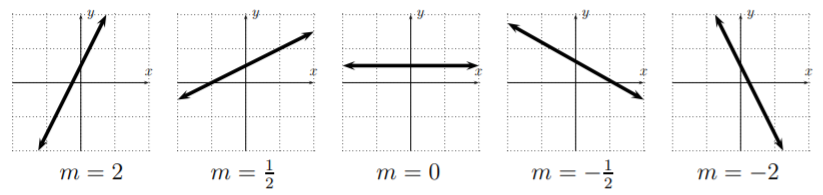
De la Ecuación\ ref {pendiente}, vemos que para una pendiente dada\(m\) y un punto\(P_1(x_1,y_1)\) en la línea, cualquier otro punto\((x,y)\) de la línea satisface\(m=\dfrac{y-y_1}{x-x_1}\). Multiplicar\((x-x_1)\) en ambos lados da lo que se llama la forma punto-pendiente de la línea:
\[\label{point-slope-form} \boxed{y-y_1=m\cdot (x-x_1)}\]
Otras características prominentes de una gráfica de una línea (u otras gráficas) incluyen dónde la gráfica cruza el\(x\) eje y el\(y-\) eje. Para una línea dada\(L\), recordemos cuáles son las\(x\) - y\(y\) -intercepciones. El\(x\) -intercept es el punto en el\(x\) eje -donde la línea se cruza con el\(x\) eje -eje. De manera similar, la\(y\) -intercepción es el punto en el\(y\) eje -donde la línea cruza el\(y\) eje -eje.
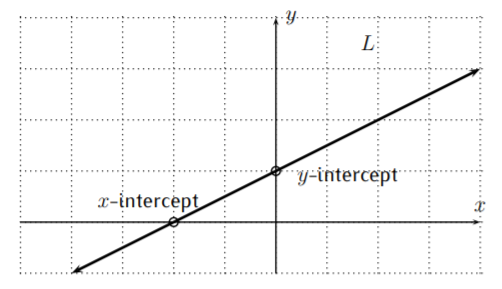
Una forma de describir una línea usando la pendiente e\(y\) -intercepción es la llamada forma pendiente-intercepción de la línea.
La forma pendiente-intercepción de la línea es la ecuación
\[\label{slope-intercept} \boxed{y=m\cdot x+b}\]
Aquí,\(m\) está la pendiente y\((0,b)\) es la \(y\)-intercepción de la línea.
Aquí hay un ejemplo de una línea en forma de pendiente-intercepción.
Grafica la línea\(y=2x+3\).
Solución
Calculamos\(y\) para diversos valores de\(x\). Por ejemplo, cuando\(x\) es\(-2, -1, 0, 1, 2\), o\(3\), calculamos
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & -2 & -1 & 0 & 1 & 2 & 3\
\ hline\ hline\ hline y & -1 & 1 & 3 & 5 & 7 & 9\
\\ hline
\ end {array}\ nonumber\]
En la tabla anterior cada\(y\) valor se calcula sustituyendo el\(x\) valor correspondiente en nuestra ecuación\(y=2x+3\):
\ [\ begin {array} {llll}
x=-2 &\ LongRightarrow & y=2\ cdot (-2) +3=-4+3=-1\
x=-1 &\ LongRightarrow & y=2\ cdot (-1) +3=-2+3=1\
x=0 &\ LongRightarrow & y=2\ cdot (0) +3=0+3=3\\
x=1 &\ LongRightarrow & y=2\ cdot (1) +3=2+3=5\\
x=2 &\ Longrightarrow & y=2\ cdot (2) +3=4+3=7\
x=3 &\ Longrightarrow & y=2\ cdot (3) +3=6+3=9
\ end {array}\ nonumber\]
En el cálculo anterior, los valores para\(x\) fueron elegidos arbitrariamente. Dado que una línea se determina completamente al conocer dos puntos en ella, dos valores cualesquiera para\(x\) habrían funcionado con el propósito de graficar la línea.
Dibujar los puntos anteriores en el plano de coordenadas y conectarlos da la gráfica de la línea\(y=2x+3\):
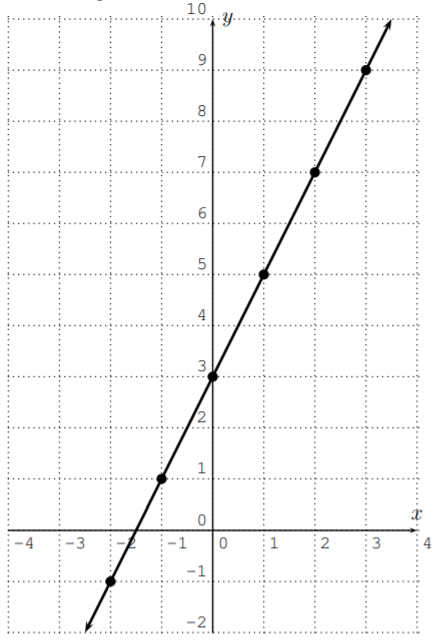
Alternativamente, tenga en cuenta que la\(y\) intersección es\((0,3)\) (\(3\)es la constante aditiva en nuestra ecuación inicial\(y=2x+3\)) y la pendiente\(m=2\) determina la velocidad a la que crece la línea: para cada paso a la derecha, tenemos que mover dos escalones hacia arriba.
Para trazar la gráfica, primero trazamos la\(y\) -intercepción\((0,3)\). Entonces a partir de ese punto, sube\(2\) y corre\(1\) para que te encuentres en\((1,5)\) (que debe estar en la gráfica), y de manera similar subir\(2\) y correr\(1\) para llegar a\((2,7)\) (que debe estar en la gráfica), etc. Trazar estos puntos en la gráfica y conectar los puntos para formar una línea recta. Como se señaló anteriormente, cualquier punto\(2\) distinto en la gráfica de una línea recta es suficiente para trazar la línea completa.
Antes de dar más ejemplos, brevemente queremos justificar por qué, en la expresión\(y=mx+b\), el número\((0,b)\) es la\(y\) intersección y\(m\) es la pendiente. Esta prueba puede omitirse en una primera lectura.
Dada la línea\(y=mx+b\), queremos calcular su\(y\) -intercepción y su pendiente. El\(y\) -intercepto es el valor de\(y\) donde\(x=0\). Por lo tanto, tenemos que la\(y-\) coordenada de la\(y\) -intercepción es
\[y=m\cdot 0 + b = b \nonumber \]
Esto muestra el primer reclamo.
A continuación, para ver por qué\(m\) es la pendiente, tenga en cuenta que\(P_1(x_1,y_1)\) se encuentra en la línea exactamente cuándo\(y_1=m x_1 +b\). Del mismo modo,\(P_2(x_2,y_2)\) se encuentra en la línea exactamente cuándo\(y_2=m x_2 +b\). Restando\(y_1=m x_1 +b\) de\(y_2=m x_2 +b\), obtenemos:
\[y_2-y_1= (m x_2+b)-(m x_1+b)=m x_2+ b - m x_1 -b = m\cdot (x_2-x_1).\nonumber \]
Dividiendo por\((x_2-x_1)\) da
\[\dfrac{y_2-y_1}{(x_2-x_1)}=\dfrac{m\cdot (x_2-x_1)}{ (x_2-x_1)}=\dfrac m 1 = m \nonumber \]
Por Ecuación\ ref {pendiente} la fracción\(\dfrac{y_2-y_1}{x_2-x_1}\) es la pendiente, estableciendo que nuestra\(m\) es efectivamente la pendiente, como afirmamos.
Encuentra la ecuación de la línea en forma de pendiente-intercepción.
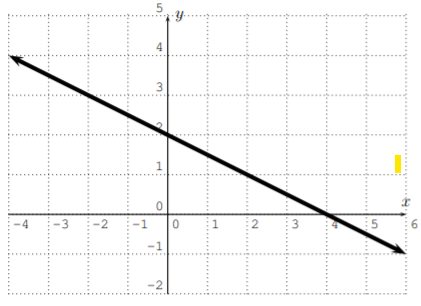
Solución
El\(y\) -intercepto se puede leer fuera de la gráfica dándonos eso\(b=2\).
En cuanto a la pendiente, utilizamos la fórmula\ ref {pendiente} y los dos puntos en la línea\(P_1(0,2)\) y\(P_2(4,0)\).
Obtenemos:
\[m=\dfrac{0-2}{4-0}=\dfrac{-2}{4}=-\dfrac{1}{2} \nonumber\]
Así, la línea tiene la forma pendiente-intercepción\(y=-\dfrac 1 2 x +2\).
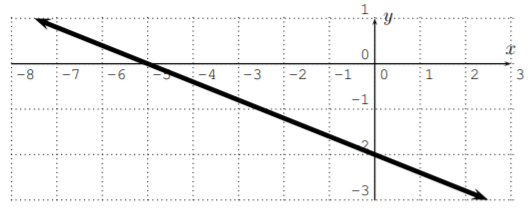
Encuentra la ecuación de la línea en forma de pendiente-intercepción.
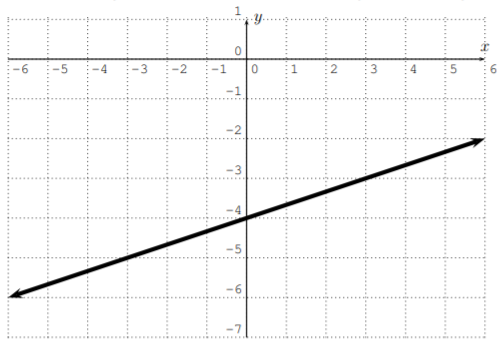
Solución
El\(y\) -intercepto es\(b=-4\). Para obtener la pendiente podemos volver a utilizar la\(y\) -intercepción\(P_1(0,-4)\). Para usar\ ref {slope}, necesitamos otro punto\(P_2\) en la línea. Podremos escoger cualquier segundo punto de la línea, por ejemplo,\(P_2(3,-3)\). Con esto, obtenemos
\[m=\dfrac{(-3)-(-4)}{3-0}=\dfrac{-3+4}{3}=\dfrac{1}{3} \nonumber \]
Así, la línea tiene la forma pendiente-intercepción\(y=\dfrac 1 3 x -4\).
Encuentra la ecuación de la línea en forma de punto-pendiente\ ref {punto-pendiente-forma}.
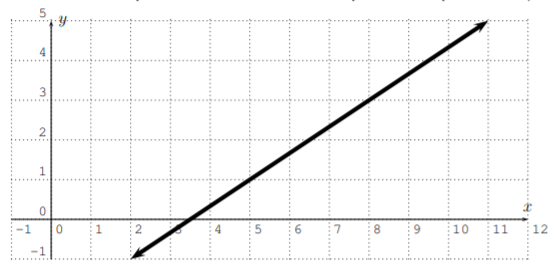
Solución
Necesitamos identificar un punto\((x_1,y_1)\) en la línea junto con la pendiente\(m\) de la línea para que podamos escribir la línea en forma de punto-pendiente:\(y-y_1=m(x-x_1)\). Por inspección directa, identificamos los dos puntos\(P_1(5,1)\) y\(P_2(8,3)\) en la línea, y con esto calculamos la pendiente como
\[m=\dfrac{3-1}{8-5}=\dfrac{2}{3} \nonumber \]
Usando el punto\((5,1)\) escribimos la línea en forma de punto-pendiente de la siguiente manera:
\[y-1=\dfrac{2}{3}(x-5) \nonumber \]
Tenga en cuenta que nuestra respuesta depende del punto elegido\((5,1)\) en la línea. En efecto, si elegimos un punto diferente en la línea, tal como\((8,3)\), obtenemos una ecuación diferente, (que sin embargo representa la misma línea):
\[y-3=\dfrac{2}{3}(x-8) \nonumber \]
Tenga en cuenta, que no necesitamos resolver esto para\(y\), ya que estamos buscando una respuesta en forma de punto-pendiente.
Encuentra la pendiente, encuentra la\(y\) intercepción y grafica la línea
\[4x+2y -2=0 \nonumber \]
Solución
Primero reescribimos la ecuación en forma de pendiente-intercepción.
\ [\ begin {alineado}
4 x+2 y-2=0 &\ stackrel {(-4 x+2)} {\ Longrightarrow} 2 y=-4 x+2\\
&\ stackrel {(\ text {divide} 2)} {\ Longrightarrow} y=-2 x+1
\ end {alineado}\ nonumber\]
Vemos que la pendiente es\(-2\) y la\(y\) -intercepción es\((0,1)\).
Luego podemos trazar la\(y-\) intercepción\((0,1)\) y usar la pendiente\(m=\dfrac{-2}{1}\) para encontrar otro punto\((1,-1)\). Trace ese punto, conecte los dos puntos trazados y extiéndalo para ver la gráfica a continuación.
También podemos graficar trazando puntos. Podemos calcular los\(y\) -valores para algunos\(x\) -valores. Por ejemplo cuando\(x=-2,-1,\dots,3\), obtenemos:
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & -2 & -1 & 0 & 1 & 2 & 3\
\ hline\ hline\ hline y & 5 & 3 & 1 & -1 & -3 & -5\
\ hline
\ end {array}\ nonumber\]
Esto da la siguiente gráfica:
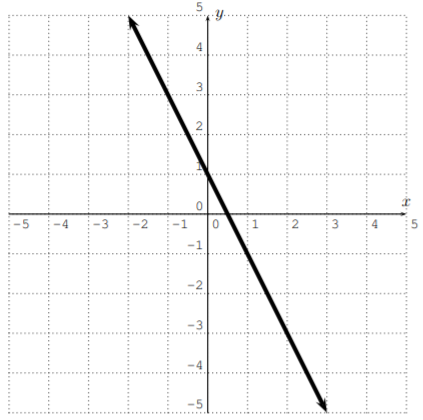
Encuentre la pendiente,\(y\) -intercepte y grafique la línea\(5y+2x =-10\).
Solución
Nuevamente, primero reescribimos la ecuación en forma de pendiente-intercepción.
\ [\ begin {array} {cl}
5 y+2 x=-10 &\ stackrel {\ text {(restar} 2 x)} {\ Longrightarrow}\ quad 5 y=-2 x-10\
&\ stackrel {(\ text {divide} 5)} {\ Longrightarrow}\ quad y=\ dfrac {-2 x-10} {5}\\
&\ Longrightarrow\ quad y=-\ dfrac {2} {5} x-2
\ fin { matriz}\ nonumber\]
Ahora, la pendiente es\(-\dfrac 2 5\) y la\(y\) -intercepción es\((0,-2)\).
Podemos trazar la\(y-\) intercepción y de ahí mover\(2\) unidades hacia abajo y\(5\) unidades a la derecha para encontrar otro punto en la línea. La gráfica se da a continuación.
Para graficarlo trazando puntos necesitamos encontrar puntos en la línea. De hecho, dos puntos cualesquiera serán suficientes para determinar completamente la gráfica de la línea. Para algunas elecciones “inteligentes”\(x\) o\(y\) el cálculo del valor correspondiente puede ser más fácil que para otras. Te sugerimos que encuentres el\(x-\) e\(y-\) intercepta, es decir, el punto de la forma\((?,0)\) (\(y=0\)en la ecuación y encontrar\(x\)) y\((0,?)\) (establecer\(x=0\) en la ecuación y encontrar \(y\)). \(x=0\)Conectando a\(5y+2x=-10\), obtenemos
\[\stackrel{x=0}{\Longrightarrow} 5 y+2 \cdot 0=-10 \quad \Longrightarrow 5 y=-10 \quad \Longrightarrow y=-2 \nonumber \]
Del mismo modo, sustituyendo\(y=0\) en\(5y+2x=-10\) da
\[\stackrel{y=0}{\Longrightarrow} 5 \cdot 0+2 x=-10 \quad \Longrightarrow 2 x=-10 \quad \Longrightarrow x=-5 \nonumber \]
Obtenemos la siguiente tabla:
\ [\ begin {array} {|c||c|c|}
\ hline x & 0 & -5\\ hline
\ hline\ hline y & -2 & 0\
\ hline
\ end {array}\ nonumber\]
Esto da la siguiente gráfica: