2.2: Introducción a las funciones
- Page ID
- 117643
Ahora introducimos formalmente la noción de una función. Un primer ejemplo fue proporcionado por una línea recta como, por ejemplo,\(y=5x+4\). Tenga en cuenta, que para cada dado\(x\) obtenemos un inducido\(y\). (Por ejemplo, para\(x=3\), obtenemos\(y=5\cdot 3+4=19\).)
Una función\(f\) consta de dos conjuntos, un conjunto\(D\) de entradas llamado dominio y un conjunto\(C\) de posibles salidas llamadas codomain, y una asignación que asigna a cada entrada\(x\) exactamente una salida\(y\).
Una función\(f\) con dominio\(D\) y codominio\(C\) se denota por
\[f:D\to C \nonumber \]
Si\(x\) está en el dominio\(D\) (una entrada), entonces denotamos por\(f(x)=y\) la salida que es asignada por\(f\) a\(x\).
A veces es de interés conocer el conjunto de todos los elementos en el codominio que realmente ocurren como salida. Este conjunto es un subconjunto del codominio y se llama el rango. Contamos con:
El rango\(R\) de una función\(f\) es un subconjunto del codominio dado por\(R=\{f(x) \,|\, x\text{ in the domain of }f\}\). Es decir, el rango es el conjunto de todas las salidas.
Algunos autores utilizan una convención ligeramente diferente al llamar al rango lo que llamamos el codominio anterior.
Ya que estaremos tratando con muchas funciones es conveniente nombrar varias funciones (generalmente con letras\(f, g, h\), etc). A menudo asumiremos implícitamente que un dominio y un codominio se dan sin especificarlos explícitamente. Si se puede determinar el rango y el codominio no se da explícitamente, entonces tomamos el codominio como el rango. Si el rango no se puede determinar fácilmente y el codominio no se da explícitamente, entonces el codominio debe tomarse como un conjunto 'simple' que contiene claramente el rango.
Hay varias formas de representar una función particular (todas las cuales pueden no aplicarse a una función específica): a través de una tabla de valores (enumerando los pares de entrada-salida), a través de una fórmula (con el dominio y el rango dados explícita o implícitamente), a través de una gráfica (que representa pares de entrada-salida en un plano de coordenadas), o en palabras, sólo por nombrar algunas. Hemos visto ejemplos de los tres primeros de estos en secciones anteriores. Nuestra discusión en esta sección entra en mayor detalle.
Defina la asignación\(f\) mediante la siguiente tabla:
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & 2 & 5 & -3 & 0 & 7 & 4\
\ hline\ hline\ hline y & 6 & 8 & 4 & -1 & 8\
\ hline
\ end {array}\ nonumber\]
Solución
La asignación\(f\) asigna a la entrada\(2\) la salida\(6\), que también se escribe como
\[f(2)=6 \nonumber \]
De igual manera,\(f\) asigna\(5\) al número\(8\), en resumen\(f(5)=8\), etc:
\[f(5)=8,\quad f(-3)=6,\quad f(0)=4,\quad f(7)=-1,\quad f(4)=8 \nonumber \]
El dominio\(D\) es el conjunto de todas las entradas. El dominio es por lo tanto
\[D=\{-3,0,2,4,5,7\}\nonumber \]
El rango\(R\) es el conjunto de todas las salidas. Por lo tanto, el rango es
\[R=\{-1,4,6,8\}\nonumber \]
La asignación\(f\) es de hecho una función ya que a cada elemento del dominio se le asigna exactamente un elemento en el rango. Tenga en cuenta que para un número de entrada que no esté en el dominio,\(f\) no le asigna una salida. Por ejemplo,
\[f(1)=\text{undefined}\nonumber \]
Tenga en cuenta también eso\(f(5)=8\) y\(f(4)=8\), de manera que se\(f\) asigna a las entradas\(5\) y\(4\) la misma salida\(8\). De igual manera,\(f\) también asigna la misma salida a las entradas\(2\) y\(-3\). Por lo tanto vemos que:
- ¡Una función puede asignar la misma salida a dos entradas diferentes!
Considera la tarea\(f\) que viene dada por la siguiente tabla.
\ [\ begin {array} {|c||c|c|c|c|c|c|c|}
\ hline x & 2 & 5 & -3 & 0 & 5 & 4\
\ hline\ hline\ hline y & 6 & 8 & 4 & -1 & 8\
\ hline
\ end {array}\ nonumber\]
¡Esta asignación no define una función! ¿Qué salió mal?
Solución
Considera el valor de entrada\(5\). ¿Qué\(f\) asigna a la entrada\(5\)? La tercera columna establece que\(f\) asigna a\(5\) la salida\(8\), mientras que la sexta columna indica que\(f\) asigna a\(5\) la salida\(-1\),
\[f(5)=8, \quad\quad f(5)=-1 \nonumber \]
Sin embargo, por la definición de una función, a cada entrada tenemos que asignar exactamente una salida. Entonces, aquí, a la entrada\(5\) hemos asignado dos salidas\(8\) y\(-1\). Por lo tanto, no\(f\) es una función.
- ¡Una función no puede asignar dos salidas a una entrada!
Repetimos las dos viñetas de los dos últimos ejemplos, que son cruciales para la comprensión de una función.
- \(f\left(x_{1}\right)=y\)y\(f\left(x_{2}\right)=y\) con\(x_{1} \neq x_{2}\) está permitido!
- \(f(x)=y_1\)y\(f(x)=y_2\) con no\(y_{1} \neq 2_{2}\) está permitido!
Una universidad crea un programa de mentoría, que relaciona a cada estudiante de primer año con un estudiante de último año como su mentor. Dentro de este programa se garantiza que cada estudiante de primer año obtenga precisamente un mentor, sin embargo dos estudiantes de primer año pueden recibir el mismo mentor. ¿La asignación de estudiantes de primer año como mentores o mentores de estudiantes de primer año describe una función? Si es así, ¿cuál es su dominio, cuál es su rango?
Solución
Dado que un estudiante de último año puede ser mentor de varios estudiantes de primer año, no podemos tomar a un mentor como “aporte”, ya que él o ella serían asignados a varios estudiantes de primer año de “salida”. Entonces el estudiante de primer año no es una función de mentor.
Por otro lado, podemos asignar a cada estudiante de primer año exactamente a un mentor, que por lo tanto describe una función. El dominio (el conjunto de todas las entradas) viene dado por el conjunto de todos los estudiantes de primer año. El rango (el conjunto de todos los resultados) viene dado por el conjunto de todos los estudiantes de último año que son mentores. La función asigna a cada estudiante de primer año de “entrada” a su mentor único de “salida”.
La precipitación en una ciudad para cada uno de los 12 meses se muestra en el siguiente histograma.
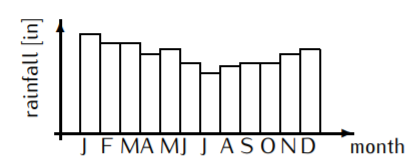
- ¿La precipitación es una función del mes?
- ¿El mes es una función de las precipitaciones?
Solución
- Cada mes tiene exactamente una cantidad de lluvia asociada a él. Por lo tanto, la asignación que asocia a un mes su precipitación (en pulgadas) es una función.
- Si tomamos una cierta cantidad de lluvia como nuestros datos de entrada, ¿podemos asociarle un mes único? Por ejemplo, febrero y marzo tienen la misma cantidad de precipitaciones. Por lo tanto, a una cantidad de lluvia de entrada no podemos asignar un mes único. El mes no es una función de las precipitaciones.
Considera la función que\(f\) se describe a continuación.
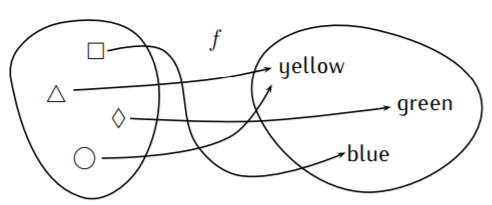
Aquí, la función\(f\) mapea el símbolo de entrada\(\Box\) al color azul de salida. Otras asignaciones de\(f\) son las siguientes:
\[\begin{aligned} f(\Box)=\text{blue}, \quad\quad\,\,\, & f(\triangle)=\text{yellow} \\ f(\Diamond)=\text{green}, \quad\quad& f(\bigcirc)=\text{yellow}\end{aligned}\]
¿Qué es el Dominio y Rango de la función f?
Solución
El dominio es el conjunto de símbolos\(D=\{\Box,\triangle, \Diamond, \bigcirc\}\), y el rango es el conjunto de colores\(R=\{\) azul\(,\) verde\(,\) amarillo\(\}\). Observe, en particular, que las entradas\(\triangle\) y\(\bigcirc\) ambas tienen la misma salida amarilla, lo que sin duda está permitido para una función.
Considere la función\(y=5x+4\) con dominio todos los números reales y rango todos los números reales. Tenga en cuenta que para cada entrada\(x\), obtenemos exactamente una salida inducida\(y\). Por ejemplo, para la entrada\(x=3\) obtenemos la salida\(y=5\cdot 3+4=19\), etc.
Considere la función\(y=x^2\) con dominio todos los números reales y rango números no negativos. La función toma un número real como entrada y lo cuadra. Por ejemplo si\(x=-2\) es la entrada, entonces\(y=4\) es la salida.
Para cada número real\(x\), denota por\(\lfloor x\rfloor\) el mayor número entero que es menor o igual a\(x\). Llamamos\(\lfloor x\rfloor\) al piso de \(x\). Por ejemplo, para calcular\(\lfloor4.37\rfloor\), tenga en cuenta que todos los enteros\(4, 3, 2, \dots\) son menores o iguales a\(4.37\):
\[\dots,-3,-2,-1,0,1,2,3,4\quad\quad \leq \quad 4.37 \nonumber \]
El mayor de estos enteros es\(4\), así que eso\(\lfloor 4.37\rfloor=4\). Definimos la función de piso como\(f(x)=\lfloor x\rfloor\). Aquí hay más ejemplos de valores de función de la función floor.
\[\begin{aligned} && \lfloor 7.3\rfloor=7, \quad\quad\quad\,\, \lfloor \pi\rfloor=3, \quad\quad\quad\,\, \lfloor -4.65\rfloor=-5, \\ && \lfloor 12\rfloor=12, \quad\quad\quad \left\lfloor \frac{-26}{3}\right\rfloor= \lfloor -8.667\rfloor=-9 \end{aligned}\]
El dominio de la función floor es el conjunto de todos los números reales, es decir\(D=\mathbb{R}\). El rango es el conjunto de todos los enteros,\(R=\mathbb{Z}\).
Dejar\(A\) ser el área de un triángulo rectángulo isósceles con longitud lateral base\(x\). \(A\)Expresar en función de\(x\).
Solución
Ser un triángulo rectángulo isósceles significa que dos longitudes de lado son\(x\), y los ángulos son\(45^\circ\)\(45^\circ\), y\(90^\circ\) (o en medida de radianes\(\dfrac\pi 4\)\(\dfrac\pi 4\), y\(\dfrac\pi 2\)):
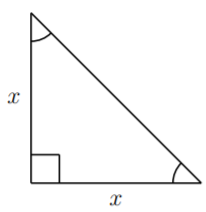
Recordemos que el área de un triángulo es: área =\(\cdot\) altura\(\dfrac 1 2\) base. En este caso, tenemos base\(=x\), y altura\(=x\), para que el área
\[A = \dfrac 1 2 x \cdot x = \dfrac 1 2 x^2 \nonumber \]
Por lo tanto, la zona\(A(x)=\dfrac 1 2 \cdot x^2\).
Considera la ecuación\(y=x^2+3\). Encuentra el dominio y el rango.
Solución
Esta ecuación asocia a cada número de entrada\(a\) exactamente un número de salida\(b=a^2+3\). Por lo tanto, la ecuación define una función. Por ejemplo:
\[\text{To the input }5 \text{ we assign the output } 5^2+3=25+3=28 \nonumber \]
El dominio\(D\) es todo números reales,\(D=\mathbb{R}\). Ya que\(x^2\) es siempre\(\geq 0\), vemos eso\(x^2+3\geq 3\), y viceversa cada número\(y\geq 3\) puede escribirse como\(y=x^2+3\). (Para ver esto, tenga en cuenta que la entrada\(x=\sqrt{y-3}\) para\(y\geq 3\) da la salida\(x^2-3=(\sqrt{y-3})^2+3=y-3+3=y\).) Por lo tanto, el rango es\(R=[3,\infty)\).
Considera la ecuación\(x^2+y^2=25\). ¿Esta ecuación define\(y\) como una función de\(x\)? Es decir, ¿esta ecuación asigna a cada entrada\(x\) exactamente una salida\(y\)?
Solución
Un número de entrada\(x\) se asigna a\(y\) con\(x^2+y^2=25\). Resolviendo esto para\(y\), obtenemos
\[y^2=25-x^2 \quad\implies\quad y=\pm\sqrt{25-x^2} \nonumber \]
Por lo tanto, hay dos posibles salidas asociadas a la entrada\(x(\not=5)\):
\[\text{either }\quad y=+\sqrt{25-x^2} \quad \quad \text{ or } \quad y=-\sqrt{25-x^2} \nonumber \]
Por ejemplo, la entrada\(x=0\) tiene dos salidas\(y=5\) y\(y=-5\). Sin embargo, ¡una función no puede asignar dos salidas a una entrada\(x\)! ¡La conclusión es que\(x^2+y^2=25\) no determina\(y\) como una función!
Tenga en cuenta que si\(y=f(x)\) entonces\(x\) se llama la variable independiente y\(y\) se llama la variable dependiente (ya que depende de\(x\)). Si\(x=g(y)\) entonces\(y\) es la variable independiente y\(x\) es la variable dependiente (ya que depende de\(y\)).


