7.1: Funciones uno a uno

Última actualización
Guardar como PDF

Page ID: 117801

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Hemos visto que algunas funciones$f$ pueden tener las mismas salidas para diferentes entradas. Por ejemplo para$f(x)=x^2$, las entradas$x=2$ y$x=-2$ tienen la misma salida$f(2)=4$ y$f(-2)=4$. Una función es uno a uno, precisamente cuando no es así.

Definición: Uno a uno

Una función$f$ se llama uno a uno (o inyectivo), si dos entradas diferentes$x_1\neq x_2$ siempre tienen diferentes salidas$f(x_1)\neq f(x_2)$.

Ejemplo$\PageIndex{1}$

Como se señaló anteriormente, la función no$f(x)=x^2$ es uno a uno, porque, por ejemplo, para entradas$2$ y$-2$, tenemos la misma salida

\[f(-2)=(-2)^2=4, \quad\quad f(2)=2^2=4 \nonumber \]

Por otro lado,$g(x)=x^3$ es uno a uno, ya que, por ejemplo, para entradas$-2$ y$2$, tenemos diferentes salidas:

\[g(-2)=(-2)^3=-8, \quad\quad g(2)=2^3=8 \nonumber \]

La diferencia entre las funciones$f$ y se$g$ puede ver a partir de sus gráficas.

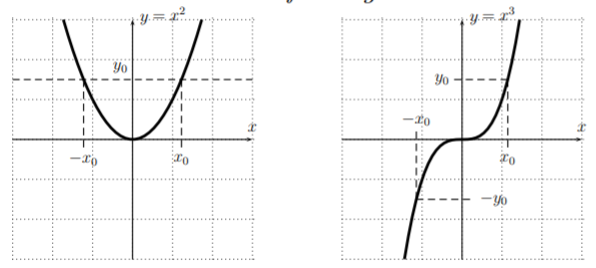
$clipboard_e0ab95ab482dd5250cfbc6c3ec2e40be6.png$

La gráfica de$f(x)=x^2$ la izquierda tiene para diferentes entradas ($x_0$y$-x_0$) la misma salida ($y_0=(x_0)^2=(-x_0)^2$). Esto se muestra en la gráfica ya que la línea horizontal en$y_0$ intersecta la gráfica en dos puntos diferentes. En general, dos entradas que tienen la misma salida$y_0$ dan dos puntos en la gráfica que también se encuentran en la línea horizontal en$y_0$.

Ahora, la gráfica de$g(x)=x^3$ la derecha se cruza con una línea horizontal en alguna$y_0$ sólo una vez. Esto demuestra que para dos entradas diferentes, nunca podremos tener la misma salida$y_0$, por lo que la función$g$ es uno-a-uno.

Podemos resumir la observación del último ejemplo en el siguiente enunciado.

Definición: Prueba de Línea Horizontal

Una función es uno a uno exactamente cuando cada línea horizontal intersecta el gráfico de la función como máximo una vez.

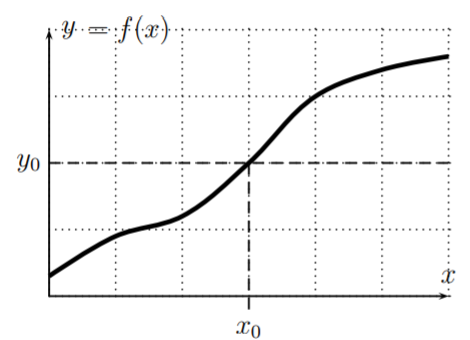
$clipboard_e63172b767625c993eabaf11e17d32ed2.png$

Ejemplo$\PageIndex{2}$

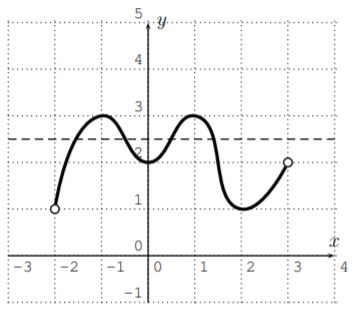
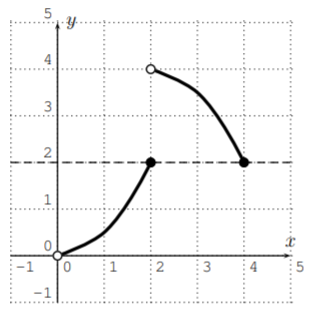
¿Cuáles de las siguientes son o representan funciones uno-a-uno?

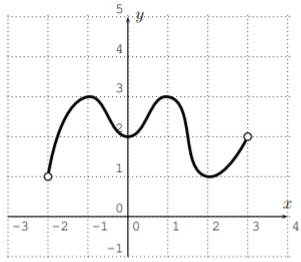
$clipboard_ed42aa128043a792776b74bb629407875.png$
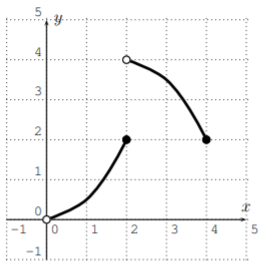
$clipboard_eb1857a23d169b5a49020815c595bf969.png$
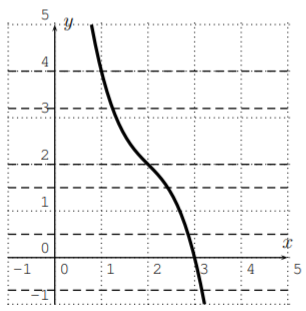
$f(x)=-x^3+6x^2-13x+12$
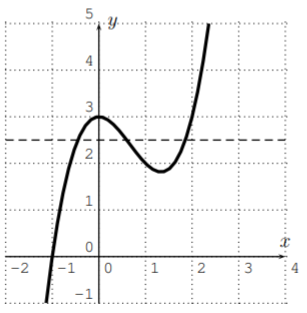
$f(x)=x^3-2x^2+3$

Solución

Utilizamos la prueba de línea horizontal para ver qué funciones son uno a uno. Para (a) y (b), vemos que las funciones no son uno-a-uno ya que hay una línea horizontal que se cruza con la gráfica más de una vez:

$clipboard_ebadce30096002e3875a33f5b544b3a4b.png$
$clipboard_e46a5ffe125f02b9b1f9a3cb13cbf986b.png$

Para (c), usando la calculadora para graficar la función$f(x)=-x^3+6x^2-13x+12$, vemos que todas las líneas horizontales se cruzan con la gráfica exactamente una vez. Por lo tanto, la función en la parte (c) es uno a uno. Sin embargo, la función en la parte (d) tiene una gráfica que cruza alguna línea horizontal en varios puntos. Por lo tanto, no$f(x)=x^3-2x^2+3$ es uno a uno:

$clipboard_ee071c7aa7956bd8047b3e12db60dd39e.png$
$clipboard_ed4346bf457936af6862e541dd62e0d27.png$

Definición: Uno a uno

Ejemplo\(\PageIndex{1}\)

Definición: Prueba de Línea Horizontal

Ejemplo\(\PageIndex{2}\)