7.2: Función inversa
- Page ID
- 117806
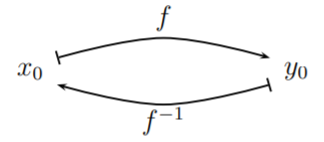
Una función es uno a uno, cuando cada salida está determinada por exactamente una entrada. Por lo tanto, podemos construir una nueva función, llamada función inversa, donde invertimos los roles de entradas y salidas. Por ejemplo, cuando\(y=x^3\), cada uno\(y_0\) proviene exactamente de uno\(x_0\) como se muestra en la imagen de abajo:
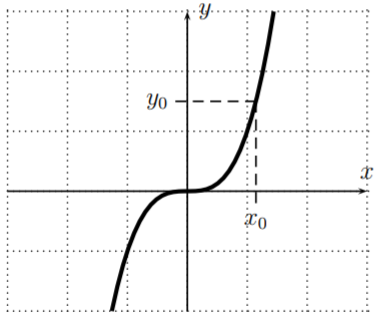
La función inversa asigna a la entrada\(y_0\) la salida\(x_0\).
Dejar\(f\) ser una función con dominio\(D_f\) y rango\(R_f\), y asumir que\(f\) es uno a uno. La inversa de\(f\) es una función\(f^{-1}\) para que\[f(x)=y \quad \text{ means precisely that } \quad f^{-1}(y)=x \nonumber \]
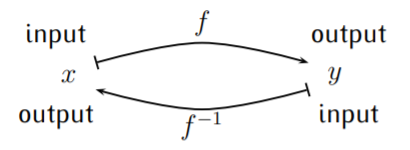
Aquí las salidas de\(f\) son las entradas de\(f^{-1}\), y las entradas de\(f\) son las salidas de\(f^{-1}\). Por lo tanto, la función inversa\(f^{-1}\) tiene un dominio igual al rango de\(f\)\(D_{f^{-1}}=R_f\),, y\(f^{-1}\) tiene un rango igual al dominio de\(f\),\(R_{f^{-1}}=D_f\). En resumen, cuando\(f\) es una función\(f:D_f\to R_f\), entonces la función inversa\(f^{-1}\) es una función\(f^{-1}:R_f\to D_f\).
La función inversa invierte los roles de entradas y salidas.
Encuentra la inversa de la siguiente función vía álgebra.
- \(f(x)=2x-7\)
- \(g(x)=\sqrt{x+2}\)
- \(h(x)=\dfrac{1}{x+4}\)
- \(j(x)=\dfrac{x+1}{x+2}\)
- \(k(x)=(x-2)^2+3\)para\(x\geq 2\)
Solución
- Primero, revertir el papel de entrada y salida en\(y=2x-7\) intercambiando las variables\(x\) y\(y\). Es decir, escribimos\(x=2y-7\). Necesitamos resolver esto para\(y\): Por\[\stackrel{\text{(add $7$)}}\implies\quad x+7 = 2y \implies\quad y=\dfrac{x+7}{2} \nonumber \] lo tanto, obtenemos que la inversa de\(f\) es\(f^{-1}(x)=\dfrac{x+7} 2\).
Para las otras partes, siempre intercambiamos\(x\)\(y\) y resolvemos por\(y\):
- Escribir\(y=\sqrt{x+2}\) e intercambiar\(x\) y\(y\):\[\begin{aligned} x=\sqrt{y+2} &\implies & x^2 =y+2 \quad \implies y= x^2-2\\ &\implies & g^{-1}(x)=x^2-2\end{aligned} \nonumber \]
- Escribir\(y=\dfrac{1}{x+4}\) e intercambiar\(x\) y\(y\):\[\begin{aligned} x=\dfrac{1}{y+4}& \implies & y+4 =\dfrac 1 x \quad\implies y= \dfrac 1 x -4\\ &\implies& h^{-1}(x)=\dfrac 1 x -4\end{aligned} \nonumber \]
- Escribir\(y=\dfrac{x+1}{x+2}\) e intercambiar\(x\) y\(y\):\[\begin{aligned} x=\dfrac{y+1}{y+2} & \stackrel{\times (y+2)}\implies & x(y+2) =y+1 \quad \implies xy+2x= y+1\\ &\implies & xy-y=1-2x \quad \implies y(x-1)=1-2x \\ &\implies & y= \dfrac{1-2x}{x-1} \quad \implies j^{-1}(x)=\dfrac{1-2x}{x-1},\end{aligned} \nonumber \]
- Escribir\(y=(x-2)^2+3\) e intercambiar\(x\) y\(y\):\[\begin{aligned} x=(y-2)^2+3 & \implies & x-3 =(y-2)^2 \quad \implies \sqrt{x-3}=y-2\\ &\implies & y=2+\sqrt{x-3} \quad\implies k^{-1}(x)=2+\sqrt{x-3}\end{aligned} \nonumber \]
La función en el último ejemplo no es uno-a-uno cuando\(x\) permite ser cualquier número real. Es por ello que tuvimos que restringir el ejemplo a las entradas\(x\geq 2\). Ejemplificamos la situación en el siguiente ejemplo.
Tenga en cuenta que la función\(y=x^2\) puede restringirse a una función uno a uno eligiendo que el dominio sea todos números no negativos\([0,\infty)\) o eligiendo que el dominio sea todos números no positivos\((-\infty,0]\).
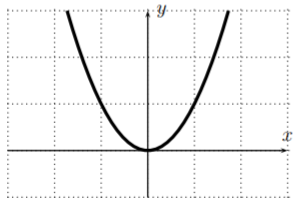
Solución
Dejar\(f:[0,\infty)\to [0,\infty)\) ser la función\(f(x)=x^2\), de manera que\(f\) tenga un dominio de todos los números no negativos. Entonces, lo inverso es la función\(f^{-1}(x)=\sqrt{x}\).
Por otro lado, podemos tomar\(g(x)=x^2\) cuyo dominio consiste en todos los números no positivos\((-\infty,0]\), es decir\(g:(-\infty,0]\to [0,\infty)\). Entonces, la función inversa\(g^{-1}\) debe revertir dominio y rango, es decir\(g^{-1}: [0,\infty)\to (-\infty,0]\). La inversa se obtiene intercambiando\(x\) y\(y\) en\(y=x^2\) lo siguiente:
\[x=y^2 \quad \implies y=\pm \sqrt{x}\quad \implies g^{-1}(x)=-\sqrt{x} \nonumber \]
Restringir la función a una función uno a uno. Encuentra la función inversa, si es posible.
- \(f(x)=(x+3)^2+1\)
- \(g(x)=\dfrac{1}{(x-2)^2}\)
- \(h(x)=x^3-3x^2\)
Solución
- La gráfica de\(f\) se muestra a continuación.
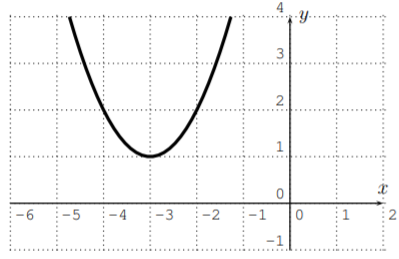
El gráfico muestra que\(f\) es uno a uno cuando se restringe a todos los números\(x\geq -3\), que es la elección que hacemos para encontrar una función inversa. A continuación, reemplazamos\(x\) y\(y\) en\(y=(x+3)^2+1\) dar\(x=(y+3)^2+1\). Al resolver esto para\(y\), ahora debemos recordar que nuestra elección de\(x\geq -3\) se convierte\(y\geq -3\) después de reemplazarlo\(x\) con\(y\). Ahora resolvemos para\(y\).
\[\begin{aligned} x=(y+3)^2+1 & \implies & x-1=(y+3)^2 \quad \implies y+3=\pm \sqrt{x-1} \\ & \implies & y=-3\pm \sqrt{x-1}\end{aligned} \nonumber \]
Ya que hemos elegido la restricción de\(y\geq -3\), utilizamos la expresión con el signo positivo,\(y=-3+\sqrt{x-1}\), para que la función inversa sea\(f^{-1}(x)=-3+\sqrt{x-1}\).
- La gráfica de\(g\) se muestra a continuación.
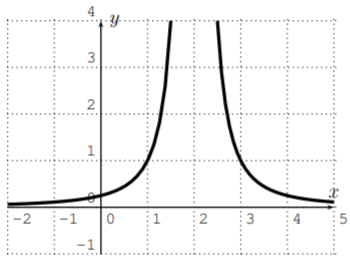
Para la función\(g\), la gráfica muestra que podemos restringir\(g\)\(x> 2\) a para obtener una función uno a uno. El inverso para esta elección se da de la siguiente manera. Sustitución\(x\) y\(y\) en\(y=\dfrac{1}{(x-2)^2}\) da\(x=\dfrac{1}{(y-2)^2}\), por lo que resolvemos esto\(y\) bajo la condición\(y>2\).
\[\begin{aligned} x=\dfrac{1}{(y-2)^2} & \implies & (y-2)^2=\dfrac{1}{x} \quad \implies y-2=\pm \dfrac 1 {\sqrt{x}} \\ & \implies & y=2\pm \dfrac 1 {\sqrt{x}} \quad \implies g^{-1}(x)=2+\dfrac{1}{\sqrt{x}}\end{aligned} \nonumber \]
- Finalmente, se\(h(x)=x^3-3x^2\) puede graficar con la calculadora de la siguiente manera:
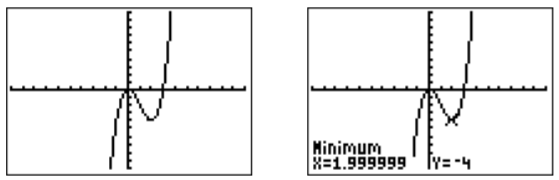
La imagen de la derecha muestra que la aproximación del mínimo local es (aproximadamente) en\(x=2\). Por lo tanto, si restringimos\(h\) a todos\(x\geq 2\), obtenemos una función uno a uno. Reemplazamos\(x\) y\(y\) en\(y=x^3-3x^2\), para que la función inversa se obtenga resolviendo la ecuación\(x=y^3-3y^2\) para\(y\). Sin embargo, esta ecuación es bastante complicada y resolverla está más allá de nuestras capacidades en este momento. Por lo tanto, simplemente decimos que\(h^{-1}(x)\) es\(y\geq 2\) aquello para lo cual\(y^3-3y^2=x\), y dejamos el ejemplo con esto.
Dejar\(f\) ser una función uno a uno. Si\(f\) mapea\(x_0\) a\(y_0=f(x_0)\), luego\(f^{-1}\) mapea\(y_0\) a\(x_0\). En otras palabras, la función inversa es precisamente la función para la cual
\[\boxed{f^{-1}(f(x_0))=f^{-1}(y_0)=x_0} \quad \text{ and } \quad \boxed{f(f^{-1}(y_0))=f(x_0)=y_0} \nonumber \]
Dejar\(f\) y\(g\) ser dos funciones uno a uno. Entonces\(f\) y\(g\) son inversos el uno del otro exactamente cuando
\[\boxed{f(g(x))=x}\quad \text{ and } \quad \boxed{g(f(x))=x}\quad \text{ for all }x \nonumber \]
En este caso escribimos eso\(g=f^{-1}\) y\(f=g^{-1}\).
¿Las siguientes funciones son inversas entre sí?
- \(f(x)=5x+7, \quad g(x)=\dfrac{x-7}{5}\)
- \(f(x)=\dfrac{3}{x-6}, \quad g(x)=\dfrac{3}{x}+6\)
- \(f(x)=\sqrt{x}-3, \quad g(x)=x^2+3\)
Solución
Calculamos las composiciones\(f(g(x))\) y\(g(f(x))\).
- \(\begin{aligned}f(g(x)) &= f\left (\dfrac{x-7}{5}\right ) = 5\cdot\dfrac{x-7}{5}+7 = (x-7)+7 =x,\\ g(f(x)) &= g(5x+7)=\dfrac{(5x+7)-7}{5}=\dfrac{5x}{5}=x \nonumber \end{aligned}\)
- \(\begin{aligned}f(g(x)) &= f\left(\dfrac3 x +6 \right )=\dfrac{3}{(\frac{3}{x}+6)-6}=\dfrac{3}{\frac{3}{x}}=3\cdot \dfrac{x}{3}=x, \\ g(f(x)) &= \left(\dfrac{3}{x-6}\right)=\dfrac{3}{\frac{3}{x-6}}+6=3\cdot \dfrac{x-6}{3}+6=(x-6)+6=x\end{aligned} \)
Usando las Inversas de Observación, vemos que tanto en la parte (a) como en la (b), las funciones son inversas entre sí. Para la parte (c), calculamos para un general\(x\) en el dominio de\(g\):
\[f(g(x))=\sqrt{x^2+3}-3\neq x \nonumber \]
Basta con demostrar que para una composición\((f\circ g)(x)\) no equivale\(x\) a concluir eso\(f\) y no\(g\) son inversos. (No es necesario calcular también la otra composición\(g(f(x))\).)
Es cierto que cuando tenemos una relación\(f(g(x))=x\), entonces también tenemos la otra relación\(g(f(x))=x\). Sin embargo, recomendamos verificar siempre ambas ecuaciones. El motivo es que es fácil confundir una de las relaciones, cuando no se tiene cuidado con el dominio y el rango.
Por ejemplo, vamos\(f(x)=x^2\) y\(g(x)=-\sqrt{x}\). Entonces, ingenuamente, calcularíamos\(f(g(x))=(-\sqrt{x})^2=x\) y\(g(f(x))=-\sqrt{x^2}=-|x|\), para que la primera ecuación dijera\(f\) y\(g\) sean inversas, mientras que la segunda ecuación dice que no son inversas.
Podemos resolver la aparente contradicción restringiendo\(f\) a una función uno a uno. Por ejemplo, si tomamos el dominio de\(f\) para ser todos los números positivos o cero,\(D_f=[0,\infty)\), entonces\(f(g(x))=f(-\sqrt{x})\) que es indefinido, ya que\(f\) sólo toma entradas no negativas. También, lo es\(g(f(x))=-\sqrt{x^2}=-x\). Por lo tanto, ¡las funciones\(f\) y no\(g\) son inversas entre sí!
Por otro lado, si restringimos la función\(f(x)=x^2\) a todos los números negativos y cero,\(D_f=(-\infty,0]\), entonces\(f(g(x))=(-\sqrt{x})^2=x\), ya que ahora\(f\) se define para la entrada negativa\(-\sqrt{x}\). También, para un número negativo\(x<0\), lo es\(g(f(x))=-\sqrt{x^2}=-|x|=x\). Entonces, en este caso, ¡\(f\)y\(g\) son inversos el uno al otro!
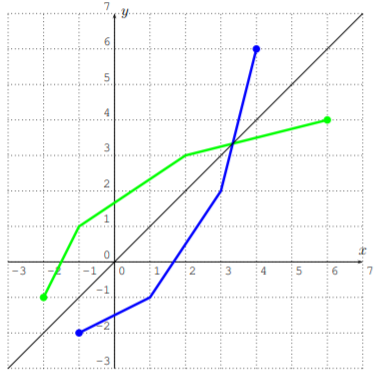
Nuestra última observación se refiere a la gráfica de funciones inversas. Si\(f(x_0)=y_0\) entonces\(f^{-1}(y_0)=x_0\), y el punto\(P(x_0,y_0)\) está en la gráfica de\(f\), mientras que el punto\(Q(y_0,x_0)\) está en la gráfica de\(f^{-1}\).
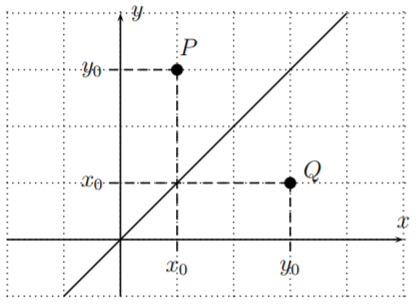
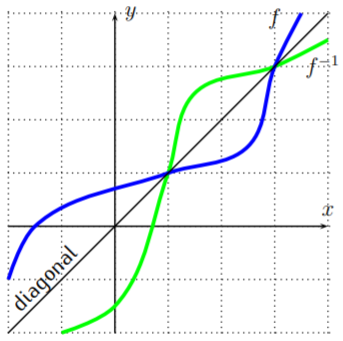
Vemos que\(Q\) es el reflejo de\(P\) lo largo de la diagonal\(y=x\). Ya que esto es cierto para cualquier punto de la gráfica de\(f\) y\(f^{-1}\), tenemos la siguiente observación general.
La gráfica de\(f^{-1}\) es la gráfica de\(f\) reflejada a lo largo de la diagonal.
Encuentre la gráfica de la función inversa de la función dada a continuación.
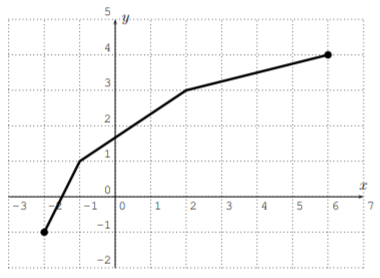
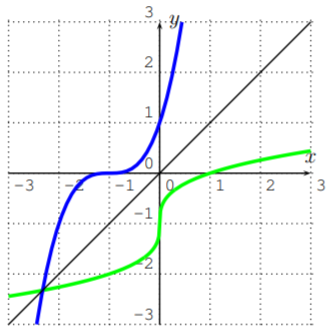
- \(f(x)=(x+1)^{3}\)
Solución
Reflegar cuidadosamente las gráficas dadas en las partes (a) y (b) da la siguiente solución. La función\(f(x)=(x+1)^3\) en la parte (b) se puede graficar primero con una calculadora.