12.1: Desigualdades polinomiales

Última actualización
Guardar como PDF

Page ID: 117760

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Consideramos ahora las desigualdades. Resolver desigualdades es bastante similar a resolver igualdades. Hay una consideración extra, que multiplicar o dividir por un número negativo en ambos lados de una desigualdad cambia la dirección del signo de desigualdad.

\ [\ begin {array} {cccc}
& -2 x\ leq-6 &\ Longrightarrow & x {\ color {Rojo}\ geq} 3\\
\ text {pero} & 2 x\ leq 6 &\ Longrightarrow & x\ leq 3
\ end {array}\ nonumber\]

Ejemplo$\PageIndex{1}$

Resolver para$x$.

$-3x+7> 19$
$2x+5\geq 4x-11$
$3 <-6x-4\leq 13$
$-2x-1\leq 3x+4< 4x-20$

Solución

$-3 x+7>19 \quad \stackrel{(-7)}{\Longrightarrow} \quad-3 x>12 \stackrel{(\div(-3))}{\Longrightarrow} \quad x<-4$
$2 x+5 \geq 4 x-11 \stackrel{(-4 x-5)}{\Longrightarrow} \quad-2 x \geq-16 \stackrel{(\div(-2))}{\Longrightarrow} \quad x \leq 8$
\[3<-6 x-4 \leq 13 \quad \stackrel{(+4)}{\Longrightarrow} \quad 7<-6 x \leq 17 \quad \stackrel{(\div(-6))}{\Longrightarrow} \quad \dfrac{7}{-6}>x \geq \dfrac{17}{-6} \quad \Longrightarrow \quad-\dfrac{17}{6} \leq x<-\dfrac{7}{6} \nonumber \]La última implicación se obtuvo cambiando los términos derecho e izquierdo de la desigualdad. El conjunto de soluciones es el intervalo$[-\dfrac{17}{6},-\dfrac{7}{6})$.
Para la parte d), lo mejor es considerar ambas desigualdades por separado.
\[\begin{aligned} -2x-1\leq 3x+4 \quad \stackrel{(-3x+1)} \implies \quad -5x\leq 5 \stackrel{(\div(-5))} \implies \quad x\geq -1 \\ 3x+4< 4x-20 \quad\stackrel{(-4x-4)} \implies \quad -x<-24 \stackrel{(\cdot(-1))} \implies \quad x> 24\end{aligned} \nonumber \]

La solución tiene que satisfacer tanto las desigualdades$x\geq -1$ como$x>24$. Ambas desigualdades son ciertas para$x>24$ (desde entonces también$x\geq -1$), por lo que esta es de hecho la solución:$x>24$.

Al tratar las desigualdades polinomiales, utilizamos la misma estrategia de tres pasos que usamos en la sección 1.4. Más precisamente, el primer paso es resolver la igualdad correspondiente, y el segundo paso es determinar la solución investigando los subintervalos inducidos a partir del paso 1. Para ambos pasos ahora también podemos usar la gráfica de la función y su visualización en la calculadora gráfica. El tercer paso es verificar los puntos finales de cada intervalo.

Ejemplo$\PageIndex{2}$

Resolver para$x$.

$x^2-3x-4\geq 0$
$x^3-9x^2+23x-15\leq 0$
$x^4-x^2 > 5(x^3-x)$
$x^3+15x>7x^2+9$
$x^5-6x^4-26x^3+144x^2-47x-210\leq 0$

Solución

Podemos encontrar las raíces del polinomio a la izquierda por factorización.

\[x^2-3x-4=0 \implies \quad (x-4)(x+1)=0 \implies \quad x=4 \text{ or }x=-1 \nonumber \]

Para ver dónde$f(x)=x^2-3x-4$ está$\geq 0$, lo graficamos con la calculadora.

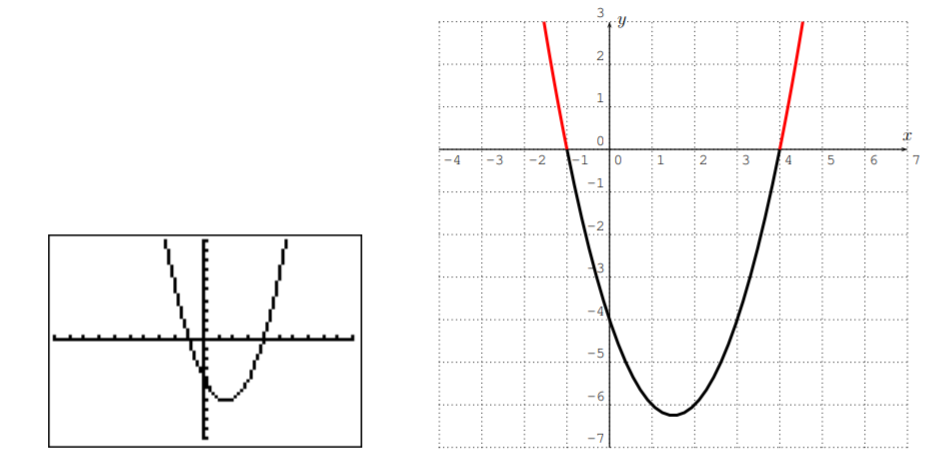
$clipboard_e308c4a18603d3f51d3e22da512cc2930.png$

Vemos que$f(x)\geq 0$ cuando$x\leq -1$ y cuando$x\geq 4$ (las partes de la gráfica por encima del$x$ eje -axis). Por lo tanto, el conjunto de soluciones es

\[\{x|x\leq -1,\text{ or }x\geq 4\}=(-\infty,-1]\cup [4,\infty) \nonumber \]

Aquí está la gráfica de la función$f(x)=x^3-9x^2+23x-15$ con el TI-84 en la ventana estándar.

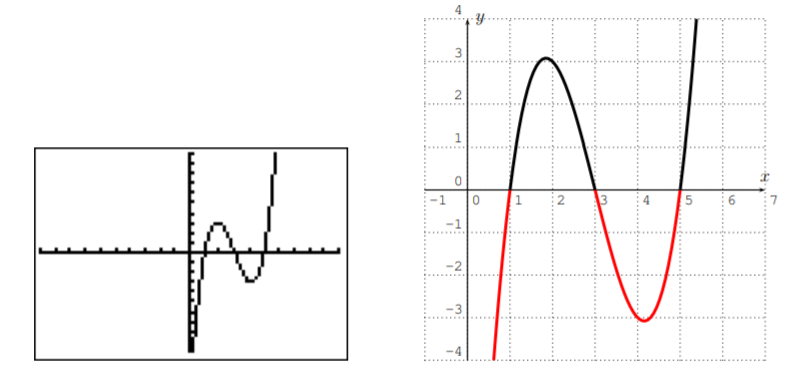
$clipboard_e912d6fbeac79ab622aa4e01a513a754f.png$

Esta gráfica muestra que hay dos intervalos donde$f(x)\leq 0$ (las partes de la gráfica debajo del$x$ eje -eje). Para determinar los intervalos exactos, calculamos dónde$f(x)=x^3-9x^2+23x-15=0$. La gráfica sugiere que las raíces de$f(x)$ están en$x=1$,$x=3$, y$x=5$. Esto se puede confirmar mediante un cálculo:

\[\begin{aligned} f(1)&= 1^3-9\cdot 1^2+23\cdot 1-15=1-9+23-15=0\\ f(3)&= 3^3-9\cdot 3^2+23\cdot 3-15=27-81+69-15=0\\ f(5)&= 5^3-9\cdot 5^2+23\cdot 5-15=125-225+115-15=0\end{aligned} \nonumber \]

Dado que$f$ es un polinomio de grado$3$, las raíces$x=1, 3, 5$ son todas de las raíces de$f$. (Alternativamente, podríamos haber dividido$f(x)$, por ejemplo, por$x-1$ y utilizado esto para factorial completamente$f$ y con esto obtener todas las raíces de$f$.) Con esto, podemos determinar el conjunto de soluciones para que sea el conjunto:

\[\begin{aligned} \text{solution set}&=\{x\in \mathbb{R} | x\leq 1, \text{ or } 3\leq x\leq 5\} \\ &=(-\infty,1]\cup [3,5] \end{aligned} \nonumber \]

Nótese que incluimos las raíces$1$$3$,, y$5$ en el conjunto de soluciones ya que la desigualdad original era “$\leq$” (y no “$<$”), que incluye las soluciones de la igualdad correspondiente.

Para utilizar la calculadora gráfica, reescribimos la desigualdad para obtener cero en un lado de la desigualdad.

\ [\ begin {alineado}
x^ {4} -x^ {2} >5\ izquierda (x^ {3} -x\ derecha) (\ text {distribuir} 5) &\ largederrow\ quad x^ {4} -x^ {2} >5 x^ {3} -5 x\
\ izquierda (\ texto {restar} 5 x^ {3},\ texto {sumar} 5 x\ derecha) &\ Longrightarrow\ quad x^ {4} -5 x^ {3} -x^ {2} +5 x>0
\ end {alineado}\ nonumber\ ]

Gráficamos$f(x)=x^4-5x^3-x^2+5x$ con el TI-84.

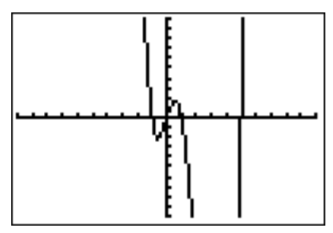
$clipboard_e672d3d0cffdc8cf82a4fbf56adcbb07d.png$

La gráfica sugiere las raíces$x=-1$,$0$,$1$, y$5$. Esto se puede confirmar mediante un cálculo sencillo.

\[\begin{aligned} f(-1)&= (-1)^4-5\cdot (-1)^3-(-1)^2+5\cdot (-1)=1+5-1-5=0\\ f(0)&= 0^4-5\cdot 0^3-0^2-5\cdot 0=0\\ f(1)&= 1^4-5\cdot 1^3-1^2+5\cdot 1=1-5-1+5=0\\ f(5)&= 5^4-5\cdot 5^3-5^2+5\cdot 5=125-125-25+25=0\end{aligned} \nonumber \]

Las raíces$x=-1$,$0$,$1$, y$5$ son las únicas raíces ya que$f$ es de grado$4$. Los intervalos de la solución para$f(x)>0$ pueden ser leídos de la gráfica:

\[\text{solution set}=(-\infty,-1)\cup (0,1)\cup (5, \infty) \nonumber \]

(Observe que las raíces$-1$,$0$,$1$, y no$5$ están incluidas en el conjunto de soluciones ya que nuestra desigualdad lee$f(x)>0$ y no$f(x)\geq 0$.)

Nuevamente, traemos todos los términos a un lado:

\[x^3+15x>7x^2+9 \implies x^3-7x^2+15x-9>0 \nonumber \]

(¡Aquí no importa si traemos los términos a la derecha o al lado izquierdo del signo de desigualdad! La desigualdad resultante es diferente, pero la solución al problema es la misma). Con esto, ahora usamos el TI-84 para encontrar la gráfica de la función$f(x)=x^3-7x^2+15x-9$.

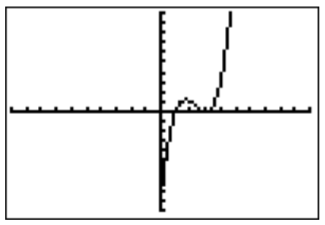
$clipboard_eca938263320b7e15e2e5db8c257fa5ea.png$

La gráfica sugiere al menos una raíz (el punto de intersección más a la izquierda), pero posiblemente una o dos raíces más. Para comprender mejor si la gráfica se cruza con el$x$ eje -eje de la derecha, reescalamos el tamaño de ventana de la gráfica anterior.

$clipboard_eed157b5a58e3880d7d2e4141e08f3e56.png$

Esta ventana de observación sugiere que hay dos raíces$x=1$ y$x=3$. Confirmamos que estas son las únicas raíces con un cómputo algebraico. Primero, comprobamos eso$x=1$ y de hecho$x=3$ son raíces:

\[\begin{aligned} f(1)&= 1^3-7\cdot 1^2+15\cdot 1-9=1-7+15-9=0\\ f(3)&= 3^3-7\cdot 3^2+15\cdot 3-9=27-63+45-9=0\end{aligned}\]

Para confirmar que estas son las únicas raíces (y no solo nos hemos perdido una de las raíces que posiblemente podrían hacerse visibles después de acercar suficientemente la gráfica), facetamos$f(x)$ completamente. Dividimos$f(x)$ por$x-1$:

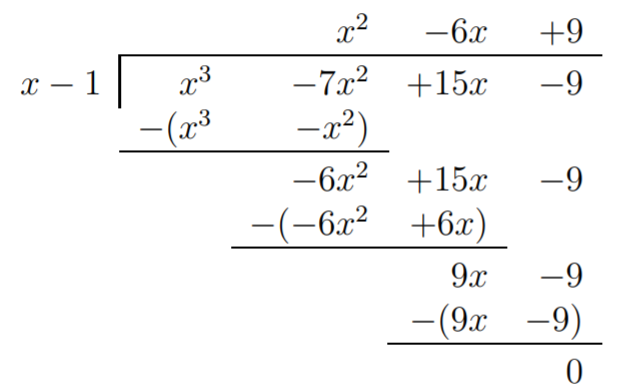
$clipboard_e0fd8bc4134b685257c2c1055542e7d17.png$

y utilícelo para faccionar$f$:

\[\begin{aligned} f(x)&= x^3-7x^2+15x-9 = (x-1)(x^2-6x+9) \\ &= (x-1)(x-3)(x-3)\end{aligned} \nonumber \]

Esto demuestra, que$3$ es una raíz de multiplicidad$2$, y así no$f$ tiene otras raíces que$x=1$ y$x=3$. El conjunto de soluciones consiste en aquellos números$x$ para los cuales$f(x)>0$. De la gráfica vemos que este es el caso cuando$1<x<3$ y cuando$x>3$ (las raíces$x=1$ y no$x=3$ se incluyen como soluciones). Podemos escribir el conjunto de soluciones de varias maneras diferentes:

\[\text{solution set}= \{x | 1<x<3 \text{ or } x>3 \} = \{x|1<x\}-\{3\} \nonumber \]

o en notación de intervalo:

\[\text{solution set}= (1,3)\cup (3,\infty) = (1,\infty)-\{3\} \nonumber \]

Si establecemos$f(x)=x^5-6x^4-26x^3+144x^2-47x-210$ entonces necesitamos encontrar esos números$x$ con$f(x)\leq 0$. Primero graficamos$f$ en la ventana estándar.

$clipboard_e605e100189d6cccb1681525f17427b3f.png$

Para obtener una mejor vista de la gráfica, reescalamos a una ventana apropiada:

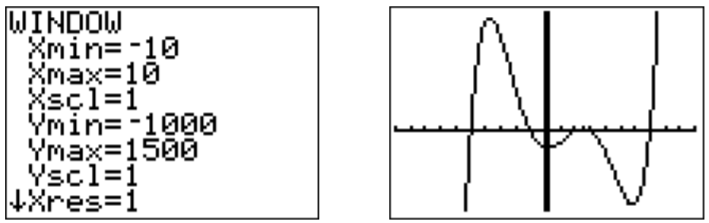
$clipboard_e4eb5bb808c119c84128b22a775be621e.png$

Parecen haber tres intervalos, donde$f(x)\leq 0$. Para determinar los números exactos, adivinamos algunas de las raíces de la gráfica. Estos serían$x=-5, -1, 2, 3, 7$. Para confirmar estas raíces, calculamos los siguientes valores de función.

\[\begin{aligned} f(-5)&= (-5)^5-6\cdot (-5)^4-26 \cdot (-5)^3+144\cdot (-5)^2-47\cdot (-5)-210\\ &= -3125-3750+3250+3600+235-210=0 \\ f(-1)&= (-1)^5-6\cdot (-1)^4-26 \cdot (-1)^3+144\cdot (-1)^2-47\cdot (-1)-210\\ &= -1-6+26+576+47-210=0\\ f(2)&= 2^5-6\cdot 2^4-26 \cdot 2^3+144\cdot 2^2-47\cdot 2-210\\ &= 32-96-208+576-94-210=0\\ f(3)&= 3^5-6\cdot 3^4-26 \cdot 3^3+144\cdot 3^2-47\cdot 3-210\\ &= 243-486-702+1296-141-210=0\\ f(7)&= 7^5-6\cdot 7^4-26 \cdot 7^3+144\cdot 7^2-47\cdot 7-210\\ &= 16807-14406-8918+7056-329-210=0\end{aligned} \nonumber \]

Ya que$f(x)$ es de grado$5$, sabemos que estas son todas las raíces de$f(x)$. El conjunto de soluciones para se$f(x)\leq 0$ puede leer en los gráficos anteriores:

\[\text{solution set}=(-\infty,-5]\cup [-1,2]\cup [3,7] \nonumber \]

(Obsérvese nuevamente, que las raíces están todas incluidas en el conjunto de soluciones.)

Las desigualdades polinomiales surgen, por ejemplo, al encontrar el dominio de funciones que involucran una raíz cuadrada, como mostraremos en el siguiente ejemplo.

Ejemplo$\PageIndex{3}$

Encuentra el dominio de las funciones dadas.

$ f(x)=\sqrt{x^2-4}$
$g(x)=\sqrt{x^3-5x^2+6x}$

Solución

El dominio de$f(x)=\sqrt{x^2-4}$ está dado por todos$x$ para los cuales la raíz cuadrada es no negativa. En otras palabras el dominio viene dado por números$x$ con$x^2-4\geq 0$. Graficando la función$y=x^2-4=(x+2)(x-2)$, vemos que este es precisamente el caso, cuándo$x\leq -2$ o$x\geq 2$.

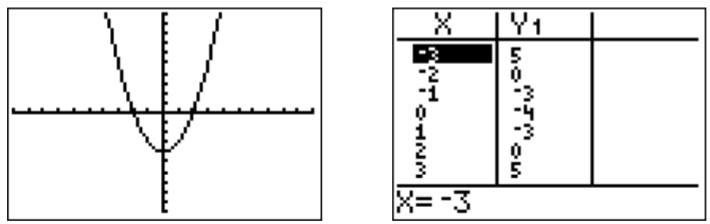
$clipboard_e901b3be50c3c3363b3ef97f39662fafa.png$

Por lo tanto, el dominio es$D_f=(-\infty,-2]\cup [2,\infty)$.

Para el dominio de$g(x)=\sqrt{x^3-5x^2+6x}$, necesitamos encontrar aquellos$x$ con$x^3-5x^2+6x\geq 0$. Para ello, graficamos$y=x^3-5x^2+6x$ y verificamos sus raíces.

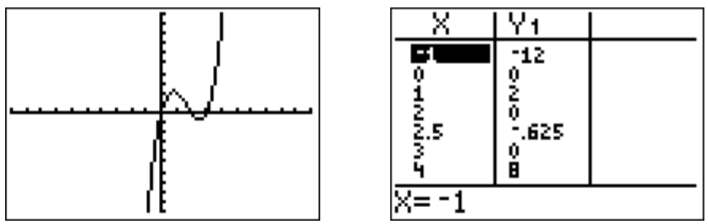
$clipboard_e742340ffabce74fc5916de9cace5a5c1.png$

A partir de la gráfica y tabla anterior, calculamos las raíces de$y=x^3-5x^2+6x$ at$x=0$,$x=2$, y$x=3$. Además, la gráfica y la tabla muestran que$x^3-5x^2+6x\geq 0$ precisamente cuando$0\leq x\leq 2$ o$3\leq x$. El dominio es por lo tanto,$D_g=[0,2]\cup [3,\infty)$.

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Ejemplo\(\PageIndex{3}\)