12.2: Desigualdades racionales y desigualdades de valor absoluto

Última actualización
Guardar como PDF

Page ID: 117761

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Las desigualdades racionales se resuelven con el mismo proceso de tres pasos que se utilizó para resolver las desigualdades polinomiales y de valores absolutos antes (ver página). Es decir, en el paso 1, encontramos la solución de la igualdad correspondiente, y luego, en el paso 2, utilizamos puntos de muestra de la gráfica para determinar los intervalos de la solución. Finalmente, en el paso 3, verificamos los puntos finales de cada intervalo.

Ejemplo$\PageIndex{1}$

Resolver para$x$.

$\dfrac{x^2-5x+6}{x^2-5x}\geq 0$
$\dfrac{5}{x-2}\leq 3$
$\dfrac{4}{x+5}<\dfrac{3}{x-3}$
$|2x-3|>7$

Solución

Aquí está la gráfica de$\dfrac{x^2-5x+6}{x^2-5x}$ en la ventana estándar.

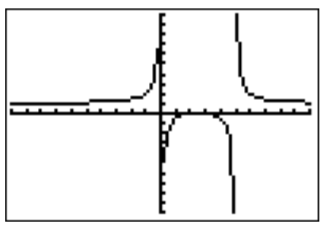
$clipboard_ebd87149b27b30be501fe8bec32454d45.png$

Factorizando numerador y denominador, podemos determinar asíntotas verticales, agujeros e$x$ intercepciones.

\[\dfrac{x^2-5x+6}{x^2-5x}=\dfrac{(x-2)(x-3)}{x(x-5)} \nonumber \]

Las asíntotas verticales están en$x=0$ y$x=5$, los$x$ -interceptos están en$x=2$ y$x=3$. Ya que para grandes$x$, la fracción se reduce a$\dfrac{x^2}{x^2}=1$, vemos que la asíntota horizontal está en$y=1$. Así,$\dfrac{x^2-5x+6}{x^2-5x}\geq 0$ para$x< 0$ y$x>5$. Para ver dónde está la gráfica$\geq 0$ entre$0$ y$5$, ampliamos la gráfica:

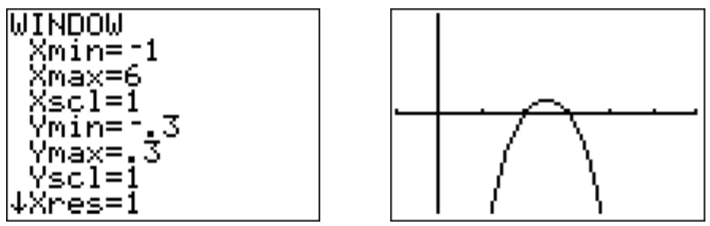
$clipboard_ef3c93b76af25649a789bcf3ecc2db5c3.png$

Combinando toda la información anterior, obtenemos el conjunto de soluciones:

\[\text{solution set}=(-\infty,0)\cup[2,3]\cup(5,\infty) \nonumber \]

Observe que las$x-$ coordenadas de las$x-$ intercepciones son$x=2$ y$x=3$ están incluidas en el conjunto de soluciones, mientras que los valores$x=0$ y$x=5$ asociados a las asíntotas verticales no están incluidos ya que la fracción no está definida para$x=0$ y$x=5$.

Para encontrar los números$x$ donde$\dfrac{5}{x-2}\leq 3$, podemos graficar las dos funciones a la derecha e izquierda de la desigualdad.

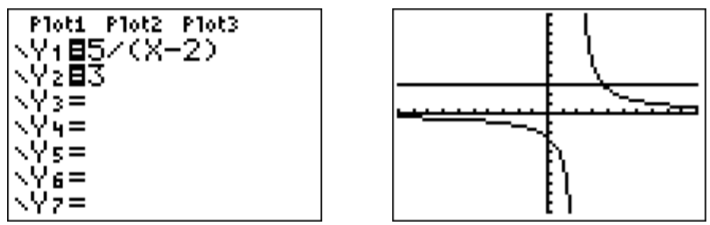
$clipboard_ee97d1a806312249ad4747db4cb49e7dc.png$

Sin embargo, esto a veces puede resultar confuso, y recomendamos reescribir la desigualdad para que un lado se convierta en cero. Entonces, graficamos la función al otro lado de la nueva desigualdad.

\[\begin{aligned} \dfrac{5}{x-2}\leq 3 &\implies \quad \dfrac{5}{x-2}-3\leq 0 \implies \quad \dfrac{5-3(x-2)}{x-2}\leq 0\\ & \implies \quad \dfrac{5-3x+6}{x-2}\leq 0 \implies \quad \dfrac{11-3x}{x-2}\leq 0\end{aligned} \nonumber \]

Por lo tanto, graficamos la función$f(x)=\dfrac{11-3x}{x-2}$.

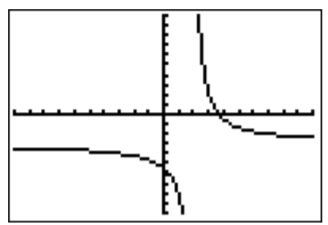
$clipboard_e40ddd7ed22046aa88a318b3cbd3ba9d1.png$

La asíntota vertical es$x=2$, y el$x$ -intercepto encontrado así

\[11-3x=0\implies \quad 11=3x \implies \quad x=\dfrac {11}{3} \nonumber \]

Esto junto con la gráfica y el hecho de que$f$ está indefinido en$2$ y$f(\dfrac{11}{2})=0$ da el siguiente conjunto de soluciones:

\[\text{solution set}=\Big(-\infty,2\Big)\cup \Big[\dfrac{11}{3},\infty\Big) \nonumber \]

Queremos encontrar esos números$x$ para los cuales$\dfrac{4}{x+5}<\frac{3}{x-3}$. Una forma de hacerlo se da graficando ambas funciones$f_1(x)=\dfrac{4}{x+5}$ y$f_2(x)=\dfrac{3}{x-3}$, y tratando de determinar dónde$f_1(x)<f_2(x)$. Sin embargo esto a veces puede ser bastante confuso, como los dos gráficos para$f_1$ y$f_2$ muestran a continuación.

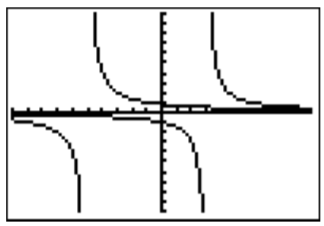
$clipboard_e0a6517e31b3e2b9580e4ce4e082b79a3.png$

Como antes, recomendamos reescribir la desigualdad para que un lado de la desigualdad se convierta en cero:

\[\begin{aligned} \dfrac{4}{x+5}<\dfrac{3}{x-3} & \implies \dfrac{4}{x+5}-\dfrac{3}{x-3} <0 \implies \quad \dfrac{4(x-3)-3(x+5)}{(x+5)(x-3)} <0 \\ & \implies \dfrac{4x-12-3x-15}{(x+5)(x-3)} <0 \implies \quad \dfrac{x-27}{(x+5)(x-3)}<0 \end{aligned} \nonumber \]

Por lo tanto, graficamos la función$f(x)=\dfrac{x-27}{(x+5)(x-3)}$.

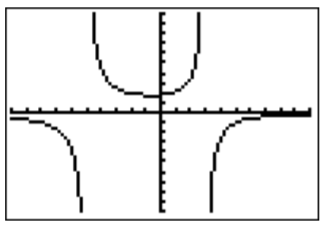
$clipboard_e52075872a51dc9e11d7661dec0ebf9d2.png$

Las asíntotas verticales de$f(x)=\dfrac{x-27}{(x+5)(x-3)}$ son$x=-5$ y$x=3$. El$x$ -intercepto es$(27,0)$. Vemos de la gráfica que$f(x)<0$ para$x<-5$. Para ver la gráfica en$x>3$, hacemos zoom a la$x$ -intercepción en$x=27$.

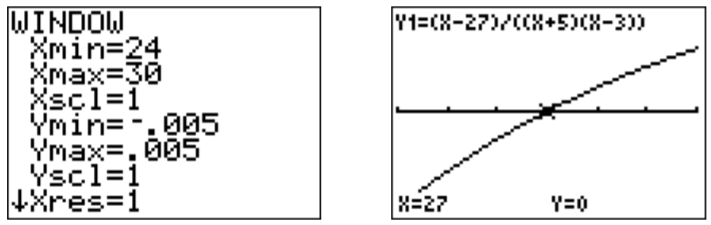
$clipboard_eb5d31816def294b8d857bf5b9ba3d608.png$

Por lo tanto, el conjunto de soluciones es

\[\text{solution set}=\{x| x<-5,\text{ or } 3<x<27\}=(-\infty,-5)\cup (3,27) \nonumber \]

(La$x$ -intercepción no$x=27$ está incluida en el conjunto de soluciones ya que la ecuación original tenía un signo “$<$” y no “$\leq$”.)

Para analizar$|2x-3|>7$, graficamos la función$f(x)=|2x-3|-7$.

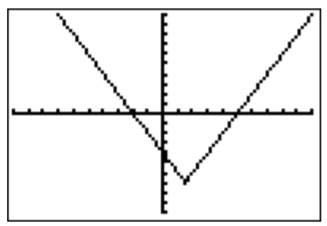
$clipboard_efc9dcd19d74a0fe7428de6f50bcb0dbd.png$

Para ver dónde$f(x)>0$, encontramos los ceros de$f(x)$.

\[|2x-3|-7=0 \implies \quad |2x-3|=7 \implies \quad 2x-3=\pm 7 \nonumber \]

\ [\ begin {aligned}
&\ Longrightarrow 2 x-3=7\
(\ text {add} 3) &\ Longrightarrow 2 x=10\
(\ text {divide por} 2) &\ Longrightarrow x=5
\ end {alineado}\ quad\ begin {alineado}
&\ LongRightarrow 2 x-3=-7\
(\ text {add} 3) &\ Longrightarrow 2 x=-4\\
(\ text {divide por} 2) &\ Longrightarrow x=-2
\ end {alineado}\ nonumber\]

\[\text{solution set}=(-\infty,-2)\cup(5,\infty) \nonumber \]