13.1: Funciones exponenciales y sus gráficas
- Page ID
- 117669
Ahora consideramos funciones que difieren mucho de polinomios y fracciones racionales en su complejidad. Más precisamente, exploraremos funciones exponenciales y logarítmicas desde un punto de vista teórico de funciones. Comenzamos recordando la definición de funciones exponenciales y estudiando sus gráficas.
Una función\(f\) se llama función exponencial si es de la forma\[f(x)=c\cdot b^x \nonumber \] para algún número real\(c\) y número real positivo\(b\). La constante\(b\) se llama la base.
Grafica las funciones
\[f(x)=2^x, \quad g(x)=3^x, \quad h(x)=10^x, \quad k(x)=\left(\dfrac 1 2\right)^x, \quad l(x)=\left(\dfrac 1 {10}\right)^x \nonumber \]
Solución
Primero, graficaremos la función\(f(x)=2^x\) calculando los valores de la función en una tabla y luego trazando los puntos en el\(y\) plano\(x\) -. Podemos calcular los valores a mano, o simplemente usar la función de tabla de la calculadora para encontrar los valores de la función.
\[\begin{aligned} f(0)&= 2^0=1\\ f(1)&= 2^1=2\\ f(2)&= 2^2=4\\ f(3)&= 2^3=8\\ f(-1)&= 2^{-1}=0.5\\ f(-2)&= 2^{-2}=0.25\end{aligned} \nonumber \]
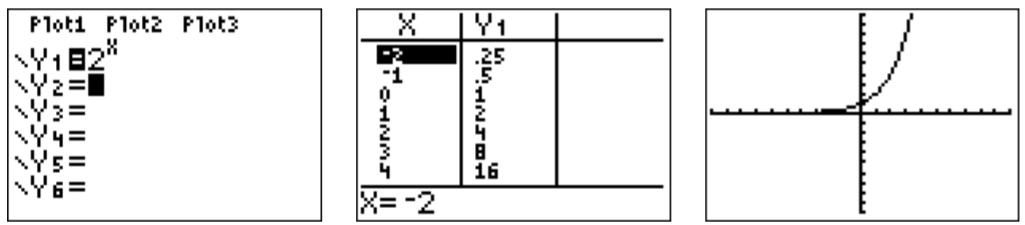
De igual manera, podemos calcular la tabla para las otras funciones\(g\)\(h\),\(k\) e\(l\) ingresando las funciones en los spots en Y2, Y3, Y4 e Y5. Los valores en la tabla para estas funciones se pueden ver moviendo el cursor hacia la derecha con la\(\boxed {\triangleright }\) tecla.
Podemos ver las gráficas pulsando la\(\boxed {\text {graph}}\) tecla.
Para poder ver estas gráficas con mayor claridad, ajustamos la ventana gráfica a un tamaño más apropiado.
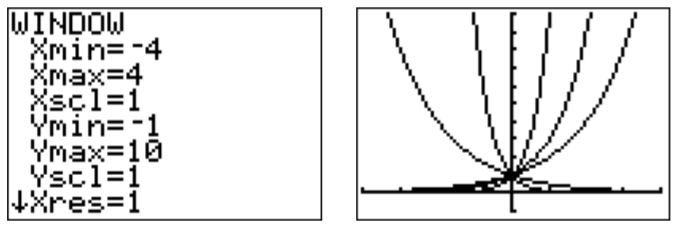
Dado que todas estas funciones están graficadas en una misma ventana, es difícil asociar las gráficas con sus funciones correspondientes. Para distinguir entre las gráficas, podemos usar el TI-84 para dibujar las gráficas en diferentes estilos de línea. En el menú de funciones (\(\boxed {y = }\)), mueva el cursor hacia la izquierda con\(\boxed {\triangleleft }\), y presione\(\boxed {\text {enter}}\) hasta que la línea se convierta en una línea gruesa, o una línea punteada, según se desee. Al mover el cursor hacia abajo\(\boxed {\bigtriangledown }\) y presionar\(\boxed {\text {enter}}\), también podemos ajustar los estilos de línea de las otras gráficas.
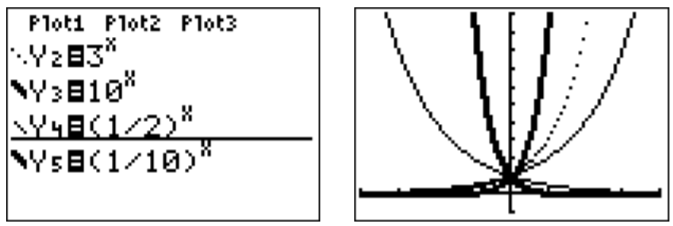
Tenga en cuenta que la función también se\(k\) puede escribir como\[k(x)=\left(\dfrac{1}{2}\right)^x=(2^{-1})^x =2^{-x} \nonumber \] y de manera similar,\[l(x)=\left(\dfrac{1}{10}\right)^x=10^{-x} \nonumber \].
Este ejemplo muestra que la función exponencial tiene las siguientes propiedades.
La gráfica de la función exponencial\(f(x)=b^x\) con\(b>0\) y\(b\neq 1\) tiene una asíntota horizontal en\(y=0\).
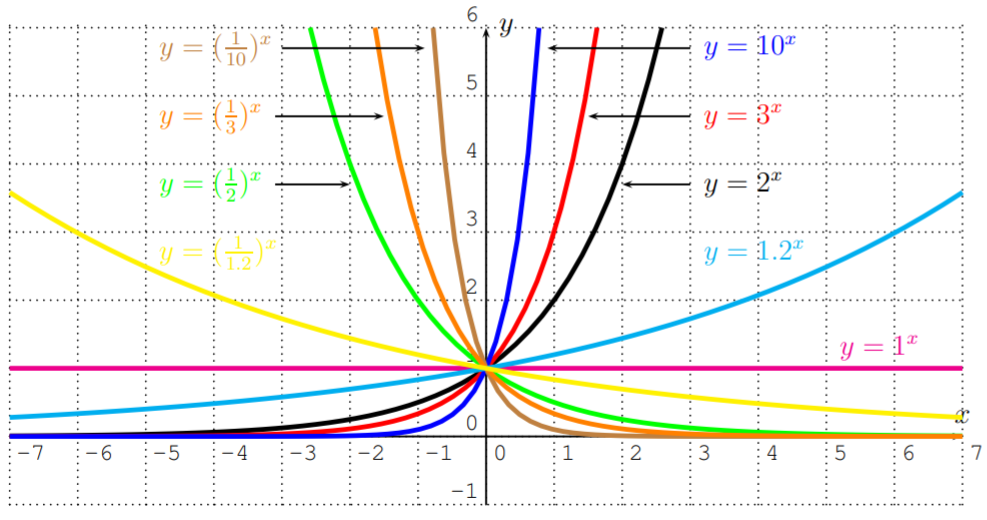
- Si\(b>1\), entonces se\(f(x)\) acerca\(+\infty\) cuando se\(x\) acerca\(+\infty\), y\(0\) se\(f(x)\) acerca cuando se\(x\) acerca\(-\infty\).
- Si\(0<b<1\), entonces se\(f(x)\) acerca\(0\) cuando se\(x\) acerca\(+\infty\), y\(+\infty\) se\(f(x)\) acerca cuando se\(x\) acerca\(-\infty\).
Una base importante que con frecuencia necesitaremos considerar es la base de\(e\), donde\(e\) está el número de Euler.
El número de Euler\(e\) es un número irracional que es aproximadamente
\[\boxed{e= 2.718281828459045235\dots} \nonumber \]
Para ser precisos, podemos definir\(e\) como el número que es la asíntota horizontal de la función\(f(x)=\left(1+\dfrac 1 x\right)^x\) cuando se\(x\) acerca\(+\infty\).
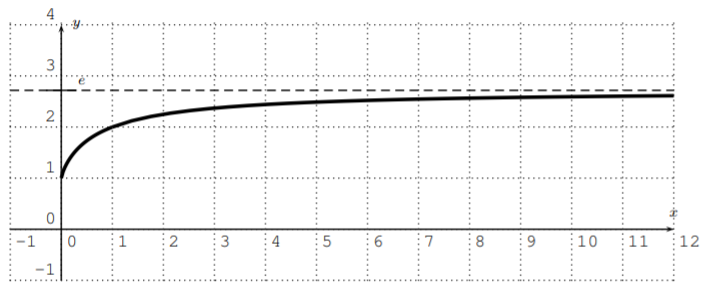
Se puede demostrar que\(f\) tiene, efectivamente, una asíntota horizontal, y este límite se define como\(e\).
\[\boxed{e:=\lim_{x\to \infty}\left(1+\dfrac 1 x\right)^x} \nonumber \]
Además, se puede demostrar que la función exponencial con base\(e\) tiene una expresión límite similar.
\[\label{EQU:exp(r)-limit} \boxed{e^r=\lim_{x\to \infty}\left(1+\dfrac r x\right)^x} \]
Alternativamente, el número de Euler y la función exponencial con base también se\(e\) pueden definir usando una serie infinita, a saber,\(e^r=1+r+\dfrac{r^2}{1\cdot 2}+\dfrac{r^3}{1\cdot 2 \cdot 3}+\dfrac{r^4}{1\cdot 2 \cdot 3\cdot 4}+\dots\). Estas ideas serán exploradas más a fondo en un curso de cálculo.
Grafica las funciones.
- \(y=e^x\)
- \(y=e^{-x}\)
- \(y=e^{-x^2}\)
- \(y=\dfrac{e^{x}+e^{-x}}{2}\)
Solución
Usando la calculadora, obtenemos las gráficas deseadas. La función exponencial\(y=e^x\) puede ser ingresada vía\(\boxed {\text {2nd}}\)\(\boxed {\text {ln}}\).
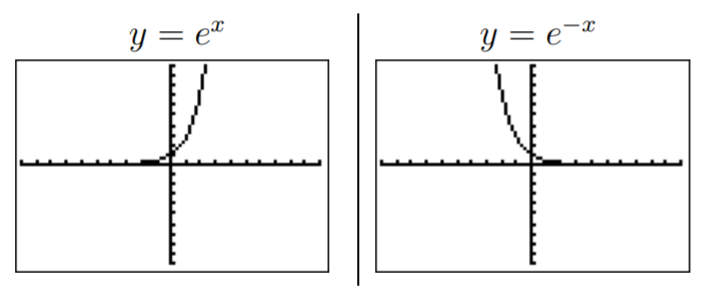
Tenga en cuenta que el signo menos se ingresa en la última expresión (y también en las dos funciones siguientes) a través de la\(\boxed {(-)}\) clave.
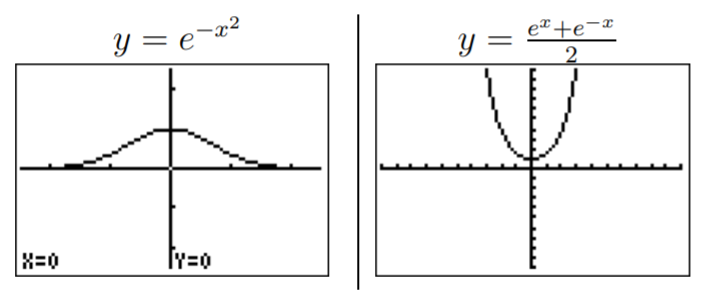
La última función\(y=\dfrac{e^{x}+e^{-x}}{2}\) se llama coseno hiperbólico, y se denota por\(\cosh(x)=\dfrac{e^{x}+e^{-x}}{2}\).
Ahora estudiamos cómo diferentes factores multiplicativos\(c\) afectan la forma de una función exponencial.
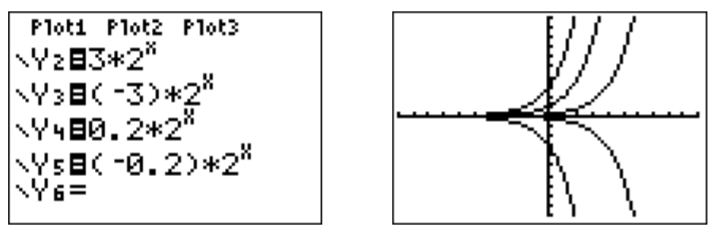
Grafica las funciones.
- \(y=2^x\)
- \(y=3\cdot 2^x\)
- \(y=(-3)\cdot 2^x\)
- \(y=0.2\cdot 2^x\)
- \(y=(-0.2)\cdot 2^x\)
Solución
Gráficamos las funciones en una ventana de visualización.
Aquí están las gráficas de funciones\(f(x)=c\cdot 2^x\) para diversas opciones de\(c\).
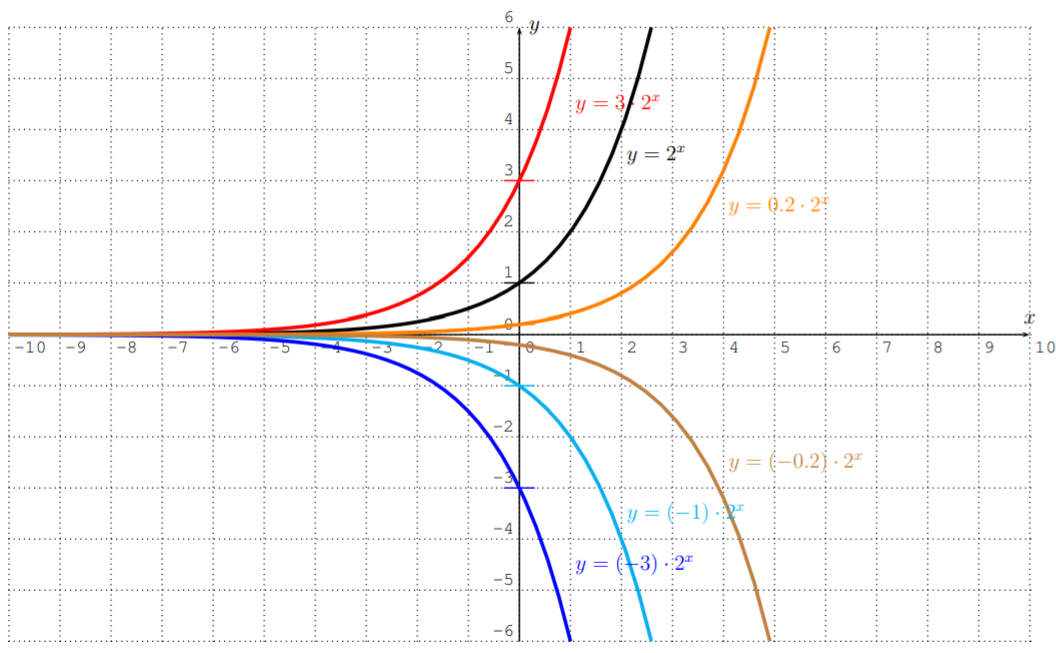
Tenga en cuenta que para\(f(x)=c\cdot 2^x\), la\(y\) -intercepción se da en\(f(0)=c\).
Finalmente, podemos combinar nuestro conocimiento de las transformaciones gráficas para estudiar funciones exponenciales que se desplazan y estiran.
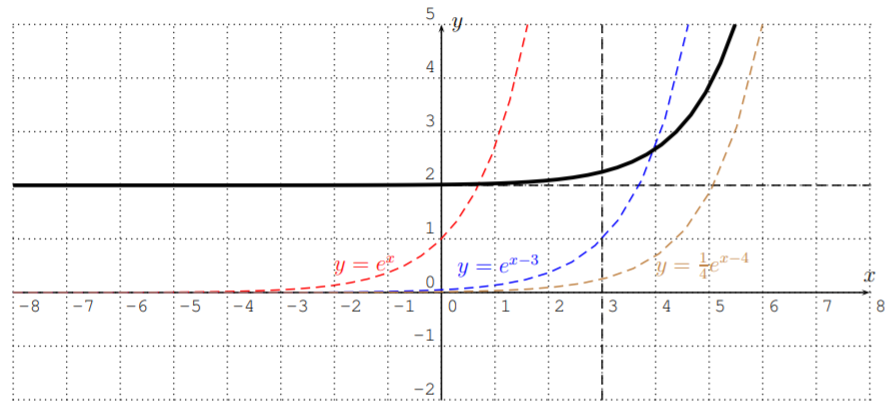
Grafica las funciones.
- \(y=3^x-5\)
- \(y=e^{x+4}\)
- \(y=\dfrac{1}{4}\cdot e^{x-3}+2\)
Solución
Las gráficas se muestran a continuación.
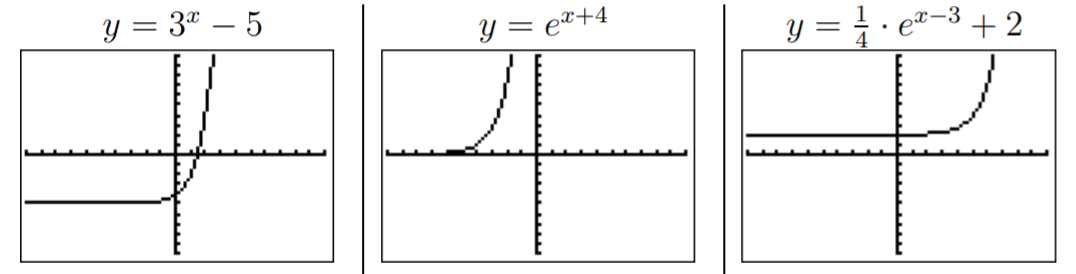
El primer gráfico\(y=3^x-5\) es el gráfico de\(y=3^x\) desplazado hacia abajo por\(5\).
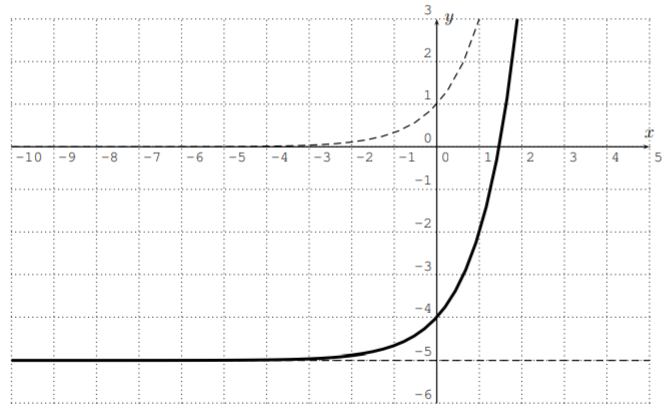
La gráfica de\(y=e^{x+4}\) es la gráfica de\(y=e^x\) desplazada a la izquierda por\(4\).
Finalmente,\(y=\dfrac{1}{4}e^{x-3}+2\) es la gráfica de\({\color{Red} y=e^x}\) desplazada a la derecha por\(3\) (ver la gráfica de\({\color{Blue} y=e^{x-3}}\)), luego comprimida por un factor\(4\) hacia el\(x\) eje -eje (ver la gráfica de\({\color{Brown} y=\dfrac 1 4 e^{x-3}}\)), y luego se desplazó hacia arriba por\(2\).