13.2: Funciones logarítmicas y sus gráficas
- Page ID
- 117665
La función logarítmica está estrechamente relacionada con la función exponencial. Específicamente, el logaritmo es la función inversa de la función exponencial.
\(0<b\neq 1\)Sea un número real positivo que no sea igual a\(1\). Para\(x>0\), el logaritmo de\(x\) con base\(b\) se define por la equivalencia
\[\label{EQU:def-of-log} \boxed{ \quad y=\log_b(x) \quad\quad \Leftrightarrow \quad\quad b^y=x \quad }\]
Para la base particular\(b=10\) utilizamos la forma corta\[\boxed{\log(x):=\log_{10}(x)} \nonumber \]
Para la base particular\(b=e\), donde\(e\approx 2.71828\) está el número de Euler, llamamos al logaritmo con base\(e\) el logaritmo natural, y escribimos
\[\boxed{\ln(x):=\log_e(x)} \nonumber \]
La función logarítmica es la función\(y=\log_b(x)\) con dominio\(D=\{x\in \mathbb{R} | x>0\}\) de todos los números reales positivos, y rango\(R=\mathbb{R}\) de todos los números reales. Es la inversa de la función exponencial\(y=b^x\) con base\(b\).
Reescribir la ecuación como una ecuación logarítmica.
- \(3^4=81\)
- \(10^{3}=1000\)
- \(e^x=17\)
- \(2^{7\cdot a}=53\)
Solución
Podemos aplicar de inmediato la ecuación\(\ref {EQU:def-of-log}\).
- Para la parte (a), tenemos\(b=3\),\(y=4\), y\(x=81\). Por lo tanto tenemos:
\[3^4=81 \quad \Leftrightarrow \quad \log_3(81)=4 \nonumber \]
De igual manera, obtenemos las soluciones para (b), (c) y (d).
- \(10^3=1000\)&\(\Leftrightarrow\) &\(\log(1000)=3\)
- \(e^x=17\)&\(\Leftrightarrow\) &\(\ln(17)=x\)
- \(2^{7a}=53\)&\(\Leftrightarrow\) &\(\log_2(53)=7a\)
Evaluar la expresión reescribiéndola como una expresión exponencial.
- \(\log_2(16)\)
- \(\log_5(125)\)
- \(\log_{13}(1)\)
- \(\log_4(4)\)
- \(\log(10,000)\)
- \(\log(0.001)\)
- \(\ln(e^7)\)
- \(\log_b(b^x)\)
Solución
- Si establecemos\(y=\log_2(16)\), entonces esto es equivalente a\(2^y=16\). Ya que, claramente\(2^4=16\),, vemos eso\(y=4\). Por lo tanto, tenemos\(\log_2(16)=4\).
- \ (\ begin {alineado}
\ log _ {5} (125) =y &\ Leftrightarrow 5^ {y} =125\\
&\ izquierda (\ text {desde} 5^ {3} =125\ derecha)\\
&\ Longrightarrow\ quad 3=y=\ log _ {5} (125)
\ end {alineado}\)
- \ (\ begin {alineado}
\ log _ {13} (1) =y &\ Leftrightarrow 13^ {y} =1\\
& {\ left (\ text {since} 13^ {0} =1\ derecha)}\\
&\ Longrightarrow 0=y=\ log _ {13} (1)
\ end {alineado}\)
- \ (\ begin {alineado}
\ log _ {4} (4) =y &\ Leftrightarrow 4^ {y} =4\\
&\ izquierda (\ text {desde} 4^ {1} =4\ derecha)\\
&\ Longrightarrow\ quad 1=y=\ log _ {4} (4)
\ end {alineado}\)
- \ (\ begin {aligned}
\ log (100,000) =y &\ Leftrightarrow\ quad 10^ {y} =100,000\\
&\ izquierda (\ text {desde} 10^ {5} =100,000\ derecha)\\ &\ Longrightarrow\ quad 5=y=\ log (100,000)
\ end {alineado}\)
- \ (\ begin {alineado}
\ log (0.001) =y &\ Leftrightarrow\ quad 10^ {y} =0.001\\
&\ izquierda (\ text {desde} 10^ {-3} =0.001\ derecha)\\
& {\ Longrightarrow}\ quad-3=y=\ log (0.001)
\ end {alineado}\) - \(\ln \left(e^{7}\right)=y \quad \Leftrightarrow \quad e^{y}=e^{7} \quad \Longrightarrow \quad 7=y=\ln \left(e^{7}\right)\)
- \(\log _{b}\left(b^{x}\right)=y \quad \Leftrightarrow \quad b^{y}=b^{x} \quad \Longrightarrow \quad x=y=\log _{b}\left(b^{x}\right)\)
En el ejemplo anterior (en las partes (c), (d) y (h)), pudimos encontrar ciertos logaritmos elementales. Los registramos en la siguiente observación.
Tenemos los logaritmos elementales:
\[\label{EQU:elementary-log} \boxed{\log_b(b^x) =x} \quad\quad\quad \boxed{\log_b(b)=1} \quad\quad\quad \boxed{\log_b(1)=0} \nonumber \]
En general, cuando el argumento no es una potencia de la base, podemos usar la calculadora para aproximar los valores de un logaritmo a través de las fórmulas:
\[\label{EQU:log-change-basis-calculator} \boxed{\log_b(x) = \dfrac{\log(x)}{\log(b)}}\quad\quad\quad \text{or}\quad\quad\quad \boxed{\log_b(x) = \dfrac{\ln(x)}{\ln(b)}}\]
Las dos últimas fórmulas se probarán en la proposición 14.1. Por ahora, queremos mostrar cómo se pueden usar para calcular cualquier expresión logarítmica con la calculadora.
Calcular:
- \(\log_3(13)\)
- \(\log_{2.34}(98.765)\)
Solución
- Calculamos\(\log_3(13)\) usando la primera fórmula en\(\ref{EQU:log-change-basis-calculator}\).
\[\log_3(13)=\dfrac{\log(13)}{\log(3)}\approx 2.335 \nonumber \]
Alternativamente, también podemos calcular esto con la segunda fórmula en\(\ref{EQU:log-change-basis-calculator}\).
\[\log_3(13)=\dfrac{\ln(13)}{\ln(3)}\approx 2.335 \nonumber \]
- Para la parte (b) tenemos\(\log_{2.34}(98.765)=\dfrac{\log(98.765)}{\log(2.34)}\approx 5.402\).
También queremos comprender la gráfica de una función logarítmica. Considera la gráfica\(y=2^x\) de la sección anterior. Recordemos que la gráfica de la inversa de una función es el reflejo de la gráfica de la función sobre la línea diagonal\(y=x\). Entonces en este caso tenemos:
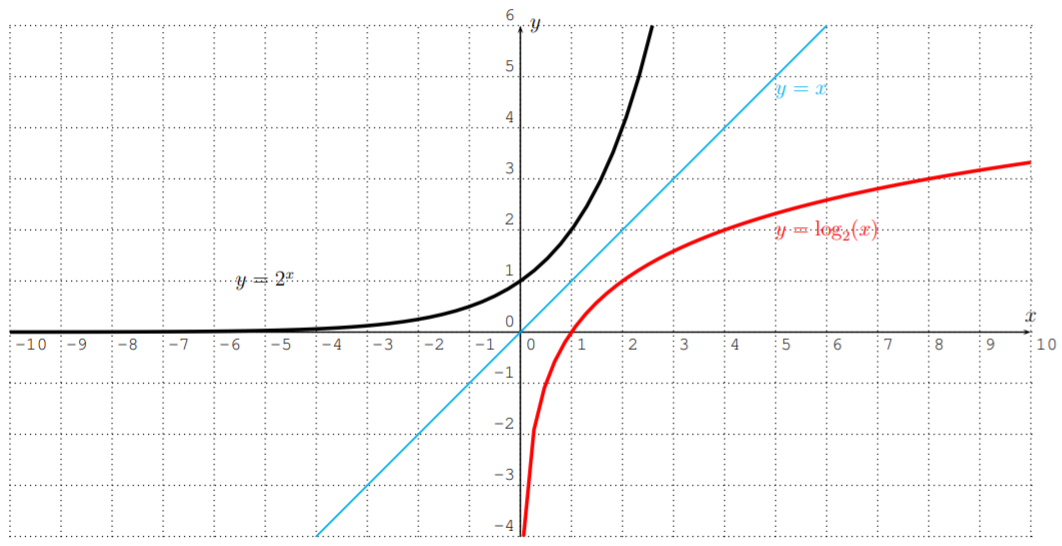
La gráfica también se puede obtener usando una calculadora gráfica.
- Grafique las funciones\(f(x)=\ln(x)\),\(g(x)=\log(x)\),\(h(x)=\log_2(x)\), y\(k(x)=\log_{0.5}(x)\). ¿Cuáles son los dominios de\(f\)\(g\),\(h\), y\(k\)? ¿En qué se diferencian estas funciones?
- Grafica la función\(p(x)= -3\cdot \ln(x)+4\). ¿De qué es el dominio\(p\)?
- Grafica la función\(q(x)= \ln(5-x)\). ¿De qué es el dominio\(q\)?
- Grafica la función\(r(x)= \log_7(2x+8)\). ¿De qué es el dominio\(r\)?
Solución
- Sabemos por la definición que el dominio de\(f\),\(g\), y\(h\) es todo números positivos reales,\(D_f=D_g=D_h=D_k=\{x|x>0\}\). Las funciones\(f\) y\(g\) se pueden ingresar inmediatamente en la calculadora. La ventana estándar da las siguientes gráficas.
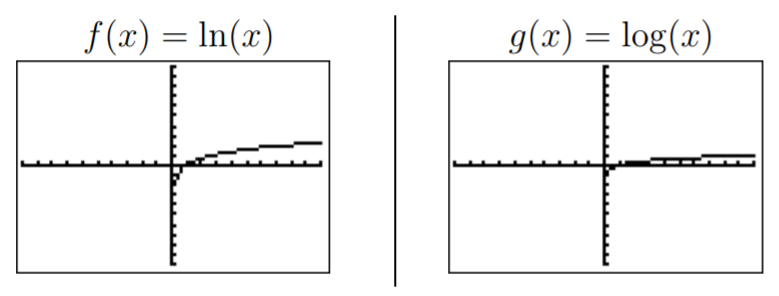
Tenga en cuenta que podemos reescribir\(g(x)\)\(h(x)\),, y\(k(x)\) como tiempos constantes\(f(x)\):
\[\begin{aligned} g(x)&= \log(x)=\log_{10}(x)=\dfrac{\ln(x)}{\ln(10)}=\dfrac{1}{\ln(10)}\cdot f(x) \\ h(x)&= \log_{2}(x)=\dfrac{\ln(x)}{\ln(2)}=\dfrac{1}{\ln(2)}\cdot f(x) \\ k(x)&= \log_{0.5}(x)=\dfrac{\ln(x)}{\ln(0.5)}=\dfrac{1}{\ln(0.5)}\cdot f(x) \end{aligned} \nonumber \]
Ya que\(\dfrac{1}{\ln(10)}\approx 0.434<1\), vemos que la gráfica de\(g\) es la de\(f\) comprimida hacia el\(x\) eje -por un factor\(\dfrac{1}{\ln(10)}\). De igual manera\(\dfrac{1}{\ln(2)}\approx 1.443>1\),, de manera que la gráfica de\(h\) es la de\(f\) estirada alejada del\(x\) eje -por un factor\(\dfrac{1}{\ln(2)}\). Por último\(\dfrac{1}{\ln(0.5)}\approx -1.443\), o más precisamente,\(\dfrac{1}{\ln(0.5)}=\dfrac{1}{\ln(2^{-1})}=-\dfrac{1}{\ln(2)}\), para que la gráfica de\(k\) sea la de\(h\) reflejada alrededor del\(x\) eje.
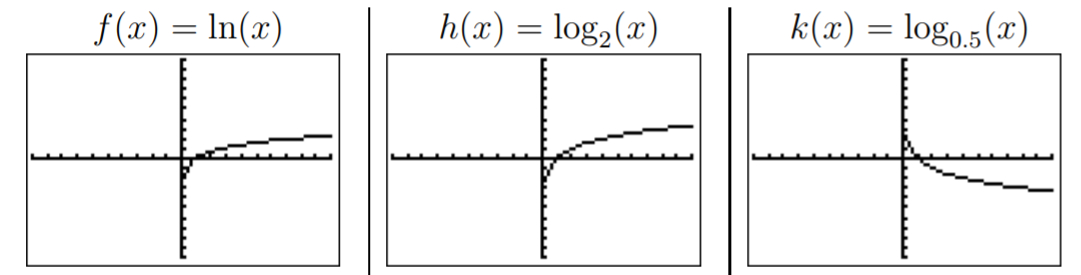
Tenga en cuenta que todas estas gráficas tienen una\(x\) intercepción común en\(x=1\):
\[f(1)=g(1)=h(1)=k(1)=0 \nonumber \]
Para visualizar las diferencias entre las gráficas, las graficamos juntas en un solo sistema de coordenadas.
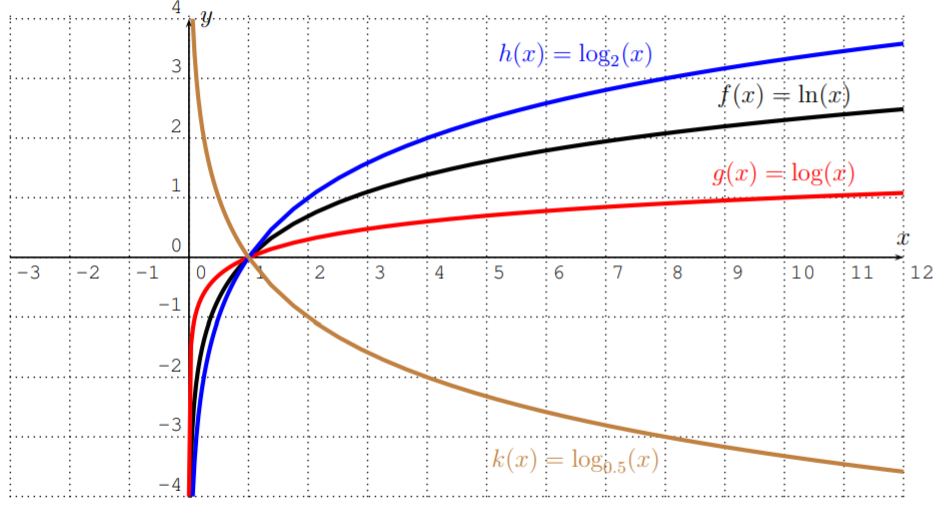
- Usando nuestro conocimiento de las transformaciones de las gráficas, esperamos que\(p(x)=-3\cdot \ln(x)+4\) sea el de\(y=\ln(x)\) reflejado y estirado lejos del\(x\) eje -( por un factor\(3\)), y luego desplazado hacia arriba por\(4\). La gráfica estirada y reflejada se encuentra en el centro de abajo, mientras que la gráfica de la función desplazada\(p\) se encuentra a la derecha debajo.
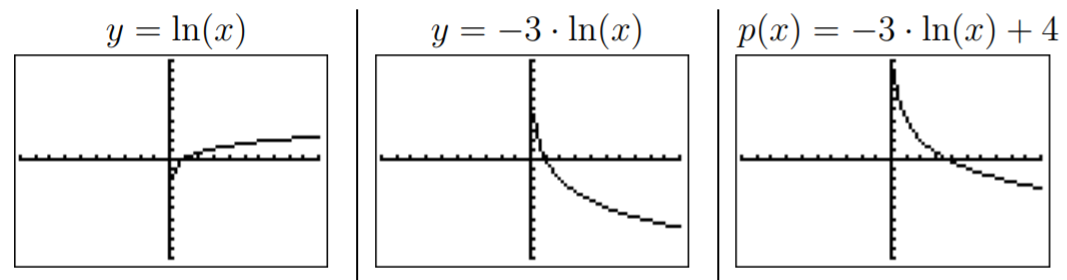
El dominio consiste en números\(x\) para los que\(\ln(x)\) se define el, es decir,\(D_p=\{x|x>0\}\).
- Para determinar el dominio de\(q(x)=\ln(5-x)\), tenemos que ver para cuál\(x\) el logaritmo tiene un argumento positivo. Más precisamente, necesitamos\(5-x>0\), es decir,\(5>x\), para que el dominio sea\(D_q=\{x|x<5\}\). La calculadora muestra la siguiente gráfica.
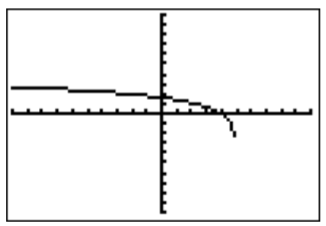
Tenga en cuenta que el gráfico, tal como lo muestra la calculadora, parece terminar en un punto que está aproximadamente en\((5,-2.5)\). Sin embargo, la gráfica real del logaritmo no se detiene en ningún punto, ya que tiene una asíntota vertical en\(x=5\), es decir, la gráfica se acerca\(-\infty\) como se\(x\) acerca\(5\). La calculadora solo muestra una aproximación, lo que puede ser engañoso ya que esta aproximación está determinada por el tamaño de la ventana y el tamaño de cada píxel. Por lo tanto, la gráfica se vería de la siguiente manera.
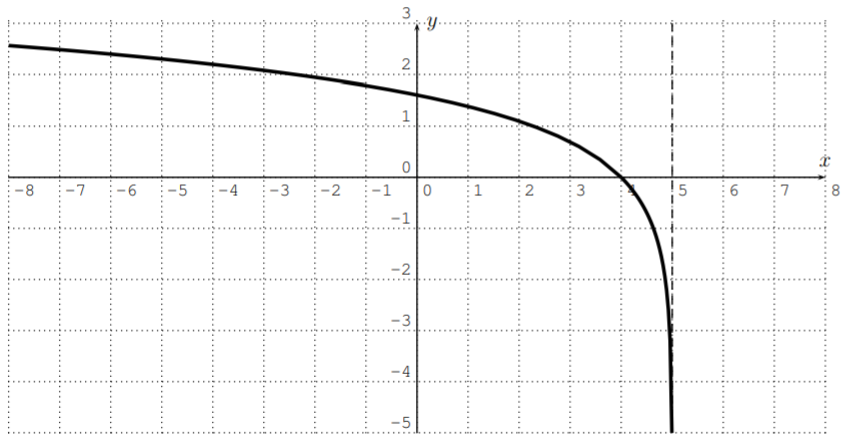
- El dominio de\(r(x)= \log_7(2x+8)\) consiste en aquellos números\(x\) para los que el argumento del logaritmo es positivo.
\[2x+8>0 \stackrel{\text{(subtract $8$)}}\implies \quad 2x>-8 \stackrel{\text{(divide by $2$)}}\implies \quad x>-4 \nonumber \]
Por lo tanto, el dominio es\(D_r=\{x|x>-4\}\). Para graficar la función\(r(x)= \log_7(2x+8)\), podemos\(r(x)=\dfrac{\ln(2x+8)}{\ln(7)}\) ingresar a la calculadora. La gráfica se ve de la siguiente manera.
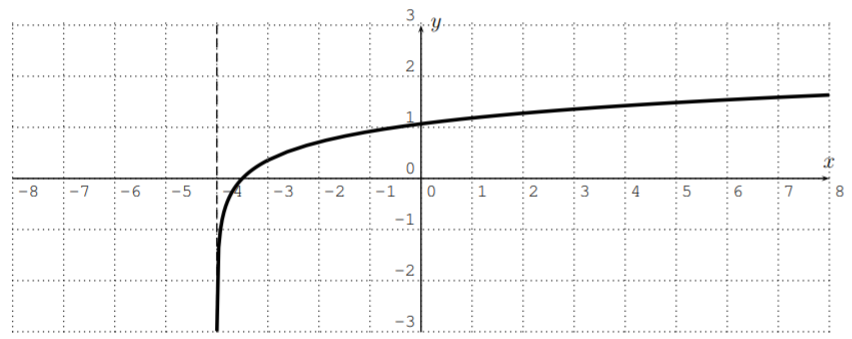
El ejemplo anterior analiza la gráfica de la función logaritmo. Aquí está el resumen.
La gráfica de una función logarítmica\(y=\log_b(x)\) con base\(b\) es la del logaritmo natural\(y=\ln(x)\) estirada alejada del\(x\) eje -, o comprimida hacia el\(x\) eje -cuando\(b>1\). Cuando\(0<b<1\), la gráfica se refleja además alrededor del\(x\) eje -eje.
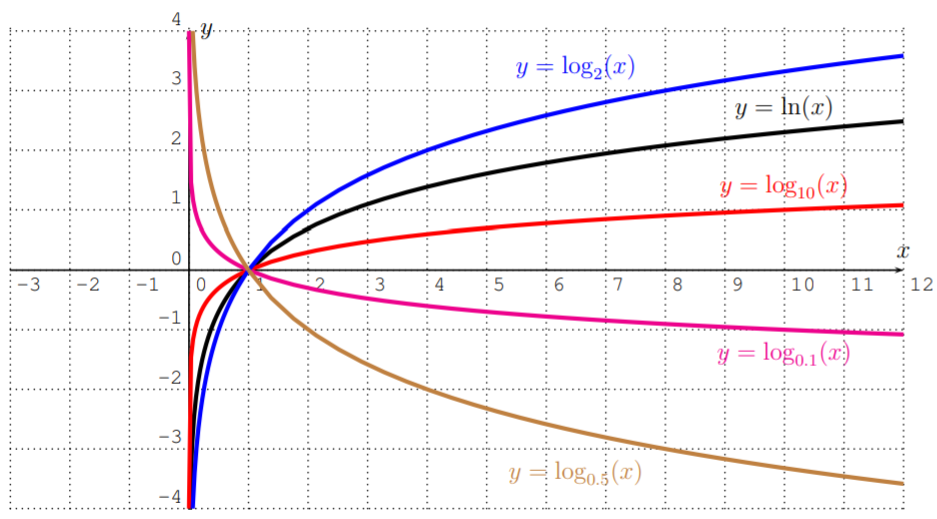
La gráfica\(y=\log_b(x)\) tiene dominio\(D=\{x|x>0\}\), y una asíntota vertical en\(x=0\). No hay asíntota horizontal, como\(f(x)\)\(x\) enfoques\(+\infty\) cuando se acerca\(+\infty\) para\(b>1\), y\(f(x)\) enfoques\(-\infty\) cuando\(x\) enfoques\(+\infty\) para\(0<b<1\). Por último, hay una\(x\) -intercepción en\(x=1\).


