15.1: Aplicaciones de funciones exponenciales

Antes de dar aplicaciones específicas, observamos que la función exponencial\(y=c\cdot b^x\) se determina de manera única proporcionando dos de sus valores de función cualesquiera.

Ejemplo\(\PageIndex{1}\)

Vamos\(f(x)=c\cdot b^x\). Determinar la constante\(c\) y la base\(b\) bajo las condiciones dadas.

1. \(f(0)=5\),\(f(1)=20\)
2. \(f(0)=3\),\(f(4)=48\)
3. \(f(2)=160\),\(f(7)=5\)
4. \(f(-2)=55\),\(f(1)=7\)

Solución

1. Aplicando\(f(0)=5\) a\(f(x)=c\cdot b^x\), obtenemos

\[5=f(0)=c\cdot b^0=c\cdot 1 =c \nonumber \]

Efectivamente, en general, siempre tenemos\(f(0)=c\) para cualquier función exponencial. Luego\(b\) se determina la base sustituyendo la segunda ecuación\(f(1)=20\).

\[20=f(1)=c\cdot b^1=5 \cdot b \quad\stackrel{(\div 5)}\implies \quad b=4 \nonumber \]

Por lo tanto,\(f(x)=5\cdot 4^x\). Obsérvese que en la última implicación, se utilizó que la base debe ser positiva.

2. Como antes, obtenemos\(3=f(0)=c\cdot b^0=c\), y

\[48=f(4)=c\cdot b^4=3\cdot b^4 \quad\stackrel{(\div 3)}\implies \quad 16=b^4 \quad\stackrel{(\text{exponentiate by }\frac 1 4)}\implies \quad b=16^{\frac 1 4}=2 \nonumber\]

Por lo tanto,\(f(x)=3\cdot 2^x\).

3. Cuando no\(f(0)\) se da, es más fácil de resolver por\(b\) primera vez. Esto lo podemos ver de la siguiente manera. Desde\(160=f(2)=c\cdot b^2\) y\(5=f(7)=c\cdot b^7\), el cociente de estas ecuaciones elimina\(c\).

\ [\ begin {alineado}
\ dfrac {160} {5} &=\ dfrac {c\ cdot b^2} {c\ cdot b^7} =\ dfrac {1} {b^5}\
\ implica 32&=b^ {-5}\\\\
\ fila larga derecha b&=32^ {-\ frac 1 5}\ quad (\ texto {exponente derecha por} (-\ frac {1} 5))\\
&=\ dfrac {1} {32^ {\ frac 1 5}}\\
&=\ dfrac 1 2
\ end {alineado}\ nonumber\]

Entonces\(c\) se determina por cualquiera de las ecuaciones originales.

\[160=f(2)=c\cdot b^2=c\cdot \Big(\frac 1 2\Big)^2=c \cdot \frac 1 4 \quad \implies \quad c=4\cdot 160=640 \nonumber \]

Por lo tanto,\(f(x)=640\cdot \Big(\dfrac 1 2\Big)^x\).

4. Esta solución es similar a la parte (c).

\ [\ begin {alineado}
\ dfrac {55} {7} &=\ dfrac {f (-2)} {f (1)} =\ dfrac {c\ cdot b^ {-2}} {c\ cdot b^1} =\ dfrac {1} {b^3}\
\ implica b^3&=\ dfrac {7} {55}\
\ implica b&=\ Grande (\ dfrac {7} {55}\ Grande) ^ {\ frac 1 3}\ aproximadamente 0.503
\ final {alineado}\ nonumber\]

\[\begin{gathered} 55=f(-2)=c\cdot b^{-2}=c\cdot \Big(\Big(\frac {7}{55}\Big)^{\frac 1 3}\Big)^{-2}=c\cdot \Big(\frac {7}{55}\Big)^{\frac {-2} 3} \\ \implies c=\frac{55}{\Big(\dfrac {7}{55}\Big)^{\frac {-2} 3}}=55\cdot \Big(\frac {7^{\frac {2} 3}}{55^{\frac {2} 3}}\Big)=55^{\frac 1 3}\cdot 7^{\frac 2 3}=\sqrt[3]{55\cdot 7^2}=\sqrt[3]{2695} \approx 13.916\end{gathered}\]

por lo tanto,\(f(x)=\sqrt[3]{2695}\cdot \Big(\sqrt[3]{\dfrac 7 {55}}\,\,\Big)^x\).

Muchas situaciones son modeladas por funciones exponenciales.

Ejemplo\(\PageIndex{2}\)

La masa de una muestra de bacterias es de\(2\cdot 1.02^t\) gramos después de\(t\) horas.

1. ¿Cuál es la masa de la muestra de bacterias después de\(4\) horas?
2. ¿Cuándo llegará la masa a los\(10\) gramos?

Solución

1. La fórmula para la masa\(y\) en gramos después de\(t\) horas es\(y(t)=2\cdot 1.02^t\). Por lo tanto, después de\(4\) horas, la masa en gramos es

\[y(4)=2\cdot 1.02^4 \approx 2.16 \nonumber \]

2. Estamos buscando el número de horas\(t\) para las cuales\(y=10\) gramos. Por lo tanto, tenemos que resolver:

\[10=2\cdot 1.02^t \quad\quad \stackrel{\text{($\div 2$)}}\implies \quad\quad 5=1.02^t \nonumber \]

Tenemos que resolver para la variable en el exponente. En general, para resolver una variable en el exponente se requiere una aplicación de un logaritmo en ambos lados de la ecuación.

\[5=1.02^t \quad\quad \stackrel{\text{(apply $\log$)}}\implies \quad\quad \log(5)=\log(1.02^t) \nonumber \]

Recordemos una de las principales propiedades que necesitamos resolver para\(t\):

\[\label{EQU:log(xt)} \log(x^t)=t\cdot \log(x) \nonumber \]

Usando este hecho, ahora podemos resolver para\(t\):

\ [\ begin {aligned}
\ log (5) &=\ log (1.02^t)\\
\ implica\ log (5) &=t\ cdot\ log (1.02)\\
\ implica\ dfrac {\ log (5)} {\ log (1.02)} &=t\ quad\ text {(dividir por $\ log (1.02) $)}
\ fin {alineado}\ umber\]

Usando la\(\boxed{log}\) clave de la calculadora, podemos aproximar esto como

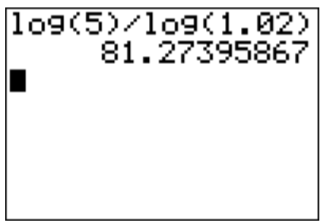
\(t=\dfrac{\log (5)}{\log (1.02)} \approx 81.3\)

Después de aproximadamente\(81.3\) horas, la masa será de\(10\) gramos.

Tenga en cuenta que la fórmula\(2\cdot 1.02^t\) proviene de los siguientes cálculos. Supongamos que después de cada hora hay un incremento del 2 por ciento de la masa y que la masa inicial de la bacteria es de 2 gramos. Entonces después de la primera hora vemos que la masa en gramos es

\[2+2\cdot(.02)=2(1+.02)=2(1.02) \nonumber \]

y que después de la segunda hora la misa es

\[2(1.02)+2(1.02)(.02)=2(1.02)(1+.02)=2(1.02)^2 \nonumber\]

y que después de tres horas la misa es

\[2(1.02)^2+2(1.02)^2(.02)=2(1.02)^2(1+.02)=2(1.02)^3 \nonumber \]

Continuando de esta manera podemos ver que, al menos para números enteros de horas\(t\), el peso viene dado por

\[2\cdot 1.02^t \nonumber \]

El mismo tipo de idea se puede utilizar en todas las siguientes aplicaciones.

Ejemplo\(\PageIndex{3}\)

El tamaño de la población de un país era\(12.7\) de millones en el año\(2000\), y\(14.3\) de millones en el año\(2010\).

1. Asumiendo un crecimiento exponencial para el tamaño de la población, encuentra la fórmula para la población dependiendo del año\(t\).
2. ¿Cuál será el tamaño de la población en el año\(2015\), suponiendo que la fórmula se mantenga hasta entonces?
3. ¿Cuándo llegará la población al\(18\) millón?

Solución

1. Se supone que el crecimiento es exponencial, por lo que se\(y(t)=c\cdot b^t\) describe el tamaño de la población dependiendo del año\(t\), donde establecemos\(t=0\) correspondiente al año\(2000\). Entonces el ejemplo describe\(y(0)=c\) como\(c=12.7\), que asumimos en unidades de millones. Para encontrar la base\(b\), sustituimos los datos de\(t=10\) y\(y(t)=14.3\) en\(y(t)=c\cdot b^t\).

\ [\ begin {alineado}
14.3&=12.7\ cdot b^ {10}\\
\ implica\ dfrac {14.3} {12.7} &=b^ {10}\
\ implica\ Grande (\ dfrac {14.3} {12.7}\ Grande) ^ {\ frac 1 {10}} & =( b^ {10}) ^ {\ frac 1 {10}} =b\\
\ implica b&=\ Grande (\ dfrac {14.3} {12.7}\ Grande) ^ {\ frac 1 {10}}\ aprox 1.012
\ end {alineado}\ nonumber\]

La fórmula para el tamaño de la población es\(y(t)\approx 12.7\cdot 1.012^t\).

2. Calculamos el tamaño de la población en el año\(2015\) estableciendo\(t=15\):

\[y(15)=12.7\cdot 1.012^{15}\approx 15.2 \nonumber \]

3. Buscamos\(t\) para que\(y(t)=18\). Resolvemos por\(t\) usar el logaritmo.

\ [\ begin {aligned}
18&=12.7\ cdot 1.012^ {t}\\
\ implica\ dfrac {18} {12.7} &=1.012^ {t}\
\\ implica\ log\ Grande (\ dfrac {18} {12.7}\ Grande) &=\ log (1.012^t)\
\ implica\ log\ Grande (\ dfrac {18} 12.7}\ Grande) &=t\ cdot\ log (1.012)\\
\ implica t& ; =\ dfrac {\ log\ Grande (\ frac {18} {12.7}\ Grande)} {\ log (1.012)}\ aprox 29.2
\ end {alineado}\ nonumber\]

La población alcanzará\(18\) millones en el año\(2029\).

En muchos casos la función exponencial\(f(x)=c\cdot b^x\) se da a través de una tasa de crecimiento\(r\).

Definición: Tasa de crecimiento

Una función exponencial con una tasa de crecimiento\(r\) es una función\(f(x)=c\cdot b^x\) con base

\[\boxed{b=1+r} \nonumber \]

Para un ejemplo de por qué esta es una definición razonable ver la nota siguiente Ejemplo\(\PageIndex{2}\).

Nota

Queremos señalar que algunos autores utilizan una convención diferente a la dada en la definición Tasa de crecimiento anterior. En efecto, a veces una función con tasa de crecimiento\(r\) se define como una función exponencial con base\(b=e^r\), mientras que para nosotros tiene base\(b=1+r\). Ya que se\(e^r\) puede ampliar como\(e^r=1+r+\dfrac{r^2}{2}+\dots\), vemos que las dos versiones sólo difieren por un error de orden\(2\).

Ejemplo\(\PageIndex{4}\)

El número de PCs que se venden en Estados Unidos en el año\(2011\) es de aproximadamente\(350\) millones con una\(3.6\%\) tasa de crecimiento anual. Suponiendo que la tasa se mantenga constante durante los próximos años, ¿cuántas PCs se venderán en el año\(2015\)?

Solución

Dado que la tasa de crecimiento es\(r=3.6\%=0.036\), obtenemos una base de\(b=1+r=1.036\), dando el número de PCs a modelar\(c(1.036)^t\). Si fijamos\(t=0\) para el año\(2011\), nos encontramos con eso\(c=350\), por lo que el número de ventas viene dado por\(y(t)=350\cdot 1.036^t\). Dado que el año\(2015\) corresponde a\(t=4\), podemos calcular el número de ventas en el año\(2015\) como

\[y(4)=350\cdot 1.036^4\approx 403 \nonumber \]

Aproximadamente\(403\) millones de PCs se venderán en el año\(2015\).

Ejemplo\(\PageIndex{5}\)

El tamaño de una colonia de hormigas está disminuyendo a una\(1\%\) tasa mensual. ¿Cuánto tiempo pasará hasta que la colonia haya alcanzado\(80\%\) su tamaño original?

Solución

Ya que\(r=-1\%=-0.01\), obtenemos la base\(b=1+r=1-0.01=0.99\). Tenemos un tamaño de colonia de\(y(t)=c\cdot 0.99^t\) después de\(t\) meses, donde\(c\) está el tamaño original. Tenemos que encontrar para\(t\) que el tamaño esté en\(80\%\) su tamaño original\(c\), es decir,\(y(t)=80\%\cdot c=0.8\cdot c\).

\ [\ begin {aligned}
0.8\ cdot c&=c\ cdot 0.99^ {t}\
\ implica 0.8&=0.99^ {t}\ quad\ text {($\ div c$)}\
\ implica\ log (0.8) &=\ log (0.99^t)\
\ implica\ log (0.8) &=t\ cdot\ log (0.99)\
\ implica t&=\ dfrac {\ log (0.8)} {\ log (0.99) }\ aprox 22.2
\ final {alineado}\ nonumber\]

Después de aproximadamente\(22.2\) meses, la colonia\(80\%\) de hormigas ha disminuido a su tamaño original.

Ejemplo\(\PageIndex{6}\)

1. El tamaño de la población de un país está aumentando a una\(4\%\) tasa anual. ¿Cuánto tiempo tarda en que el país haya duplicado su tamaño poblacional?
2. El número de nuevos casos de gripe está disminuyendo a un ritmo de\(5\%\) por semana. ¿Después de cuánto tiempo llegará el número de nuevos casos de gripe a una cuarta parte de su nivel actual?

Solución

1. La tasa de cambio es\(r=4\%=0.04\), por lo que el tamaño de la población es una función exponencial con base\(b=1+0.04=1.04\). Por lo tanto,\(f(x)=c\cdot 1.04^x\) denota el tamaño de la población,\(c\) siendo la población inicial en el año correspondiente a\(x=0\). Para que el tamaño de la población se duplique,\(f(x)\) tiene que alcanzar el doble de su tamaño inicial, es decir:

\ [\ begin {alineado}
f (x) &=2c\
\\ implica c\ cdot 1.04^x&=2c\
\ implica 1.04^x&=2\ quad (\ div c)\
\ implica\ log (1.04^x) &=\ log (2)\
\ implica x\ log (1.04) &=\ log (2)\
\ implica x&=\ dfrac {\ log (2)} {\ log (1. 04)}\ aprox 17.7
\ final {alineado}\ nonumber\]

Pasarán unos\(17.7\) años hasta que el tamaño de la población se haya duplicado.

2. Dado que el número de nuevos casos de gripe está disminuyendo, la tasa de crecimiento es negativa,\(r=-5\%=-0.05\) por semana, por lo que tenemos una función exponencial con base\(b=1+r=1+(-0.05)=0.95\). Para llegar a una cuarta parte de su número inicial de casos de gripe, establecemos\(f(x)=c\cdot 0.95^x\) igual a\(\dfrac 1 4 c\).

\ [\ begin {alineado}
c\ cdot 0.95^x&=\ dfrac 1 4 c\\
\ implica 0.95^x&=\ cfrac 1 4\ quad (\ div c)\
\ implica x\ log (0.95) &=\ log (\ cfrac 1 4)\
\ implica x&=\ cfrac {\ log (\ frac 1 4)} {log (0.95)}\ aprox. 27.0
\ end {alineado}\ nonumber\ ]

Por lo tanto, tomará alrededor de\(27\) semanas hasta que el número de nuevos casos de gripe haya disminuido a una cuarta parte de su nivel actual.