17.1: Definiciones trigonométricas básicas y hechos
- Page ID
- 117833
En esta parte, investigaremos las funciones trigonométricas\(y=\sin(x)\), como\(y=\cos(x)\), y\(y=\tan(x)\) en términos de sus aspectos teóricos de función. Antes de graficar estas funciones, recordamos las definiciones básicas y los hechos principales, que consideraremos como material de fondo conocido.
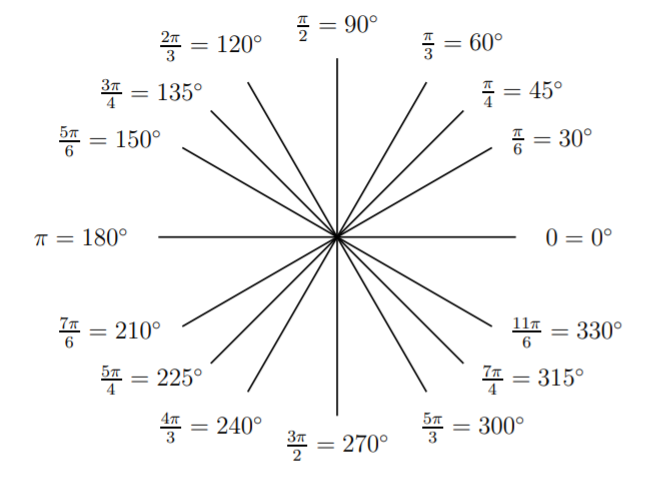
Un ángulo se puede expresar en grado o en medida de radianes. La relación entre grados y radianes viene dada por
\[\boxed{\pi=180^\circ} \nonumber \]
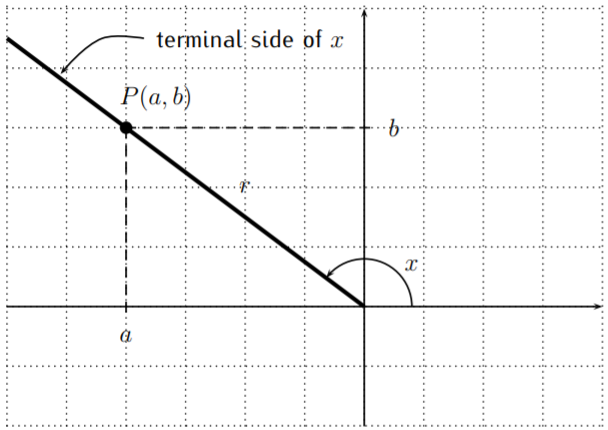
Dejar\(x\) ser un ángulo. Considere el lado terminal del ángulo\(x\), y asuma que el punto\(P(a,b)\) es un punto en el lado terminal de\(x\). Si\(r\) es la distancia desde\(P\) el origen\((0,0)\), entonces definimos el seno, coseno, tangente, cosecante, secante y cotangente como sigue:
\ [\ boxed {\ begin {alineado}
& a^ {2} +b^ {2} =r^ {2}\
\ implica & r=\ sqrt {a^ {2} +b^ {2}}
\ end {alineado}}\ nonumber\]
\ [\ boxed {\ begin {array} {ll}
\ sin (x) =\ dfrac {b} {r} &\ csc (x) =\ dfrac {r} {b}\\ cos (x) =
\ dfrac {a} {r} &\ sec (x) =\ dfrac {r} {a}\\\ (tan x) =\ dfrac {r} {a}\\ (tan x) =\ dfrac ac {b} {a} &\ cot (x) =\ dfrac {a} {b}
\ end {array}}\ nonumber\]
Hay algunas consecuencias inmediatas de la definición anterior.
\[\begin{aligned} \boxed{\csc(x)=\dfrac{1}{\sin(x)}} && \boxed{\sec(x)=\dfrac{1}{\cos(x)}} \\ \boxed{\tan(x)=\dfrac{\sin(x)}{\cos(x)}} && \boxed{\cot(x)=\dfrac{\cos(x)}{\sin(x)}=\dfrac{1}{\tan(x)}}\end{aligned}\]
Si tomamos\(r=1\) en lo anterior tenemos la siguiente definición de 'círculo unitario' de\(\sin\) y\(\cos\):
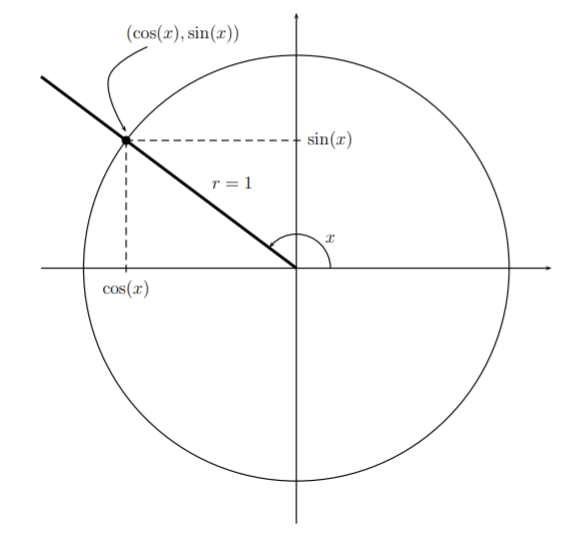
Es decir, que el punto donde el lado terminal del ángulo se\(x\) cruza con el círculo unitario es\((\cos(x),\sin(x))\) (que puede servir como definición\(\cos\) y\(\sin\) como funciones de\(x\)).
Para lo siguiente, utilizamos la notación de mano corta:
\[\sin^2\alpha:=(\sin \alpha)^2, \quad \cos^2\alpha:=(\cos \alpha)^2 , \quad\text{ and }\quad \tan^2\alpha:=(\tan \alpha)^2 \nonumber \]
A partir de estas definiciones, obtenemos que
\[\label{EQU:sin2+cos2=1} \boxed{\sin^2(x)+\cos^2(x)=1} \quad \quad \boxed{\sec^2(x)=1+\tan^2(x)}\]
ya que\(\sin^2(x)+\cos^2(x)=\left(\dfrac{b}{r}\right)^2+\left(\dfrac{a}{r}\right)^2=\dfrac{b^2+a^2}{r^2}=\dfrac{r^2}{r^2}=1\), y, de manera similar,\(1+\tan^2(x)=1+\left(\dfrac{b}{a}\right)^2=\dfrac{a^2+b^2}{a^2}=\dfrac{r^2}{a^2}=\left(\dfrac{r}{a}\right)^2=\sec^2(x)\). Además, podemos ver en la definición que
\[\label{EQU:basic-trig-eqns-wrt-pi} \begin{matrix} \boxed{\sin(x+2\pi)=\sin(x)}&\boxed{\sin(-x)=-\sin(x)}&\boxed{\sin(\pi-x)=\sin(x)}\\&&\\ \boxed{\cos(x+2\pi)=\cos(x)}&\boxed{\cos(-x)=\cos(x)}&\boxed{\cos(\pi-x)=-\cos(x)} \end{matrix} \]
Para un punto\(P(a,b)\) la\(x\) coordenada\(a\) -es positiva cuando\(P\) está en el cuadrante I y IV, mientras que la\(y\) coordenada\(b\) -es positiva cuando\(P\) está en el cuadrante I y II. La duración del hipotenuso\(r\) es siempre positiva. Así, las funciones trigonométricas son positivas/negativas según la gráfica:
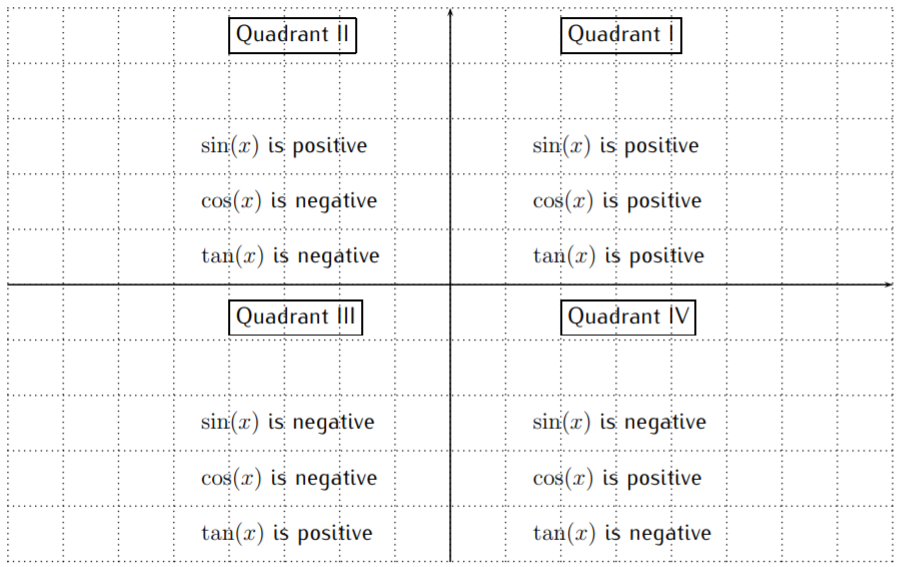
Existen dos triángulos básicos que se utilizan para calcular los valores exactos de las funciones trigonométricas. Estos dos triángulos son los\(30^\circ-60^\circ-90^\circ\) triángulos\(45^\circ-45^\circ-90^\circ\) y, los cuales pueden describirse con longitudes laterales específicas.
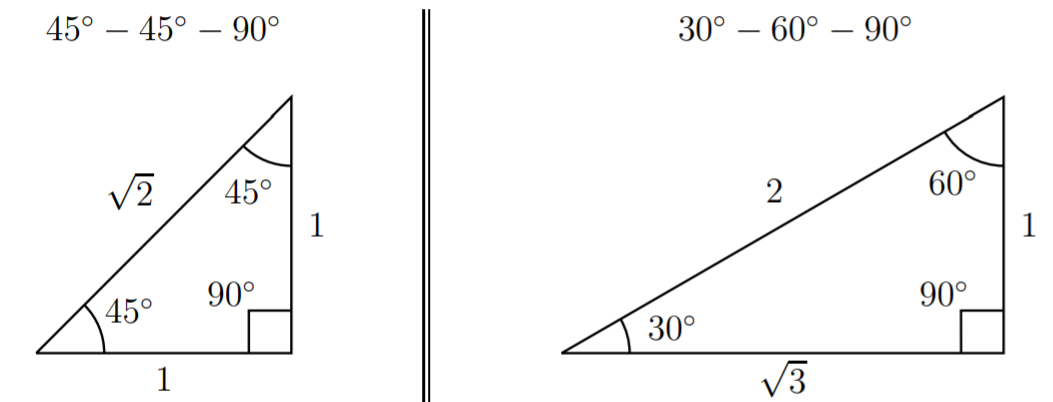
Estos triángulos básicos pueden ser utilizados para calcular las funciones trigonométricas de ciertos ángulos.
Encontrar\(\sin(x)\),\(\cos(x)\), y\(\tan(x)\) para los ángulos
\[x=30^\circ,\quad x=45^\circ, \quad x=60^\circ,\quad x=90^\circ,\quad x=0^\circ \nonumber \]
Solución
Dibujamos el ángulo\(x=30^\circ\) en el plano, y usamos el triángulo especial para encontrar un punto en el lado terminal del ángulo. A partir de esto, luego leemos las funciones trigonométricas. Aquí están los valores de función para\(30^\circ\),\(45^\circ\), y\(60^\circ\).
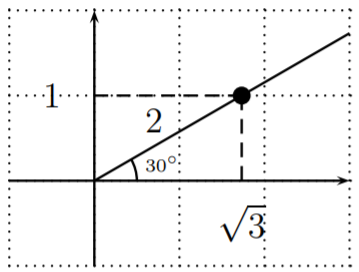
\ sin\ izquierda (30^ {\ circ}\ derecha) &=\ dfrac {b} {r} =\ dfrac {1} {2}\
\ cos\ izquierda (30^ {\ circ}\ derecha) &=\ dfrac {a} {r} =\ dfrac {\ sqrt {3}} {2}\ tan
\\ izquierda (30^ {\ circ}\ derecha) &=\ dfrac {b} {a} =\ dfrac {1} {\ sqrt {3}} =\ dfrac {\ sqrt {3}} {3}
\ end {alineado}\)
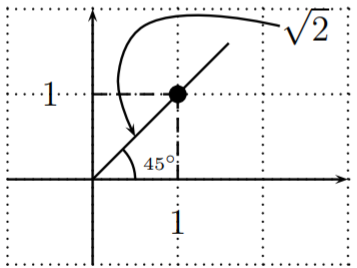
\ sin\ izquierda (45^ {\ circ}\ derecha) &=\ dfrac {b} {r} =\ dfrac {1} {\ sqrt {2}} =\ dfrac {\ sqrt {2}} {2}\
\ cos\ izquierda (45^ {\ circ}\ derecha) &=\ dfrac {a} {} =\ dfrac {1} {\ sqrt {2}} =\ dfrac {\ sqrt {2}} {2}\\
\ tan\ izquierda (45^ {\ circ}\ derecha) &=\ dfrac {b} {a} =\ dfrac {1} {1} =1
\ end {alineado}\)
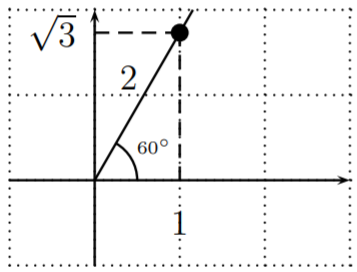
\ sin\ izquierda (60^ {\ circ}\ derecha) &=\ dfrac {b} {r} =\ dfrac {\ sqrt {3}} {2}\
\ cos\ izquierda (60^ {\ circ}\ derecha) &=\ dfrac {a} {r} =\ dfrac {1} {2}\ tan
\\ izquierda (60^ {\ circ}\ derecha) &=\ dfrac {b} {a} =\ dfrac {\ sqrt {3}} {1} =\ sqrt {3}
\ end {alineado}\)
Aquí están las funciones trigonométricas para\(90^\circ\) y\(0^\circ\).
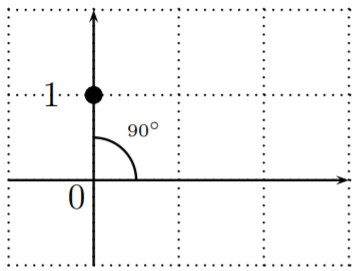
\ sin\ izquierda (90^ {\ circ}\ derecha) &=\ dfrac {b} {r} =\ dfrac {1} {1} =1\
\ cos\ izquierda (90^ {\ circ}\ derecha) &=\ dfrac {a} {r} =\ dfrac {0} {1} =0\
\ tan izquierda\ (90^ {\ circ}\ derecha) &=\ dfrac {b} {a} =\ dfrac {1} {0}\ quad\ text {es indefinido}
\ end {alineado}\)
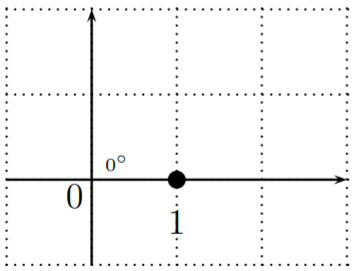
\ sin\ izquierda (0^ {\ circ}\ derecha) &=\ dfrac {b} {r} =\ dfrac {0} {1} =0\
\ cos\ izquierda (0^ {\ circ}\ derecha) &=\ dfrac {a} {r} =\ dfrac {1} {1} =1\
\ tan izquierda\ (0^ {\ circ}\ derecha) &=\ dfrac {b} {a} =\ dfrac {0} {1} =0
\ end {alineado}\)
Recopilamos los resultados del ejemplo anterior en una tabla:
\ [\ begin {array} {c||c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ pi} {2} =90^ {\ circ}\\ hline
\ hline\ hline\ sin (x) & 0 &\ dfrac {1} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {\ sqrt {3}} {2} & amp; 1\
\ hline\ cos (x) & 1 &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {1} {2} & 0\
\ hline\ tan (x) & 0 &\ dfrac {\ sqrt {3}} {3} & 1 &\ sqrt {3} &\ texto {undef.}
\ end {array}\ nonumber\]
Hay una manera fácil de recordar el valor de función dado en la tabla anterior escribiendo el numerador de\(\sin(x)\) como\(\sqrt{0}, \sqrt{1}, \sqrt{2}, \sqrt{3}, \sqrt{4}\) en orden creciente, y para\(\cos(x)\) en orden decreciente:
\ [\ begin {array} {c|c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} y dfrac {\ pi} {2} =90^ {\ circ}\\ hline\ sin (x) &\ dfrac {\ sqrt {0}} {2} &\ dfrac {\ sqrt {1}} {2} &\ dfrac {\ sqrt {2}} {2} &\
dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {4}} {2}\
\ hline\ cos (x) &\ dfrac {\ sqrt {4}} {2} &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {\ sqrt {1}} {2} &\ dfrac {\ sqrt {0}} {2}
\ end {array}\ nonumber\]
Los valores de entonces\(\tan(x)\) se determinan a partir de esto por\(\tan (x)=\dfrac{\sin (x)}{\cos (x)}\):
\ [\ begin {array} {c|c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} y dfrac {
\ pi} {2} =90^ {\ circ}\\ hline\ tan (x) &\ dfrac {0} {1} =0 &\ dfrac {\ frac {1} {2}} {\ frac {\ sqrt {3}} {2}} =\ dfrac {1} {\ sqrt {3}} =\ dfrac {\ sqrt {3}} {3} &\ dfrac {\ sqrt {2}} {\ frac {\ sqrt {2}} {2}} =1 &\ dfrac {\ sqrt {3}} {\ frac {1} {2}} =\ sqrt {3} & {}”\ dfrac {1} {0} {}”\ texto {es undef.}
\ end {array}\ nonumber\]
Podemos utilizar el especial\(45^\circ-45^\circ-90^\circ\) y los\(30^\circ-60^\circ-90^\circ\) triángulos para encontrar también otros valores de las funciones trigonométricas.
Encuentra\(\sin(x)\),\(\cos(x)\), y\(\tan(x)\) para los siguientes ángulos.
- \(x=240^\circ\)
- \(x=495^\circ\)
- \(x=\dfrac{11\pi}{6}\)
- \(x=\dfrac{-9\pi}{4}\)
Solución
- Graficamos el ángulo\(x=240^\circ\), e identificamos un\(30^\circ-60^\circ-90^\circ\) triángulo especial usando el lado terminal de\(x\).
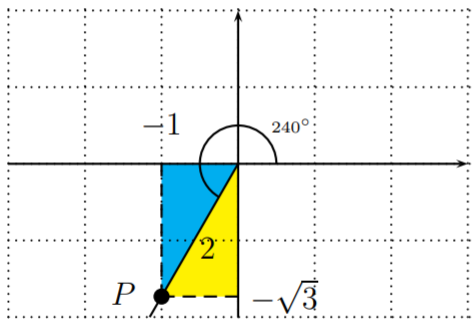
Identificamos un punto\(P\) en el lado terminal de\(x\). Este punto\(P\) tiene coordenadas\(P(-1,-\sqrt{3})\), las cuales se pueden ver considerando uno de los dos\(30^\circ-60^\circ-90^\circ\) triángulos en el plano (sombreado arriba). La longitud del segmento de línea desde\(P\) el origen\((0,0)\) es\(2\). Así,\(a=-1, b=-\sqrt{3}, r=2\). Obtenemos
\[\sin(240^\circ)=\dfrac{-\sqrt{3}}{2}, \quad \cos(240^\circ)=\dfrac{-1}{2},\quad \tan(240^\circ)=\dfrac{-\sqrt{3}}{-1}=\sqrt{3} \nonumber \]
- El ángulo\(x=495^\circ\) es mayor que\(360^\circ\). Sin embargo, las funciones trigonométricas son invariantes bajo suma o resta de\(360^\circ\):
\[\boxed{\sin(x\pm 360^\circ)=\sin(x)} \,\,\, \boxed{\cos(x\pm 360^\circ)=\cos(x)} \,\,\, \boxed{\tan(x\pm 360^\circ)=\tan(x)} \nonumber \]
Ya que\(495^\circ-360^\circ=135^\circ\), tenemos\(\sin(495^\circ)=\sin(135^\circ)\), y de manera similar para\(\cos\) y\(\tan\). Graficando el lado terminal e identificando un\(45^\circ-45^\circ-90^\circ\) triángulo especial, encontramos las coordenadas de un punto\(P\) en el lado terminal con coordenadas\(P(-1,1)\).\(x\)
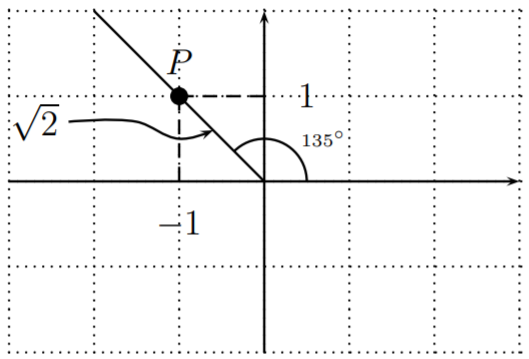
Por lo tanto,\(a=-1, b=1, r=\sqrt{2}\). Obtenemos
\[\sin(495^\circ)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}, \quad \cos(495^\circ)=\dfrac{-1}{\sqrt{2}}=\dfrac{-\sqrt{2}}{2},\quad \tan(495^\circ)=\dfrac{1}{-1}=-1 \nonumber \]
- \(\dfrac{11\pi}{6}\)Convertiéndose en grados, tenemos
\[x=\dfrac{11\pi}{6}=\dfrac{11\pi}{6}\cdot \dfrac{180^\circ}{\pi}=11\cdot 30^\circ=330^\circ \nonumber \]
Dibujando el lado terminal, obtenemos el punto\(P\).
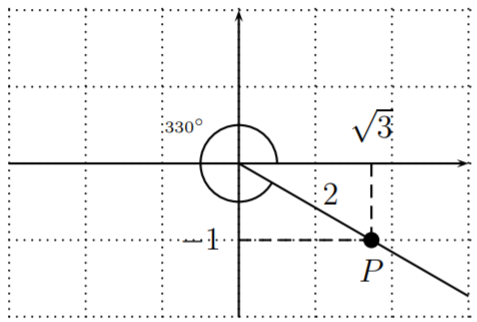
El punto\(P\) tiene coordenadas\(P(\sqrt{3},-1)\). Por lo tanto\(a=\sqrt{3}, b=-1, r=2\),, y
\[\sin\Big(\dfrac{11\pi}{6}\Big)=\dfrac{-1}{2}, \quad \cos\Big(\dfrac{11\pi}{6}\Big)=\dfrac{\sqrt{3}}{2},\quad \tan\Big(\dfrac{11\pi}{6}\Big)=\dfrac{-1}{\sqrt{3}}=\dfrac{-\sqrt{3}}{3} \nonumber \]
- Al convertir el ángulo\(x=\dfrac{-9\pi}{4}=\dfrac{-9\pi}{4}\cdot \dfrac{180^\circ}{\pi}=-9\cdot 45^\circ=-405^\circ\), vemos que las funciones trigonométricas de\(x\) son las mismas que de\(-405^\circ+360^\circ=-45^\circ\), y también de\(-45^\circ+360^\circ=315^\circ\). Podemos dibujar ya sea\(-45^\circ\) o\(315^\circ\) para encontrar un punto\(P\) en el lado terminal de\(x\).
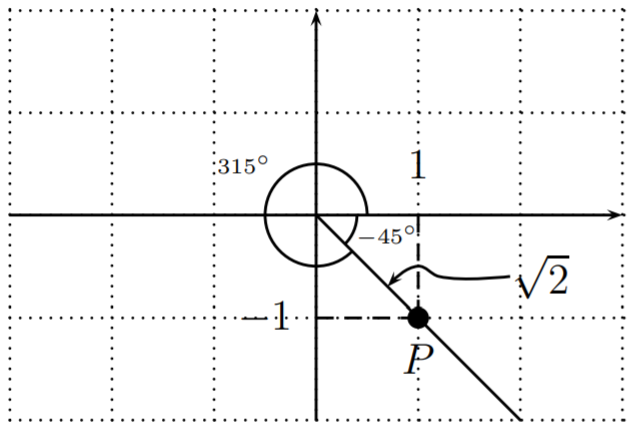
El punto\(P(1,-1)\) determina\(a=1, b=-1, r=\sqrt{2}\), y así
\[\begin{aligned} && \sin\Big(\dfrac{-9\pi}{4}\Big)=\dfrac{-1}{\sqrt{2}}=\dfrac{-\sqrt{2}}{2}, \quad \cos\Big(\dfrac{-9\pi}{4}\Big)=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}, \\ && \tan\Big(\dfrac{-9\pi}{4}\Big)=\dfrac{-1}{1}=-1 \end{aligned} \nonumber \]


