17.2: pecado, cos y bronceado como funciones

Última actualización
Guardar como PDF

Page ID: 117827

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

Pasamos ahora a aspectos teóricos de función de las funciones trigonométricas definidas en la última sección. En particular, nos interesará entender las gráficas de las funciones$y=\sin(x)$,$y=\cos(x)$, y$y=\tan(x)$. Con un ojo hacia el cálculo, tomaremos los ángulos$x$ en medida de radián.

Ejemplo$\PageIndex{1}$

Gráficamos las funciones$y=\sin(x)$,$y=\cos(x)$, y$y=\tan(x)$.

Solución

Una forma de proceder es calcular y recolectar diversos valores de función en una tabla y luego graficarlos. Sin embargo, esto es bastante elaborado, como muestra la siguiente tabla.

\ [\ begin {array} {c||c|c|c|c|c|c|c|c|c|c|c}
x & 0 &\ dfrac {\ pi} {6} &\ dfrac {\ pi} {4} &\ dfrac {\ pi} {3} &\ dfrac {\ pi} {2} &\ dfrac {2\ pi} {3}} &\ dfrac {3\ pi} {4} &\ dfrac {5\ pi} {6} &\ pi &\ ldots\\ hline
\ hline\ hline\ sin (x) & 0 &\ dfrac {1} {2} & \ dfrac {\ sqrt {2}} {2} &\ dfrac {\ sqrt {3}} {2} & 1 &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2}} {2} &\ dfrac {1} {2} & 0 &\ ldots
\\ hline\ cos (x) y 1 &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {1} {2} & 0 &\ dfrac {-1} {2} &\ dfrac {-\ sqrt {2}} {2} &\ dfrac {-\ sqrt {3}} {2} & -1 &\ ldots\
\ hline\ tan (x) & 0 &\ dfrac {\ sqrt {3}} {3} & 1 &\ sqrt {3} &\ text {undef.} & -\ sqrt {3} & -1 &\ dfrac {-\ sqrt {3}} 3} & 0 &\ ldots
\ end {array}\ nonumber\]

Un enfoque más fácil es usar el TI-84 para graficar cada función. Antes de ingresar a la función, necesitamos asegurarnos de que la calculadora esté en modo radián. Para esto, presione la$\boxed{\text{mode}}$ tecla, y en caso de que el tercer elemento esté configurado en grado, cambie a radián y presione$\boxed{\text{enter}}$.

$clipboard_eea526ccc6cb58ddd905e7979a401b79f.png$

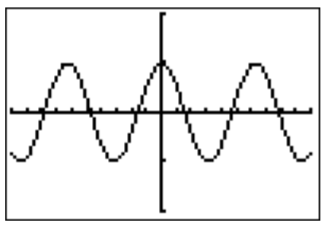
Ahora podemos ingresar a la función$y=\sin(x)$ y estudiar su gráfica.

$clipboard_e6d5bd276be62b98b500502173c40d7f2.png$

A partir de esto, podemos hacer algunas observaciones inmediatas (que también se pueden ver usando la definición sin-cos-tan). Primero, la gráfica está delimitada entre$-1$ y$+1$, porque por definición sin-cos-tan, tenemos$\sin(x)=\dfrac b r$ con$-r\leq b \leq r$, de manera que

\[-1\leq \sin(x)\leq 1, \quad \text{ for all }x \nonumber \]

Por lo tanto, cambiamos la ventana de la gráfica para mostrar$y$ entre$-2$ y$2$, para obtener una vista más cercana.

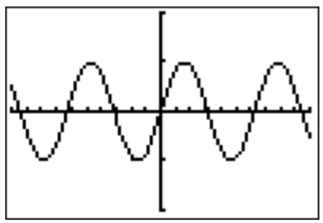
$clipboard_ec10c022393b0caa29d437347ee06815f.png$

$y=\sin (x)$

Segundo, vemos que$y=\sin(x)$ es una función periódica con punto$2\pi$, ya que la función no cambia su valor al$360^\circ=2\pi$ sumar a su argumento (y este es el número más pequeño distinto de cero con esa propiedad):

\[\sin(x+2\pi)=\sin(x) \nonumber \]

La gráfica de$y=\sin(x)$ tiene los siguientes valores específicos:

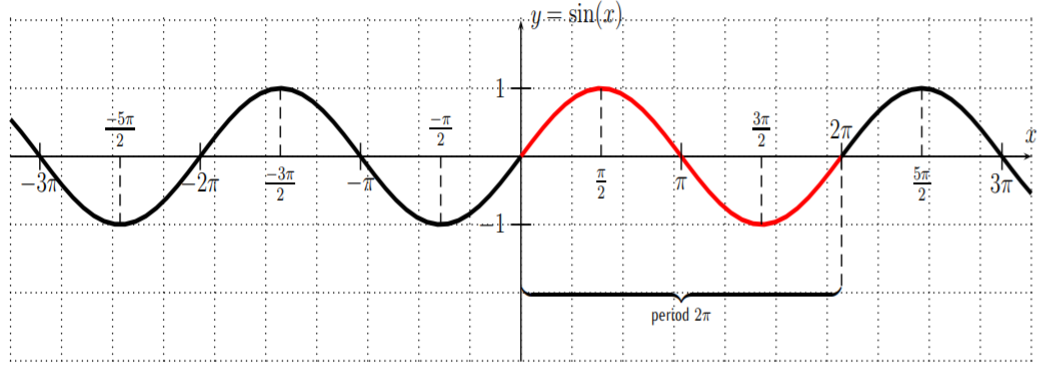
$clipboard_ec5024c7de96a419bbef1bda2c12141f2.png$

La gráfica de$y=\sin(x)$ tiene un periodo de$2\pi$, y una amplitud de$1$.

Del mismo modo, podemos graficar la función$y=\cos(x)$. Ya que$-1\leq \cos(x)\leq 1$ para todos$x$, lo graficamos también con la configuración de la ventana ampliada.

$clipboard_e3fc157b6bb1d641156fad4901a9da487.png$

$y=\cos (x)$

Vemos que también$y=\cos(x)$ es periódico con periodo$2\pi$, es decir\[\cos(x+2\pi)=\cos(x) \nonumber \] y$y=\cos(x)$ también tiene una amplitud de$1$, ya que$-1\leq\cos(x)\leq 1$.

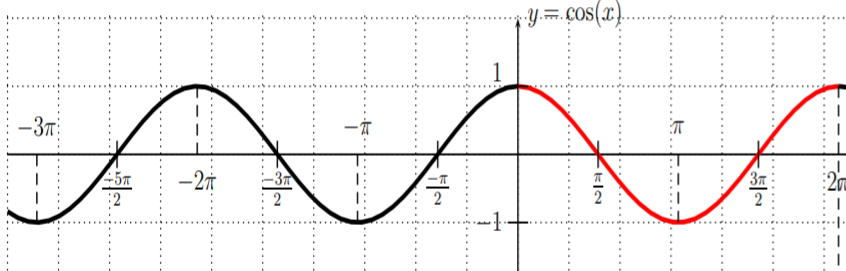
$clipboard_e98701f47f35b3fb0486f63a568c7ee9a.png$

En efecto, la gráfica de$y=\cos(x)$ es la de$y=\sin(x)$ desplazado a la izquierda por$\dfrac{\pi}{2}$. La razón de esto es que

\[\label{EQ:cos=sin+pi2} \boxed{\cos(x)=\sin\left(x+\dfrac{\pi}{2}\right)} \]

Muchas otras propiedades de$\sin$ y se$\cos$ pueden observar a partir de la gráfica (o de la definición del círculo unitario). Por ejemplo, recordando Observación par-impar de la página, vemos que la función seno es una función impar, ya que la gráfica de$y=\sin(x)$ es simétrica con respecto al origen. De igual manera, la función coseno es una función par, ya que la gráfica de$y=\cos(x)$ es simétrica con respecto al$y$ eje -eje. Álgebraicamente, Definición par-impar de página por lo tanto muestra que estas funciones satisfacen las siguientes relaciones:

\[\label{EQ:sin-odd-cos-even} \boxed{\sin(-x)=-\sin(x)} \quad\text{and}\quad \boxed{\cos(-x)=\cos(x)} \]

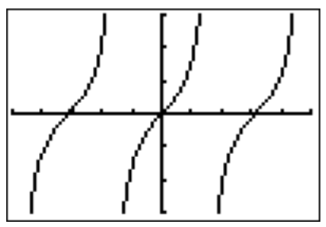
Por último, llegamos a la gráfica de$y=\tan(x)$. Graficando esta función en la ventana estándar, obtenemos:

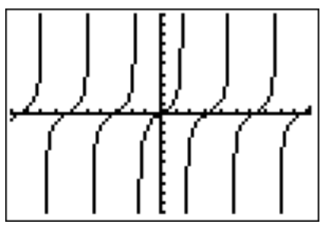
$clipboard_ec15aa126207a50ee7871c7609c002604.png$

$y=\tan (x)$

Al hacer zoom en esta gráfica, vemos que$y=\tan(x)$ tiene asíntotas verticales$x=\dfrac{\pi}{2}\approx 1.6$ y$x=\dfrac{-\pi}{2}\approx-1.6$.

$clipboard_e19b4de9c6ddc1c327da11fa53fc1072b.png$

$y=\tan (x)$

Esto también se sustenta en el hecho de que$\tan \left(\dfrac{\pi}{2} \right)$ y$\tan \left(-\dfrac{\pi}{2} \right)$ son indefinidos. A continuación se muestra la gráfica de$y=\tan(x)$ con algunos valores de función más específicos.

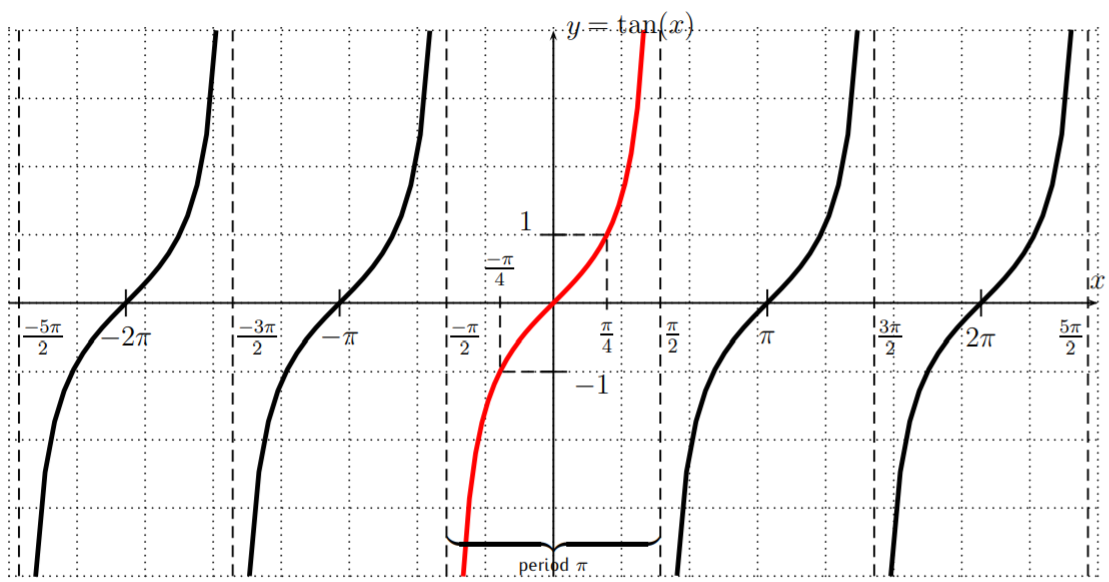
$clipboard_ecb7254386d387eaab4192629f12b7778.png$

Vemos que la tangente es periódica con un periodo de$\pi$:

\[\label{EQU:tan-period} \tan(x+\pi)=\tan(x) \nonumber \]

Hay asíntotas verticales:$x=\dfrac{\pi}{2}, \dfrac{-\pi}{2}, \dfrac{3\pi}{2}, \dfrac{-3\pi}{2}, \dfrac{5\pi}{2}, \dfrac{-5\pi}{2}, \dots$, o, en definitiva

\[\text{asymptotes of }y=\tan(x): \quad x=n\cdot \dfrac{\pi}{2}, \text{ where }n=\pm1, \pm3, \pm5, \dots \nonumber\]

Además, la tangente es una función impar, ya que es simétrica con respecto al origen (ver Observación par-impar):

\[\label{EQ:tan-odd} \boxed{\tan(-x)=-\tan(x)} \]

Recordemos de la sección 5.2 cómo cambiar la fórmula de una función afecta a la gráfica de la función, como por ejemplo:

la gráfica de$c\cdot f(x)$ (for$c>0$) es la gráfica de$f(x)$ estirado lejos del$x$ eje -por un factor$c$ (o comprimido cuando$0<c<1$)
la gráfica de$f(c\cdot x)$ (for$c>0$) es la gráfica de$f(x)$ comprimida hacia el$y$ eje por un factor$c$ (o$y$ estirada el eje cuando$0<c<1$)
gráfico de$f(x)+c$ es el gráfico de$f(x)$ desplazado hacia arriba por$c$ (o hacia abajo cuando$c<0$)
gráfico de$f(x+c)$ es el gráfico de$f(x)$ desplazado a la izquierda por$c$ (o a la derecha cuando$c<0$)

Con esto podemos graficar algunas variaciones de las funciones trigonométricas básicas.

Ejemplo$\PageIndex{2}$

Grafica las funciones:

\[\begin{aligned} && f(x)=\sin(x)+3, \,\, g(x)=4\cdot \sin(x), \,\, h(x)=\sin(x+2), \,\, i(x)=\sin(3x), \\ && j(x)=2\cdot \cos(x)+3, \,\,\, k(x)=\cos(2x-\pi), \,\,\, l(x)=\tan(x+2)+3 \end{aligned} \nonumber \]

Solución

Las funciones$f$,$g$,$h$, y$i$ tienen gráficas que son variaciones de la$y=\sin(x)$ gráfica básica. La gráfica de$f(x)=\sin(x)+3,$ desplaza la gráfica de$y=\sin(x)$ hacia arriba$3$, mientras que la gráfica de$g(x)=4\cdot \sin(x)$ se extiende$y=\sin(x)$ alejándose del$x$ eje -eje.

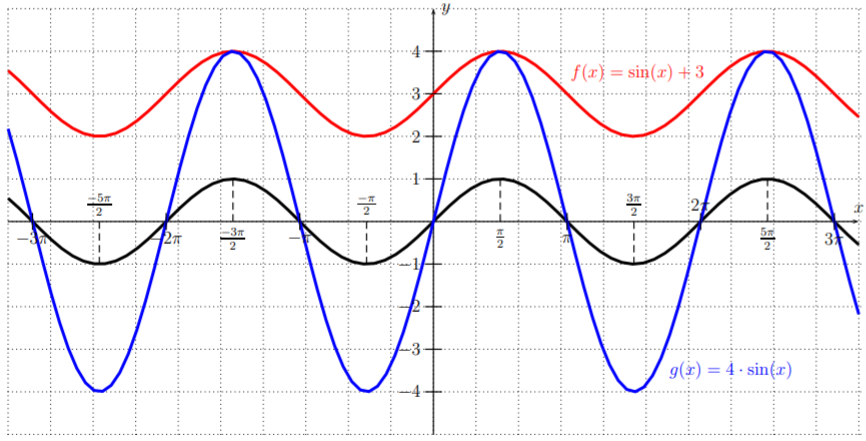
$clipboard_e5f5e59e1d3b8682d723b67a9fd0df51b.png$

La gráfica de$h(x)=\sin(x+2)$ desplaza la gráfica de$y=\sin(x)$ a la izquierda por$2$, y$i(x)=\sin(3x)$ comprime$y=\sin(x)$ hacia el$y$ eje -eje.

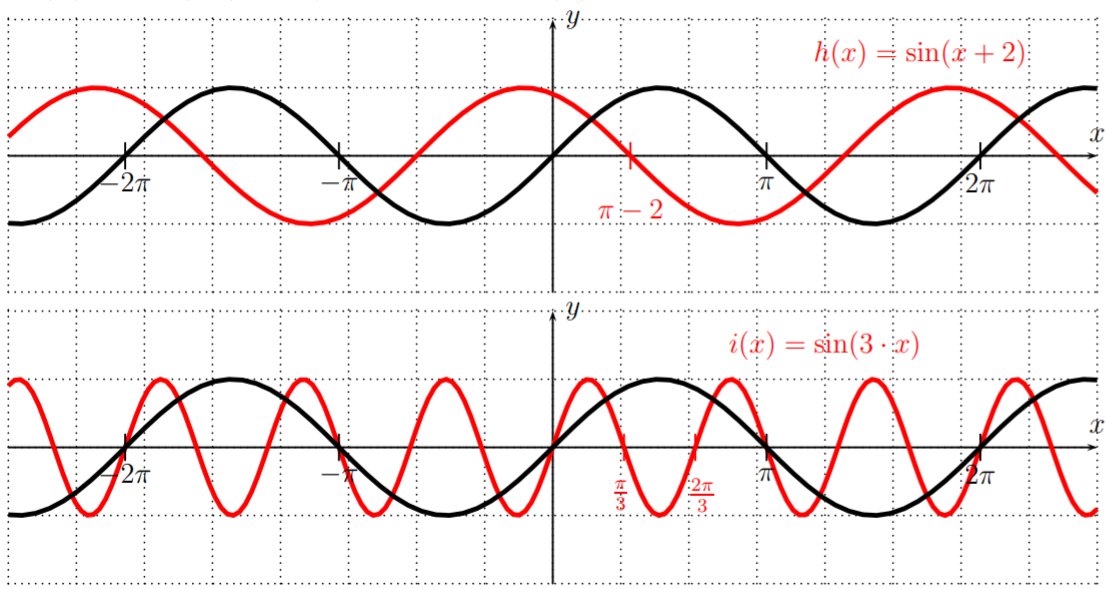
$clipboard_e75c491d55c5016c4fb6fa5588aaacbfa.png$

A continuación,$j(x)=2\cdot \cos(x)+3$ tiene una gráfica de$y=\cos(x)$ estirado por un factor$2$ lejos del$x$ eje -y desplazado hacia arriba por$3$.

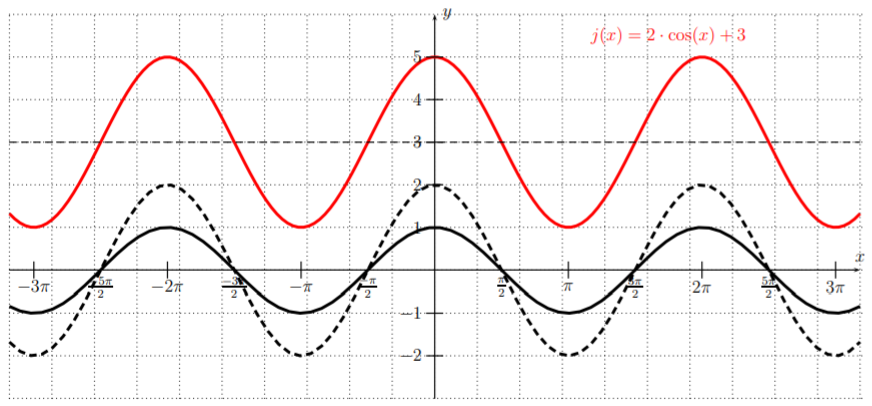
$clipboard_ec66e82e24792d584fc75733ca37b9d14.png$

Para la gráfica de$k(x)=\cos(2x-\pi)=\cos\left(2\cdot \left(x-\dfrac{\pi}{2}\right)\right)$, necesitamos comprimir la gráfica de$y=\cos(x)$ por un factor$2$ (obtenemos la gráfica de la función$y=\cos(2x)$) y luego desplazarla$\dfrac{\pi}{2}$ hacia la derecha.

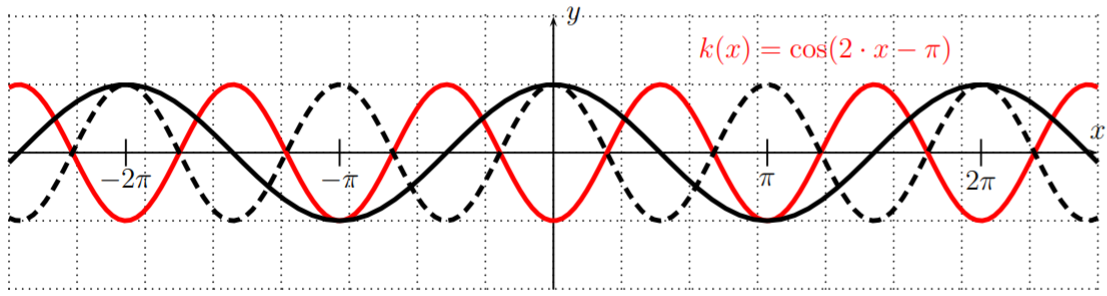
$clipboard_e6497fca20f8e99323bbe633253c15b42.png$

Exploraremos este caso a continuación con más generalidad. De hecho, siempre que$y=\cos(b\cdot x +c)=\cos\Big(b\cdot \Big(x-\dfrac{-c}{b}\Big)\Big)$, la gráfica de$y=\cos(x)$ se desplaza hacia la derecha por$\dfrac{-c}{b}$, y comprimida por un factor$b$, de manera que tenga un periodo de$\dfrac{2\pi}{b}$.

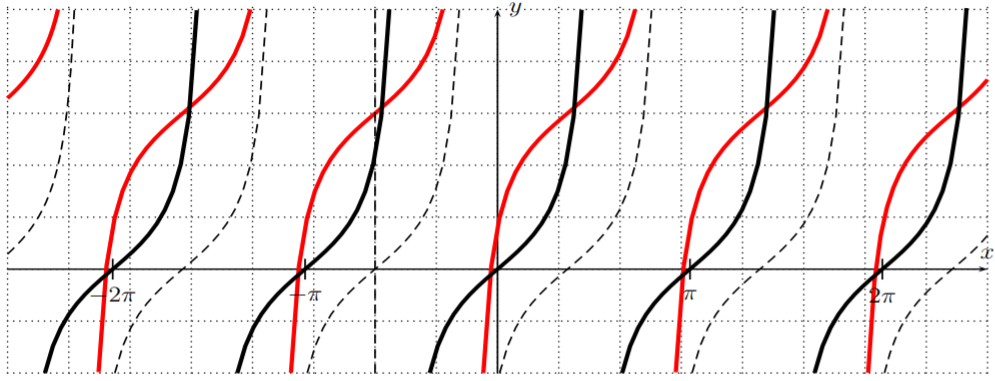
Por último,$l(x)=\tan(x+2)+3$ desplaza la gráfica de$y=\tan(x)$ arriba por$3$ y hacia la izquierda por$2$.

$clipboard_e244b6707a0a4bf9ebd2f44c9b0ff2877.png$

Recopilamos algunas de las observaciones que se hicieron en los ejemplos anteriores en la siguiente definición.

Definición: Amplitud-Periódico-Desplazamiento de Fase

$f$Sea una de las funciones:

\[f(x)=a\cdot \sin(b\cdot x +c) \quad \text{or} \quad f(x)=a\cdot \cos(b\cdot x +c) \nonumber \]

El número$|a|$ se llama amplitud, el número$\left|\dfrac{2\pi}{b}\right|$ es el período y el número$\dfrac{-c}{b}$ se llama desplazamiento de fase.

En aplicaciones físicas, el período a veces se denota por$T=\left|\dfrac{2\pi}{b}\right|$ y la frecuencia es el recíproco\[f=\dfrac 1 T \nonumber \]

Usando la amplitud, el período y el desplazamiento de fase, podemos dibujar la gráfica de, por ejemplo, una función a$f(x)=a\cdot \sin(b\cdot x +c)$ lo largo de un período desplazando la gráfica de$\sin(x)$ por el desplazamiento de fase$\dfrac{-c}{b}$ hacia la derecha, luego marcando un período completo de longitud$\left|\dfrac{2\pi}{b}\right|$, y luego dibujar la$\sin(x)$ gráfica básica con una amplitud de$a$ (o la gráfica reflejada de$-\sin(x)$ cuándo$a$ es negativa).

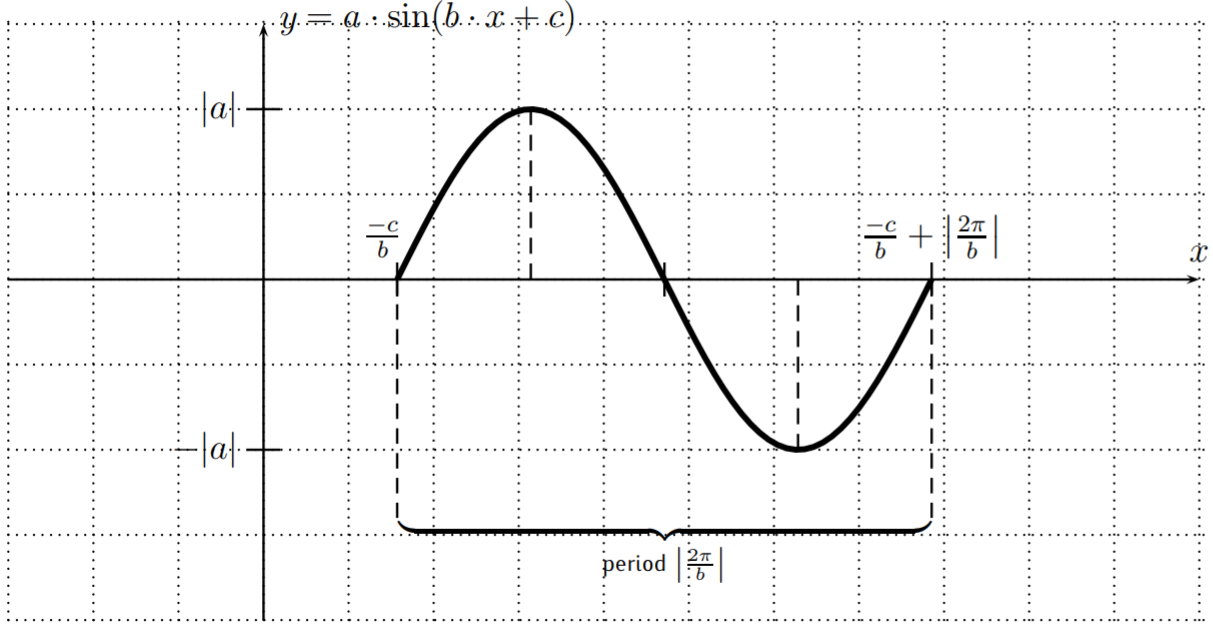
$clipboard_eb1a1c825a1e932d00e2ed9e4bbbfdd88.png$

Los cero (s), máximos y mínimos de la gráfica dentro del período dibujado se pueden encontrar calculando el punto medio entre$\left(\dfrac{-c}{b},0\right)$ y$\left(\dfrac{-c}{b}+\dfrac{2\pi}{b},0\right)$ y los puntos medios entre estos y el punto medio resultante.

Se puede obtener una gráfica similar$f(x)=a\cdot \cos(b\cdot x +c)$ reemplazando la$\sin(x)$ gráfica por la$\cos(x)$ gráfica en un periodo.

Ejemplo$\PageIndex{3}$

Encuentre la amplitud, el período y el desplazamiento de fase, y dibuje el gráfico durante un período completo.

$f(x)=3 \sin(2 x)$
$f(x)=-2\cos(\pi\cdot x)$
$f(x)=\cos(x-2)$
$f(x)=\cos(2 x+\pi)$
$f(x)=-4\cdot \sin\left(\dfrac{x}{2}+3\right)$
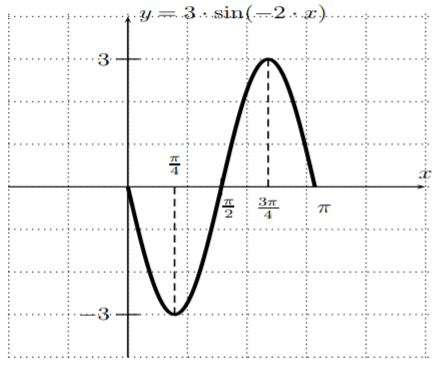
$f(x)=3 \sin(-2 x)$

Solución

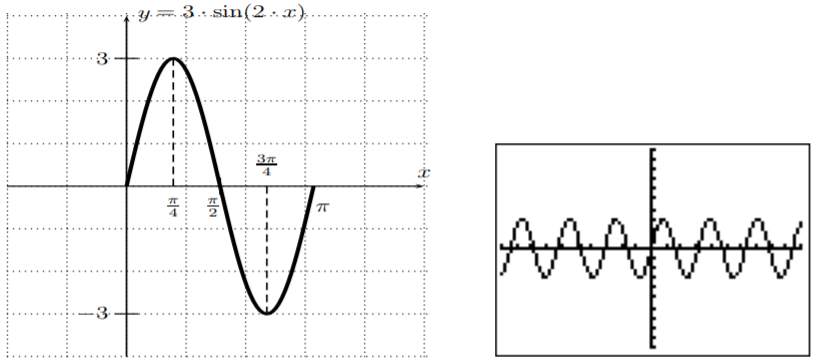
La amplitud es$|3|=3$, y desde$f(x)=3\cdot \sin(2\cdot x+0)$, es$b=2$ y$c=0$, de manera que el periodo es$\left|\dfrac{2\pi}{2}\right|=\pi$ y el desplazamiento de fase es$\dfrac{-0}{2}=0$. Esto también se apoya graficando la función con la calculadora; en particular la gráfica se repite después de un periodo completo, que es at$\pi\approx 3.1$.

$clipboard_e4f27022195faf0219ffc43bae6a9c0ba.png$

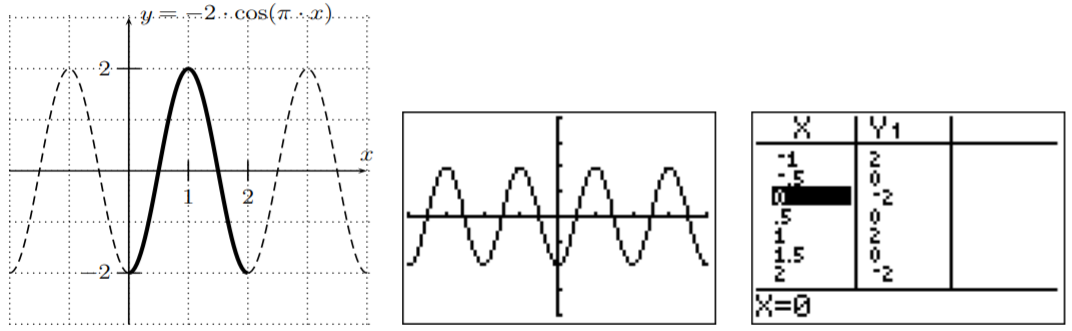
Porque$f(x)=-2\cos(\pi\cdot x)$, la amplitud es$|-2|=2$, el periodo es$\left|\dfrac{2\pi}{\pi}\right|=2$, y el desplazamiento de fase es$0$. Obsérvese, que el primer coeficiente es negativo, de manera que el$\cos(x)$ tiene que reflejarse alrededor del$x$ eje -eje. Un período completo se grafica a continuación con una línea continua (y la continuación de la gráfica es discontinua). Esta gráfica vuelve a ser apoyada por la gráfica y la tabla según lo dado por la calculadora.

$clipboard_ea30106bfe5f409b90ee6c517fb0b6dd7.png$

La amplitud de$f(x)=\cos(x-2)$ es$1$, el periodo es$2\pi$, y el desplazamiento de fase es$\dfrac{-(-2)}{1}=2$. A continuación se muestra la gráfica de un periodo.

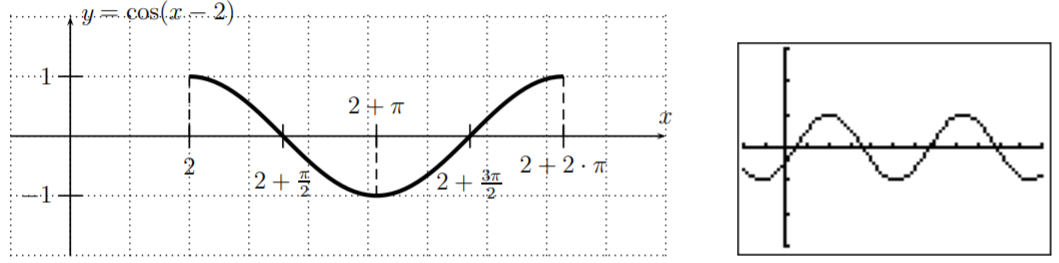
$clipboard_e77dec4e015c5e09cfa9a4b16478f787d.png$

El mínimo de la función$f$ en este periodo se da tomando el valor en la mitad del intervalo$[2,2+2\pi]$, es decir, at$2+\pi$. Con esto, los ceros se dan tomando el valor en medio de los intervalos$[2,2+\pi]$ y$[2+\pi,2+2\pi]$, que están en$2+\dfrac{\pi}{2}$ y$2+\dfrac{3\pi}{2}$.

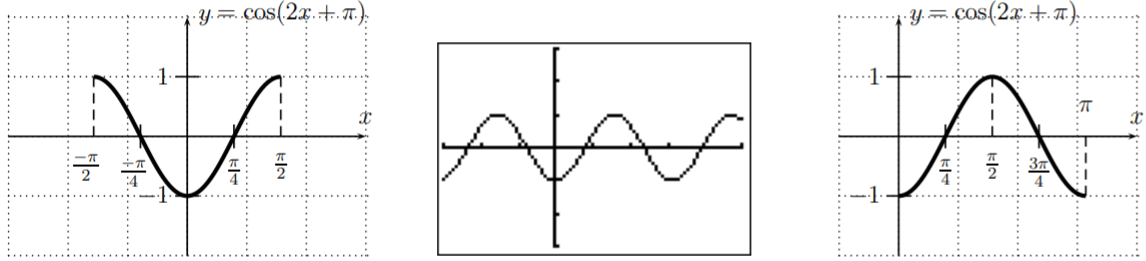
La función$f(x)=\cos(2 x+\pi)$ tiene amplitud$1$$\dfrac{2\pi}{2}=\pi$, periodo y desplazamiento de fase$\dfrac{-\pi}{2}$. Así podemos dibujar la gráfica durante un periodo de$\dfrac{-\pi}{2}$ a$\dfrac{-\pi}{2}+\pi=\dfrac{\pi}{2}$; ver gráfico de la izquierda a continuación. Sin embargo, también podemos graficar la función a lo largo de otro periodo completo, como por ejemplo$[0,\pi]$ (ver la gráfica de la derecha).

$clipboard_eb88b0896f697605f64444ae282d03fe2.png$

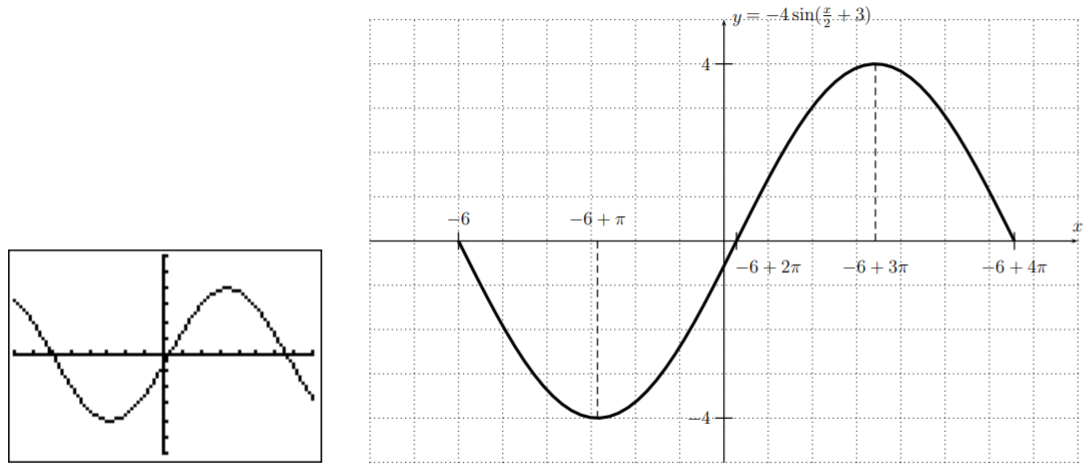
La gráfica de$f(x)=-4\cdot \sin\left(\dfrac{x}{2}+3\right)$ tiene una amplitud de$|-4|=4$, un período de$\dfrac{2\pi}{\frac{1}{2}}=4\pi$, y un desplazamiento de fase de$\dfrac{-3}{\frac{1}{2}}=-6$. Usando esta información, y confirmando esto con la calculadora, podemos dibujar un periodo completo de la gráfica de$f$.

$clipboard_ecf608eff09087ce1598b11db6f309b12.png$

Porque$f(x)=3\sin(-2x)$, tenemos una amplitud de$3$, un periodo de$\left|\dfrac{2\pi}{-2}\right|=\pi$ y un desplazamiento de fase de$\dfrac{-0}{-2}=0$. Comparando esto con el ejemplo (a) anterior, vemos que tenemos los mismos datos que para la función$y=3\sin(2x)$ de la parte (a). Sin embargo, en este caso, tenemos que dibujar la función seno a lo largo de un periodo moviéndose hacia la izquierda, lo que significa que la gráfica tiene que iniciar el periodo como una función decreciente. Esto también se puede ver observando que la función sinusoidal es una función impar, es decir, ecuación$\ref{EQ:sin-odd-cos-even}$, de modo que

\[f(x)=3\sin(-2x) = -3\sin(2x) \nonumber \]

Por tanto, la gráfica se dibuja de la siguiente manera.

$clipboard_eab8512093290c7a52d9555a05b2f36fd.png$

Ejemplo\(\PageIndex{1}\)

Ejemplo\(\PageIndex{2}\)

Definición: Amplitud-Periódico-Desplazamiento de Fase

Ejemplo\(\PageIndex{3}\)