18.1: Suma y resta de ángulos

En la sección anterior encontramos valores exactos de las funciones trigonométricas para ángulos específicos de\(0, \dfrac{\pi}{3}, \dfrac{\pi}{4}, \dfrac{\pi}{6}\) más posiblemente cualquier múltiplo de\(\dfrac{\pi}{2}\). Usando estos valores, podemos encontrar muchos otros valores de funciones trigonométricas a través de las siguientes fórmulas de suma y resta de ángulos, que exponemos ahora.

Proposición: Fórmulas de suma y resta de ángulos

Para cualquier ángulo\(\alpha\) y\(\beta\), tenemos:

\ [\ comenzar {alineado}
\ sin (\ alfa+\ beta) &=\ sin\ alfa\ cos\ beta+\ cos\ alfa\ sin\ beta
\\ sin (\ alfa-\ beta) &=\ sin\ alfa\ cos\ beta-\ cos\ alfa\ sin\ beta
\\ cos (\ alpha+\ beta) &=\ cos\ alpha\ cos\ beta-\ sin\ alpha\ beta\\
\ cos (\ alfa-\ beta) &=\ cos\ alfa\ cos\ beta+\ sin\ alfa\ sin\ beta\
\ tan (\ alpha+\ beta) &=\ dfrac {\ tan\ alpha+\ tan\ beta} {1-\ tan\ alfa\ tan\ beta}\
\ tan (\ alfa-\ beta) &=\ dfrac {tan\ alfa- 1+\ tan\ beta} {\ tan\ alfa\ tan\ beta}
\ final {alineado}\ nonumber\]

Prueba

Comenzamos con la prueba de las fórmulas para\(\sin(\alpha+\beta)\) y\(\cos(\alpha+\beta)\) cuándo\(\alpha\) y\(\beta\) son ángulos entre\(0\) y\(\dfrac \pi 2=90^\circ\). Demostramos las fórmulas de adición (for\(\alpha,\beta\in \left (0,\dfrac \pi 2\right)\)) de una manera bastante elemental, y luego mostramos que las fórmulas de adición también se mantienen para ángulos arbitrarios\(\alpha\) y\(\beta\).

Para encontrar\(\sin(\alpha+\beta)\), considere la siguiente configuración.

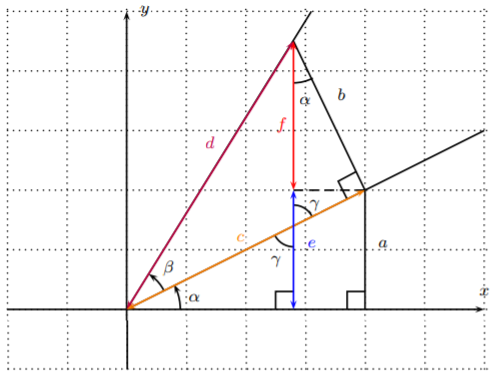
Tenga en cuenta, que hay ángulos verticalmente opuestos, etiquetados por\(\gamma\), que por lo tanto son iguales. Estos ángulos son ángulos en dos triángulos rectos, siendo el tercer ángulo\(\alpha\). Por lo tanto vemos que el ángulo\(\alpha\) aparece de nuevo como el ángulo entre los lados\(b\) y\(f\). Con esto, ya podemos calcular\(\sin(\alpha+\beta)\).

\[\begin{aligned} \sin(\alpha+\beta)&=\dfrac{\text{opposite}}{\text{hypotenuse}}=\dfrac{e+f}{d}=\dfrac{e}{d}+\dfrac{f}{d}=\dfrac{a}{d}+\dfrac{f}{d}=\dfrac{a}{c}\cdot \dfrac{c}{d}+\dfrac{f}{b}\cdot \dfrac{b}{d}\\ &=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta)\end{aligned} \nonumber \]

La figura anterior muestra la situación cuando\(\alpha+\beta\leq \dfrac \pi 2\). Hay una cifra similar para\(\dfrac \pi 2< \alpha+\beta<\pi\). (Recomendamos como ejercicio dibujar la figura correspondiente para el caso de\(\dfrac \pi 2< \alpha+\beta<\pi\).)

A continuación, demostramos la fórmula de adición para\(\cos(\alpha+\beta)\). La siguiente figura representa los objetos relevantes.

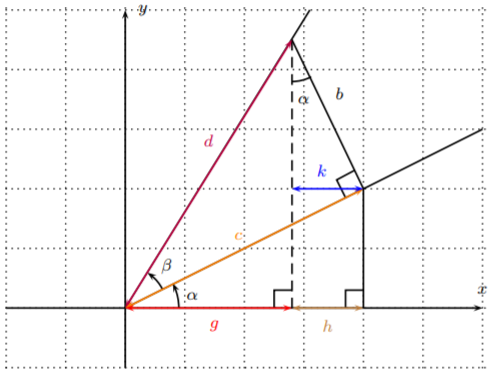
Calculamos de\(\cos(\alpha+\beta)\) la siguiente manera.

\[\begin{aligned} \cos(\alpha+\beta)&=\dfrac{\text{adjacent}}{\text{hypotenuse}}=\dfrac{g}{d}=\dfrac{g+h}{d}-\dfrac{h}{d}=\dfrac{g+h}{d}-\dfrac{k}{d}=\dfrac{g+h}{c}\cdot \dfrac{c}{d}-\dfrac{k}{b}\cdot \dfrac{b}{d}\\ &=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta)\end{aligned} \nonumber \]

Nuevamente, hay una cifra correspondiente cuando el ángulo\(\alpha+\beta\) es mayor que\(\dfrac \pi 2\). (Alentamos al estudiante a verificar la fórmula de adición para esta situación también).

Por lo tanto, hemos demostrado las fórmulas de adición para\(\sin(\alpha+\beta)\)\(\alpha\) y\(\cos(\alpha+\beta)\) cuándo y\(\beta\) son ángulos entre\(0\) y\(\dfrac \pi 2\), que ahora extenderemos a todos los ángulos\(\alpha\) y \(\beta\). Primero, tenga en cuenta que las fórmulas de adición son trivialmente ciertas cuando\(\alpha\) o\(\beta\) son\(0\). (¡Comprueba esto!) Ahora, al observar eso\(\sin(x)\) y se\(\cos(x)\) pueden convertir entre sí a través de los desplazamientos de\(\dfrac \pi 2\), (o, alternativamente, usando las identidades [equ:basic-TRIG-EQNS-WRT-PI] y [EQ:cos=SIN+pi2]), obtenemos, que

\[\begin{aligned} \sin\left (x+\dfrac \pi 2 \right)=\,\,\,\,\,\cos x, && \cos\left (x+\dfrac \pi 2 \right) = -\sin(x), \\ \sin\left (x-\dfrac \pi 2\right)=-\cos x, && \cos\left(x-\dfrac \pi 2 \right) = \,\,\,\,\,\sin(x). \end{aligned} \nonumber \]

Con esto, ampliamos las identidades de adición para\(\alpha\) por\(\pm \dfrac \pi 2\) lo siguiente:

\[\begin{aligned} \sin\left(\left(\alpha+\dfrac \pi 2\right)+\beta\right)&= \sin\left(\alpha+\beta+\dfrac \pi 2\right)=\cos(\alpha+\beta)=\cos(\alpha)\cos(\beta)-\sin(\alpha)\sin(\beta) \\ &= \sin\left(\alpha+\dfrac \pi 2\right)\cos(\beta)+\cos\left(\alpha+\dfrac \pi 2\right)\sin(\beta) \\ \sin\left(\left(\alpha-\dfrac \pi 2\right)+\beta\right)&= \sin\left(\alpha+\beta-\dfrac \pi 2\right)=-\cos(\alpha+\beta)=-\cos(\alpha)\cos(\beta)+\sin(\alpha)\sin(\beta) \\ &= \sin\left(\alpha-\dfrac \pi 2\right)\cos(\beta)+\cos\left(\alpha-\dfrac \pi 2\right)\sin(\beta) \\ \cos\left(\left(\alpha+\dfrac \pi 2\right)+\beta\right)&= \cos\left(\alpha+\beta+\dfrac \pi 2\right)=-\sin(\alpha+\beta)=-\sin(\alpha)\cos(\beta)-\cos(\alpha)\sin(\beta) \\ &= \cos\left(\alpha+\dfrac \pi 2\right)\cos(\beta)-\sin\left(\alpha+\dfrac \pi 2\right)\sin(\beta) \\ \cos\left(\left(\alpha-\dfrac \pi 2\right)+\beta\right)&= \cos\left(\alpha+\beta-\dfrac \pi 2\right)=\sin(\alpha+\beta)=\sin(\alpha)\cos(\beta)+\cos(\alpha)\sin(\beta) \\ &= \cos\left(\alpha-\dfrac \pi 2\right)\cos(\beta)-\sin\left(\alpha-\dfrac \pi 2\right)\sin(\beta)\end{aligned} \nonumber \]

Hay pruebas similares para extender las identidades\(\beta\). Un argumento de inducción muestra la validez de las fórmulas de adición para ángulos arbitrarios\(\alpha\) y\(\beta\).

Las fórmulas restantes siguen ahora a través del uso de identidades trigonométricas.

\[\tan(\alpha+\beta)=\dfrac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\dfrac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}=\dfrac{\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta}}{\frac{\cos\alpha\cos\beta-\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}=\dfrac{\frac{\sin\alpha}{\cos\alpha}+\frac{\sin\beta}{\cos\beta}}{1-\frac{\sin\alpha}{\cos\alpha}\frac{\sin\beta}{\cos\beta}} \nonumber \]

Esto demuestra que\(\tan(\alpha+\beta)=\dfrac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\). Para las relaciones con\(\alpha-\beta\), utilizamos el hecho de que\(\sin\) y\(\tan\) son funciones impares, mientras que\(\cos\) es una función par, ver identidades [EQ:sin-odd-cos-par] y [EQ:tan-Odd].

\[\begin{aligned} \sin(\alpha-\beta)&=\sin(\alpha+(-\beta))=\sin(\alpha)\cos(-\beta)+\cos(\alpha)\sin(-\beta) =\sin\alpha\cos\beta-\cos\alpha\sin\beta \\ \cos(\alpha-\beta)&=\cos(\alpha+(-\beta))=\cos(\alpha)\cos(-\beta)-\sin(\alpha)\sin(-\beta)= \cos\alpha\cos\beta+\sin\alpha\sin\beta \\ \tan(\alpha-\beta)&=\tan(\alpha+(-\beta))=\dfrac{\tan(\alpha)+\tan(-\beta)}{1-\tan(\alpha)\tan(-\beta)}=\dfrac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta} \end{aligned} \nonumber \]

Esto completa la prueba de la proposición.

Antes de dar ejemplos de la proposición anterior, recordamos los valores elementales de la función\(\sin\),\(\cos\), y\(\tan\) de la sección anterior:

\ [\ begin {array} {c||c|c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ pi} {2} =90^ {\ circ} &\ pi=180^ {\ circ}\\ hline
\ hline\ hline\ sin (x) & 0 &\ dfrac {1} {2} &\ dfrac {\ sqrt {2}} {2} & amp;\ dfrac {\ sqrt {3}} {2} & 1 & 0\
\ hline\ cos (x) & 1 &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2}} {2} &\ dfrac {1} {2} & 0 & -1
\\ hline\ tan (x) & 0 &\ dfrac {\ sqrt {3}} {3} & 1 &\ sqrt {3} &\ text {undef.} & 0
\ end { matriz}\ nonumber\]

Ejemplo\(\PageIndex{1}\)

Encuentra los valores exactos de las funciones trigonométricas.

1. \(\cos\left(\dfrac{\pi}{12}\right)\)
2. \(\tan\left(\dfrac{5\pi}{12}\right)\)
3. \(\cos\left(\dfrac{11\pi}{12}\right)\)

Solución

1. La clave es realizar el ángulo\(\dfrac{\pi}{12}\) como una suma o diferencia de ángulos con valores de función trigonométrica conocidos. Tenga en cuenta, eso\(\dfrac{\pi}{3}-\dfrac{\pi}{4}=\dfrac{4\pi-3\pi}{12}=\dfrac{\pi}{12}\), para que

\ [\ comenzar {alineado}
\ cos\ izquierda (\ dfrac {\ pi} {12}\ derecha) &=\ cos\ izquierda (\ dfrac {\ pi} {3} -\ dfrac {\ pi} {4}\ derecha)\\
&=\ cos\ dfrac {\ pi} {3}\ cos\ dfrac {\ pi} {4} +\ sin dfrac\ {\ pi} {3}\ sin\ dfrac {\ pi} {4}\\
&=\ dfrac {1} {2}\ cdot\ dfrac {\ sqrt {2}} {2} +\ dfrac {\ sqrt {3}} {2}\ cdot\ dfrac { \ sqrt {2}} {2}\\
&=\ dfrac {\ sqrt {2}} {4} +\ dfrac {\ sqrt {6}} {4}\\
&=\ dfrac {\ sqrt {2} +\ sqrt {6}} {4}
\ end {alineado}\ nonumber\]

Observamos que la última expresión está en la forma más simple y no se puede simplificar más.

2. Nuevamente podemos escribir el ángulo\(\dfrac{5\pi}{12}\) como una suma que involucra solo ángulos especiales dados en la tabla anterior:\(\dfrac{5\pi}{12}=\dfrac{2\pi}{12}+\dfrac{3\pi}{12}=\dfrac{\pi}{6}+\dfrac{\pi}{4}\). Por lo tanto,

\ [\ begin {alineado}
\ tan\ izquierda (\ dfrac {5\ pi} {12}\ derecha) &=\ tan\ izquierda (\ dfrac {\ pi} {6} +\ dfrac {\ pi} {4}\ derecha)\\
&=\ dfrac {\ tan\ frac {\ pi} {6} + tan\ frac {\ frac {\ pi} {4}} {1-\ tan\ frac {\ pi} {6}\ tan\ frac {\ pi} {4}}\\
&=\ dfrac {\ frac {\ frac {\ sqrt {3}} {3} +1} {1-\ frac {\ sqrt {3}} {3}\ cdot 1}\\
&=\ dfrac {\ frac {\ sqrt {3} +3} {3}} {\ frac {3-\ sqrt {3}} {3}}\\
&=\ dfrac {\ sqrt {3} +3} {3}\ cdot\ dfrac {3} {3-\ sqrt {3}}\\
&=\ dfrac {\ sqrt 3} +3} {3-\ sqrt {3}}\\
&\ aproximadamente 3.732
\ final {alineado}\ nonumber\]

Aquí, podemos simplificar aún más la última expresión racionalizando el denominador. Esto se hace multiplicando\((3+\sqrt{3})\) a numerador y denominador.

\ [\ begin {alineado}
\ tan\ izquierda (\ dfrac {5\ pi} {12}\ derecha) &=\ dfrac {(\ sqrt {3} +3)\ cdot (3+\ sqrt {3})} {(3-\ sqrt {3})\ cdot (3+\ sqrt {3})}\\
&=\ dfrac {3\ sqrt {3} +\ sqrt {3} ^2+9+3\ sqrt {3}} {3^2-\ sqrt {3} ^2}\\
&=\ dfrac {3+9+6\ sqrt {3}} {9-3}\\
&=\ dfrac {12+6 \ sqrt {3}} {6}\\
&= 2+\ sqrt {3}\\
&\ aproximadamente 3.732
\ final {alineado}\ nonumber\]

3. Nuevamente necesitamos escribir el ángulo\(\dfrac{11\pi}{12}\) como una suma o diferencia de los ángulos anteriores. De hecho, podemos hacerlo de al menos dos formas distintas:\(\dfrac{11\pi}{12}=\dfrac{6\pi}{12}+\dfrac{5\pi}{12}\) y también\(\dfrac{11\pi}{12}=\dfrac{12\pi}{12}-\dfrac{\pi}{12}=\pi-\dfrac{\pi}{12}\). En cualquier caso, primero necesitamos calcular algunas otras funciones trigonométricas, a saber, las de cualquiera\(\dfrac{5\pi}{12}\) o\(\dfrac{\pi}{12}\). Elegimos la segunda solución, y usando la parte (a), tenemos

\[\cos\left(\dfrac{\pi}{12}\right) = \dfrac{\sqrt{2}+\sqrt{6}}{4}\nonumber \]

y

\ [\ comenzar {alineado}
\ sin\ izquierda (\ dfrac {\ pi} {12}\ derecha) &=\ sin\ izquierda (\ dfrac {\ pi} {3} -\ dfrac {\ pi} {4}\ derecha)\\
&=\ sin\ dfrac {\ pi} {3}\ cos\ dfrac {\ pi} {4} -\ cos dfrac {\ pi} {\ pi} {3}\ sin\ dfrac {\ pi} {4}\\
&=\ dfrac {\ sqrt {3}} {2}\ cdot\ dfrac {\ sqrt {2}} {2} -\ dfrac {1} {2}\ cdot\ dfrac {\ sqrt {2}} {2}\\
&=\ dfrac {\ sqrt {6}} {4} -\ dfrac {\ sqrt {2}} {4}\\
&=\ dfrac {\ sqrt {6} -\ sqrt {2}} {4}
\ end {alineado}\ nonumber\]

Con esto, tenemos

\ [\ comenzar {alineado}
\ cos\ izquierda (\ dfrac {11\ pi} {12}\ derecha) &=\ cos\ izquierda (\ pi-\ dfrac {\ pi} {12}\ derecha)\\
&=\ cos\ pi\ cos\ dfrac {\ pi} {12} +\ sin\ pi\ sin\ dfrac {\ pi} {12}\
&= (-1)\ cdot\ dfrac {\ sqrt {2} +\ sqrt {6}} {4} +0\ cdot\ dfrac {\ sqrt {6} -\ sqrt {2}} {4}\\
&= \ dfrac {- (\ sqrt {2} +\ sqrt {6})} {4}\\
&\ aproximadamente 0.9569
\ final {alineado}\ nonumber\]

Generalizando el ejemplo anterior, podemos obtener cualquier múltiplo de\(\dfrac{\pi}{12}\) como suma o diferencia de ángulos conocidos provenientes de los\(45^\circ-45^\circ-90^\circ\) triángulos\(30^\circ-60^\circ-90^\circ\) y.

Nota

Partiendo de los ángulos\(\dfrac{\pi}{6}=\dfrac{2\pi}{12}\)\(\dfrac{\pi}{4}=\dfrac{3\pi}{12}\),\(\dfrac{\pi}{3}=\dfrac{4\pi}{12}\),\(\dfrac{\pi}{2}=\dfrac{6\pi}{12}\), y, obtenemos múltiplos del ángulo\(\dfrac{\pi}{12}\) por suma y resta, tales como:

\ [\ begin {alineado}
\ dfrac {\ pi} {12} &=\ dfrac {4\ pi} {12} -\ dfrac {3\ pi} {12},\
\ dfrac {5\ pi} {12} &=\ dfrac {2\ pi} {12} +\ dfrac {3\ pi} {12},\
\ dfrac {7\ pi} {12} &=\ dfrac {4\ pi} {12} +\ dfrac {3\ pi} {12},\
\ dfrac {8\ pi} {12} &=\ dfrac {4\ pi} {12} +\ dfrac {4\ pi} {12},\
\ dfrac {9\ pi} {12} &=\ dfrac {6\ pi} {12} +\ dfrac {3\ pi} {12},\
\ dfrac {10\ pi} {12} &=\ dfrac {6\ pi} {12} +\ dfrac {4\ pi} {12},\
\ dfrac {11\ pi} {12} &=\ dfrac {6\ pi} {12} +\ dfrac {5\ pi} {12} =\ dfrac {12\ pi} {12} -\ dfrac {\ pi} {12}
\ end {alineado}\ nonumber \]

Aquí, los valores de función trigonométrica de la última fracción se obtienen a partir de los valores trigonométricos previamente obtenidos, como en la parte (c) del ejemplo\(\PageIndex{1}\) anterior. Los múltiplos superiores de se\(\dfrac{\pi}{12}\) pueden obtener de la lista anterior agregando múltiplos de\(\pi\) a la misma. Obsérvese también que en muchos casos hay varias formas de escribir un ángulo como suma o diferencia. Por ejemplo:\(\dfrac{8\pi}{12}=\dfrac{4\pi}{12}+\dfrac{4\pi}{12}=\dfrac{6\pi}{12}+\dfrac{2\pi}{12}=\dfrac{12\pi}{12}-\dfrac{4\pi}{12}\)

Ejemplo\(\PageIndex{2}\)

Usando proposition [prop:TRIG-ADD-Subt-formulas] podemos probar otras identidades trigonométricas relacionadas con las fórmulas de suma y resta. Reescribimos\(\cos\left(x+\dfrac{\pi}{2}\right)\) usando la fórmula de resta.

Solución

\[\cos\left(x+\dfrac{\pi}{2}\right) = \cos x\cdot \cos\dfrac{\pi}{2}-\sin x\cdot \sin\dfrac{\pi}{2} = \cos x\cdot 0+\sin x\cdot 1=\sin(x) \nonumber \]