19.1: Las funciones de arcsin, arccos y arctan
- Page ID
- 117694
Las funciones trigonométricas inversas son las funciones inversas del\(y=\sin x\),\(y=\cos x\), y\(y=\tan x\) funciones restringidas a dominios apropiados. En esta sección damos una definición precisa de estas funciones.
La función de tangente inversa
Comenzamos con la función inversa a la tangente\(y=\tan(x)\). Recordemos que la gráfica de\(y=\tan(x)\) es la siguiente:
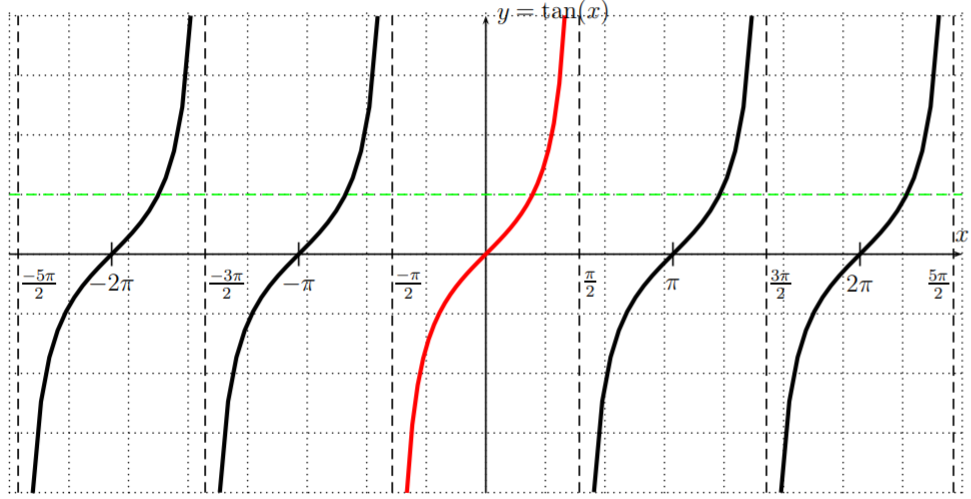
Tiene asíntotas verticales en\(x=\pm\dfrac{\pi}{2}, \pm\dfrac{3\pi}{2}, \pm\dfrac{5\pi}{2}, \dots\). Tenga en cuenta que esa no\(y=\tan(x)\) es una función uno a uno en el sentido de definición [DEF:1-to-1] en la página. (Por ejemplo, la línea horizontal\(y=1\) cruza la gráfica en\(x=\dfrac{\pi}{4}\),\(x=\dfrac{\pi}{4}\pm\pi\)\(x=\dfrac{\pi}{4}\pm2\pi\),, etc.) Sin embargo, cuando restringimos la función al dominio\(D=(\dfrac{-\pi}{2},\dfrac{\pi}{2})\) la función restringida es uno a uno, y, para esta función restringida, podemos tomar su función inversa.
La inversa de la función\(y=\tan(x)\) con dominio\(D=(\dfrac{-\pi}{2},\dfrac{\pi}{2})\) y rango restringidos\(R=\mathbb{R}\) se llama la función tangente inversa o arcotangente. Se denota por
\[y=\tan^{-1}(x) \quad \text{ or } \quad y= \arctan(x) \quad \iff \quad \tan(y)=x, \quad y\in\left(-\dfrac{\pi}2,\dfrac{\pi}{2}\right) \nonumber \]
El arcotangente invierte la entrada y salida de la función tangente, de modo que el arcotangente tiene dominio\(D=\mathbb{R}\) y rango\(R=\left(\dfrac{-\pi}{2},\dfrac{\pi}{2}\right)\). El gráfico se muestra a continuación.
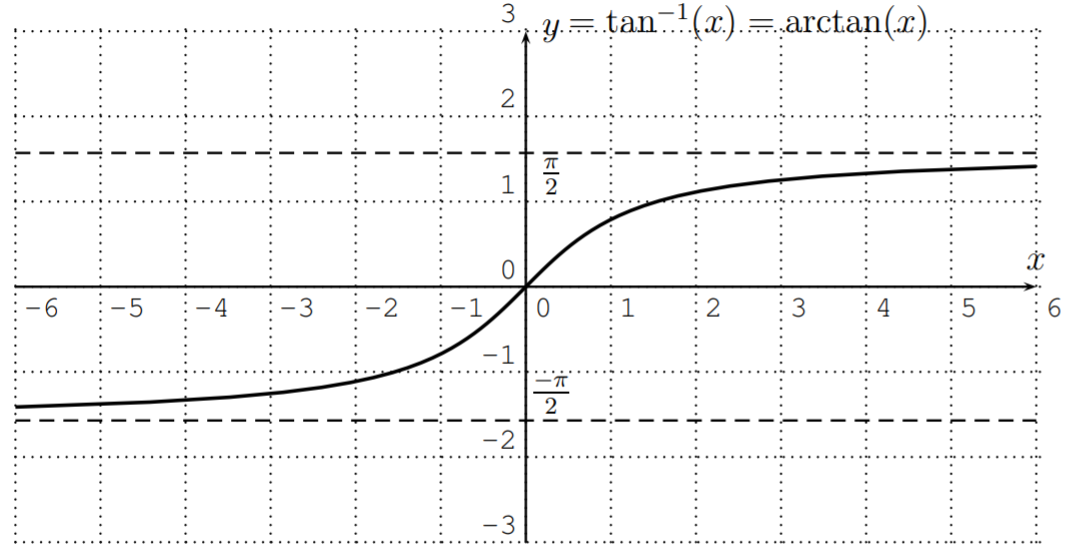
La notación de\(\tan^{-1}(x)\) y\(\tan^2(x)\) es ligeramente inconsistente, ya que el símbolo de exponenciación se usa arriba de dos maneras diferentes. De hecho,\(\tan^{-1}(x)=\arctan(x)\) se refiere a la función inversa de la\(\tan(x)\) función. Sin embargo, cuando escribimos\(\tan^2(x)\), nos referimos a
\[\tan^2(x)=(\tan(x))^2=\tan(x)\cdot \tan(x) \nonumber \]
Por lo tanto,\(\tan^{-1}(x)\) es la función inversa de\(\tan(x)\) respecto a la operación de composición, mientras que\(\tan^2(x)\) es el cuadrado con respecto al producto habitual en\(\mathbb{R}\). Obsérvese también que la función inversa de la tangente con respecto al producto en\(\mathbb{R}\) es\(y=\dfrac{1}{\tan(x)}=\cot(x)\), que es la cotangente.
La función tangente inversa es una función impar:
\[\label{EQU:tan-1(-x)} \boxed{\tan^{-1}(-x)=-\tan^{-1}(x)} \nonumber \]
Esto se puede observar observando que la tangente\(y=\tan(x)\) es una función impar (es decir\(\tan(-x)=-\tan(x)\)), o directamente desde la simetría de la gráfica con respecto al origen\((0,0)\).
El siguiente ejemplo calcula los valores de función de la función tangente inversa.
Recordemos los valores exactos de la función tangente de la sección 17.1:
\ [\ begin {array} {c||c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ pi} {2} =90^ {\ circ}\
\ hline\ hline\ tan (x) & 0 &\ dfrac {\ sqrt {3}} {3} & 1 &\ sqrt {3} &\ text {undef.}
\ end {array}\ nonumber\]
Solución
A partir de esto, podemos deducir valores de función invirtiendo entradas y salidas, tales como:
\[\begin{aligned} \tan\Big(\dfrac{\pi}{6}\Big)=\dfrac{\sqrt{3}}{3} &\implies & \tan^{-1}\Big(\dfrac{\sqrt{3}}{3} \Big)=\dfrac{\pi}{6} \\ \tan\Big(\dfrac{\pi}{4}\Big)=1 &\implies & \tan^{-1}\big(1 \big)=\dfrac{\pi}{4} \end{aligned} \nonumber \]
También, ya que\(\tan^{-1}(-x)=-\tan^{-1}(x)\), obtenemos la tangente inversa de números negativos.
\[\begin{aligned} \tan^{-1}(-\sqrt{3})&=&-\tan^{-1}(\sqrt{3})=-\dfrac{\pi}{3} \\ \tan^{-1}(-1)&=&-\tan^{-1}(1)=-\dfrac{\pi}{4} \end{aligned} \nonumber \]
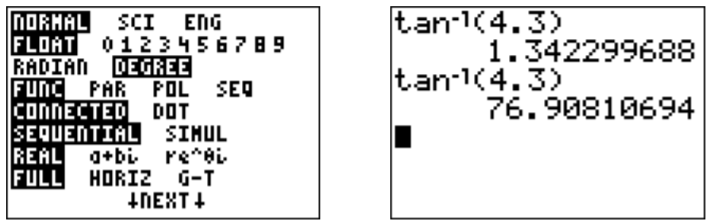
Podemos calcular la tangente inversa de valores específicos con la calculadora usando las\(\boxed {\text{tan}}\) claves\(\boxed {\text{2nd}}\) y. Por ejemplo,\(\tan^{-1}(4.3)\approx 1.34\).
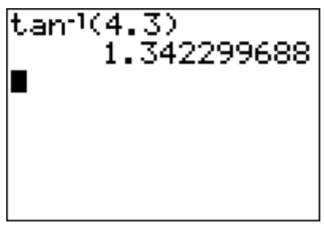
Tenga en cuenta, que la respuesta difiere, al cambiar el modo de radianes a grado, ya que\(\tan^{-1}(4.3) \approx 76.9^\circ \approx 1.34\).
La función\(y=\sin^{-1}(x)\)
A continuación, definimos la función sinusoidal inversa. Para ello, nuevamente recordamos primero la gráfica de la\(y=\sin(x)\) función, y notamos que tampoco es uno a uno.
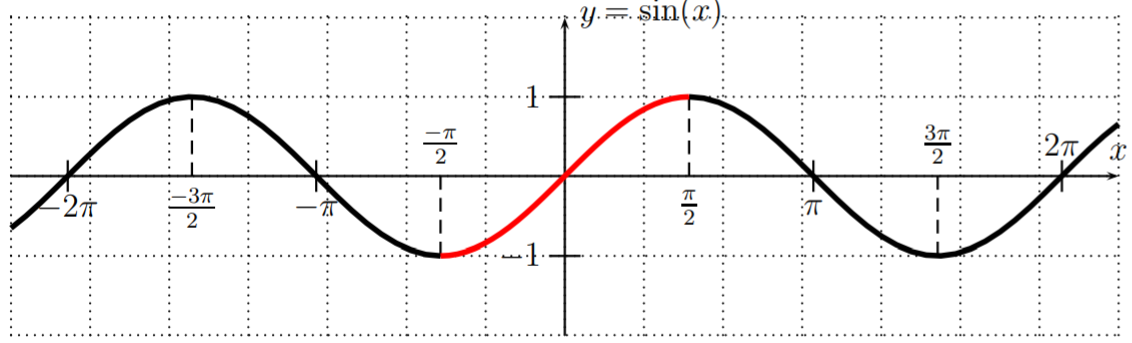
Sin embargo, cuando se restringe el seno al dominio\(\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\), la función restringida es uno a uno. Tenga en cuenta además, que al restringir el dominio a\(\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\), el rango es\([-1,1]\), y por lo tanto no podemos extender esto a un dominio más grande de una manera tal que la función siga siendo una función uno a uno. Utilizamos el dominio\(\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\) para definir la función sinusoidal inversa.
La inversa de la función\(y=\sin(x)\) con dominio\(D=\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\) y rango restringidos\(R=[-1,1]\) se llama la función sinusoidal inversa o arcoseno. Se denota por
\[y=\sin^{-1}(x) \quad \text{ or } \quad y= \arcsin(x) \quad \iff \quad \sin(y)=x, \quad y\in\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right] \nonumber \]
El arcoseno invierte la entrada y salida de la función sinusoidal, de modo que el arcoseno tiene dominio\(D=[-1,1]\) y rango\(R=\left[\dfrac{-\pi}{2},\dfrac{\pi}{2}\right]\). A continuación se dibuja la gráfica del arcoseno.
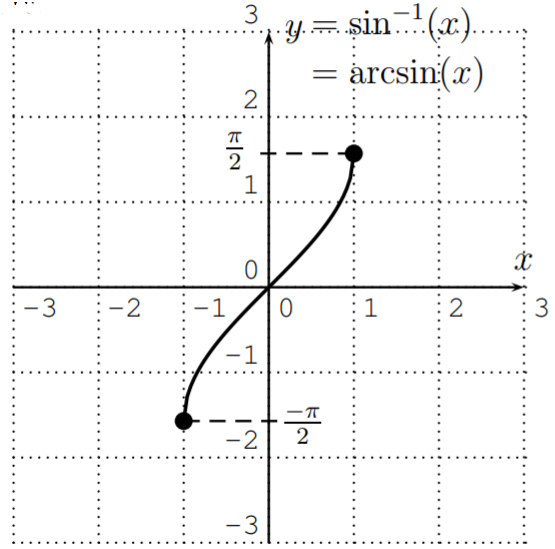
La función sinusoidal inversa es impar:
\[\label{EQU:sin-1(-x)} \boxed{\sin^{-1}(-x)=-\sin^{-1}(x)} \nonumber \]
Esto se puede ver nuevamente observando que el seno\(y=\sin(x)\) es una función impar (es decir\(\sin(-x)=-\sin(x)\)), o alternativamente directamente desde la simetría de la gráfica con respecto al origen\((0,0)\).
Ahora calculamos valores de función específicos del seno inverso.
Primero recordamos los valores conocidos del seno.
\ [\ begin {array} {c||c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ pi} {2} =90^ {\ circ}\\ hline
\ hline\ hline\ sin (x) & 0 &\ dfrac {1} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {\ sqrt {3}} {2} & amp; 1
\ end {array}\ nonumber\]
Solución
Estos valores junto con el hecho de que el seno inverso es impar, es decir\(\sin^{-1}(-x)=-\sin^{-1}(x)\), nos proporciona ejemplos de sus valores de función.
\[\begin{aligned} \sin^{-1}\Big(\dfrac{\sqrt{2}}{2}\Big) &= \dfrac{\pi}{4}\\\sin^{-1}(1) &=\dfrac{\pi}{2}\\ \sin^{-1}(0) &= 0\\\sin^{-1}\Big(\dfrac{-1}{2}\Big) &=-\sin^{-1}\Big(\dfrac{1}{2}\Big)=-\dfrac{\pi}{6}\end{aligned} \nonumber \]
Tenga en cuenta que el dominio de\(y=\sin^{-1}(x)\) es\(D=[-1,1]\), de manera que los números de entrada que no están en este intervalo dan salidas indefinidas del seno inverso:
\[\sin^{-1}(3) \text{ is undefined} \nonumber \]
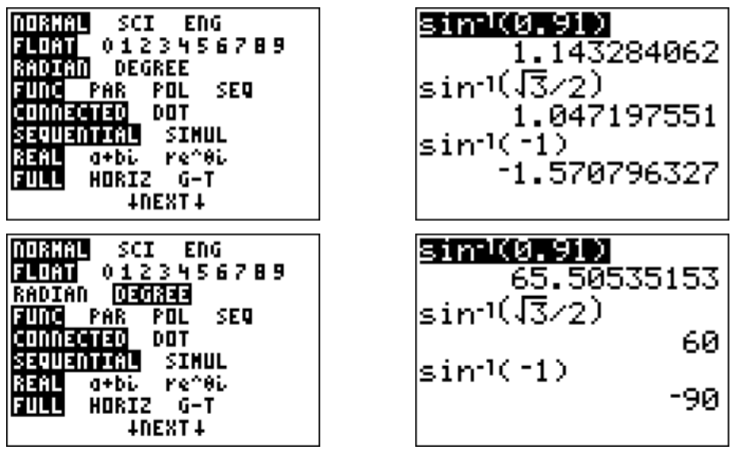
Los valores de entrada que no están en la tabla anterior se pueden encontrar con la calculadora a través de las\(\boxed {\text{2nd}}\)\(\boxed {\text{sin}}\) teclas. Señalamos, que los valores de salida dependen de si la calculadora está establecida en modo radián o grado. (Recordemos que el\(\boxed {\text{mode}}\) puede ser cambiado a través de la clave).
La función\(y=\cos^{-1}(x)\)
Finalmente, definimos el coseno inverso. Recordemos la gráfica de\(y=\cos(x)\), y anote nuevamente que la función no es uno-a-uno.
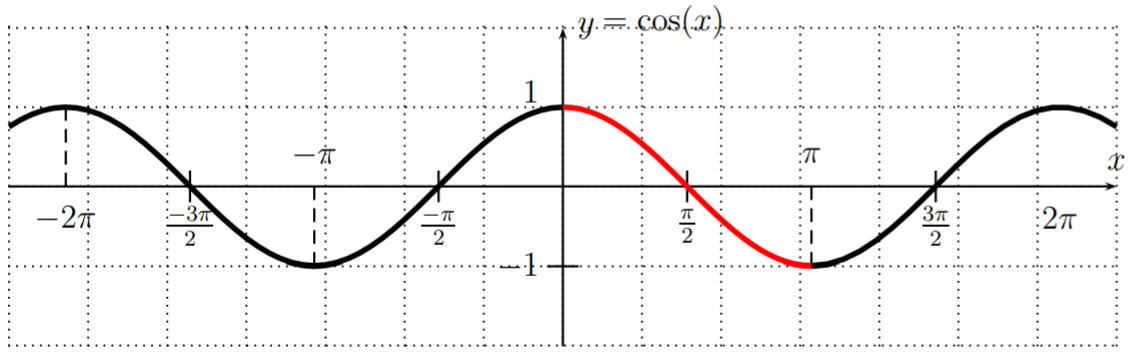
En este caso, la forma de restringir el coseno a una función uno a uno no es tan clara como en los casos anteriores para el seno y la tangente. Por convención, el coseno está restringido al dominio\([0,\pi]\). Esto proporciona una función que es uno a uno, que se utiliza para definir el coseno inverso.
La inversa de la función\(y=\cos(x)\) con dominio\(D=[0,\pi]\) y rango restringidos\(R=[-1,1]\) se llama la función coseno inversa o arcoseno. Se denota por
\[y=\cos^{-1}(x) \quad \text{ or } \quad y= \arccos(x) \quad \iff \quad \cos(y)=x,\quad y\in [0,\pi] \nonumber \]
El arccosino invierte la entrada y salida de la función coseno, de modo que el arccosino tiene dominio\(D=[-1,1]\) y rango\(R=[0,\pi]\). A continuación se dibuja la gráfica del arcoseno.
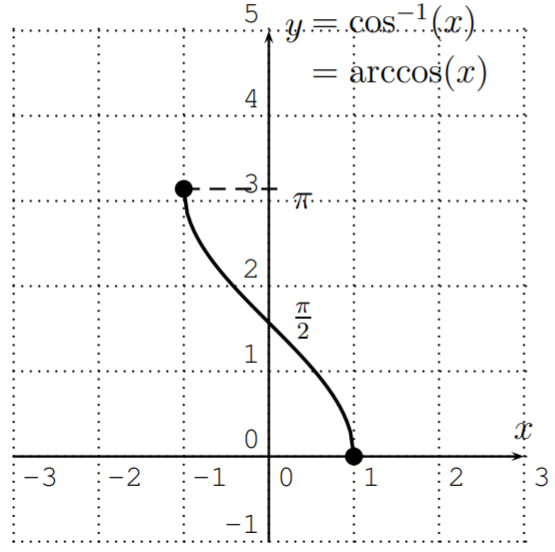
La función coseno inversa no es ni par ni impar. Es decir, la función\(\cos^{-1}(-x)\) no se puede computar simplemente tomando\(\pm\cos^{-1}(x)\). Pero sí tiene cierta simetría dada algebraicamente por la relación más complicada
\[\label{EQU:cos-1(-x)} \boxed{\cos^{-1}(-x)=\pi-\cos^{-1}(x)} \nonumber \]
- Prueba
-
Podemos ver que si desplazamos la gráfica hacia abajo por\(\dfrac{\pi}{2}\) la función resultante es impar. Es decir, la función con la regla\(\cos^{-1}(x)-\dfrac{\pi}{2}\) es impar:
\[\cos^{-1}(-x)-\dfrac{\pi}{2}=-(\cos^{-1}(x)-\dfrac{\pi}{2}) \nonumber\]
que rinde\(\ref{EQU:cos-1(-x)}\) al distribuir y agregar\(\dfrac{\pi}{2}\).
Otro enfoque más formal es el siguiente. La relación inferior derecha de [equ:basic-TRIG-EQNS-WRT-PI] en la página afirma, que tenemos la relación\(\cos(\pi-y)=-\cos(y)\) para todos\(y\). Dejar\(-1\leq x\leq 1\), y denotar por\(y=\cos^{-1}(x)\). Ese\(y\) es el número\(0\leq y\leq \pi\) con\(\cos(y)=x\). Entonces tenemos
\(-x=-\cos(y)=\cos(\pi-y) \)(por la ecuación 17.1.2)
Aplicar\(\cos^{-1}\) a ambos lados da:
\[\cos^{-1}(-x)=\cos^{-1}(\cos(\pi-y))=\pi-y \nonumber \]
Sigue la última igualdad, ya que\(\cos\) y\(\cos^{-1}\) son inversas entre sí, y\(0\leq y\leq \pi\), por lo que también\(0\leq \pi-y\leq \pi\) están en el rango de la\(\cos^{-1}\). La reescritura\(y=\cos^{-1}(x)\) da el resultado deseado:
\[\cos^{-1}(-x)=\pi-\cos^{-1}(x) \nonumber \]
Esta es la ecuación\(\ref{EQU:cos-1(-x)}\) que queríamos probar.
Ahora calculamos valores de función específicos del coseno inverso.
Primero recordamos los valores conocidos del coseno.
\ [\ begin {array} {c||c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ pi} {2} =90^ {\ circ}\
\ hline\ hline\ cos (x) & 1 &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {1} {2} & amp; 0
\ end {array}\ nonumber\]
Solución
Aquí hay algunos ejemplos de valores de función del coseno inverso.
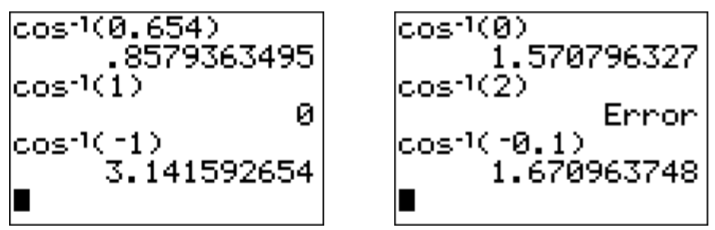
\[\cos^{-1}\Big(\dfrac{\sqrt{3}}{2}\Big)=\dfrac{\pi}{6}, \quad\quad \cos^{-1}(1)=0,\quad\quad \cos^{-1}(0) =\dfrac{\pi}{2} \nonumber \]
Las entradas negativas al arcoseno se pueden calcular con la ecuación\(\ref{EQU:cos-1(-x)}\), es decir\(\cos^{-1}(-x)=\pi-\cos^{-1}(x)\), o volviendo a la definición del círculo unitario.
\[\begin{aligned} \cos^{-1}\Big(-\dfrac{1}{2}\Big)&=\pi-\cos^{-1}\Big(\dfrac{1}{2}\Big)=\pi-\dfrac{\pi}{3}=\dfrac{3\pi-\pi}{3}=\dfrac{2\pi}{3}\\ \cos^{-1}(-1)&=\pi-\cos^{-1}(1)=\pi-0=\pi\end{aligned} \nonumber \]
Además, el dominio de\(y=\cos^{-1}(x)\) es\(D=[-1,1]\), de manera que los números de entrada que no están en este intervalo dan salidas indefinidas del coseno inverso.
\[\cos^{-1}(17) \text{ is undefined} \nonumber \]
Otros valores de entrada se pueden obtener con la calculadora presionando las\(\boxed {\text{2nd}}\)\(\boxed {\text{cos}}\) teclas. Por ejemplo, obtenemos los siguientes valores de función (aquí usando la medida de radianes).