21.1: Forma polar de números complejos
- Page ID
- 117747
Ahora recordamos la definición de números complejos y mostramos cómo se representan en el plano complejo.
Definimos la unidad imaginaria o unidad compleja para ser
\[\label{DEF:imaginary-unit} \text{imaginary unit: } \boxed{i=\sqrt{-1}} \nonumber \]
En otras palabras,\(i\) es una solución de la ecuación:
\[\boxed{i^2=-1} \nonumber \]
Un número complejo es un número de la forma\(a+b\cdot i\). (Alternativamente también escribimos esto como\(a+bi\) sin el punto para la multiplicación.) Aquí\(a\) y\(b\) están los números reales. El número\(a\) se llama la parte real de\(a+b\cdot i\), y\(b\) se llama la parte imaginaria de\(a+b\cdot i\). El conjunto de todos los números complejos se denota por\(\mathbb{C}\).
Aquí hay algunos ejemplos de números complejos:
\[3+2i, \quad 1-1\cdot i, \quad \sqrt{2}+\pi \cdot i, \quad 5+0\cdot i, \quad 0+3\cdot i \nonumber \]
Tenga en cuenta que en los dos últimos ejemplos\(5+0\cdot i=5\), tenemos, para que veamos que el número real también\(5\) es un número complejo. En efecto, cualquier número real también\(a=a+0\cdot i\) es un número complejo. Del mismo modo, así\(0+3\cdot i=3i\) como cualquier múltiplo de también\(i\) es un número complejo (a estos números se les suele llamar números imaginarios puros).
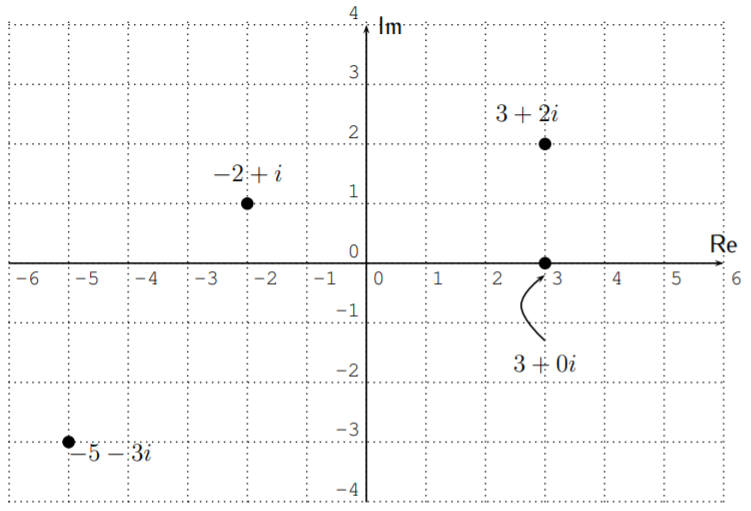
En analogía con la sección 1.1, donde representamos los números reales en la recta numérica, podemos representar los números complejos en el plano complejo:
El número complejo\(a+bi\) se representa como el punto con coordenadas\((a,b)\) en el plano complejo.
Realizar la operación.
- \((2-3i)+(-6+4i)\)
- \((3+5i)\cdot (-7+i)\)
- \(\dfrac{5+4i}{3+2i}\)
Solución
- Agregar partes reales e imaginarias, respectivamente, da,
\[(2-3i)+(-6+4i) = 2-3i-6+4i = -4+i \nonumber \]
- Multiplicamos (usando FOIL), y usamos eso\(i^2=-1\).
\[\begin{aligned} (3+5i)\cdot (-7+i) &=-21+3i-35i+5i^2\\&=-21-32i+5\cdot(-1)\\ &=-21-32i-5\\&=-26-32i\end{aligned} \nonumber \]
- Recordemos que podemos simplificar un cociente de números complejos multiplicando el numerador y el denominador por el conjugado del denominador.
\[\begin{aligned} \dfrac{5+4i}{3+2i} &= \dfrac{(5+4i)\cdot (3-2i)}{(3+2i)\cdot (3-2i)}\\& =\dfrac{15-10i+12i-8i^2}{9-6i+6i-4i^2}\\ &= \dfrac{15+2i+8}{9+4}\\&=\dfrac{23+2i}{13}\\&=\dfrac{23}{13}+\dfrac{2}{13}i\end{aligned} \nonumber \]
La parte real de la solución es\(\dfrac{23}{13}\); lo es la parte imaginaria\(\dfrac{2}{13}\).
También existe una noción de valor absoluto\(|a+bi|\) para cualquier número complejo\(a+bi\).
Dejar\(a+bi\) ser un número complejo. El valor absoluto de\(a+bi\), denotado por\(|a+bi|\) es la longitud entre el punto\(a+bi\) en el plano complejo y el origen\((0,0)\).
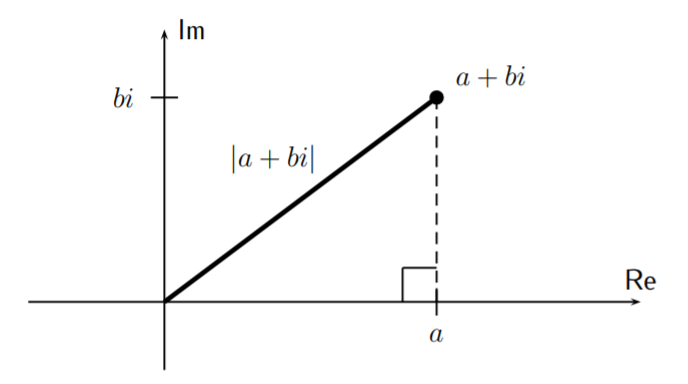
Usando el teorema de Pitágoras, podemos calcular\(|a+bi|\) como
\[|a+bi|^2=a^2+b^2 \nonumber \]
para que
\[\boxed{ |a+bi|= \sqrt{a^2+b^2} } \nonumber \]
Encuentre el valor absoluto de los números complejos a continuación.
- \(5-3i\)
- \(-8+6i\)
- \(7i\)
Solución
Los valores absolutos se calculan de la siguiente manera.
- \(|5-3 i|=\sqrt{5^{2}+(-3)^{2}}=\sqrt{25+9}=\sqrt{34}\)
- \(|-8+6 i|=\sqrt{(-8)^{2}+6^{2}}=\sqrt{64+36}=\sqrt{100}=10\)
- \(|7 i|=\sqrt{0^{2}+(7)^{2}}=\sqrt{0+49}=7\)
Podemos escribir un número complejo en la forma\(a+bi\), o alternativamente, podemos usar el valor absoluto y “ángulo” para escribir el número en la llamada forma polar, que discutimos ahora.
Dejar\(a+bi\) ser un número complejo. Las coordenadas en el plano se pueden expresar en términos del valor absoluto\(r=|a+bi|\) y el ángulo\(\theta\) con el eje real como se muestra a continuación.
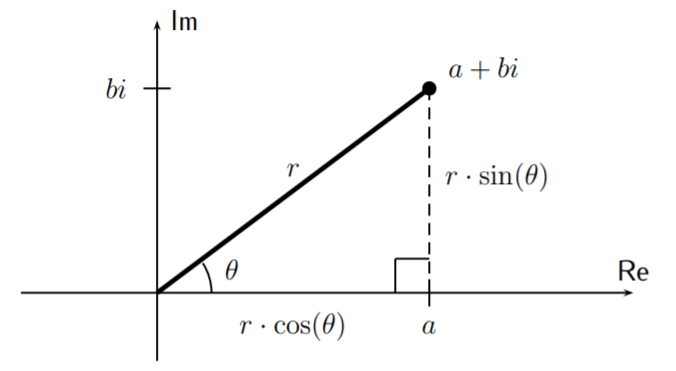
Desde el triángulo rectángulo como se muestra en el plano complejo anterior, vemos que las coordenadas\(a\) y\(b\) en el plano están dadas por:
\[\label{EQU:a-and-b-in-complex-number} a=r\cdot \cos(\theta)\quad\text{ and }\quad b=r\cdot \sin(\theta) \]
Por lo tanto, el número complejo es\(a+bi = r\cdot \cos(\theta) + r\cdot \sin(\theta)\cdot i\), o factorizando\(r\) a partir de esta expresión:
\[\boxed{a+bi = r\cdot \big(\cos(\theta)+i\cdot \sin(\theta)\big)} \]
Escribir el número complejo de esta manera se llama la forma polar del número complejo. Aquí, el número\(r\) es el valor absoluto, y\(\theta\) viene dado por\(\ref{EQU:a-and-b-in-complex-number}\) vía del cálculo\(\dfrac{b}{a}=\dfrac{r\cdot \sin(\theta)}{r\cdot \cos(\theta)}=\dfrac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)\). Por lo tanto,
\[\label{EQU:r-and-theta} \boxed{r=\sqrt{a^2+b^2}} \quad\text{ and }\quad \boxed{\tan(\theta)=\dfrac{b}{a}}\]
Al encontrar el ángulo direccional\(\theta\) de un número complejo vía ecuación\(\ref{EQU:r-and-theta}\), tenemos que recordar que se\(\tan(\theta)\) puede obtener por los dos ángulos\(\theta\) y\(\pi+\theta\); es decir, tenemos
\[\tan(\pi+\theta)=\tan(\theta) \nonumber \]
Por lo tanto, tenemos que verificar que nuestra respuesta para\(\theta\) yace en el cuadrante correcto. Esto se muestra en el siguiente ejemplo.
Convertir el número complejo a forma polar.
- \(2+3i\)
- \(-2-2\sqrt{3}i\)
- \(4-3i\)
- \(-4i\)
Solución
- Primero, el valor absoluto es\(r=|2+3i|=\sqrt{2^2+3^2}=\sqrt{13}\). Además, desde\(a=2\) y\(b=3\), tenemos\(\tan(\theta)=\dfrac{3}{2}\). Para obtener\(\theta\), calculamos
\[\tan^{-1}\Big(\dfrac{3}{2}\Big)\approx 56.3^\circ \nonumber \]
Tenga en cuenta que\(56.3^\circ\) está en el primer cuadrante, y también lo está el número complejo\(2+3i\)
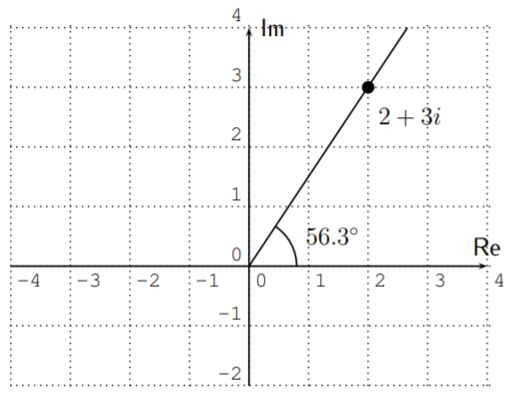
Por lo tanto\(\theta\approx 56.3^\circ\),, y obtenemos nuestra respuesta:
\[2+3i\approx \sqrt{13}\cdot \left(\cos(56.3^\circ)+i\sin(56.3^\circ)\right) \nonumber \]
- Para\(-2-2\sqrt{3}i\), primero calculamos el valor absoluto:
\[r=\sqrt{(-2)^2+(-2\sqrt{3})^2}=\sqrt{4+4\cdot 3}=\sqrt{4+12}=\sqrt{16}=4 \nonumber \]
Además,\(\tan(\theta)=\dfrac{b}{a}=\dfrac{-2\sqrt{3}}{-2}=\sqrt{3}\). Ahora,\(\tan^{-1}(\sqrt{3})=60^\circ=\dfrac{\pi}{3}\). Sin embargo, graficando el ángulo\(\dfrac{\pi}{3}=60^\circ\) y el número\(-2-2\sqrt{3}i\), vemos que\(60^\circ\) está en el primer cuadrante, mientras que\(-2-2\sqrt{3}i\) está en el tercer cuadrante.
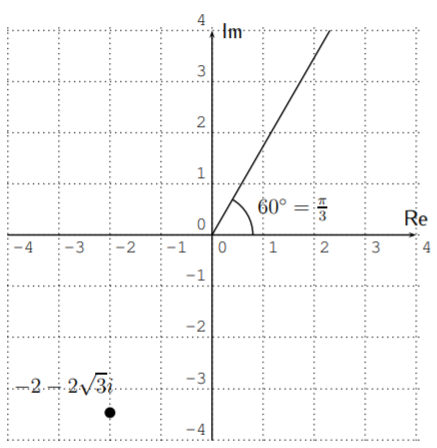
Por lo tanto, tenemos que\(\pi\) sumar\(\dfrac \pi 3\) a para obtener el ángulo correcto para\(-2-2\sqrt{3} i\), es decir\(\theta=\dfrac{\pi}{3}+\pi=\dfrac{\pi+3\pi}{3}=\dfrac{4\pi}{3}\). Nuestro número complejo en forma polar es
\[-2-2\sqrt{3}i = 4\cdot \left(\cos\left(\dfrac{4\pi}{3}\right)+i\sin\left(\dfrac{4\pi}{3}\right)\right) \nonumber \]
- Para\(4-3i\) calculamos\(r=\sqrt{4^2+(-3)^2}=\sqrt{16+9}=\sqrt{25}=5\). El ángulo\(\tan^{-1}\left(\dfrac{-3}{4}\right)\approx -36.9^\circ\), que está en el cuarto cuadrante, igual que el número\(4-3i\).
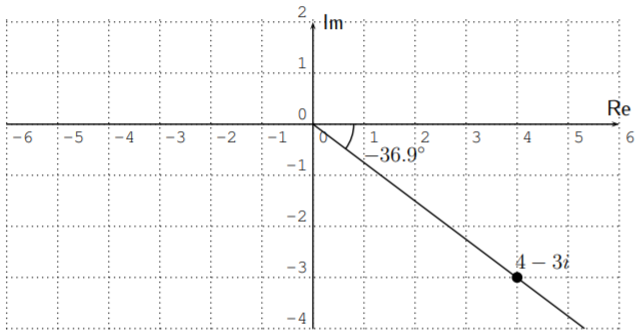
Por lo tanto\(\theta\approx-36.9^\circ\),, y escribimos
\[4-3i\approx 5\cdot (\cos(-36.9^\circ)+i\sin(-36.9^\circ)) \nonumber \]
- Calculamos el valor absoluto de\(0-4i\) as\(r=\sqrt{0^2+(-4)^2}=\sqrt{16}=4\). No obstante, a la hora de calcular el ángulo\(\theta\) de\(0-4i\), nos llevan a considerar\(\tan^{-1}\left(\dfrac{-4}{0}\right)\), ¡lo cual no está definido! La razón de esto se puede ver trazando el número\(-4i\) en el plano complejo.
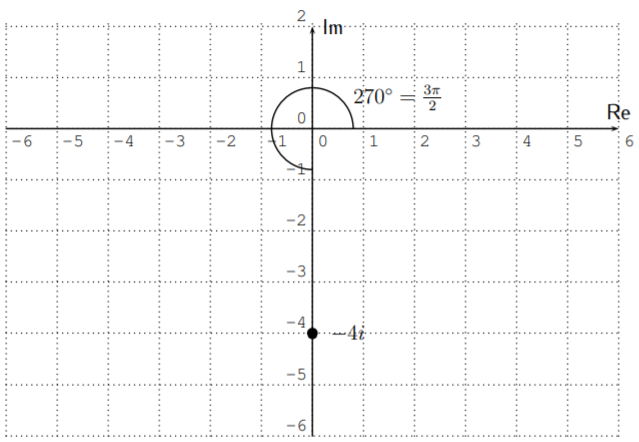
El ángulo\(\theta=270^\circ\) (o alternativamente\(\theta=-90^\circ\)), de modo que el número complejo es
\[\begin{aligned} -4i &= 4\cdot (\cos(270^\circ)+i\sin(270^\circ)) \\ &= 4\cdot \left(\cos\left(\dfrac{3\pi}{2}\right)+i\sin\left(\dfrac{3\pi}{2}\right)\right) \end{aligned} \nonumber \]
Tenga en cuenta que podemos escribir nuestra respuesta ya sea en grado o modo radián como lo hicimos anteriormente.
También podemos realizar la conversión inversa de un número complejo de forma polar a “forma estándar”\(a+bi\).
Convierte el número de forma polar a la forma estándar\(a+bi\).
- \(3\cdot (\cos(117^\circ)+i\sin(117^\circ))\)
- \(4\cdot \left(\cos\left(\dfrac{5\pi}{4}\right)+i\sin\left(\dfrac{5\pi}{4}\right)\right)\)
Solución
- Como no tenemos una fórmula exacta para\(\cos(117^\circ)\) o\(\sin(117^\circ)\), utilizamos la calculadora para obtener valores aproximados.
\[3\cdot (\cos(117^\circ)+i\sin(117^\circ))\approx 3\cdot (-0.454+i \cdot 0.891)=-1.362+2.673 i \nonumber \]
- Recordamos eso\(\cos\left(\dfrac{5\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\) y\(\sin\left(\dfrac{5\pi}{4}\right)=-\dfrac{\sqrt{2}}{2}\). (Esto se puede ver como en el Ejemplo 17.1.2 considerando el punto\(P(-1,-1)\) en el lado terminal del ángulo\(\dfrac{5\pi}{4}=\dfrac{5\cdot 180^\circ}{4}=225^\circ\).
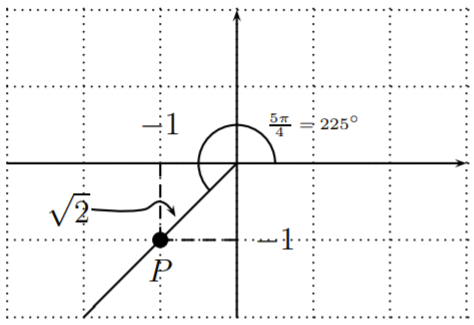
Por lo tanto,\(\cos\left(\dfrac{5\pi}{4}\right)=\dfrac{-1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\) y\(\sin\left(\dfrac{5\pi}{4}\right)=\dfrac{-1}{\sqrt{2}}=-\dfrac{\sqrt{2}}{2}\).
Con esto, obtenemos el número complejo en forma estándar.
\[\begin{aligned} 4\cdot \left(\cos\left(\dfrac{5\pi}{4}\right)+i\sin\left(\dfrac{5\pi}{4}\right)\right) &= 4\cdot \left(-\dfrac{\sqrt{2}}{2}-i\dfrac{\sqrt{2}}{2}\right)\\ &= -4\dfrac{\sqrt{2}}{2}-i\cdot 4\dfrac{\sqrt{2}}{2}\\&=-2\sqrt{2}-2\sqrt{2}\cdot i\end{aligned} \nonumber\]


