27.4: Revisión de funciones trigonométricas

Última actualización
Guardar como PDF

Page ID: 117667

Thomas Tradler and Holly Carley
CUNY New York City College of Technology via New York City College of Technology at CUNY Academic Works

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$ \newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$

( \newcommand{\kernel}{\mathrm{null}\,}\) $ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\id}{\mathrm{id}}$

$ \newcommand{\Span}{\mathrm{span}}$

$ \newcommand{\kernel}{\mathrm{null}\,}$

$ \newcommand{\range}{\mathrm{range}\,}$

$ \newcommand{\RealPart}{\mathrm{Re}}$

$ \newcommand{\ImaginaryPart}{\mathrm{Im}}$

$ \newcommand{\Argument}{\mathrm{Arg}}$

$ \newcommand{\norm}[1]{\| #1 \|}$

$ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$

$ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\AA}{\unicode[.8,0]{x212B}}$

$ \newcommand{\vectorA}[1]{\vec{#1}} % arrow$

$ \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow$

$ \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vectorC}[1]{\textbf{#1}} $

$ \newcommand{\vectorD}[1]{\overrightarrow{#1}} $

$ \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} $

$ \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} $

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $

$ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $

$\newcommand{\avec}{\mathbf a}$ $\newcommand{\bvec}{\mathbf b}$ $\newcommand{\cvec}{\mathbf c}$ $\newcommand{\dvec}{\mathbf d}$ $\newcommand{\dtil}{\widetilde{\mathbf d}}$ $\newcommand{\evec}{\mathbf e}$ $\newcommand{\fvec}{\mathbf f}$ $\newcommand{\nvec}{\mathbf n}$ $\newcommand{\pvec}{\mathbf p}$ $\newcommand{\qvec}{\mathbf q}$ $\newcommand{\svec}{\mathbf s}$ $\newcommand{\tvec}{\mathbf t}$ $\newcommand{\uvec}{\mathbf u}$ $\newcommand{\vvec}{\mathbf v}$ $\newcommand{\wvec}{\mathbf w}$ $\newcommand{\xvec}{\mathbf x}$ $\newcommand{\yvec}{\mathbf y}$ $\newcommand{\zvec}{\mathbf z}$ $\newcommand{\rvec}{\mathbf r}$ $\newcommand{\mvec}{\mathbf m}$ $\newcommand{\zerovec}{\mathbf 0}$ $\newcommand{\onevec}{\mathbf 1}$ $\newcommand{\real}{\mathbb R}$ $\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}$ $\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}$ $\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}$ $\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}$ $\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}$ $\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}$ $\newcommand{\laspan}[1]{\text{Span}\{#1\}}$ $\newcommand{\bcal}{\cal B}$ $\newcommand{\ccal}{\cal C}$ $\newcommand{\scal}{\cal S}$ $\newcommand{\wcal}{\cal W}$ $\newcommand{\ecal}{\cal E}$ $\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}$ $\newcommand{\gray}[1]{\color{gray}{#1}}$ $\newcommand{\lgray}[1]{\color{lightgray}{#1}}$ $\newcommand{\rank}{\operatorname{rank}}$ $\newcommand{\row}{\text{Row}}$ $\newcommand{\col}{\text{Col}}$ $\renewcommand{\row}{\text{Row}}$ $\newcommand{\nul}{\text{Nul}}$ $\newcommand{\var}{\text{Var}}$ $\newcommand{\corr}{\text{corr}}$ $\newcommand{\len}[1]{\left|#1\right|}$ $\newcommand{\bbar}{\overline{\bvec}}$ $\newcommand{\bhat}{\widehat{\bvec}}$ $\newcommand{\bperp}{\bvec^\perp}$ $\newcommand{\xhat}{\widehat{\xvec}}$ $\newcommand{\vhat}{\widehat{\vvec}}$ $\newcommand{\uhat}{\widehat{\uvec}}$ $\newcommand{\what}{\widehat{\wvec}}$ $\newcommand{\Sighat}{\widehat{\Sigma}}$ $\newcommand{\lt}{<}$ $\newcommand{\gt}{>}$ $\newcommand{\amp}{&}$ $\definecolor{fillinmathshade}{gray}{0.9}$

Ejercicio$\PageIndex{1}$

Rellene todos los valores de las funciones trigonométricas en la siguiente tabla.

\ [\ begin {array} {c||c|c|c|c|c}
& 0 &\ dfrac {\ pi} {6} &\ dfrac {\ pi} {4} &\ dfrac {\ pi} {3} &\ dfrac {\ pi} {2}\
\ hline\ hline\ hline\ sin (x) & & & &
\\ hline\ cos (x) & & & & &\
\ hline\ tan (x) & & amp; & & &
\ end {array}\ nonumber\]

Contestar: \ (\ begin {array} {c||c|c|c|c|c}
x & 0=0^ {\ circ} &\ dfrac {\ pi} {6} =30^ {\ circ} &\ dfrac {\ pi} {4} =45^ {\ circ} &\ dfrac {\ pi} {3} =60^ {\ circ} &\ dfrac {\ pi} {2} =90^ {\ circ}\\ hline
\ hline\ hline\ sin (x) & 0 &\ dfrac {1} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {\ sqrt { 3}} {2} & 1\
\ hline\ cos (x) & 1 &\ dfrac {\ sqrt {3}} {2} &\ dfrac {\ sqrt {2}} {2} &\ dfrac {1} {2} & 0\
\ hline\ tan (x) & 0 &\ dfrac {\ sqrt {3}} {3} & 1 &\ sqrt {3} &\ text {undef.}
\ end {array}\)

Ejercicio$\PageIndex{2}$

Encuentra los valores exactos de

$\cos\left(-\dfrac{\pi}{6}\right)$
$\sin\left(-\dfrac{\pi}{4}\right)$
$\tan\left(-\dfrac{\pi}{3}\right)$

Contestar

$\dfrac{\sqrt{3}}{2}$
$\dfrac{-\sqrt{2}}{2}$
$-\sqrt{3}$

Ejercicio$\PageIndex{3}$

Encuentra el valor exacto de la función trigonométrica.

$\sin\left(\dfrac{5\pi}{4}\right)$
$\cos\left(\dfrac{11\pi}{6}\right)$

[Pista: Usa el especial$45^\circ-45^\circ-90^\circ$ o$30^\circ-60^\circ-90^\circ$ triángulos para encontrar la solución.]

Contestar

$\dfrac{-\sqrt{2}}{2}$
$\dfrac{\sqrt{3}}{2}$

Ejercicio$\PageIndex{4}$

Encuentra la amplitud, el periodo y el desplazamiento de fase de la función dada. Dibuja la gráfica en un intervalo de un periodo. Etiquetar todos los máximos, mínimos e intercepciones.

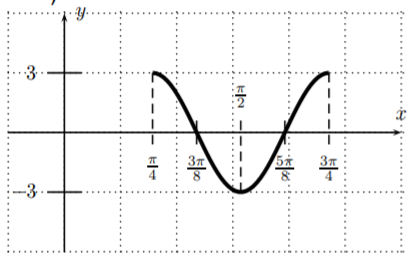
$y=3 \cos\left(4 x-\pi\right)$
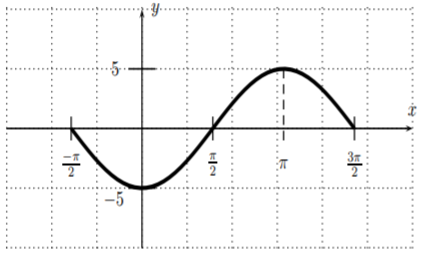
$y=-5\sin\left(x+\dfrac{\pi}{2}\right)$

Contestar

amplitud$3$, periodo$\dfrac{\pi}{2}$, desplazamiento de fase$\dfrac{\pi}{4}$ $clipboard_eae7381b7075b464c7074552724f5f1ed.png$
amplitud$5$, periodo$2\pi $, desplazamiento de fase$\dfrac{-\pi}{2}$ $clipboard_e24e4d7c331858767be9f4c23ff7a2c75.png$

Ejercicio$\PageIndex{5}$

Encuentra el valor exacto de la función trigonométrica.

$\cos\left(\dfrac{\pi}{12}\right)$[Pista: Utilice las fórmulas de suma y resta de ángulos.]
$\cos\left(\dfrac{3\pi}{8}\right)$[Pista: Usa las fórmulas de medio ángulos.]

Contestar

$\dfrac{\sqrt{2}+\sqrt{6}}{4}$
$\dfrac{\sqrt{2-\sqrt{2}}}{2}$

Ejercicio$\PageIndex{6}$

Dejemos$\sin(\alpha)=-\dfrac{4}{5}$ y dejemos$\alpha$ estar en el cuadrante III. Encontrar$\sin(2\alpha)$,$\cos(2\alpha)$, y$\tan(2\alpha)$.

Contestar: $\sin (2 \alpha)=\dfrac{24}{25}, \cos (2 \alpha)=\dfrac{-7}{25}, \tan (2 \alpha)=\dfrac{-24}{7}$

Ejercicio$\PageIndex{7}$

Encuentra el valor exacto de:

$\sin^{-1}\left(-\dfrac{1}{2}\right)$
$\cos^{-1}\left(-\dfrac{\sqrt{3}}{2}\right)$
$\tan^{-1}\left(-\dfrac{\sqrt{3}}{3}\right)$

Contestar

$\dfrac{-\pi}{6}$
$\dfrac{5 \pi}{6}$
$\dfrac{-\pi}{6}$

Ejercicio$\PageIndex{8}$

Resolver para$x$:$2\sin(x)+\sqrt{3}=0$

Contestar: $x=(-1)^{n+1} \dfrac{\pi}{3}+n \pi$, donde$n=0, \pm 1, \ldots $

Ejercicio$\PageIndex{9}$

Resolver para$x$:$\tan^2(x)-1=0$

Contestar: $x=\pm \dfrac{\pi}{4}+n \pi $donde$n=0, \pm 1, \ldots $

Ejercicio$\PageIndex{10}$

Resolver para$x$.

$2\cos^2(x)-1=0$
$2\sin^2(x)+15\sin(x)+7=0$

Contestar

$x=\pm \dfrac{\pi}{4}+2 n \pi$o$x=\pm \dfrac{3 \pi}{4}+2 n \pi$ donde$n=0, \pm 1, \ldots$
$(-1)^{n+1} \dfrac{\pi}{6}+n \pi$donde$n=0, \pm 1, \ldots$

Search

Text Color

Text Size

Margin Size

Font Type

Ejercicio\(\PageIndex{1}\)

Ejercicio\(\PageIndex{2}\)

Ejercicio\(\PageIndex{3}\)

Ejercicio\(\PageIndex{4}\)

Ejercicio\(\PageIndex{5}\)

Ejercicio\(\PageIndex{6}\)

Ejercicio\(\PageIndex{7}\)

Ejercicio\(\PageIndex{8}\)

Ejercicio\(\PageIndex{9}\)

Ejercicio\(\PageIndex{10}\)