2.4: Gráficas y Gráficas

Última actualización
Guardar como PDF

Page ID: 114011

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En cálculo, estaremos analizando gráficas para conocer más sobre las funciones que representan. Es importante que tengamos una buena comprensión de la relación entre una función y su gráfica. Específicamente en el cálculo diferencial, aprenderemos a usar derivadas (que es una tasa de cambio o la pendiente local) para determinar dónde está aumentando o disminuyendo una gráfica. Además, en el cálculo integral, podrías aprender a calcular el trabajo requerido para bombear un fluido, lo que da la oportunidad de explorar el valor de usar diferentes ubicaciones para el origen, resultando efectivamente en un desplazamiento de la función y su gráfica.

2.4.1 Gráficas de Funciones Generales

Muchas personas toman un enfoque muy tedioso para graficar; para el dominio que les interesa graficar, toman cada posible valor entero de$x$, evalúan la función para ese valor, y luego grafican un solo punto. Después de haber graficado varios puntos en todo el dominio, “conectarán los puntos”. Si bien este método es confiable, consume mucho tiempo y puede ser difícil dependiendo de la función. En esta sección, daremos una visión general de la forma general de las funciones comunes y luego hablaremos sobre cómo estas funciones generales se pueden desplazar, estirar y voltear para esbozar rápidamente funciones relacionadas. Adicionalmente, hablaremos sobre las funciones por partes y cómo graficarlas correctamente.

Líneas

La forma más rápida de graficar una línea es usando un punto y la pendiente. Esto se debe en gran parte a que ambas formas, pendiente-intercepción y punto-pendiente, le proporcionan esta información. Comience trazando el punto. Entonces, a partir de ese punto usa la pendiente para trazar un segundo punto. Por ejemplo, si la pendiente es$-\frac{2}{3}$, comenzaría en el punto inicial, movería$3$ las unidades a la derecha (porque el cambio horizontal es 3) y luego bajaría$2$ unidades en la dirección y (porque la pendiente es negativa y el cambio vertical es 2). (Nota: también puedes moverte verticalmente y luego horizontalmente, de cualquier manera da el mismo resultado.) Trace este nuevo punto, y luego use una recta para conectar ambos puntos. Asegúrese de continuar más allá de cada uno de los puntos. Si la pendiente es un número entero, mueve esas muchas unidades verticalmente y solo una unidad a la derecha para trazar tu segundo punto.

Ejemplo$\PageIndex{1}$: Graphing a Line

Grafica la línea$y=2x-3$

Solución

Empecemos por identificar la pendiente y un punto. Estamos en forma de pendiente-intercepción, así podemos ver que la pendiente es$m=2$ y la intercepción y lo es$(0,-3)$. Empezaremos trazando un punto en$(0,-3)$. Después, nos moveremos a la derecha 1 unidad y subiremos 2 unidades y trazaremos un segundo punto. Entonces, usamos los dos puntos para trazar nuestra línea. El proceso completo se muestra en las siguientes tres gráficas:

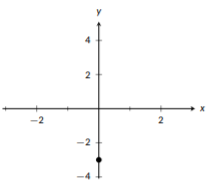
$clipboard_ef8a60f94209297d950c83c236a58f590.png$

Figura$\PageIndex{1}$: Trazar la$y$ -intercepción

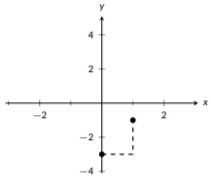
$clipboard_e8da68b92f6fd6855af96765042d286ba.png$

Figura$\PageIndex{2}$: Usar la pendiente para trazar un segundo punto

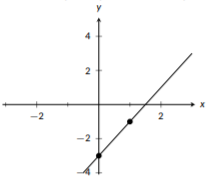
$clipboard_e7603f4d13e2187e9c08958a3d43d12b6.png$

Figura$\PageIndex{3}$: Completar la línea

Funciones cuadráticas

La función cuadrática más básica es$f(x)=x^2$ .Más adelante, discutiremos cómo cada otra función cuadrática se puede graficar desplazando y estirando esta función. La forma general de esta función es una “U” y es simétrica sobre el eje y, lo que significa que los lados izquierdo y derecho de la gráfica son un reflejo el uno del otro. Esta función crece rápidamente; esto significa que a medida que$x$ se hace grande,$f(x)$ se hace grande más rápido que$x$ lo hace. No tiene asíntotas horizontales, es decir, que como$x$ se hace grande,$f(x)$ no se nivela.

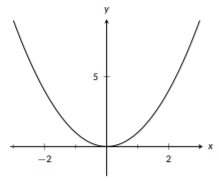
$clipboard_e1f4c290b751dc977869473b659a3909b.png$

Figura$\PageIndex{4}$: La gráfica de$f(x)=x^{2}$.

Funciones cúbicas

La función cúbica más básica es$f(x)=x^3$. De manera similar a las funciones cuadráticas, todas las demás funciones cúbicas se pueden graficar desplazando y estirando esta función. Esta función tiene simetría rotacional alrededor del origen; si tratas$(0,0)$ como un punto de pivote y giras la gráfica$180^{\circ}$, se verá exactamente igual. Para valores positivos de$x$, esta función crece rápidamente, pero para valores negativos de la$x$ misma se vuelve cada vez más negativa. Tampoco tiene asíntotas horizontales.

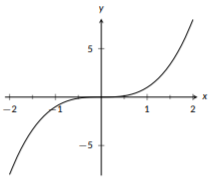
$clipboard_ee04399b88b329174c878980654f77598.png$

Figura$\PageIndex{5}$: La gráfica de$f(x)=x^{3}$.

Incluso polinomios

Un polinomio par es cualquier polinomio donde cada monomio tiene un grado par. Por ejemplo,$f(x)=x^6+3x^4-5x^2+7$ es un polinomio par porque los grados son 6, 4, 2 y 0. Sin embargo, no$g(x)=x^4-x^2+x-4$ es un polinomio par porque tiene$x$ como término (y$x$ tiene grado 1). Incluso los polinomios comparten características con la función cuadrática básica: son simétricos alrededor del eje y y ambas “colas” de la función tienen el mismo signo. Esto significa que como$x$ se pone muy grande o muy negativo,$f(x)$ tendrá el mismo signo; o ambas colas son positivas o ambas colas son negativas. Esta es una característica clave de incluso polinomios. El signo en el término de grado más alto te indica si ambas colas serán positivas o si ambas serán negativas.

Un tipo de función relacionado, pero ligeramente diferente, es un polinomio de orden par, también conocido como polinomio de grado par. Aquí, solo nos importa que el término de grado más alto sea parejo, así que tanto como$f(x)$$g(x)$ desde arriba son polinomios de orden par. Estos polinomios no tienen que ser simétricos alrededor del eje y, pero sí exhiben el mismo comportamiento “final” donde ambas colas son positivas o ambas son negativas.

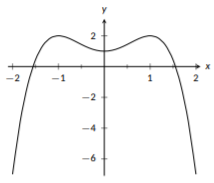
$clipboard_e46a8838ee1b305231c7bc89f233f6fc5.png$

Figura$\PageIndex{6}$: La gráfica de$f(x)=-x^{4}+2x^{2}+1$, un polinomio par.

Polinomios impares

Un polinomio impar es cualquier polinomio donde cada monomio tiene un grado impar. Por ejemplo,$f(x)=4x^5+2x^3-7x$ es un polinomio impar porque los grados son 5, 3 y 1. Sin embargo, no$g(x)=2x^3+x-7$ es e impar polinomio porque tiene$-7$ como término (y$-7$ tiene grado 0). Los polinomios impares comparten características con las funciones cúbicas básicas: tienen simetría rotacional sobre el origen y las colas tienen signos opuestos. Los polinomios impares siempre tienen una cola positiva y una cola negativa.

Nuevamente, tenemos un tipo de función relacionada, un polinomio de orden impar, también conocido como polinomio de grado impar. Para estos polinomios, el grado más alto debe ser impar, pero los términos de grado más pequeños pueden ser pares, como en$h(x)=x^3+2x^2$. Estos polinomios no son todos simétricos sobre el origen, pero las colas tendrán signos opuestos.

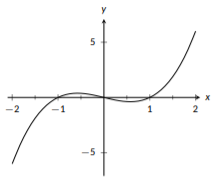
$clipboard_e40ad8d69dee85c7ba8d1d37fdeec0ea0.png$

Figura$\PageIndex{7}$: La gráfica de$f(x)=x^{3}-x$, un polinomio impar.

Funciones exponenciales

Para una función exponencial básica,$f(x)=b^x$,$b$ debe ser un número real positivo con$b\neq 1$. Todas las funciones exponenciales básicas con$b>1$ comparten algunas características clave: todas contienen el punto$(0,1)$, todas contienen el punto$(1,b)$, crecen rápidamente para valores positivos de$x$, y para valores negativos de$x$ se acercan a$y=0$, el eje x. Una función exponencial básica nunca cruzará el eje x, solo se acercará cada vez más a medida que$x$ se vuelva cada vez más negativa. Este comportamiento a largo plazo se describe como tener una asíntota horizontal en$y=0$. Al graficar una función exponencial, trazamos los dos puntos clave enumerados anteriormente y usamos la forma general para guiar el resto de nuestra gráfica.

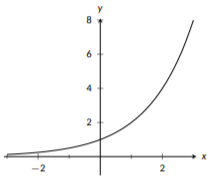
$clipboard_e38e782605d04e49e6721cc30e773b116.png$

Figura$\PageIndex{8}$: La gráfica de$f(x)-2^{x}$, una función exponencial básica.

Funciones logarítmicas

Las funciones logarítmicas tienen la misma forma que las funciones exponenciales básicas, pero reflejadas sobre la línea$y=x$. Esto significa que las características clave de las funciones de la forma$f(x)=\log_b{(x)}$ son: todas contienen el punto$(1,0)$; todas contienen el punto$(b,1)$; para valores positivos muy pequeños de$x$,$f(x)$ se vuelve cada vez más negativo si $b>1$y cada vez más positivo si$b<1$; como$x$ se vuelve muy grande, también lo hace$f(x)$ si$b>1$ y muy negativo si$b<1$. Es importante a la hora de graficar funciones logarítmicas recordar que su dominio es solo$(0,\infty)$; no debes graficar nada para valores negativos de$x$ y nada para$x=0$. Las funciones logarítmicas tienen una asíntota vertical en$x=0$, el eje y. El gráfico se acerca mucho a esta línea vertical, pero nunca la cruzará.

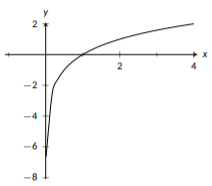
$clipboard_e42ae753574652530e459aef545f74ea9.png$

Figura$\PageIndex{9}$: La gráfica de$f(x)=\log_{2}(x)$, una función logarítmica básica.

Funciones trigonométricas

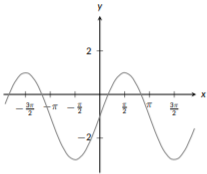
Una característica clave de las funciones trigonométricas$\sin{(x)}$$\cos{(x)}$, y$\tan{(x)}$ es que las tres son funciones periódicas; exhiben el mismo patrón una y otra vez. Adicionalmente, las funciones seno y coseno nunca crecen sin ataduras; sus$y$ valores siempre están entre$-1$ y$1$. La función tangente crece sin encuadernación y tiene asíntotas verticales repetidas. Para las tres funciones, hay puntos clave cuando$x$ es un múltiplo de$\pi$, como$x=\frac{\pi}{2}$,$x=\pi$,$x=\frac{3\pi}{2}$, y$x=2\pi$. Adicionalmente, podrías notar que las gráficas de seno y coseno son muy similares. De hecho, si tomas la gráfica de seno y la desplazas hacia la izquierda por$\frac{\pi}{2}$ ti obtendrías la gráfica de coseno. De hecho, se trata de una identidad trigonométrica que se puede ver solo a partir de las gráficas. Las gráficas de estas tres funciones se pueden ver a continuación:

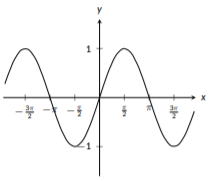
$clipboard_e47d7116d5902be94ae289b51d78a7098.png$

Figura$\PageIndex{10}$: La gráfica de$f(x)=\sin (x)$

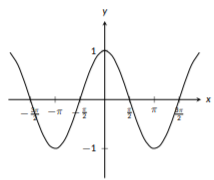
$clipboard_eb1b3ee116d2973fa244ff4bae0bddfb5.png$

Figura$\PageIndex{11}$: La gráfica de$f(x)=\cos(x)$

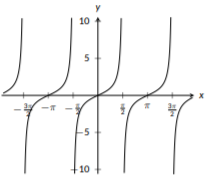
$clipboard_e923ccc4c9db569e934c3271b04d0b59d.png$

Figura$\PageIndex{12}$: La gráfica de$f(x)=\tan(x)$

2.4.2: Modificación de funciones

Ahora que hemos visto las formas de algunas funciones básicas como$f(x)=x^2$, hablemos de cómo podemos usar estas formas básicas para ayudar a graficar muchas funciones. Tendremos que ser capaces de identificar la función base con la que estamos trabajando e identificar cómo se ha modificado. Los desglosaremos en dos tipos principales de modificaciones: modificaciones verticales y modificaciones horizontales. Las modificaciones verticales afectarán, como su nombre lo indica, a las funciones verticalmente, ya sea desplazando la función hacia arriba o hacia abajo, o estirando o reduciendo la altura de la función. De igual manera, las modificaciones horizontales afectarán la función horizontalmente, desplazándola hacia la izquierda o hacia la derecha, o estirando o reduciendo su “ancho”.

Modificaciones Verticales

El primer tipo de modificaciones verticales que discutiremos son los turnos, donde cada punto de las funciones se desplaza hacia arriba o hacia abajo por la misma distancia. Esta es una de las modificaciones más fáciles de detectar; todo lo que tenemos que hacer es sumar o restar una constante a la función. Echemos un vistazo a un ejemplo.

Ejemplo$\PageIndex{2}$: Shifting a Function Vertically

Grafica la función$f(x)=x^2+3$.

Solución

Aquí podemos ver que tenemos una función con una constante añadida a ella; esto nos dice que necesitamos graficar$x^2$, pero con un desplazamiento vertical. La constante, nos$+3$ dice que tomaremos esta función base y la desplazaremos hacia arriba$3$ unidades (si esto fuera$-3$ desplazaríamos la función hacia abajo en 3 unidades).

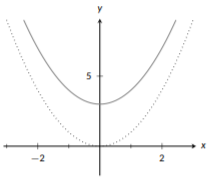
$clipboard_e0b839479f0ed6cdd622c2e2e6e287d39.png$

Figura$\PageIndex{13}$: Desplazamiento vertical

Aquí, la gráfica muestra tanto nuestra función base,$x^2$ (punteada) como nuestra función desplazada deseada,$f(x)=x^2+3$ (sólida). Si tomas un trozo de alambre y lo moldeas para que coincida con la gráfica de$x^2$, puedes mover el cable hacia arriba 3 unidades y ver que obtienes exactamente la gráfica de$f(x)=x^2+3$.

Observe que con un desplazamiento vertical, la forma de la función no cambia en absoluto, solo cambia su posicionamiento relativo al eje x. Con nuestra siguiente modificación, estiramiento vertical y encogimiento, no cambiamos su posicionamiento, ni la forma, sino que cambiamos lo empinada que es la función. Con estiramientos verticales, todo en el eje x es fijo, por lo que el posicionamiento no cambia. La forma no cambia en el sentido de que cada cuadrático seguirá pareciendo una “U” y cada seno o coseno seguirá pareciendo ondas interminables (de manera similar para nuestras otras funciones). Entonces, ¿cómo reconocemos cuando una función se está estirando o encogiendo verticalmente? Tendremos una función base que se está modificando con multiplicación escalar, tal como$f(x)=3\sin{(x)}$$g(t)= -\frac{1}{2} t^3$ o.Aquí, si multiplicamos por un número mayor que 1 o menor que$-1$, estiraremos la función y la haremos más pronunciada. Si lo multiplicamos por cualquier cosa entre$-1$ y$1$, se encogerá y se volverá menos empinada. Si multiplicamos por un número negativo, no sólo se está estirando o encogiendo la función, sino que también se volteará; todo lo que esté por encima del eje x se reflejará hasta debajo del eje x y todo lo que esté debajo será reflejo hacia arriba del eje x.

Ejemplo$\PageIndex{3}$: Stretching/Shrinking a Function Vertically

Graficar las funciones$f(x)=\frac{1}{2} x^3$ y$g(x)=-\frac{1}{2}x^3$.

Solución

Para ambos$f(x)$ y$g(x)$ tenemos la misma función base,$x^3$. Ya que$f(x)$ se forma multiplicando esto por$\frac{1}{2}$, se está encogiendo, pero no volteando.

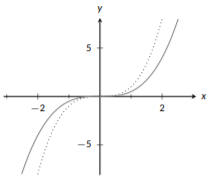
$clipboard_ece9ded63e33073910669fab46d4089d6.png$

Figura$\PageIndex{14}$: Encogimiento vertical

Aquí podemos ver nuestra función base,$x^3$ (punteada) y$f(x)=\frac{1}{2}x^3$ (sólida). Verás que la forma y la posición siguen siendo las mismas, pero$f(x)$ se mantiene más cerca del eje x; no llega a ser alto tan rápido como lo$x^3$ hace porque encogimos la gráfica verticalmente. Ahora que hemos encogido la gráfica, voltearla nos dará la gráfica de$g(x)$ (sólido):

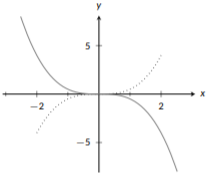
$clipboard_e1b53b463113dc60a9b7a3073027f078e.png$

Figura$\PageIndex{15}$: Encogimiento vertical

Esta gráfica tiene tanto$f(x)$ (punteada) como$g(x)$ (sólida); ambas tienen la misma posición y la misma pendiente, pero$g(x)$ está al revés.

El ejemplo anterior muestra cómo reducir y voltear una gráfica. Aquí, podrías hacer cualquiera de los dos pasos primero; si volteas y luego te encoges obtendrías exactamente el mismo resultado. Te recomendamos hacer bocetos muy rápidos en los márgenes de tu página al tratar múltiples transformaciones al mismo tiempo; me facilita el asegurarme de que dibujemos la gráfica final con precisión capturando cada etapa, sin embargo, después de la práctica puedes sentirte cómodo haciendo ambos pasos a la vez.

Ya hemos visto cómo trabajamos las modificaciones verticales de forma individual, pero ¿qué sucede cuando las combinamos?

Ejemplo$\PageIndex{4}$: Multiple Vertical Modifications

Gráfica$h(x) = 2\sin{(x)} - 1$.

Solución

Primero, identifiquemos nuestra función base. Aquí, estamos trabajando con$\sin{(x)}$. Vemos que estamos multiplicando por 2 y restando 1; esto nos dice que tenemos un estiramiento vertical y un desplazamiento vertical. ¿Qué debemos hacer primero? La respuesta viene de nuestro orden de operaciones: la multiplicación debe hacerse antes de la resta. Seguiremos esa misma regla aquí estirándola$\sin{(x)}$ y luego desplazándola. Como tenemos$2\sin{(x)}$ en nuestra función, comenzaremos graficando$\sin{(x)}$ (punteado) y luego haciéndola dos veces más “alta” (es decir, dos veces más lejos del eje x; gráfica sólida).

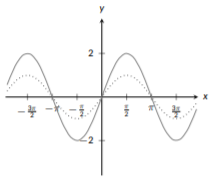
$clipboard_ed9b560570e5d6d4a3644bf2f6ed5c3c1.png$

Figura$\PageIndex{16}$: Sine

Ahora que lo hemos estirado, podemos encargarnos de la suma y desplazarla hacia abajo 1 unidad:

$clipboard_ef399ac9297ad4fdc6a6d7a91f6f3bb5c.png$

Figura$\PageIndex{17}$: Desplazado sinusoidal

Modificaciones Horizontales

Podemos hacer las mismas modificaciones horizontalmente que hicimos verticalmente: estiramiento, encogimiento y desplazamiento. Con modificaciones verticales, las modificaciones se presentaron en el exterior de la función, con cambios agregados al final y con estiramientos viniendo como multiplicación al frente. Con cambios horizontales trabajaremos en el interior de la función. Por ejemplo, si queremos desplazar la función$f(x)$ 2 unidades a la izquierda, la graficaríamos$f(x+2)$. Esto mueve la gráfica de$f$ hacia la izquierda porque, en esencia, siempre miramos una entrada más grande que lo que realmente es x, por ejemplo$x=4$, si, realmente estamos mirando$f(4+2)=f(6)$. De igual manera, si queremos$f$ desplazarnos hacia la derecha, usaríamos una resta:$f(x-2)$.

De igual manera, si queremos estirar o reducir la función horizontalmente, el cambio también se mostrará en el interior. Para estirar una función por$a>0$, nosotros graficaríamos$f(\frac{1}{a}x)$. Usamos$\frac{1}{a}$ porque para estirarlo horizontalmente necesitamos$x$ cambiar más lentamente. Para encogerlo por un factor de$a>0$ multiplicaríamos:$f(ax)$. Si queremos voltear la gráfica horizontalmente, seguiremos multiplicando por un negativo:$f(-x)$. Observe que muchas de las modificaciones horizontales no funcionan inmediatamente de la manera que esperaría, a diferencia de las modificaciones verticales. Si te sientes un poco confundido por estos, te recomendamos graficar algunos usando el método punto por punto. Del mismo modo, el proceso para lidiar con múltiples modificaciones es un poco diferente de lo que podría esperar: primero identificaremos la función base, luego incluiremos cualquier turno, y luego incluiremos cualquier tramo o contracción. Veamos un ejemplo:

Ejemplo$\PageIndex{5}$: Multiple Horizontal Modifications

Grafica la función$f(x)=4x^2+4x+1=(2x+1)^2$.

Solución

Nuestra función base aquí es$x^2$ (punteada). No tenemos ninguna modificación vertical, solo modificaciones horizontales ya que todo está sucediendo dentro de la función. Vemos que tenemos un turno a la izquierda de 1, debido a la$+1$, y luego necesitamos encogernos por un factor de 2 ya que$x$ se multiplica por 2. Primero, incluimos el turno (sólido):

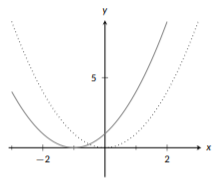
$clipboard_e13b260cf71178c6038e3db08e9c5f34a.png$

Figura$\PageIndex{18}$: Desplazamiento cuadrático

entonces, reducimos la función horizontalmente (sólido):

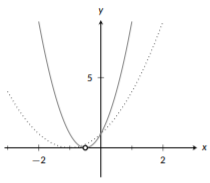
$clipboard_e80fea6ece407d048952fdeb1fc75460d.png$

Figura$\PageIndex{19}$: Desplazamiento cuadrático

Observe que cuando lo encojamos, el punto en el eje y$(0,1)$,, es el único punto que es el mismo entre ambas gráficas. Esto se debe a que nos encogimos y estiramos alrededor del eje y, no alrededor del centro de la gráfica. Podemos ver esto también al ver que la intercepción x cambia de$(-1,0)$ a$(-\frac{1}{2},0)$ (etiquetada con un punto abierto).

Si se está modificando una función tanto vertical como horizontalmente, primero debes encargarte de todos los cambios horizontales. Veamos cómo se ve esto.

Ejemplo$\PageIndex{6}$: Graph Transformation

Grafica la función$g(x)=-(\frac{1}{2}x+2)^2+3$.

Solución

Al igual que con nuestros ejemplos anteriores, el primer paso es identificar la función base. Aquí nuestras funciones base son$x^2$ (punteadas). Dijimos que deberíamos comenzar con cambios horizontales, así que veamos esos primero. Con modificaciones horizontales, necesitamos trabajar con el turno y luego el estiramiento. Dentro de nuestra función tenemos$+2$; esto nos dice que comenzamos desplazando a la izquierda 2 unidades (sólido):

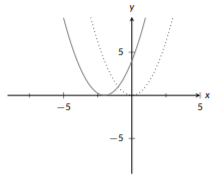
$clipboard_e13b81eec363e33a5b31338ff02bba811.png$

Figura$\PageIndex{20}$: Transformación cuadrática

A continuación, estiraremos nuestra gráfica horizontalmente (sólida) por un factor de 2 ya que$x$ se multiplica por$\frac{1}{2}$ en el interior de la función:

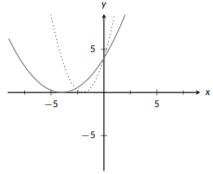
$clipboard_e7f8e478d1c70d1f55e3cd9ff6d06b0d0.png$

Figura$\PageIndex{21}$: Transformación cuadrática

Ahora que hemos completado todos los cambios horizontales, podemos trabajar en cambios verticales. Tenemos dos: un flip y un turno. Tenemos que hacer el flip primero (sólido):

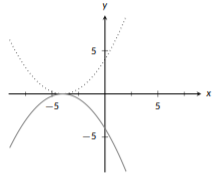
$clipboard_ebc8a8003b191b7144d36faf284bb485b.png$

Figura$\PageIndex{22}$: Transformación cuadrática

La última modificación para completar es un cambio hacia arriba 3 unidades (sólido):

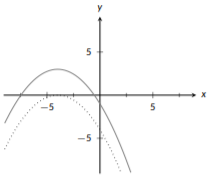
$clipboard_ec4350d71702ab51f27b92ef3245644a0.png$

Figura$\PageIndex{23}$: Transformación cuadrática

En todos nuestros ejemplos hasta el momento, se nos ha dado la función transformada y se nos ha pedido que la graficemos. ¿Y si se nos pide que ideemos la nueva función?

Ejemplo$\PageIndex{7}$: Functions for a Transformation

Determinar la ecuación para la gráfica de$f(x)=x^3$ después de que haya sido desplazada 2 unidades a la derecha, volteada verticalmente y desplazada 2 unidades hacia arriba.

Solución

Aquí las transformaciones se han dado en el mismo orden en que las aplicaríamos. Nuestro primer paso, es desplazar la función a la derecha, así vamos a cambiar a$(x-2)^3$. A continuación, queremos voltear la función verticalmente, así que obtenemos$-(x-2)^3$. Por último, queremos cambiar hacia arriba 2 unidades, así obtenemos$g(x)=-(x-2)^3+2$ como nuestra nueva función. le dimos un nuevo nombre a la función$g$, en lugar de para$f$ que no nos confundamos usando el mismo nombre para ambos.

2.4.3: Gráficas de Funciones por Piezas

El último tema de graficar que discutiremos en esta sección es graficar funciones por partes. Una función por partes es una función que se define en piezas; para parte de su dominio se define de una manera y para otras partes se define de manera diferente. Al graficar estas funciones, la parte más difícil es asegurarse de usar la parte correcta de la definición de función para cada parte del dominio. Para que esto sea un poco más fácil de mantener recto, nos aseguramos de graficar solo una pieza a la vez.

Al cambiar entre diferentes piezas, es importante hacerlo correctamente. A veces el punto “final” de esa pieza no está realmente incluido. Esto sucede cuando el dominio para esa pieza está abierto, es decir, no incluye ese punto final. Esto se indica con un paréntesis o un “$<$” o un “$>$” diciéndonos que no se debe incluir el punto final. Aquí, trazaríamos un punto abierto, un círculo con un interior blanco, para mostrar que no está incluido. Si se incluye el punto final, trazaremos un punto cerrado, un círculo con un interior relleno, para mostrar que está incluido. Si el dominio de la función para una pieza continúa hasta$\infty$ o hasta$-\infty$, lo indicaremos dibujando una pequeña punta de flecha en el borde de la gráfica para mostrar que continúa para siempre.

Ejemplo$\PageIndex{8}$: Graphing a Piecewise Function

Graficar la función$f(x) = \left\{\begin{array}{cc} 3-x & 0<x \leq 1 \\ x^2 & 1<x<2 \end{array}\right.$

Solución

Esta función tiene dos piezas: una línea cuando$x$ está adentro$(0,1]$ y una función cuadrática cuando$x$ está adentro$(1,2)$. Nos gusta trabajar de izquierda a derecha, así que primero vamos a graficar la línea, pero podrías graficar las piezas en cualquier orden.

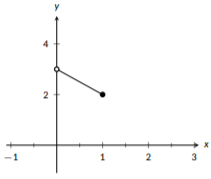
$clipboard_e618d8b71d8b096c1cf73ff62adec5583.png$

Figura$\PageIndex{24}$: Por tramos

Aquí, graficamos la línea trazando los dos puntos finales y conectándolos. Ya que son los puntos finales, no queremos pasar de ellos. Desde la línea aplicada cuando$0<x\leq1$, trazamos un punto abierto$x=0$ para mostrar que no está incluido y un punto cerrado$x=1$ para mostrar que está incluido.

A continuación, agregaremos la pieza cuadrática a esta gráfica.

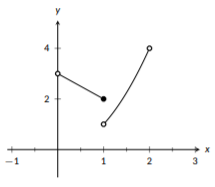
$clipboard_ef2d958eb08727726079aabd53cee12fc.png$

Figura$\PageIndex{25}$: Por tramos

Con la cuadrática, ambos extremos están abiertos ya que esta pieza sólo se aplica cuando$1<x<2$. Esto significa que necesitamos puntos abiertos en ambos extremos.