3.4: Introducción a las funciones trigonométricas

En esta sección, introduciremos funciones trigonométricas. Examinaremos las relaciones entre estas funciones y discutiremos cómo evaluar estas funciones para entradas de uso común. Las funciones trigonométricas se utilizan frecuentemente en cálculos y cursos posteriores debido a la amplia gama de fenómenos que pueden modelar estas funciones, desde el flujo de aire en nuestros bronquios hasta las vibraciones sísmicas en un edificio.

3.4.1 Definiciones trigonométricas

En esta sección, nos centraremos en seis funciones trigonométricas: seno, coseno, tangente, cosecante, secante y cotangente. Todas estas funciones están relacionadas entre sí, y típicamente los matemáticos se centran en el seno y el coseno ya que las otras cuatro funciones pueden expresarse en términos de seno y coseno. Estas relaciones son:

• \(\displaystyle \tan{(\theta)} = \frac{\sin{(\theta)}}{\cos{(\theta)}}\)

• \(\displaystyle \csc{(\theta)} = \frac{1}{\sin{(\theta)}}\)

• \(\displaystyle \sec{(\theta)} = \frac{1}{\cos{(\theta)}}\)

• \(\displaystyle \cot{(\theta)} = \frac{\cos{(\theta)}}{\sin{(\theta)}}\)

Aquí\(\tan{(\theta)}\) está la notación comúnmente utilizada para la función tangente;\(\csc{(\theta)}\) es la notación para la función cosecante;\(\sec{(\theta)}\) es la notación para la función secante; y\(\cot{(\theta)}\) es la notación para la función cotangente. Observe que cada uno de estos toma un valor de entrada; por sí mismo “\(\sin{}\)” no tiene más significado que “\(\sqrt{}\)” tiene; todas son funciones y todas requieren una entrada. Adicionalmente, observe que usamos\(\theta\) (la letra griega theta) como nuestra variable de entrada. Los matemáticos suelen (pero no siempre) usan letras griegas cuando se refieren a ángulos, por lo que a menudo verás\(\theta\) y otras letras griegas utilizadas para etiquetar ángulos, como\(\alpha\) (alfa) y\(\beta\) (beta).

3.4.2 El Círculo de Unidades

Todas las funciones trigonométricas tienen patrones repetitivos; como tal, la mayoría de los matemáticos utilizan una herramienta conocida como círculo unitario para ayudar a evaluar estas funciones. El círculo unitario es un círculo de radio 1 donde etiquetaremos puntos clave. Antes de ver el círculo de unidades, hablemos un poco sobre cómo usar el círculo unitario.

Para cada función trigonométrica, los matemáticos suelen pensar en la entrada como medir un ángulo. Probablemente estés acostumbrado a medir ángulos en grados, pero en cálculo mediremos ángulos con una unidad llamada radianes. Los radianes son solo un tipo diferente de unidad para medir ángulos, al igual que los pies y los metros son diferentes unidades para medir la distancia. Probablemente estés familiarizado con la idea que tiene un círculo completo\(360^{\circ}\); en radianes esto es lo mismo que\(2\pi\) los radianes. Los matemáticos prefieren radianes a grados por varias razones. En primer lugar, es que los radianes relacionan los ángulos con la longitud del arco, la distancia alrededor del círculo. Para un círculo completo, tenemos un nombre especial para la longitud del arco: circunferencia. Quizás recuerdes que la fórmula para la circunferencia es\(C=2\pi r\); con radianes esto es lo mismo que decir el tamaño del ángulo por el radio. Una segunda razón se mostrará en el cálculo cuando aprendas derivadas.

Al usar el círculo unitario, medimos el ángulo a medida que nos movemos en sentido contrario a las agujas del reloj, usando el eje x positivo como nuestro punto de partida. Esto quiere decir que para cuando alcanzamos el eje y positivo hemos recorrido una cuarta parte del camino alrededor del círculo; hemos barrido un ángulo de\(\frac{2 \pi}{4} = \frac{\pi}{2}\) radianes. Esto se ilustra en la Figura\(\PageIndex{1}\). Si nos movemos alrededor del círculo en sentido contrario, en el sentido de las agujas del reloj, decimos que los ángulos son negativos. Esto significa que hemos barrido\(-\frac{3 \pi}{2}\) radianes si nos movemos hacia el eje y positivo en el sentido de las agujas del reloj.

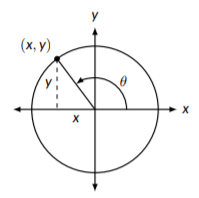
Figura\(\PageIndex{1}\): Medición de ángulos; reproducida a partir de\(\text{A}^{\text{P}}_{\text{E}}\text{X}\) Cálculo, Versión 3.0

Una vez que hayamos barrido el ángulo que nos interesa, necesitaremos conocer las coordenadas x e y del punto asociado en el círculo. La coordenada x en el punto es el valor de\(\cos{(\theta)}\) para ese ángulo y la coordenada y es el valor de\(\sin{(\theta)}\) para ese ángulo. El círculo unitario, mostrado en la Figura\(\PageIndex{2}\), muestra estas coordenadas para una variedad de entradas comunes. Aquí, el círculo unitario se muestra con ambos ángulos medidos tanto en grados como en radianes, pero recuerda que nos estamos enfocando en radianes.

Figura\(\PageIndex{2}\): El círculo unitario; reproducido de\(\text{A}^{\text{P}}_{\text{E}}\text{X}\) Cálculo, Versión 3.0

Veamos algunos ejemplos de cómo usar el círculo unitario para evaluar las funciones trigonométricas. Recuerde, el círculo unitario nos ayudará a determinar qué coordenadas x e y se emparejan con cada ángulo. La coordenada x nos da el valor del coseno para el ángulo y la coordenada y nos da el valor de seno para el ángulo.

Ejemplo\(\PageIndex{1}\): Evaluating Trigonometric Functions

Evaluar cada uno de los siguientes:

\[\begin{array}{lll}{\text{1. }\sin\left(\frac{\pi}{4}\right)}&{\qquad}&{\text{4. }\cos\left(-\frac{3\pi}{4}\right)} \\ {\text{2. }\tan\left(\frac{\pi}{6}\right)}&{\qquad}&{\text{5. }\csc\left(\frac{2\pi }{3}\right)} \\ {\text{3. }\sec(3\pi)}&{\qquad}&{\text{6. }\cot\left(\frac{5\pi}{6}\right)}\end{array}\nonumber\]

Solución

Empecemos:

1. Aquí, nuestro ángulo de entrada es\(\frac{\pi}{4}\). Esto corresponde al par de coordenadas\((\frac{\sqrt{2}}{2}, \frac{\sqrt{2}}{2})\). Nos interesa el valor del seno, por lo que queremos mirar la coordenada y. Esto nos da
   \[\sin\left(\frac{\pi}{4}\right)=\frac{\sqrt{2}}{2}\]
2. Aquí, nuestro ángulo de entrada es el\(\frac{\pi}{6}\) que corresponde al par de coordenadas\((\frac{\sqrt{3}}{2}, \frac{1}{2})\). Los pares de coordenadas nos dan los valores para coseno y seno, pero no nos dan directamente un valor para tangente, por lo que necesitaremos usar nuestra definición de tangente. Tenemos\[\begin{align}\begin{aligned}\begin{split} \tan{\bigg(\frac{\pi}{6}\bigg)} &= \frac{\sin{(\frac{\pi}{6})}}{\cos{(\frac{\pi}{6})}} \\[6pt] &=\frac{\frac{\sqrt{3}}{2}}{\frac{1}{2}} \\[6pt] &= \frac{\sqrt{3}}{2} \times \frac{2}{1} \\[6pt] & = \sqrt{3} \end{split}\end{aligned}\end{align}\] Entonces, nuestra respuesta final es
   \[\tan\left(\frac{\pi}{6}\right)=\sqrt{3}\]
3. Aquí, nuestro ángulo de entrada es\(3\pi\). No hay ángulo etiquetado como\(3\pi\) en el círculo unitario, por lo que este requiere un poco más de pensamiento. Dijimos antes que el círculo tiene\(2\pi\) radianes, así que si damos la vuelta por completo al círculo, hemos cubierto\(2\pi\). Tenemos que ir a otros\(3\pi-2\pi=\pi\) radianes, para que podamos usar las coordenadas en\(\pi\) radianes para obtener nuestros valores para\(3\pi\) radianes. En\(\pi\) radianes, nuestras coordenadas son\((-1,0)\). Esto nos da:\[\begin{align}\begin{aligned}\begin{split} \sec{(3\pi)} & = \frac{1}{\cos{(3\pi)}} \\[6pt] & = \frac{1}{-1} \\[6pt] & = -1 \end{split}\end{aligned}\end{align}\] Entonces, tenemos
   \[\sec (3\pi )=-1\]
4. Aquí, nuestro ángulo de entrada es\(-\frac{3\pi}{4}\). Esto significa que estamos cubriendo el círculo unitario moviéndonos en el sentido de las agujas del reloj. Tenemos que comenzar en\(0\) radianes, y mover\(\frac{3\pi}{4}\) radianes en el sentido de las agujas del reloj. Esto nos pondría en\(\frac{5\pi}{4}\) radianes. Las coordenadas son\((-\frac{\sqrt{2}}{2}, -\frac{\sqrt{2}}{2})\), entonces
   \[\cos\left(-\frac{3\pi}{4}\right)=-\frac{\sqrt{2}}{2}\]
5. Aquí, nuestro ángulo de entrada es\(\frac{2\pi}{3}\) radianes, lo que da coordenadas de\((-\frac{1}{2}, \frac{\sqrt{3}}{2})\). Cosecante se basa en seno, por lo que tenemos\[\begin{align}\begin{aligned}\begin{split} \csc{\bigg(\frac{2\pi}{3}\bigg)} & = \frac{1}{\sin{(\frac{2\pi}{3})}} \\[6pt] & = \frac{1}{\frac{\sqrt{3}}{2}} \\[6pt] & = \frac{2}{\sqrt{3}} \\[6pt] & = \frac{2}{\sqrt{3}} \times \frac{\sqrt{3}}{\sqrt{3}} \\[6pt] & = \frac{2\sqrt{3}}{3} \end{split}\end{aligned}\end{align}\] Aviso que racionalizamos el denominador. Esto quiere decir que reescribimos la fracción para que no tuviera un número irracional,\(\sqrt{3}\), en el denominador. Este es un último paso común en matemáticas para estandarizar la forma de la respuesta. La mayoría de las claves de respuesta escribirán la respuesta en la forma racionalizada, por lo que es un buen hábito racionalizar el denominador para que puedas verificar tus respuestas. Nuestra respuesta final es
   \[\csc\left(\frac{2\pi}{3}\right)=\frac{2\sqrt{3}}{3}\]
6. Aquí, tenemos un ángulo de\(\frac{5\pi}{6}\), que tiene coordenadas\((-\frac{\sqrt{3}}{2}, \frac{1}{2})\). Esto nos da\[\begin{split} \cot{\bigg( \frac{5\pi}{6}\bigg)} & = \frac{\cos{(\frac{5\pi}{6})}}{\sin{(\frac{5\pi}{6})}} \\ & = \frac{-\frac{\sqrt{3}}{2}}{\frac{1}{2}} \\ & = \frac{-\sqrt{3}}{2} \times \frac{2}{1} \\ & = -\sqrt{3} \end{split}\]
   \[\cot\left(\frac{5\pi}{6}\right)=-\sqrt{3}\]

3.4.3 Propiedades de las Funciones Trigonométricas

Observe que en el círculo unitario, los valores de las coordenadas x e y oscilan entre -1 y 1. Dado que estos son los valores de salida de las funciones seno y coseno, decimos que el rango, o los valores de salida, de seno y coseno es\([-1,1]\), lo que significa que la salida puede llegar a ser tan pequeña como -1 y tan grande como 1. Adicionalmente, se definen seno y coseno para cualquier valor de entrada, por lo que para cada dominio es\((-\infty,\infty)\).

Las otras cuatro funciones trigonométricas se definen en términos de seno y coseno, donde ya sea seno o coseno está en el denominador de una fracción. Esto significa que los dominios de estas funciones son limitados. Tanto la secante como la tangente tienen coseno en el denominador, lo que significa que estarán indefinidos cada vez que el coseno sea 0. El coseno es 0 en los múltiplos impares de\(\frac{\pi}{2}\). Esto nos dice que estos impares múltiplos de\(\frac{\pi}{2}\)\(-\frac{3\pi}{2}\), valores como\(-\frac{\pi}{2}\)\(\frac{\pi}{2}\),,, y no\(\frac{3\pi}{2}\) forman parte del dominio para tangente o para secante. Al igual que seno y coseno, los valores de salida de secante son limitados; su rango es\((-\infty,-1]\cup [1,\infty)\), pero el rango para tangente no está limitado; su rango es\((-\infty,\infty)\).

Tanto cosecante como cotangente tienen seno en el denominador para sus definiciones; esto significa que están indefinidas cuando seno es 0. Seno es 0 en los múltiplos enteros de\(\pi\):\(-5\pi\)\(-3\pi\),\(-\pi\),\(\pi\),\(3\pi\),, etc. Al igual que con secante, los valores de salida de cosecante están limitados por lo que su rango es también\((-\infty,-1] \cup [1,\infty)\); el rango de cotangente no está limitado y es\((-\infty,\infty)\).