3.5: Funciones trigonométricas y triángulos

Última actualización
Guardar como PDF

Page ID: 113946

$ \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } $ $ \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} $$\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$ $\newcommand{\id}{\mathrm{id}}$ $ \newcommand{\Span}{\mathrm{span}}$ $ \newcommand{\kernel}{\mathrm{null}\,}$ $ \newcommand{\range}{\mathrm{range}\,}$ $ \newcommand{\RealPart}{\mathrm{Re}}$ $ \newcommand{\ImaginaryPart}{\mathrm{Im}}$ $ \newcommand{\Argument}{\mathrm{Arg}}$ $ \newcommand{\norm}[1]{\| #1 \|}$ $ \newcommand{\inner}[2]{\langle #1, #2 \rangle}$ $ \newcommand{\Span}{\mathrm{span}}$$\newcommand{\AA}{\unicode[.8,0]{x212B}}$

En esta sección, discutiremos más a fondo las funciones trigonométricas. Examinaremos la relación entre las funciones trigonométricas y los triángulos rectos, y examinaremos algunas propiedades más de las funciones trigonométricas.

3.5.1 Triángulos rectos

En la última sección, nos centramos en las relaciones entre las funciones trigonométricas y el círculo unitario. Ahora, examinaremos la relación de estas funciones y el círculo unitario con triángulos rectos. En Figura$\PageIndex{1}$, comenzamos dibujando un círculo unitario con un ángulo$\theta$ y marcando las coordenadas correspondientes en el círculo. Si bajamos de estas coordenadas al eje x, podemos formar un triángulo rectángulo.

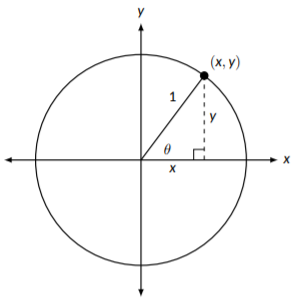
$clipboard_ef7c2d29f7b291fea0d71f5710e846c24.png$

Figura$\PageIndex{1}$: Triángulo recto dentro del círculo unitario

Este triángulo tiene una hipotenusa de 1 porque la hipotenusa tiene la misma longitud que el radio del círculo unitario, y longitudes laterales de$x=\cos{(\theta)}$ y$y=\sin{(\theta)}$. Si aplicamos el Teorema de Pitágoras a este triángulo, descubrimos una identidad interesante:

\[\begin{align}\begin{aligned}\begin{split} a^2 + b^2 & = c^2 \\ (x)^2 + (y)^2 & = (1)^2 \\ (\cos{(\theta)})^2 + (\sin{(\theta)})^2 &= 1^2 \\ \cos^2{(\theta)} + \sin^2{(\theta)} & = 1 \end{split}\end{aligned}\end{align}\]

No hay nada especial en la elección de que$\theta$ se muestra en la Figura$\PageIndex{1}$; esta identidad es cierta para todas las entradas. Observe que la entrada para coseno y la entrada para seno son las mismas; si las entradas son diferentes, no podemos garantizar que la suma sea igual a 1.

Este triángulo rectángulo también nos da una manera diferente de evaluar las funciones trigonométricas, en general. Con el círculo unitario, vimos que$\cos{(\theta)}$ es la coordenada x y$\sin{(\theta)}$ es la coordenada y, y nuestro triángulo rectángulo tiene una hipotenusa de 1. Si escalamos el triángulo, las longitudes laterales también escalarán, pero el tamaño de los ángulos seguirá siendo el mismo, por lo que los valores de$\cos{(\theta)}$ y también$\sin{(\theta)}$ deberían permanecer iguales. Para que esto sea cierto, no podemos simplemente decir que el coseno es la longitud del lado adyacente y el seno es la longitud del opuesto; en cambio, necesitaremos dividir ambos por la longitud de la hipotenusa para ajustarnos a la escala (ver Figura$\PageIndex{2}$ para una explicación visual de los lados opuesto y adyacente) . Esto nos da las siguientes identidades:

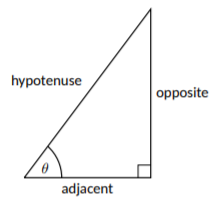
$clipboard_ee323021193a86fff9a0908dd0d4a3b2c.png$

Figura$\PageIndex{2}$: Uso de un triángulo rectángulo para evaluar funciones trigonométricas

\[\begin{array}{lll}{\text{1. }\sin(\theta )=\frac{\text{opposite}}{\text{hypotenuse}}}&{\qquad}&{\text{4. }\csc(\theta )=\frac{\text{hypotenuse}}{\text{opposite}}} \\ {\text{2. }\cos(\theta )=\frac{\text{adjacent}}{\text{hypotenuse}}}&{\qquad}&{\text{5. }\sec(\theta )=\frac{\text{hypotenuse}}{\text{adjacent}}} \\ {\text{3. }\tan(\theta )=\frac{\text{opposite}}{\text{adjacent}}}&{\qquad}&{\text{6. }\cot(\theta )=\frac{\text{adjacent}}{\text{opposite}}}\end{array}\nonumber\]

Mucha gente resume los tres primeros de estos con SOH-CAH-TOA para ayudar a recordar las identidades. SOH-CAH-TOA significa El seno es opuesto sobre hipotenusa; el coseno es adyacente sobre hipotenusa y la tangente es opuesta sobre adyacente. Las tres identidades restantes se pueden formar a partir de las definiciones de cosecante, secante y cotangente. Echemos un vistazo a cómo podemos usar triángulos rectos para ayudarnos a evaluar nuestras funciones trigonométricas.

Ejemplo$\PageIndex{1}$: Using a Right Triangle

Supongamos que$\cos{(\theta)} = \frac{12}{13}$. Determinar todos los valores posibles de$\sin{(\theta)}$.

Solución

Para ayudar a encontrar los posibles valores de$\sin{(\theta)}$, dibujaremos un triángulo rectángulo y lo etiquetaremos usando los valores que ya conocemos. Lo sabemos$\cos{(\theta)} = \frac{12}{13}$, así podemos usar 12 como la longitud del lado adyacente y 13 como la longitud de la hipotenusa:

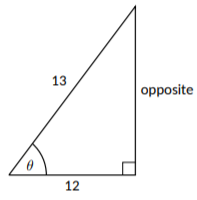
$clipboard_ecc9130ebba78923bb50f95b8cc3e149e.png$

Figura$\PageIndex{3}$

Ahora, podemos usar el Teorema de Pitágoras para encontrar la longitud lateral faltante:

\[\begin{align}\begin{aligned}\begin{split} a^2 + b^2 &= c^2 \\ (12)^2 + b^2 & = 13^2 \\ 144 + b^2 & = 169 \\ b^2 & = 25 \\ b & = \pm5 \end{split}\end{aligned}\end{align}\]

Ahora, podemos actualizar nuestro dibujo:

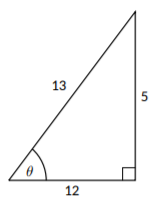
$clipboard_e927d75fd0866588adb80069a8fb2dadc.png$

Figura$\PageIndex{4}$

En nuestro dibujo, etiquetamos todos los lados con valores positivos porque cuando medimos el lado de un triángulo obtendremos una longitud positiva. De este triángulo, obtenemos$\sin{(\theta)} = \frac{\text{opposite}}{\text{hypotenuse}} = \frac{5}{13}$. Sin embargo, este no es el único valor posible de$\sin{(\theta)}$. No conocemos el verdadero valor de$\theta$ y en nuestro dibujo asumimos que está entre 0 y$\frac{\pi}{2}$. En realidad, también podría ser entre$\frac{3\pi}{2}$ y$2\pi$. Esto significaría que también$\sin{(\theta)}$ podría tener un valor negativo.

Los posibles valores de$\sin (\theta )$ son$\frac{5}{13}$ y$-\frac{5}{13}$

3.5.2 Funciones trigonométricas inversas

A menudo, tendremos información sobre las longitudes laterales del triángulo, pero querremos saber el valor del ángulo. Aquí es donde necesitaremos las funciones trigonométricas inversas. Cada función trigonométrica tiene una inversa, pero las inversas de seno, coseno y tangente son las más utilizadas. La notación para las funciones es un poco complicada. Hemos visto que podemos escribir$(\sin{(\theta)})^2$ ya que$\sin^2{(\theta)}$, sin embargo, la notación$\sin^{-1}{(\theta)}$ se usa a menudo para representar la función sinusoidal inversa en lugar de la función$\frac{1}{\sin{(\theta)}}$. En este libro, usaremos la notación$\arcsin{(x)}$ para representar la función sinusoidal inversa. Esto elimina la confusión sobre la notación, pero debes tener en cuenta que no todas las referencias hacen esto. Del mismo modo, utilizamos$\arccos{(x)}$ para la función coseno inverso y$\arctan{(x)}$ para la función tangente inversa. Estos pueden denominarse arcoseno, arcoseno y arcotangente por escrito.

Observe que para cada una de estas funciones trigonométricas inversas, utilizamos$x$ como nuestra entrada en lugar de$\theta$. Esto se debe a que ya no estamos ingresando un ángulo, sino una relación de longitudes. Para estas funciones, nuestra salida será un ángulo. Recuerden, cuando decimos que dos funciones son inversas, queremos decir que existe una relación como la siguiente:$\arccos{(\cos{(\theta)})}=\theta$ y$\cos{(\arccos{(x)})} = x$. Otra forma de expresar esta relación es decir que si$\cos{(\theta)} =x$, entonces$\arccos{(x)} = \theta$. Sin embargo, esto no es exactamente cierto aquí. Cuando miramos las funciones trigonométricas, sabemos que hay muchos ángulos que dan como resultado el mismo valor para el seno, muchos ángulos que dan como resultado el mismo valor para el coseno y muchos ángulos que dan como resultado el mismo valor para la tangente. Debido a que solo queremos una salida por cada entrada, las funciones trigonométricas inversas utilizan salidas restringidas. Arccosine está restringido a valores de salida entre$0$ y$\pi$, lo que significa que su rango es$[0,\pi]$. Esto funciona porque cada salida posible de coseno aparece una vez para ángulos de 0 a$\pi$. Arcoseno y arcotangente están restringidos a valores de salida entre$-\frac{\pi}{2}$ y$\frac{\pi}{2}$, lo que significa que cada uno tiene un rango de$[-\frac{\pi}{2}, \frac{\pi}{2}]$. Tanto para tangente como para seno, cada valor de salida posible aparece una vez para los ángulos entre$-\frac{\pi}{2}$ y$\frac{\pi}{2}$. Al restringir los rangos, nos aseguramos de que estas funciones estén bien definidas, lo que significa que solo producen una salida por cada entrada.

En la práctica, todavía podemos usar el círculo unitario para ayudar a evaluar las funciones trigonométricas inversas. Por ejemplo, si queremos evaluar$\arcsin{(\frac{1}{2})}$, vamos a querer mirar el círculo unitario para ver dónde$\sin{(\theta)}=\frac{1}{2}$. Obtenemos dos ángulos:$\frac{\pi}{6}$ y$\frac{5\pi}{6}$. Dado que el rango de arcoseno está restringido a$[-\frac{\pi}{2},\frac{\pi}{2}]$, decimos eso$\arcsin{(\frac{1}{2})} = \frac{\pi}{6}$. De igual manera, diríamos eso$\arccos{(\frac{1}{2})} = \frac{\pi}{3}$, y$\arctan{(1)} =\frac{\pi}{4}$.