15: Medidas Homogéneas de Riesgo
- Page ID
- 67950
Objetivos de aprendizaje
Después de completar este capítulo, debe ser capaz de: (1) definir y medir el riesgo; (2) comprender cómo la aversión al riesgo de una persona afecta su asignación de recursos; (3) distinguir entre variables de resultado directas e indirectas; y (4) evaluar estrategias alternativas de respuesta al riesgo disponibles para gerentes financieros incluyendo compartir resultados de riesgo, comprar seguros, diversificar inversiones, comprar inversiones para reducir el riesgo y elegir una estructura de capital óptima.
Para lograr tus metas de aprendizaje, debes completar los siguientes objetivos:
- Aprenda a describir eventos riesgosos asignando una variable aleatoria a sus resultados y asignando una función de densidad de probabilidad (pdf) a la variable aleatoria.
- Aprender a medir la variabilidad y tendencias centrales de variables aleatorias utilizando los valores esperados y varianzas de sus funciones de densidad de probabilidad.
- Conozca cómo se pueden usar las primas de riesgo para medir el costo del riesgo.
- Aprenda a describir el conjunto de opciones riesgosas que enfrentan los gerentes de la empresa utilizando conjuntos eficientes de varianza de valor esperado (EV).
- Conozca la función de densidad de probabilidad normal y comprenda por qué es tan importante a la hora de describir eventos riesgosos.
- Aprenda cómo compartir el riesgo con otros puede ser una respuesta útil al riesgo.
- Aprenda cómo comprar un seguro puede ser una respuesta útil al riesgo.
- Aprenda cómo la diversificación puede ser una respuesta útil al riesgo.
- Aprenda cómo comprar insumos para reducir el riesgo puede ser una respuesta útil al riesgo.
- Conozca cómo el apalancamiento afecta el nivel de riesgo que enfrenta la firma.
Introducción
El adjetivo “incierto” describe un evento (como un huracán o un partido de fútbol) cuyos resultados no se conocen con certeza. Un evento incierto debe tener al menos dos posibles resultados, y suele tener más. En un tiempo anterior, se hizo una distinción entre eventos de riesgo y eventos inciertos con base en la información disponible para identificar los posibles resultados de un evento y predecir las probabilidades de esos resultados. Por ejemplo, el volteo de una moneda es un evento familiar con dos resultados: cabezas (H) y colas (T). Con base en pruebas pasadas o lógica, podemos inferir que la probabilidad de que aparezca una cabeza (cola) cuando se arroja una moneda justa es de alrededor del 50 por ciento. Algunos pueden llamar a este evento riesgoso porque tenemos buena información sobre los posibles resultados y la probabilidad de que ocurran.
Ahora considera un evento diferente: el tiro de una chincheta. [1] ¿Cuál es la probabilidad de que la chincheta aterrice de costado frente a aterrizar en su cabeza? Debido a que no estamos familiarizados con este evento y no podemos asignar probabilidades a sus resultados basados en nuestra experiencia o lógica pasada, este evento podría llamarse incierto.
Para muchos, la distinción entre eventos riesgosos y eventos inciertos ya no es importante, y la mayoría de los investigadores asignan los adjetivos inciertos y riesgosos a los eventos indistintamente. Una razón por la que muchos no distinguen entre eventos riesgosos e inciertos es porque la asignación de probabilidades a los resultados del evento es subjetiva (nunca tenemos suficiente información para estar absolutamente seguros sobre los posibles resultados o sus probabilidades) y puede estar basado en otros factores además de la lógica y las observaciones pasadas, incluyendo corazonadas, presagios, experiencias ajenas en circunstancias irrelevantes y consejos de personas no calificadas, por mencionar algunas.
Una distinción entre eventos riesgosos e inciertos aún puede ser útil. Las personas parecen referirse a los eventos como inciertos cuando los resultados del evento no se conocen con certeza. También parece popular referirse a eventos inciertos como riesgosos cuando son inciertos y su ocurrencia altera el bienestar del tomador de decisiones. Por lo tanto, solo importan los eventos riesgosos, independientemente de la confianza de uno en las probabilidades de varios resultados (por ejemplo, el lanzamiento de una moneda versus el lanzamiento de una chincheta).
El estudio de eventos riesgosos, por supuesto, tiene aplicación a problemas de presupuestación de capital. Cuando estimamos el flujo de caja futuro utilizado en el análisis de decisiones de presupuestación de capital, estamos estimando resultados riesgosos asociados a un evento riesgoso. Así, nos encontramos ante el reto de satisfacer el principio de medidas homogéneas aplicado al riesgo ajustando las proyecciones de flujo de caja futuras de un retador y las predicciones de flujo de caja utilizadas para encontrar la TIR del defensor a su certeza valor equivalente que definiremos en este capítulo.
Conceptos estadísticos útiles para describir eventos riesgosos y resultados riesgosos
Función de densidad de probabilidad. Una función de densidad de probabilidad (pdf) es una función que asigna probabilidades a los resultados de eventos de riesgo. Por ejemplo, el tiro de una moneda justa es un evento con resultados que muestran una cabeza (H) o una cola (T). El pdf para este evento podrá asignar a H la probabilidad de 50% de ocurrencia y 50% a la ocurrencia de T. Un pdf puede ser discreto o continuo. Si los resultados de un evento son finitos, entonces su probabilidad de ocurrir se describe mediante un pdf discreto. Si los resultados de un evento son infinitos, entonces su probabilidad de ocurrir se describe mediante un pdf continuo.
Variables aleatorias. Una variable aleatoria es un valor numérico asignado por una función o regla a los resultados de eventos de riesgo. La probabilidad de un valor particular descrito por una variable aleatoria es la misma que las probabilidades de su resultado de evento subyacente. Por ejemplo, supongamos que un suceso fue el tiro de una moneda. Podríamos asignar al resultado de cabezas el número uno, y al resultado de colas el valor de cero. Entonces la probabilidad de que una variable aleatoria tome el valor uno es la misma probabilidad que H que ocurre al arrojar una moneda.
Valores esperados. Un valor esperado es una medida utilizada para describir las propiedades de un pdf. A veces se le llama el primer momento del pdf porque mide el centro de la masa de un pdf (como el fulcro de un tamborazo).
El valor esperado de un pdf se determina calculando un promedio ponderado de los valores posibles de los valores de la variable aleatoria multiplicada por su probabilidad de ocurrir. Para ilustrar, considere dos posibles inversiones A y B. El evento es la operación de la economía con tres posibles resultados: una recesión con 20% de probabilidad, una economía estable con 60% de probabilidad y una economía de crecimiento con 20% de probabilidad. El valor de las variables aleatorias que describen los tres resultados para las inversiones A y B se describen en el Cuadro 15.1 y representan tasas alternativas de rendimiento de las inversiones.
| Resultados económicos | pdf asociado a resultados económicos | Retornos de la inversión A (una variable aleatoria) | Retornos de la inversión B (una variable aleatoria) |
|---|---|---|---|
| Recesión | 20% | — 20% | — 40% |
| Estable | 60% | 20% | 20% |
| Crecimiento | 20% | 40% | 60% |
| Valores esperados de las inversiones A y B | 16% | 16% | |
| Varianzas (desviaciones estándar) de las inversiones A y B | .039 (19.6%) | .103 (32.0%) |
El operador de valor esperado se expresa como E (). El valor esperado de la inversión A es la suma de las variables aleatorias de A ponderadas por sus respectivas probabilidades y se escribe como:
\ [E (\ text {Inversión} A) = (.2) (-.20) + (.6) (.20) + (.2) (.4) =16\%\ etiqueta {15.1}\]
El valor esperado de la inversión B se escribe como:
\ [E (\ text {Inversión} B) = (.2) (-.40) + (.6) (.20) + (.2) (.60) =16\%\ etiqueta {15.2}\]
En general, el valor esperado de la variable aleatoria y j que ocurre con probabilidad discreta p j con j = 1,..., n resultados se expresa como:
\[ \label{15.3} E(y)=\sum_{j=1}^{n} p_{j} y_{j}\]
y donde la suma de todas las probabilidades de yj ocurran igual a 1:
\[ \label{15.4} \sum_{j=1}^{n} p_{j}=1\]
Un tipo especial de valor esperado es la media. Se calcula una media para n observaciones a partir de un pdf desconocido donde cada observación es igualmente probable. Supongamos que observamos cinco sorteos de una distribución desconocida igual a 8, 4, 0, 2 y 6. Dado que suponemos que cada observación fue igualmente probable, 1/ n, o 1/5, en este caso el valor esperado es igual a la media calculada como
\ [\ begin {align}\ bar {x} =\ frac {\ sum x_ {i}} {n} \ label {15.5a}\\ =\ frac {8+4+0+2+6} {5} =\ frac {20} {5} =4\ etiqueta {15.5b} \ end {align}\]
Varianza y desviación estándar. Aunque los valores esperados de las inversiones A y B descritos anteriormente son iguales, la mayoría de los inversionistas no los considerarían igualmente atractivos debido a las amplias diferencias en la variabilidad de los valores asumidos por sus variables aleatorias. Un enfoque para medir la variabilidad de una variable aleatoria es calcular su varianza o la raíz cuadrada de su varianza igual a su desviación estándar. Podemos encontrar la varianza de una variable aleatoria y j con n posibles resultados sumando y j menos E (y) cantidad al cuadrado ponderada por la probabilidad de que ocurra una variable aleatoria. Escribimos la fórmula de varianza para la variable aleatoria y j como:
\ [\ nombreoperador {Varianza} (y) =\ sigma_ {y} ^ {2} =\ suma_ {j=1} ^ {n} p_ {j}\ izquierda [y_ {j} -E (y)\ derecha] ^ {2}\ etiqueta {15.6}\]
Ilustramos la fórmula de varianza calculando las varianzas y desviaciones estándar para las inversiones A y B. La varianza para la inversión A se calcula como:
\ [\ sigma_ {A} ^ {2} =.2 (-.2-.16) ^ {2} +.6 (.2-.16) ^ {2} +.2 (.4-.16) ^ {2} =.039 \ label {15.7}\]
En tanto, la desviación estándar para la inversión A se puede encontrar calculando la raíz cuadrada de la varianza de inversión A y es igual a:
\ [ \ sigma_ {A} =\ sqrt {\ sigma_ {A} ^ {2}} =\ sqrt {.039} =.196\ texto {o} 19.6 \%\ etiqueta {15.8}\]
La varianza para la inversión B se calcula como:
(15.9)
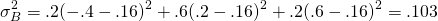
En tanto, la desviación estándar para la inversión B se encuentra igual a:
\ [\ sigma_ {B} =\ sqrt {\ sigma_ {B} ^ {2}} =\ sqrt {.320} =.320\ texto {o} 32 \%\ etiqueta {15.10}\]
Una razón para medir la variabilidad de la variable aleatoria al cuadrar sus desviaciones de su valor esperado es porque si encontráramos el promedio de la desviación de la variable aleatoria a partir de sus valores esperados, siempre sumarían a cero. Sumarían a cero porque las desviaciones ponderadas por probabilidad por encima del valor esperado son exactamente iguales a desviaciones ponderadas por probabilidad por debajo del valor esperado. Tomando la raíz cuadrada de la varianza de retornos convierte la medida de desviación en unidades comparables con las de la variable aleatoria original. Así, de las desviaciones estándar calculadas anteriormente, podemos inferir que, en promedio, la variable aleatoria que representa la inversión A se desviará 19.6% de su valor esperado mientras que la variable aleatoria que representa la inversión B se desviará 32.0% de su valor esperado. Claramente, los resultados de riesgo para la inversión B son más variables —y algunos dirían más riesgosos— que los resultados asociados a la inversión A. Añadimos a las descripciones en el Cuadro 15.1 de las inversiones A y B sus respectivas varianzas ( desviaciones estándar).
La varianza de la muestra se encuentra como antes sumando y cuadrando las desviaciones de la media ponderada por su probabilidad de ocurrencia. Sin embargo, por razones no discutidas aquí, la varianza de la muestra de observaciones se divide por n —1 en lugar de n donde n es el número de observaciones. Así, la desviación estándar de una distribución muestral se denota S x para observaciones sobre la variable aleatoria x. De lo contrario, la varianza de la variable aleatoria x extraída de la población verdadera se divide por n. Por lo tanto en nuestro ejemplo, la desviación estándar de la muestra, la raíz cuadrada de la varianza es:
\ [S=\ sqrt {\ frac {\ left (\ sum x_ {i} -\ bar {x}\ derecha) ^ {2}} {n-1}}\ etiqueta {15.11a}\]
(15.11b)
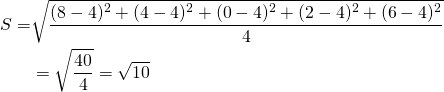
Primas de riesgo e ingresos equivalentes a certidumbre. Si bien no son propiedades de pdfs, conceptos importantes relacionados con pdfs que describen inversiones son primas de riesgo e ingresos equivalentes a certidumbre. Si bien estos conceptos están relacionados con las propiedades pdf, también dependen de las preferencias de riesgo de los tomadores de decisiones individuales para la varianza y el rendimiento esperado inherentes a la inversión. Las primas de riesgo, los ingresos equivalentes de certeza y las preferencias de riesgo se pueden explicar fácilmente.
Supongamos que un inversionista enfrentó la inversión A descrita en el Cuadro 15.1 y tuvo la oportunidad de recibir su valor esperado con certeza a cambio de pagar una prima de riesgo. ¿Cuál es la mayor prima de riesgo que el inversionista pagaría para recibir con certeza el valor esperado de la inversión? La respuesta dependería de las preferencias de riesgo del inversionista. Si el inversionista pagara una prima de riesgo positiva para recibir con certeza el valor esperado de la inversión A, entonces el inversionista es reacio al riesgo. Si el inversionista no pagara nada por recibir el valor esperado de la inversión A con certeza, el inversionista es neutral en el riesgo. Si el inversionista pagara para mantener la variabilidad (el inversionista disfruta del juego), diríamos que el inversionista prefiere el riesgo.
Una vez que conocemos la prima de riesgo del inversionista para el pdf de una inversión en particular, podemos encontrar su ingreso equivalente de certeza restándolo del valor esperado de la inversión. Podemos describir la relación entre la prima de riesgo del primer inversor, el ingreso equivalente de certeza, las actitudes de riesgo y el valor esperado y varianza de la variable aleatoria en la siguiente expresión:
\ [y_ {C E} ^ {i} =E (y) -\ frac {\ lambda^ {i}} {2} \ sigma_ {y} ^ {2}\ etiqueta {15.12}\]
En la Ecuación\ ref {15.12}, el ingreso equivalente de certeza del inversionista
i ésimo
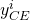 para una inversión cuyos valores posibles están representados por la variable
aleatoria y es igual al valor esperado de
y menos una prima de riesgo. En Ecuación\ ref {15.13}, podemos
resolver para la mayor prima de seguro que el inversionista estaría
dispuesto a pagar para recibir con
certeza el valor esperado de la inversión.
para una inversión cuyos valores posibles están representados por la variable
aleatoria y es igual al valor esperado de
y menos una prima de riesgo. En Ecuación\ ref {15.13}, podemos
resolver para la mayor prima de seguro que el inversionista estaría
dispuesto a pagar para recibir con
certeza el valor esperado de la inversión.
\ [\ label {1\ frac {\ lambda^ {i}} {2} \ sigma_ {y} ^ {2} =E (y) -y_ {C E} ^ {i} 5.13}\]
La prima de riesgo del inversionista es igual a la medida de preferencia de riesgo λ i del tomador de decisiones dividida por 2 veces la varianza de la variable aleatoria y. El coeficiente de aversión al riesgo λ i /2 del inversor se entiende mejor como un coeficiente de pendiente que indica la respuesta sobre el ingreso equivalente de certeza del inversionista por un incremento en una unidad de varianza de la variable aleatoria y.
Criterio de varianza de valor esperado. Supongamos que tenemos un conjunto de pdfs que representan cada uno la probabilidad de m variables aleatorias alternativas. Además, supongamos que cada una de las m inversiones se describieron usando sus valores esperados y varianzas. Entonces, suponiendo que todos los inversionistas eran reacio al riesgo y sin conocer el coeficiente de aversión al riesgo de cada inversionista, sabemos que por cada dos inversiones con valores esperados iguales (varianzas) y varianzas desiguales (valores esperados) el inversionista preferiría la inversión con la varianza menor (mayor valor esperado). Por otro lado, no pudimos clasificar dos inversiones en las que una tuviera un valor esperado y varianza mayores que la otra. El conjunto de inversiones y clasificado preferido para los tomadores de decisiones con aversión al riesgo se denomina conjunto eficiente de varianza de valor esperado (EV). A continuación se muestra la gráfica de un determinado conjunto de vehículos eléctricos.
Figura 15.1. Una Frontera Eficiente Valor Esperado-Varianza de las Inversiones Representadas por sus Valores Esperados E (y) y Varianzas σ 2.
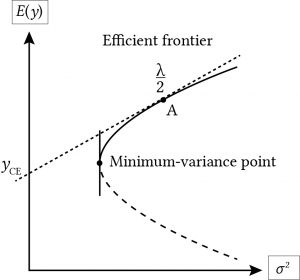
Supongamos que íbamos a trazar una línea tangente a la sección relevante del EV en el punto A, representando una inversión A. Entonces la pendiente de la línea en el punto A equivaldría al coeficiente de riesgo del tomador de decisiones en el punto. Además, si extendiéramos la línea tangente para intersectar con el eje vertical, el punto de intersección equivaldría a la certeza equivalente de la inversión.
La función de densidad de probabilidad normal (pdf)
Si tienes una muestra suficientemente grande de resultados de una distribución normal, la distribución se verá como una curva en forma de campana.
Figura 15.2. Una distribución de probabilidad normal que describe la probabilidad en áreas divididas a desviaciones estándar de la media.
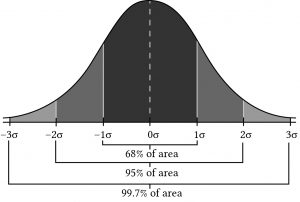
La distribución normal es simétrica respecto a su valor esperado. Los números en la gráfica corresponden a desviaciones estándar medidas a partir de la media de la distribución normal. Todas las características de la distribución normal se describen completamente por la media y varianza (o equivalentemente, la desviación estándar). La media especifica el valor promedio de la tasa de retorno. La probabilidad de obtener un retorno por encima o por debajo de la media por una cierta cantidad está determinada por el tamaño de la desviación estándar.
Si los rendimientos se distribuyen normalmente, existe un 68% de probabilidad de que el rendimiento para un periodo dado esté dentro de una desviación estándar del valor esperado; una probabilidad del 95% de que cualquier retorno observado en particular esté dentro de 2 desviaciones estándar del valor esperado; y un 99.74% probabilidad de que cualquier retorno esté dentro de 3 desviaciones estándar de la media. Claramente, cuanto mayor sea la desviación estándar, más dispersos estarán los rendimientos reales que se produzcan. Supongamos que los rendimientos de acciones comunes que vimos antes fueron generados por una distribución normal. Estimamos que el valor esperado de la distribución era r = 18.92% y la desviación estándar para ser σ (r) = 16.18%. Si nos interesara predecir cuál será el rendimiento del próximo año sobre las acciones ordinarias, podríamos decir que el valor esperado será de alrededor de 18.92%, pero, además, existe una probabilidad de 68.26% de que los rendimientos estén entre 2.74% y 35.1%; una probabilidad de 95.44% de que los rendimientos estén entre —13. 44% y 51.28%; y un 99.74% de probabilidad de que los rendimientos estén entre — 29.62% y 67.46%. Cuanto menor sea la desviación estándar, menos dispersos serán los rendimientos y más precisa será la media como predictor de retornos futuros.
Error de muestreo. La distribución normal es una distribución importante tanto desde el punto de vista teórico como práctico. Es importante tener en cuenta que si estás viendo una pequeña muestra de datos, es probable que su pdf de base empírica no tenga la forma de una distribución normal aunque realmente se genere a partir de una distribución normal. En una muestra pequeña, la distribución tendrá huecos y agujeros en ella y es poco probable que tenga una forma que se parezca a la distribución verdadera que generó los datos. Si sigues agregando observaciones de la distribución, eventualmente los huecos se llenarán, y empezará a parecerse a la distribución verdadera que generó los datos. El punto aquí es, aunque el pdf de muestra generado por una distribución normal sí se vea como una distribución normal, esto puede deberse a que el tamaño de la muestra es demasiado pequeño. Por lo tanto, debido a su utilidad y trazabilidad, muchas veces asumimos que nuestros pdfs de muestra se distribuyen normalmente.
Variables de resultados directos e indirectos
Por lo general, conectamos un evento riesgoso a una variable aleatoria y (). Por ejemplo, puede representar precios inciertos e y () puede representar ingresos que dependen de precios inciertos. Nos referiremos a como la variable de resultado directo e y () como la variable de resultado indirecto sobre la que se define la utilidad de la empresa.
En la mayoría de los modelos de riesgo, la relación entre e y () es monótona, si la variable de resultado directo sube (baja) también lo hace la variable de resultado indirecto. Si los precios aumentan, también lo hace el ingreso; si la varianza de aumenta, también lo hace la varianza de y (). Sin embargo, se pueden construir fácilmente ejemplos en los que el enlace no es tan directo. Por ejemplo, supongamos que la firma enfrenta estrés financiero y que sólo resultados muy favorables permitirán a la firma cumplir con sus obligaciones de flujo de caja y sobrevivir. En tales circunstancias, la firma puede aumentar sus ingresos esperados y su probabilidad de sobrevivir eligiendo una estrategia que incremente su varianza de resultados directos. Considera tal problema definiendo una variable de resultado indirecto w = 0 si la empresa no logra sobrevivir y w = 1 si la firma sobrevive. En este modelo la variable de resultado directo es y. Luego conectamos la variable de resultado indirecto w a la variable de resultado directo y definiendo un ingreso de supervivencia yd y definiendo w en términos de y de la siguiente manera:
\ [w=\ left\ {\ begin {array} {ll} {0} & {\ text { for}\ quad y<y_ {d}}\\ {1} & {\ text {for}\ quad y\ geq y_ {d}}\ end {array}\ right. \ nonumber\]
La regla de decisión ad hoc puede expresarse de la siguiente manera:
\ [V (y) =\ left\ {\ begin {array} {lll} {U (0)} & {\ text {for}} & {y<y_ {d}}\\ {U (1)} & {\ text {for}} & {y\ geq y_ {d}}\ end {array}\ right. \ nonumber\]
Dado que U (0) y U (1) son valores asignados arbitrariamente, vamos U (0) = 0 y U (1) = 1. Entonces, la regla de decisión ad hoc a maximizar es:
(15.14)
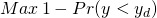
que llama a minimizar Pr (y < y d). Esta regla se conoce como la regla de la seguridad primero de Roy. Cuando los resultados directos se definen en términos de ganar o perder, la regla de seguridad primero de Roy es consistente con un modelo de utilidad esperado.
Por supuesto, se puede pensar en otras relaciones de variables de resultado directas e indirectas. Por ejemplo, y podría representar ingresos no asegurados y w podría representar ingresos asegurados, o y podría representar ingresos no cubiertos y w podría representar ingresos cubiertos, o y podría representar ingresos producidos sin insumos que reduzcan el riesgo y w podría representar ingresos producidos con insumos reductores de riesgo.
Entonces, ¿qué hemos aprendido? Aprendimos que las respuestas de riesgo se definen sobre las variables de resultado directo. La falta de distinción entre variables de resultado indirectas y directas puede llevarnos a ver las respuestas a las variables de resultado indirectas como las que prefieren el riesgo cuando efectivamente están evitando el riesgo.
Respuestas Firmas al Riesgo
Los individuos y las empresas enfrentan eventos de riesgo, incluida la posibilidad de pérdidas que los dejan menos acomodados que antes de que ocurriera el resultado asociado con el evento de riesgo. Estos resultados pueden incluir a usted o alguien a quien le importa enfermarse o estar desempleado. Los negocios también enfrentan la posibilidad de perder clientes, fallas de producción, precios decrecientes y pérdida de apoyo financiero.
En la siguiente sección se describen respuestas alternativas a eventos de riesgo disponibles para empresas y particulares. Si las empresas y los individuos limitan sus respuestas de riesgo descritas por alternativas en una frontera de vehículos eléctricos y seleccionan alternativas de riesgo consistentes con sus preferencias de riesgo subyacentes, entonces maximizarán su ingreso equivalente de certeza. Los tomadores de decisiones con mayor aversión al riesgo seleccionarán inversiones con valores esperados y varianzas más bajos. Los tomadores de decisiones con menos aversión al riesgo seleccionarán inversiones con mayores valores esperados y varianzas. Si la posición de riesgo actual de la empresa es una combinación de valor y varianza esperada fuera de la frontera, entonces las respuestas de riesgo de la empresa pueden diseñarse para acercar a la empresa a una posición en la frontera EV.
Más al punto, subir o bajar su frontera de vehículos eléctricos implica pagar a otra unidad para absorber parte o la totalidad de su riesgo (por ejemplo, comprar un seguro) o cambiar la cantidad relativa de inversiones seguras y riesgosas en su cartera.
Alguien alguna vez afirmó que los economistas pueden predecir correctamente el pasado solo el 50% de las veces. ¿Imagina cuán exitosos son los economistas para predecir resultados futuros para eventos de riesgo? Esto debería sugerir que aunque presentemos soluciones de respuesta al riesgo en formas cerradas, debemos ser cautelosos y explorar supuestos y predicciones alternativas para explorar la robustez de nuestras estimaciones. Con esa precaución en mente, procedemos a explorar las respuestas de riesgo externas (pagar a otros para que absorban nuestro riesgo) y las respuestas de riesgo internas (cambiar las tenencias de la empresa de inversiones riesgosas y seguras).
Nuestra discusión sobre eventos riesgosos e inciertos y cómo medir las probabilidades de sus resultados nos ha preparado para evaluar respuestas de riesgo alternativas que incluyen: (1) compartir el riesgo con otros a través de diversos arreglos que incluyen la formación de asociaciones y cooperativas, (2) compra de seguros, (3) diversificar las tenencias de inversiones de riesgo, (4) comprar insumos para reducir el riesgo y (5) elegir una estructura de capital óptima. Además, introduciremos el criterio de varianza de valor esperado para clasificar las inversiones alternativas de riesgo. Finalmente exploraremos cómo convertir el flujo de caja riesgoso a sus equivalentes de certeza puede proporcionar los medios para introducir el riesgo en los modelos PV para que se cumpla el principio de medidas homogéneas aplicado al riesgo.
Cómo compartir resultados riesgosos
Una forma de mitigar el impacto de los resultados adversos asociados con eventos de riesgo es mediante la formación de acuerdos de riesgo compartido con otros, incluso cuando se enfrentan a riesgos similares. La clave para lograr combinaciones exitosas de reducción de riesgos con otras es combinar operaciones que sean estadísticamente independientes entre sí. La independencia estadística tiene un significado preciso, pero esencialmente significa que el valor esperado del producto de dos variables aleatorias es igual al producto de sus valores esperados. En una sección posterior discutiremos la combinación de las operaciones de las empresas dentro de otras firmas cuyos rendimientos tienden a moverse juntos.
Para hacer el punto de que combinar unidades que
experimentan resultados de riesgo independientes puede mitigar
el riesgo, considere lo siguiente. Sea x una variable aleatoria con
valor esperado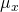 y varianza
y varianza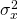 respectivamente. Deje que “a” y “b” sean iguales a constantes numéricas. Luego,
defina una nueva variable aleatoria:
respectivamente. Deje que “a” y “b” sean iguales a constantes numéricas. Luego,
defina una nueva variable aleatoria:
(15.15)
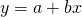
La varianza de y,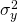 ,
es igual a:
,
es igual a:
(15.16)
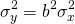
La explicación para la Ecuación\ ref {15.16} es que la varianza de la constante “a” o cualquier constante es siempre cero mientras que la varianza de una constante por una variable aleatoria es la constante cuadrada por la varianza de la variable aleatoria.
En Ecuación\ ref {15.15} creamos una nueva variable aleatoria y transformando linealmente la variable aleatoria x. Ahora considere otra forma de crear una nueva variable aleatoria, tomando el promedio de dos (o más variables aleatorias). Por ejemplo, supongamos que dos negocios enfrentaban ingresos riesgosos distribuidos de forma independiente. Un dueño de negocio enfrentó la variable aleatoria x 1 y el segundo dueño de negocio enfrentó la variable aleatoria x 2. También supongamos que los dos dueños de negocios decidieron combinar sus negocios y acordaron que cada uno recibiría la mitad de las ganancias promedio. En este proceso definimos una nueva variable aleatoria.
(15.17)
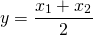
Primero, reconoce que cada variable aleatoria se multiplica por la constante (1/2). Entonces cada socio ganaría en promedio el valor esperado
(15.18)
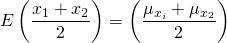
y la varianza que enfrentaría cada propietario sería la varianza de la rentabilidad esperada multiplicada por la constante (1/2) cuadrada. La varianza de las ganancias promedio que recibiría cada empresa, σ y 2, es igual a:
(15.19)
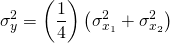
n el caso de que las distribuciones se distribuyeran
idénticamente con el valor esperado y la varianza de
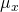 y
y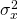 ,
cada socio enfrentaría el mismo valor esperado que antes,
,
cada socio enfrentaría el mismo valor esperado que antes,
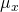 .
Pero, la varianza de sus ganancias individuales sería
.
Pero, la varianza de sus ganancias individuales sería![]() ,
la mitad de lo que era antes sin combinar sus negocios.
Además, la desviación estándar de las ganancias
que enfrentaría cada socio sería:
,
la mitad de lo que era antes sin combinar sus negocios.
Además, la desviación estándar de las ganancias
que enfrentaría cada socio sería:
(15.20)
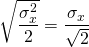
Y si n socios
se unían, entonces cada uno enfrentaría el
mismo valor esperado que antes, pero la varianza que recibiría cada socio es![]() .
Ahora ilustramos
estos importantes resultados.
.
Ahora ilustramos
estos importantes resultados.
Supongamos que las ganancias de uno de los negocios están determinadas por los resultados asociados con el tiro de una moneda justa. Si el resultado del lanzamiento de la moneda es colas, la firma paga (pierde) $5,000. Si el tiro es una cabeza, la firma gana $8,000. Así, la firma gana ya sea $8,000 o pierde $5,000 y gana en promedio (.5) (—5,000) + (.5) (8,000) = $1500.
La desviación estándar de estos resultados riesgosos es:
(15.21)
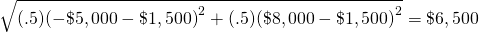
Además, asumiendo una distribución normal, 68% del tiempo, el resultado promedio estará entre la media y más o menos una desviación estándar: ($1,500 + $6,500) = $8,000 y ($1,500 — $6,500) = —$5,000.
Ahora supongamos que dos personas deciden combinar sus operaciones y compartir el promedio de los resultados. Entonces los posibles resultados de dos tiradas de monedas son dos cabezas (H, H) que gana en promedio $16,000/2 = $8,000 y ocurre con una probabilidad de .25; dos colas (T, T) que gana en promedio —$10,000/2 = —$5,000 y ocurre con una probabilidad de .25, y una cabeza y una cola (H, T) o una cola y una cabeza (T, H) que ambas ganan en promedio $3,000/2 = $1,500 y cada una ocurre con una probabilidad de .25. El valor esperado para cada uno de los dos jugadores ahora se puede expresar como:
(15.22)
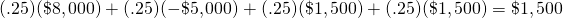
Los dos jugadores ahora reciben en promedio lo mismo que antes, $1.500, pero considera la desviación estándar del resultado promedio:
(15.23)

Además, asumiendo una distribución normal, 68% del tiempo, el resultado promedio estará entre la media y más o menos una desviación estándar: ($1,500 + $4,596) = $6,096 y ($1,500 — $4,596) = —$3,096. Obsérvese que aunque el valor esperado no cambió cuando los resultados se promediaron sobre dos personas, la desviación estándar se redujo casi 30%. También tenga en cuenta que los resultados están de acuerdo con la Ecuación\ ref {15.24}:
(15.24)
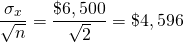
Ahora imagina diez personas cada una enfrentando resultados de ingresos distribuidos independientes e idénticos, entonces la desviación estándar que enfrentaría cada una sería igual:
(15.25)
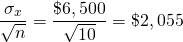
Además, asumiendo una distribución normal, 68% del tiempo, el resultado promedio oscilará entre ($1,500 — $2,055) = —$555.48 y ($1,500 + $2,055) = $3,555. Obsérvese que aunque el valor esperado no cambió cuando los resultados se promediaron sobre diez personas, la desviación estándar se redujo casi por encima del 70%. La reducción de la variabilidad para cada persona en más del 70% mediante la combinación de diez eventos de riesgo independientes (enfrentados a cada una de las 10 firmas independientes) ilustra el poder de reducir el riesgo al compartir eventos de riesgo independientes.
En el ejemplo anterior asumimos que cada
socio aportó una participación igual. Ahora supongamos que dos personas
decidieron formar una sociedad y compartir el riesgo y los rendimientos
esperados ponderados por sus acciones aportadas al negocio. Asumir
socio 1 aportó w 1 = 30% de los activos
y socio 2 aportó w 2 = 70% del
negocio. La tasa de rendimiento comercial de cada socio puede describirse
mediante variables aleatorias y 1 e
y 2 con valores esperados y varianzas para el
socio uno de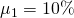 y
y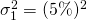 para el primer socio y
para el primer socio y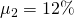 y
y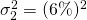 para el segundo socio. Queremos encontrar el valor esperado de la
asociación y la participación de cada socio del valor esperado. Entonces,
queremos encontrar la varianza de la asociación y la varianza de
rendimientos que enfrentaría cada socio.
para el segundo socio. Queremos encontrar el valor esperado de la
asociación y la participación de cada socio del valor esperado. Entonces,
queremos encontrar la varianza de la asociación y la varianza de
rendimientos que enfrentaría cada socio.
Primero, para encontrar el valor esperado de la asociación, ponderamos la contribución de cada socio por el porcentaje de sus contribuciones. Llame al retorno esperado de la asociación E (y p):
(15.26)
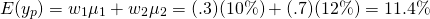
En tanto, la varianza del rendimiento esperado de la asociación es la suma de las varianzas individuales multiplicadas por las acciones de los socios al cuadrado:
(15.27)
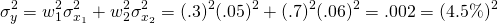
Además, la desviación estándar de la cartera es de 4.5%. Así, la sociedad gana 11.4% sobre sus inversiones y enfrenta una desviación estándar de rendimientos igual a 4.5% que es menor que su desviación estándar de rendimientos enfrentados solos igual a 5.0% o 6.0%. Por supuesto, tendrían que ponerse de acuerdo sobre cómo distribuir las ganancias, pero asumimos que estaría basado en las acciones que aportaron.
Reducción del riesgo mediante la compra de seguros
Puede ser difícil para una firma individual ponerse de acuerdo con otras firmas independientes sobre cómo compartir las ganancias y el riesgo. Sin embargo, una compañía de seguros que absorbe el riesgo de las empresas individuales a cambio de una prima de seguro puede reducir el riesgo general al combinar el riesgo que enfrenta un gran número de firmas individuales. Además, al seleccionar cuidadosamente negocios de diferentes áreas geográficas y de diferentes tipos, el riesgo absorbido por las empresas individuales puede ser casi insignificante.
Para la mayoría de las personas y negocios, los seguros ofrecen una forma de reducir su riesgo cuando no se dispone de otras medidas. El seguro es un arreglo práctico mediante el cual una compañía o agencia gubernamental proporciona compensación por una amplia variedad de pérdidas y resultados adversos. Por ejemplo, podemos adquirir un seguro médico en caso de que nos enfermemos, seguro contra incendios en caso de incendio, seguro a término y de vida completa para nuestros herederos si morimos, seguro de ingresos en caso de que nuestros gastos excedan los ingresos, seguro de viaje en caso de que nuestro vuelo se cancele, y casi cualquier otro resultado adverso siempre y cuando estemos dispuestos a pagarle a alguien para que asuma la posibilidad de pérdida. A continuación se describe este tipo de seguro, el seguro discreto de eventos de desastre.
Seguro discreto para eventos de desastre.
Considerar una firma con riqueza compuesta por un activo de riesgo, cuyo valor
es W en el mejor estado de la naturaleza y cero en el peor
estado de la naturaleza, y activos libres de riesgo valorados en
W 0 independientemente del estado de la naturaleza. Una compañía de
seguros está dispuesta a absorber el riesgo de posibles pérdidas
de riqueza a cambio de una prima de seguro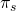 .
La firma debe determinar la prima máxima de seguro
.
La firma debe determinar la prima máxima de seguro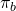 que puede pagar para evitar un desastre sin reducir el nivel de su
certeza equivalente de riqueza por debajo del nivel alcanzado sin cobertura de
seguro. La firma puede incrementar su certeza equivalente de
ingresos mediante la compra de seguros si
que puede pagar para evitar un desastre sin reducir el nivel de su
certeza equivalente de riqueza por debajo del nivel alcanzado sin cobertura de
seguro. La firma puede incrementar su certeza equivalente de
ingresos mediante la compra de seguros si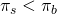 .
.
Supongamos que la firma está considerando una póliza integral de seguro
contra incendios y W representa el valor de los bienes inflamables de la
firma asegurados. Para encontrar la prima máxima de
seguro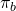 que la firma puede pagar sin reducir su certeza de
ingresos equivalentes, formamos la matriz de decisión que se muestra en la Tabla 15.2.
que la firma puede pagar sin reducir su certeza de
ingresos equivalentes, formamos la matriz de decisión que se muestra en la Tabla 15.2.
La matriz tiene dos posibles estados de la naturaleza, dos
opciones y cuatro posibles resultados diferentes. Los estados de la naturaleza
son (1) un estado de fuego s 1, y (2) un
estado sin fuego s 2. Las opciones son comprar un seguro
(opción A 1) y permanecer sin seguro (opción
A 2). Si se
selecciona la opción A1, el resultado en ambos estados s 1 y
s 2 es inicial rico W +
W 0 menos una prima de seguro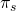 .
Este resultado se obtiene porque si ocurre un incendio, la aseguradora
reembolsa a la firma sus pérdidas y recibe una
prima de riesgo. Si no hay incendio, la aseguradora no paga
pérdidas mientras sigue ganando la prima del seguro. En ambos estados
la firma que compra el seguro paga una prima. Si, por otro
lado, la firma decide permanecer sin seguro (opción
A 2) y no se produce ningún incendio, la firma quedará tanto
con su patrimonio seguro W 0 como con su
riqueza riesgosa W y habrá ahorrado la prima del seguro
porque no compró un seguro. No obstante, si se produce un incendio, la
firma perderá su arriesgada riqueza W. Estos resultados se
resumen a continuación.
.
Este resultado se obtiene porque si ocurre un incendio, la aseguradora
reembolsa a la firma sus pérdidas y recibe una
prima de riesgo. Si no hay incendio, la aseguradora no paga
pérdidas mientras sigue ganando la prima del seguro. En ambos estados
la firma que compra el seguro paga una prima. Si, por otro
lado, la firma decide permanecer sin seguro (opción
A 2) y no se produce ningún incendio, la firma quedará tanto
con su patrimonio seguro W 0 como con su
riqueza riesgosa W y habrá ahorrado la prima del seguro
porque no compró un seguro. No obstante, si se produce un incendio, la
firma perderá su arriesgada riqueza W. Estos resultados se
resumen a continuación.
Cuadro 15.2. Matriz de Decisiones para Seguros Versus No Seguros con un Desastre Discreto.
| Opciones | |||
| Estados de la naturaleza | Probabilidad de resultados | Resultados A 1 (comprar seguro) | A 2 (No compre seguros) resultados |
| (s 1) fuego | 0 < p < 1 |
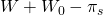 |
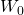 |
| (s 2) sin fuego | 1 — p |
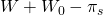 |
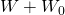 |
Si la probabilidad de incendio es p y la probabilidad de no incendio es 1 — p, los valores esperados de las dos opciones E (A1) y E (A2) son:
(15.28)
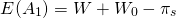
Y
(15.29)
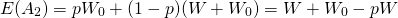
La diferencia entre E (A1) y E (A2) se puede expresar como:
(15.30)
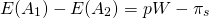
Si el tomador de decisiones era neutral en cuanto al riesgo y
decidiera entre opciones en función de su valor esperado,
el máximo que pagaría el cliente por el seguro contra incendios sería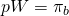 ,
y siempre y cuando
,
y siempre y cuando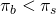 el cliente estaría mejor comprando un seguro que no
comprarlo.
el cliente estaría mejor comprando un seguro que no
comprarlo.
Para ilustrar, supongamos que la
propiedad inflamable fue W = $100,000 y p = 1%. Entonces,
lo máximo que un cliente podría pagar y el equilibrio basado en sus
valores esperados sería Pw = (.01) ($100,000) = $1,000. Si una póliza de
seguro estuviera disponible por menos de $1,000, se le
recomendaría al cliente que comprara el seguro. Supongamos que el cliente es reacio al
riesgo y se despierta por la noche preocupándose por la posibilidad
de un incendio, y tal vez el cliente esté dispuesto a pagar una prima de
seguro adicional basada en alguna función de p y
W igual a U (p, W) $150 para saber
que, pase lo que pase, el resultado será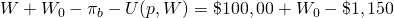 .
.
Seguro de ingresos. Una de las formas más importantes de seguros disponibles para individuos y empresas es el seguro de ingresos. Los principios generales del seguro de ingresos pueden ser complicados. Describimos una versión simplificada del seguro de ingresos con resultados discretos.
Supongamos que un resultado de una operación de cultivo es un evento
riesgoso con tres posibles resultados: ingreso normal y, ingreso
reducido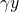 donde
donde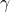 hay un porcentaje entre uno y cero, o un cultivo fallido que resulta en
y = 0. Que la probabilidad de y sea
p 1. Que la probabilidad de
hay un porcentaje entre uno y cero, o un cultivo fallido que resulta en
y = 0. Que la probabilidad de y sea
p 1. Que la probabilidad de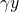 ser p 2. Y que las probabilidades de un
cultivo fallido y un ingreso cero sean (1 — p 1 —
p 2).
ser p 2. Y que las probabilidades de un
cultivo fallido y un ingreso cero sean (1 — p 1 —
p 2).
El seguro proporcionado no compensa completamente a los agricultores por sus pérdidas por razones de riesgo moral; quieren que los agricultores experimenten algunas pérdidas por no producir un cultivo normal.
En consecuencia, los ingresos perdidos sólo se compensan
por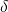 ciento. Además, existe un proceso complicado para determinar
qué es un rendimiento normal que produce y. Si
se produce un resultado fallido de cosecha, la empresa recibe
ciento. Además, existe un proceso complicado para determinar
qué es un rendimiento normal que produce y. Si
se produce un resultado fallido de cosecha, la empresa recibe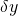 o
o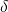 porcentaje de lo que normalmente gana. Si
se produce un resultado parcial de la cosecha, entonces la firma también gana
porcentaje de lo que normalmente gana. Si
se produce un resultado parcial de la cosecha, entonces la firma también gana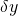 porque la compañía
porque la compañía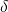 de seguros paga los ingresos perdidos de la firma igual a
de seguros paga los ingresos perdidos de la firma igual a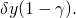
Para describir el programa de seguro de ingresos descrito anteriormente construimos el Cuadro 15.3.
Cuadro 15.3. Matriz de Decisiones para Ingresos con Seguros Versus Sin Seguros con Resultados Discretos.
| Opciones | |||
| Estados de la naturaleza | Probabilidad de resultados | Resultados A 1 (comprar seguro) | A 2 (No compre seguros) resultados |
| (s 1) cosecha completa | p 1 |
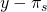 |
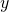 |
| (s 2) cultivo parcial | p 2 |
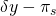 |
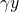 |
| (s 3) fracaso del cultivo | (1 — p 1 — p 2) |
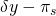 |
0 |
Para resolver para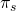 equiparamos el valor esperado para las dos opciones de elección:
equiparamos el valor esperado para las dos opciones de elección:
(15.31)
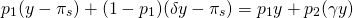
Y resolviendo para la prima del seguro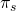 encontramos:
encontramos:
(15.32)
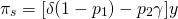
Para ilustrar, supongamos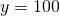 y para
y para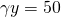 que
que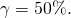 Supongamos que la probabilidad de un ingreso normal es del 60%, la
probabilidad de un cultivo parcial y un ingreso reducido es del 30%, y la
probabilidad de un fracaso completo del cultivo y ningún ingreso es del 10%.
Por último, suponga que tu póliza de seguro de ingresos cubre
Supongamos que la probabilidad de un ingreso normal es del 60%, la
probabilidad de un cultivo parcial y un ingreso reducido es del 30%, y la
probabilidad de un fracaso completo del cultivo y ningún ingreso es del 10%.
Por último, suponga que tu póliza de seguro de ingresos cubre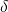 = 80% de los ingresos perdidos. Reafirmamos estas condiciones en la Tabla 15.4
y luego resolvemos la prima del seguro de equilibrio
= 80% de los ingresos perdidos. Reafirmamos estas condiciones en la Tabla 15.4
y luego resolvemos la prima del seguro de equilibrio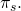
Cuadro 15.4. Matriz de Decisión para Seguros de Ingresos Versus Sin Seguro con Resultados Discretos.
| Opciones | |||
| Estados de la naturaleza | Probabilidad de resultados | Resultados A 1 (comprar seguro) | A 2 (No compre seguros) resultados |
| (s 1) cosecha completa | p 1 = 60% | 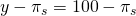 |
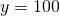 |
| (s 2) cultivo parcial | p 2 = 30% | 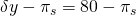 |
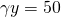 |
| (s 3) fracaso del cultivo | (1 — p 1 — p 2) = 10% | 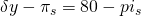 |
0 |
Finalmente, resolvemos para la
prima de seguro de equilibrio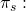
(15.33)
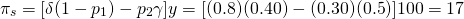
Es decir, un directivo podría permitirse pagar hasta 17% de sus ingresos normales como seguro de ingresos en las condiciones descritas en la Tabla 15.3.
Diversificación de Inversiones Firmas
Los inversionistas rara vez mantienen inversiones de manera aislada. En efecto, mantener una sola inversión por sí mismo puede ser muy arriesgado. La mayoría de los inversionistas intentan reducir el riesgo manteniendo una cartera de (dos o más) inversiones. Agregar una inversión riesgosa a una cartera de inversiones puede disminuir el riesgo de la cartera sin afectar negativamente el rendimiento esperado de la cartera. Ilustramos el punto de que agregar inversiones riesgosas a la cartera de uno puede disminuir el riesgo con un ejemplo.
Sombrillas y gafas de sol. Supongamos que en un día cualquiera hay tres posibles resultados climáticos: puede haber lluvia, puede haber una mezcla de nubes y sol, y puede haber cielos brillantes y soleados. Por simplicidad, supongamos que la probabilidad de cada resultado es 1/3. Una firma cuyos resultados dependen del estado meteorológico puede invertir en sombrillas o gafas de sol o en una mezcla de ambos. Tanto las inversiones en sombrillas como en gafas de sol obtienen una tasa de rendimiento esperada igual al 10%. Estos resultados se resumen en la Tabla 15.5 siguiente:
Cuadro 15.5. Rentabilidades esperadas y variaciones en inversiones en gafas de sol y paraguas
| Estados meteorológicos i = 1,2,3: | Probabilidad de estados meteorológicos | Devoluciones Aleatorias en Gafas de Sol en el estado meteorológico i º: r i S | Devoluciones aleatorias en Paraguas en el estado meteorológico i th: r i W | Rentabilidad sobre cartera |
| Lluvia | 1/3 | 0% | 20% | .5 (0) +.5 (20%) = 10% |
| Mezcla nubes y sol | 1/3 | 10% | 10% | .5 (10) +.5 (10%) = 10% |
| Soleado | 1/3 | 20% | 0% | .5 (20) +.5 (0%) = 10% |
| Retorno esperado de las inversiones: | E (r i S) = (1/3) (0% + 10% + 20%) = 10% | E (r i W) = (1/3) (20% + 10% + 0%) = 10% | .5E (r i S) + .5E (r i S) = (1/3) (10% + 10% + 10%) = 10% | |
| Desviación estándar de retornos: | 8.16% | 8.16% | 0% | |
Observe que cuando llueve, el retorno en sombrillas es favorable (20%) pero el retorno en gafas de sol es bajo, 0%. Lo contrario es cierto cuando hay cielos brillantes y soleados; el retorno de las sombrillas es bajo (0%) mientras que el retorno de las gafas de sol es favorable, 20%. La desviación estándar para ambas inversiones es igual a:
(15.34a)
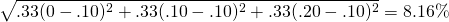
Ahora supongamos que la firma se diversificó y creó una cartera en la que el 50% de sus inversiones fueron en gafas de sol y el otro 50% fueron en paraguas. Los resultados se describen en la última columna del Cuadro 15.5. Observe que el retorno en cada estado es del 10% porque cuando las devoluciones en bajas en gafas de sol, el retorno en sombrillas son favorables y viceversa. Tenga en cuenta también que si bien cada inversión individual tiene una desviación estándar de rendimientos igual a 8.16%, el rendimiento de la cartera es constante y la desviación estándar de los rendimientos de la cartera es cero.
(15.34b)
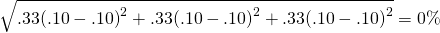
Este es un ejemplo extremo de cómo agregar una inversión riesgosa en realidad puede disminuir el riesgo de la firma. Sin embargo, este resultado favorable se dio porque los rendimientos en sombrillas y gafas de sol se correlacionaron perfecta y negativamente.
Medidas de covarianza. Estar perfecta y negativamente correlacionado significa que los rendimientos de una inversión están por encima de su media exactamente por la misma cantidad que la otra inversión está por debajo de su media en el mismo estado. Una medida de correlación entre dos variables aleatorias es la medida de covarianza. Usando la notación del ejemplo de paraguas y gafas de sol, definimos la covarianza como:
(15.35)
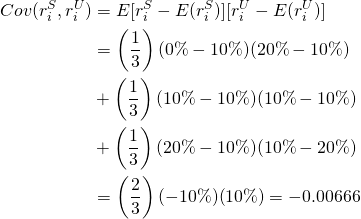
Observe que la covarianza es similar a una medida de varianza excepto que en lugar de que una desviación del valor esperado sea cuadrada, la desviación para ambas variables en el mismo estado se multiplica, por lo que la covarianza mide si las dos variables se están moviendo en direcciones opuestas desde su medias (covarianza negativa) o si las dos variables se mueven en la misma dirección desde sus medias (covarianza positiva). Para enfatizar la diferencia entre las medidas de varianza y covarianza, al calcular la varianza, se calcularon desviaciones al cuadrado de la media, y como resultado todas las varianzas son positivas. En contraste, la desviación en las medidas de covarianza no son cuadradas lo que les permite ser positivas o negativas. Obsérvese que el primer y tercer término en el cálculo de covarianza en la Ecuación\ ref {15.35} fueron negativos mientras que el segundo término fue cero. Así, la covarianza de las inversiones en gafas de sol y sombrillas es negativa.
Obviamente el ejemplo de gafas de sol y sombrillas se
simplifica para ilustrar un punto, ese riesgo se
elimina por completo porque los rendimientos de las dos inversiones tienen
perfecta correlación negativa. El nivel de correlación entre
rendimientos se mide por el coeficiente de correlación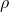 definido como:
definido como:
(15.36)
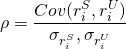
Así, en nuestro ejemplo, el coeficiente de correlación es negativo:
(15.37)
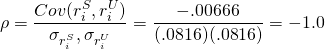
Obviamente, al igual que otras cosas, preferiríamos agregar inversiones a nuestra cartera que estén correlacionadas negativamente con los rendimientos generales de nuestra cartera.
Volvamos a nuestra investigación de la asociación, solo que esta vez permitan que una sola firma considere su tasa de rendimiento en su cartera de inversiones. Supongamos que tiene dos inversiones y el porcentaje de la cartera total invertida en cada inversión se indica por un peso w 1 y w 2 que suman a uno. El valor esperado para la cartera de la firma se puede expresar como antes:
(15.38)
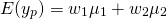
Consideremos ahora la varianza de la cartera del inversionista. Si las inversiones están representadas por variables aleatorias independientes, la varianza de cartera es como antes, la suma ponderada de las varianzas individuales. Cuando las inversiones no son independientes, la varianza de cartera también incluye un término de covarianza. Podemos escribir la varianza de la cartera permitiendo la dependencia entre las dos inversiones como:
(15.39)
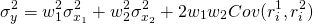
Ahora aplicamos nuestro enfoque de portafolio al ejemplo de paraguas y gafas de sol. Recordemos que ambas inversiones obtuvieron una tasa de rendimiento esperada del 10% y sus desviaciones estándar fueron ambas iguales a 8.16%. Si la firma dividiera su cartera entre las dos inversiones, entonces escribiríamos el valor esperado y la varianza de la cartera como:
(15.40)
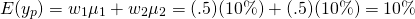
Y escribimos la varianza de cartera como:
(15.41)
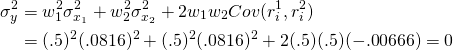
En este ejemplo especial, que los rendimientos de las gafas de sol y los paraguas se movieran en dirección perfectamente opuesta significa que combinar inversiones en ambos eliminó la variabilidad de los rendimientos en la cartera de la firma.
Coeficientes beta y diversificación de riesgos. Un concepto de riesgo importante aplicado a los mercados de valores pero que también tiene aplicación a la firma es el coeficiente beta (β). El coeficiente beta es una medida asociada a una inversión individual que refleja la tendencia de los rendimientos de una inversión a moverse con el rendimiento promedio en el mercado. Aplicado a la firma individual, el coeficiente beta mide la tendencia de los rendimientos de una inversión individual a moverse con el rendimiento promedio de la cartera de inversiones de la firma.
Para explicar el coeficiente beta, supongamos que tenemos observaciones anteriores de tasa de retorno r t j sobre una nueva inversión potencial y sobre la cartera de rendimientos de la firma r t p en periodo de tiempo t . La Tabla 15.6 resume nuestras observaciones:
Cuadro 15.6. Observaciones de Rentabilidades sobre la Cartera de Inversiones de la Firma r t p y sobre una Nueva Inversión Potencial (a Challenger).
| Tiempo t | Rentabilidad observada en la cartera de la firma a lo largo del tiempo r t p | Rentabilidad observada de una nueva inversión potencial para r t j de la firma |
| 2012 | 10% | 7% |
| 2013 | 6% | 8% |
| 2014 | 7% | 5% |
| 2015 | 3% | 2% |
| 2016 | 5% | 3% |
Otra forma de representar las dos tasas de medidas de retorno y su relación entre sí es representarlas en un gráfico de dispersión bidimensional.
Podemos observar visualmente cómo los dos conjuntos de tasas de retorno se mueven juntos dibujando una línea a través de los puntos en la gráfica de tal manera que se minimice la distancia cuadrada del punto a la línea. Nuestro gráfico de dispersión se identifica como Figura 15.3.
Figura 15.3. Gráfico de dispersión de rendimientos de la cartera de inversiones de la firma y rendimientos de la nueva inversión potencial
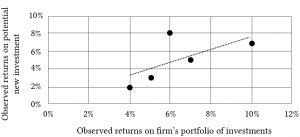
La relación entre los rendimientos de la nueva inversión y la cartera de la firma se puede expresar como:
(15.42)
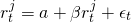
Observe que la ecuación anterior describe la línea recta dibujada a través del punto más la distancia vertical de la línea a cada punto. La pendiente de la línea es el coeficiente beta β y nos dice cómo los rendimientos de la cartera y la nueva inversión potencial se han movido juntos en el pasado. Podemos encontrar la ecuación para esta línea utilizando un método estadístico llamado análisis de regresión de “mínimos cuadrados”. El método esencialmente encuentra una línea de manera que se minimizan las desviaciones cuadradas promedio de la línea, ε t 2. La fórmula para beta es igual a la covarianza entre los rendimientos de la nueva inversión r t j y los rendimientos de la cartera de la firma r t p durante algún periodo de tiempo dividido por el varianza de los rendimientos de la cartera:
(15.43)
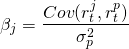
Afortunadamente, los cálculos para el coeficiente beta así como los coeficientes en la Ecuación\ ref {15.16} se pueden encontrar usando Excel. [2] Encontramos el coeficiente beta y los coeficientes para la Ecuación \ ref {15.16} utilizando los datos de la Tabla 15.6.
La ecuación estimada para la línea es:
(15.44)
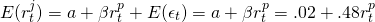
Riesgo diversificable y no diversificable. Supongamos un coeficiente beta de menos uno (—1). Esto significaría que para un incremento (disminución) de 10% en la tasa general de rendimiento de la firma, la tasa de retorno esperada de la inversión potencialmente nueva disminuye (aumenta) en 10%. Al igual que las inversiones en gafas de sol y sombrillas, una inversión suficiente en la nueva inversión eliminaría el riesgo de la firma. Así, una beta de —1 significa que todo su riesgo puede diversificarse. En contraste, supongamos un coeficiente beta de uno. Esto significaría que para un incremento (disminución) de 10% en la tasa general de rendimiento de la firma, que la tasa de retorno esperada de la inversión potencialmente nueva aumenta (disminuye) en 10%. A diferencia de invertir en gafas de sol y sombrillas, agregar la inversión potencialmente nueva a la cartera de inversión de la firma solo acentúa su riesgo, y la nueva inversión no tiene potencial para diversificar el riesgo general de la firma.
Inversiones para reducir el riesgo de compra
Es útil distinguir entre dos razones principales para invertir: primero, para aumentar las ganancias esperadas para la firma y segundo, para reducir la variabilidad de las ganancias. Si se puede aumentar los rendimientos esperados sin aumentar la varianza de rendimiento, el ingreso equivalente de certeza ha aumentado. Si se puede reducir la varianza de los rendimientos sin reducir también los rendimientos esperados, el ingreso equivalente de certeza ha aumentado. Ver Ecuación\ ref {15.12}. Por supuesto, si a partir de la posición actual de varianza de valor esperado, uno podría aumentar el valor esperado de los rendimientos sin aumentar la varianza de los rendimientos, o si se pudiera reducir la varianza de uno sin reducir también el valor esperado, entonces la empresa estaría en un esperado ineficiente posición valor-varianza fuera de la frontera EV. Sin embargo, podemos identificar inversiones cuyo propósito principal es reducir la variabilidad aunque alteren los ingresos esperados. A estas las llamamos inversiones reductoras de riesgos. Analizamos los insumos reductores de riesgo utilizando el modelo de ingresos equivalentes de certeza descrito en la Ecuación\ ref {15.12} que da cuenta tanto de la varianza como del valor esperado en el criterio de clasificación.
Ilustraremos inversiones que reducen riesgos con
un estudio de caso que involucra una inversión en riego. Considera una empresa
que enfrenta cinco estados de humedad con una probabilidad igual de probable de
ocurrir: normal, estrés bajo, estrés moderado, estrés alto y
sequía. Los rendimientos por acre con y sin el
sistema de riego se reportan en el Cuadro 15.7. El costo anualizado del sistema de
riego, que se espera tenga una vida útil de 20 años y ningún valor de
liquidación, es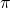 por acre. Asumimos que la TIR del defensor asociada al flujo de caja equivalente a
certeza es de 8%.
por acre. Asumimos que la TIR del defensor asociada al flujo de caja equivalente a
certeza es de 8%.
Cuadro 15.7. Devoluciones por Acre bajo Estados Alternativos de Humedad con y sin Sistema de Riego.
| Estados de humedad | Probabilidad de estados de humedad | Retorno por acre sin la inversión de riego r i w /0 | Retorno por acre con el sistema de riego r i w menos costos de riego por acre π |
| Normal | 20% | $128.00 | $113— π |
| Bajo estrés | 20% | $105.00 | $100 — π |
| Estrés moderado | 20% | $90.00 | $80 — π |
| Alto estrés | 20% | $75.00 | $75 — π |
| Sequía | 20% | $50.00 | $70— π |
| Retornos esperados | $89.60 | $87.60 | |
| Desviación estándar de retornos | 26,43$ | $16.28 | |
Supongamos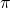 que son 15 dólares por acre. Entonces el valor esperado de la producción de cultivos por
acre sin riego sigue siendo de $89.60 y superior a $87.60. Si
el tomador de decisiones fuera neutral en el riesgo, no invertiría en
el sistema de riego. Permitir que el tomador de decisiones sea reacio al riesgo
y elija entre inversiones en base a su certeza
ingresos equivalentes en lugar de la diferencia en sus valores esperados. Si
este fuera el caso, entonces la certeza del ingreso equivalente sin
riego es:
que son 15 dólares por acre. Entonces el valor esperado de la producción de cultivos por
acre sin riego sigue siendo de $89.60 y superior a $87.60. Si
el tomador de decisiones fuera neutral en el riesgo, no invertiría en
el sistema de riego. Permitir que el tomador de decisiones sea reacio al riesgo
y elija entre inversiones en base a su certeza
ingresos equivalentes en lugar de la diferencia en sus valores esperados. Si
este fuera el caso, entonces la certeza del ingreso equivalente sin
riego es:
(15.45)
![]()
En contraste, la certeza de ingresos equivalentes con el sistema de riego es:
(15.46)
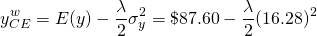
No podemos decidir entre los dos sistemas porque
uno tiene un valor esperado mayor y el otro tiene una varianza menor.
Todo depende de cuán reacio al riesgo sea el tomador de decisiones. Recordemos
que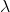 refleja la compensación preferida del tomador de decisiones entre el
rendimiento esperado por varianza. El λ de equilibrio en este caso se encuentra
equiparando los dos ingresos equivalentes de certeza:
refleja la compensación preferida del tomador de decisiones entre el
rendimiento esperado por varianza. El λ de equilibrio en este caso se encuentra
equiparando los dos ingresos equivalentes de certeza:
(15.47)
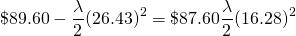
y resolviendo para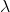 :
:
(15.48)
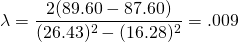
De esta manera, todos los tomadores de decisiones más reacios al riesgo de lo que
se refleja en el coeficiente de aversión al riesgo de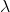 = .009 estarán ganando un valor esperado menor en promedio que el que
se obtendría sin el sistema de riego.
= .009 estarán ganando un valor esperado menor en promedio que el que
se obtendría sin el sistema de riego.
Elegir una estructura de capital óptima
Apalancamiento y riesgo. En un capítulo anterior, utilizamos el apalancamiento como medida del riesgo de la empresa sin indicar explícitamente la conexión. Ahora hacemos explícita la conexión reconsiderando la ecuación 8.5 y haciendo un ajuste. El ajuste es que dado que solo consideramos las ganancias de capital realizadas al encontrar ROA—IRR, ignoramos las ganancias de capital no realizadas (V 1 — V 0) lo que nos permite reescribir la ecuación 8.5 como:
(15.49)
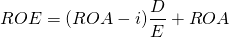
En la Ecuación\ ref {15.49}, anote el ratio de apalancamiento D/E y que multiplica la diferencia entre el ROA y la tasa de interés promedio i. Y ahora volvemos a un principio de riesgo introducido anteriormente, que multiplicando una variable aleatoria por una constante, en este caso el ratio de apalancamiento, aumenta la varianza de la variable aleatoria por la constante al cuadrado. Considerar la aplicación de este principio.
Supongamos que la variable aleatoria ROA es descrita por pdf f (r ROA) con valor esperado r ROA y varianza σ 2. Ahora supongamos que íbamos a multiplicar la variable aleatoria ROA por algún escalar, digamos 2. Entonces el valor esperado de la variable aleatoria sería 2 r ROA y la varianza sería 2 2 σ 2, o 4σ 2.
En la Ecuación\ ref {15.49}, la relación deuda-capital es el escalador que multiplica y exagera la diferencia entre r ROA e i. Para ilustrar, supongamos que ROA puede tomar valores de — 8%, — 3%, 3%, 5% y 12% e i = 3%. Después en el Cuadro 15.8 encontramos ROE para ratios de apalancamiento de 0, 2, 5 y 10.
Cuadro 15.8. ROE cuyos valores esperados y desviaciones estándar dependen de las relaciones de apalancamiento.
| Valores de la variable aleatoria ROA (i = 3%) | Valores ROE para relaciones de apalancamiento alternativas (L = D/E) y valores de la variable aleatoria ROA | |||
| L = 0 | L = 2 | L = 5 | L = 10 | |
| — 8% | — 8% | — 30% | — 63% | — 118% |
| — 3% | — 3% | — 15% | — 33% | — 63% |
| 3% | 3% | 3% | 3% | 3% |
| 5% | 5% | 9% | 15% | 25% |
| 12% | 12% | 30% | 57% | 102% |
| Desviaciones estándar para ROE asociadas con cada relación de apalancamiento L | ||||
| Valores esperados | 1.8% | — .6% | — 4.2% | — 10.2% |
| Desviación estándar σ | .077 | .23 | .460 | .843 |
Lo primero a tener en cuenta sobre los resultados en el Cuadro 15.8 es que siempre que el ROA supere la tasa de interés promedio i, ese ROE > ROA. Por ejemplo, para un ratio de apalancamiento de 2 y un ROA de 5%, ROE es 9%. El segundo punto a observar es que a pesar de que la E (ROA) > 0, a medida que aumentaba la relación de apalancamiento, la E (ROE) fue en su mayoría inferior a cero. En otras palabras, el efecto del apalancamiento fue más pronunciado cuando el ROA < i que cuando ROA > i. Otra cosa a tener en cuenta es que si el resultado de ROA es — 8% y la firma tiene un ratio de apalancamiento de 10, pierde 118% de su patrimonio. En otras palabras, un resultado desfavorable con un alto índice de apalancamiento puede destruir a la firma. Finalmente, debido al costo de la deuda que debe pagarse independientemente de los resultados del ROA, el costo de la deuda menor que el promedio de ROA con altos ratios de apalancamiento tiene efectos adversos significativos en el capital de la firma. Así, concluimos que un ratio de apalancamiento alto, aunque puede exagerar resultados de ROA inusualmente altos, sigue siendo un estado riesgoso para la firma. Por esa razón, muchas firmas ven la reducción del apalancamiento como una estrategia importante para reducir el riesgo de los resultados que enfrentan.
Estructura de capital. La estructura de capital de una empresa es su combinación de deuda y capital utilizada para financiar sus operaciones generales y crecimiento. La pequeña y mediana empresa puede financiar sus operaciones generales y su crecimiento mediante el uso de deuda a largo plazo, acciones y pagarés por pagar. Discutiremos la estructura de capital óptima de la pequeña a mediana empresa utilizando un modelo simplificado de ganancia de varianza de valor esperado (EV).
En nuestro modelo simplificado, permitimos que los activos
A de la firma sean financiados por una combinación de deuda D y capital
E. Dejamos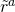 ser la tasa estocástica de rendimiento de los activos de la firma cuya
varianza es
ser la tasa estocástica de rendimiento de los activos de la firma cuya
varianza es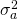 y cuya tasa de rendimiento esperada es r a. Dejamos que
el costo promedio no estocástico de la deuda por dólar esté representado
por la variable i D. La compensación
riesgo-rendimiento del tomador de decisiones en firme se mide por
y cuya tasa de rendimiento esperada es r a. Dejamos que
el costo promedio no estocástico de la deuda por dólar esté representado
por la variable i D. La compensación
riesgo-rendimiento del tomador de decisiones en firme se mide por![]()
Representamos las ganancias estocásticas de la firma
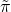 para igualar la tasa estocástica de rendimiento de los activos por activos menos
el costo promedio de la deuda de la empresa por la deuda de la empresa. Entonces
sustituimos por activos A la suma de deuda D más
capital E y cobramos términos similares y expresamos los
resultados estocásticos en la Ecuación\ ref {15.50}.
para igualar la tasa estocástica de rendimiento de los activos por activos menos
el costo promedio de la deuda de la empresa por la deuda de la empresa. Entonces
sustituimos por activos A la suma de deuda D más
capital E y cobramos términos similares y expresamos los
resultados estocásticos en la Ecuación\ ref {15.50}.
(15.50)
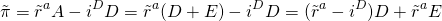
Escribimos el valor esperado de las ganancias estocásticas como:
(15.51)
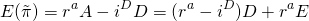
Escribimos la varianza de las ganancias como:
(15.52)
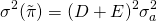
Finalmente, sustituimos el valor esperado y la
varianza de ganancias por la Ecuación\ ref {15.51} para encontrar la
certeza equivalente de ganancias de la firma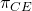 que denominamos modelo EV.
que denominamos modelo EV.
(15.53)
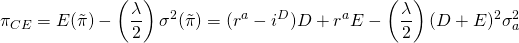
Encontrar la
estructura de capital óptima de la firma. [3]
Teniendo nuestro modelo EV definido sobre el valor esperado y la varianza de
ganancias y teniendo en cuenta las actitudes de riesgo del tomador de decisiones,
utilizamos el cálculo para encontrar el nivel óptimo de deuda diferenciando la función equivalente de
certeza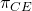 con respecto a D.
con respecto a D.
(15.54)
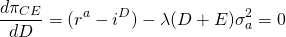
Se cumplen las condiciones de segundo orden que nos permiten resolver para la deuda óptima D * (asumiendo capital fijo). Encontramos la deuda óptima D * igual:
(15.55)
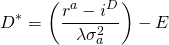
La ecuación (15.55) revela un detalle interesante. Si el costo de la deuda es igual al rendimiento esperado de los activos, la firma mantiene una deuda negativa, prefiriendo prestar su capital a una tasa segura i D en lugar de obtener un rendimiento estocástico de los activos de la empresa.
Dividiendo la Ecuación\ ref {15.55} por el capital E de la firma, podemos encontrar su ratio de apalancamiento óptimo l * igual a:
(15.56)
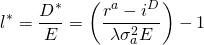
Ilustramos la Ecuación\ ref {15.56} usando
los datos de HQN. Sustituimos por r a el valor ROA igual
a 6.5% (ecuación 5.13), el costo promedio de la deuda
i D igual a 6% (ecuación 5.21), equidad
E igual a $8,000 (Cuadro 4.1), el
coeficiente de aversión al riesgo calculado en la Ecuación\ ref {15.48} igual a .009, y
finalmente, dejamos que la desviación estándar —la cantidad que los rendimientos de
los activos varían en promedio— sea igual a 1.25% o .0125 que cuadramos para encontrar
la varianza de ganancias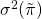 igual a .000156. Haciendo las sustituciones para las variables en la
Ecuación\ ref {15.56} encontramos que el ratio de apalancamiento óptimo de la empresa es
igual a:
igual a .000156. Haciendo las sustituciones para las variables en la
Ecuación\ ref {15.56} encontramos que el ratio de apalancamiento óptimo de la empresa es
igual a:
(15.57)
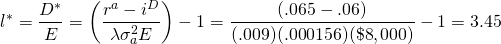
en comparación con la relación de apalancamiento real de la empresa de 4.0.
Variables cambiantes que afectan a la estructura de capital óptima. Podemos imaginar cómo cambiaría el apalancamiento óptimo en respuesta a los cambios en el valor de las variables incluidas en la Ecuación\ ref {15.57}. En otras palabras, nos preguntamos: ¿cómo cambiaría el apalancamiento óptimo si cambiara el valor de una de las variables en la Ecuación\ ref {15.57}? Podemos inferir la respuesta a esta pregunta observando los cambios en la relación óptima de apalancamiento en respuesta a un cambio en una de las variables que mantienen constantes las otras variables.
Aumentar el valor esperado de los rendimientos de los activos
r a hace que sea más rentable el uso de
fondos prestados y aumenta el ratio de apalancamiento óptimo. Aumentar el costo
promedio de la deuda i D hace que el uso de la deuda sea menos
rentable y reduce el ratio de apalancamiento óptimo. A medida que un
tomador de decisiones se vuelve más reacio al riesgo, representado por un aumento en el coeficiente de aversión al
riesgo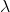 ,
el tomador de decisiones está menos dispuesto a arriesgarse a perder capital con un resultado
desfavorable y reduce el apalancamiento. A medida que
aumenta el capital de la empresa, puede lograr la misma combinación de riesgo y rentabilidad con
menos deuda y disminuye el ratio de apalancamiento óptimo. Finalmente, a medida que
,
el tomador de decisiones está menos dispuesto a arriesgarse a perder capital con un resultado
desfavorable y reduce el apalancamiento. A medida que
aumenta el capital de la empresa, puede lograr la misma combinación de riesgo y rentabilidad con
menos deuda y disminuye el ratio de apalancamiento óptimo. Finalmente, a medida que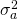 aumenta la
varianza del rendimiento de los activos de la empresa, la firma reduce su ratio de apalancamiento para regresar a su trade-off
preferido entre capital y deuda.
aumenta la
varianza del rendimiento de los activos de la empresa, la firma reduce su ratio de apalancamiento para regresar a su trade-off
preferido entre capital y deuda.
Además de describir cómo la firma encuentra su estructura de capital óptima en respuesta a cambios en el valor de las variables que determinan la estructura de capital óptima, creamos la Tabla 15.9. Las columnas en la Tabla 15.9 incluyen la lista de variables, sus valores originales para HQN, una columna que muestra valores incrementados de las variables, el ratio de apalancamiento óptimo revisado y el cambio en el ratio de apalancamiento óptimo en comparación con el ratio de apalancamiento óptimo original de 3.45.
Tabla 15.9 Ratios de apalancamiento óptimos y cambios en el ratio de apalancamiento óptimo en respuesta a incrementos en una de las variables de la Ecuación\ ref {15.57} manteniendo constantes las otras variables.
| Variable | Valor original | Mayor valor | Ratio de apalancamiento óptimo revisado | Cambio en la relación óptima de apalancamiento |
| r a | 6.5% | 7.0% | 7.903134 | 4.45 |
| i D | 6% | 6.5% | (1) | (4.45) |
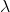 |
.009 | .001 | 3.01 | (.44) |
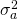 |
0.000156 | .000175 | 2.97 | (.48) |
| E | $8,000 | $9,000 | 2.96 | (.49) |
Resumen y Conclusiones
Se informa que algún sabio ha dicho que sólo la muerte y los impuestos son ciertos. Si esa afirmación está cerca de ser cierta, entonces el riesgo y la incertidumbre llenan el mundo en el que vivimos y tratamos de manejar. Un paso importante hacia el manejo de los resultados de eventos de riesgo es comprender las herramientas que se han desarrollado para reportarlo y medirlo. En este esfuerzo, no se espera precisión. Lo mejor es explorar la influencia del riesgo en una variedad de entornos y suposiciones.
Lo segundo a tener en cuenta sobre el riesgo, enfatizado en el ejemplo de riego, es que las preferencias individuales de riesgo pueden tener efectos significativos. Como resultado, dos individuos que enfrentan las mismas oportunidades de inversión pueden tomar decisiones diferentes debido a las diferentes preferencias de riesgo. En consecuencia, es importante que los directivos exploren sus propias preferencias de riesgo y las apliquen a la hora de tomar decisiones riesgosas.
Preguntas
- Esta pregunta tiene varias partes.
- ¿Cuál es la diferencia entre una muestra de observaciones y la población de posibles valores?
- Explicar la diferencia entre un valor esperado y varianza (desviación estándar) calculada a partir de una muestra y el valor esperado y varianza (desviación estándar) de una población.
- Encuentra el valor esperado y la varianza (desviación estándar) para los números 5, 8, —3, 9 y 0. Supongamos que cada número tiene una probabilidad igualmente probable de ser observado.
- Encuentre el valor esperado y la varianza poblacional ( desviación estándar) para los números 5, 8, —3, 9 y 0 si su probabilidad de ocurrir fue .1, .2, .4, .2 y .1 respectivamente.
- Comparar los resultados obtenidos en las partes c y d.
- Volver a la Tabla 15.1 en el texto. Supongamos que el inversionista decidió invertir la mitad de sus activos en inversión A y la mitad en inversión B. Describir la variable aleatoria para la inversión combinada. Luego describa su pdf, valor esperado y varianza (desviación estándar). Con base en los respectivos valores esperados y varianzas para la inversión A, la inversión B y la inversión combinada, ¿cuál preferiría, asumiendo que es reacio al riesgo?
- Supongamos que dos personas deciden formar una sociedad y comparten el riesgo y los rendimientos esperados en función de sus acciones aportadas al negocio. Asumir socio 1 aportó 40% de los activos y socio 2 aportó 60% de los activos. El negocio de cada socio puede describirse mediante variables aleatorias y 1 e y 2 con valores esperados y varianzas de μ 1 = 8% y σ 1 2 = 0.006 para el primer socio y μ 2 = 12% y σ 2 2 = .007 para el segundo socio. Encuentra el valor esperado desviación estándar de la sociedad.
- Supongamos que Kelly quiere mantener a sus herederos en caso de que fallezca durante el próximo año. Por lo tanto, compra una póliza de seguro de vida a término que paga $1,000,000 en caso de que fallezca a cambio de una prima de seguro de $800. Asumiendo que Kelly es neutral en cuanto al riesgo, ¿qué debe asumir Kelly es la probabilidad de su muerte para que pueda adquirir la póliza de seguro?
- Asumir las condiciones descritas en el Cuadro 15.3 excepto permitir que la cobertura del seguro δ aumente de 80% a 85%. Encuentra el incremento en la prima del seguro de equilibrio.
- Asumir las condiciones descritas en la Tabla 15.4. También suponga que en lugar de comprar un seguro de ingresos el inversionista podría adquirir un sistema de riego que aumentaría la probabilidad de un año de ingresos normales de 60% a 75%, reduciría la probabilidad de un año de ingresos reducidos de 30% a 20%, y reduciría la probabilidad de cero ingresos de 10% a 5%. ¿Qué sería lo máximo que podría pagar el directivo para reducir su riesgo a través de la compra de un sistema de riego y aún así estar tan bien como estaba antes? (Consejo: comparar el valor proporcionado por el sistema de riego menos el costo del sistema de riego en comparación con los resultados sin un sistema de riego.)
- Una de las diferencias entre la compra de un sistema de riego y el seguro de ingresos es que se tiene que adquirir un seguro de ingresos cada año mientras que el sistema de riego continúa brindando servicios de reducción de riesgos durante su vida útil. Si el sistema de riego descrito en la pregunta anterior estuvo disponible desde hace 10 años y la tasa de descuento fue del 8%, ¿cuál es el VPN del sistema de riego?
- Utilice los datos del Cuadro 15.5 para encontrar el coeficiente beta para la inversión en sombrillas y gafas de sol.
- Una firma tiene dos inversiones en su cartera. A continuación se reportan las tasas históricas de rendimiento de las dos inversiones. Encuentre la tasa de rendimiento esperada para la cartera de la firma, la covarianza entre las dos inversiones y la varianza de los rendimientos de la cartera. Clasifique la inversión 1, la inversión 2 y la inversión combinada utilizando el criterio EV.
Cuadro Q15.1. Observaciones de los rendimientos de las dos inversiones de la firma
| Tiempo t | Rentabilidad observada sobre la inversión uno. | Rentabilidad observada sobre la inversión dos. |
| 2012 | 10% | 7% |
| 2013 | 6% | 8% |
| 2014 | 7% | 5% |
| 2015 | 3% | 6% |
| 2016 | 5% | 4% |
- Los autores agradecen a Jack Meyer por el ejemplo de chincheta de un evento incierto.
- La ecuación de regresión lineal que incluye el coeficiente Beta se encuentra en Excel trazando primero un diagrama de dispersión y luego pasando el cursor sobre un punto de datos en la gráfica. Una discusión completa de los modelos de regresión lineal está fuera del alcance de esta clase.
- Esta sección utiliza el cálculo para encontrar el nivel óptimo de deuda de la firma y su óptima estructura de capital o ratio de apalancamiento (D/E). Los que no estén interesados en la derivación podrán pasar a la siguiente sección sin pérdida de continuidad en la discusión.


