2.2: Cuantificación de la incertidumbre a través de modelos de probabilidad

Objetivos de aprendizaje

• En esta sección, aprenderá a cuantificar la frecuencia relativa de ocurrencias de eventos inciertos mediante el uso de modelos de probabilidad.
• Aprenderás sobre las medidas de frecuencia, severidad, verosimilitud, distribuciones estadísticas y valores esperados.
• Utilizarás ejemplos para calcular estos valores.

Al considerar la incertidumbre, utilizamos rigurosos estudios cuantitativos del azar, el reconocimiento de su regularidad empírica en situaciones inciertas. Muchos de estos métodos se utilizan para cuantificar la ocurrencia de eventos inciertos que representan hitos intelectuales. A medida que creamos modelos basados en la probabilidad y las estadísticas, probablemente reconocerá que la probabilidad y las estadísticas tocan casi todos los campos de estudio hoy en día. A medida que hemos interiorizado la regularidad predictiva de repetidos eventos fortuitos, toda nuestra cosmovisión ha cambiado. Por ejemplo, nos hemos convencido de las probabilidades de que las cabezas en una moneda volteen tanto que es difícil imaginar lo contrario. Estamos acostumbrados a ver declaraciones como “vida media de 1,000 horas” en un paquete de bombillas. Entendemos tal frase porque podemos pensar en la duración de la vida de una bombilla como incierta pero estadísticamente predecible. Rutinariamente escuchamos declaraciones como “La probabilidad de lluvia mañana es del 20 por ciento”. Nos cuesta imaginar que hace apenas unos siglos la gente no creyera ni siquiera en la existencia de sucesos fortuitos o eventos aleatorios o en accidentes, y mucho menos explorar cualquier método de cuantificación de eventos aparentemente fortuitos. Hasta hace muy poco, la gente ha creído que Dios controlaba cada detalle minucioso del universo. Esta creencia descarta cualquier tipo de conceptualización del azar como fenómeno regular o predecible. Por ejemplo, hasta hace poco el costo de comprar una renta vitalicia que pagaba a los compradores 100 dólares mensuales de por vida era el mismo para un joven de treinta años que para un joven de setenta años. No importaba que empíricamente, la “esperanza de vida” de un niño de treinta años era cuatro veces mayor que la de un setenta años.El gobierno de Guillermo III de Inglaterra, por ejemplo, ofrecía anualidades del 14 por ciento independientemente de que el anuitante fuera 30 o 70 por ciento; (Karl Pearson, La historia de la estadística En los siglos XVII y XVIII contra el trasfondo cambiante del pensamiento intelectual, científico y religioso (Londres: Charles Griffin & Co., 1978), 134. Después de todo, la gente creía que la hora particular de muerte de una persona era “la voluntad de Dios”. Nadie creía que la duración de la vida de alguien pudiera ser juzgada o predicha estadísticamente por cualquier regularidad notada o exhibida entre las personas. A pesar de los avances en matemáticas y ciencias desde el inicio de la civilización, notablemente, el desarrollo de medidas de frecuencia relativa de ocurrencia de eventos inciertos no ocurrió hasta el siglo XVII. Este nacimiento de las ideas “modernas” del azar ocurrió cuando un jugador frecuente le planteó un problema al matemático Blaisé Pascal. Como suele ocurrir, el problema resultó ser menos importante a largo plazo que la solución desarrollada para resolver el problema.

El problema planteado fue: Si dos personas están apostando y el juego se interrumpe y se suspende antes de que cualquiera de las dos haya ganado, ¿cuál es una manera justa de dividir el bote de dinero sobre la mesa? Claramente la persona por delante en ese momento tenía más posibilidades de ganar el juego y debería haber conseguido más. El jugador a la cabeza recibiría la mayor porción del bote de dinero. No obstante, la persona perdedora podría venir de atrás y ganar. Podría suceder y tal posibilidad no debería excluirse. ¿Cómo se debe dividir la olla de manera justa? Pascal formuló una aproximación a este problema y, en una serie de cartas con Pierre de Fermat, desarrolló una aproximación al problema que implicaba anotar todos los resultados posibles que pudieran ocurrir y luego contar el número de veces que ganó el primer jugador. La proporción de veces que ganó el primer jugador (calculada como el número de veces que ganó el jugador dividido por el número total de resultados posibles) se tomó como la proporción del bote que el primer jugador podría reclamar de manera justa. En el proceso de formulación de esta solución, Pascal y Fermat desarrollaron de manera más general un marco para cuantificar la frecuencia relativa de resultados inciertos, lo que ahora se conoce como probabilidad. Crearon la noción matemática del valor esperado de un evento incierto. Fueron los primeros en modelar la regularidad exhibida de azar o eventos inciertos y aplicarla para resolver un problema práctico. De hecho, su solución apuntaba a muchas otras aplicaciones potenciales a problemas en derecho, economía y otros campos.

A partir del trabajo de Pascal y Fermat, quedó claro que para gestionar los riesgos futuros bajo incertidumbre, necesitamos tener alguna idea no solo sobre los posibles resultados o estados del mundo sino también la probabilidad de que ocurra cada resultado. Necesitamos un modelo, o en otras palabras, una representación simbólica de los posibles resultados y sus probabilidades o frecuencias relativas.

Un Preludio Histórico a la Cuantificación de la Incertidumbre Vía Probabilidades

Históricamente, el desarrollo de medidas de azar (probabilidad) solo comenzó a mediados del 1600. ¿Por qué en la Edad Media, y no con los griegos? La respuesta, en parte, es que los griegos y sus predecesores no tenían los conceptos matemáticos. Tampoco, lo que es más importante, los griegos tenían la perspectiva psicológica para siquiera contemplar estas nociones, y mucho menos desarrollarlas en una teoría cogente capaz de reproducción y expansión. En primer lugar, los griegos no contaban con el sistema matemático notacional necesario para contemplar una aproximación formal al riesgo. Carecían, por ejemplo, del sistema simbólico simple y completo que incluyera un signo cero y otro igual útiles para el cálculo, contribución que posteriormente fue desarrollada por los árabes y posteriormente adoptada por el mundo occidental. El uso de números romanos podría haber sido suficiente para el conteo, y tal vez suficiente para la geometría, pero ciertamente no fue propicio para cálculos complejos. El signo igual no fue de uso común hasta finales de la Edad Media. Imagínese hacer cálculos (incluso cálculos tan simples como dividir fracciones o resolver una ecuación) en números romanos sin un signo igual, un elemento cero o un punto decimal!

Pero matemáticos y científicos resolvieron estos impedimentos mil años antes del advenimiento de la probabilidad. ¿Por qué no surgió el análisis de riesgos con el advenimiento de un sistema de numeración más completo como lo hicieron los cálculos sofisticados en astronomía, ingeniería y física? La respuesta es más psicológica que matemática y va al meollo de por qué consideramos el riesgo como un concepto tanto psicológico como numérico en este libro. A los griegos (y a los milenios de otros que los siguieron), se creía que los cielos, divinamente creados, eran estáticos y perfectos y estaban gobernados por la regularidad y las reglas de la perfección: círculos, esferas, los seis sólidos geométricos perfectos, etc. La esfera terrenal, en cambio, era fuente de imperfección y caos. Los griegos aceptaron que no encontrarían sentido en estudiar los eventos caóticos de la Tierra. Los antiguos griegos encontraron el camino hacia la verdad al contemplar la perfección de los cielos y otras entidades perfectas vírgenes o incorruptas. ¿Por qué un dios (o dioses) lo suficientemente poderosos como para conocer y crear todo intencionalmente crearía un mundo usando un modelo menos que perfecto? Los griegos, y otros que los siguieron, creían que el razonamiento puro, no empírico, la observación conduciría al conocimiento. Estudiar la regularidad en la caótica esfera terrenal fue peor que una inútil pérdida de tiempo; distrajo la atención de importantes contemplaciones que en realidad podrían impartir conocimiento verdadero.

Se necesitó un cambio radical de mentalidad para comenzar a contemplar la regularidad en los eventos en el dominio terrenal. Todos somos criaturas de nuestra época, y no podíamos plantearnos las preguntas necesarias para desarrollar una teoría de probabilidad y riesgo hasta que nos sacáramos estos grilletes de la mente. Hasta la era de la razón, cuando las reformas de la iglesia y una creciente clase mercantil (que pragmáticamente examinaba y contaba las cosas empíricamente) creaban un tremendo crecimiento en el comercio, permanecíamos atrapados en las viejas formas de pensar. Mientras la sociedad estuviera estática y estacionaria, siendo los pueblos este año esencialmente los mismos que el año pasado o una década o siglo antes, había poca necesidad de plantear o resolver estos problemas. M. G. Kendall capta esto de manera sucinta cuando señaló que “las matemáticas nunca llevan al pensamiento, sino que solo lo expresan” * El mundo occidental simplemente no estaba todavía listo para tratar de cuantificar el riesgo o la probabilidad de eventos (probabilidad) o para contemplar la incertidumbre. Si se cree que todas las cosas están gobernadas por un dios omnipotente, entonces no es de confiar en la regularidad, tal vez incluso se pueda considerar engañosa, y la variación es irrelevante e ilusoria, siendo meramente un reflejo de la voluntad de Dios. Además, el hecho de que cosas como los dados y el sorteo de lotes fueran utilizados simultáneamente por magos, por jugadores, y por figuras religiosas para la adivinación no dio ningún impulso hacia la búsqueda de regularidad en los esfuerzos terrenales.

* M. G. Kendall, “Los inicios de un cálculo de probabilidad”, en Estudios en Historia de la Estadística y la Probabilidad, vol. 1, ed. E. S. Pearson y Sir Maurice Kendall (Londres: Charles Griffin & Co., 1970), 30.

Técnicas de medición para medidas de frecuencia, gravedad y distribución de probabilidad para cuantificar eventos inciertos

Cuando podamos ver el patrón de las pérdidas y/o ganancias experimentadas en el pasado, esperamos que el mismo patrón continúe en el futuro. En algunos casos, queremos poder modificar los resultados pasados de una manera lógica como inflarlos por el tiempo valor del dinero discutido en “4: Gestión del riesgo en evolución - Herramientas fundamentales”. Si los patrones de ganancias y pérdidas continúan, nuestras predicciones de pérdidas o ganancias futuras serán informativas. De igual manera, podemos desarrollar un patrón de pérdidas basado en constructos teóricos o físicos ( como modelos de predicción de huracanes basados en la física o probabilidad de obtener una cabeza en un tirón de una moneda basada en modelos teóricos de igual probabilidad de cabeza y cola). La verosimilitud es la noción de la frecuencia con que ocurrirá un determinado evento. Las inexactitudes en nuestras habilidades para crear una distribución correcta surgen de nuestra incapacidad para predecir los resultados de futuros con precisión. La distribución es la visualización de los eventos en un mapa que nos indica la probabilidad de que ocurra el evento o eventos. De alguna manera, se asemeja a una imagen de la probabilidad y regularidad de los eventos que ocurren. Pasemos ahora a la creación de modelos y medidas de los resultados y su frecuencia.

Medidas de Frecuencia y Gravedad

El Cuadro 2.1 y el Cuadro 2.2 muestran la compilación del número de siniestros y sus montos en dólares para viviendas quemadas durante un periodo de cinco años en dos localidades distintas etiquetadas como Ubicación A y Ubicación B. Tenemos información sobre el número total de siniestros por año y el monto del incendio pérdidas en dólares por cada año. Cada ubicación tiene el mismo número de viviendas (1,000 viviendas). Cada ubicación tiene un total de 51 siniestros para el quinquenio, un promedio (o media) de 10.2 siniestros anuales, que es la frecuencia. El monto promedio en dólares de las pérdidas por siniestro para todo el periodo es también el mismo para cada ubicación, $6,166.67, que es la definición de severidad.

Cuadro 2.1 Reclamaciones y pérdidas por incendio para un grupo de viviendas en la ubicación A

Año	Número de reclamaciones por incendio	Número de Pérdidas por Incendio ($)	Pérdida promedio por reclamo ($)
1	11	16,500.00	1,500.00
2	9	40,000.00	4,444.44
3	7	30,000.00	4,285.71
4	10	123,000.00	12,300.00
5	14	105,000.00	7,500.00
Total	51.00	314,500.00	6,166.67
Media	10.20	62,900.00	6,166.67
	Frecuencia promedio =	10.20
	Gravedad promedio =	6,166.67 para el periodo de 5 años

Cuadro 2.2 Reclamaciones y Pérdidas por Incendio ($) para Viviendas en Ubicación B

Año	Número de reclamaciones por incendio	Pérdidas por incendio	Pérdida promedio por reclamo ($)
1	15	16,500.00	1,100.00
2	5	40,000.00	8,000.00
3	12	30,000.00	2,500.00
4	10	123,000.00	12,300.00
5	9	105,000.00	11,666.67
Total	51.00	314,500.00	6,166.67
Media	10.20	62,900.00	6,166.67
	Frecuencia promedio =	10.20
	Gravedad promedio =	6,166.67 para el periodo de 5 años

Como se muestra en el Cuadro 2.1 y el Cuadro 2.2, el número total de reclamos por incendio para las dos ubicaciones A y B es el mismo, al igual que lo es el monto total en dólares de las pérdidas que se muestra. Tal vez recuerdes de antes, el número de reclamos por año se llama la frecuencia. La frecuencia promedio de siniestros para las ubicaciones A y B es de 10.2 por año. El tamaño de la pérdida en términos de dólares perdidos por siniestro se denomina severidad, como señalamos anteriormente. El promedio de dólares perdidos por siniestro al año en cada ubicación es de $6,166.67.

Las medidas más importantes para los gestores de riesgo cuando abordan las pérdidas potenciales que surgen de la incertidumbre suelen ser las asociadas con la frecuencia y severidad de las pérdidas durante un periodo de tiempo determinado. El uso de datos de frecuencia y severidad es muy importante tanto para las aseguradoras como para los gerentes de firmas que se preocupan por juzgar el riesgo de diversos esfuerzos. Los gestores de riesgos intentan emplear actividades (construcción física, sistemas de respaldo, cobertura financiera, seguros, etc.) para disminuir la frecuencia o severidad (o ambas) de posibles pérdidas. En “4: Evolving Risk Management - Fundamental Tools”, veremos los datos de frecuencia y datos de gravedad representados. Por lo general, el gerente de riesgos relacionará el número de incidentes bajo investigación con una base, como el número de empleados si examina la frecuencia y gravedad de las lesiones en el lugar de trabajo. En los ejemplos del Cuadro 2.1 y Cuadro 2.2, la severidad se relaciona con el número de reclamos por incendio en el quinquenio por mil viviendas. Es importante señalar que en estas tablas la distribución precisa (frecuencias y pérdidas en dólares) a lo largo de los años para las reclamaciones por año que surgen en la Ubicación A es diferente de la distribución para la Ubicación B. Esto se discutirá más adelante en este capítulo. A continuación, se discute el concepto de frecuencia en términos de probabilidad o verosimilitud.

Frecuencia y Probabilidad

Volviendo a la cuantificación de la noción de incertidumbre, primero observamos que nuestro uso intuitivo de la palabra probabilidad puede tener dos significados o formas diferentes en relación con declaraciones de resultados inciertos. Esto es ejemplificado por dos declaraciones diferentes:Véase Patrick Brockett y Arnold Levine Brockett, Estadísticas, probabilidad y sus aplicaciones (W. B. Saunders Publishing Co., 1984), 62.

1. “Si navego hacia el oeste desde Europa, tengo un 50 por ciento de posibilidades de que me caiga del borde de la tierra”.
2. “Si le doy la vuelta a una moneda, tengo un 50 por ciento de posibilidades de que aterrice en cabezas”.

Conceptualmente, estos representan dos tipos distintos de declaraciones de probabilidad. El primero es una declaración sobre la probabilidad como un grado de creencia sobre si ocurrirá un evento y qué tan firme se sostiene esta creencia. El segundo es una declaración sobre la frecuencia con la que se esperaría que una cabeza apareciera en repetidas vueltas de una moneda. La diferencia importante es que se manifestará la validez o verdad de la primera declaración. Podemos aclarar la veracidad de la declaración para todos navegando por todo el mundo.

El segundo enunciado, sin embargo, sigue sin resolverse. Incluso después del primer volteo de monedas, todavía tenemos una probabilidad del 50 por ciento de que el siguiente giro resulte en una cabeza. El segundo proporciona una interpretación diferente de la “probabilidad”, es decir, como una frecuencia relativa de ocurrencia en ensayos repetidos. Esta conceptualización de frecuencia relativa de probabilidad es más relevante para la gestión del riesgo. Uno quiere aprender de eventos pasados sobre la probabilidad de que ocurran en el futuro. Los descubridores de la teoría de probabilidad adoptaron el enfoque de frecuencia relativa para formalizar la probabilidad de eventos de azar.

Pascal y Fermat marcaron el comienzo de un gran avance conceptual: el concepto de que, en repetidos juegos de azar (o en muchas otras situaciones encontradas en la naturaleza) que involucran incertidumbre, surgieron frecuencias relativas fijas de ocurrencia de los posibles resultados individuales. Estas frecuencias relativas fueron estables a lo largo del tiempo y los individuos pudieron calcularlas simplemente contando el número de formas en que el resultado podría ocurrir dividido por el número total de posibles resultados igualmente probables. Además, empíricamente la frecuencia relativa de ocurrencia de eventos en una larga secuencia de ensayos repetidos (por ejemplo, juegos de azar repetidos) correspondió con el cálculo teórico del número de formas en que un evento podría ocurrir dividido por el número total de resultados posibles. Este es el modelo de resultados igualmente probables o definición de frecuencia relativa de probabilidad. Fue una desviación muy distinta de la anterior conceptualización de la incertidumbre que tenía todos los eventos controlados por Dios sin un patrón humanamente discernible. En el marco Pascal-Fermat, la predicción se convirtió en una cuestión de contar que cualquiera podía hacer. ¡La probabilidad y la predicción se habían convertido en una herramienta de la gente! La figura \(\PageIndex{1}\) proporciona un ejemplo que representa todos los resultados posibles en el lanzamiento de dos dados de colores junto con sus probabilidades asociadas.

Figura\(\PageIndex{1}\): Posibles resultados para una tirada de dos dados con la probabilidad de tener un número particular de puntos hacia arriba

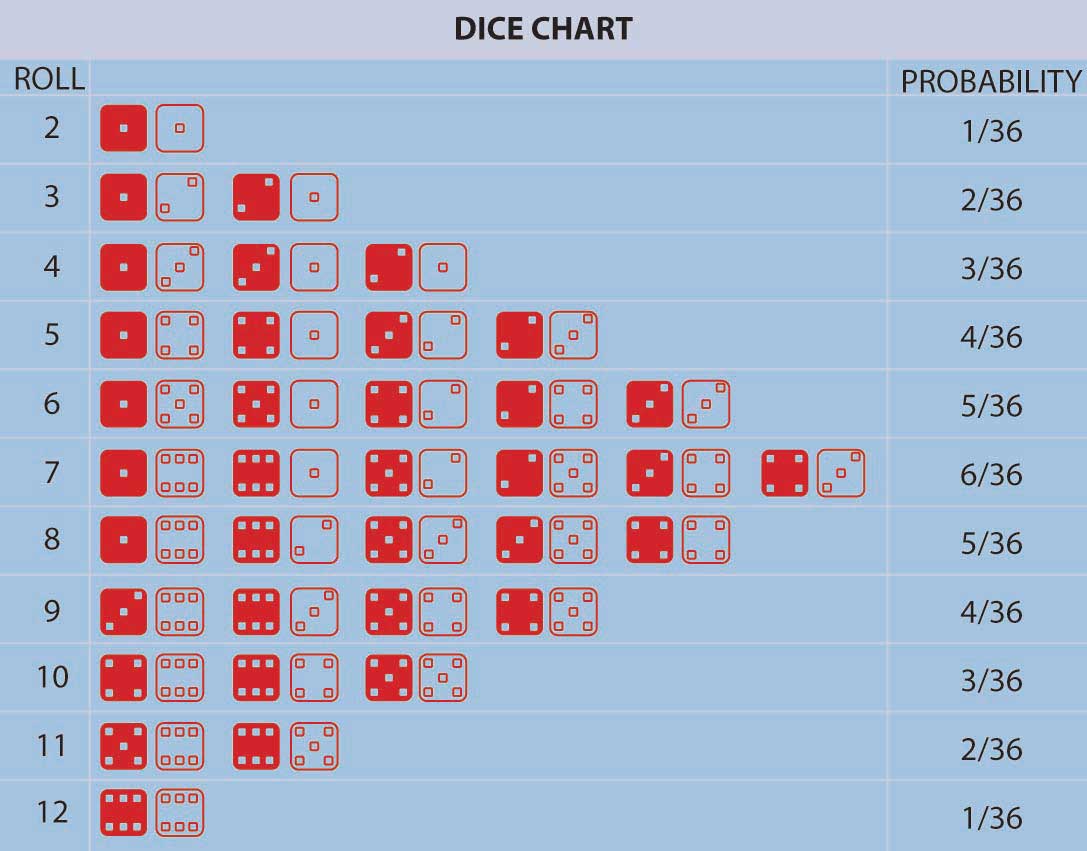
La figura\(\PageIndex{1}\) enumera las probabilidades para el número de puntos orientados hacia arriba (2, 3, 4, etc.) en una tirada de dados de dos colores. Podemos calcular la probabilidad para cualquiera de estos números (2, 3, 4, etc.) sumando el número de resultados (tiradas de dos dados) que dan como resultado este número de puntos hacia arriba dividido por el número total de posibilidades. Por ejemplo, un rollo de treinta y seis posibilidades en total cuando tiramos dos dados (contarlos). La probabilidad de rodar un 2 es 1/36 (solo podemos rodar un 2 de una manera, es decir, cuando ambos dados tienen un 1 boca arriba). La probabilidad de rodar un 7 es\(\frac{6}{36}\) =\(\frac{1}{6}\) (ya que los rollos pueden caer cualquiera de seis formas para rodar un 7—1 y 6 dos veces, 2 y 5 dos veces, 3 y 4 dos veces). Para cualquier otra elección de número de puntos orientados hacia arriba, podemos obtener la probabilidad simplemente sumando el número de formas en que el evento puede ocurrir dividido por treinta y seis. La probabilidad de rodar un 7 o un 11 (5 y 6 dos veces) en un lanzamiento de los dados, por ejemplo, es \(\frac{6+2}{36}\) =\(\frac{2}{9}\).

Las nociones de “resultados igualmente probables” y el cálculo de probabilidades como la relación de “el número de formas en que podría ocurrir un evento, dividido por el número total de resultados igualmente probables” es seminal e instructivo. Pero, no incluía situaciones en las que el número de posibles resultados era (al menos conceptualmente) ilimitado o infinito o no era igualmente probable.Tampoco se entendió fácilmente en ese momento la lógica de la noción de resultados igualmente probables. Por ejemplo, el famoso matemático D'Alembert cometió el siguiente error al calcular la probabilidad de que una cabeza apareciera en dos volteretas de una moneda (Karl Pearson, La historia de la estadística en los siglos XVII y XVIII contra el trasfondo cambiante de intelectual, científico y Pensamiento Religioso [Londres: Charles Griffin & Co., 1978], 552). D'Alembert dijo que la cabeza podría aparecer en la primera voltereta, lo que asentaría esa materia, o podría aparecer una cola en la primera vuelta seguida de una cabeza o una cola en la segunda vuelta. Hay tres resultados, dos de los cuales tienen cabeza, y así afirmó que la probabilidad de obtener una cabeza en dos volteretas es\(\frac{2}{3}\). Evidentemente, no se tomó el tiempo para realmente voltear monedas para ver que la probabilidad era \(\frac{3}{4}\), ya que los posibles resultados igualmente probables son en realidad (H, T), (H, H), (T, T) con tres pares de volteretas dando como resultado una cabeza. El error es que los resultados establecidos en la solución de D'Alembert no son igualmente probables utilizando sus resultados H, (T, H), (T, T), por lo que su denominador está equivocado. La moraleja de esta historia es que los modelos teóricos postulados deben ser siempre probados contra datos empíricos siempre que sea posible para descubrir posibles errores. Necesitábamos una extensión. Al darse cuenta de que la probabilidad de un evento, cualquier evento, siempre que esa extensión. Además, extender la teoría a posibles resultados no igualmente probables surgió al notar que la probabilidad de que ocurra un evento, cualquier evento, podría calcularse como la frecuencia relativa de un evento que ocurre en una larga serie de ensayos en los que el evento puede ocurrir o no. Así, diferentes eventos podrían tener diferentes posibilidades desiguales de ocurrir en una larga repetición de escenarios que involucran las posibles ocurrencias de los eventos. En el cuadro 2.3 se ofrece un ejemplo de ello. Podemos extender la teoría aún más a una situación en la que el número de posibles resultados es potencialmente infinito. Pero, ¿qué pasa con una situación en la que no se pueda encontrar ningún límite fácilmente definible en el número de posibles resultados? Podemos abordar esta situación utilizando de nuevo la interpretación de frecuencia relativa de la probabilidad también. Cuando tenemos un continuo de posibles resultados (por ejemplo, si un resultado es tiempo, podemos verlo como un resultado variable continuo), entonces se crea una curva de frecuencia relativa. Así, la probabilidad de que un resultado caiga entre dos números x e y es el área bajo la curva de frecuencia entre x e y. El área total bajo la curva es una que refleja que es 100 por ciento seguro que se producirá algún resultado.

La llamada distribución normal o curva en forma de campana de la estadística nos proporciona un ejemplo de tal curva de distribución de probabilidad continua. La curva en forma de campana representa una situación en la que surge un continuo de posibles resultados. La figura \(\PageIndex{2}\) proporciona dicha curva en forma de campana para la rentabilidad de implementar un nuevo proyecto de investigación y desarrollo. Puede tener ganancias o pérdidas.

Figura\(\PageIndex{2}\): Distribución normal del beneficio potencial de un proyecto de investigación y desarrollo

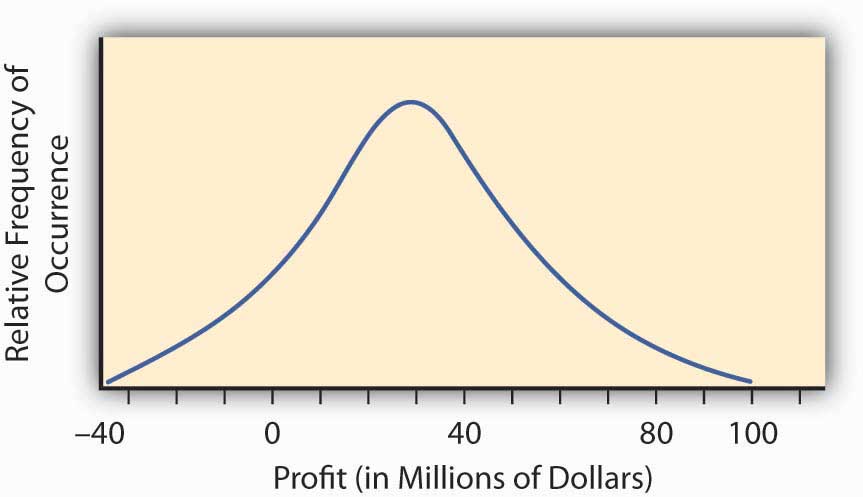
Para encontrar la probabilidad de cualquier rango de valores de rentabilidad para este proyecto de investigación y desarrollo, encontramos el área bajo la curva en Figura\(\PageIndex{2}\) entre el rango deseado de valores de rentabilidad. Por ejemplo, la distribución en Figura \(\PageIndex{2}\) se construyó para tener lo que se llama una distribución normal con la joroba sobre el punto $30 millones y una medida de spread de 23 millones de dólares. Este spread representa la desviación estándar que discutiremos en la siguiente sección. Podemos calcular el área bajo la curva por encima de $0, que será la probabilidad de que obtengamos ganancias implementando el proyecto de investigación y desarrollo. Esto lo hacemos por referencia a una tabla de distribución normal de valores disponible en cualquier libro de estadísticas. El área bajo la curva es de 0.904, lo que significa que tenemos aproximadamente un cambio de 90 por ciento (probabilidad de 0.9) de que el proyecto resulte en una ganancia.

En la práctica, construimos tablas de distribución de probabilidad o curvas de probabilidad como las de la Figura\(\PageIndex{1}\)\(\PageIndex{2}\), Figura y Tabla 2.3 utilizando estimaciones de la probabilidad (probabilidad) de varios estados diferentes de la naturaleza basados en la frecuencia relativa histórica de ocurrencia o datos teóricos. Por ejemplo, los datos empíricos pueden provenir de observaciones repetidas en situaciones similares como con tablas de vida o mortalidad históricamente construidas. Los datos teóricos pueden provenir de una evaluación física o de ingeniería de la probabilidad de falla de un puente o nave de contención de una planta de energía nuclear. En algunas situaciones, sin embargo, podemos determinar las probabilidades subjetivamente o por opinión experta. Por ejemplo, las evaluaciones de derrocamiento político de los gobiernos se utilizan para fijar los precios de los seguros de riesgo político que necesitan las corporaciones que hacen negocios en mercados emergentes. Independientemente de la fuente de las probabilidades, podemos obtener una evaluación de las probabilidades o frecuencias relativas de la ocurrencia futura de cada evento concebible. El conjunto resultante de posibles eventos junto con sus respectivas probabilidades de ocurrencia se denomina distribución de probabilidad, un ejemplo de lo cual se muestra en la Tabla 2.3.

Medidas del Valor Resultado: Gravedad de la Pérdida, Valor de Ganancia

Hemos desarrollado una medida cuantificada de la probabilidad de los diversos resultados inciertos que una empresa o individuo podría enfrentar, estos también se llaman probabilidades. Ahora podemos recurrir para abordar las consecuencias de la incertidumbre. Las consecuencias de la incertidumbre suelen ser un tema vital desde el punto de vista financiero. La razón por la que la incertidumbre es inquietante no es la incertidumbre en sí, sino los diversos resultados que pueden impactar planes estratégicos, rentabilidad, calidad de vida y otros aspectos importantes de nuestra vida o la viabilidad de una empresa. Por lo tanto, necesitamos evaluar cómo nos impactan en cada estado del mundo. Para cada resultado, asociamos un valor que refleja cómo nos afecta estar en este estado del mundo.

Como ejemplo, considere que una firma minorista ingresa a un nuevo mercado con un producto recién creado. Pueden ganar mucho dinero aprovechando el estatus de “primeros en mover”. Pueden perder dinero si el producto no es aceptado suficientemente por el mercado. Además, aunque han tratado de anticiparse a cualquier problema, pueden enfrentar una posible responsabilidad del producto. Si bien naturalmente intentan que sus productos sean lo más seguros posible, tienen que considerar la responsabilidad potencial debido a la limitada experiencia con el producto. Pueden ser capaces de evaluar la probabilidad de una demanda así como las consecuencias (pérdidas) que podrían derivarse de tener que defender tales demandas. La incertidumbre de las consecuencias hace que este esfuerzo sea riesgoso y el potencial de ganancia que motiva la entrada de la compañía al nuevo mercado. ¿Cómo se calculan estas ganancias y pérdidas? Ya demostramos algunos cálculos en los ejemplos anteriores en el Cuadro 2.1 y el Cuadro 2.2 para las reclamaciones y pérdidas por incendio para viviendas en las localidades A y B. Estos ejemplos se concentraron en las consecuencias de la incertidumbre sobre los incendios. Otra forma de calcular el mismo tipo de consecuencias se proporciona en el ejemplo del Cuadro 2.3 para la distribución de probabilidad para esta nueva entrada al mercado. También buscamos una evaluación de las consecuencias financieras de la entrada al mercado. Este ejemplo analiza algunos resultados posibles, no solo el resultado de las pérdidas por incendio. Estos resultados pueden tener consecuencias positivas o negativas. Por lo tanto, utilizamos aquí la terminología de oportunidad en lugar de solo las posibilidades de pérdida.

Cuadro 2.3 Consecuencias de la evaluación de oportunidades y pérdidas de la entrada al mercado de nuevos

Estado de la Naturaleza	Evaluación de Probabilidad de Probabilidad de Estado	Consecuencias financieras de estar en este estado (en millones de dólares)
Sujeto a una pérdida en una demanda de responsabilidad por productos	.01	−10.2
La aceptación del mercado es limitada y temporal	.10	−.50
Alguna aceptación en el mercado pero sin gran demanda de los consumidores	.40	.10
Buena aceptación en el mercado y desempeño de ventas	.40	1
Gran demanda del mercado y desempeño de ventas	.09	8

Como puede ver, no es la incertidumbre de los propios estados lo que hace que los tomadores de decisiones reflexionen sobre la conveniencia de la entrada al mercado de un nuevo producto. Son las consecuencias de los diferentes resultados los que provocan la deliberación. La firma podría perder 10.2 millones de dólares o ganar 8 millones de dólares. Si supiéramos qué estado se materializaría, la decisión sería sencilla. Abordamos el tema de cómo combinamos la evaluación de probabilidad con el valor de la ganancia o pérdida con el propósito de evaluar el riesgo (consecuencias de la incertidumbre) en la siguiente sección.

Combinar probabilidad y valor de resultado juntos para obtener una evaluación general del impacto de un esfuerzo incierto

Los desarrolladores de probabilidad temprana preguntaron cómo podríamos combinar las diversas probabilidades y valores de resultado para obtener un solo número que refleje el “valor” de la multitud de diferentes resultados y las diferentes consecuencias de estos resultados. Querían un solo número que resumiera de alguna manera toda la distribución de probabilidad. En el contexto de los juegos de azar de la época en que los resultados fueron la cantidad que ganaste en cada estado potencial incierto del mundo, afirmaron que este valor era el “valor razonable” de la apuesta. Definimos el valor razonable como el promedio numérico de la experiencia de todos los resultados posibles si jugaste el juego una y otra vez. A esto también se le llama el “valor esperado”. El valor esperado se calcula multiplicando cada probabilidad (o frecuencia relativa) por su respectiva ganancia o pérdida.De alguna manera es una pena que se haya utilizado el término “valor esperado” para describir este concepto. Un término mejor es “valor promedio a largo plazo” o “valor medio” ya que este valor en particular realmente no es de esperar en ningún sentido real y puede que ni siquiera sea una posibilidad de ocurrir (por ejemplo, el valor calculado a partir de la Tabla 2.3 es 1.008, lo que ni siquiera es una posibilidad). Sin embargo, estamos pegados con esta terminología, y sí transmite alguna concepción de lo que queremos decir siempre y cuando la interpretemos como el número esperado como un valor promedio en una larga serie de repeticiones del escenario que se está evaluando. También se le conoce como el valor medio, o el valor promedio. Si X denota el valor que da como resultado una situación incierta, entonces el valor esperado (o valor promedio o valor medio) a menudo se denota por\(E(X)\), a veces también referido por los economistas como\(E(U)\) —utilidad esperada y\(E(G)\) —ganancia esperada. A la larga, la pérdida o ganancia experimentada total dividida por el número de ensayos repetidos sería la suma de las probabilidades por la experiencia en cada estado. En la Tabla 2.3 el valor esperado es\ ((.01) × (—10.2) + (.1) × (−.50) + (.4) × (.1) + (.4) × (1) + (.09) × (8) = 1.008\). Así, diríamos que el resultado esperado de la situación incierta descrita en el Cuadro 2.3 fue de $1.008 millones, o $1,008,000.00. De igual manera, el valor esperado del número de puntos al lanzar un par de dados calculado a partir del ejemplo en la Figura\(\PageIndex{1}\) es\ (2× ((\ frac {1} {36}) +3× (\ frac {2} {36}) +4 × (\ frac {3} {36}) +5× (\ frac {4} {36}) +6× (\ frac {5} {36}) +6× (\ frac {5} {36}}) +7× (\ frac {6} {36}) +8× (\ frac {5} {36}) +9× (\ frac {4} {36}) +10× (\ frac {3} {36}) +11× (\ frac {2 } {36}) +12× (\ frac {1} {36}) = 7\). En situaciones económicas inciertas que involucren posibles ganancias o pérdidas financieras, el valor medio o valor promedio o valor esperado se suele utilizar para expresar los rendimientos esperados.Otras medidas de rentabilidad de uso común en una oportunidad incierta, distintas del valor medio o esperado, son las mode (el valor más probable) y la mediana (el número con la mitad de los números por encima y la mitad de los números por debajo de él, la marca del 50 por ciento). Representa el retorno esperado de un emprendimiento; sin embargo, no expresa el riesgo que implica el escenario incierto. Pasamos ahora a esto.

Relativo al Cuadro 2.1 y Cuadro 2.2, para las ubicaciones A y B de pérdidas por siniestros por incendio, el valor esperado de las pérdidas es la gravedad de las reclamaciones por incendio, $6,166.67, y el número esperado de siniestros es la frecuencia de ocurrencia, 10.2 reclamaciones por año.

Conclusiones clave

En esta sección aprendiste sobre la cuantificación de resultados inciertos a través de modelos de probabilidad. Más específicamente, profundizó en métodos de computación:

• La severidad como medida de la consecuencia de la incertidumbre, es el valor esperado o valor promedio de la pérdida que surge en diferentes estados del mundo. La gravedad se puede obtener sumando todos los valores de pérdida en una muestra y dividiendo por el tamaño total de la muestra.
• Si tomamos una tabla de probabilidades (distribución de probabilidad), el valor esperado se obtiene multiplicando la probabilidad de que ocurra una pérdida particular por el tamaño de la pérdida y sumando sobre todas las posibilidades.
• La frecuencia es el número esperado de ocurrencias de la pérdida que surge en diferentes estados del mundo.
• La distribución de verosimilitud y probabilidad representan la frecuencia relativa de ocurrencia (frecuencia de ocurrencia del evento dividida por la frecuencia total de todos los eventos) de diferentes eventos en situaciones inciertas.

Preguntas de Discusión

1. Un estudio de las pérdidas de datos en las que incurrieron las empresas debido a que piratas informáticos penetraron en la seguridad de Internet de la firma encontró que el 60 por ciento de las firmas de la industria estudiada habían experimentado brechas de seguridad y que la pérdida promedio por brecha de seguridad fue de $15,000
   1. ¿Cuál es la probabilidad de que una firma no tenga una brecha de seguridad?
   2. Una firma tuvo dos incumplimientos en un año y está contemplando gastar dinero para disminuir la probabilidad de una infracción. Suponiendo que el próximo año sería el mismo que este año en términos de incumplimientos de seguridad, ¿cuánto debería estar dispuesta a pagar la firma para eliminar las incumplimientos de seguridad (es decir, cuál es el valor esperado de su pérdida)?
2. A continuación se presenta la experiencia de la Aseguradora A durante los últimos tres años:

   Año	Número de exposiciones	Número de reclamaciones por colisión	Pérdidas por colisión ($)
   1	10,000	375	350,000
   2	10,000	330	250,000
   3	10,000	420	400,000

   1. ¿Cuál es la frecuencia de pérdidas en el año 1?
   2. Calcular la probabilidad de una pérdida en el año 1.
   3. Calcular las pérdidas medias anuales para las reclamaciones y pérdidas por colisión.
   4. Calcular las pérdidas medias por exposición.
   5. Calcular las pérdidas medias por siniestro.
   6. ¿Cuál es la frecuencia de las pérdidas?
   7. ¿Cuál es la gravedad de las pérdidas?
3. A continuación se presenta la experiencia de la Aseguradora B durante los últimos tres años:

   Año	Número de exposiciones	Número de reclamaciones por colisión	Pérdidas por colisión ($)
   1	20,000	975	650,000
   2	20,000	730	850.000
   3	20,000	820	900,000

   1. Calcular la media o promedio del número de siniestros anuales para la aseguradora durante el trienio.
   2. Calcular el valor medio o promedio en dólares de las pérdidas por colisión por exposición para el año 2.
   3. Calcular el valor esperado (media o promedio) de las pérdidas por siniestro durante el trienio.
   4. Para cada uno de los tres años, calcule la probabilidad de que una unidad de exposición presente un reclamo.
   5. ¿Cuál es la frecuencia promedio de pérdidas?
   6. ¿Cuál es la severidad promedio de las pérdidas?
   7. ¿Cuál es la desviación estándar de las pérdidas?
   8. Calcular el coeficiente de variación.