2.3: Medidas de Riesgo - Armarlo

Objetivos de aprendizaje

• En esta sección, aprenderás a calcular varias medidas comunes de riesgo utilizando diversos métodos y conceptos estadísticos.

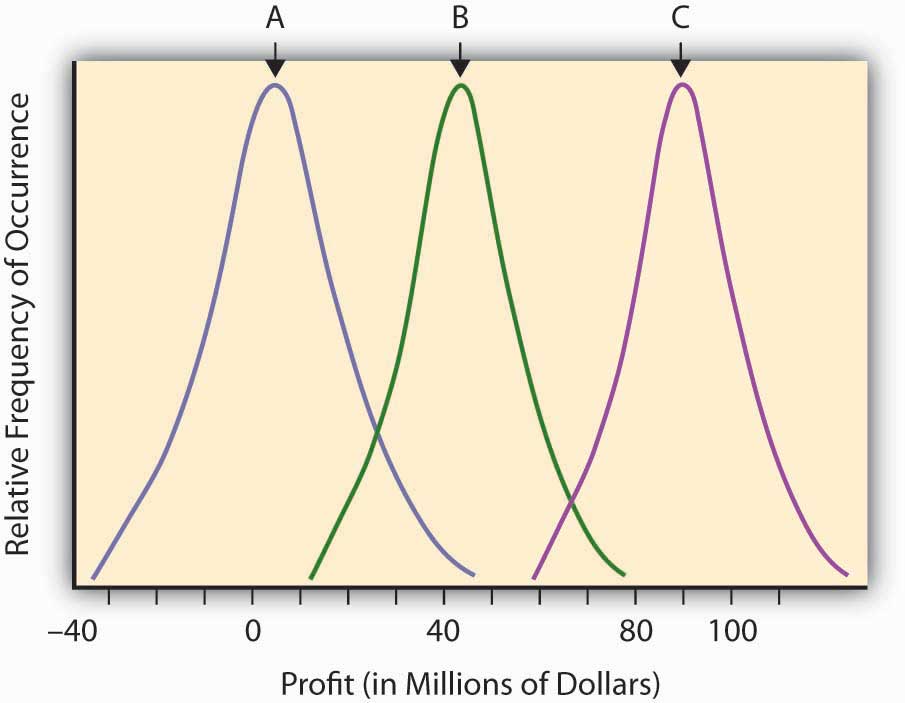
Habiendo desarrollado el concepto de probabilidad para cuantificar la probabilidad relativa de un evento incierto, y habiendo desarrollado una medida de “valor esperado” para un evento incierto, ahora estamos listos para intentar cuantificar el riesgo mismo. El “valor esperado” (o valor medio o valor razonable) cuantificando el resultado potencial derivado de un escenario o situación incierta en la que se han asignado probabilidades es un insumo común en el proceso de toma de decisiones sobre la conveniencia de tomar ciertas acciones, pero no lo es la única consideración. Los resultados de retorno financiero de diversas investigaciones y desarrollo inciertos, podrían, por ejemplo, ser casi idénticos salvo que las distribuciones de retorno se desplazan en una u otra dirección. Tal situación se muestra en la Figura\(\PageIndex{1}\). Esta cifra describe las distribuciones (continuas) de la rentabilidad anticipada para cada uno de los tres posibles gastos de capital en proyectos inciertos de investigación y desarrollo. Estos están etiquetados A, B y C, respectivamente.

Figura\(\PageIndex{1}\): Posible rentabilidad de tres proyectos potenciales de investigación y desarrollo

Intuitivamente, en términos económicos un riesgo es un resultado “sorpresa” que es consecuencia de la incertidumbre. Puede ser una sorpresa positiva o una sorpresa negativa, como discutimos en “1: La naturaleza del riesgo - pérdidas y oportunidades”.

Utilizando los términos explicados en la última sección, podemos considerar el riesgo como la desviación del valor esperado. Cuanto más se desvía una observación de lo que esperábamos, más nos sorprendería que nos volviéramos si la vemos, y de ahí más riesgoso (en sentido económico) consideramos que es el resultado. Intuitivamente, cuanto más sorpresa “esperemos” de una aventura o de un escenario, más riesgosos juzgamos que es esta aventura o escenario.

Mirando hacia atrás en la Figura\(\PageIndex{1}\), podríamos decir que las tres curvas en realidad representan el mismo nivel de riesgo en que cada una difiere de su valor esperado (la media o joroba de la distribución) de manera idéntica. Solo difieren en su respectivo nivel esperado de rentabilidad (la joroba en la curva). Tenga en cuenta que los escenarios inciertos “B” y “C” todavía describen situaciones de riesgo, aunque prácticamente todos los posibles resultados de estos escenarios inciertos están en el rango de beneficio positivo. El “riesgo” reside en las desviaciones del valor esperado que pudieran resultar (el potencial sorpresa), ya sea en promedio el resultado es negativo o positivo. Observe la distribución etiquetada como “A”, que describe un escenario u descripción de oportunidad/pérdida donde muchos más de los posibles resultados están en el rango negativo (daños o pérdidas). Los economistas no consideran que “A” sea más riesgoso (o más peligroso) que “B” o “C”, sino simplemente menos rentable. La desviación de cualquier riesgo esperado define el riesgo aquí. Podemos planificar resultados negativos así como positivos si sabemos qué esperar. Un cierto valor negativo puede ser desafortunado, pero no es riesgoso.

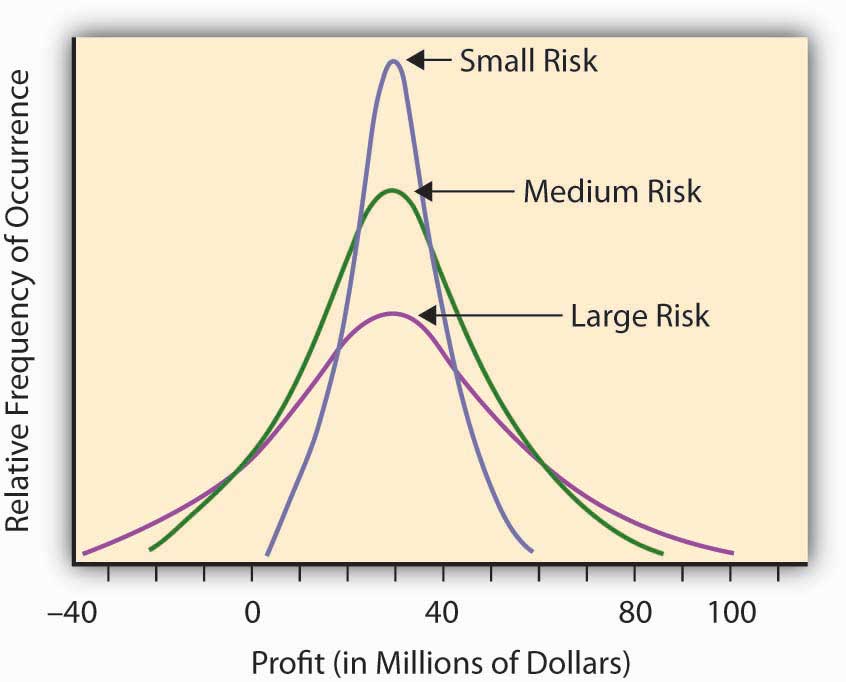
Algunas otras situaciones o escenarios inciertos tendrán el mismo nivel esperado de “rentabilidad”, pero diferirán en la cantidad de “sorpresa” que puedan presentar. Por ejemplo, supongamos que tenemos tres oportunidades potenciales de inversión en proyectos corporativos. Esperamos que, a lo largo de una década, la rentabilidad promedio en cada oportunidad sea de 30 millones de dólares. Los proyectos difieren, sin embargo, por el nivel de incertidumbre que implica esta evaluación de rentabilidad (ver Figura\(\PageIndex{2}\)). En la Oportunidad A, el posible rango de rentabilidad es de $5—$60 millones, mientras que la Oportunidad B tiene un rango mayor de posibles ganancias, entre —$20 millones y + $90 millones. La tercera oportunidad aún tiene un rendimiento esperado de 30 millones de dólares, pero ahora el rango de valores va de —40 millones a +$100. Podrías ganar más con la Oportunidad C, pero podrías perder más, también. La desviación de los resultados alrededor del valor esperado puede medir el nivel de potencial “sorpresa” que contiene la situación incierta o el escenario de ganancias/pérdidas. La situación incierta respecto a la rentabilidad en la Oportunidad B contiene en ella una sorpresa potencial mayor que A, ya que podríamos obtener una desviación mayor del valor esperado en B que en A. Por eso consideramos que la Oportunidad B es más riesgosa que A. La oportunidad C es la más riesgosa de todas, teniendo la posibilidad de un rendimiento gigante de 100 millones de dólares, con el potencial bajista de crear una pérdida de 40 millones de dólares.

Figura\(\PageIndex{2}\): Tres oportunidades corporativas que tienen la misma rentabilidad esperada pero que difieren en riesgo o potencial sorpresa

Nuestra discusión anterior se basa en la intuición más que en las matemáticas. Para hacerlo específico, necesitamos definir cuantitativamente lo que queremos decir con los términos “una sorpresa” y “más sorprendido”. Para ello, debemos enfocarnos en el objetivo del análisis. Una secuencia de lanzamientos de un par de dados de colores en los que el dado rojo siempre aterriza a la izquierda del dado verde puede ser sorprendente, pero esta sorpresa es irrelevante si el propósito del lanzamiento de dados es jugar un juego en el que el número de puntos hacia arriba determina la amortización. Reconocemos así que debemos definir el riesgo en un contexto de la meta del esfuerzo o estudio. Si estamos más preocupados por el riesgo de insolvencia, podemos usar una medida de riesgo, mientras que si estamos interesados en la susceptibilidad de la cartera de activos a cambios moderados en las tasas de interés, podemos usar otra medida de riesgo. El contexto lo es todo. Discutamos varias medidas de riesgo que son apropiadas en diferentes situaciones.

Algunas medidas comunes de riesgo

Como mencionamos anteriormente, intuitivamente, una medida de riesgo debe reflejar el nivel de potencial “sorpresa” intrínseco en los diversos resultados de una situación o escenario incierto. Para ello, la literatura propone una variedad de medidas estadísticas para los niveles de riesgo. Todas estas medidas intentan expresar la variabilidad de resultados para cada resultado relevante en la situación incierta. Las siguientes son algunas medidas de riesgo.

La gama

Podemos usar el rango de la distribución, es decir, la distancia entre el valor de resultado más alto posible y el más bajo, como una medida aproximada de riesgo. La gama proporciona una idea sobre la dispersión “peor de los casos” de sorpresas sucesivas. Al tomar el “mejor escenario menos el peor de los casos” definimos la amplitud potencial de resultados que podrían surgir en la situación incierta.

Como ejemplo, considere el número de siniestros por año en la Ubicación A del Cuadro 2.1. En el cuadro 2.1 se observa un mínimo de siete siniestros anuales hasta un máximo de catorce siniestros anuales, para un rango de siete siniestros anuales. Para la Ubicación B del Cuadro 2.2, tenemos un rango en el número de siniestros desde un mínimo de cinco en un año hasta un máximo de quince siniestros por año, lo que nos da un rango de diez siniestros por año. Usando la medida de rango de riesgo, diríamos que la Ubicación A es menos riesgosa que la Ubicación B en esta situación, sobre todo porque el reclamo promedio es el mismo (10.2) en cada caso y tenemos más variabilidad o potencial sorpresa en la Ubicación B. Como otro ejemplo, si volvemos a la distribución de los valores posibles en el Cuadro 2.3, los extremos varían de −$10.2 millones a +$8 millones, por lo que el rango es de $18.2 millones.

Esta medida de riesgo deja el cuadro incompleto porque no puede distinguir en riesgosidad entre dos distribuciones de situaciones donde los posibles resultados no están acotados, ni toma en cuenta la frecuencia o probabilidad de los valores extremos. El valor más bajo de —$10.2 millones en la Tabla 2.3 solo ocurre el 1 por ciento de las veces, por lo que es muy poco probable que obtengas un valor tan pequeño. Podría haber tenido un valor extremo de —$100 millones, lo que ocurrió con probabilidad 0.0000000001, en cuyo caso el rango habría reflejado esta posibilidad. Tenga en cuenta que es extremadamente improbable que alguna vez experimente un evento de uno en un billón. Por lo general, no querría que sus actividades de gestión de riesgos o acciones gerenciales fueran dictadas por un evento de uno en un billón.

Desviación de un valor central

Una manera más sofisticada (y más tradicional) de medir el riesgo consideraría no solo los valores más extremos de la distribución sino todos los valores y sus respectivas probabilidades de ocurrencia. Una forma de hacerlo es promediar las desviaciones de los posibles valores de la distribución desde un valor central, como el valor esperado\(E(V)\) o el valor medio discutido anteriormente. Desarrollamos esta idea más adelante.

Varianza y Desviación Estándar

Continuando con el ejemplo de la Tabla 2.1 y la Tabla 2.2, ahora nos preguntamos qué diferencia la distribución de siniestros de la Ubicación A y B, ambas poseen la misma frecuencia y severidad esperadas. Ya hemos visto que la gama es diferente. Ahora examinamos cómo las dos ubicaciones difieren en términos de su desviación de la media común o valor esperado. Esencialmente, queremos examinar en qué se diferencian en cuanto a la cantidad de sorpresa que esperamos ver en las observaciones de las distribuciones. Una de esas medidas de desviación o sorpresa es mediante el cálculo de la distancia cuadrada esperada de cada uno de los diversos resultados a partir de su valor medio. Se trata de una distancia cuadrática promedio ponderada de cada valor posible a partir de la media de todas las observaciones, donde los pesos son las probabilidades de ocurrencia. Computacionalmente, lo hacemos al cuadrar individualmente la desviación de cada posible resultado del valor esperado, multiplicando este resultado por su respectiva probabilidad o probabilidad de ocurrir, y luego sumando los productos resultantes.Calcular la desviación promedio firmada de la media o valor esperado ya que es un ejercicio inútil ya que el resultado siempre será cero. Tomando el cuadrado de cada desviación para el valor medio o esperado se deshace del signo algebraico y hace que la suma sea positiva y significativa. Alternativamente, se podría tomar el valor absoluto de las desviaciones de la media para obtener otra medida llamada desviación absoluta, pero esto generalmente no se hace porque resulta en una formulación matemáticamente inconveniente. Nos apegaremos a la desviación cuadrada y sus variantes aquí. Esto produce una medida conocida como varianza. La varianza proporciona una medida de riesgo muy utilizada en contextos financieros y es una de las bases de la noción de selección eficiente de cartera en finanzas y el Modelo de Precios de Activos de Capital, que se utiliza para mostrar explícitamente el trade-off entre riesgo y retorno de activos en un capital mercado.

Primero ilustramos el cálculo de la varianza utilizando la distribución de probabilidad que se muestra en la Tabla 2.2. Ya calculamos el valor esperado en $1.008 millones, por lo que podemos calcular la varianza para que sea\ ((.01) × (—10.2 —1.008) ^2 + (.1) × (—.5 —1.008) ^2+ (.4) × (.1 — 1.008) ^2+ (.4) × (1 — 1.008) ^2 + (.09) × (8 — 1.008) ^2= 7.445\). Por lo general, la varianza se denota con el símbolo griego sigma cuadrado,\(σ^2\), o simplemente V.

Como otro ejemplo, el Cuadro 2.4 y el Cuadro 2.5 muestran el cálculo de la varianza para las dos muestras de siniestros dadas en las ubicaciones A y B de la Tabla 2.1 y la Tabla 2.2, respectivamente. En este caso, todos los años se tratan por igual por lo que la desviación cuadrada promedio de la media es solo la media simple de las desviaciones cuadráticas de cinco años de la media. Calculamos la varianza del número de siniestros únicamente.

Cuadro 2.4 Varianza y Desviación Estándar de Reclamaciones de Incendio de

Año	Número de reclamaciones por incendio	Diferencia entre el número observado de reclamaciones y el número medio de reclamaciones	Diferencia al cuadrado
1	11	0.8	0.64
2	9	−1.2	1.44
3	7	−3.2	10.24
4	10	−0.2	0.04
5	14	3.8	14.44
Total	51	0	26.8
Media	10.2		\(\frac{26.8}{4}\)= 6.7
Varianza 6.70
Desviación estándar = Raíz cuadrada (6.7) = 2.59

Cuadro 2.5 Varianza y Desviación Estándar de Reclamaciones de Incendio de

Año	Número de reclamaciones por incendio	Diferencia entre el número observado de reclamaciones y el número medio de reclamaciones	Diferencia al cuadrado
1	15	4.8	23.04
2	5	−5.2	27.04
3	12	1.8	3.24
4	10	−0.2	0.04
5	9	−1.2	1.44
Total	51	0	54.8
Media	10.2		\(\frac{54.8}{4}\)= 13.70
Varianza 13.70
Desviación estándar 3.70

Un problema con la varianza como medida de riesgo es que al cuadrar las desviaciones individuales de la media, terminas con una medida que está en unidades cuadradas (por ejemplo, si las pérdidas originales se miden en dólares, entonces la varianza se mide en dólares-cuadrados). Para volver a las unidades de medida originales comúnmente tomamos la raíz cuadrada y obtenemos una medida de riesgo conocida como la desviación estándar, denotada por la letra griega sigma (σ). Para proporcionar una medida más significativa del riesgo denominada en las mismas unidades que los datos originales, los economistas y los profesionales del riesgo suelen utilizar esta raíz cuadrada de la variación, la desviación estándar, como medida de riesgo. Proporciona un valor comparable con los resultados esperados originales. Recuerde que la varianza utiliza diferencias cuadradas; por lo tanto, tomar la raíz cuadrada devuelve la medida a su unidad de medida inicial.

Así, la desviación estándar es la raíz cuadrada de la varianza. Para la distribución en el Cuadro 2.3, calculamos la varianza en 7.445, por lo que la desviación estándar es la raíz cuadrada de 7.445 o $2.73 millones. De igual manera, las desviaciones estándar de las ubicaciones A y B del Cuadro 2.1 y Cuadro 2.2 aparecen en las Tablas 2.4 y 2.5. Como puede ver, la desviación estándar de la muestra para la Ubicación A es de sólo 2.59, mientras que la desviación estándar de la muestra de la Ubicación B es de 2.70. El número de reclamos por incendio en la Ubicación B está más distribuido de año en año que los de la Ubicación A. La desviación estándar es la representación numérica de ese diferencial.

Si comparamos una desviación estándar con otra distribución de igual media pero mayor desviación estándar, como cuando comparamos la distribución de siniestros de la Ubicación A con la Ubicación B, podríamos decir que la segunda distribución con la desviación estándar mayor es más riesgosa que la primera. Es más riesgoso porque las observaciones están, en promedio, más alejadas de la media (más dispersas y, por lo tanto, proporcionan más potencial de “sorpresa”) que las observaciones en la primera distribución. Desviaciones estándar mayores, por lo tanto, representan un mayor riesgo, siendo todo lo demás igual.

Por supuesto, las distribuciones rara vez tienen la misma media. ¿Y si estamos comparando dos distribuciones con diferentes medias? En este caso, un enfoque sería considerar el coeficiente de variación, que es la desviación estándar de una distribución dividida por su media. Esencialmente negocia el riesgo (medido por la desviación estándar) con el rendimiento ( medido por el valor medio o esperado). El coeficiente de variación puede ser utilizado para darnos un valor relativo de riesgo cuando las medias de las distribuciones no son iguales.

La Semivariancia

Las medidas de riesgo anteriores dieron la misma atención o importancia a las desviaciones tanto positivas como negativas del valor medio o esperado. Algunas personas prefieren medir el riesgo por las sorpresas en una sola dirección. Por lo general, solo las desviaciones negativas por debajo del valor esperado se consideran riesgosas y con necesidad de control o manejo. Por ejemplo, un tomador de decisiones podría estar especialmente preocupado por desviaciones por debajo del nivel esperado de ganancia y recibiría con agrado desviaciones por encima del valor esperado. Para ello una “semivariancia” podría servir como medida de riesgo más apropiada que la varianza, que trata las desviaciones en ambos sentidos de la misma manera. La semivariancia es la desviación cuadrada promedio. Ahora solo se suman las desviaciones por debajo del valor esperado. Si la distribución de pérdidas y ganancias es simétrica, el uso de la semivariancia resulta en la misma clasificación exacta de resultados inciertos con respecto al riesgo que el uso de la varianza. Sin embargo, si la distribución no es simétrica, entonces estas medidas pueden diferir y las decisiones tomadas sobre qué distribución de resultados inciertos es más riesgosa serán diferentes, y las decisiones tomadas sobre cómo manejar el riesgo medido por estas dos medidas pueden ser diferentes. Como la mayoría de las distribuciones financieras y de pérdida pura son asimétricas, los profesionales suelen preferir la semivarianza en el análisis financiero como medida de riesgo, aunque la varianza (y desviación estándar) también se utilizan comúnmente.

Valor en Riesgo (VaR) y Pérdida Anual Máxima Probable (MPAL)

¿Cómo gestionan los bancos y otras instituciones financieras los riesgos sistémicos o fundamentales del mercado a los que se enfrentan? El modelado de VaR se ha convertido en la herramienta estándar de medición de riesgos en la industria bancaria para evaluar la exposición al riesgo Después de que la industria bancaria adoptara VaR, muchas otras firmas financieras también lo adoptaron. Esto se debe en parte a la aceptación de esta técnica por parte de los reguladores, como las condiciones escritas en los acuerdos de Basilea II sobre regulación bancaria.Comité de Basilea sobre Supervisión Bancaria (BCBS), Convergencia Internacional de Medición de Capital y Estándares de Capital: A Revised Framework (Basilea, Suiza, 2004). Además, las instituciones financieras necesitan saber cuánto dinero necesitan reservar para poder soportar un choque o pérdida de capital y seguir siendo solventes. Para ello, necesitan una medida de riesgo con una probabilidad alta especificada. Intuitivamente, VaR se define como la pérdida de valor en dólares del peor escenario (hasta un nivel de probabilidad especificado) que podría ocurrir para una empresa expuesta a un conjunto específico de riesgos (tasas de interés, precios de acciones, tipos de cambio y precios de materias primas). Esta es la cantidad necesaria a tener en reserva para evitar la insolvencia con el nivel de probabilidad especificado.

En realidad, para muchas exposiciones al riesgo, la pérdida absoluta del “peor de los casos” que podría experimentarse es concebiblemente ilimitada. Es concebible que se pueda perder una cantidad muy grande pero puede ser muy poco probable que se pierda tanto. Así, en lugar de elegir la mayor pérdida posible para prepararse contra, la firma selecciona un nivel de probabilidad con el que puedan vivir (generalmente, están interesados en que su exposición al riesgo financiero cubra algo así como 95 por ciento o 99 por ciento del tiempo), y preguntan: “¿Cuál es lo peor caso que puede suceder hasta estar cubierto el 95 por ciento o 99 por ciento de las veces?” Para un determinado nivel de confianza (en este caso 95 por ciento o 99 por ciento) y en un horizonte de tiempo específico, VaR puede medir riesgos en cualquier valor único (ya sea una inversión específica representada en sus valores de inversión o préstamo de un cliente específico) o una cartera completa siempre y cuando tener suficientes datos históricos. VaR da respuesta a la pregunta “¿Cuál es la peor pérdida que podría ocurrir y para la que debo prepararme?”

En la práctica, los profesionales examinan un registro histórico de rendimientos para el activo o cartera bajo consideración y construyen una distribución de probabilidad de rendimientos. Si selecciona un VaR del 95 por ciento, entonces elige el 5 por ciento más bajo de la distribución, y cuando se multiplica por el valor del activo o de la cartera, obtiene el 95 por ciento de VaR. Si se desea un VaR del 99 por ciento, entonces se determina el 1 por ciento más bajo de la distribución de rendimientos y esto se multiplica por el valor del activo o cartera para obtener el VaR del 99 por ciento.

Figura\(\PageIndex{3}\): El VaR del 95 por ciento para la distribución de pérdidas y ganancias de la Figura 2.2.1

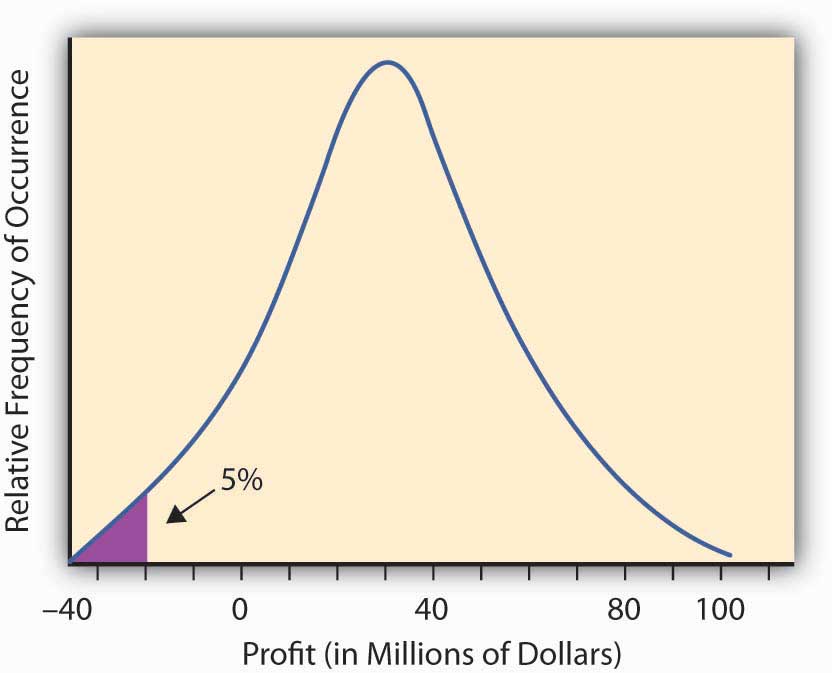
Esto lo ilustramos más a fondo con la Figura\(\PageIndex{3}\), relativa a Hometown Bank.

Caso: Riesgo de Mercado Bancario de la ciudad natal

El riesgo de mercado es el cambio en el valor de mercado de los activos y pasivos bancarios resultante de las cambiantes condiciones del mercado. Por ejemplo, a medida que aumentan las tasas de interés, los préstamos que Hometown Bank hizo a tasas fijas bajas se vuelven menos valiosos para el banco. Los valores totales de mercado de sus activos disminuyen a medida que el valor de mercado de los préstamos pierde valor. Si los préstamos se negocian en el mercado secundario, Hometown registraría una pérdida real. Otros activos y pasivos bancarios también están en riesgo debido a los cambios en los precios del mercado. Hometown acepta posiciones de capital como garantía (por ejemplo, una hipoteca sobre la casa incluye la casa como garantía) contra préstamos que están sujetos a cambios en los precios de las acciones. A medida que caen los precios de las acciones, la garantía contra el préstamo es menos valiosa. Si la caída del precio es precipitada, el préstamo podría quedar subgarantizado donde el valor del patrimonio neto, como una vivienda, es menor que el monto del préstamo tomado y puede que no brinde suficiente protección a Hometown Bank en caso de incumplimiento del cliente.

Otro ejemplo de riesgo incluye las actividades bancarias en servicios cambiarios. Esto los somete al riesgo de tipo de cambio de divisas. También se incluye el riesgo de precio de las materias primas asociado con los préstamos en la industria agrícola.

Hometown Bank tiene un total de 65.5 millones de dólares en valores de inversión. Por lo general, los bancos mantienen estos valores hasta que los clientes bancarios necesitan el dinero como préstamos, pero la Reserva Federal requiere que algo de dinero se mantenga en reserva para pagar a los depositantes que soliciten su devolución de dinero. Hometown tiene una política de inversión que enumera sus valores aprobados para inversión. Debido a que la cartera consiste en valores sensibles a las tasas de interés, a medida que suben las tasas de interés, el valor de los valores disminuye. La valoración de los bonos está cubierta en el texto de finanzas Valor del bono = valor presente de cupones + valor presente del valor nominal del bono. El director general de Hometown Bank, el señor Allen, está interesado en estimar su riesgo a lo largo de un periodo de cinco días medido por el peor de los casos que probablemente enfrentará en términos de pérdidas en el valor de cartera. Entonces puede retener esa cantidad de dinero en reserva para que pueda evitar enfrentar problemas de liquidez. Este problema plagó a numerosos bancos durante la crisis financiera de finales de 2008. Allen podría posiblemente perder la totalidad de 65.5 millones de dólares, pero esto es increíblemente improbable. Él elige un nivel de cobertura de riesgo del 99 por ciento y elige medir este riesgo potencial de pérdida de cinco días utilizando el 99 por ciento, el VaR o el valor en riesgo. Es decir, quiere encontrar la cantidad de dinero que necesita para mantener disponible para que tenga una oferta de dinero suficiente para satisfacer la demanda con probabilidad de al menos 0.99. Para ilustrar el cálculo de VaR, utilizamos una base de datos histórica para rastrear el valor de los diferentes bonos que posee Hometown Bank como valores de inversión. ¿Cuántas veces a lo largo de un período de tiempo determinado —un año, en nuestro ejemplo—, Hometown experimentó un movimiento negativo de precios en sus inversiones y en cuánto? Para simplificar el ejemplo, asumiremos que toda la cartera está invertida en bonos del Tesoro de Estados Unidos a dos años. Un año de datos históricos crearía aproximadamente 250 puntos de datos de movimiento de precios para la cartera.El número 250 proviene de una estimación aproximada del número de días que los valores pueden negociarse en el mercado abierto durante un año determinado. Cincuenta y dos semanas a los cinco días de la semana rinde 260 días laborables, y hay aproximadamente diez días festivos a lo largo del año por los que el mercado está cerrado. De esos 250 resultados, ¿ con qué frecuencia el valor de la cartera disminuyó 5 por ciento o más desde el valor inicial? ¿Cuál fue la frecuencia de veces que la cartera de notas del Tesoro de Estados Unidos aumentó en valor más de 5 por ciento? Hometown Bank ahora puede construir una distribución de probabilidad de rendimientos registrando observaciones del desempeño de la cartera. Esta distribución de probabilidad aparece en la Figura\(\PageIndex{4}\).

Figura\(\PageIndex{4}\): Distribución de frecuencia bancaria de la ciudad natal del movimiento diario de precios de la cartera de valores de inversión

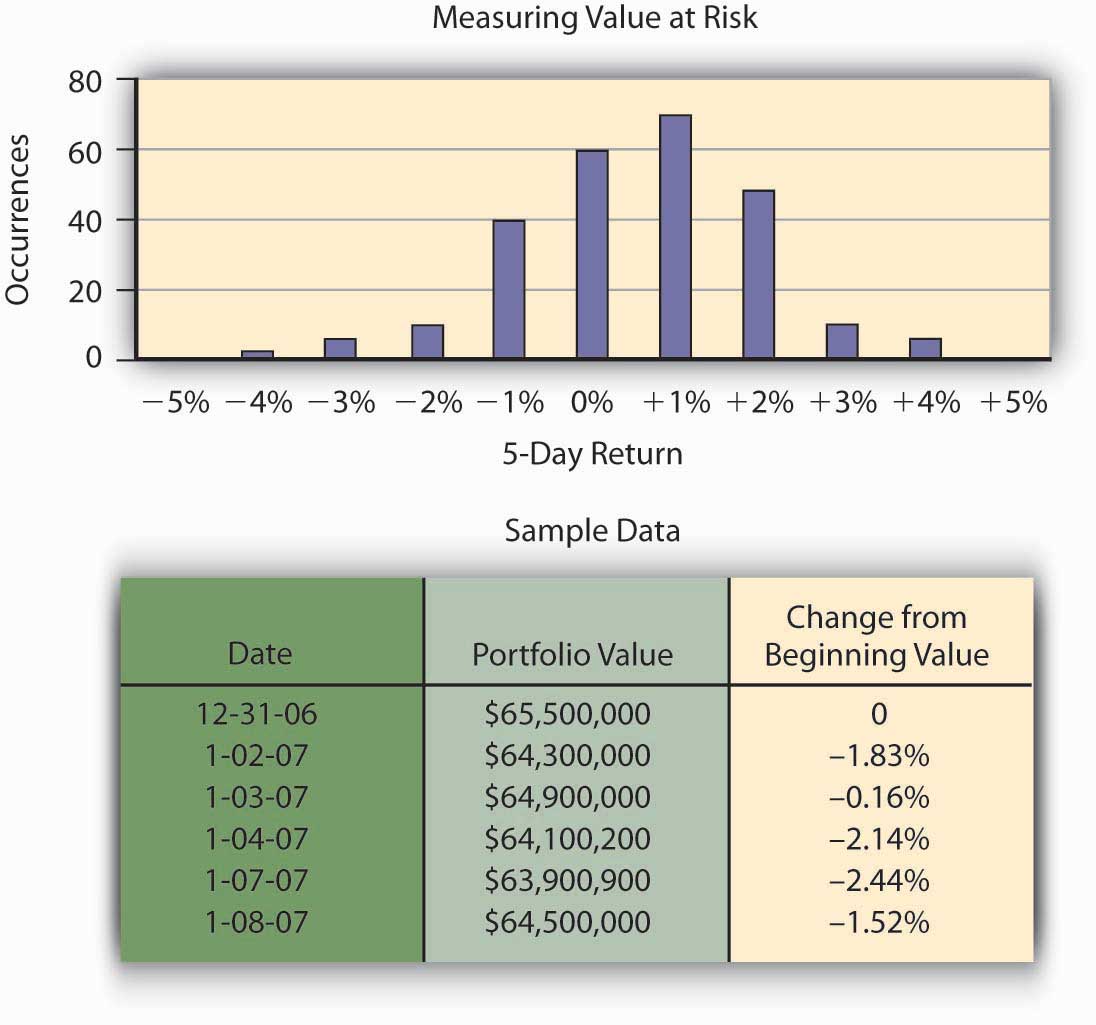
La curva de distribución de frecuencias del movimiento de precios para la cartera aparece en la Figura\(\PageIndex{1}\). A partir de esos datos, Hometown puede medir el 99 por ciento de VaR de una cartera durante un período de cinco días al encontrar el percentil inferior para la distribución de probabilidad. VaR describe la probabilidad de pérdida potencial de valor de los bonos del Tesoro de Estados Unidos que se relaciona con el riesgo de precio de mercado. Del gráfico, observamos que el 1 por ciento inferior de las 250 observaciones es aproximadamente una pérdida de 5 por ciento, es decir, 99 por ciento de las veces el retorno es mayor que —5 por ciento. Así, el 99 por ciento de VaR sobre los rendimientos es —5 por ciento. El VaR para la cartera es el VaR en los tiempos de retorno $65.5 millones, o —.05× ($65.5 millones) = −$3,275,000. Esto responde a la pregunta de cuánto capital de riesgo necesita retener el banco frente a contingencias que solo deberían ocurrir una vez en ciento periodos de cinco días, es decir, deben tener $3,275,000 en reserva. Con esta cantidad de dinero, la probabilidad de que los movimientos en los valores de mercado provoquen una pérdida de más de $3,275,000 es del 1 por ciento.

El riesgo ahora se puede comunicar con el comunicado: En condiciones normales de mercado, lo más que perderá la cartera de valores de inversión en un periodo de cinco días es de aproximadamente $3,275,000 con un nivel de confianza del 99 por ciento .Philippe Jorion, Valor en Riesgo: El Nuevo Benchmark para la Gestión del Riesgo Financiero, 2a ed. (McGraw Hill, 2001), ch. 1. “1:La Naturaleza del Riesgo - Pérdidas y Oportunidades”.

En el contexto de exposiciones de riesgo puro, la noción equivalente a VaR es la Pérdida Anual Máxima Probable (MPAL). Al igual que con la medida VaR, se observa una distribución de probabilidad, en este caso de pérdidas a lo largo de un periodo de un año y luego elige el valor del percentil inferior seleccionado como MPAL. Por ejemplo, si la distribución de pérdidas viene dada por la Figura 2.1.2, y se selecciona el nivel de confianza del 95 por ciento, entonces el MPAL es el mismo que el valor de VaR del 95 por ciento. En contextos de seguros a menudo se encuentra con el término MPAL, mientras que en las finanzas a menudo se encuentra con el término VaR. Su cálculo es el mismo y su interpretación como medida de riesgo es la misma.

También observamos que el debate se desata sobre las debilidades percibidas al usar VaR como medida de riesgo en las finanzas. “En definitiva, los modelos VaR no proporcionan una medida precisa de las pérdidas que ocurren en eventos extremos. Simplemente no puede representar la textura completa y el alcance de sus riesgos de mercado solo con VaR” Gleason, capítulo 12. Además, el VaR examina el tamaño de la pérdida que se produciría sólo el 1 por ciento de las veces, pero no especifica el tamaño del déficit que se esperaría que la compañía tuviera que compensar por una liquidación de bienes de auxilio en caso de que ocurriera una pérdida tan grande. Para ello se utiliza otra medida denominada el déficit esperado. El lector interesado es remitido a Brockett y AIPatrick L. Brockett y Jing Ai, “Enterprise Risk Management (ERM)”, en Encyclopedia of Quantitative Risk Assessment and Analysis, ed. E. Melnick y B. Everitt (Chichester, Reino Unido: John Wiley & Sons Ltd., 2008), 559—66. para este cálculo.

Medida beta del riesgo de cartera no diversificable de CAPM

Algunas exposiciones de riesgo afectan a muchos activos de una firma al mismo tiempo. En las finanzas, por ejemplo, los movimientos en el mercado en su conjunto o en toda la economía pueden afectar el valor de muchas acciones individuales (y empresas) simultáneamente. Vimos esto muy dramáticamente ilustrado en la crisis financiera de 2008—2009 donde todo el mercado de valores bajó y arrastró a muchas acciones (y firmas) hacia abajo con ella, algunas más que otras. En “1: La naturaleza del riesgo - pérdidas y oportunidades” nos referimos a este tipo de riesgo como riesgo sistemático, fundamental o no diversificable. Para una empresa (o individuo) que tenga una cartera de activos grande y bien diversificada, el impacto financiero negativo total de cualquier riesgo idiosincrásico sobre el valor de la cartera es mínimo ya que constituye solo una pequeña fracción de su riqueza.

Por lo tanto, el riesgo idiosincrásico específico del activo generalmente se ignora al tomar decisiones sobre la cantidad adicional de riesgo involucrada al adquirir un activo adicional para ser agregado a una cartera de activos ya bien diversificada. La pregunta es cómo desenredar lo sistemático del riesgo no sistemático incrustado en cualquier activo. Los profesores de finanzas Jack Treynor, William Sharpe, John Lintner y Jan Mossin trabajaron de forma independiente y desarrollaron un modelo llamado Capital Asset Pricing Model (CAPM). A partir de este modelo podemos obtener una medida de cómo el rendimiento de un activo varía sistemáticamente con las variaciones en el mercado, y en consecuencia podemos obtener una medida del riesgo sistemático. La idea es similar al viejo adagio de que una marea ascendente levanta todos los barcos. En este caso un mercado o economía ascendente (o descendente) eleva (o baja) todos los activos en mayor o menor grado dependiendo de su covariación con el mercado. Esta covariación con el mercado es fundamental para obtener una medida de riesgo sistemático. Lo desarrollamos ahora.

Esencialmente, el modelo CAPM asume que los inversionistas en activos esperan ser compensados tanto por el valor temporal del dinero como por el riesgo sistemático o no diversificable que soportan. Al respecto, se supone que el rendimiento de un activo A\(R_A\),, es igual al rendimiento de una inversión absolutamente segura o libre de riesgo,\(r_f\) (el valor temporal de la parte monetaria) y una prima de riesgo, que mide la compensación por el riesgo sistemático que están soportando. Para medir el monto de este riesgo sistemático, primero analizamos la correlación entre los rendimientos del activo y los rendimientos en una cartera de mercado de todos los activos. El supuesto es que la cartera de mercado cambia con los cambios en la economía en su conjunto, por lo que los cambios sistemáticos en la economía se ven reflejados por cambios en el nivel de la cartera de mercado. Se asume que la variación de los rendimientos de los activos con respecto a los rendimientos del mercado es lineal y, por lo tanto, el marco general se expresa como

\[R_A= r_f+β_A× (R_m − r_f )+ ε,\]

donde ε denota un término aleatorio que no está relacionado con el rendimiento del mercado. Así, el término\(β_A× (R_m − r_f )\) representa un retorno sistemático y ε representa un componente específico de la empresa o idiosincrásico no sistemático del retorno.

Observe que al tomar varianzas, tenemos\ (σ_A^ {2} = .β_A^2×β_M^2, + σ_ε^2\), por lo que el primer término se denomina varianza sistemática y el segundo término es la varianza idiosincrática o específica de la firma.

La idea detrás del CAPM es que los inversionistas serían compensados por el riesgo sistemático y no el riesgo idiosincrásico, ya que el riesgo idiosincrásico debería ser diversificable por los inversionistas que poseen una gran cartera diversificada de activos, mientras que el riesgo sistemático o de mercado los afecta a todos. En términos de valores esperados, a menudo escribimos la ecuación como

\[E[R_A]= r_f+ β_A×(E[R_m]− r_f),\]

que es el llamado modelo CAPM. Al respecto la tasa esperada de rendimiento de un activo\(E[R_A]\), es la inversión libre de riesgo \(r_f\), más una prima de riesgo de mercado igual a\ (β_A× (E [R_M] − r_f)\). El coeficiente\(β_A\) se denomina riesgo de mercado o riesgo sistemático de activo A.

Al ejecutar una regresión lineal de los rendimientos experimentados en el activo A con los rendimientos experimentados en una cartera de mercado ( como la cartera de acciones de Dow Jones Industrial) y el rendimiento de los activos sin riesgo (como la tasa de retorno de la factura T de Estados Unidos), se puede encontrar la medida de riesgo\(β_A\). Una regresión es una técnica estadística que crea una tendencia basada en los datos. Se utiliza una regresión lineal real para calcular la frecuencia y gravedad futuras con base en una tendencia en “4: Gestión del riesgo en evolución - Herramientas fundamentales” para el análisis de la gestión de riesgos. Libros estadísticos mostrarVéase Patrick Brockett y Arnold Levine Brockett, Estadísticas, probabilidad y sus aplicaciones (W. B. Saunders Publishing Co., 1984). que \(β_A. = \tfrac{COV(R_A, R_m)}{β_m^2}\) donde\(COV(R_A,R_m)\) está la covarianza del rendimiento del activo con el rendimiento en el mercado y es definido por

\ [COV (R_A, R_m) = E [{R_A, −E (R_A)} × {R_m , -E (R_m)}],\]

es decir, el valor promedio del producto de la desviación del rendimiento del activo con respecto a su valor esperado y los rendimientos del mercado a partir de su valor esperado. En cuanto al coeficiente de correlación \(ρ_{Am}\) entre el rendimiento del activo y el mercado, tenemos \(β_A= ρ_{Am}×(\frac{β_A}{β_m})\), por lo que también podemos pensar en beta como escalar la volatilidad de los activos por la volatilidad del mercado y la correlación del activo con el mercado.

El término\(β\) (beta) en las ecuaciones anteriores intenta cuantificar el riesgo asociado a las fluctuaciones o oscilaciones del mercado en el mercado. Una beta de 1 significa que se espera que el rendimiento del activo se mueva en conjunto con el mercado, es decir, un movimiento del 5 por ciento (medido en términos de unidades de desviación estándar del mercado) en el mercado dará como resultado un movimiento del 5 por ciento en el activo (medido en términos de unidades de desviación estándar del activo ). Una beta menor a una indica que el activo es menos volátil que el mercado en que cuando el mercado sube (o baja) en un 5 por ciento el activo subirá (o bajará) en menos de 5 por ciento. Una beta mayor a uno significa que se espera que el precio del activo se mueva más rápidamente que el mercado, por lo que si el mercado sube (o baja) en un 5 por ciento, entonces el activo subirá (o bajará) en más de un 5 por ciento. Una beta de cero indica que el rendimiento del activo no se correlaciona con los rendimientos del mercado.

Conclusiones clave

• Las medidas de riesgo cuantifican la cantidad de potencial sorpresa contenido en una distribución de probabilidad.
• Medidas como el rango y el Valor en Riesgo (VaR) y la Pérdida Anual Máxima Probable (MPAL) se centran en los extremos de las distribuciones y son medidas de riesgo adecuadas cuando el interés se centra en la solvencia o asegurarse de que se destina suficiente capital para manejar cualquier pérdida extrema realizada.
• Medidas como la varianza, la desviación estándar y la semivariancia son útiles cuando se observan desviaciones promedio de lo que se espera con el propósito de planificar las desviaciones esperadas de los resultados esperados.
• La medida de riesgo de mercado del Modelo de Precios de Activos de Capital es útil para evaluar el riesgo financiero sistemático o el riesgo adicional que implica agregar un activo a una cartera diversificada ya existente.

Preguntas de Discusión

1. Compare el riesgo relativo de la Aseguradora A con la Aseguradora B en las siguientes preguntas.
   1. ¿Qué aseguradora conlleva más riesgo en pérdidas y cuál conlleva más riesgo de siniestros? Explique.
   2. Comparar también la severidad y frecuencia de las aseguradoras.
2. La experiencia de la Aseguradora A durante los últimos tres años dada en el Problema 2 fue la siguiente:

   Año	Número de exposiciones	Número de reclamaciones por colisión	Pérdidas por colisión ($)
   1	10,000	375	350,000
   2	10,000	330	250,000
   3	10,000	420	400,000

   1. ¿Cuál es el rango de pérdidas por colisión por año?
   2. ¿Cuál es la desviación estándar de las pérdidas por año?
   3. Calcular el coeficiente de variación de las pérdidas por año.
   4. Calcular la varianza del número de siniestros por año.
3. La experiencia de la Aseguradora B durante los últimos tres años dada en el Problema 3 fue la siguiente:

   Año	Número de exposiciones	Número de reclamaciones por colisión	Pérdidas por colisión
   1	20,000	975	650,000
   2	20,000	730	850.000
   3	20,000	820	900,000

   1. ¿Cuál es el rango de pérdidas por colisión?
   2. Calcular la varianza en el número de reclamaciones por colisión por año.
   3. ¿Cuál es la desviación estándar de las pérdidas por colisión?
   4. Calcular el coeficiente de variación de colisión.
   5. Comparando los resultados de la Aseguradora A y la Aseguradora B, ¿qué aseguradora tiene un libro de negocios más riesgoso en cuanto al rango de posibles pérdidas que podrían experimentar?
   6. Al comparar los resultados de la Aseguradora A y la Aseguradora B, ¿qué aseguradora tiene un libro de negocios más riesgoso en términos de la desviación estándar en las pérdidas por colisión que puedan experimentar?