3.4: Elección bajo incertidumbre - Teoría de la utilidad esperada

Objetivos de aprendizaje

• En esta sección el alumno aprende que el objetivo de un individuo es maximizar la utilidad esperada a la hora de tomar decisiones bajo incertidumbre.
• También aprendemos que las personas son reacias al riesgo, neutrales al riesgo o buscan riesgos (amorosas).

Vimos antes que en cierto mundo, a la gente le gusta maximizar la utilidad. En un mundo de incertidumbre, parece intuitivo que los individuos maximizarían la utilidad esperada. Esto se refiere a un constructo utilizado para explicar el nivel de satisfacción que obtiene una persona cuando se enfrenta a elecciones inciertas. La intuición es sencilla, demostrarlo axiomáticamente fue una tarea muy desafiante. John von Neumann y Oskar Morgenstern (1944) abogaron por un enfoque que nos lleve a una representación matemática formal de maximización de la utilidad esperada.

También hemos visto que existe una representación de función de utilidad si se mantienen los cuatro supuestos discutidos anteriormente. Los señores von Neumann y Morgenstern agregaron dos suposiciones más y se les ocurrió una función de utilidad esperada que existe si estos axiomas se mantienen. Si bien las discusiones sobre estas supuestasEstas se llaman las suposiciones de continuidad e independencia. está más allá del alcance del texto, basta con decir que la función de utilidad esperada tiene la forma

\[E(U)= \sum_{i= 1}^{n} πi Ui\]

donde u es una función que adjunta números que miden el nivel de satisfacción u _i asociado con cada resultado i. u se llama la función Bernoulli mientras que \(E(U)\) es la función de utilidad esperada von Neumann-Morgenstern.

Nuevamente, tenga en cuenta que la función de utilidad esperada no es única, sino que varias funciones pueden modelar las preferencias del mismo individuo sobre un conjunto dado de elecciones o juegos inciertos. Lo que importa es que exista tal función (que refleja las preferencias de un individuo sobre los juegos inciertos). La teoría de la utilidad esperada dice entonces si los axiomas proporcionados por von Neumann-Morgenstern están satisfechos, entonces los individuos se comportan como si estuvieran tratando de maximizar la utilidad esperada.

La visión más importante de la teoría es que el valor esperado de los resultados en dólares puede proporcionar una clasificación de opciones diferentes a las dadas por la utilidad esperada. La teoría de la utilidad esperada dice entonces que las personas elegirán una opción (un juego de azar o lotería) que maximice su utilidad esperada en lugar de la riqueza esperada. Esa clasificación de utilidad esperada difiere del ranking de riqueza esperada se explica mejor usando el siguiente ejemplo.

Pensemos en un individuo cuya función de utilidad viene dada por\(u(W)=W\) y tiene una dotación inicial de $10. Esta persona se enfrenta a las siguientes tres loterías, basadas en un lanzamiento de monedas:

Tabla 3.1 Función de Utilidad con Dotación Inicial de $10

Resultado (Probabilidad)	Lotería de recompensa 1	Lotería de recompensa 2	Lotería de recompensa 3
H (0.5)	10	20	30
T (0.5)	−2	−5	−10
E (G)	4	7.5	10

Podemos calcular el pago esperado de cada lotería tomando el producto de probabilidad y el pago asociado con cada resultado y sumando este producto sobre todos los resultados. El ranking de las loterías basado en las ganancias esperadas en dólares es la lotería 3, 2 y 1—en ese orden. Pero consideremos el ranking de las mismas loterías por parte de esta persona que las clasifica en orden en función de la utilidad esperada.

Calculamos la utilidad esperada tomando el producto de probabilidad y la utilidad asociada correspondiente a cada resultado para todas las loterías. Cuando el pago es de $10, el patrimonio final equivale a dotación inicial ($10) más ganancias = ($20). La utilidad de esta riqueza final viene dada por 20 =4.472. A continuación se muestra la tabla de servicios públicos terminada.

Tabla 3.2 Rankings de lotería por utilidad esperada

Resultado (Probabilidad)	Lotería de Utilidades 1	Lotería de Utilidad 2	Lotería de Utilidad 3
\(H(0.5)\)	4.472	5.477	6.324
\(T(0.5)\)	2.828	2.236	0
\(E(U)\)=	3.650	3.856	3.162

La utilidad esperada clasifica las loterías en el orden 2—1—3. Entonces, el principio de maximización de utilidad esperada conduce a elecciones que difieren de las elecciones de riqueza esperadas.

El ejemplo muestra que el ranking de juegos de azar difiere cuando uno utiliza la teoría de utilidad esperada (\(E(U)\)) que cuando se aplica el\(E(G)\) principio de ganancia esperada Esto nos lleva a la idea de que si dos loterías proporcionan lo mismo\(E(G)\), el principio de ganancia esperada se clasificará ambas loterías por igual, mientras que la \(E(U)\) teoría puede conducir a clasificaciones únicas de las dos loterías. ¿Qué sucede cuando la\(E(U)\) teoría lleva a un mismo ranking? La teoría dice que la persona es indiferente entre las dos loterías.

Tipos de riesgo y sus representaciones de funciones de utilidad

¿Qué característica de los juegos de azar puede llevar a lo mismo \(E(G)\) pero diferente\(E(U)\)? La característica es el “riesgo” asociado a cada juego. En esta coyuntura, solo nos importa esa noción de riesgo, que captura la variabilidad inherente en los resultados (incertidumbre) asociados a cada lotería. Entonces la \(E(U)\) teoría predice que la “actitud” de riesgo de los individuos para cada lotería puede llevar a diferentes clasificaciones entre loterías. Además, la teoría es “robusta” en el sentido de que también permite que las actitudes hacia el riesgo varíen de un individuo a otro. Como veremos ahora, la\(E(U)\) teoría sí nos permite captar diferentes actitudes de riesgo de los individuos. Técnicamente, la diferencia en las actitudes de riesgo entre los individuos se llama “heterogeneidad de las preferencias de riesgo” entre los agentes económicos.

Desde la perspectiva\(E(U)\) teórica, podemos categorizar a todos los agentes económicos en una de las tres categorías como se señala en “1: La naturaleza del riesgo - pérdidas y oportunidades”:

• Aversión al riesgo
• Neutro de riesgo
• Búsqueda de riesgo (o amor)

Exploraremos cómo\(E(U)\) capta estas actitudes y el significado de cada actitud de riesgo a continuación.

Considere la\(E(U)\) función dada por\ (E (U) =\ displaystyle \ sum_ {i= 1} ^ {n} πi U (Wi)\). Que las preferencias sean tales que la adición a utilidad que uno obtiene de un dólar adicional a niveles más bajos de riqueza siempre es mayor que la utilidad adicional de un dólar extra en niveles más altos de riqueza. Entonces, digamos que cuando una persona tiene cero riqueza (sin dinero), entonces la persona tiene cero utilidad. Ahora si la persona recibe un dólar, su utilidad salta a 1 util. Si ahora se le da a esta persona un dólar adicional, entonces según la suposición de monotonicidad (más es mejor), su utilidad subirá. Digamos que sube a 1.414 utils para que el incremento de utilidad sea de sólo 0.414 utils, mientras que antes era una unidad entera (1 util). A 2 dólares de riqueza, si el individuo recibe otro dólar, entonces nuevamente la utilidad de sus familias sube a un nuevo nivel, pero sólo a 1.732 utils, un incremento de 0.318 unidades (1.732 −1.414). Esto está aumentando la utilidad a un ritmo decreciente por cada unidad adicional de riqueza. En la figura se\(\PageIndex{1}\) muestra una gráfica de la utilidad.

Figura\(\PageIndex{1}\): Una función de utilidad para un individuo con aversión al riesgo

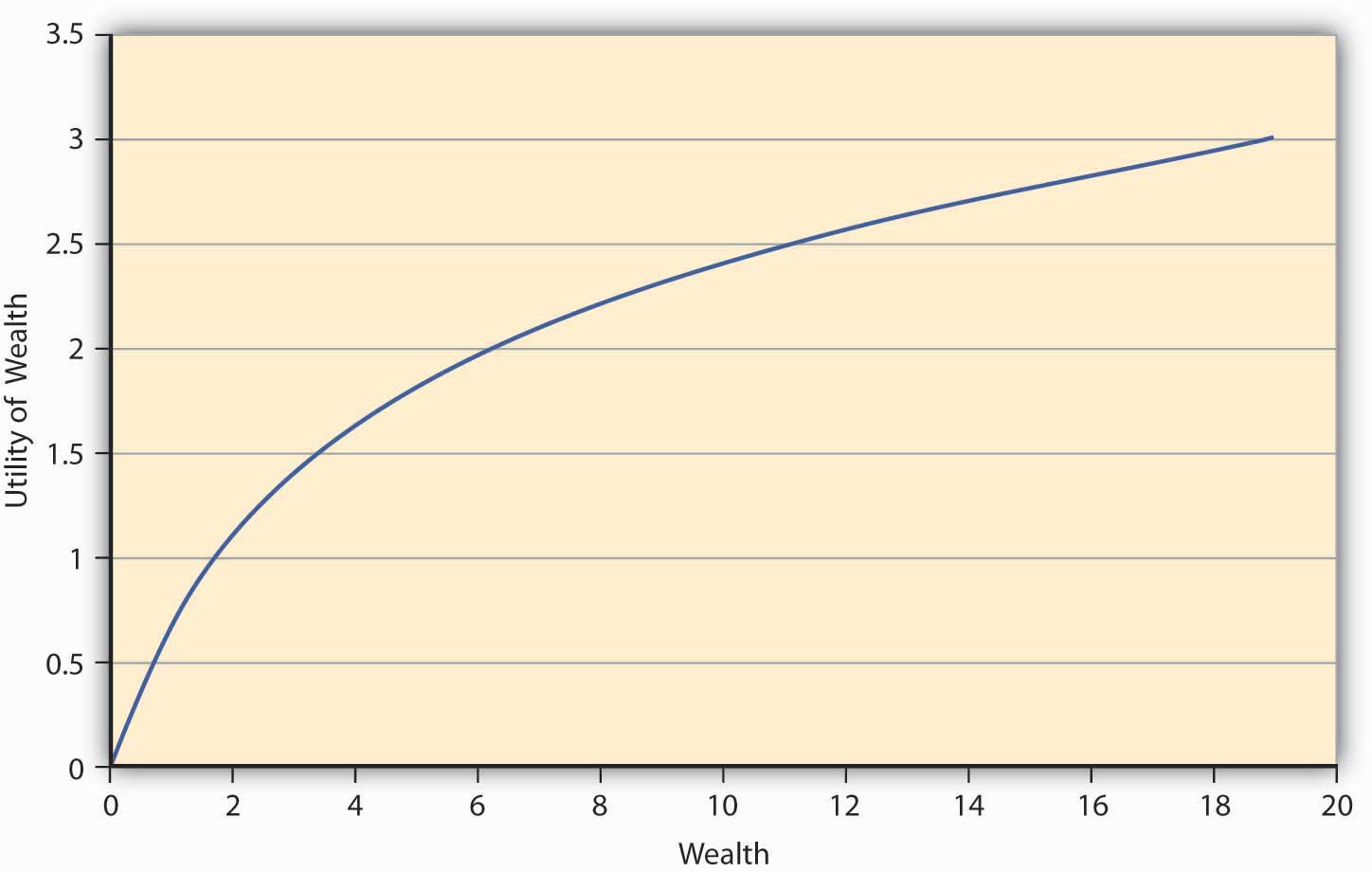
Lo primero que notamos de Figura\(\PageIndex{1}\) es su concavidad, lo que significa que si uno dibuja una cuerda conectando dos puntos cualesquiera de la curva, el acorde quedará estrictamente por debajo de la curva. Además, la utilidad siempre va en aumento aunque a un ritmo decreciente. Esta característica de esta función de utilidad particular se llama utilidad marginal decreciente. La utilidad marginal en cualquier nivel de riqueza dado no es más que la pendiente de la función de utilidad en ese nivel de riqueza.Matemáticamente, la propiedad que la utilidad está aumentando a una tasa decreciente puede escribirse como una combinación de restricciones sobre la primera y segunda derivada (tasa de cambio de pendiente) de la función de utilidad,\(u^\prime\) (W) >0, \(u^{\prime\prime}\) (W) <0. Algunas funciones que satisfacen esta propiedad son\(u(W)= W\),\(LN(W)\),\(−e −aW\). \(u^\prime\)(W) >0,\(u^{\prime\prime}\) (W) <0,\(u(W)= W\), \(LN(W)\),\(−e −2W\). La forma funcional representada en la Figura \(\PageIndex{1}\) es\(LN(W)\).

La pregunta que nos hacemos ahora es si un individuo así, cuya función de utilidad tiene la forma en la Figura\(\PageIndex{1}\), estará dispuesto a pagar el precio actuarialmente justo (AFP), que equivale a las ganancias esperadas, para jugar un juego de azar? Que se le ofrezca el juego que le ofrezca los beneficios. En el Juego 1, las mesas tienen juegos de playoffs por Juego 1 en la Tabla 3.1 basados en el lanzamiento de una moneda. El AFP para el juego es de 4 dólares. Supongamos que una persona llamada Terry lleva este costo por adelantado y gana; entonces su riqueza final es\($10−$4+$10= $16\) (riqueza original menos el costo del juego, más la ganancia de $10), o de lo contrario equivale a\ ($10− $4− $2= $4\) (riqueza original menos el costo del juego, menos la pérdida de $2) en caso de que pierde. Que la función de utilidad de este individuo sea dada por W. Entonces la utilidad esperada cuando el juego cuesta AFP equivale a 0.5 16 +0.5 4 =3 utils. Por otro lado, supongamos que Terry no juega el juego; su utilidad se mantiene en 10 =3.162. Dado que la utilidad es mayor cuando Terry no juega el juego, concluimos que cualquier individuo cuyas preferencias sean representadas por Figura\(\PageIndex{1}\) renunciará a un juego de azar si su costo es igual a AFP. Este es un resultado importante para una función de utilidad cóncava como se muestra en la Figura\(\PageIndex{1}\).

Tal persona necesitará incentivos para estar dispuesta a jugar el juego. Podría venir como una reducción de precio por jugar a la lotería, o como una prima que compense al individuo por el riesgo. Si Terry ya enfrenta un riesgo, pagará una cantidad mayor al valor actuarialmente razonable para reducir o eliminar el riesgo. Por lo tanto, funciona en ambos sentidos: los consumidores exigen una prima por encima de AFP para asumir riesgos. Así, las compañías de seguros cobran primas individuales por transferencia de riesgos a través de seguros.

Un individuo —llamémosle Johann— tiene preferencias que se caracterizan por las que se muestran en la Figura\(\PageIndex{1}\) (es decir, por una función de utilidad marginal cóncava o decreciente). Johann es una persona reacia al riesgo. Hemos visto que una persona reacia al riesgo se niega a jugar un juego actuarialmente limpio. Dichas aversiones de riesgo también proporcionan un incentivo natural para que Johann exija (o, de manera equivalente, pague) una prima de riesgo por encima de AFP para asumir (o, equivalentemente, deshacerse de) el riesgo. Quizás recuerdes de “1: La naturaleza del riesgo - pérdidas y oportunidades” que introdujo una medida más matemática a la descripción de la aversión al riesgo. En un estudio experimental, Holt y Laury (2002) encuentran que la mayoría de los sujetos en estudio tomaron “decisiones seguras”, es decir, mostraron aversión al riesgo. Dado que las situaciones de la vida real pueden ser más riesgosas que los entornos de laboratorio, podemos asumir con seguridad que la mayoría de las personas son reacias al riesgo la mayor parte del tiempo. ¿Y el resto de la población?

Sabemos que la mayoría de nosotros no nos comportamos como personas reacias al riesgo todo el tiempo. A finales de la década de 1990, se consideró que el mercado de valores era una “burbuja”, y muchas personas invirtieron en el mercado de valores a pesar de las preferencias que exhibían antes de esta época. En su momento, el presidente de la Junta de la Reserva Federal, Alan Greenspan, introdujo el término “exuberancia irracional” en un discurso pronunciado en el American Enterprise Institute. La frase se ha convertido en una forma regular de describir las desviaciones de las personas de las preferencias normales. Dicho comportamiento también se repitió a principios y mediados de la década de 2000 con una burbuja inmobiliaria. Las personas sin los medios racionales para comprar casas las compraron y tomaron “riesgos no convencionales”, lo que llevó a la crisis financiera y crediticia 2008-2009 y a grandes recesiones (quizás incluso depresión) cuando el presidente Obama asumió el cargo en enero de 2009. Podemos considerar que las condiciones del mercado externo y la “mentalidad de rebaño” contribuyen significativamente a cambiar los rasgos racionales de aversión al riesgo.

Un individuo puede hacer paracaidismo, ala delta y participar en comportamientos de alto riesgo. Nuestra pregunta es, ¿puede la teoría de la utilidad esperada capturar ese comportamiento también? De hecho puede, y eso nos lleva a la conducta de búsqueda de riesgos y su caracterización en \(E(U)\) teoría. Dado que el comportamiento de búsqueda de riesgo exhibe preferencias que parecen ser lo opuesto a la aversión al riesgo, la representación funcional matemática también puede mostrar un comportamiento opuesto. Para una persona amante del riesgo, la función de utilidad mostrará la forma dada en la Figura\(\PageIndex{2}\). Demuestra que cuanto mayor sea el nivel de riqueza del individuo, mayor es el incremento en la utilidad cuando se le da un dólar adicional a la persona. Llamamos a esta característica de la función, en la que la utilidad siempre está aumentando a un ritmo creciente, incrementando la utilidad marginal. Resulta que todas las funciones de utilidad convexas se parecen a Figura\(\PageIndex{2}\). La curva se encuentra estrictamente por debajo de la cuerda uniendo dos puntos cualesquiera de la curva. La curva convexa en la Figura\(\PageIndex{1}\) tiene algunos ejemplos que incluyen la función matemática\ (u (W) = W^2\), e W. \(u(W)=W^2\), e W.

Figura\(\PageIndex{2}\): Una función de utilidad para un individuo que busca riesgos

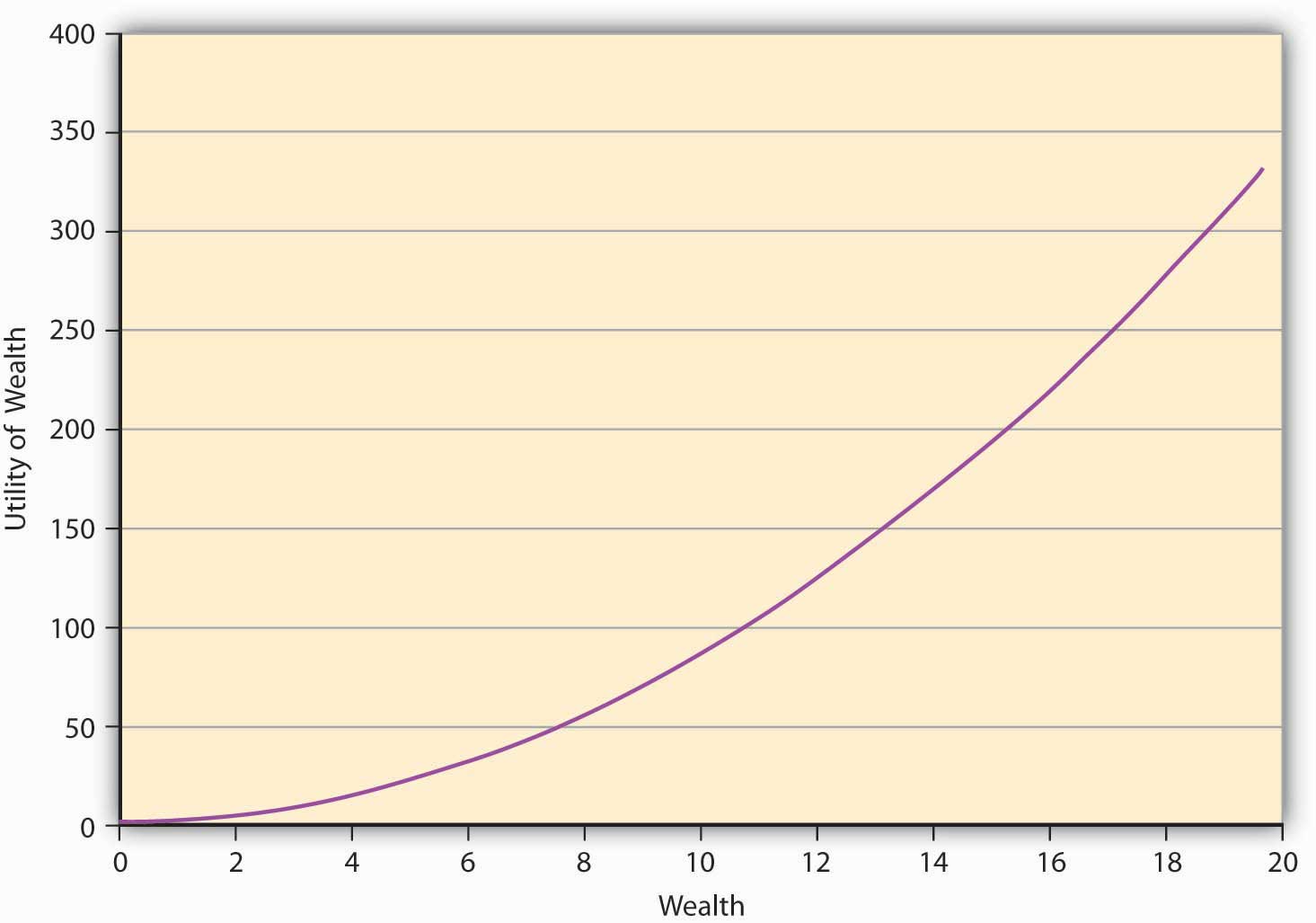
Un individuo que busca riesgos siempre elegirá jugar una apuesta en su AFP. Por ejemplo, supongamos que las preferencias del individuo están dadas por\(u(W)= W²\). Como antes, el individuo posee $10, y tiene que decidir si jugar o no una lotería basada en un lanzamiento de moneda. El pago si aparece una cabeza es de $10 y −$2 si es una cola. Hemos visto anteriormente (en la Tabla 3.1) que la AFP por jugar a esta lotería es de 4 dólares.

El cálculo de utilidad esperado es el siguiente. Después de asumir el costo de la lotería por adelantado, la riqueza es de 6 dólares. Si aparecen cabezas, la riqueza final se vuelve\($16 ($6 + $10)\). En caso de que las colas se vuelvan boca arriba, entonces la riqueza final equivale a $4 ($6 − $2). La utilidad esperada de la gente si juegan la lotería es\ (u (W) =0.5× 16^2+0.5× 4^2=136\) utils.

Por otro lado, si un individuo llamado Ray decide no jugar a la lotería, entonces el\(E(U)= 10^2=100\). Dado que el\(E(U)\) es mayor si Ray juega la lotería en su AFP, jugará la lotería. De hecho, esta es la mentalidad de los jugadores. Es por ello que vemos a tanta gente en las máquinas tragamonedas de las casas de juego.

El contraste entre las decisiones tomadas por los individuos reacios al riesgo y los individuos que buscan riesgos es claramente claro en el ejemplo anterior. Matemáticamente hablando, para una persona reacia al riesgo, tenemos \(E(U[W])≤U[E(W)]\). De igual manera, para una persona que busca riesgos tenemos \(E(U[W])≥U[E(W)]\). A este resultado se le llama desigualdad de Jensen. Para resumir, una persona que busca riesgos siempre juega la lotería en su AFP, mientras que una persona reacia al riesgo siempre la abandona. Sus funciones de utilidad cóncavas (Figura 3.1.1\(\PageIndex{1}\)) versus convexas (Figura) y sus implicaciones se encuentran en el centro de su toma de decisiones.

Por último, llegamos al tercer tipo de actitud de riesgo donde un individuo es indiferente entre jugar una lotería y no jugarlo. A tal individuo se le llama riesgo neutral. Las preferencias de tal individuo pueden ser capturadas en\(E(U)\) teoría por una función de utilidad lineal de la forma\(u(W)=aW\), donde a es un número real > 0. Tal individuo gana una utilidad marginal constante de la riqueza, es decir, cada dólar adicional agrega la misma utilidad a la persona independientemente de que el individuo esté dotado de $10 o 10,000 dólares. La función de utilidad de tal individuo se representa en la Figura\(\PageIndex{3}\).

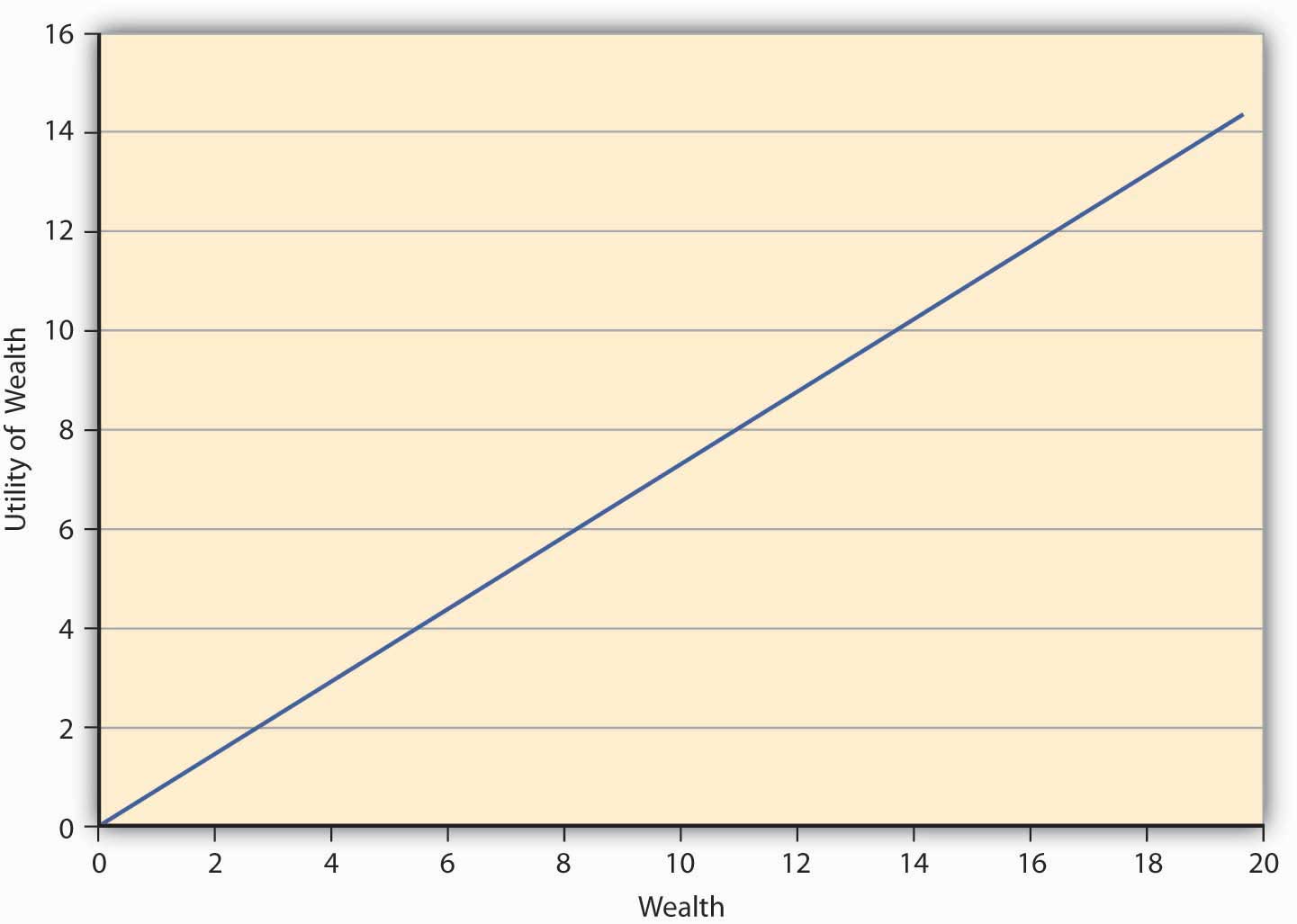Figura \(\PageIndex{3}\): Una función de utilidad para un individuo con riesgo neutro

Conclusiones clave

• Esta sección sienta las bases para el análisis del comportamiento de los individuos bajo incertidumbre. El estudiante debe ser capaz de describirlo como tal.
• El estudiante debe ser capaz de calcular las ganancias esperadas y las utilidades esperadas.
• Finalmente, y lo más importante, la concavidad y convexidad de la función de utilidad es clave para distinguir entre individuos reacios al riesgo y buscadores de riesgo.

Preguntas de Discusión

1. Discutir la función de utilidad esperada de von Neumann-Morgenstern y discutir en qué se diferencia de las ganancias esperadas.
2. Se le dice que\(U(W)= W^2\) es una función de utilidad con utilidad marginal decreciente. ¿Es correcto? Discutir, utilizando la definición de utilidad marginal decreciente.
3. Un individuo tiene una función de utilidad dada por\(U(W)=W\), y riqueza inicial de $100. Si juega una lotería sin costo en la que puede ganar o perder 10 dólares al lanzar una moneda, compute su utilidad esperada. ¿Cuál es la ganancia esperada? ¿Se clasificará a una persona así como neutral en el riesgo?
4. Discutir los tres tipos de riesgo con respecto a sus formas, formulación técnico-matemática y la interpretación económica.