1.6: El tratamiento matemático de los resultados de la medición
- Page ID
- 1798
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)Habilidades para desarrollar
- Explicar el enfoque del análisis dimensional (etiqueta de factor) para los cálculos matemáticos que involucran cantidades
- Utilizar el análisis dimensional para hacer conversiones de unidades para una propiedad dada y cálculos que involucren dos o más propiedades
A veces ocurre que una cantidad de interés no puede ser fácil (o posible) para medir directamente, sino que se debe calcular usando otras propiedades medidas directamente y relacionadas matemáticamente. Por ejemplo, considere medir la velocidad promedia de un atleta que corre esprints. Esto se logra típicamente midiendo el tiempo requerido para que el atleta corra desde la línea de inicio hasta la línea de meta, y la distancia entre estas dos líneas, y luego calculando la velocidad de la ecuación que relaciona estas tres propiedades:
\[\mathrm{speed=\dfrac{distance}{time}}\]
Un velocista olímpico puede correr 100 m en aproximadamente 10 s, lo que corresponde a una velocidad media de
\[\mathrm{\dfrac{100\: m}{10\: s}=10\: m/s}\]
Tenga en cuenta que esta simple aritmética consiste en dividir los números de cada cantidad medida para obtener el número de la cantidad calculada (100/10 = 10) y de la misma manera dividir las unidades de cada cantidad medida para obtener la unidad de la cantidad calculada (m/s = m/s). Ahora, considere usar esta misma relación para predecir el tiempo requerido para que una persona que corre a esta velocidad recorra una distancia de 25 m. Se utiliza la misma relación entre las tres propiedades, pero en este caso, las dos cantidades proporcionadas son una velocidad (10 m/s) y una distancia (25 m). Para obtener la propiedad buscada que es el tiempo en este caso, la ecuación se debe reorganizar adecuadamente:
\[\mathrm{time=\dfrac{distance}{speed}}\]
El tiempo se puede calcular como:
\[\mathrm{\dfrac{25\: m}{10\: m/s}=2.5\: s}\]
De nuevo, la aritmética en los números (25/10 = 2.5) estuvo acompañada por la misma aritmética en las unidades (m/m/s = s) para obtener el número y la unidad del resultado, 2.5 s. Tenga en cuenta que, al igual que para los números, cuando una unidad se divide por una unidad idéntica (en este caso, m / m), el resultado es "1", o, como se dice comúnmente, las unidades se "cancelan".
Estos cálculos son ejemplos de un enfoque matemático versátil conocido como el análisis dimensional (o el método de etiquetado de factores). El análisis dimensional se basa en esta premisa: las unidades de cantidades se deben someter a las mismas operaciones matemáticas que sus números asociados. Este método se puede aplicar a los cálculos que son de conversiones de unidades simples a cálculos más complejos de varios pasos que involucran varias cantidades diferentes.
Los factores de conversión y el análisis dimensional
Se puede utilizar una relación de dos cantidades equivalentes expresadas con diferentes unidades de medida como factor de conversión de unidades. Por ejemplo, las longitudes de 2.54 cm y 1 pulgada son equivalentes (por definición), se puede derivar un factor de conversión de unidad de esta relación,
\[\mathrm{\dfrac{2.54\: cm}{1\: in.}\:(2.54\: cm=1\: in.)\: or\: 2.54\:\dfrac{cm}{in.}}\]
Varios otros factores de conversión comúnmente usados se muestran en la Tabla \(\PageIndex{1}\).
| Longitud | Volumen | Masa |
|---|---|---|
| 1 m = 1.0936 yd | 1 L = 1.0567 qt | 1 kg = 2.2046 lb |
| 1 in. = 2.54 cm (exacto) | 1 qt = 0.94635 L | 1 lb = 453.59 g |
| 1 km = 0.62137 mi | 1 ft3 = 28.317 L | 1 (avoirdupois) oz = 28.349 g |
| 1 mi = 1609.3 m | 1 tbsp = 14.787 mL | 1 (troy) oz = 31.103 g |
Cuando multiplicamos una cantidad (como la distancia dada en pulgadas) por un factor de conversión de unidad apropiada, convertimos la cantidad a un valor equivalente con diferentes unidades (como la distancia en centímetros). Por ejemplo, el salto vertical de un jugador de baloncesto de 34 pulgadas se puede convertir a centímetros de la siguiente manera:
\[\mathrm{34\: \cancel{in.} \times \dfrac{2.54\: cm}{1\:\cancel{in.}}=86\: cm}\]
Dado que esta aritmética simple involucra cantidades, la premisa del análisis dimensional requiere que multipliquemos tanto los números como las unidades. Los números de estas dos cantidades se multiplican para obtener el número de la cantidad del producto, 86, mientras que las unidades se multiplican para producir
\[\mathrm{\dfrac{in.\times cm}{in.}}.\]
Al igual que para los números, una proporción de unidades idénticas también es numéricamente igual a uno,
\[\mathrm{\dfrac{in.}{in.}=1}\]
y el producto unitario se simplifica así a cm. (Cuando las unidades idénticas se dividen para obtener un factor de 1, se dice que se "cancelan".) Usando el análisis dimensional, podemos determinar que un factor de conversión de la unidad se configuró correctamente al verificar que la unidad original se cancelará, y el resultado tendrá la unidad deseada (convertida).
Ejemplo \(\PageIndex{1}\): el uso de los factores de conversión de unidades
La masa de un Frisbee de competición es 125 g. Convierte su masa a onzas usando el factor de conversión unitario derivado de la relación 1 oz = 28.349 g (Tabla \(\PageIndex{1}\)).
Solución
Si tenemos el factor de conversión, podemos determinar la masa en kilogramos utilizando una ecuación similar a la utilizada para convertir la longitud de pulgadas a centímetros.
\[x\:\mathrm{oz=125\: g\times unit\: conversion\: factor} \nonumber\]
Escribimos el factor de conversión de la unidad en sus dos formas:
\[\mathrm{\dfrac{1\: oz}{28.349\: g}\:and\:\dfrac{28.349\: g}{1\: oz}} \nonumber\]
El factor de conversión de unidad correcto es la proporción que cancela las unidades de gramos y deja onzas.
\[\begin{align*}
x\:\ce{oz}&=\mathrm{125\:\cancel{g}\times \dfrac{1\: oz}{28.349\:\cancel{g}}}\\
&=\mathrm{\left(\dfrac{125}{28.349}\right)\:oz}\\
&=\mathrm{4.41\: oz\: (three\: significant\: figures)}
\end{align*}\]
Ejercicio \(\PageIndex{1}\)
Convierta un volumen de 9.345 qt a litros.
- Respuesta
-
8.844 L
Más allá de las conversiones de unidades simples, el método de etiqueta de factor se puede usar para resolver los problemas más complejos que involucran los cálculos. Independientemente de los detalles, el enfoque básico es el mismo: todos los factores involucrados en el cálculo deben estar orientados de manera apropiada para asegurar que sus etiquetas (unidades) se cancelen y / o combinen de manera apropiada para obtener la unidad deseada en el resultado. Es por esto que se conoce como el método de etiqueta factorial. Continuando con su estudio de la química, encontrará muchas oportunidades para aplicar este enfoque.
Ejemplo \(\PageIndex{2}\): Calculando cantidades a partir de de los resultados de la medición
¿Cuál es la densidad del anticongelante común en unidades de g / ml? Una muestra de 4.00 qt de anticongelante pesa 9.26 lb.
Solución
Ya que \(\mathrm{density=\dfrac{mass}{volume}}\), necesitamos dividir la masa en gramos por el volumen en mililitros. En general: el número de unidades de B = el número de unidades del factor de conversión de unidad A \(\times\). Los factores de conversión necesarios se proporcionan en la Tabla 1.7.1: 1 lb = 453.59 g; 1 L = 1.0567 qt; 1 l = 1,000 ml. Podemos convertir la masa de libras a gramos en un solo paso:
\[\mathrm{9.26\:\cancel{lb}\times \dfrac{453.59\: g}{1\:\cancel{lb}}=4.20\times 10^3\:g} \nonumber \]
Necesitamos usar dos pasos para convertir el volumen de cuartos de galón a mililitros.
1.Convierta cuartos a litros.\[\mathrm{4.00\:\cancel{qt}\times\dfrac{1\: L}{1.0567\:\cancel{qt}}=3.78\: L} \nonumber\]
- Convierta litros a mililitros.
\[\mathrm{3.78\:\cancel{L}\times\dfrac{1000\: mL}{1\:\cancel{L}}=3.78\times10^3\:mL} \nonumber\]
Entonces,
\[\mathrm{density=\dfrac{4.20\times10^3\:g}{3.78\times10^3\:mL}=1.11\: g/mL} \nonumber\]
Alternativamente, la calculación se puede configurar de manera que usaría tres factores de conversión de unidades de forma secuencial en la siguiente manera:
\[\mathrm{\dfrac{9.26\:\cancel{lb}}{4.00\:\cancel{qt}}\times\dfrac{453.59\: g}{1\:\cancel{lb}}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\:\cancel{L}}{1000\: mL}=1.11\: g/mL} \nonumber\]
Ejercicio \(\PageIndex{2}\)
¿Cuál es el volumen en litros de 1.000 oz, dado que 1 L = 1.0567 qt y 1 qt = 32 oz (exactamente)?
- Respuesta
-
\(\mathrm{2.956\times10^{-2}\:L}\)
Ejemplo \(\PageIndex{3}\): Calculando cantidades a partir de de los resultados de la medición
Mientras se conduce desde Filadelfia a Atlanta, una distancia de aproximadamente 1250 km, un Lamborghini Aventador Roadster 2014 usa 213 L de gasolina.
- ¿Qué economía de combustible (promedio), en millas por galón obtuvo el Roadster durante este viaje?
- Si la gasolina cuesta $ 3.80 por galón, ¿Cuál fue el costo del combustible para este viaje?
Solución
(a) Primero convertimos la distancia de kilómetros a millas:
\[\mathrm{1250\: km\times\dfrac{0.62137\: mi}{1\: km}=777\: mi} \nonumber\]
y luego convertimos el volumen de litros a galones:
\[\mathrm{213\:\cancel{L}\times\dfrac{1.0567\:\cancel{qt}}{1\:\cancel{L}}\times\dfrac{1\: gal}{4\:\cancel{qt}}=56.3\: gal} \nonumber\]
Entonces,
\[\mathrm{(average)\: mileage=\dfrac{777\: mi}{56.3\: gal}=13.8\: miles/gallon=13.8\: mpg} \nonumber\]
Alternativamente, la calculación se puede configurar para que use todos los factores de conversión de forma secuencial, de la siguiente manera:
\[\mathrm{\dfrac{1250\:\cancel{km}}{213\:\cancel{L}}\times\dfrac{0.62137\: mi}{1\:\cancel{km}}\times\dfrac{1\:\cancel{L}}{1.0567\:\cancel{qt}}\times\dfrac{4\:\cancel{qt}}{1\: gal}=13.8\: mpg} \nonumber \]
(b) Al usar el volumen previamente calculado en galones, encontramos:
\[\mathrm{56.3\: gal\times\dfrac{$3.80}{1\: gal}=$214} \nonumber \]
Ejercicio \(\PageIndex{3}\)
Un Toyota Prius Hybrid usa 59.7 L de gasolina para conducir desde San Francisco a Seattle, una distancia de 1300 km (dos dígitos significativos).
- ¿Cuánto combustible (promedio), en millas por galón, obtuvo el Prius durante este viaje?
- Si la gasolina cuesta $ 3.90 por galón, ¿Cuánto costo el combustible para este viaje?
- Respuesta a
-
51 mpg
- Respuesta b
-
$62
La conversión de las unidades de la temperatura
Usamos la palabra temperatura para referir al calor o la frialdad de una sustancia. Una forma en que medimos un cambio en la temperatura es usar el hecho de que la mayoría de las sustancias se expanden cuando la temperatura sube y se contraen cuando la temperatura baja. El mercurio o el alcohol en un termómetro de vidrio cambia su volumen cuando cambia la temperatura. Debido a que el volumen del líquido cambia más que el volumen del vidrio, podemos ver que el líquido se expande cuando se calienta y se contrae cuando se enfría.
Para marcar una escala en un termómetro, necesitamos valores de referencia: dos de los más utilizados son las temperaturas de congelación y la ebullición del agua a una presión atmosférica específica. En la escala Celsius, 0°C se define como la temperatura de congelación del agua y 100° C como la temperatura de ebullición del agua. El espacio entre las dos temperaturas se divide en 100 intervalos iguales, lo que llamamos grados. En la escala Fahrenheit, el punto de congelación del agua se define como 32° F y la temperatura de ebullición es 212° F. El espacio entre estos dos puntos en un termómetro Fahrenheit se divide en 180 partes iguales (grados).
La definición de las escalas de temperatura Celsius y Fahrenheit como se describe en el párrafo anterior, resulta en una relación un poco más compleja entre los valores de temperatura en estas dos escalas que para diferentes unidades de medida para otras propiedades. La mayoría de las unidades de medida para una propiedad dada son directamente proporcionales entre sí (y = mx). Aqui se muestra un ejemplo que usa unidades de longitud familares:
\[\mathrm{length\: in\: feet=\left(\dfrac{1\: ft}{12\: in.}\right)\times length\: in\: inches}\]
dónde:
- y = longitud en pies,
- x = longitud en pulgadas
- La constante de proporcionalidad, m, es el factor de conversión.
Las escalas de temperatura Celsius y Fahrenheit no comparten un punto cero común, por eso la relación entre estas dos escalas es lineal en lugar de proporcional (\(y=mx+b\)). Por eso, convertir una temperatura de una de estas escalas a la otra requiere más que la simple multiplicación por un factor de conversión, m, también debe tener en cuenta las diferencias en los puntos cero de las escalas (\(b\)).
La ecuación lineal que relaciona las temperaturas en grados Celsius y Fahrenheit se derive fácilmente de las dos temperaturas utilizadas para definir cada escala. Al representar la temperatura en grados Celsius como \(x\) y la temperatura Fahrenheit como \(y\), la pendiente, \(m\), se calcula como:
\[\begin{align} m &=\dfrac{\Delta y}{\Delta x} \\[5pt] &= \mathrm{\dfrac{212\: ^\circ F - 32\: ^\circ F}{100\: ^\circ C-0\: ^\circ C}} \\[5pt] &= \mathrm{\dfrac{180\: ^\circ F}{100\: ^\circ C}} \\[5pt] &= \mathrm{\dfrac{9\: ^\circ F}{5\: ^\circ C} }\end{align} \]
La intersección en y de la ecuación, b, se calcula utilizando cualquiera de los pares de temperatura equivalentes, (100° C, 212° F) o (0° C, 32° F), como:
\[\begin{align} b&=y-mx \\[5pt] &= \mathrm{32\:^\circ F-\dfrac{9\:^\circ F}{5\:^\circ C}\times0\:^\circ C} \\[5pt] &= \mathrm{32\:^\circ F} \end{align} \]
La ecuación relacionando las escalas de temperatura es:
\[\mathrm{\mathit{T}_{^\circ F}=\left(\dfrac{9\:^\circ F}{5\:^\circ C}\times \mathit{T}_{^\circ C}\right)+32\:^\circ C}\]
Una forma abreviada de esta ecuación que omite las unidades de medida es:
\[\mathrm{\mathit{T}_{^\circ F}=\dfrac{9}{5}\times \mathit{T}_{^\circ C}+32}\]
El reordenamiento de esta ecuación produce la forma útil para convertir Fahrenheit a Celsius:
\[\mathrm{\mathit{T}_{^\circ C}=\dfrac{5}{9}(\mathit{T}_{^\circ F}+32)}\]
Como se mencionó anteriormente en este capítulo, la unidad de temperatura SI es el kelvin (K). Diferente a las escalas Celsius y Fahrenheit, la escala de kelvin es una escala de temperatura absoluta en la que 0 (cero) K corresponde a la temperatura más baja que se puede alcanzar teóricamente. El descubrimiento a principios del siglo XIX de la relación entre el volumen y la temperatura de un gas sugería que el volumen de un gas sería cero a −273.15 ° C. En 1848, el físico británico William Thompson, quien luego adoptó el título de Lord Kelvin, propuso una escala de temperatura absoluta basada en este concepto (en el capítulo sobre los gases de este texto se da más información sobre este tema).
La temperatura de congelación del agua en esta escala es 273.15 K y su temperatura de ebullición es 373.15 K. Observe que la diferencia numérica entre estas dos temperaturas de referencia es 100, esto es igual para la escala Celsius, y por eso la relación lineal entre estas dos escalas de temperatura mostrará una pendiente de \(\mathrm{1\:\dfrac{K}{^\circ\:C}}\). Siguiendo el mismo enfoque, las ecuaciones para convertir entre las escalas de temperatura kelvin y Celsius se derivan a ser:
\[T_{\ce K}=T_{\mathrm{^\circ C}}+273.15\]
\[T_\mathrm{^\circ C}=T_{\ce K}-273.15\]
El 273.15 en estas ecuaciones se ha determinado experimentalmente, por eso no es exacto. La figura \(\PageIndex{1}\) muestra la relación entre las tres escalas de temperatura. Recuerde que no utilizamos el signo de grado con temperaturas en la escala de kelvin.
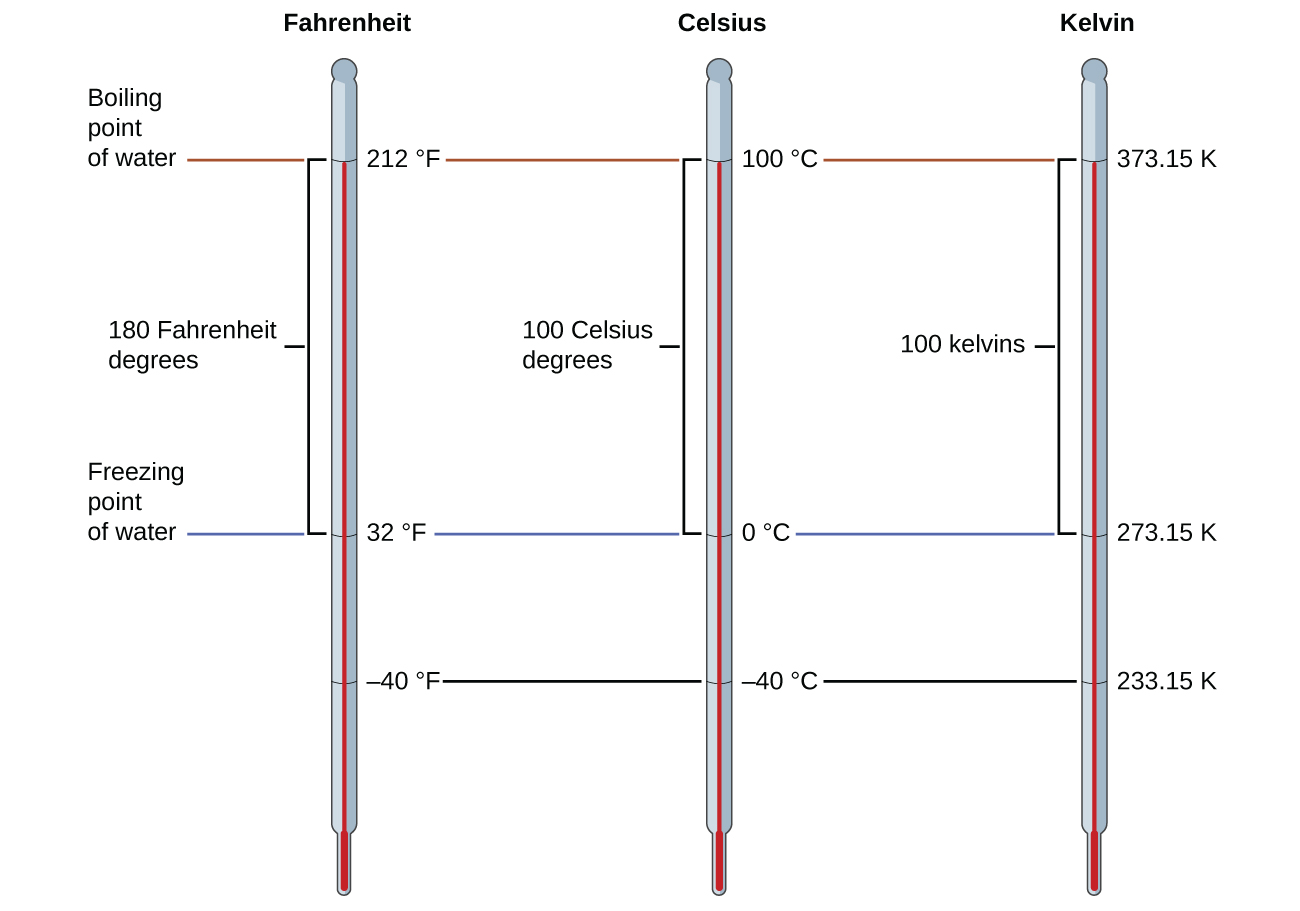
Aunque la escala de temperatura kelvin (absoluta) es la escala de temperatura oficial del SI, Celsius se usa comúnmente en muchos contextos científicos y es la escala que se escoge para contextos no científicos en casi todas las áreas del mundo. Muy pocos países (los EE. UU. Y sus territorios, las Bahamas, Belice, las Islas Caimán y Palau) todavía usan Fahrenheit para el clima, la medicina y la cocina.
Ejemplo \(\PageIndex{4}\) La conversión de centígrados
La temperatura normal del cuerpo se ha aceptado comúnmente a ser 37.0 °C (aunque varía según la hora del día y el método de medición, tanto como entre los individuos). ¿Cuál es esta temperatura en la escala de kelvin y en la escala de Fahrenheit?
Solución
\[\mathrm{K= {^\circ C}+273.15=37.0+273.2=310.2\: K} \nonumber \]
\[\mathrm{^\circ F=\dfrac{9}{5}\:{^\circ C}+32.0=\left(\dfrac{9}{5}\times 37.0\right)+32.0=66.6+32.0=98.6\: ^\circ F} \nonumber \]
Ejercicio \(\PageIndex{4}\)
Convierta 80.92 °C a K y °F.
- Respuesta
-
354.07 K, 177.7 °F
EJemplo \(\PageIndex{5}\): Conversión de Fahrenheit
Hornear una pizza preparada requiere una temperatura de horno de 450 °F. Si está en Europa y el termómetro de su horno usa la escala Celsius, ¿A cual temperatura necesita estar el horno en Celsius? ¿Cuál es la temperatura en kelvin?
Solución
\[\mathrm{^\circ C=\dfrac{5}{9}(^\circ F-32)=\dfrac{5}{9}(450-32)=\dfrac{5}{9}\times 418=232 ^\circ C\rightarrow set\: oven\: to\: 230 ^\circ C}\hspace{20px}\textrm{(two significant figures)} \nonumber\]
\[\mathrm{K={^\circ C}+273.15=230+273=503\: K\rightarrow 5.0\times 10^2\,K\hspace{20px}(two\: significant\: figures)} \nonumber\]
Ejercicio \(\PageIndex{5}\)
Convierta 50 °F a °C y K.
- Respuesta
-
10 °C, 280 K
Resumen
Las mediciones se realizan utilizando una variedad de unidades. Muy seguido, es útil o necesario convertir una cantidad medida de una unidad a otra. Estas conversiones se logran utilizando factores de conversión de unidades, que se derivan de aplicaciones simples de un enfoque matemático llamado el método de etiqueta de factor o el análisis dimensional. Esta estrategia también se usa para calcular las cantidades buscadas utilizando las cantidades medidas y las relaciones matemáticas apropiadas.
Ecuaciones Clave
- \(T_\mathrm{^\circ C}=\dfrac{5}{9}\times T_\mathrm{^\circ F}-32\)
- \(T_\mathrm{^\circ F}=\dfrac{9}{5}\times T_\mathrm{^\circ C}+32\)
- \(T_\ce{K}={^\circ \ce C}+273.15\)
- \(T_\mathrm{^\circ C}=\ce K-273.15\)
Glosario
- análisis dimensional
- (también, el método de etiqueta factorial) es un enfoque matemático versátil que se puede aplicar a los cálculos desde simples conversiones de unidades a cálculos más complejos de varios pasos que involucran varias cantidades diferentes
- Fahrenheit
- la unidad de temperatura; el agua se congela a 32 ° F y hierve a 212 ° F en esta escala
- factor de conversión de unidades
- la relación de cantidades equivalentes expresadas con diferentes unidades; se utiliza para convertir de una unidad a otra unidad diferente.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.


