1.5: La medición, incertidumbre, exactitud, y precisión
- Page ID
- 1797
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)habilidades para desarrollar
- Definir exactitud y precisión.
- Distinguir números exactos e inciertos.
- Representar correctamente la incertidumbre en cantidades utilizando cifras significativas.
- Aplicar reglas de redondeo adecuadas a las cantidades calculadas.
El conteo es el único tipo de medición que no tiene incertidumbre, dado que el número de objetos que se están contando no cambie mientras se están contando. El resultado de tal medición de conteo es un ejemplo de un número exacto. Si contamos los huevos en una caja, sabemos exactamente cuántos huevos hay en la caja. Los números de cantidades definidas también son exactos. Por definición, 1 pie es exactamente 12 pulgadas, 1 pulgada es exactamente 2.54 centímetros y 1 gramo es exactamente 0.001 kilogramo. Sin embargo, las cantidades derivadas de mediciones distintas del conteo son inciertas en diferentes grados debido a las limitaciones del proceso de medición utilizado.
Las cifras significativas en la medición
Los números de cantidades medidas, a diferencia de cantidades definidas o contadas directamente, no son exactos. Para medir el volumen de líquido en un cilindro graduado, debe hacer una medida en la parte inferior del menisco, el punto más bajo en la superficie curvada del líquido.
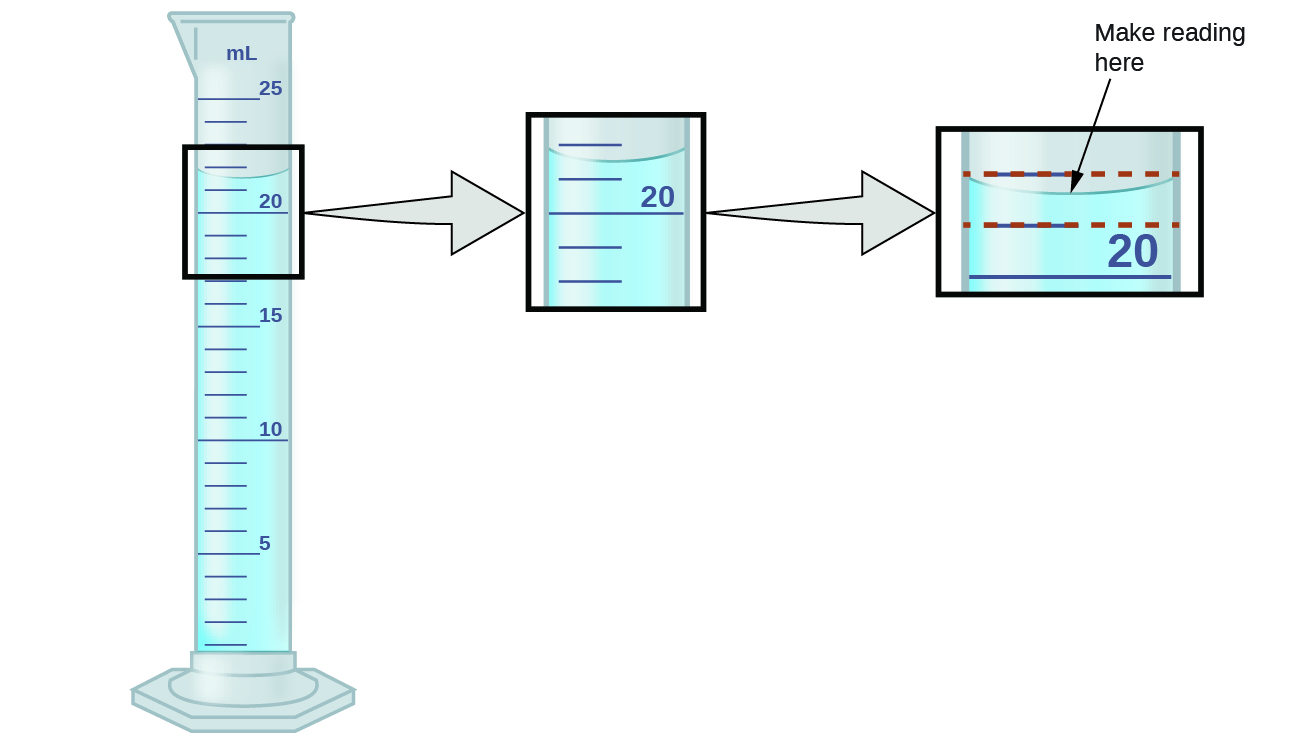
Consulte la ilustración en la Figura \(\PageIndex{1}\). La parte inferior del menisco en este caso se encuentra claramente entre las marcas 21 y 22, lo que significa que el volumen del líquido es ciertamente mayor que 21 mL, pero menor que 22 ml. El menisco parece estar un poco más cerca de la marca de 22 ml que de la marca de 21 ml, por eso una estimación razonable del volumen del líquido sería de 21.6 ml. En el número 21.6, entonces, los dígitos 2 y 1 son ciertos, pero el 6 es una estimación. Algunas personas podrían estimar que la posición del menisco está a una distancia igual de cada una de las marcas y estimar el dígito del décimo lugar como 5, mientras que otras pueden pensar que está aún más cerca de la marca de 22 ml y estimar que este dígito es 7. Nota que sería inútil intentar estimar un dígito para el centésimo puesto, dado que el dígito del décimo lugar es incierto. En general, las escalas numéricas como la de este cilindro graduado permiten realizar mediciones a una décima parte de la división de escala más pequeña. La escala en este caso tiene divisiones de 1 ml, por lo que los volúmenes se pueden medir con una precisión de 0.1 ml.
Este concepto es válido para todas las mediciones, incluso si no es una estimación. Si coloca un cuarto en una balanza electrónica estándar, puede obtener una lectura de 6.72 g. Los dígitos 6 y 7 son ciertos, y el 2 indica que la masa del trimestre es probable entre 6.71 y 6.73 gramos. El cuarto pesa alrededor de 6.72 gramos, con una incertidumbre nominal en la medida de ± 0.01 gramos. Si pesamos el cuarto en un balance más sensible, podemos encontrar que su masa es 6.723 g. Esto significa que su masa se encuentra entre 6.722 y 6.724 gramos, una incertidumbre de 0.001 gramos. Cada medida tiene cierta incertidumbre, que depende del dispositivo utilizado (y la capacidad del usuario). Todos los dígitos en una medición, incluido el último dígito incierto, se llaman cifras significativas o dígitos significativos. Tenga en cuenta que cero puede ser un valor medido; por ejemplo, si se encuentra en una escala que muestra el peso a la libra más cercana y muestra "120", entonces 1 (centenas), 2 (decenas) y 0 (unidades) son todos valores significativos (medidos).
Siempre que hace una medición correctamente, todos los dígitos en el resultado son significativos. Pero ¿qué pasaría si estuviera analizando un valor informado y tratando de determinar qué es y qué no es significativo? Bueno, para empezar, todos los dígitos que no son cero son significativos, y solo los ceros requieren cierto pensamiento. Usaremos los términos "líder", "finalización" y "cautivo" para los ceros y consideraremos cómo tratarlos.
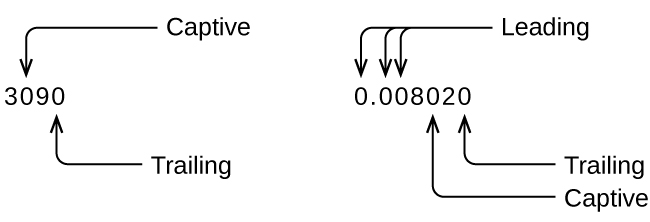
Comenzando con el primer dígito que no es cero a la izquierda, cuente este dígito y todos los dígitos que siguen a la derecha. Este es el número de cifras significativas en la medición, a menos que el último dígito sea un cero al final del punto decimal.
Los ceros cautivos resultan de la medición y por eso siempre son significativos. Sin embargo, los ceros iniciales nunca son significativos, simplemente nos dicen dónde se encuentra el punto decimal.
Los ceros a la izquierda en este ejemplo no son significativos. Podríamos usar la notación exponencial (como se describe en el Apéndice B) y expresar el número como 8.32407 \(\times\) 10-3; entonces el número 8.32407 contiene todas las cifras significativas, y 10-3 localiza el punto decimal.
El número de cifras significativas es incierto en un número que termina con un cero a la izquierda del punto decimal. Los ceros en la medida de 1.300 gramos podrían ser significativos o simplemente podrían indicar dónde se encuentra el punto decimal. La ambigüedad se puede resolver con el uso de notación exponencial: 1.3 \(\times\) 103 (dos cifras significativas), 1.30 \(\ times\) 103 (tres cifras significativas, si se midió el lugar de las decenas), o 1.300 \(\times\) 103 (cuatro cifras significativas, si también se midió el lugar). En los casos en que solo está disponible el número con formato decimal, es prudente suponer que todos los ceros finales no son significativos.
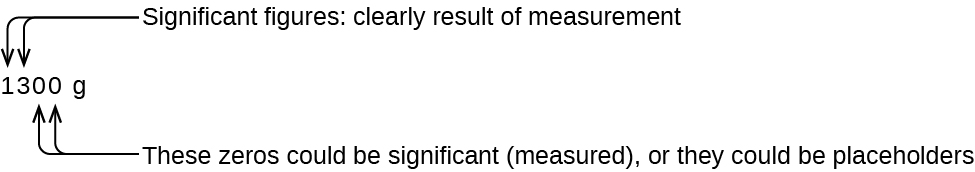
Al determinar cifras significativas, asegúrese de prestar atención a los valores informados y piense en la medición y las cifras significativas en términos de lo que es razonable o probable, es decir, si el valor tiene sentido. Por ejemplo, el censo oficial de enero de 2014 informó que la población residente de los EE. UU. Era de 317,297,725. ¿Cree que la población de EE. UU. ¿Estaba determinada correctamente a las nueve cifras significativas informadas, es decir, al número exacto de personas? La gente nace, muere, se muda adentro o afuera del país, y se asume que se tiene en cuenta la gran cantidad de personas que en realidad no se cuentan. Debido a estas incertidumbres, podría ser más razonable esperar que conozcamos a la población dentro de aproximadamente un millón o así, en este caso pues, la población debería reportarse como 317 millones o \ (3.17\times10^8\) personas.
Las cifras significativas en los cálculos
Un segundo principio importante de incertidumbre es que los resultados calculados de una medición son al menos tan inciertos como la medición. Debemos tener en cuenta la incertidumbre en nuestras mediciones para evitar una mala representación de la incertidumbre en los resultados calculados. Una forma de hacer esto es informar el resultado de un cálculo con el número correcto de cifras significativas, que se determina por las siguientes tres reglas para redondear números:
- Cuando sumamos o restamos números, debemos redondear el resultado al mismo número de lugares decimales que el número con el menor número de lugares decimales (el valor menos preciso en términos de suma y resta).
- Cuando multiplicamos o dividimos números, debemos redondear el resultado al mismo número de dígitos que el número con el menor número de cifras significativas (el valor menos preciso en términos de multiplicación y división).
- Si el dígito que se va a descartar (el que está inmediatamente a la derecha del dígito que se va a retener) es menor que 5, "redondeamos hacia abajo" y dejamos el dígito retenido sin cambios; si es más de 5, "redondeamos" y aumentamos el dígito retenido en 1; si el dígito descartado es 5, redondeamos hacia arriba o hacia abajo, lo que nos dé un valor para el dígito retenido. (La última parte de esta regla puede parecerle un poco extraño, pero se basa en estadísticas confiables y tiene el objetivo de evitar cualquier sesgo al eliminar el dígito “5”, ya que está igualmente cerca de los dos valores posibles del número retenido.)
Los siguientes ejemplos ilustran la aplicación de esta regla al redondear algunos números diferentes a tres cifras significativas:
- 0.028675 se redondea "hasta" 0.0287 (el dígito caído, 7, es mayor que 5)
- 18.3384 se redondea "hacia abajo" a 18.3 (el dígito eliminado, 3, es menor que 5)
- 6.8752 se redondea "hasta" 6.88 (el dígito eliminado es 5, y el dígito que se queda es par)
- 92.85 se redondea "hacia abajo" a 92.8 (el dígito eliminado es 5, y el dígito que se queda es par)
Vamos a trabajar con estas reglas en algunos ejemplos.
EJemplo \(\PageIndex{1}\): redondeo de números
Redondee lo siguiente al número indicado de cifras significativas:
- 31.57 (a dos cifras significativas)
- 8.1649 (a tres cifras significativas)
- 0.051065 (a cuatro cifras significativas)
- 0.90275 (a cuatro cifras significativas)
Solución
a. 31.57 se redondea "hasta" 32 (el dígito eliminado es 5, y el dígito que se queda es par)
b. 8.1649 se redondea hacia "abajo" a 8.16 (el dígito caído, 4, es menor que 5)
c. 0.051065 se redondea hacia "abajo" a 0.05106 (el dígito eliminado es 5, y el dígito que se queda es par)
d. 0.90275 se redondea "hasta" 0.9028 (el dígito perdido es 5, y el dígito que se queda es par)Ejercicio \(\PageIndex{1}\)
Redondee lo siguiente al número indicado de cifras significativas:
- 0.424 (a dos cifras significativas)
- 0.0038661 (a tres cifras significativas)
- 421.25 (a cuatro cifras significativas)
- 28,683.5 (a cinco cifras significativas)
- Respuesta a
-
0.42
- Respuesta b
-
0.00387
- Respuesta c
-
421.2
- Respuesta d
-
28,684
Ejemplo \(\PageIndex{2}\): Adición y sustracción con la regla de cifras significativas
Cuando sumamos o restamos números, debemos redondear el resultado al mismo número de lugares decimales que el número con el menor número de lugares decimales (es decir, el valor menos preciso en términos de suma y resta).
a. Suma 1.0023g y 4.383g.
b.Resta 421.23g de 486 g.
Solución
(a)
\[\begin{align*}
&\mathrm{1.0023\: g}\\ +\: &\underline{\mathrm{4.383\: g}\:\:}\\ &\mathrm{5.3853\: g}
\end{align*}\]
La respuesta es 5.385 g (redondea al lugar milésimo; tres decimales)
(b)
\[\begin{align*}
&\mathrm{486\: g}\\ -\: &\underline{\mathrm{421.23\: g}}\\ &\mathrm{\:\:64.77\: g}
\end{align*}\]
La respuesta es 65 g (redondea al lugar de los unos; sin decimales)
EJercicio \(\PageIndex{2}\)
a. Suma 2.334 ml y 0.31 ml.
b. Resta 55.8752 m de 56.533 m.
- Respuesta a
-
2.64 mL
- Respuesta b
-
0.658 m
Ejemplo \(\PageIndex{3}\): Multiplicación y división con cifras significativas
Regla: cuando multiplicamos o dividimos números, debemos redondear el resultado al mismo número de dígitos que el número con el menor número de cifras significativas (el valor menos preciso en términos de multiplicación y división).
a. Multiplica 0.6238 cm por 6.6 cm.
b. Divida 421.23 g por 486 ml.
Solución
(a)
\[\mathrm{0.6238\: cm\times6.6\:cm=4.11708\:cm^2\rightarrow result\: is\:4.1\:cm^2}\:\textrm{(round to two significant figures)}\]
\[\textrm{four significant figures}\times \textrm{two significant figures}\rightarrow \textrm{two significant figures answer}\]
(b)
\[\mathrm{\dfrac{421.23\: g}{486\: mL}=0.86728...\: g/mL\rightarrow result\: is\: 0.867\: g/mL} \: \textrm{(round to three significant figures)}\]
\[\mathrm{\dfrac{five\: significant\: figures}{three\: significant\: figures}\rightarrow three\: significant\: figures\: answer}\]
Ejercicio \(\PageIndex{3}\)
a. Multiplica 2.334 cm y 0.320 cm.
b. Divide 55.8752 m por 56.53 s.
- Respuesta a
-
0.747 cm2
- Respuesta b
-
0.9884 m/s
En medio de todos estos aspectos técnicos, es importante tener en cuenta la razón por la que utilizamos cifras y reglas de redondeo: para representar correctamente la certeza de los valores que informamos y para garantizar que un resultado calculado no se represente como más cierto que el valor menos cierto utilizado en el cálculo.
Ejemplo \(\PageIndex{4}\): CÁLCULO CON FIGURAS SIGNIFICATIVAS
Una bañera común tiene 13.44 dm de largo, 5.920 dm de ancho y 2.54 dm de profundidad. Suponga que la bañera es rectangular y calcule su volumen aproximado en litros.
Solución
\[\begin{align*}
V&=l\times w\times d\\ &=\mathrm{13.44\: dm\times 5.920\: dm\times 2.54\: dm}\\ &=\mathrm{202.09459...dm^3}\:\textrm{(value from calculator)}\\ &=\mathrm{202\: dm^3,}\textrm{ or 202 L (answer rounded to three significant figures)}
\end{align*}\]
Ejercicio \(\PageIndex{4}\): DETERMINACIÓN DE LA DENSIDAD UTILIZANDO EL DESPLAZAMIENTO DEL AGUA
¿Cuál es la densidad de un líquido con una masa de 31.1415 g y un volumen de 30.13 cm3?
- Respuesta
-
1.034 g/mL
Ejemplo \(\PageIndex{4}\)
Una pieza de barra de refuerzo se pesa y luego se sumerge en un cilindro graduado parcialmente lleno de agua, los resultados se muestran abajo.
a. Usa estos valores para determinar la densidad de esta pieza de barra de refuerzo.
b. La pieza de barra de refuerzo es en su mayoría de hierro. ¿Su resultado en (a) apoya esta afirmación? ¿Cómo?
Solución
El volumen de la barra de refuerzo es igual al volumen del agua desplazada:
\[\mathrm{volume=22.4\: mL-13.5\: mL=8.9\: mL=8.9\: cm^3} \nonumber\]
(redondeado al 0.1 mL más cercano, según la regla de suma y resta)
La densidad es la relación masa-volumen:
\[\mathrm{density=\dfrac{mass}{volume}=\dfrac{69.658\: g}{8.9\: cm^3}=7.8\: g/cm^3} \nonumber\]
(redondeado a dos cifras significativas, según la regla de multiplicación y división)
La densidad del hierro es 7.9 g/cm3, muy cercana a la de la barra de refuerzo, que apoya el hecho de que la barra de refuerzo es principalmente hierro.
Ejercicio \(\PageIndex{4}\)
Una pieza de forma irregular de un material amarillento brillante se pesa y luego se sumerge en un cilindro graduado, los resultados se muestran abajo.
a. Usa estos valores para determinar la densidad de este material.
b. ¿Tiene alguna conjetura razonable sobre la identidad de este material? Explique su razonamiento.
- Respuesta a
-
19 g/cm3
- Respuesta b
-
Es probable que sea oro; tiene la apariencia correcta para el oro y tiene una densidad muy cercana de la densidad dada para el oro.
Exactitud y Precisión
Típicamente, los científicos hacen mediciones repetidas de una cantidad para garantizar la calidad de sus resultados y para saber la precisión y la exactitud de sus resultados. Se dice que las mediciones son precisas si producen resultados muy similares cuando se repiten en la misma manera. Una medición se considera precisa si produce un resultado muy cercano al valor verdadero o aceptado. Los valores precisos concuerdan entre sí; los valores precisos concuerdan con un valor verdadero. Estas caracterizaciones pueden extenderse a otros contextos, como los resultados de una competencia de tiro con arco. (Figura \(\PageIndex{2}\)).
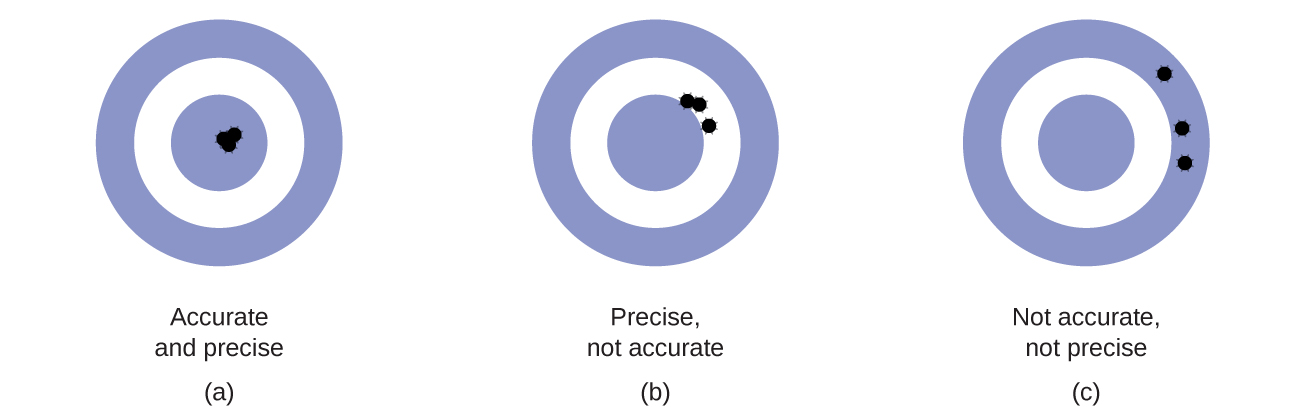
Supongamos que un químico de control de calidad en una compañía farmacéutica tiene la tarea de verificar la exactitud y la precisión de tres máquinas diferentes que están destinadas a dispensar 10 onzas (296 mL) de jarabe para la tos en botellas de almacenamiento. Ella procede a usar cada máquina para llenar cinco botellas y luego determina cuidadosamente el volumen real dispensado, obteniendo los resultados tabulados en Tabla \(\PageIndex{2}\).
| Dispensador #1 | Dispensador #2 | Dispensador #3 |
|---|---|---|
| 283.3 | 298.3 | 296.1 |
| 284.1 | 294.2 | 295.9 |
| 283.9 | 296.0 | 296.1 |
| 284.0 | 297.8 | 296.0 |
| 284.1 | 293.9 | 296.1 |
Teniendo en cuenta estos resultados, informará que el dispensador # 1 es preciso (todos los valores están cerca uno del otro, dentro de unas décimas de mililitro) pero no es preciso (ninguno de los valores está cerca del valor objetivo de 296 ml, cada uno más de 10 ml demasiado bajo). Los resultados para el dispensador # 2 representan una precisión mejorada (cada volumen está a menos de 3 ml de los 296 ml) pero la precisión es peor (los volúmenes varían en más de 4 ml). Finalmente, puede informar que el dispensador # 3 está funcionando bien, dispensando jarabe para la tos con precisión (todos los volúmenes dentro de 0.1 ml del volumen objetivo) y precisamente (volúmenes que difieren entre sí en no más de 0.2 ml).
Resumen
Las cantidades pueden ser exactas o medidas. Las cantidades medidas tienen una incertidumbre asociada que está representada por el número de cifras significativas en la medición. La incertidumbre de un valor calculado depende de las incertidumbres en los valores utilizados en el cálculo y se refleja en cómo se redondea el valor. Los valores medidos pueden ser exactos (cercanos al valor real) y/o precisos (que muestran poca variación cuando se miden repetidamente).
Glosario
- incertidumbre
- Estimación de la cantidad por la cual la medición difiere del valor verdadero.
- cifras significativas
- (también, dígitos significativos) Todos los dígitos medidos en una determinación, incluyendo el último dígito incierto.
- redondeo
- Procedimiento utilizado para garantizar que los resultados calculados reflejen correctamente la incertidumbre en las mediciones utilizadas en el cálculo.
- precisión
- qué tan cerca una medida coincide con la misma medida cuando se repite
- número exacto
- Número derivado por conteo o por definición.
- exactitud
- Qué tan cerca se alinea una medida con un valor correcto.
Contribuyentes
Paul Flowers (Universidad de Carolina del Norte - Pembroke), Klaus Theopold (Universidad de Delaware) y Richard Langley (Stephen F. Austin Universidad del Estado) con autores contribuyentes. Contenido del libro de texto producido por la Universidad de OpenStax tiene licencia de Atribución de Creative Commons Licencia 4.0 licencia. Descarge gratis en http://cnx.org/contents/85abf193-2bd...a7ac8df6@9.110)."
Ana Martinez (amartinez02@saintmarys.edu) contribuyó a la traducción de este texto.