2.3: Circuitos de corriente alterna

Una corriente continua tiene un valor fijo que es independiente del tiempo. Una corriente alterna, por otro lado, tiene un valor que cambia con el tiempo. Este cambio en la corriente sigue un patrón que podemos caracterizar por su período—el tiempo\(t_p\),, para un ciclo completo—o por su frecuencia\(f\), que es el recíproco de su periodo

\[f = \frac{1}{t_p} \label{sine1} \]

La frecuencia se reporta en hercios (Hz), lo que equivale a un ciclo por segundo.

Corrientes y voltajes sinusoidales

Aunque podemos dibujar muchas señales periódicas —y lo haremos en capítulos posteriores— la señal periódica más simple es una onda sinusoidal: como se muestra en el lado derecho de la Figura\(\PageIndex{1}\), el seno es una onda propagadora cuya amplitud,\(A\), es una función del tiempo,\(t\), que escribimos como\(a(t)\).

Figura\(\PageIndex{1}\). Ilustración que muestra cómo una onda sinusoidal puede ser explicada por un vector giratorio. Ver texto para una explicación de los símbolos.

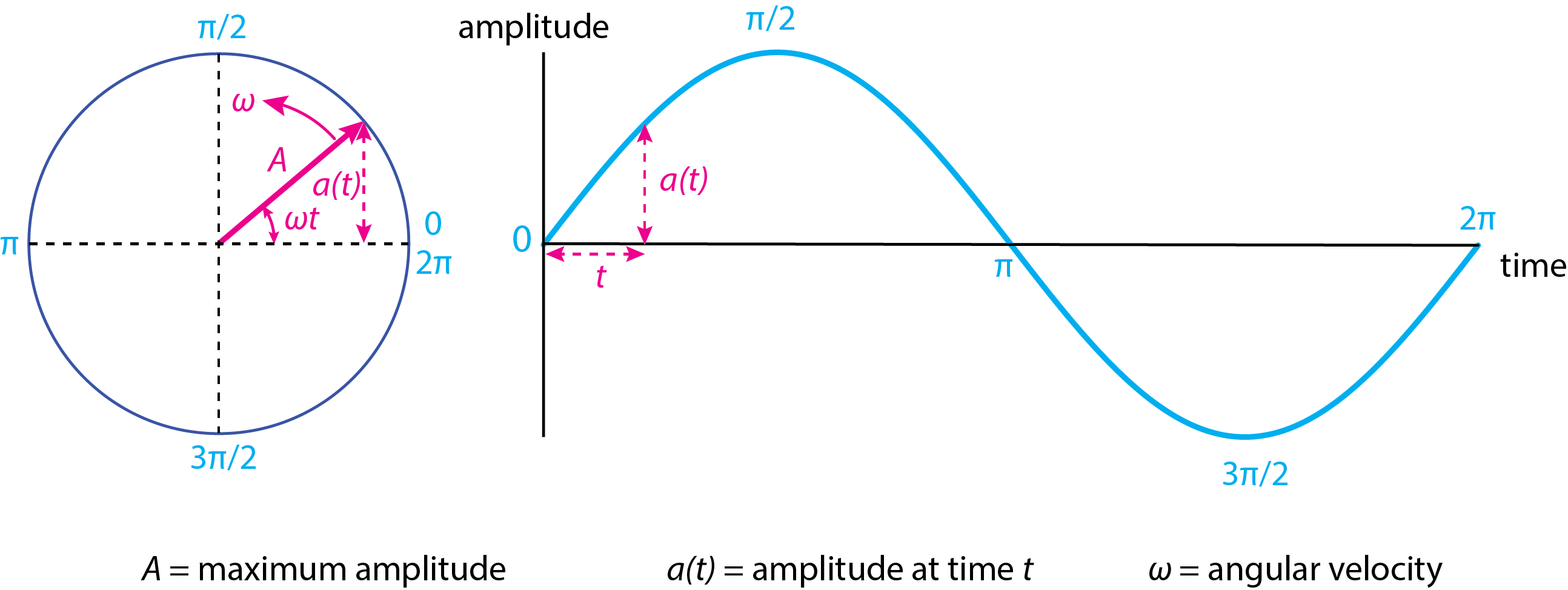
El lado izquierdo de la Figura\(\PageIndex{1}\) proporciona una representación vectorial giratoria de la onda sinusoidal (una representación que volveremos a encontrar en el Capítulo 19 sobre espectroscopia de RMN). El vector es la flecha que se extiende desde el centro del círculo hasta el borde del círculo. Está rotando hacia la izquierda con una velocidad angular dada por\(\omega\) y que se expresa en radianes por el periodo de la onda sinusoidal,\(t_p\); así

\[\omega = \frac{2 \pi}{t_p} = 2 \pi f \label{sine2} \]

donde\(f\) esta la frecuencia. La amplitud de la onda sinusoidal en función del tiempo\(a(t)\),, es equivalente a la proyección del vector giratorio sobre el eje x; así

\[a(t) = A\sin{\omega t} = A\sin{2 \pi f t} \label{sine3} \]

En el contexto de este capítulo, la amplitud es o bien una corriente\(i\), o una tensión,\(v\).

\[i(t) = I\sin{\omega t} = I\sin{2 \pi f t} \label{sine4} \]

\[v(t) = V\sin{\omega t} = V\sin{2 \pi f t} \label{sine5} \]

donde\(I\) es la corriente máxima o pico, y\(V\) es la tensión máxima o pico.

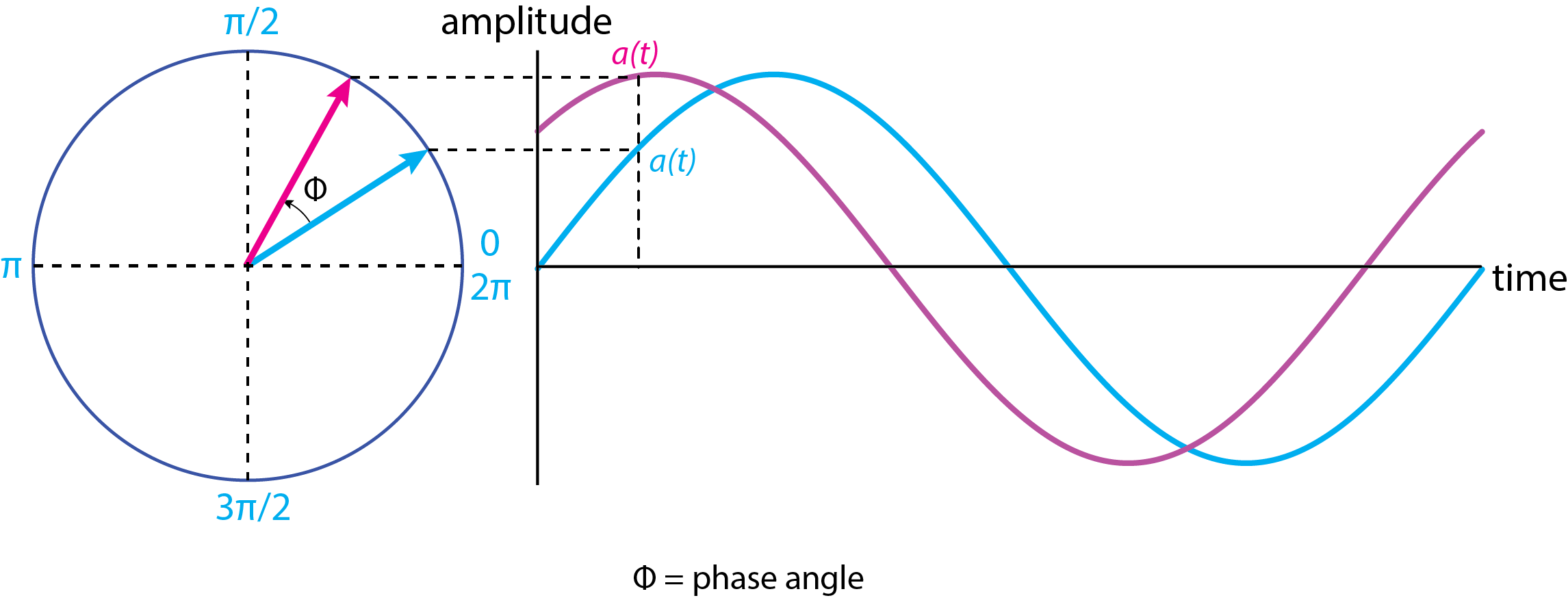
Las ecuaciones\ ref {seno4} y\ ref {seno5} requieren que la amplitud dependiente del tiempo de una onda sinusoidal\(a(t)\),, tenga un valor de cero cuando\(t = n \pi\), donde\(n\) es un entero. No hay razón para insistir en esto y dos ondas sinusoidales pueden separarse entre sí en el tiempo, como se muestra en la Figura\(\PageIndex{2}\), por un ángulo de fase,\(\Phi\). La ecuación para la onda sinusoidal cuando\(\Phi \ne 0\) se convierte

\[a(t) = A\sin{(\omega t + \Phi)} = A\sin{(2 \pi f t + \Phi)} \label{sine6} \]

Figura\(\PageIndex{2}\). Dos ondas sinusoidales que están desfasadas entre sí. El ángulo,\(\Phi\), entre los dos vectores giratorios es el ángulo de fase.

Una complicación de una corriente alterna es que la corriente neta en el transcurso de un solo ciclo es cero. Esto es un problema para nosotros porque la ecuación para la potencia en una resistencia es

\[P = \frac{I^2}{R} \ne 0 \label{sine7} \]

La figura\(\PageIndex{3}\) muestra varias formas de reportar corriente en circuitos de CA.

Figura\(\PageIndex{3}\). Diferentes formas de reportar corriente: I _p es la corriente absoluta máxima, o corriente pico; I _pp es la corriente pico a pico; I _rms es la corriente cuadrática media; y I _avg es la corriente promedio numérica.

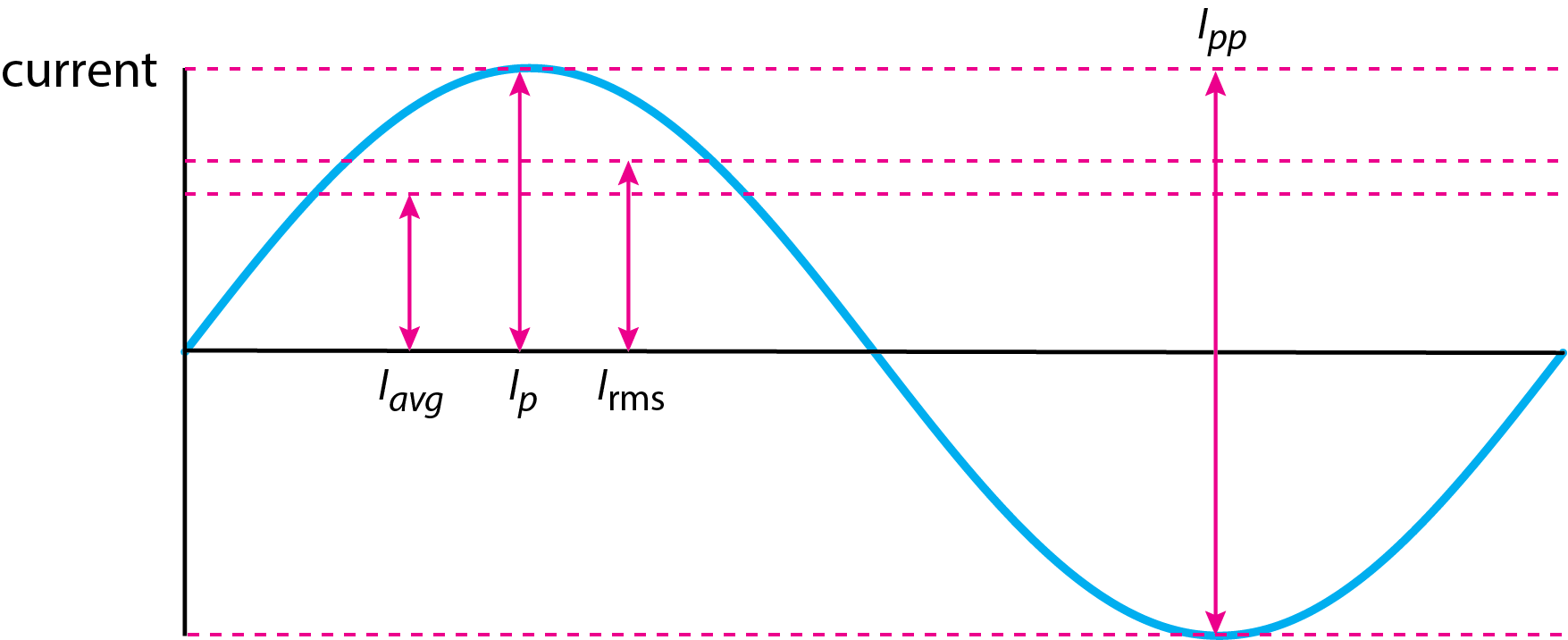
La corriente cuadrática media de raíz,\(I_{rms}\), se define como

\[I_{rms} = \sqrt{\frac{I_p^2}{2}} = \sqrt{2} \times \frac{I_p}{2} = 0.707 \times I_p \label{sine8} \]

y produce la misma potencia en un circuito de CA que una corriente continua de igual valor en un circuito de CC. La corriente promedio,\(I_{avg}\), es

\[I_{avg} = \frac{1}{\pi} \int_{0}^{\pi}I_p \sin{\omega t}\, dt = \frac{2 I_p}{\pi} = 0.6371 \times I_p \label{sine9} \]

Capacitores

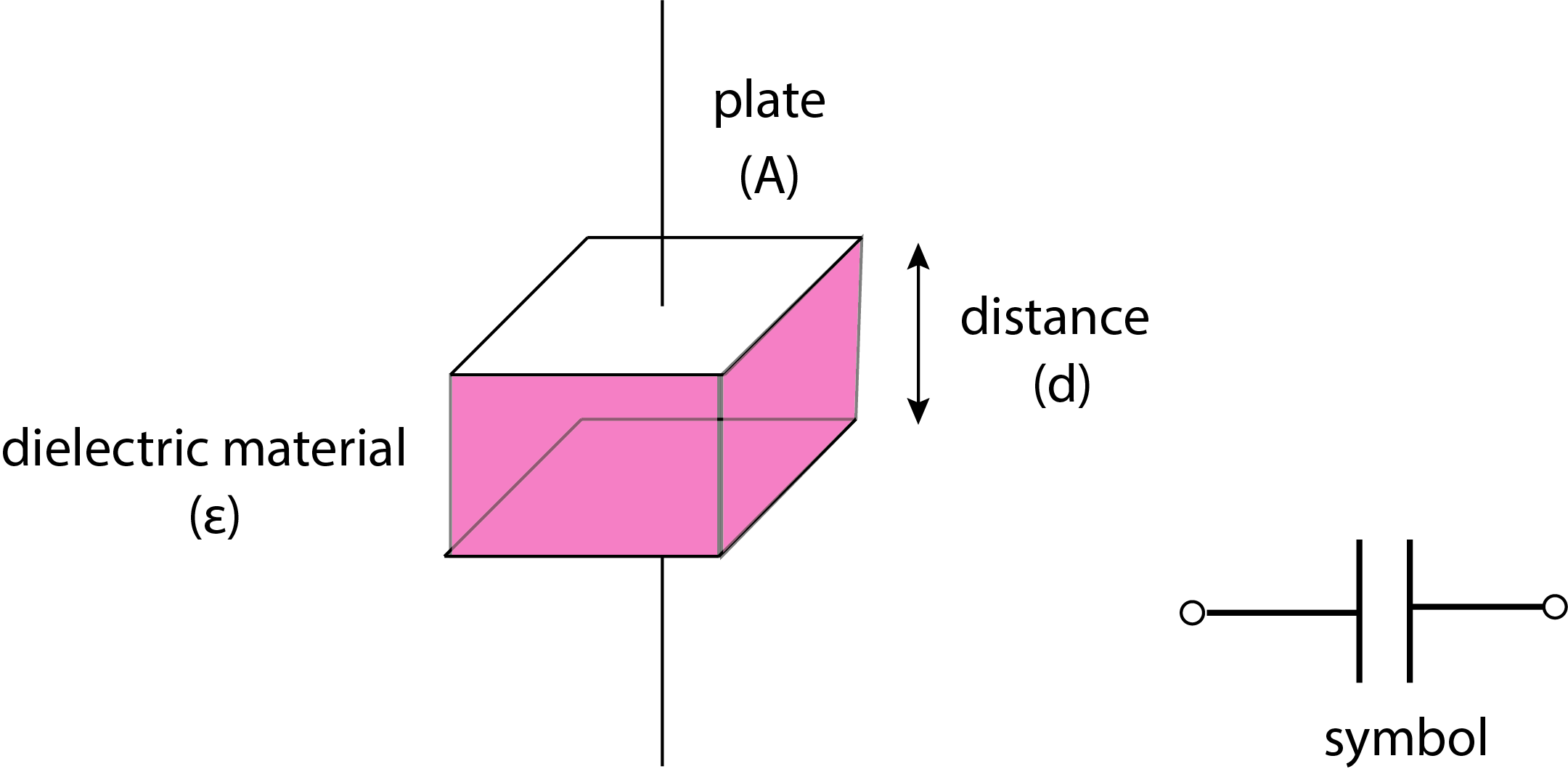
Un condensador es un componente de circuitos que es capaz de almacenar carga. La figura\(\PageIndex{4}\) muestra el diseño de un condensador típico y su símbolo al construir un circuito eléctrico. El condensador consta de dos placas conductoras separadas por una capa delgada de un material aislante o dieléctrico. Las placas tienen áreas de\(A\) y están separadas por una distancia,\(d\). El material dieléctrico tiene una constante dieléctrica,\(\epsilon\). Un condensador simple podría consistir en dos piezas de una lámina metálica separadas por aire, que sirve como material dieléctrico. La capacidad de un condensador para almacenar carga\(Q\), viene dada por

\[Q = C \times V \label{cap1} \]

dónde\(V\) está el voltaje aplicado a través de las dos placas y dónde\(C\) está la capacitancia del condensador, que, a su vez, se define como

\[C = \frac{\epsilon A}{d} \label{cap2} \]

La capacitancia se mide en unidades de faradios, donde un farado es igual a un culombo por voltio.

Figura\(\PageIndex{4}\). Diagrama esquemático de un condensador. En un circuito eléctrico, un condensador está representado por el símbolo en la parte inferior derecha.

Resistor y condensador en serie

La figura\(\PageIndex{5}\) muestra una resistencia, con una resistencia de\(R\), y un condensador, con una capacitancia de\(C\), en serie con una fuente de voltaje, con una tensión de\(V\).

Figura\(\PageIndex{5}\). Un circuito simple que consiste en una resistencia y un condensador en serie.

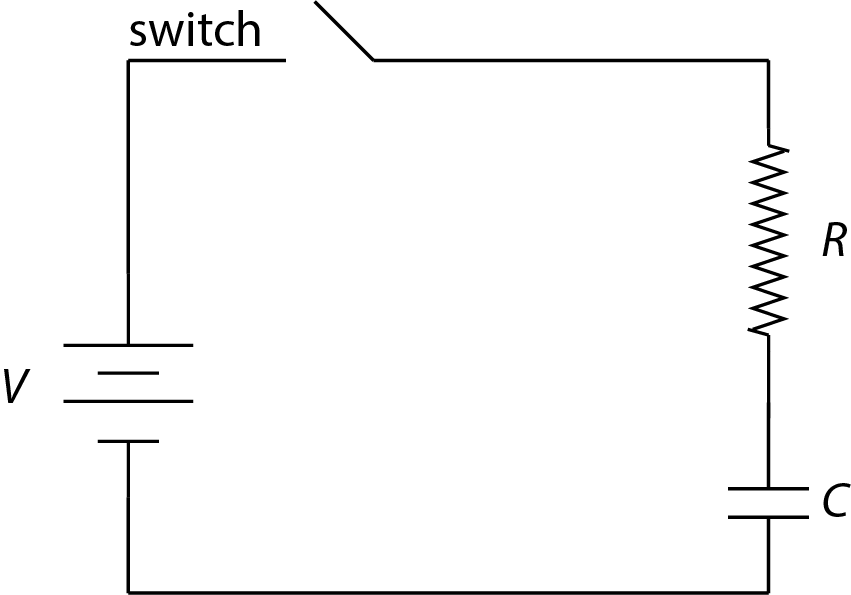
Cuando el interruptor se cerró, la corriente fluye a medida que el condensador acumula una carga. Por las leyes de Kirchoff, sabemos que

\[V = v_R + v_C = iR + \frac{Q}{C} \label{cap3} \]

donde\(v_R\) y\(v_C\) son, respectivamente, los voltajes dependientes del tiempo a través de la resistencia y el condensador. Debido a que\(V\) tiene un valor fijo, cualquier aumento a\(v_C\) medida que se carga el condensador se compensa con una disminución en\(V_r\). Dado que los valores de\(v_C\) y\(v_R\) —y las corrientes asociadas— dependen del tiempo, podemos diferenciar la Ecuación\ ref {cap3} con respecto al tiempo

\[\frac{dV}{dt} = 0 = \left( R \times \frac{di}{dt} \right) + \left( \frac{1}{C} \times \frac{dq}{dt} \right) = \left(R \times \frac{di}{dt}\right) + \frac{i}{C} \label{cap4} \]

Reordenando la ecuación\ ref {cap4} da

\[\frac{di}{i} = - \frac{1}{RC}dt \label{cap5} \]

Integrando ambos lados de esta ecuación

\[ \int_{I_{0}}^{i} \frac{1}{i} di = -\frac{1}{RC} \int_{0}^{t} dt \label{cap6} \]

conduce a la siguiente relación entre la corriente en el momento\(t\) y la corriente inicial,\(I_0\)

\[i_t = I_0 \times e^{-t/RC} \label{cap7} \]

lo que nos dice que la corriente disminuye exponencialmente a medida que el condensador se carga completamente. Reemplazar la corriente en la ecuación\ ref {cap7} con\(\frac{V}{R}\) y sustituyendo de nuevo en la Ecuación\ ref {cap3}

\[v_C = V_0 \left( 1 - e^{-t/RC} \right) \label{cap8} \]

nos muestra que durante el tiempo que se está cargando el condensador, la corriente que fluye a través del condensador disminuye exponencialmente hasta su límite de cero, y la tensión a través del condensador está aumentando exponencialmente hasta su límite de la tensión aplicada.

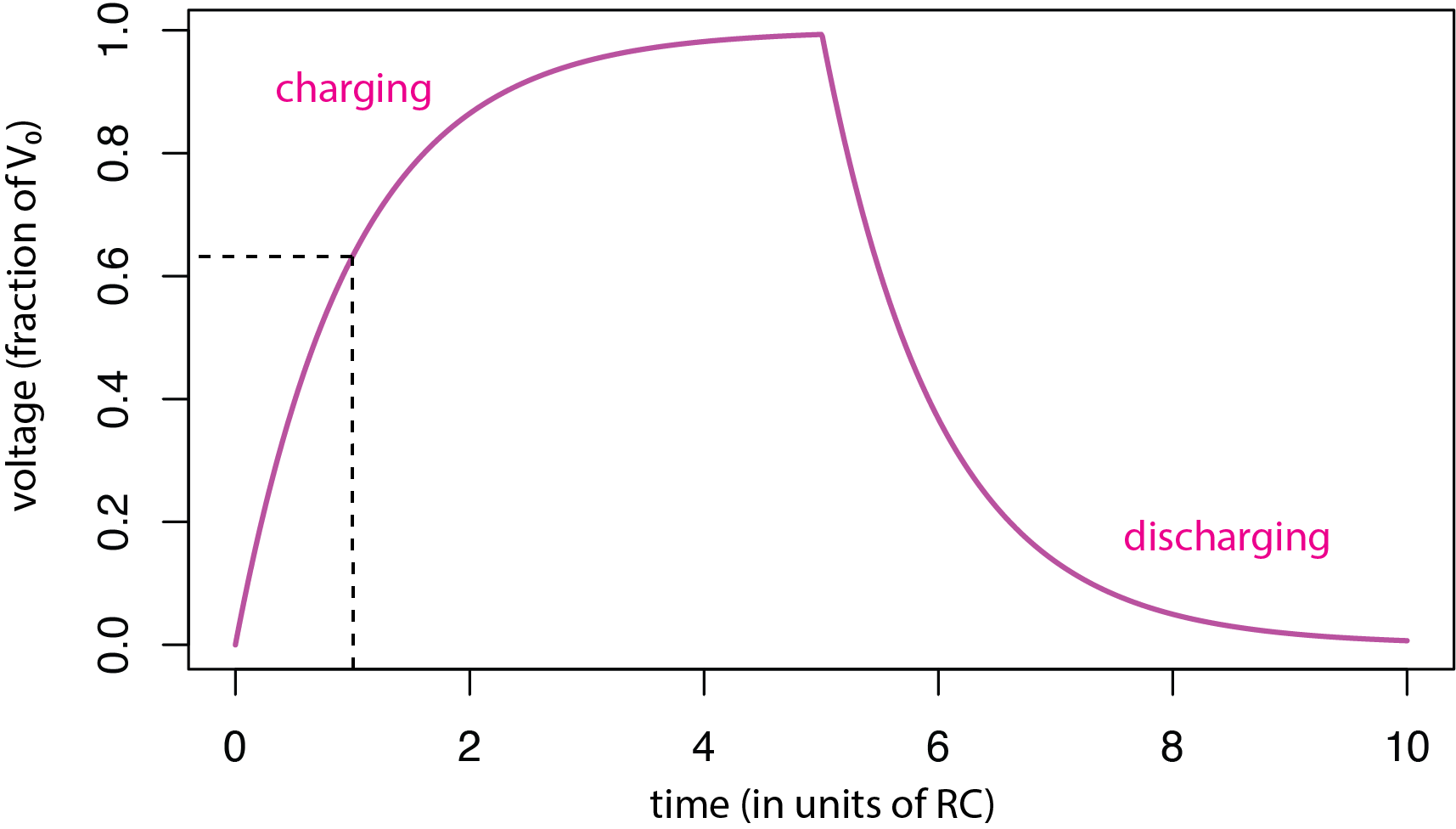
Constante de tiempo

El valor\(RC\) en la Ecuación\ ref {cap7} y en la Ecuación\ ref {cap8} es la constante de tiempo del circuito. Se necesitan aproximadamente cinco constantes de tiempo para que el condensador se cargue por completo o se descargue completamente. La figura\(\PageIndex{6}\) muestra el voltaje a través del condensador\(v_C\), ya que se permite cargar y descargar. El tiempo se muestra en términos del número de constantes de tiempo transcurrido, y el voltaje se expresa como una fracción de la tensión máxima. La línea discontinua muestra que la constante de tiempo\(RC\),, es equivalente\(0.63 \times\) al voltaje máximo.

Figura\(\PageIndex{6}\). Voltaje a través de un condensador a medida que se carga y luego se descarga. La escala en el eje x es el tiempo en incrementos de la constante de tiempo\(RC\), y la escala en el eje y es la fracción del voltaje aplicado. La línea discontinua muestra que la constante de tiempo es equivalente\(0.63 \times\) al voltaje aplicado.

Respuesta de un circuito RC en serie a una entrada sinusoidal

Si reemplazamos la fuente de voltaje de CC en la Figura\(\PageIndex{5}\) con una fuente de CA, entonces el condensador sufrirá una fluctuación continua en su voltaje y corriente en función del tiempo. Sabemos, formar Ecuación\ ref {cap1} esa carga,\(Q\), es el producto de la capacitancia,\(C\), y el voltaje\(V\),, que podemos escribir como un derivado con respecto al tiempo.

\[\frac{dq}{dt} = C \times \frac{dv}{dt} \label{ac1} \]

Desplazamiento de fase en un circuito de CA

En un circuito de CA, como aprendimos anteriormente en la Ecuación\ ref {sene4}, la corriente, que es equivalente a\(dq/dt\) es

\[i = I_p \sin{2 \pi f t} \label{ac2} \]

donde\(I_p\) está la corriente pico. Sustituir en Ecuación\ ref {ac1} da

\[i = I_p \sin{2 \pi f t} = C \times \frac{dv}{dt} \label{ac3} \]

Reorganizar esta ecuación e integrarla a lo largo del tiempo da el voltaje dependiente del tiempo a través del condensador,\(v_C\), como

\[v_C = \frac{I_p}{2 \pi f C} \left( -\cos{2 \pi f t} \right) \label{ac4} \]

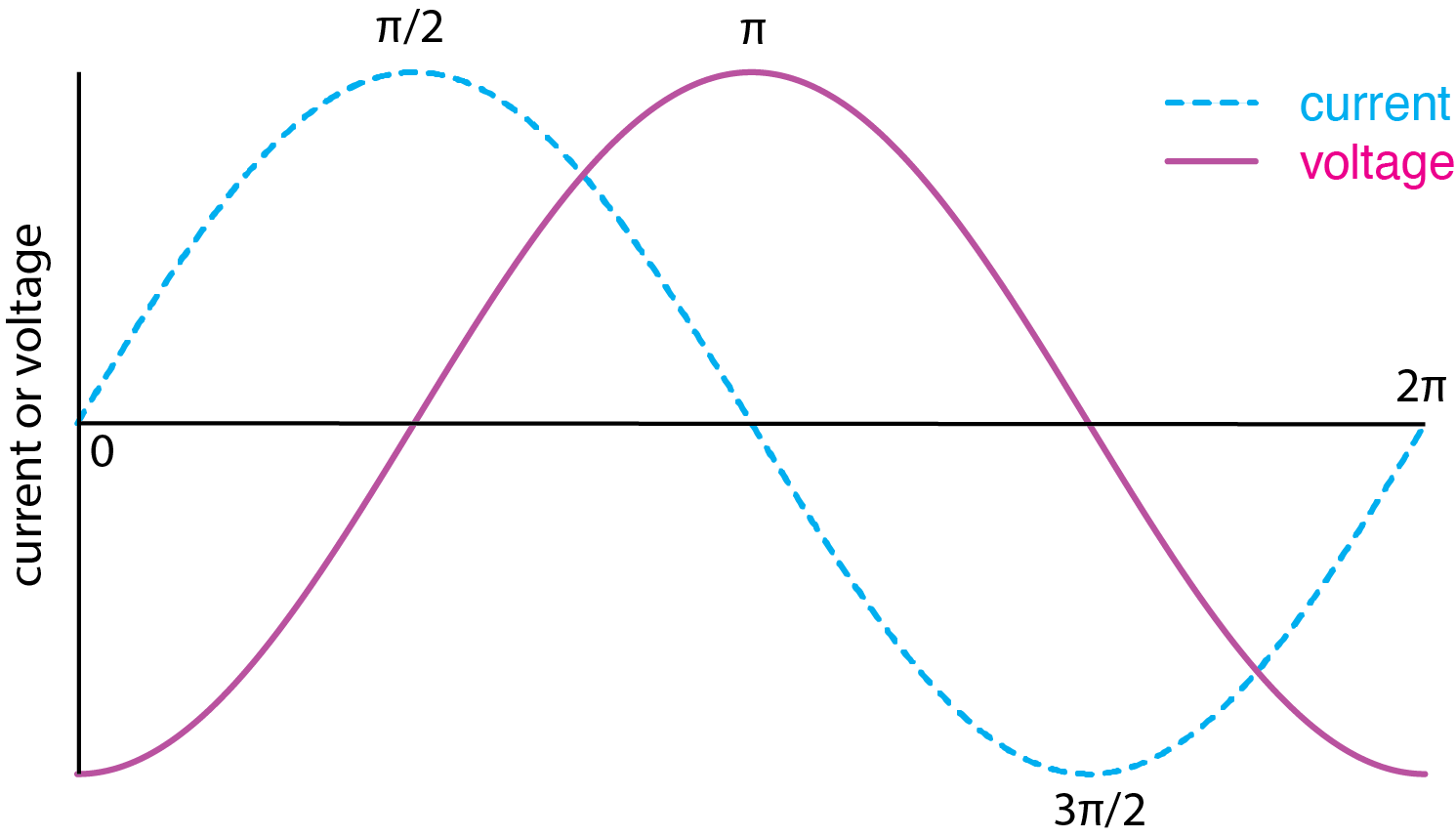
Podemos reescribir esta ecuación en términos de una función sinusoidal en lugar de una función coseno reconociendo que las dos están 90° desfasadas entre sí; así

\[v_C = \frac{I_p}{2 \pi f C} \left( \sin{2 \pi f t -90} \right) = V_p \left( \sin{2 \pi f t -90} \right) \label{ac5} \]

Comparando la Ecuación\ ref {ac2} y la Ecuación\ ref {ac5}, vemos que la corriente y el voltaje están 90° desfasados entre sí; la Figura lo\(\PageIndex{7}\) muestra visualmente.

Figura\(\PageIndex{7}\). Respuesta del voltaje de un condensador a una corriente de entrada sinusoidal que muestra que están 90° (\(\pi/2\)) fuera de fase.

Reactancia capacitiva, resistencia e impedancia

De la ecuación\ ref {ac5} vemos que

\[V_p = \frac{I_p}{2 \pi f t} \label{ac6} \]

Dividiendo ambos lados por\(I_p\) da

\[\frac{V_p}{I_p} = X_C = \frac{1}{2 \pi f t} \label{ac7} \]

donde\(X_C\) está la reactancia del condensador, que, al igual que la resistencia de una resistencia, tiene unidades de ohmios. A diferencia de una resistencia, sin embargo, la reactancia de un condensador depende de la frecuencia y, dada la relación recíproca entre\(X_C\) y\(f\), se vuelve más pequeña a frecuencias más altas.

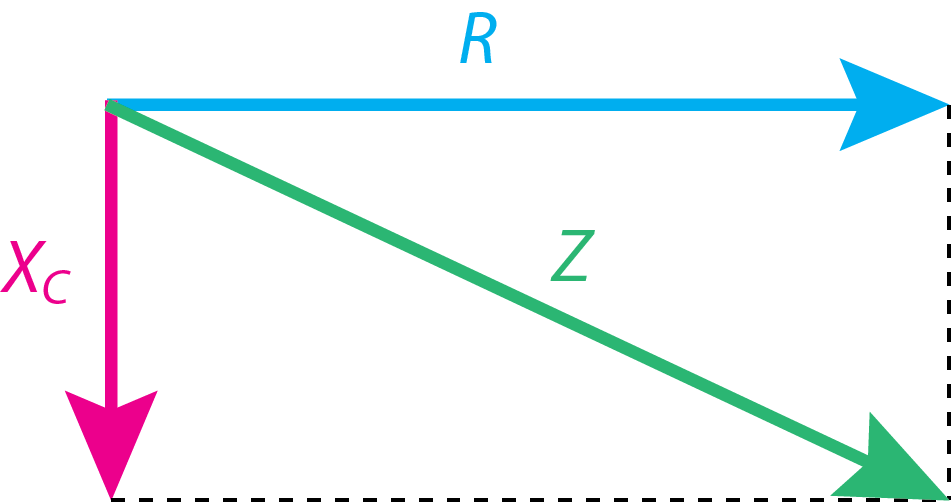
En un circuito RC, tanto la resistencia como el condensador contribuyen a la impedancia del circuito de la corriente alterna. Debido a que la contribución del condensador es 90° fuera de fase a la contribución de la resistencia, la impedancia neta,\(Z\), es

\[Z = \sqrt{R^2 + X_C^2} \label{ac8} \]

como se muestra en la Figura\(\PageIndex{8}\) donde el vector que representa\(Z\) es el hipotono de un triángulo rectángulo definido por la resistencia de la resistencia y la reactancia del condensador.

Figura\(\PageIndex{8}\): Relación entre la resistencia de una resistencia, la reactancia de un condensador y la impedancia del circuito RC.

Sustituir en la Ecuación\ ref {ac7} muestra el efecto de la frecuencia sobre la impedancia.

\[Z = \sqrt{R^2 + \left( \frac{1}{2 \pi f t} \right)^2} \label{ac9} \]

Escribir la ley de Ohm en términos de impedence\(V_p = I_p \times Z\),, y sustituirla en Ecuación\ ref {ac9}, define\(I_p\) y\(V_p\) en términos de impedence.

\[V_p = I_p \times \sqrt{R^2 + \left( \frac{1}{2 \pi f t} \right)^2} \label{ac10} \]

\[I_p = \frac{V_p}{\sqrt{R^2 + \left( \frac{1}{2 \pi f t} \right)^2}} \label{ac11} \]

Filtros basados en circuitos RC

La dependencia de frecuencia de un circuito RC nos proporciona la capacidad de atenuar algunas frecuencias y pasar otras frecuencias. Esto permite el filtrado selectivo de una señal de entrada. Aquí consideramos el diseño de un filtro de paso bajo que elimina las señales de mayor frecuencia, y el diseño de un filtro de paso alto que elimina las señales de menor frecuencia. La figura\(\PageIndex{9}\) muestra que (a) un filtro de paso bajo coloca la resistencia antes que el condensador y mide el voltaje de salida,\(V_{out}\), a través del condensador, y que (b) un filtro de paso alto coloca el condensador antes que el resistor y mide el voltaje de salida,\(V_{out}\), a través de la resistencia.

Figura\(\PageIndex{9}\). Circuitos para (a) un filtro de paso bajo y (b) un filtro de paso alto.

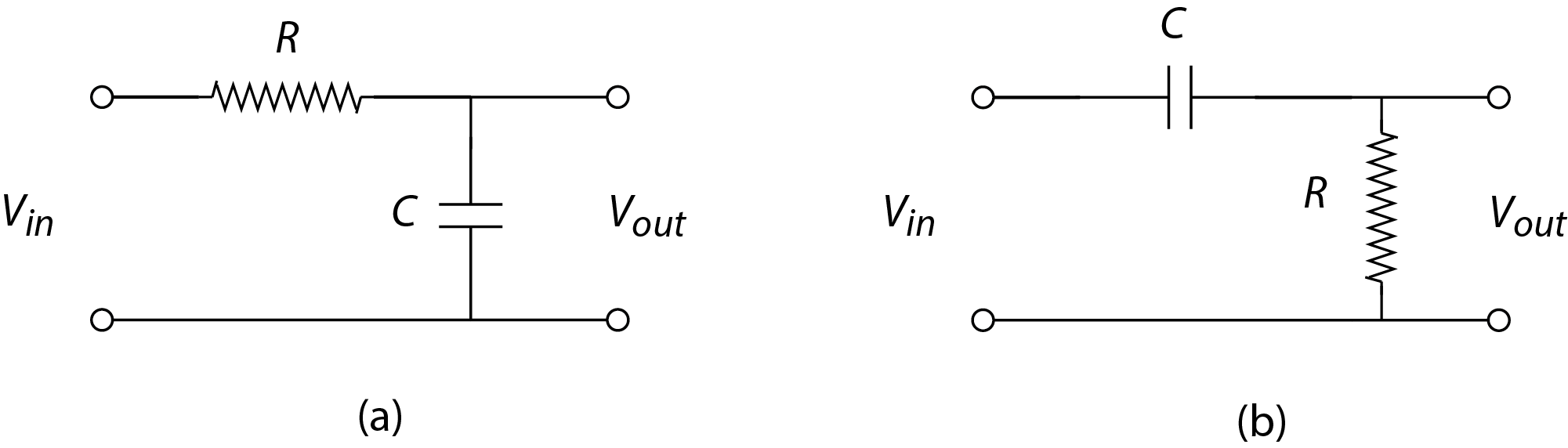
Filtro de paso bajo

Para el filtro de paso bajo en la Figura\(\PageIndex{9}a\), la relación del voltaje a través del condensador\((V_p)_{out}\),, al voltaje de entrada pico,\((V_p)_{in}\), es igual a la fracción de la impedancia del circuito,\(Z\), atribuida a la reactancia del condensador,\(X_C\), como se esperaba para un divisor de voltaje que consiste de elementos en serie.

\[\frac{(V_p)_{out}}{(V_p)_{in}} = \frac{X_C}{Z} = \frac{(2 \pi f C)^{-1}}{\sqrt{R^2 + \left( \frac{1}{2 \pi f C}\right)^2}} \label{lowpass1} \]

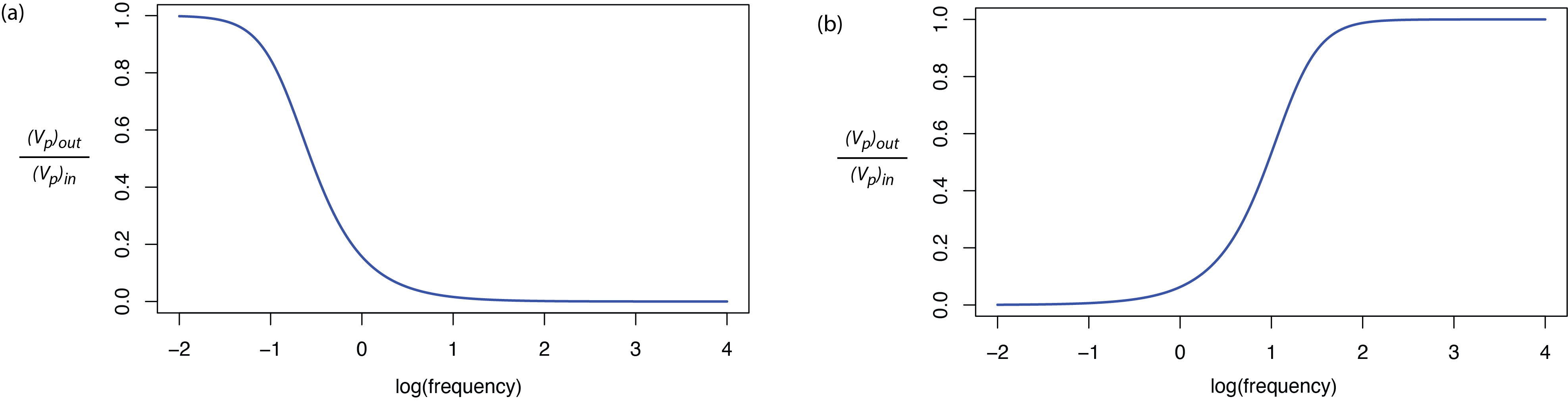
La figura\(\PageIndex{10}a\) muestra la respuesta de frecuencia para un filtro de paso bajo con una\(1 \times 10^6 \text{ Hz}\) resistencia y un\(1 \times 10^{-6} \text{ F}\) condensador, eliminando todas las frecuencias mayores a aproximadamente\(10^1\) Hz.

Figura\(\PageIndex{10}\). La salida de (a) un filtro de paso bajo y (b) un filtro de paso alto.

Filtro de paso alto

Para el filtro de paso alto en la Figura\(\PageIndex{9}b\), la relación del voltaje a través de la resistencia\((V_p)_{out}\), a la tensión de entrada pico,\((V_p)_{in}\), es igual a la fracción de la impedancia del circuito,\(Z\), atribuida a la resistencia de la resistencia,\(R\), como se esperaba para un divisor de voltaje que consiste de elementos en serie.

\[\frac{(V_p)_{out}}{(V_p)_{in}} = \frac{R}{Z} = \frac{R}{\sqrt{R^2 + \left( \frac{1}{2 \pi f C}\right)^2}} \label{lowpass2} \]

La figura\(\PageIndex{10}b\) muestra la respuesta de frecuencia para un filtro de paso bajo con una\(1 \times 10^5 \text{ Hz}\) resistencia y un\(1 \times 10^{-7} \text{ F}\) condensador, eliminando todas las frecuencias menores a aproximadamente\(10^{-1}\).