2.4: Semiconductores
- Page ID
- 78858
Un semiconductor es un material cuya resistividad al movimiento de carga cae en algún lugar entre la de un conductor, a través del cual podemos mover una carga fácilmente, y un aislante, que resiste el movimiento de carga. Algunos semiconductores son elementales, como el silicio y el germanio (los cuales examinamos más de cerca en esta sección) y algunos son multielementales, como el carburo de silicio.
Propiedades de los Semiconductores de Silicio y Germanio
Un conductor, como el aluminio o el cobre, tiene una resistividad del orden de\(10^{-8} - 10^{-6} \ \Omega \cdot m\), lo que significa que su resistencia al movimiento de electrones es lo suficientemente pequeña como para que lleve una corriente sin mucho esfuerzo. Un aislante, como el cuarzo mineral\(\ce{SiO2}\), tiene una resistividad del orden de\(10^{15} - 10^{19} \ \Omega \cdot m\). El silicio, por otro lado, tiene una resistividad de aproximadamente\(640 \ \Omega \cdot m\) y el germaino tiene una resistividad de aproximadamente\(0.46 \ \Omega \cdot m\).
La inversa de la resistividad es la conductividad.
El silicio y el germanio están en el mismo grupo que el carbono. Si usamos una visión simplificada de los átomos, podemos tratar al silicio y al germanio como que tienen cuatro electrones de valencia y una carga nuclear efectiva,\(Z_{eff}\), de
\[\begin{align*} (Z_{eff})_\ce{Si} &= Z - \text{ number of core electrons} \\[4pt] &= 14 - 10 \\[4pt] &= +4 \\[4pt] (Z_{eff})_\ce{Ge} &= Z - \text{ number of core electrons} \\[4pt] &= 32 - 28 \\[4pt] &= +4 \end{align*} \]
Podemos aumentar la conductividad del silicio y el germanio agregándoles, esto se llama dopaje, una pequeña cantidad de una impureza. Agregar una pequeña cantidad de In o Ga, que tienen tres electrones de valencia en lugar de cuatro electrones de valencia, deja un pequeño número de vacantes, u agujeros, en los que falta un electrón. Agregar una pequeña cantidad de As o Sb, que tienen cinco electrones de valencia en lugar de cuatro electrones de valencia, deja un pequeño número de electrones adicionales. La figura\(\PageIndex{1}\) muestra las tres posibilidades.
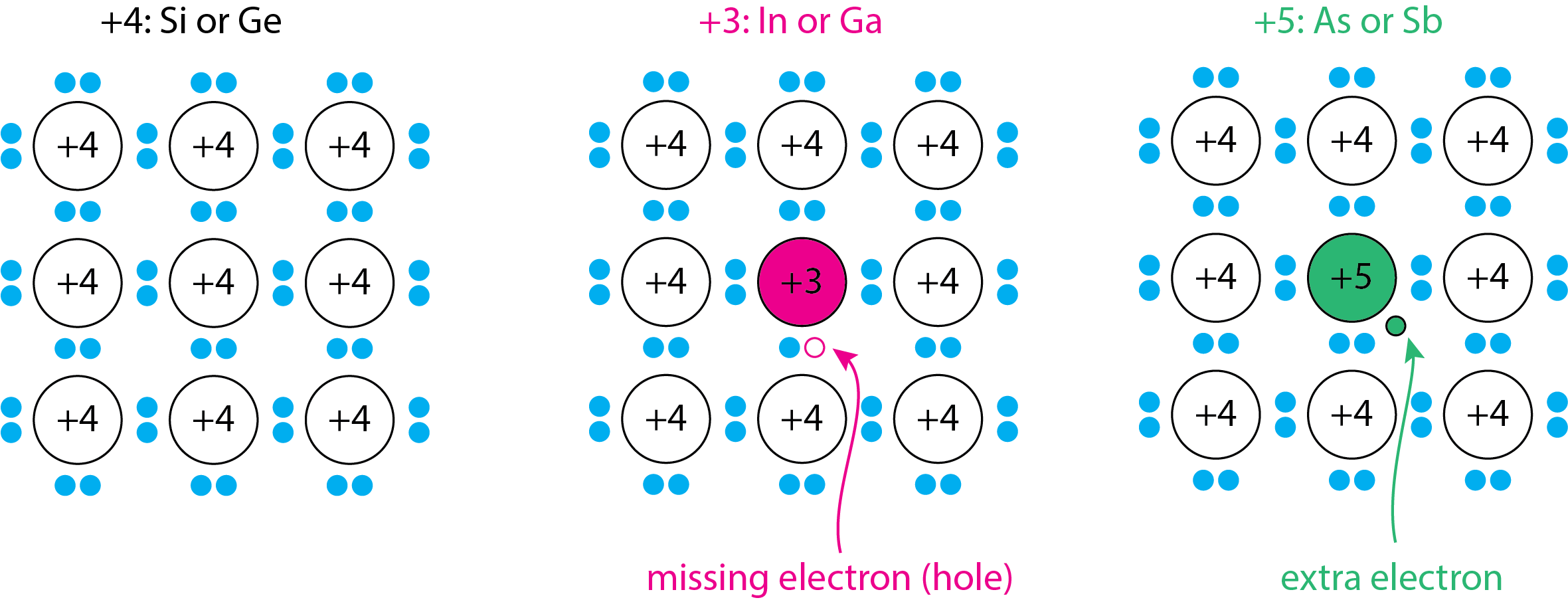
Si aplicamos un potencial a través del semiconductor dopado con As o Sb, el electrón extra se mueve hacia el polo positivo, creando una pequeña corriente y dejando atrás una vacante, o agujero. Si aplicamos un potencial a través del semiconductor dopado con In o Ga, los electrones ingresan al semiconductor desde el polo negativo, ocupando las vacantes, o agujeros, y creando una pequeña corriente. En ambos casos, los electrones se mueven hacia el polo positivo y los agujeros se mueven hacia el polo negativo. Llamamos a un semiconductor dopado As o Sb un semiconductor de tipo n porque el portador primario de carga es un electrón; llamamos a un semiconductor dopado In o Ga un semiconductor de tipo p porque el portador primario de carga es el agujero.
Diodos Semiconductores
Un diodo es un dispositivo eléctrico que es más conductor en una dirección que en la dirección opuesta. Un diodo aprovecha las propiedades de la unión entre un semiconductor tipo p y un semiconductor de tipo n.
Propiedades de pn Junctions
Usemos Figure\(\PageIndex{2}\) para dar sentido a cómo funciona un diodo semiconductor. La figura se divide en dos partes: el lado izquierdo de la figura, las partes (a), (b) y (c), muestran el comportamiento del diodo semiconductor cuando se aplica una polarización hacia adelante, y el lado derecho de la figura, las partes (d), (e) y (f), muestran su comportamiento cuando se aplica una polarización inversa. Para ambos, el diodo semiconductor consiste en una unión entre un semiconductor de tipo n, que tiene un exceso de electrones y lleva una carga negativa, y un semiconductor de tipo p, que tiene un exceso de agujeros y, por lo tanto, una carga positiva; esto se muestra en (a) y (d). La forma en que se fabrica el semiconductor no es de importancia para nosotros.
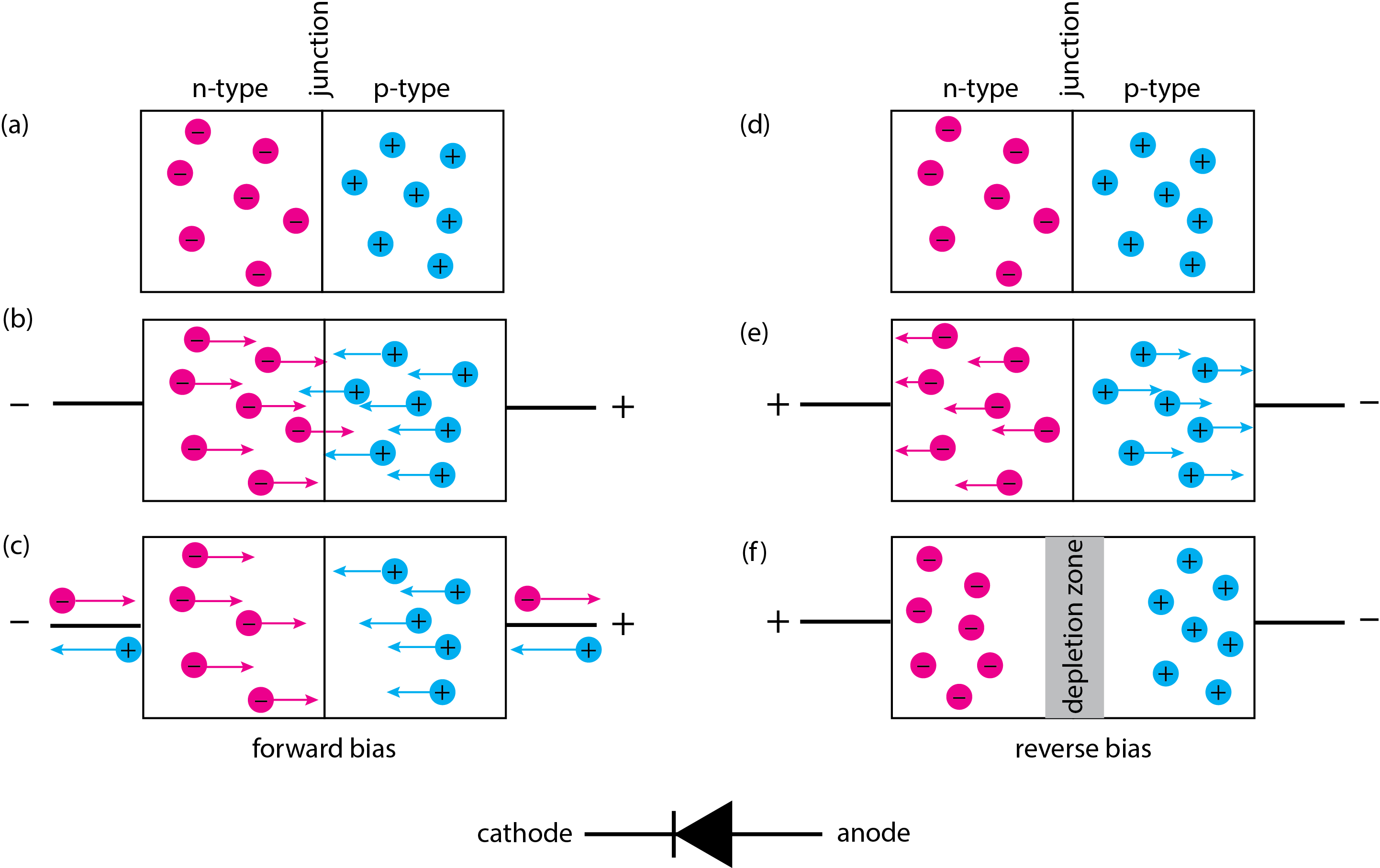
Para efectuar un sesgo directo, aplicamos un potencial positivo a la región tipo p y aplicamos un potencial negativo a la región de tipo n. Como vemos en (b), los agujeros en la región p se mueven hacia la unión y los electrones en la región n también se mueven hacia la unión. Cuando los agujeros y los electrones se encuentran se combinan y son eliminados, razón por la cual vemos menos huecos y electrones en (c). Los electrones adicionales fluyen hacia la región n y los electrones se alejan de la región p, como se ve en (c), lo que resulta en una corriente. Para efectuar un sesgo inverso, cambiamos los potenciales aplicados para que la región p tenga el potencial negativo y la región n tenga el potencial positivo. El resultado, como se ve en (e) es una breve corriente a medida que los agujeros y electrones se alejan unos de otros. dejando atrás, en (f), una zona de agotamiento que esencialmente no tiene electrones ni agujeros.
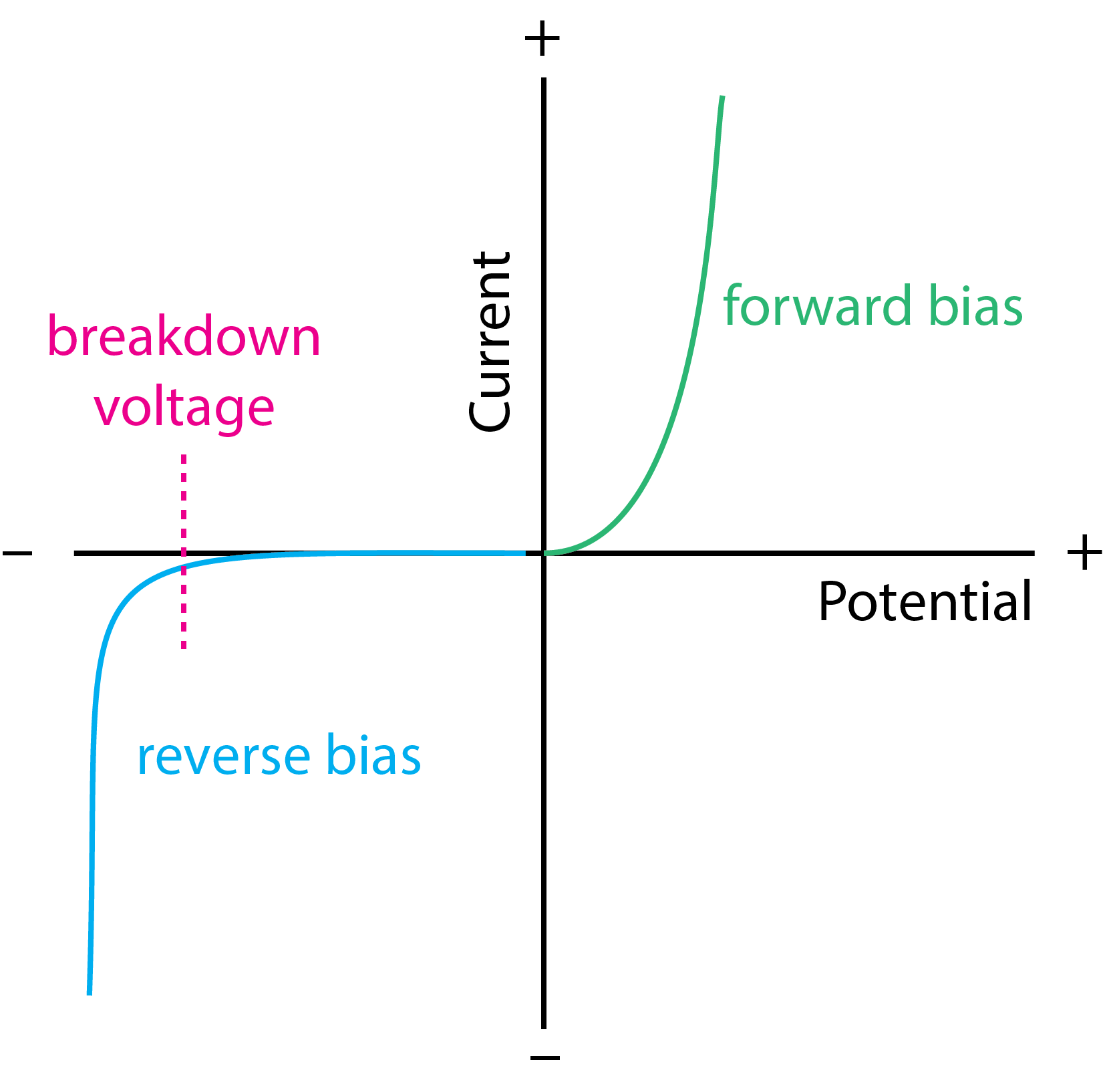
Curvas de corriente-voltaje para diodos semiconductores
La figura\(\PageIndex{3}\) muestra una gráfica de la corriente en función de la tensión para un diodo semiconductor. En el modo de polarización directa, la corriente aumenta exponencialmente con un aumento en el voltaje aplicado, pero permanece esencialmente en cero cuando se opera bajo una polarización inversa. El uso de un potencial negativo suficientemente grande, sin embargo, da como resultado un aumento repentino y dramático de la corriente; el potencial al que esto sucede se llama voltaje de ruptura.
