24.2: Coulometría de Potencial Controlado
- Page ID
- 79083
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
\( \newcommand{\dsum}{\displaystyle\sum\limits} \)
\( \newcommand{\dint}{\displaystyle\int\limits} \)
\( \newcommand{\dlim}{\displaystyle\lim\limits} \)
\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)
( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\id}{\mathrm{id}}\)
\( \newcommand{\Span}{\mathrm{span}}\)
\( \newcommand{\kernel}{\mathrm{null}\,}\)
\( \newcommand{\range}{\mathrm{range}\,}\)
\( \newcommand{\RealPart}{\mathrm{Re}}\)
\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)
\( \newcommand{\Argument}{\mathrm{Arg}}\)
\( \newcommand{\norm}[1]{\| #1 \|}\)
\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)
\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)
\( \newcommand{\vectorA}[1]{\vec{#1}} % arrow\)
\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}} % arrow\)
\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\( \newcommand{\vectorC}[1]{\textbf{#1}} \)
\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)
\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)
\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)
\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)
\(\newcommand{\longvect}{\overrightarrow}\)
\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)
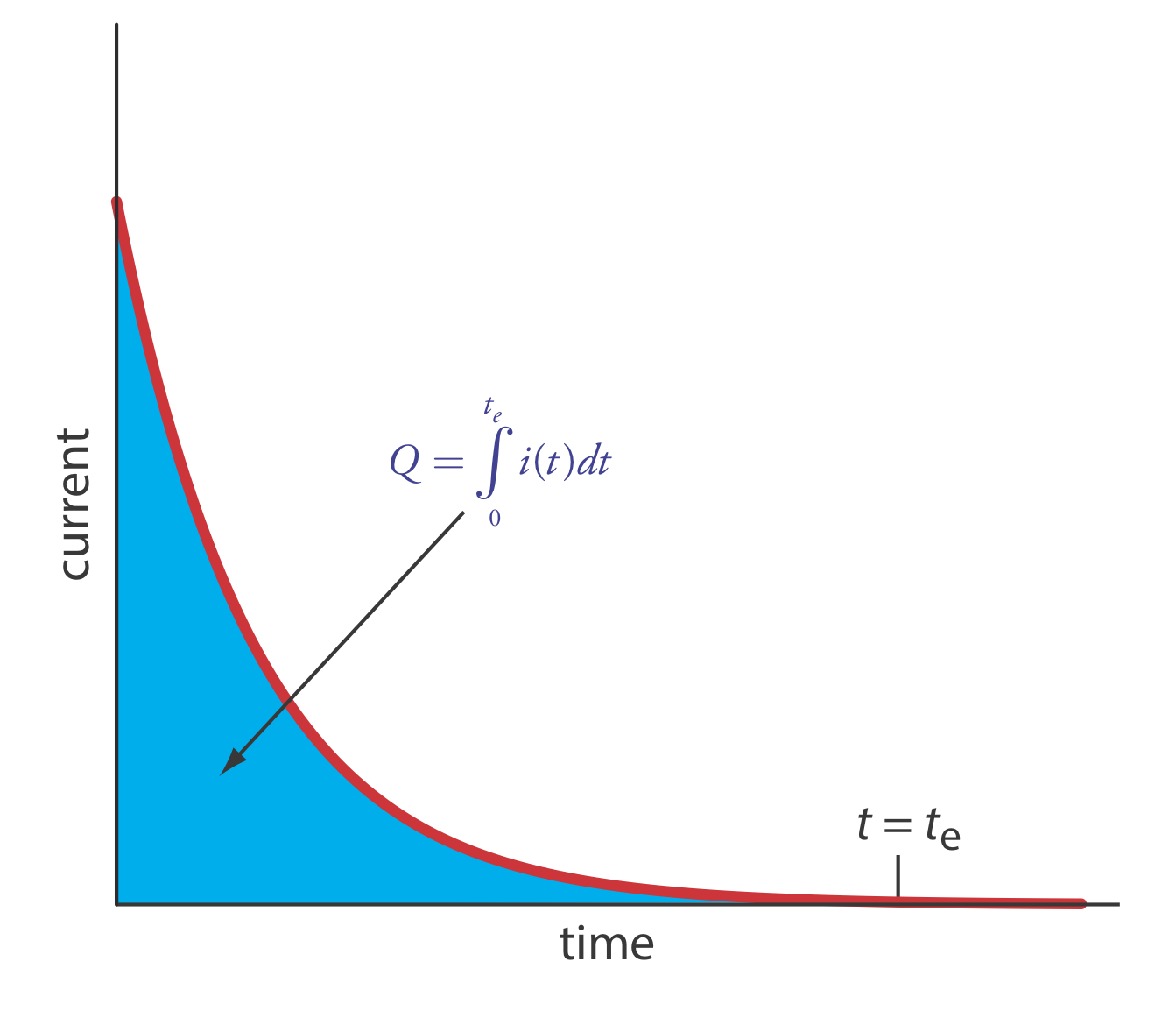
\(\newcommand{\avec}{\mathbf a}\) \(\newcommand{\bvec}{\mathbf b}\) \(\newcommand{\cvec}{\mathbf c}\) \(\newcommand{\dvec}{\mathbf d}\) \(\newcommand{\dtil}{\widetilde{\mathbf d}}\) \(\newcommand{\evec}{\mathbf e}\) \(\newcommand{\fvec}{\mathbf f}\) \(\newcommand{\nvec}{\mathbf n}\) \(\newcommand{\pvec}{\mathbf p}\) \(\newcommand{\qvec}{\mathbf q}\) \(\newcommand{\svec}{\mathbf s}\) \(\newcommand{\tvec}{\mathbf t}\) \(\newcommand{\uvec}{\mathbf u}\) \(\newcommand{\vvec}{\mathbf v}\) \(\newcommand{\wvec}{\mathbf w}\) \(\newcommand{\xvec}{\mathbf x}\) \(\newcommand{\yvec}{\mathbf y}\) \(\newcommand{\zvec}{\mathbf z}\) \(\newcommand{\rvec}{\mathbf r}\) \(\newcommand{\mvec}{\mathbf m}\) \(\newcommand{\zerovec}{\mathbf 0}\) \(\newcommand{\onevec}{\mathbf 1}\) \(\newcommand{\real}{\mathbb R}\) \(\newcommand{\twovec}[2]{\left[\begin{array}{r}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\ctwovec}[2]{\left[\begin{array}{c}#1 \\ #2 \end{array}\right]}\) \(\newcommand{\threevec}[3]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\cthreevec}[3]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \end{array}\right]}\) \(\newcommand{\fourvec}[4]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\cfourvec}[4]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \end{array}\right]}\) \(\newcommand{\fivevec}[5]{\left[\begin{array}{r}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\cfivevec}[5]{\left[\begin{array}{c}#1 \\ #2 \\ #3 \\ #4 \\ #5 \\ \end{array}\right]}\) \(\newcommand{\mattwo}[4]{\left[\begin{array}{rr}#1 \amp #2 \\ #3 \amp #4 \\ \end{array}\right]}\) \(\newcommand{\laspan}[1]{\text{Span}\{#1\}}\) \(\newcommand{\bcal}{\cal B}\) \(\newcommand{\ccal}{\cal C}\) \(\newcommand{\scal}{\cal S}\) \(\newcommand{\wcal}{\cal W}\) \(\newcommand{\ecal}{\cal E}\) \(\newcommand{\coords}[2]{\left\{#1\right\}_{#2}}\) \(\newcommand{\gray}[1]{\color{gray}{#1}}\) \(\newcommand{\lgray}[1]{\color{lightgray}{#1}}\) \(\newcommand{\rank}{\operatorname{rank}}\) \(\newcommand{\row}{\text{Row}}\) \(\newcommand{\col}{\text{Col}}\) \(\renewcommand{\row}{\text{Row}}\) \(\newcommand{\nul}{\text{Nul}}\) \(\newcommand{\var}{\text{Var}}\) \(\newcommand{\corr}{\text{corr}}\) \(\newcommand{\len}[1]{\left|#1\right|}\) \(\newcommand{\bbar}{\overline{\bvec}}\) \(\newcommand{\bhat}{\widehat{\bvec}}\) \(\newcommand{\bperp}{\bvec^\perp}\) \(\newcommand{\xhat}{\widehat{\xvec}}\) \(\newcommand{\vhat}{\widehat{\vvec}}\) \(\newcommand{\uhat}{\widehat{\uvec}}\) \(\newcommand{\what}{\widehat{\wvec}}\) \(\newcommand{\Sighat}{\widehat{\Sigma}}\) \(\newcommand{\lt}{<}\) \(\newcommand{\gt}{>}\) \(\newcommand{\amp}{&}\) \(\definecolor{fillinmathshade}{gray}{0.9}\)La manera más fácil de asegurar una eficiencia de corriente del 100% es mantener el electrodo de trabajo a un potencial constante donde el analito se oxida o se reduce por completo y donde no se oxidan o reducen las especies potenciales interferentes. A medida que avanza la electrólisis, la concentración del analito y la corriente disminuyen. El perfil de corriente contra tiempo resultante para la culombimetría de potencial controlado se muestra en la Figura\(\PageIndex{1}\). Integrar el área bajo la curva de t = 0 a t = t e da la carga total. En esta sección consideramos los parámetros experimentales y la instrumentación necesarios para desarrollar un método coulométrico de análisis de potencial controlado y sus aplicaciones.
Selección de un potencial constante
Para entender cómo se selecciona un potencial apropiado para el electrodo de trabajo, desarrollemos un método coulométrico de potencial constante para Cu 2 + basado en su reducción a cobre metálico en un electrodo de trabajo de Pt.
\[\mathrm{Cu}^{2+}(a q)+2 e^{-} \rightleftharpoons \mathrm{Cu}(s) \label{cp1} \]
La figura\(\PageIndex{2}\) muestra las tres reacciones de reducción que pueden tener lugar en una solución acuosa de Cu 2 + y sus potenciales de reducción en estado estándar: la reducción de O 2 a H 2 O, la reducción de Cu 2 + a Cu y la reducción de H 3 O + a H 2. A partir del diagrama sabemos que la reacción\ ref {cp1} se ve favorecida cuando el potencial del electrodo de trabajo es más negativo que +0.342 V frente al electrodo de hidrógeno estándar. Para asegurar una eficiencia de corriente del 100%, sin embargo, el potencial debe ser suficientemente más positivo que +0.000 V para que la reducción de H 3 O + a H 2 no contribuya significativamente a que la corriente total fluya a través de la celda electroquímica.
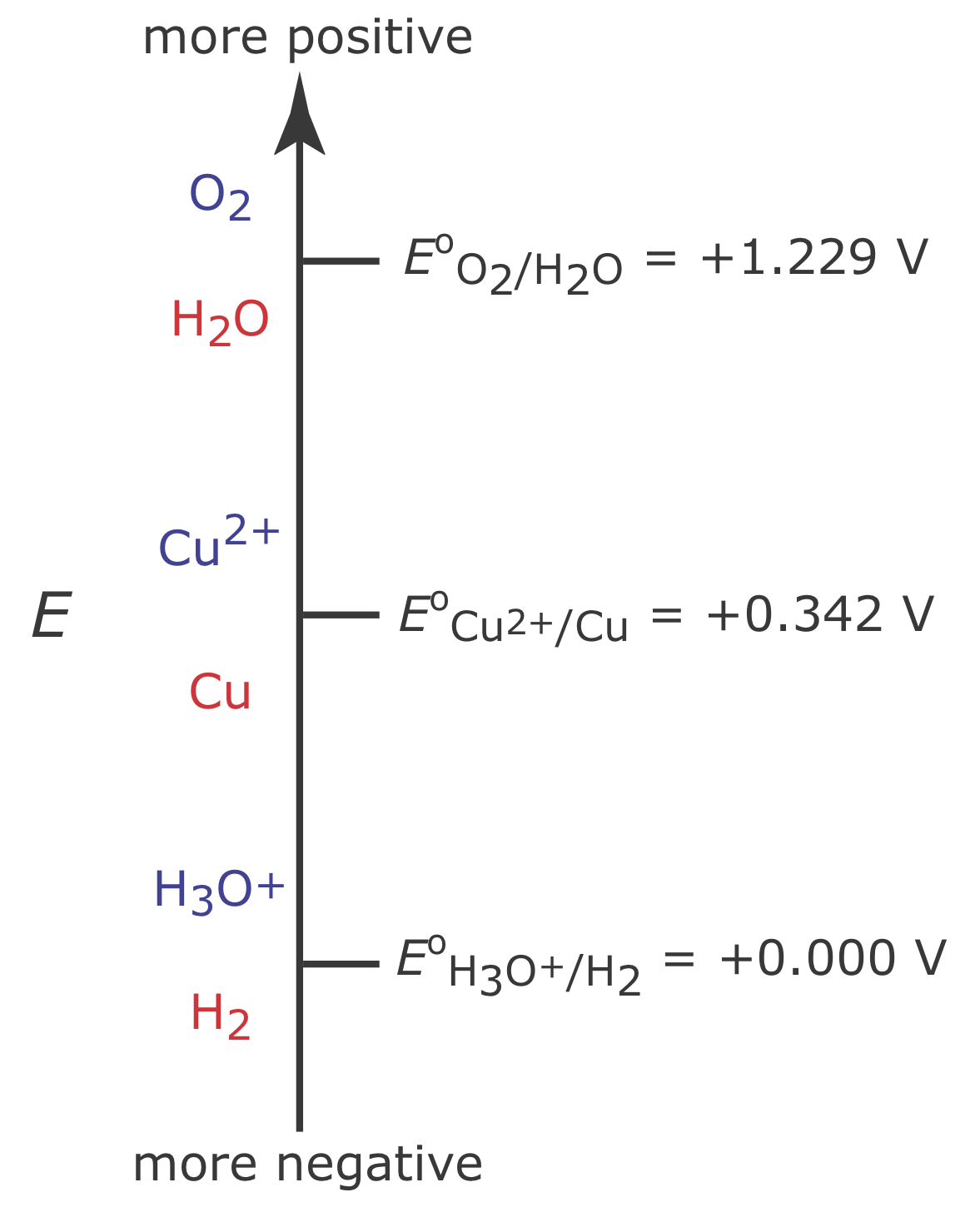
Podemos usar la ecuación de Nernst para la reacción\ ref {cp1} para estimar el potencial mínimo para reducir cuantitativamente Cu 2 +.
\[E=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\mathrm{o}}-\frac{0.05916}{2} \log \frac{1}{\left[\mathrm{Cu}^{2+}\right]} \label{cp2} \]
Entonces, ¿por qué estamos usando la concentración de Cu 2 + en la Ecuación\ ref {cp2} en lugar de su actividad como hicimos en el Capítulo 23 cuando consideramos la potenciometría? En potenciometría se utilizó la actividad porque se utilizó la célula E para determinar la concentración del analito. Aquí utilizamos la ecuación de Nernst para ayudarnos a seleccionar un potencial apropiado. Una vez que identificamos un potencial, podemos ajustar su valor según sea necesario para asegurar una reducción cuantitativa de Cu 2 +. Además, en la culometría la concentración del analito viene dada por la carga total, no por el potencial aplicado.
Si definimos una electrólisis cuantitativa como aquella en la que reducimos 99.99% de Cu2+ a Cu, entonces la concentración de Cu 2 + a t e es
\[\left[\mathrm{Cu}^{2+}\right]_{t_{e}}=0.0001 \times\left[\mathrm{Cu}^{2+}\right]_{0} \label{cp3} \]
donde [Cu 2 +] 0 es la concentración inicial de Cu 2 + en la muestra. Sustituir la Ecuación\ ref {cp3} por la Ecuación\ ref {cp2} nos permite calcular el potencial deseado.
\[E=E_{\mathrm{Cu}^{2+} / \mathrm{Cu}}^{\circ}-\frac{0.05916}{2} \log \frac{1}{0.0001 \times\left[\mathrm{Cu}^{2+}\right]} \label{cp4} \]
Si la concentración inicial de Cu 2 + es\(1.00 \times 10^{-4}\) M, por ejemplo, entonces el potencial del electrodo de trabajo debe ser más negativo que +0.105 V para reducir cuantitativamente Cu 2 + a Cu. Tenga en cuenta que a este potencial H 3 O + no se reduce a H 2, manteniendo el 100% de eficiencia de corriente.
Muchos métodos coulométricos de potencial controlado para Cu 2 + utilizan un potencial negativo en relación con el electrodo de hidrógeno estándar; véase, por ejemplo, Rechnitz, G. A. Controlled-Potential Analysis, Macmillan: New York, 1963, p.49. Con base en la Figura se podría\(\PageIndex{2}\) esperar que aplicar un potencial <0.000 V reducirá parcialmente H 3 O + a H 2, lo que resulta en una eficiencia de corriente inferior al 100%. La razón por la que podemos usar tal potencial negativo es que la velocidad de reacción para la reducción de H 3 O + a H 2 es muy lenta en un electrodo de Pt. Esto da como resultado un sobrepotencial significativo —la necesidad de aplicar un potencial más positivo o uno más negativo que el predicho por la termodinámica— que desplaza E o para el par redox H 3 O + /H 2 a un valor más negativo.
Minimización del tiempo de electró
En la coulometría de potencial controlado, como se muestra en la Figura\(\PageIndex{1}\), la corriente disminuye con el tiempo. Como resultado, la tasa de electrólisis —recordar del Capítulo 22 que la corriente es una medida de la velocidad— se vuelve más lenta y una electrólisis exhaustiva del analito puede requerir mucho tiempo. Debido a que el tiempo es una consideración importante a la hora de diseñar un método analítico, debemos considerar los factores que afectan el tiempo de análisis.
Podemos aproximar cómo cambia la corriente en función del tiempo (Figura\(\PageIndex{1}\)) como decaimiento exponencial; así, la corriente en el tiempo t es
\[i_{t}=i_{0} e^{-k t} \label{cp5} \]
donde i 0 es la corriente a t = 0 y k es una constante de velocidad que es directamente proporcional al área del electrodo de trabajo y la velocidad de agitación, y que es inversamente proporcional al volumen de solución. Para una electrólisis exhaustiva en la que oxidamos o reducimos 99.99% del analito, la corriente al final del análisis, t e, es
\[i_{t_{e}} \leq 0.0001 \times i_{0} \label{cp6} \]
Sustituyendo la Ecuación\ ref {cp6} en Ecuación\ ref {cp5} y resolviendo para t e da el tiempo mínimo para una electrólisis exhaustiva como
\[t_{e}=-\frac{1}{k} \times \ln (0.0001)=\frac{9.21}{k} \label{cp7} \]
A partir de esta ecuación vemos que un valor mayor para k reduce el tiempo de análisis. Por esta razón, solemos realizar un análisis coulométrico de potencial controlado en una celda electroquímica de pequeño volumen, utilizando un electrodo con una gran superficie y con una alta velocidad de agitación. Una electrólisis cuantitativa normalmente requiere aproximadamente 30—60 min, aunque son posibles tiempos más cortos o más largos.
Instrumentación
Podemos usar el potenciostato de tres electrodos en la Figura (\(\PageIndex{3}\)) para establecer y controlar el potencial en la culometría de potencial controlado. El potencial del electrodo de trabajo se mide en relación con un electrodo de referencia de potencial constante que se conecta al electrodo de trabajo a través de un potenciómetro de alta impedancia. Para establecer el potencial del electrodo de trabajo, ajustamos la resistencia de cable deslizante que está conectada al electrodo auxiliar. Si el potencial del electrodo de trabajo comienza a derivar, ajustamos la resistencia del cable deslizante para devolver el potencial a su valor inicial. La corriente que fluye entre el electrodo auxiliar y el electrodo de trabajo se mide con un amperímetro. Por supuesto, un estato de potencia moderno utiliza amplificadores operativos para mantener el potencial constante sin nuestra intervención.

El electrodo de trabajo suele ser uno de dos tipos: un electrodo cilíndrico de Pt fabricado a partir de gasa de platino (Figura\(\PageIndex{4}\)), o un electrodo de piscina de Hg. El gran sobrepotencial para la reducción de H 3 O + a Hg lo convierte en el electrodo de elección para un analito que requiere un potencial negativo. Por ejemplo, un potencial más negativo que —1 V versus el SHE es factible en un electrodo de Hg, pero no en un electrodo de Pt, incluso en una solución muy ácida. Debido a que el mercurio es fácil de oxidar, es menos útil si necesitamos mantener un potencial que sea positivo con respecto a la ELE. El platino es el electrodo de trabajo de elección cuando necesitamos aplicar un potencial positivo.

El electrodo auxiliar, que a menudo es un cable de Pt, está separado por un puente de sal de la solución analítica. Esto es necesario para evitar que los productos de electrólisis generados en el electrodo auxiliar reaccionen con el analito e interfieran en el análisis. Un electrodo de calomel saturado o Ag/AgCl sirve como electrodo de referencia.
La otra necesidad esencial de coulometría de potencial controlado es un medio para determinar la carga total. Un método es monitorear la corriente en función del tiempo y determinar el área bajo la curva, como se muestra en la Figura\(\PageIndex{1}\). Los instrumentos modernos utilizan la integración electrónica para monitorear la carga en función del tiempo. La carga total al final de la electrólisis se lee directamente a partir de una lectura digital.
Electrogravimetría
Si el producto de la coulometría de potencial controlado forma un depósito en el electrodo de trabajo, entonces podemos usar el cambio en la masa del electrodo como señal analítica. Por ejemplo, si aplicamos un potencial que reduce Cu 2 + a Cu en un electrodo de trabajo de Pt, la diferencia en la masa del electrodo antes y después de la electrólisis es una medición directa de la cantidad de cobre en la muestra. Una técnica analítica que utiliza la masa como señal una técnica gravimétrica; así, llamamos a esta electrogravimetría.
Aplicaciones Cuantitativas
La mayoría de los análisis coulométricos de potencial controlado implican la determinación de cationes y aniones inorgánicos, incluyendo metales traza e iones haluros. La tabla\(\PageIndex{1}\) resume varios de estos métodos.
| analito | reacción electrolítica | electrodo |
|---|---|---|
| antimonio | \(\text{Sb}(\text{III}) + 3 e^{-} \rightleftharpoons \text{Sb}\) | Pt |
| arsénico | \(\text{As}(\text{III}) \rightleftharpoons \text{As(V)} + 2 e^{-}\) | Pt |
| cadmio | \(\text{Cd(II)} + 2 e^{-} \rightleftharpoons \text{Cd}\) | Pt o Hg |
| cobalto | \(\text{Co(II)} + 2 e^{-} \rightleftharpoons \text{Co}\) | Pt o Hg |
| cobre | \(\text{Cu(II)} + 2 e^{-} \rightleftharpoons \text{Cu}\) | Pt o Hg |
| haluros (X —) | \(\text{Ag} + \text{X}^- \rightleftharpoons \text{AgX} + e^-\) | Ag |
| hierro | \(\text{Fe(II)} \rightleftharpoons \text{Fe(III)} + e^-\) | Pt |
| plomo | \(\text{Pb(II)} + 2 e^{-} \rightleftharpoons \text{Pb}\) | Pt o Hg |
| níquel | \(\text{Ni(II)} + 2 e^{-} \rightleftharpoons \text{Ni}\) | Pt o Hg |
| plutonio | \(\text{Pu(III)} \rightleftharpoons \text{Pu(IV)} + e^-\) | Pt |
| plata | \(\text{Ag(I)} + 1 e^{-} \rightleftharpoons \text{Ag}\) | Pt |
| estaño | \(\text{Sn(II)} + 2 e^{-} \rightleftharpoons \text{Sn}\) | Pt |
| uranio | \(\text{U(VI)} + 2 e^{-} \rightleftharpoons \text{U(IV})\) | Pt o Hg |
| zinc | \(\text{Zn(II)} + 2 e^{-} \rightleftharpoons \text{Zn}\) | Pt o Hg |
|
Fuente: Rechnitz, G. A. Análisis de Potencial Controlado, Macmillan: Nueva York, 1963. Las reacciones electrolíticas se escriben en términos del cambio en el estado de oxidación del analito. La especie real en solución depende del analito. |
||
La capacidad de controlar la selectividad ajustando el potencial del electrodo de trabajo hace que la culombimetría de potencial controlado sea particularmente útil para el análisis de aleaciones. Por ejemplo, podemos determinar la composición de una aleación que contiene Ag, Bi, Cd y Sb disolviendo la muestra y colocándola en una matriz de 0.2 M H 2 SO 4 junto con un electrodo de trabajo Pt y un contraelectrodo de Pt. Si aplicamos un potencial constante de +0.40 V frente al SCE, Ag (I) se deposita en el electrodo como Ag y los otros iones metálicos permanecen en solución. Cuando se completa la electrólisis, utilizamos la carga total para determinar la cantidad de plata en la aleación. A continuación, cambiamos el potencial del electrodo de trabajo a —0.08 V versus el SCE, depositando Bi en el electrodo de trabajo. Cuando se completa el análisis coulométrico para bismuto, determinamos el antimonio cambiando el potencial del electrodo de trabajo a —0.33 V versus el SCE, depositando Sb. Finalmente, determinamos cadmio después de su electrodeposición sobre el electrodo de trabajo a un potencial de —0.80 V frente al SCE.
También podemos utilizar la coulometría de potencial controlado para el análisis cuantitativo de compuestos orgánicos, aunque el número de aplicaciones es significativamente menor que el de los analitos inorgánicos. Un ejemplo es la reducción de seis electrones de un grupo nitro, —NO 2, a una amina primaria, —NH 2, en un electrodo de mercurio. Se analizan soluciones de ácido pícrico, también conocido como 2,4,6-trinitrofenol, o TNP, un pariente cercano del TNT, reduciéndolo a triaminofenol.
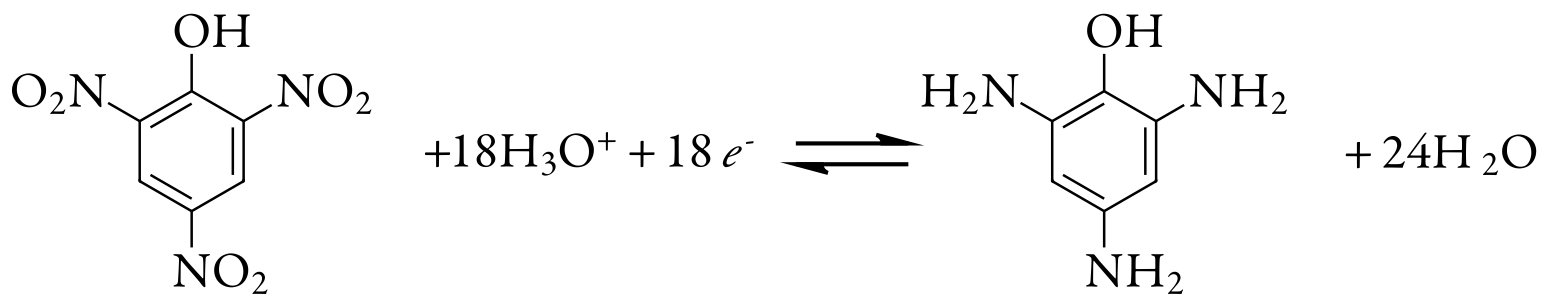
Otro ejemplo es la reducción sucesiva de tricloroacetato a dicloroacetato, y de dicloroacetato a monocloroacetato
\[\text{Cl}_3\text{CCOO}^-(aq) + \text{H}_3\text{O}^+(aq) + 2 e^- \rightleftharpoons \text{Cl}_2\text{HCCOO}^-(aq) + \text{Cl}^-(aq) + \text{H}_2\text{O}(l) \nonumber \]
\[\text{Cl}_2\text{HCCOO}^-(aq) + \text{ H}_3\text{O}^+(aq) + 2 e^- \rightleftharpoons \text{ ClH}_2\text{CCOO}^-(aq) + \text{ Cl}^-(aq) + \text{H}_2\text{O}(l) \nonumber \]
Podemos analizar una mezcla de tricloroacetato y dicloroacetato seleccionando un potencial inicial donde solo reacciona el tricloroacetato más fácilmente reducido. Cuando se completa su electrólisis, podemos reducir el dicloroacetato ajustando el potencial a un potencial más negativo. La carga total para la primera electrólisis da la cantidad de tricloroacetato, y la diferencia en la carga total entre la primera electrólisis y la segunda electrólisis da la cantidad de dicloroacetato.
Una aplicación útil de la coulometría de potencial controlado es determinar el número de electrones involucrados en una reacción redox. Para realizar la determinación, se realiza un análisis coulométrico de potencial controlado utilizando una cantidad conocida de un compuesto puro. La carga total al final de la electrólisis se utiliza para determinar el valor de n usando la ley de Faraday. Una muestra de 0.3619-g de ácido tetracloropicolínico, C 6 HNO 2 Cl 4, se disuelve en agua destilada, se transfiere a un matraz aforado de 1000 ml y se diluye a volumen. Una electrólisis exhaustiva de potencial controlado de una porción de 10.00 mL de esta solución en un cátodo esponjoso de plata requiere 5.374 C de carga. ¿Cuál es el valor de n para esta reacción de reducción?
Solución
La porción de 10.00 ml de muestra contiene 3.619 mg, o\(1.39 \times 10^{-5}\) mol de ácido tetracloropicolínico. Resolviendo para n da
\[n=\frac{Q}{F N_{A}}=\frac{5.374 \text{ C}}{\left(96478 \text{ C/mol } e^{-}\right)\left(1.39 \times 10^{-5} \text{ mol } \mathrm{C}_{6} \mathrm{HNO}_{2} \mathrm{Cl}_{4}\right)} = 4.01 \text{ mol e}^-/\text{mol } \mathrm{C}_{6} \mathrm{HNO}_{2} \mathrm{Cl}_{4} \nonumber \]
Así, reducir una molécula de ácido tetracloropicolínico requiere cuatro electrones. La reacción global, que resulta en la formación selectiva de ácido 3,6-dicloropicolínico, es



