4.4: La distribución de las mediciones y los resultados
- Page ID
- 75496
Anteriormente se reportaron resultados para una determinación de la masa de un centavo circulante de Estados Unidos, obteniendo una media de 3.117 g y una desviación estándar de 0.051 g. En la Tabla 4.4.1 se muestran resultados para una segunda determinación independiente de la masa de un centavo, así como los datos del primer experimento. Aunque las medias y desviaciones estándar para los dos experimentos son similares, no son idénticas. La diferencia entre los dos experimentos plantea algunas preguntas interesantes. ¿Los resultados de un experimento son mejores que los resultados del otro experimento? ¿Los dos experimentos proporcionan estimaciones equivalentes para la media y la desviación estándar? ¿Cuál es nuestra mejor estimación de la masa esperada de un centavo? Para responder a estas preguntas necesitamos entender cómo podríamos predecir las propiedades de todos los centavos usando los resultados de un análisis de una pequeña muestra de centavos. Comenzamos por hacer una distinción entre poblaciones y muestras.
| Primer Experimento | Segundo Experimento | ||
|---|---|---|---|
| Penny | Masa (g) | Penny | Masa (g) |
| 1 | 3.080 | 1 | 3.052 |
| 2 | 3.094 | 2 | 3.141 |
| 3 | 3.107 | 3 | 3.083 |
| 4 | 3.056 | 4 | 3.083 |
| 5 | 3.112 | 5 | 3.048 |
| 6 | 3.174 | ||
| 7 | 3.198 | ||
| \(\overline{X}\) | 3.117 | 3.081 | |
| \(s\) | 0.051 | 0.037 | |
Poblaciones y Muestras
Una población es el conjunto de todos los objetos del sistema que estamos investigando. Para los datos de la Tabla 4.4.1 , la población es de todos los centavos de Estados Unidos en circulación. Esta población es tan grande que no podemos analizar a cada miembro de la población. En su lugar, seleccionamos y analizamos un subconjunto limitado, o muestra de la población. Los datos de la Tabla 4.4.1 , por ejemplo, muestran los resultados de dos muestras de este tipo extraídas de la mayor población de todos los centavos circulantes de Estados Unidos.
Distribuciones de probabilidad para poblaciones
El cuadro 4.4.1 proporciona las medias y las desviaciones estándar para dos muestras de centavos circulantes de Estados Unidos. ¿Qué nos dicen estas muestras sobre la población de centavos? ¿Cuál es la mayor masa posible por un centavo? ¿Cuál es la masa más pequeña posible? ¿Todas las masas son igualmente probables, o algunas masas son más comunes?
Para responder a estas preguntas necesitamos saber cómo se distribuyen las masas de centavos individuales sobre la masa promedio de la población. Representamos la distribución de una población trazando la probabilidad o frecuencia de obtener un resultado específico en función de los posibles resultados. Tales parcelas se denominan distribuciones de probabilidad.
Existen muchas distribuciones de probabilidad posibles; de hecho, la distribución de probabilidad puede tomar cualquier forma dependiendo de la naturaleza de la población. Afortunadamente, muchos sistemas químicos muestran una de varias distribuciones de probabilidad comunes. Dos de estas distribuciones, la distribución binomial y la distribución normal, se discuten en esta sección.
La distribución binomial
La distribución binomial describe una población en la que el resultado es el número de veces que ocurre un evento particular durante un número fijo de ensayos. Matemáticamente, la distribución binomial se define como
\[P(X, N) = \frac {N!} {X!(N - X)!} \times p^X \times (1 - p)^{N - X} \nonumber\]
donde P (X, N) es la probabilidad de que un evento ocurra X veces durante N ensayos, y p es la probabilidad del evento para un solo ensayo. Si volteas una moneda cinco veces, P (2,5) es la probabilidad de que la moneda suba “cabezas” exactamente dos veces.
El término N! se lee como N -factorial y es el producto\(N \times (N – 1) \times (N – 2) \times \cdots \times 1\). Por ejemplo, ¡4! es\(4 \times 3 \times 2 \times 1 = 24\). Su calculadora probablemente tenga una clave para calcular factoriales.
Una distribución binomial tiene medidas bien definidas de tendencia central y propagación. El valor medio esperado es
\[\mu = Np \nonumber\]
y el spread esperado viene dado por la varianza
\[\sigma^2 = Np(1 - p) \nonumber\]
o la desviación estándar.
\[\sigma = \sqrt{Np(1 - p)} \nonumber\]
La distribución binomial describe una población cuyos miembros solo tienen valores específicos y discretos. Cuando enrolla una matriz, por ejemplo, los valores posibles son 1, 2, 3, 4, 5 o 6. Un rollo de 3.45 no es posible. Como se muestra en el Ejemplo Trabajado 4.4.1 , un ejemplo de un sistema químico que obedece a la distribución binomial es la probabilidad de encontrar un isótopo particular en una molécula.
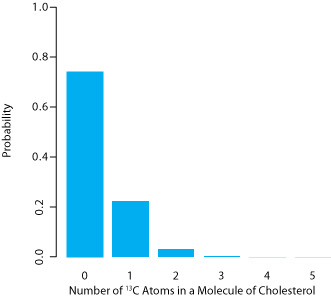
El carbono tiene dos isótopos estables, no radiactivos, 12 C y 13 C, con abundancias isotópicas relativas de 98.89% y 1.11% respectivamente.
(a) ¿Cuáles son la media y la desviación estándar para el número de 13 átomos de C en una molécula de colesterol (C 27 H 44 O)?
b) ¿Cuál es la probabilidad de que una molécula de colesterol no tenga átomos de 13 C?
Solución
La probabilidad de encontrar un átomo de 13 C en una molécula de colesterol sigue una distribución binomial, donde X es el número de 13 átomos de C, N es el número de átomos de carbono en una molécula de colesterol, y p es la probabilidad de que un átomo de carbono en 13 C.
Para (a), el número medio de 13 átomos de C en una molécula de colesterol es
\[\mu = Np = 27 \times 0.0111 = 0.300 \nonumber\]
con una desviación estándar de
\[\sigma = \sqrt{Np(1 - p)} = \sqrt{27 \times 0.0111 \times (1 - 0.0111)} = 0.544 \nonumber\]
Para (b), la probabilidad de encontrar una molécula de colesterol sin un átomo de 13 C es
\[P(0, 27) = \frac {27!} {0! \: (27 - 0)!} \times (0.0111)^0 \times (1 - 0.0111)^{27 - 0} = 0.740 \nonumber\]
Existe un 74.0% de probabilidad de que una molécula de colesterol no tenga un átomo de 13 C, resultado consistente con la observación de que el número medio de 13 átomos de C por molécula de colesterol, 0.300, es menor que uno.
Una porción de la distribución binomial para átomos de 13 C en colesterol se muestra en la Figura 4.4.1 . Obsérvese en particular que hay poca probabilidad de encontrar más de dos átomos de 13 C en cualquier molécula de colesterol.
La distribución normal
Una distribución binomial describe una población cuyos miembros solo tienen ciertos valores discretos. Este es el caso del número de 13 átomos de C en el colesterol. Una molécula de colesterol, por ejemplo, puede tener dos 13 átomos de C, pero no puede tener 2.5 átomos de 13 C. Una población es continua si sus miembros pueden tomar algún valor. La eficiencia de extraer colesterol de una muestra, por ejemplo, puede tomar cualquier valor entre 0% (no se extrae colesterol) y 100% (se extrae todo el colesterol).
La distribución continua más común es la distribución gaussiana, o normal, cuya ecuación es
\[f(X) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{- \frac {(X - \mu)^2} {2 \sigma^2}} \nonumber\]
donde\(\mu\) está la media esperada para una población con n miembros
\[\mu = \frac {\sum_{i = 1}^n X_i} {n} \nonumber\]
y\(\sigma^2\) es la varianza de la población.
\[\sigma^2 = \frac {\sum_{i = 1}^n (X_i - \mu)^2} {n} \label{4.1}\]
Ejemplos de tres distribuciones normales, cada una con una media esperada de 0 y con varianzas de 25, 100 o 400, respectivamente, se muestran en la Figura 4.4.2 . Dos características de estas curvas de distribución normal merecen atención. Primero, tenga en cuenta que cada distribución normal tiene un único máximo que corresponde a\(\mu\), y que la distribución es simétrica sobre este valor. Segundo, aumentar la varianza de la población aumenta la dispersión de la distribución y disminuye su altura; sin embargo, el área bajo la curva es la misma para las tres distribuciones.
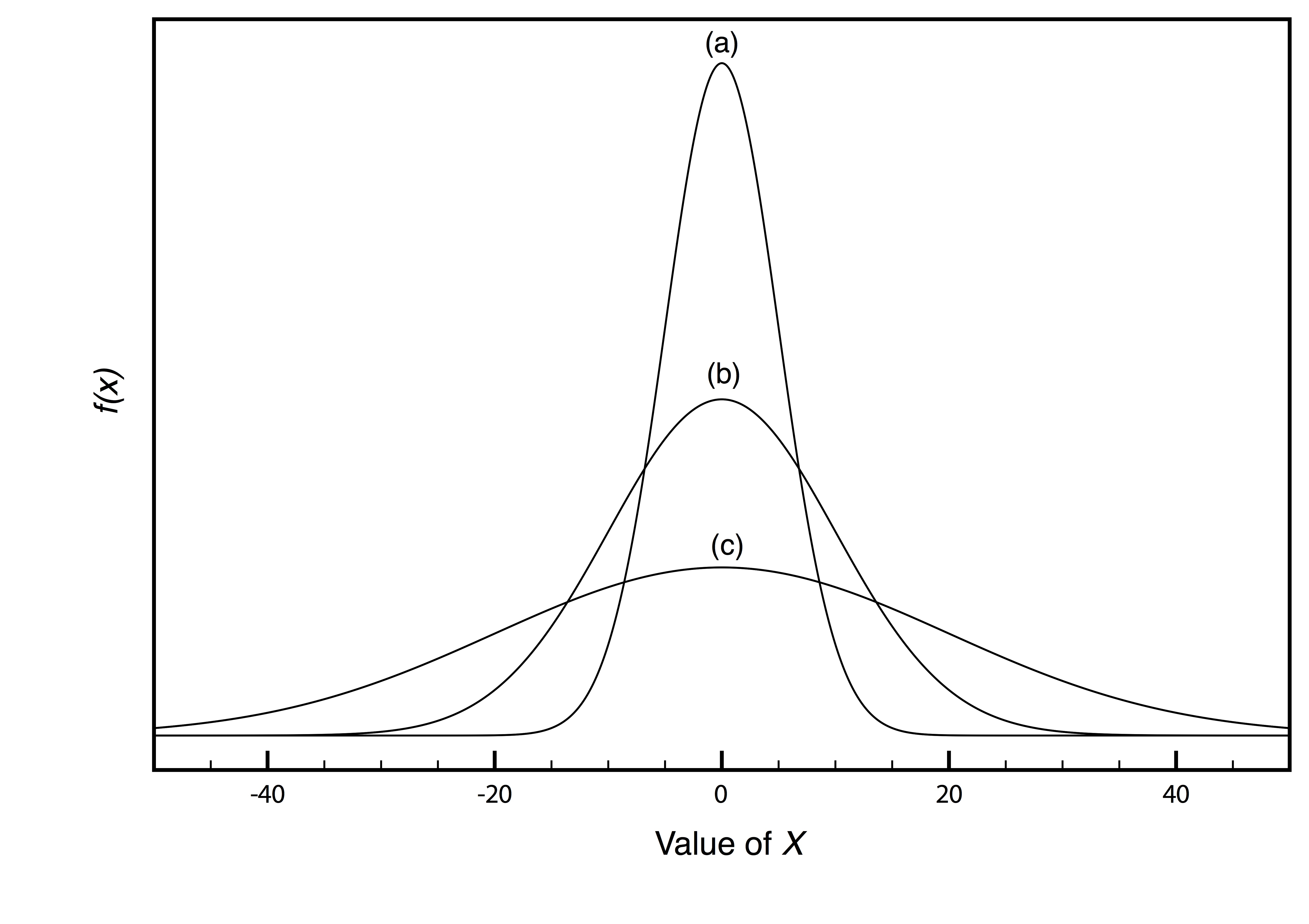
El área bajo una curva de distribución normal es una propiedad importante y útil, ya que es igual a la probabilidad de encontrar un miembro de la población dentro de un rango particular de valores. En la Figura 4.4.2 , por ejemplo, 99.99% de la población mostrada en la curva (a) tiene valores de X entre —20 y +20. Para la curva (c), 68.26% de los integrantes de la población tienen valores de X entre —20 y +20.
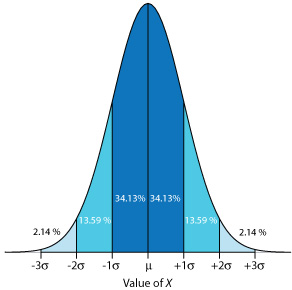
Debido a que una distribución normal depende únicamente de\(\mu\) y\(\sigma^2\), la probabilidad de encontrar un miembro de la población entre dos límites cualesquiera es la misma para todas las poblaciones normalmente distribuidas. La figura 4.4.3 , por ejemplo, muestra que 68.26% de los miembros de una distribución normal tienen un valor dentro del rango\(\mu \pm 1 \sigma\), y que 95.44% de los miembros de la población tienen valores dentro del rango\(\mu \pm 2 \sigma\). Sólo 0.27% los miembros de una población tienen valores que superan la media esperada en más de ± 3\(\sigma\). Los rangos y probabilidades adicionales se reúnen en la tabla de probabilidad incluida en el Apéndice 3. Como se muestra en el Ejemplo 4.4.2 , si conocemos la media y la desviación estándar para una población normalmente distribuida, entonces podemos determinar el porcentaje de la población entre cualquier límite definido.
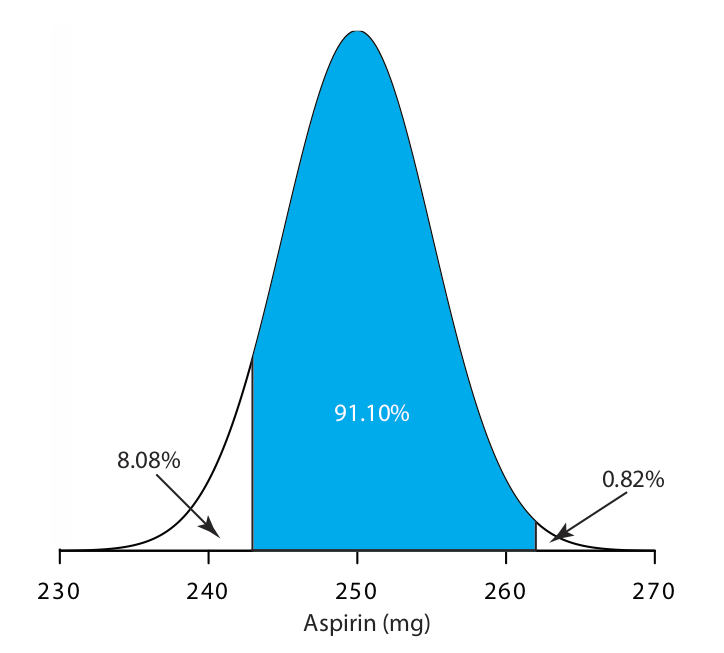
Se sabe que la cantidad de aspirina en las tabletas analgésicas de un fabricante en particular sigue una distribución normal con\(\mu\) = 250 mg y\(\sigma\) = 5. En una muestra aleatoria de tabletas de la línea de producción, ¿qué porcentaje se espera que contenga entre 243 y 262 mg de aspirina?
Solución
No se determina directamente el porcentaje de comprimidos entre 243 mg y 262 mg de aspirina. En cambio, primero encontramos el porcentaje de tabletas con menos de 243 mg de aspirina y el porcentaje de tabletas que tienen más de 262 mg de aspirina. Al restar estos resultados del 100%, se obtiene el porcentaje de comprimidos que contienen entre 243 mg y 262 mg de aspirina.
Para encontrar el porcentaje de comprimidos con menos de 243 mg de aspirina o más de 262 mg de aspirina calculamos la desviación, z, de cada límite\(\mu\) en términos de la desviación estándar de la población,\(\sigma\)
\[z = \frac {X - \mu} {\sigma} \nonumber\]
donde X es el límite en cuestión. La desviación para el límite inferior es
\[z_{lower} = \frac {243 - 250} {5} = -1.4 \nonumber\]
y la desviación para el límite superior es
\[z_{upper} = \frac {262 - 250} {5} = +2.4 \nonumber\]
Utilizando la tabla del Apéndice 3, encontramos que el porcentaje de comprimidos con menos de 243 mg de aspirina es de 8.08%, y que el porcentaje de comprimidos con más de 262 mg de aspirina es de 0.82%. Por lo tanto, el porcentaje de comprimidos que contienen entre 243 y 262 mg de aspirina es
\[100.00 \% - 8.08 \% - 0.82 \% = 91.10 \% \nonumber\]
La Figura 4.4.4 muestra la distribución de aspirantes en los comprimidos, con el área en azul mostrando el porcentaje de comprimidos que contienen entre 243 mg y 262 mg de aspirina.
Qué porcentaje de comprimidos de aspirina contendrá entre 240 mg y 245 mg de aspirina si la media de la población es de 250 mg y la desviación estándar de la población es de 5 mg.
- Contestar
-
Para encontrar el porcentaje de comprimidos que contienen menos de 245 mg de aspirina primero calculamos la desviación, z,
\[z = \frac {245 - 250} {5} = -1.00 \nonumber\]
y luego buscar la probabilidad correspondiente en el Apéndice 3, obteniendo un valor de 15.87%. Para encontrar el porcentaje de tabletas que contienen menos de 240 mg de aspirina encontramos que
\[z = \frac {240 - 250} {5} = -2.00 \nonumber\]
lo que corresponde a 2.28%. El porcentaje de comprimidos que contienen entre 240 y 245 mg de aspirante es 15.87% — 2.28% = 13.59%.
Intervalos de confianza para poblaciones
Si seleccionamos al azar un solo miembro de una población, ¿cuál es su valor más probable? Esta es una cuestión importante y, de una forma u otra, está en el centro de cualquier análisis en el que se desee extrapolar de una muestra a la población madre de la muestra. Una de las características más importantes de la distribución de probabilidad de una población es que proporciona una manera de responder a esta pregunta.
La figura 4.4.3 muestra que para una distribución normal, 68.26% de los miembros de la población tienen valores dentro del rango\(\mu \pm 1\sigma\). Dicho esto de otra manera, existe una probabilidad de 68.26% de que el resultado para una sola muestra extraída de una población normalmente distribuida esté en el intervalo\(\mu \pm 1\sigma\). En general, si seleccionamos una sola muestra esperamos su valor, X i está en el rango
\[X_i = \mu \pm z \sigma \label{4.2}\]
donde el valor de z es la confianza que tenemos en la asignación de este rango. Los valores reportados de esta manera se denominan intervalos de confianza. La ecuación\ ref {4.2}, por ejemplo, es el intervalo de confianza para un solo miembro de una población. La Tabla 4.4.2 da los intervalos de confianza para varios valores de z. Por razones discutidas más adelante en el capítulo, un nivel de confianza del 95% es una opción común en química analítica.
Cuando z = 1, llamamos a esto el intervalo de confianza del 68.26%.
| z | Intervalo de confianza |
|---|---|
| 0.50 | 38.30 |
| 1.00 | 68.26 |
| 1.50 | 86.64 |
| 1.96 | 95.00 |
| 2.00 | 95.44 |
| 2.50 | 98.76 |
| 3.00 | 99.73 |
| 3.50 | 99.95 |
¿Cuál es el intervalo de confianza del 95% para la cantidad de aspirina en una sola tableta analgésica extraída de una población para la cual\(\mu\) es 250 mg y para la cual\(\sigma\) es 5?
Solución
Usando Table 4.4.2 , encontramos que z es 1.96 para un intervalo de confianza del 95%. Sustituyendo esto en la Ecuación\ ref {4.2} da el intervalo de confianza para una sola tableta como
\[X_i = \mu \pm 1.96\sigma = 250 \text{ mg} \pm (1.96 \times 5) = 250 \text{ mg} \pm 10 \text{mg} \nonumber\]
Un intervalo de confianza de 250 mg ± 10 mg significa que 95% de los comprimidos en la población contienen entre 240 y 260 mg de aspirina.
Alternativamente, podemos reescribir la Ecuación\ ref {4.2} para que dé el intervalo de confianza es para\(\mu\) basado en la desviación estándar de la población y el valor de un solo miembro extraído de la población.
\[\mu = X_i \pm z \sigma \label{4.3}\]
Se sabe que la desviación estándar poblacional para la cantidad de aspirina en un lote de tabletas analgésicas es de 7 mg de aspirina. Si selecciona y analiza aleatoriamente un solo comprimido y encuentra que contiene 245 mg de aspirina, ¿cuál es el intervalo de confianza del 95% para la media de la población?
Solución
El intervalo de confianza del 95% para la media poblacional se da como
\[\mu = X_i \pm z \sigma = 245 \text{ mg} \pm (1.96 \times 7) \text{ mg} = 245 \text{ mg} \pm 14 \text{ mg} \nonumber\]
Por lo tanto, con base en esta muestra, estimamos que existe 95% de probabilidad de que la media de la población,\(\mu\), se encuentre dentro del rango de 231 mg a 259 mg de aspirina.
Tenga en cuenta la calificación para la que la predicción\(\mu\) se basa en una muestra; una muestra diferente probablemente dará un intervalo de confianza diferente del 95%. Nuestro resultado aquí, por lo tanto, es una estimación para\(\mu\) basada en esta muestra.
Es inusual predecir la media esperada de la población a partir del análisis de una sola muestra; en cambio, recolectamos n muestras extraídas de una población de conocidos\(\sigma\), y reportamos la media, X. La desviación estándar de la media\(\sigma_{\overline{X}}\), que también se conoce como el error estándar de la media, es
\[\sigma_{\overline{X}} = \frac {\sigma} {\sqrt{n}} \nonumber\]
El intervalo de confianza para la media de la población, por lo tanto, es
\[\mu = \overline{X} \pm \frac {z \sigma} {\sqrt{n}} \nonumber\]
¿Cuál es el intervalo de confianza del 95% para las tabletas analgésicas en el Ejemplo 4.4.4 , si un análisis de cinco comprimidos produce una media de 245 mg de aspirina?
Solución
En este caso el intervalo de confianza es
\[\mu = 245 \text{ mg} \pm \frac {1.96 \times 7} {\sqrt{5}} \text{ mg} = 245 \text{ mg} \pm 6 \text{ mg} \nonumber\]
Estimamos una probabilidad del 95% de que la media de la población esté entre 239 mg y 251 mg de aspirina. Como era de esperar, el intervalo de confianza al usar la media de cinco muestras es menor que el de una sola muestra.
Un análisis de siete comprimidos de aspirina de una población conocida por tener una desviación estándar de 5, da los siguientes resultados en mg de aspirina por comprimido:
\(246 \quad 249 \quad 255 \quad 251 \quad 251 \quad 247 \quad 250\)
¿Cuál es el intervalo de confianza del 95% para la media esperada de la población?
- Contestar
-
La media es de 249.9 mg de aspirina/comprimido para esta muestra de siete comprimidos. Para un intervalo de confianza del 95% el valor de z es 1.96, lo que hace que el intervalo de confianza
\[249.9 \pm \frac {1.96 \times 5} {\sqrt{7}} = 249.9 \pm 3.7 \approx 250 \text{ mg} \pm 4 \text { mg} \nonumber\]
Distribuciones de probabilidad para muestras
En Ejemplos 4.4.2 — 4.4.5 asumimos que la cantidad de aspirina en las tabletas analgésicas se distribuye normalmente. Sin analizar a cada miembro de la población, ¿cómo podemos justificar esta suposición? En una situación en la que no podemos estudiar a toda la población, o cuando no podemos predecir la forma matemática de la distribución probabilística de una población, debemos deducir la distribución a partir de un muestreo limitado de sus miembros.
Distribuciones de muestra y teorema del límite central
Volvamos al problema de determinar la masa de un centavo para explorar más a fondo la relación entre la distribución de una población y la distribución de una muestra extraída de esa población. Los dos conjuntos de datos en la Tabla 4.4.1 son demasiado pequeños para proporcionar una imagen útil de la distribución de una muestra, por lo que usaremos la muestra más grande de 100 centavos que se muestra en la Tabla 4.4.3 . La media y la desviación estándar para esta muestra son 3.095 g y 0.0346 g, respectivamente.
| Penny | Peso (g) | Penny | Peso (g) | Penny | Peso (g) | Penny | Peso (g) |
|---|---|---|---|---|---|---|---|
| 1 | 3.126 | 26 | 3.073 | 51 | 3.101 | 76 | 3.086 |
| 2 | 3.140 | 27 | 3.084 | 52 | 3.049 | 77 | 3.123 |
| 3 | 3.092 | 28 | 3.148 | 53 | 3.082 | 78 | 3.115 |
| 4 | 3.095 | 29 | 3.047 | 54 | 3.142 | 79 | 3.055 |
| 5 | 3.080 | 30 | 3.121 | 55 | 3.082 | 80 | 3.057 |
| 6 | 3.065 | 31 | 3.116 | 56 | 3.066 | 81 | 3.097 |
| 7 | 3.117 | 32 | 3.005 | 57 | 3.128 | 82 | 3.066 |
| 8 | 3.034 | 33 | 3.115 | 58 | 3.112 | 83 | 3.113 |
| 9 | 3.126 | 34 | 3.103 | 59 | 3.085 | 84 | 3.102 |
| 10 | 3.057 | 35 | 3.086 | 60 | 3.086 | 85 | 3.033 |
| 11 | 3.053 | 36 | 3.103 | 61 | 3.084 | 86 | 3.112 |
| 12 | 3.099 | 37 | 3.049 | 62 | 3.104 | 87 | 3.103 |
| 13 | 3.065 | 38 | 2.998 | 63 | 3.107 | 88 | 3.198 |
| 14 | 3.059 | 39 | 3.063 | 64 | 3.093 | 89 | 3.103 |
| 15 | 3.068 | 40 | 3.055 | 65 | 3.126 | 90 | 3.126 |
| 16 | 3.060 | 41 | 3.181 | 66 | 3.138 | 91 | 3.111 |
| 17 | 3.078 | 42 | 3.108 | 67 | 3.131 | 92 | 3.126 |
| 18 | 3.125 | 43 | 3.114 | 68 | 3.120 | 93 | 3.052 |
| 19 | 3.090 | 44 | 3.121 | 69 | 3.100 | 94 | 3.113 |
| 20 | 3.100 | 45 | 3.105 | 70 | 3.099 | 95 | 3.085 |
| 21 | 3.055 | 46 | 3.078 | 71 | 3.097 | 96 | 3.117 |
| 22 | 3.105 | 47 | 3.147 | 72 | 3.091 | 97 | 3.142 |
| 23 | 3.063 | 48 | 3.104 | 73 | 3.077 | 98 | 3.031 |
| 24 | 3.083 | 49 | 3.146 | 74 | 3.178 | 99 | 3.083 |
| 25 | 3.065 | 50 | 3.095 | 75 | 3.054 | 100 | 3.104 |
Un histograma (Figura 4.4.5 ) es una forma útil de examinar los datos en la Tabla 4.4.3 . Para crear el histograma, dividimos la muestra en intervalos, por masa, y determinamos el porcentaje de centavos dentro de cada intervalo (Tabla 4.4.4 ). Tenga en cuenta que la media de la muestra es el punto medio del histograma.
| Intervalo de masa | Frecuencia (como% de la Muestra) | Intervalo de masa | Frecuencia (como% de la Muestra) |
|---|---|---|---|
| 2.991 — 3.009 | 2 | 3.105 — 3.123 | 19 |
| 3.010 — 3.028 | 0 | 3.124 — 3.142 | 12 |
| 3.029 — 3.047 | 4 | 3.143 — 3.161 | 3 |
| 3.048 — 3.066 | 19 | 3.162 — 3.180 | 1 |
| 3.067 — 3.085 | 14 | 3.181 — 3.199 | 2 |
| 3.086 — 3.104 | 24 | 3.200 — 3.218 | 0 |
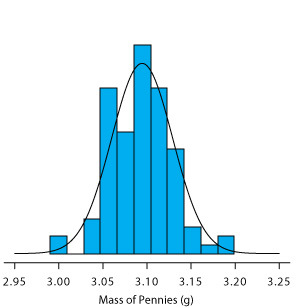
La Figura 4.4.5 también incluye una curva de distribución normal para la población de centavos, con base en el supuesto de que la media y la varianza para la muestra son estimaciones apropiadas para la media y varianza de la población. Aunque el histograma no es de forma perfectamente simétrica, proporciona una buena aproximación de la curva de distribución normal, lo que sugiere que la muestra de 100 centavos se distribuye normalmente. Es fácil imaginar que el histograma se aproximará más a una distribución normal si incluimos centavos adicionales en nuestra muestra.
No ofreceremos una prueba formal de que la muestra de centavos en la Tabla 4.4.3 y la población de todos los centavos de Estados Unidos circulantes están normalmente distribuidos; sin embargo, la evidencia en la Figura 4.4.5 sugiere fuertemente que esto es cierto. Aunque no podemos afirmar que los resultados de todos los experimentos se distribuyen normalmente, en la mayoría de los casos nuestros datos se distribuyen normalmente. Según el teorema del límite central, cuando una medición está sujeta a una variedad de errores indeterminados, los resultados para esa medición se aproximarán a una distribución normal [Mark, H.; Workman, J. Spectroscopy 1988, 3, 44—48]. El teorema del límite central es válido incluso si las fuentes individuales de error indeterminado no se distribuyen normalmente. La principal limitación al teorema del límite central es que las fuentes de error indeterminado deben ser independientes y de similar magnitud para que ninguna fuente de error domine la distribución final.
Una característica adicional del teorema del límite central es que una distribución de medias para muestras extraídas de una población con alguna distribución se aproximará estrechamente a una distribución normal si el tamaño de cada muestra es suficientemente grande. Por ejemplo, la Figura 4.4.6 muestra la distribución para dos muestras de 10 000 extraídas de una distribución uniforme en la que cada valor entre 0 y 1 ocurre con una frecuencia igual. Para muestras de tamaño n = 1, la distribución resultante se aproxima estrechamente a la distribución uniforme de la población. La distribución de las medias para muestras de tamaño n = 10, sin embargo, se aproxima estrechamente a una distribución normal.
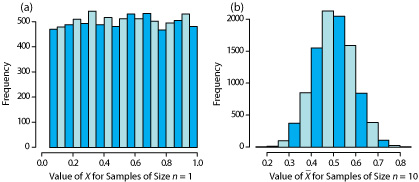
Podría preguntarse razonablemente si este aspecto del teorema del límite central es importante ya que es poco probable que completemos 10 000 análisis, cada uno de los cuales es el promedio de 10 ensayos individuales. Esto es engañoso. Cuando adquirimos una muestra de suelo, por ejemplo, consiste en muchas partículas individuales cada una de las cuales es una muestra individual del suelo. Nuestro análisis de esta muestra, por lo tanto, da la media para este gran número de partículas individuales de suelo. Debido a esto, el teorema del límite central es relevante. Para una discusión de las circunstancias en las que el teorema del límite central puede no aplicarse, consulte “¿Considera que está normalmente distribuido?” , cuya referencia completa es Majewsky, M.; Wagner, M.; Farlin, J. Sci. Total Environ. 2016, 548—549, 408—409.
Grados de Libertad
¿Notó las diferencias entre la ecuación para la varianza de una población y la varianza de una muestra? Si no, aquí están las dos ecuaciones:
\[\sigma^2 = \frac {\sum_{i = 1}^n (X_i - \mu)^2} {n} \nonumber\]
\[s^2 = \frac {\sum_{i = 1}^n (X_i - \overline{X})^2} {n - 1} \nonumber\]
Ambas ecuaciones miden la varianza alrededor de la media, utilizando\(\mu\) para una población y\(\overline{X}\) para una muestra. Aunque las ecuaciones utilizan diferentes medidas para la media, la intención es la misma tanto para la muestra como para la población. Una diferencia más interesante es entre los denominadores de las dos ecuaciones. Cuando calculamos la varianza de la población dividimos el numerador por el tamaño de la población, n; para la varianza de la muestra, sin embargo, dividimos por n — 1, donde n es el tamaño de la muestra. ¿Por qué dividimos por n — 1 cuando calculamos la varianza de la muestra?
Una varianza es la desviación cuadrada promedio de los resultados individuales en relación con la media. Cuando calculamos un promedio dividimos la suma por el número de mediciones independientes, o grados de libertad, en el cálculo. Para la varianza de la población, los grados de libertad son iguales al tamaño de la población, n. Cuando medimos a cada miembro de una población tenemos información completa sobre la población.
Cuando calculamos la varianza de la muestra, sin embargo,\(\mu\) reemplazamos por\(\overline{X}\), que también calculamos usando los mismos datos. Si hay n miembros en la muestra, podemos deducir el valor del n-ésimo miembro de los n — 1 miembros restantes y la media. Por ejemplo, si\(n = 5\) y sabemos que las primeras cuatro muestras son 1, 2, 3 y 4, y que la media es 3, entonces el quinto miembro de la muestra debe ser
\[X_5 = (\overline{X} \times n) - X_1 - X_2 - X_3 - X_4 = (3 \times 5) - 1 - 2 - 3 - 4 = 5 \nonumber\]
Debido a que solo tenemos cuatro mediciones independientes, hemos perdido un grado de libertad. El uso de n — 1 en lugar de n cuando calculamos la varianza de la muestra asegura que\(s^2\) es un estimador imparcial de\(\sigma^2\).
Aquí hay otra forma de pensar sobre los grados de libertad. Analizamos muestras para hacer predicciones sobre la población subyacente. Cuando nuestra muestra consiste en n mediciones no podemos hacer más de n predicciones independientes sobre la población. Cada vez que estimamos un parámetro, como la media de la población, perdemos un grado de libertad. Si hay n grados de libertad para calcular la media de la muestra, entonces n — 1 grados de libertad permanecen cuando calculamos la varianza de la muestra.
Intervalos de confianza para muestras
Anteriormente se introdujo el intervalo de confianza como una forma de reportar el valor más probable para la media de una población,\(\mu\)
\[\mu = \overline{X} \pm \frac {z \sigma} {\sqrt{n}} \label{4.4}\]
donde\(\overline{X}\) es la media para una muestra de tamaño n, y\(\sigma\) es la desviación estándar de la población. Para la mayoría de los análisis desconocemos la desviación estándar de la población. Todavía podemos calcular un intervalo de confianza, sin embargo, si hacemos dos modificaciones a la Ecuación\ ref {4.4}.
La primera modificación es sencilla: reemplazamos la desviación estándar de la población,\(\sigma\), por la desviación estándar de la muestra, s. La segunda modificación no es tan obvia. Los valores de z en la Tabla 4.4.2 son para una distribución normal, que es una función de\(sigma^2\), no s 2. Aunque la varianza de la muestra, s 2, es una estimación imparcial de la varianza de la población\(\sigma^2\), el valor de s 2 rara vez será igual\(\sigma^2\). Para dar cuenta de esta incertidumbre en la estimación\(\sigma^2\), reemplazamos la variable z en la Ecuación\ ref {4.4} por la variable t, donde t se define de tal manera que\(t \ge z\) en todos los niveles de confianza.
\[\mu = \overline{X} \pm \frac {t s} {\sqrt{n}} \label{4.5}\]
Los valores para t en el nivel de confianza del 95% se muestran en la Tabla 4.4.5 . Tenga en cuenta que t se vuelve más pequeño a medida que aumenta el número de grados de libertad, y que se acerca a z cuando n se acerca al infinito. Cuanto mayor sea la muestra, más se aproxima su intervalo de confianza para una muestra (Ecuación\ ref {4.5}) al intervalo de confianza para la población (Ecuación\ ref {4.3}). El apéndice 4 proporciona valores adicionales de t para otros niveles de confianza.
| Grados de Libertad | t | Grados de Libertad | t | Grados de Libertad | t | Grados de Libertad | t |
|---|---|---|---|---|---|---|---|
| 1 | 12.706 | 6 | 2.447 | 12 | 2.179 | 30 | 2.042 |
| 2 | 4.303 | 7 | 2.365 | 14 | 2.145 | 40 | 2.021 |
| 3 | 3.181 | 8 | 2.306 | 16 | 2.120 | 60 | 2.000 |
| 4 | 2.776 | 9 | 2.262 | 18 | 2.101 | 100 | 1.984 |
| 5 | 2.571 | 10 | 2.228 | 20 | 2.086 | \ (\ infty | 1.960 |
¿Cuáles son los intervalos de confianza del 95% para las dos muestras de centavos en la Tabla 4.4.1 ?
Solución
La media y la desviación estándar para el primer experimento son, respectivamente, 3.117 g y 0.051 g. Debido a que la muestra consta de siete mediciones, hay seis grados de libertad. El valor de t de Table 4.4.5 , es 2.447. Sustituyendo en Ecuación\ ref {4.5} da
\[\mu = 3.117 \text{ g} \pm \frac {2.447 \times 0.051 \text{ g}} {\sqrt{7}} = 3.117 \text{ g} \pm 0.047 \text{ g} \nonumber\]
Para el segundo experimento la media y la desviación estándar son 3.081 g y 0.073 g, respectivamente, con cuatro grados de libertad. El intervalo de confianza del 95% es
\[\mu = 3.081 \text{ g} \pm \frac {2.776 \times 0.037 \text{ g}} {\sqrt{5}} = 3.081 \text{ g} \pm 0.046 \text{ g} \nonumber\]
Con base en el primer experimento, el intervalo de confianza del 95% para la media de la población es de 3.070—3.164 g. Para el segundo experimento, el intervalo de confianza del 95% es de 3.035—3.127 g. Aunque los dos intervalos de confianza no son idénticos, recuerde, cada intervalo de confianza proporciona una estimación diferente para\(\mu\) — la media para cada experimento está contenida dentro del intervalo de confianza del otro experimento. También hay un solapamiento apreciable de los dos intervalos de confianza. Ambas observaciones son consistentes con muestras extraídas de una misma población.
Tenga en cuenta que nuestra comparación de estos dos intervalos de confianza en este punto es algo vaga e insatisfactorio. Volveremos a este punto en la siguiente sección, cuando consideramos un enfoque estadístico para comparar los resultados de los experimentos.
¿Cuál es el intervalo de confianza del 95% para la muestra de 100 centavos en la Tabla 4.4.3 ? La media y la desviación estándar para esta muestra son 3.095 g y 0.0346 g, respectivamente. Compara tu resultado con los intervalos de confianza para las muestras de centavos en la Tabla 4.4.1 .
- Contestar
-
Con 100 centavos, tenemos 99 grados de libertad para la media. Aunque Table 4.4.3 no incluye un valor para t (0.05, 99), podemos aproximar su valor usando los valores para t (0.05, 60) y t (0.05, 100) y asumiendo un cambio lineal en su valor.
\[t(0.05, 99) = t(0.05, 60) - \frac {39} {40} \left\{ t(0.05, 60) - t(0.05, 100\} \right) \nonumber\]
\[t(0.05, 99) = 2.000 - \frac {39} {40} \left\{ 2.000 - 1.984 \right\} = 1.9844 \nonumber\]
El intervalo de confianza del 95% para los centavos es
\[3.095 \pm \frac {1.9844 \times 0.0346} {\sqrt{100}} = 3.095 \text{ g} \pm 0.007 \text{ g} \nonumber\]
Del Ejemplo 4.4.6 , los intervalos de confianza del 95% para las dos muestras en la Tabla 4.4.1 son 3.117 g ± 0.047 g y 3.081 g ± 0.046 g. Como se esperaba, el intervalo de confianza para la muestra de 100 centavos es mucho menor que el de las dos más pequeñas muestras de centavos. Obsérvese, también, que el intervalo de confianza para la muestra más grande se ajusta dentro de los intervalos de confianza para las dos muestras más pequeñas.
Una declaración de precaución
Existe la tentación cuando analizamos datos simplemente para enchufar números en una ecuación, realizar el cálculo y reportar el resultado. Esto nunca es una buena idea, y debes desarrollar el hábito de revisar y evaluar tus datos. Por ejemplo, si analizas cinco muestras y reportas la concentración media de un analito como 0.67 ppm con una desviación estándar de 0.64 ppm, entonces el intervalo de confianza del 95% es
\[\mu = 0.67 \text{ ppm} \pm \frac {2.776 \times 0.64 \text{ ppm}} {\sqrt{5}} = 0.67 \text{ ppm} \pm 0.79 \text{ ppm} \nonumber\]
Este intervalo de confianza estima que la concentración real del analito está entre —0.12 ppm y 1.46 ppm. Incluir una concentración negativa dentro del intervalo de confianza debería llevarte a reevaluar tus datos o tus conclusiones. Un examen más detallado de sus datos puede convencerle de que la desviación estándar es mayor de lo esperado, lo que hace que el intervalo de confianza sea demasiado amplio, o puede concluir que la concentración del analito es demasiado pequeña para reportarlo con confianza.
Volveremos al tema de los límites de detección cerca del final de este capítulo.
Aquí hay un segundo ejemplo de por qué deberías examinar de cerca tus datos: los resultados obtenidos en muestras extraídas al azar de una población normalmente distribuida deben ser aleatorios. Si los resultados de una secuencia de muestras muestran un patrón o tendencia regular, entonces la población subyacente o bien no se distribuye normalmente o hay un error determinado dependiente del tiempo. Por ejemplo, si seleccionamos aleatoriamente 20 centavos y encontramos que la masa de cada centavo es mayor que la del centavo anterior, entonces podríamos sospechar que nuestro saldo se está desviando de la calibración.


