6.10: Uso de Excel y R para resolver problemas de equilibrio
- Page ID
- 75726
Al resolver problemas de equilibrio normalmente hacemos una o más suposiciones para simplificar el álgebra. Estas suposiciones son importantes porque nos permiten reducir el problema a una ecuación en x que podemos resolver simplemente tomando una raíz cuadrada, una raíz de cubo o usando la ecuación cuadrática. Sin estas suposiciones, la mayoría de los problemas de equilibrio resultan en una ecuación cúbica (o una ecuación de orden superior) que es más difícil de resolver. Tanto Excel como R son herramientas útiles para resolver tales ecuaciones.
Aunque aquí nos enfocamos en el uso de Excel y R para resolver problemas de equilibrio, también puede usar WolframAlpha; para más detalles, consulte Cleary, D. A. “Uso de WolframAlpha en los cálculos de equilibrio”, Chem. Educador, 2014, 19, 182—186.
Excel
Excel ofrece una herramienta útil, la función Solver, para encontrar la raíz químicamente significativa de una ecuación polinómica. Además, es fácil resolver un sistema de ecuaciones simultáneas mediante la construcción de una hoja de cálculo que permite probar y evaluar múltiples soluciones. Trabajemos a través de dos ejemplos.
Ejemplo 1: Solubilidad de Pb (IO 3) 2 en Pb 0.10 M (NO 3) 2
En nuestro tratamiento anterior de este problema llegamos a la siguiente ecuación cúbica
\[4 x^{3}+0.40 x^{2}=2.5 \times 10^{-13} \nonumber\]
donde x es la concentración de equilibrio de Pb 2 +. Aunque existen varios enfoques para resolver ecuaciones cúbicas con papel y lápiz, ninguno es computacionalmente fácil. Un enfoque es iterar sobre la respuesta encontrando dos valores de x, uno que lleve a un resultado mayor que\(2.5 \times 10^{-13}\) y otro que dé un resultado menor que\(2.5 \times 10^{-13}\). Con límites establecidos para el valor de x, desplazamos el límite superior y el límite inferior hasta que la precisión de nuestra respuesta sea satisfactoria. Sin entrar en detalles, así es como funciona la función Solver de Excel.
Para resolver este problema, primero reescribimos la ecuación cúbica para que su lado derecho sea igual a cero.
\[4 x^{3}+0.40 x^{2}-2.5 \times 10^{-13}=0 \nonumber\]
A continuación, configuramos la hoja de cálculo que se muestra en la Figura 6.10.1 a, colocando la fórmula para la ecuación cúbica en la celda B2, e ingresando nuestra suposición inicial para x en la celda B1. Debido a que Pb (IO 3) 2 no es muy soluble, esperamos que x sea pequeño y establezca nuestra suposición inicial en 0. Finalmente, accedemos a la función Solver seleccionando Solver... desde el menú Herramientas, que abre la ventana Parámetros del Solver.
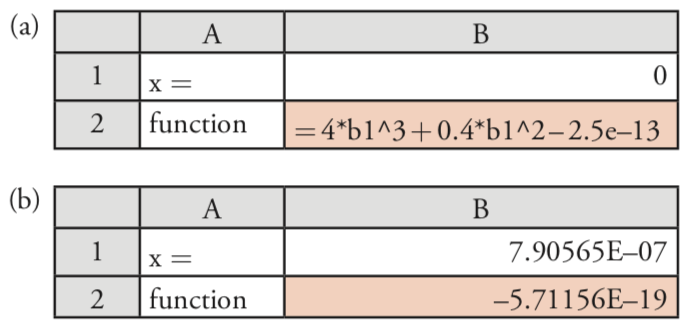
Para definir el problema, coloque el cursor en el cuadro de Establecer celda de destino y luego haga clic en la celda B2. Seleccione el botón de opción Valor de: e ingrese 0 en la casilla. Coloque el cursor en el cuadro de Por cambio de celdas: y haga clic en la celda B1. Juntas, estas acciones instruyen a la función Solver para cambiar el valor de x, que está en la celda B1, hasta que la ecuación cúbica en la celda B2 sea igual a cero. Antes de resolver realmente la función, debemos considerar si hay alguna limitación para un resultado aceptable. Por ejemplo, sabemos que x no puede ser menor que 0 porque no es posible una concentración negativa. También queremos asegurarnos de que la precisión de la solución sea aceptable. Haga clic en el botón etiquetado Opciones... para abrir la ventana Opciones de Solver. Marcar la opción de Asumir no negativo obliga al Solver a mantener un valor positivo para el contenido de la celda B1, cumpliendo con uno de nuestros criterios. Establecer la precisión requiere un poco más de pensamiento. La función Solver utiliza la precisión para decidir cuándo detener su búsqueda, haciéndolo cuando
\[|\text { expected value }-\text { calculated value } | \times 100=\text { precision }(\%) \nonumber\]
donde el valor esperado es el valor deseado de la celda objetivo (0 en este caso), el valor calculado es el valor actual de la función (celda B1 en este caso), y la precisión es el valor que ingresamos en la casilla de Precisión. Debido a que nuestra suposición inicial de x = 0 da un resultado calculado de\(2.5 \times 10^{-13}\), aceptar la precisión predeterminada del Solver\(1 \times 10^{-6}\) detendrá la búsqueda después de un ciclo. Para estar seguros, fijemos la precisión en\(1 \times 10^{-18}\). Haga clic en Aceptar y luego en Solucionar. Cuando la función Solver encuentra una solución, los resultados aparecen en su hoja de cálculo (ver Figura 6.10.1 b). Haga clic en Aceptar para conservar el resultado o en Cancelar para volver a los valores originales. Tenga en cuenta que la respuesta aquí concuerda con nuestro resultado anterior de\(7.91 \times 10^{-7}\) M para la solubilidad de Pb (IO 3) 2.
Asegúrese de evaluar la razonabilidad de la respuesta de Solver. Si es necesario, repita el proceso usando un valor menor para la precisión.
Ejemplo 2: pH de 1.0 M HF
Al desarrollar nuestra solución anterior a este problema comenzamos identificando cuatro incógnitas y escribiendo las siguientes cuatro ecuaciones.
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=6.8 \times 10^{-4} \nonumber\]
\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \nonumber\]
\[C_{\mathrm{HF}}=[\mathrm{HF}]+\left[\mathrm{F}^{-}\right] \nonumber\]
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{F}^{-}\right] \nonumber\]
A continuación, hicimos dos suposiciones que nos permitieron simplificar el problema a una ecuación que es fácil de resolver.
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a}} C_{\mathrm{HF}}}=\sqrt{\left(6.8 \times 10^{-4}\right)(1.0)}=2.6 \times 10^{-2} \nonumber\]
Aunque no lo notamos en su momento, sin hacer suposiciones la solución a nuestro problema es una ecuación cúbica
que podemos resolver usando la función Solver de Excel. ¡Por supuesto, esto supone que completamos con éxito la derivación!
Otra opción es usar Excel para resolver las cuatro ecuaciones simultáneamente iterando en los valores para [HF], [F —], [H 3 O +] y [OH —]. La figura 6.10.2 a muestra una hoja de cálculo para este propósito. Las celdas de la primera fila contienen conjeturas iniciales para el pH de equilibrio. Usando el diagrama de escalera en la Figura 6.8.1, los valores de pH entre 1 y 3 parecen razonables. Puede agregar columnas adicionales si desea incluir más valores de pH. Las fórmulas en las filas 2—5 utilizan la definición de pH para calcular [H 3 O +], K w para calcular [OH —], la ecuación del saldo de carga para calcular [F —] y K a para calcular [HF]. Para evaluar las conjeturas iniciales, utilizamos la expresión de balance de masa para HF, reescribiéndola como
\[[\mathrm{HF}]+\left[\mathrm{F}^{-}\right]-C_{\mathrm{HF}}=[\mathrm{HF}]+[\mathrm{F}]-1.0=0 \nonumber\]
e ingresándolo en la última fila; los valores en estas celdas dan el error del cálculo para cada pH.
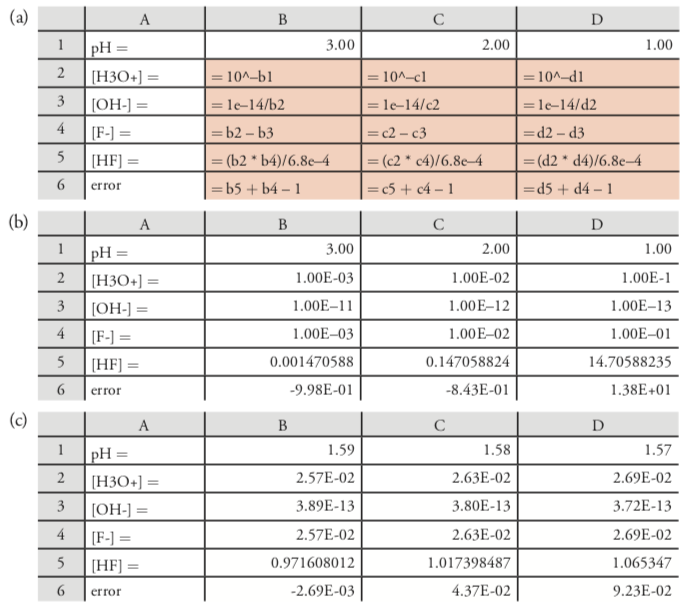
La Figura 6.10.2 b muestra los valores reales para la hoja de cálculo en la Figura 6.10.2 a. El valor negativo en las celdas B6 y C6 significa que las concentraciones combinadas de HF y F — son demasiado pequeñas, y el valor positivo en la celda D6 significa que sus concentraciones combinadas son demasiado grande. El pH real, por lo tanto, está entre 1.00 y 2.00. Usando estos valores de pH como nuevos límites para la primera fila de la hoja de cálculo, continuamos estrechando el rango para el pH real. La figura 6.10.2 c muestra un conjunto final de conjeturas, con el pH real cayendo entre 1.59 y 1.58. Debido a que el error para 1.59 es menor que el de 1.58, aceptamos un pH de 1.59 como respuesta. Obsérvese que se trata de un acuerdo con nuestro resultado anterior.
También puedes resolver este conjunto de ecuaciones simultáneas usando la función Solver de Excel. Para ello, cree la hoja de cálculo en la Figura 6.10.2 a, pero omita todas las columnas que no sean A y B. Seleccione Solver... desde el menú Herramientas y defina el problema usando B6 para Establecer celda de destino, estableciendo su valor deseado en 0 y seleccionando B1 para Cambiando celdas:. Es posible que tengas que jugar con las opciones del Solver para encontrar una solución adecuada al problema, y es aconsejable probar varias conjeturas iniciales diferentes. La función Solver funciona bien para problemas relativamente simples, como encontrar el pH de 1.0 M HF. A medida que los problemas se vuelven más complejos e incluyen más incógnitas, la función Solver se convierte en una herramienta menos confiable para resolver problemas de equilibrio.
Usando Excel, calcula la solubilidad de AGi en 0.10 M NH 3 sin hacer ningún supuesto. Consulte nuestro tratamiento anterior de este problema para conocer las reacciones y constantes de equilibrio relevantes.
- Contestar
-
Para obtener una lista de las reacciones de equilibrio y constantes de equilibrio relevantes, consulte nuestro tratamiento anterior de este problema. Para resolver este problema usando Excel, vamos a configurar la siguiente hoja de cálculo
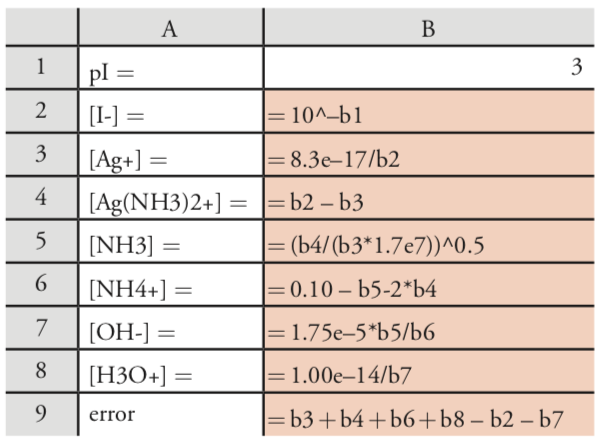
copiar el contenido de las celdas B1‐B9 en varias columnas adicionales. La suposición inicial para pI en la célula B1 da la concentración de I — en la célula B2. Las células B3-B8 calculan las concentraciones restantes, usando la K sp para obtener [Ag +], usando el balance de masas sobre yoduro y plata para obtener [\(\text{Ag(NH}_3)_2^+\)], usando b2 para calcular [NH 3], usando el balance de masas sobre amoníaco para encontrar [\(\text{NH}_4^+\)], usando K b para calcular [OH —], y usando K w para calcular [H 3 O +]. La ecuación de saldo de carga del sistema proporciona un medio para determinar el error del cálculo.
\[\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-\left[\mathrm{I}^{-}\right]+\left[\mathrm{OH}^{-}\right]=0 \nonumber\]
El mayor valor posible para pI, que corresponde a la menor concentración de I — y la menor solubilidad posible, ocurre para una solución simple y saturada de AGi. Cuando [Ag +] = [I —], la concentración de yoduro es
\[\left[\mathrm{I}^{-}\right]=\sqrt{K_{\mathrm{sp}}}=\sqrt{8.3 \times 10^{-17}}=9.1 \times 10^{-9} \nonumber\]
lo que corresponde a un pI de 8.04. Al ingresar conjeturas iniciales para pI de 4, 5, 6, 7 y 8, se muestra que el error cambia de signo entre un pI de 5 y 6. Continuando de esta manera para estrechar el rango para pI, encontramos que la función de error es más cercana a cero a un pI de 5.42. La concentración de I — en equilibrio, y la solubilidad molar de AGi, es\(3.8 \times 10^{-6}\) mol/L, lo que concuerda con nuestra solución anterior a este problema.
R
R tiene un comando simple, uniroot, para encontrar la raíz químicamente significativa de una ecuación polinómica. Además, es fácil escribir una función para resolver un conjunto de ecuaciones simultáneas iterando en una solución. Trabajemos a través de dos ejemplos.
Ejemplo 1: Solubilidad de Pb (IO 3) 2 en Pb 0.10 M (NO 3) 2
En nuestro tratamiento anterior de este problema llegamos a la siguiente ecuación cúbica
\[4 x^{3}+0.40 x^{2}=2.5 \times 10^{-13} \nonumber\]
donde x es la concentración de equilibrio de Pb 2 +. Aunque existen varios enfoques para resolver ecuaciones cúbicas con papel y lápiz, ninguno es computacionalmente fácil. Un enfoque para resolver el problema es iterar sobre la respuesta encontrando dos valores de x, uno que lleve a un resultado mayor que\(2.5 \times 10^{-13}\) y otro que dé un resultado menor que\(2.5 \times 10^{-13}\). Habiendo establecido límites para el valor de x, cambiamos entonces el límite superior y el límite inferior hasta que la precisión de nuestra respuesta sea satisfactoria. Sin entrar en detalles, así es como funciona el comando uniroot.
La forma general del comando uniroot es
uniroot (función, inferior, superior, tol)
donde function es un objeto que contiene la ecuación cuya raíz buscamos, inferior y superior son límites para la raíz, y tol es la precisión deseada para la raíz. Para crear un objeto que contenga la ecuación, la reescribimos de manera que su lado derecho sea igual a cero.
\[4 x^{3}+0.40 x^{2}-2.5 \times 10^{-13} = 0 \nonumber\]
A continuación, ingresamos el siguiente código, que define nuestra ecuación cúbica como una función con el nombre eqn.
> eqn = función (x) {4*x^3 + 0.4*x^2 — 2.5e—13}
Debido a que nuestra ecuación es una función, el comando uniroot puede enviar un valor de x a eqn y recibir el valor correspondiente de la ecuación.
Por ejemplo, ingresando
> eqn (2)
pasa el valor x = 2 a la función y devuelve una respuesta de 33.6.
Finalmente, usamos el comando uniroot para encontrar la raíz.
> uniroot (eqn, inferior = 0, superior = 0.1, tol = 1e—18)
Debido a que Pb (IO 3) 2 no es muy soluble, esperamos que x sea pequeño y establezca el límite inferior en 0. La elección del límite superior es menos crítica. Para asegurar que la solución tenga suficiente precisión, establecemos la tolerancia a un valor que es menor que la raíz esperada. La figura 6.10.3 muestra la salida resultante. El valor $root es la raíz de la ecuación, que está en buena concordancia con nuestro resultado anterior de\(7.91 \times 10^{-7}\) para la solubilidad molar de Pb (IO 3) 2. Los otros resultados son el valor de la ecuación para la raíz, el número de iteraciones necesarias para encontrar la raíz y la precisión estimada de la raíz.
![Salida R que muestra $root; [1] 7.905663e-07; $f.root; [1] 0; $iter; [1] 46; $estim.prec; [1] 1.827271e-12.](https://chem.libretexts.org/@api/deki/files/195630/Figure6.19.png)
Ejemplo 2: pH de 1.0 M HF
Al desarrollar nuestra solución anterior a este problema comenzamos identificando cuatro incógnitas y escribiendo las siguientes cuatro ecuaciones.
\[K_{\mathrm{a}}=\frac{\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{F}^{-}\right]}{[\mathrm{HF}]}=6.8 \times 10^{-4} \nonumber\]
\[K_{w}=\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]\left[\mathrm{OH}^{-}\right]=1.00 \times 10^{-14} \nonumber\]
\[C_{\mathrm{HF}}=[\mathrm{HF}]+\left[\mathrm{F}^{-}\right] \nonumber\]
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\left[\mathrm{OH}^{-}\right]+\left[\mathrm{F}^{-}\right] \nonumber\]
A continuación, hicimos dos suposiciones que nos permitieron simplificar el problema a una ecuación que es fácil de resolver.
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]=\sqrt{K_{\mathrm{a}} C_{\mathrm{HF}}}=\sqrt{\left(6.8 \times 10^{-4}\right)(1.0)}=2.6 \times 10^{-2} \nonumber\]
Aunque no lo notamos en su momento, sin hacer suposiciones la solución a nuestro problema es una ecuación cúbica
\[\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{3}+K_{\mathrm{a}}\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]^{2}- \left(K_{a} C_{\mathrm{HF}}+K_{\mathrm{w}}\right)\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-K_{\mathrm{a}} K_{\mathrm{w}}=0 \nonumber\]
que podemos resolver usando el comando uniroot. ¡Por supuesto, esto supone que completamos con éxito la derivación!
Otra opción es escribir una función para resolver las cuatro ecuaciones simultáneamente. Aquí está el código para esta función, que llamaremos eval.
> eval = función (pH) {
+ h3o = 10^—pH
+ oh = 1e—14/h3o
+ hf = (h3o * f) /6.8e—4
+ error= hf + f — 1
+ salida= data.frame (pH, error)
+ impresión (salida)
+}
Las llaves abiertas, {, le dice a R que pretendemos ingresar a nuestra función sobre varias líneas. Cuando presionamos enter al final de una línea, R cambia su prompt de > a +, indicando que seguimos ingresando el mismo comando. La llave cerrada,}, en la última línea indica que hemos completado la función. El comando data.frame combina dos o más objetos en una tabla, que luego imprimimos para que podamos ver los resultados de los cálculos. Puede adaptar esta función a otros problemas cambiando la variable que pasa a la función y las ecuaciones que incluya dentro de la función.
Examinemos más de cerca cómo funciona esta función. La función acepta una suposición para el pH y utiliza la definición de pH para calcular [H 3 O +], K w para calcular [OH —], la ecuación de equilibrio de carga para calcular [F —] y K a para calcular [HF]. Luego, la función evalúa la solución usando la expresión de balance de masa para HF, reescribiéndola como
\[[\mathrm{HF}]+\left[\mathrm{F}^{-}\right]-C_{\mathrm{HF}}=[\mathrm{HF}]+\left[\mathrm{F}^{-}\right]-1.0=0 \nonumber\]
La función luego reúne la suposición inicial para el pH y el error y los imprime como una tabla.
La belleza de esta función es que el objeto que le pasamos, pH, puede contener muchos valores, lo que facilita la búsqueda de una solución. Debido a que el HF es un ácido, sabemos que la solución es ácida. Esto establece un límite superior de 7 para el pH. También sabemos que el pH de 1.0 M HF no es menor que 0 ya que este es el pH si el HF era un ácido fuerte. Para nuestro primer pase, ingresemos el siguiente código
> pH= c (7, 6, 5, 4, 3, 2, 1)
> eval (pH)
que varía el pH dentro de estos límites. El resultado, que se muestra en la Figura 6.10.4 a, indica que el pH es menor que 2 y mayor que 1 porque es en este intervalo donde el error cambia de signo.
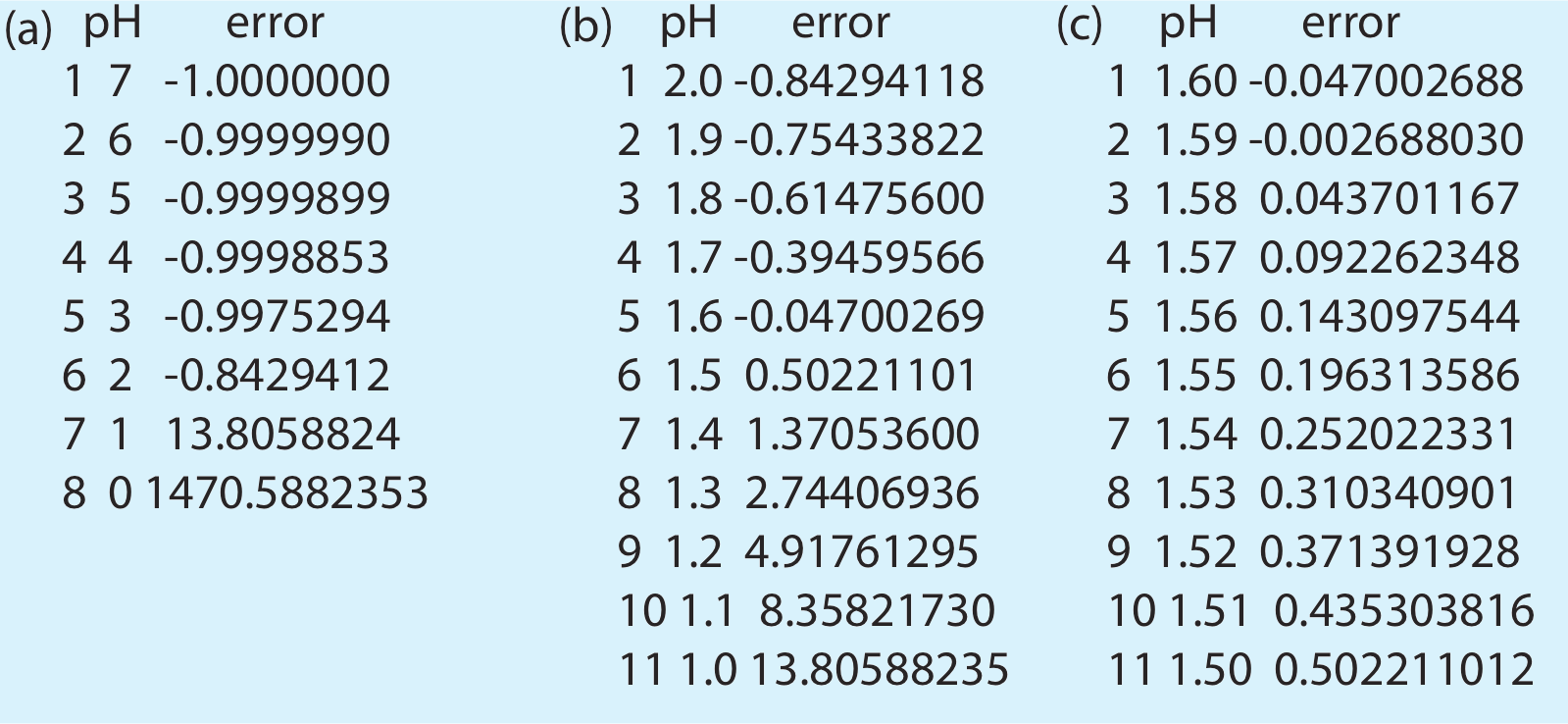
Para nuestra segunda pasada, exploremos valores de pH entre 2.0 y 1.0 para reducir aún más la solución del problema.
> pH = c (2.0, 1.9, 1.8, 1.7, 1.6, 1.5, 1.4, 1.3, 1.2, 1.1, 1.0)
> eval (pH)
El resultado en la Figura 6.10.4 b muestra que el pH debe ser menor que 1.6 y mayor que 1.5. Un tercer paso entre estos límites da el resultado mostrado en la Figura 6.10.4 c, que es consistente con nuestro resultado anterior de un pH 1.59.
Usando R, se calcula la solubilidad de AGi en 0.10 M NH 3 sin hacer ningún supuesto. Consulte nuestro tratamiento anterior de este problema para conocer las reacciones y constantes de equilibrio relevantes.
- Contestar
-
Para resolver este problema, usemos la siguiente función
> eval = función (pI) {
+ I = 10^—Pi
+ Ag = 8.3E—17/i
+ AgNH3 = Ag — I
+ NH3 = (AGNH3/ (1.7E7*Ag)) ^0.5
+ NH4 = 0.10‐NH3 — 2 * AgNH3
+ OH = 1.75e—5 * NH3/NH4
+ H3O = 1E—14/OH
+ error = Ag + AgNH3 + NH4 + H3O — OH — I
+ salida = data.frame (pI, error)
+ impresión (salida)
+}
La función acepta una suposición inicial para pI y calcula las concentraciones de cada especie en solución usando la definición de pI para calcular [I —], usando la K sp para obtener [Ag +], usando el balance de masas sobre yoduro y plata para obtener [\(\text{Ag(NH}_3)_2^+\)], usando \(\beta_2\)para calcular [NH 3], usando el balance de masa sobre amoníaco para encontrar [\(\text{NH}_4^+\)], usando K b para calcular [OH —], y usando K w para calcular [H 3 O +]. La ecuación de saldo de carga del sistema proporciona un medio para determinar el error del cálculo.
\[\left[\mathrm{Ag}^{+}\right]+\left[\mathrm{Ag}\left(\mathrm{NH}_{3}\right)_{2}^{+}\right]+\left[\mathrm{NH}_{4}^{+}\right]+\left[\mathrm{H}_{3} \mathrm{O}^{+}\right]-\left[\mathrm{I}^{-}\right]+\left[\mathrm{OH}^{-}\right]=0 \nonumber\]
El mayor valor posible para PI, que corresponde a la concentración más pequeña de I, y la menor solubilidad posible, ocurre para una solución simple y saturada de AGi. Cuando [Ag +] = [I —], la concentración de yoduro es
\[\left[\mathrm{I}^{-}\right]=\sqrt{K_{\mathrm{sp}}}=\sqrt{8.3 \times 10^{-17}}=9.1 \times 10^{-9} \nonumber\]
correspondiente a un pI de 8.04. En la siguiente sesión se muestra la función en acción.
> pi=C (4, 5, 6, 7, 8)
> eval (pI)
Error de PI
1 4 ‐2.56235615
2 5 ‐0.16620930
3 6 0.07337101
4 7 0.09734824
5 8 0.09989073> pI =c (5.1, 5.2, 5.3, 5.4, 5.5, 5.6, 5.7, 5.8, 5.9, 6.0)
> eval (pI)
Error de PI
1 5.1 ‐0.111446582 5.2 ‐0.06794105
3 5.3 ‐0.03336475
4 5.4 ‐0.00568116
5 5.5 0.01571549
6 5.6 0.03308929
7 5.7 0.04685937
8 5.8 0.05779214
9 5.9 0.06647475
10 6.0 0.07337101> pI =c (5.40, 5.41, 5.42, 5.43, 5.44, 5.45, 5.46, 5.47, 5.48, 5.49, 5.50)
> eval (pI)
Error de pI
1 5.40 ‐0.0056811605
2 5.41 ‐0.0030715484
3 5.42 0.0002310369
4 5.43 ‐0.0005134898
5 5.44 0.0028281878
6 5.45 0.0052370980
7 5.46 0.0074758181
8 5.47 0.0096260370
9 5.48 0.0117105498
10 5.49 0.0137387291
11 5.50 0.0157154889
La función de error es la más cercana a cero a un pI de 5.42. La concentración de I — en equilibrio, y la solubilidad molar de AGi, es\(3.8 \times 10^{-6}\) mol/L, lo que concuerda con nuestra solución anterior a este problema.


