14.1: Optimización del Procedimiento Experimental
- Page ID
- 75331
En presencia de H 2 O 2 y H 2 SO 4, una solución de vanadio forma un color marrón rojizo que se cree que es un compuesto con la fórmula general (VO) 2 (SO 4) 3. La intensidad del color de la solución depende de la concentración de vanadio, lo que significa que podemos usar su absorbancia a una longitud de onda de 450 nm para desarrollar un método cuantitativo para el vanadio.
La intensidad del color de la solución también depende de las cantidades de H 2 O 2 y H 2 SO 4 que añadimos a la muestra; en particular, un gran exceso de H 2 O 2 disminuye la absorbancia de la solución a medida que cambia de un color marrón rojizo a un color amarillento [Vogel's Textbook of Quantitative Inorganic Analysis, Longman: London, 1978, p. 752.]. El desarrollo de un método estándar para vanadio basado en esta reacción requiere optimizar la cantidad de H 2 O 2 y H 2 SO 4 añadidos para maximizar la absorbancia a 450 nm. Utilizando la terminología de los estadísticos, llamamos a la absorbancia de la solución la respuesta del sistema. El peróxido de hidrógeno y el ácido sulfúrico son factores cuyas concentraciones, o niveles de factores, determinan la respuesta del sistema. Para optimizar el método necesitamos encontrar la mejor combinación de niveles de factores. Por lo general se busca una respuesta máxima, como es el caso para el análisis cuantitativo de vanadio como (VO) 2 (SO 4) 3. En otras situaciones, como minimizar el error porcentual de un análisis, buscamos una respuesta mínima.
Volveremos a este método analítico para vanadio en Ejemplo 14.1.4 y Problema 11 de los problemas de fin de capítulo.
Superficies de respuesta
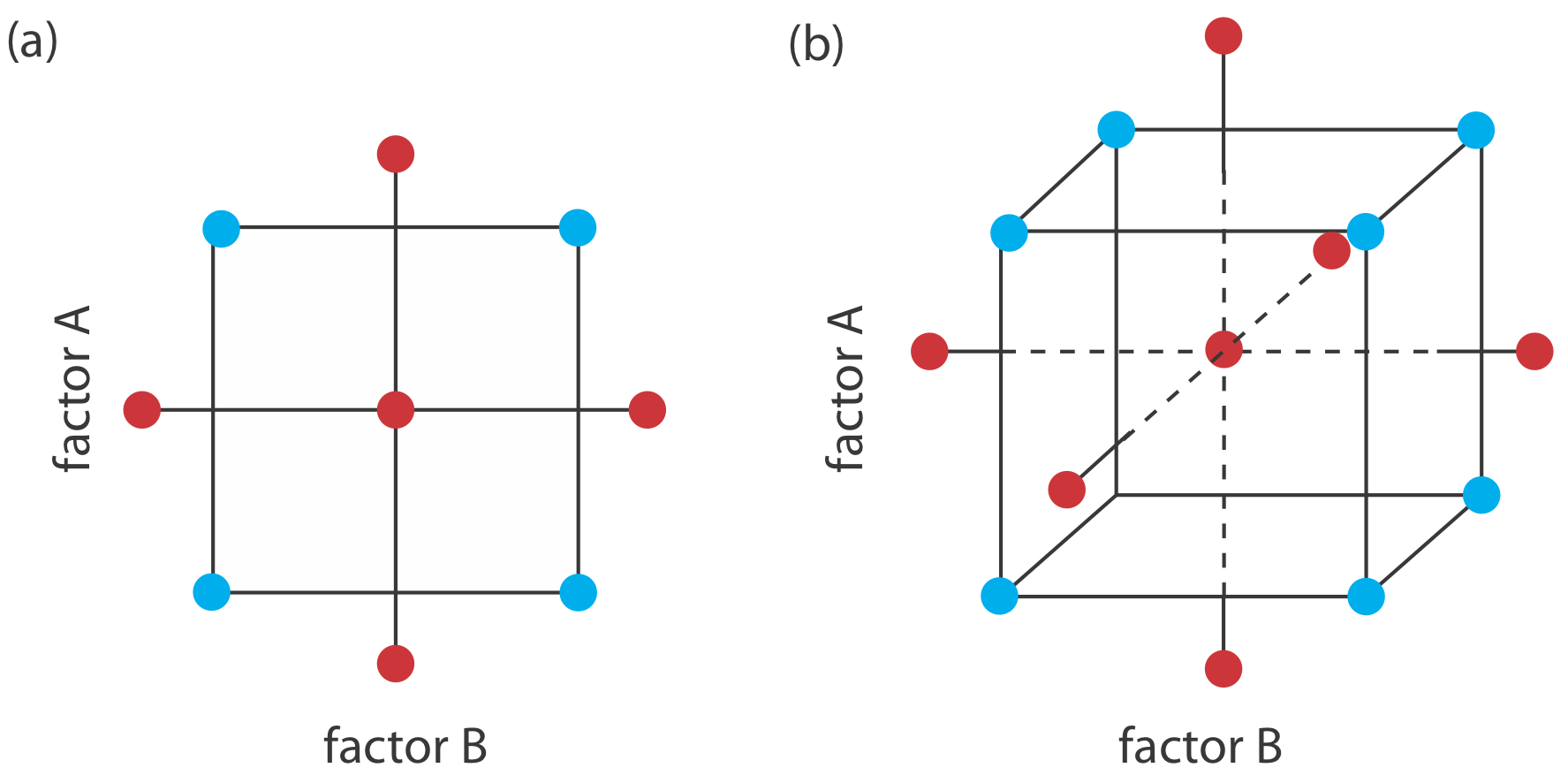
Una de las formas más efectivas de pensar en una optimización es visualizar cómo cambia la respuesta de un sistema cuando aumentamos o disminuimos los niveles de uno o más de sus factores. Llamamos a una gráfica de la respuesta del sistema en función de los niveles factoriales una superficie de respuesta. La superficie de respuesta más simple tiene un factor y se dibuja en dos dimensiones colocando las respuestas en el eje y y los niveles del factor en el eje x. La curva de calibración en la Figura 14.1.1 es un ejemplo de una superficie de respuesta de un factor. También podemos definir matemáticamente la superficie de respuesta. La superficie de respuesta en la Figura 14.1.1 , por ejemplo, es
\[A = 0.008 + 0.0896C_A \nonumber\]
donde A es la absorbancia y C A es la concentración del analito en ppm.
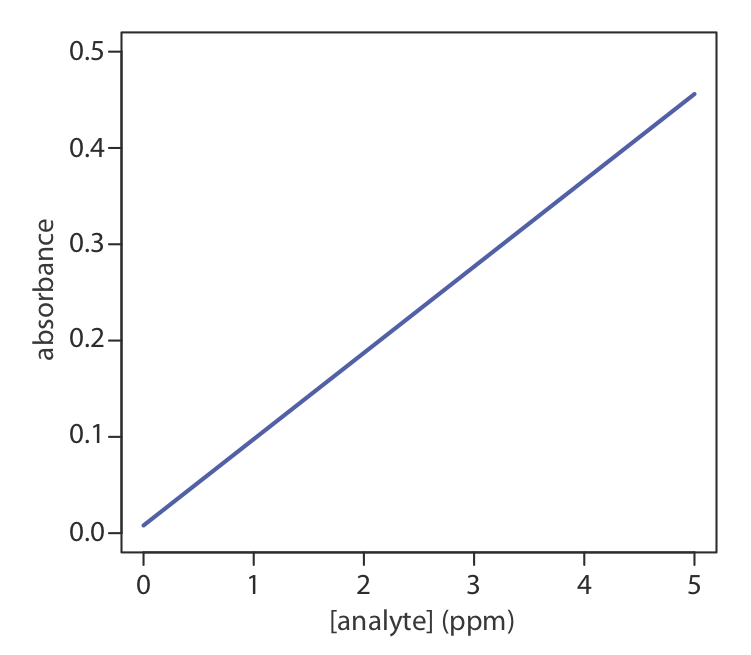
Para un sistema de dos factores, como el análisis cuantitativo para vanadio descrito anteriormente, la superficie de respuesta es un plano plano o curvo en tres dimensiones. Como se muestra en la Figura 14.1.2 a, colocamos la respuesta en el eje z y los niveles de factor en el eje x y el eje y. La figura 14.1.2 a muestra una gráfica de estructura de alambre pseudo-tridimensional para un sistema que obedece a la ecuación
\[R = 3.0 - 0.30A + 0.020AB \nonumber\]
donde R es la respuesta, y A y B son los factores. También podemos representar una superficie de respuesta de dos factores usando la gráfica de nivel bidimensional en la Figura 14.1.2 b, que usa un gradiente de color para mostrar la respuesta en una cuadrícula bidimensional, o usando la gráfica de contorno bidimensional en la Figura 14.1.2 c, que usa curvas de nivel para mostrar la superficie de respuesta.
También podemos superponer una gráfica de nivel y una gráfica de contorno. Vea la Figura 14.1.7 b para un ejemplo típico.
Las superficies de respuesta en la Figura 14.1.2 cubren un rango limitado de niveles de factores (0 ≤ A ≤ 10, 0 ≤ B ≤ 10), pero podemos extender cada uno a valores más positivos o más negativos porque no hay restricciones sobre los factores. La mayoría de las superficies de respuesta de interés para un químico analítico tienen restricciones naturales impuestas por los factores, o tienen límites prácticos establecidos por el analista. La superficie de respuesta en la Figura 14.1.1 , por ejemplo, tiene una restricción natural en su factor porque la concentración del analito no puede ser menor que cero.
Expresamos esta restricción como C A ≥ 0.
Si tenemos una ecuación para la superficie de respuesta, entonces es relativamente fácil encontrar la respuesta óptima. Desafortunadamente, al desarrollar un nuevo método analítico, rara vez conocemos detalles útiles sobre la superficie de respuesta. En cambio, debemos determinar la forma de la superficie de respuesta y ubicar su respuesta óptima realizando experimentos apropiados. El enfoque de esta sección se centra en métodos experimentales útiles para caracterizar una superficie de respuesta. Estos métodos experimentales se dividen en dos amplias categorías: métodos de búsqueda, en los que un algoritmo guía una búsqueda sistemática de la respuesta óptima, y métodos de modelado, en los que se utiliza un modelo teórico o un modelo empírico de la superficie de respuesta para predecir la respuesta óptima.
Búsqueda de algoritmos para superficies de respuesta
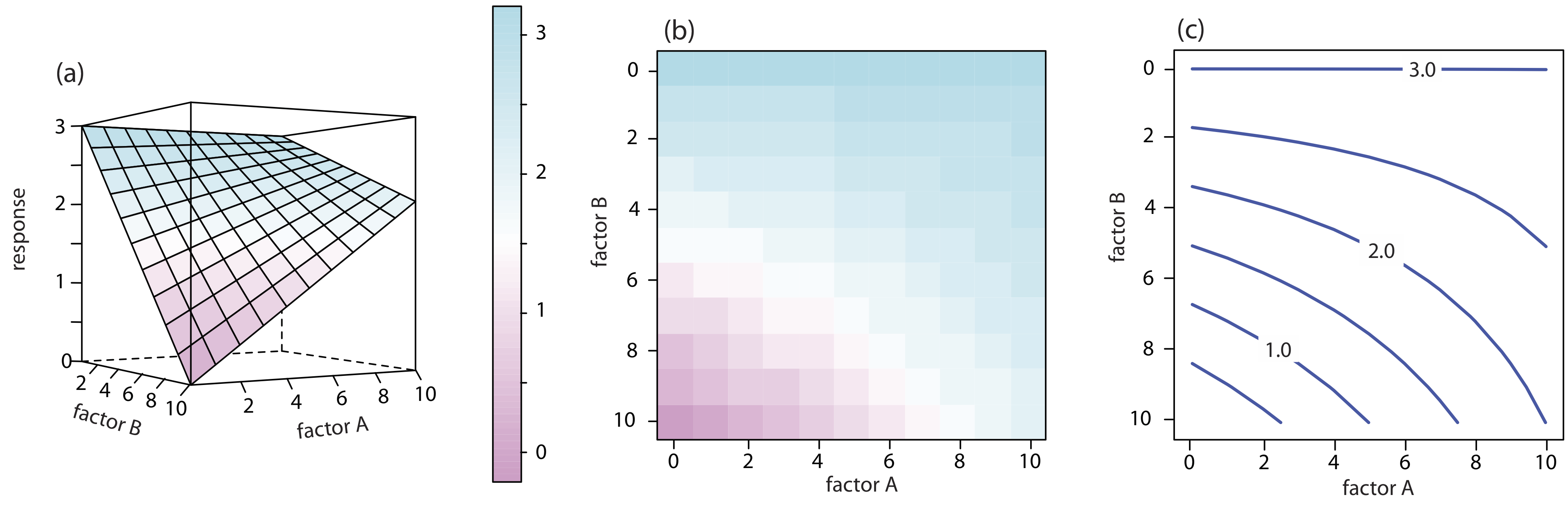
La figura 14.1.3 muestra una porción de las tierras baldías de Dakota del Sur, un paisaje árido que incluye muchas crestas estrechas formadas a través de la erosión. Supongamos que desea subir al punto más alto de esta cresta. Debido a que el camino más corto hasta la cima no es obvio, podrías adoptar la siguiente regla simple: mira a tu alrededor y da un paso en la dirección que tenga el mayor cambio de elevación, para luego repetir hasta que no sea posible más paso. La ruta que sigues es el resultado de una búsqueda sistemática que utiliza un algoritmo de búsqueda. Por supuesto que hay tantas rutas posibles como puntos de partida, tres ejemplos de los cuales se muestran en la Figura 14.1.3 . Tenga en cuenta que algunas rutas no alcanzan el punto más alto, lo que llamamos el óptimo global. En cambio, muchas rutas alcanzan un óptimo local desde el que es imposible seguir moviéndose.
Podemos utilizar un algoritmo de búsqueda sistemática para localizar la respuesta óptima para un método analítico. Comenzamos por seleccionar un conjunto inicial de niveles de factores y medir la respuesta. A continuación, aplicamos las reglas de nuestro algoritmo de búsqueda para determinar un nuevo conjunto de niveles factoriales y medir su respuesta, continuando con este proceso hasta alcanzar una respuesta óptima. Antes de considerar dos algoritmos de búsqueda comunes, consideremos cómo evaluamos un algoritmo de búsqueda.
Eficacia y Eficiencia
Un algoritmo de búsqueda se caracteriza por su efectividad y su eficiencia. Para ser efectivo, un algoritmo de búsqueda debe encontrar el óptimo global de la superficie de respuesta, o al menos llegar a un punto cercano al óptimo global. Un algoritmo de búsqueda puede no encontrar el óptimo global por varias razones, incluyendo un algoritmo mal diseñado, incertidumbre en la medición de la respuesta y la presencia de optima local. Consideremos cada uno de estos problemas potenciales.
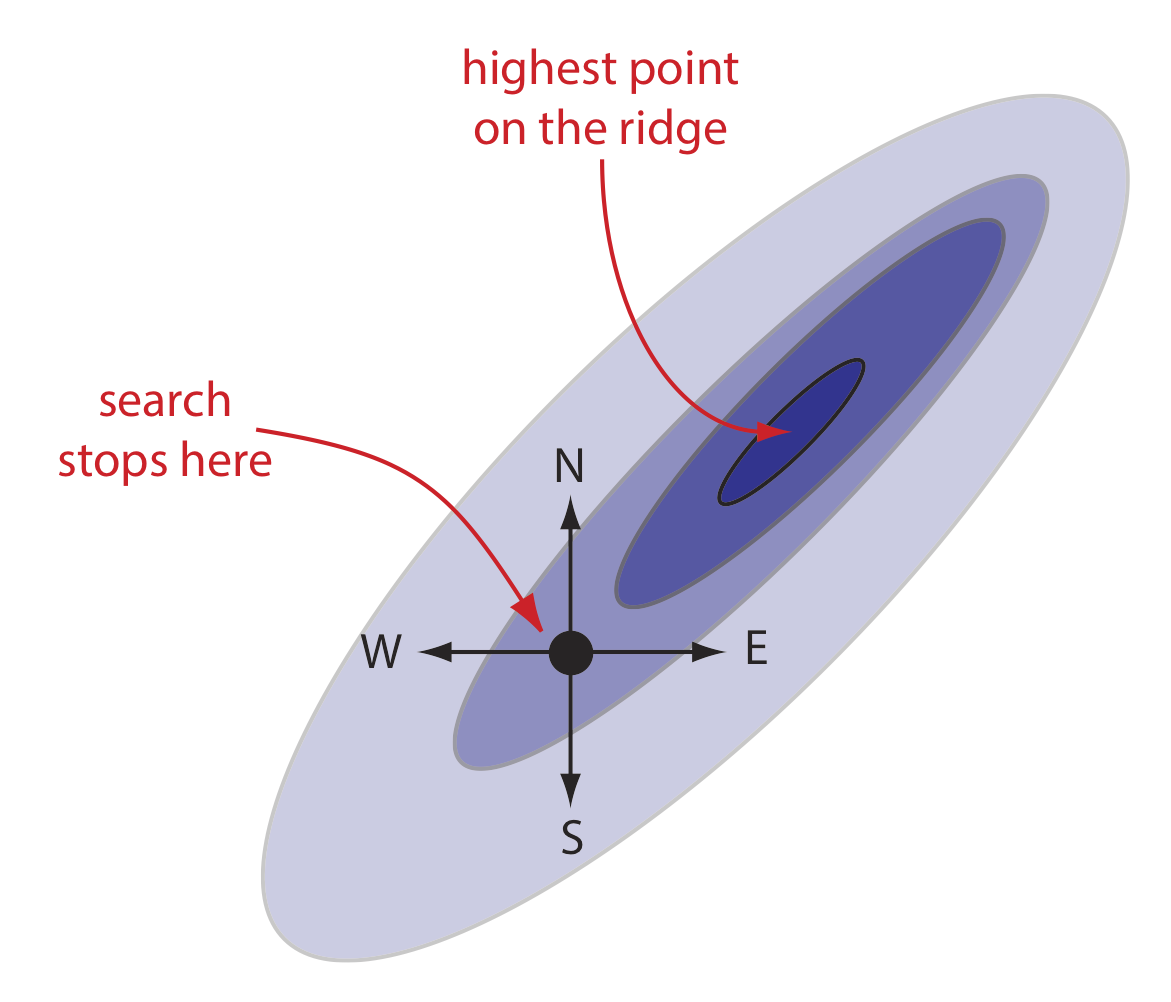
Un algoritmo mal diseñado puede terminar prematuramente la búsqueda antes de que alcance el óptimo global de la superficie de respuesta. Como se muestra en la Figura 14.1.4 , al escalar una cresta que se inclina hacia el noreste, es probable que un algoritmo la falle si limita sus pasos solo hacia el norte, sur, este u oeste. Un algoritmo que no pueda responder a un cambio en la dirección del ascenso más empinado no es un algoritmo efectivo.
Todas las mediciones contienen incertidumbre, o ruido, que afecta nuestra capacidad para caracterizar la señal subyacente. Cuando el ruido es mayor que el cambio local en la señal, entonces es probable que un algoritmo de búsqueda termine antes de que alcance el óptimo global. La Figura 14.1.5 proporciona una vista diferente de la Figura 14.1.3 , que nos muestra que el terreno relativamente plano que conduce a la cresta está muy degradado y muy desigual. Debido a que la variación en la altura local (el ruido) excede la pendiente (la señal), nuestro algoritmo de búsqueda termina la primera vez que nos acercamos a una superficie local menos erosionada.

Finalmente, una superficie de respuesta puede contener varios óptimos locales, solo uno de los cuales es el óptimo global. Si comenzamos la búsqueda cerca de un óptimo local, es posible que nuestro algoritmo de búsqueda nunca llegue al óptimo global. La cresta en la Figura 14.1.3 , por ejemplo, tiene muchos picos. Sólo aquellas búsquedas que comiencen en el extremo derecho llegarán al punto más alto de la cresta. Idealmente, un algoritmo de búsqueda debería alcanzar el óptimo global independientemente de dónde comience.
Un algoritmo de búsqueda siempre alcanza un óptimo. Nuestro problema, por supuesto, es que no sabemos si es el óptimo global. Un método para evaluar la efectividad de un algoritmo de búsqueda es utilizar varios conjuntos de niveles de factores iniciales, encontrar la respuesta óptima para cada uno y comparar los resultados. Si llegamos a o cerca de la misma respuesta óptima después de comenzar desde ubicaciones muy diferentes en la superficie de respuesta, entonces estamos más seguros de que es el óptimo global.
La eficiencia es la segunda característica deseable de un algoritmo de búsqueda. Un algoritmo eficiente se mueve desde el conjunto inicial de niveles de factores a la respuesta óptima en los pocos pasos posibles. Al buscar el punto más alto de la cresta en la Figura 14.1.5 , podemos aumentar la velocidad a la que nos acercamos al óptimo dando pasos más grandes. Sin embargo, si el tamaño del paso es demasiado grande, la diferencia entre el óptimo experimental y el óptimo verdadero puede ser inaceptablemente grande. Una solución es ajustar el tamaño del paso durante la búsqueda, usando pasos más grandes al principio y pasos más pequeños a medida que nos acercamos al óptimo global.
Optimización de un factor a la vez
Un algoritmo simple para optimizar el método cuantitativo para vanadio descrito anteriormente es seleccionar concentraciones iniciales para H 2 O 2 y H 2 SO 4 y medir la absorbancia. A continuación, optimizamos un reactivo aumentando o disminuyendo su concentración, manteniendo constante la concentración del segundo reactivo, hasta que disminuya la absorbancia. Luego variamos la concentración del segundo reactivo, manteniendo la concentración óptima del primer reactivo, hasta que ya no vemos un aumento en la absorbancia. Podemos detener este proceso, al que llamamos optimización de un factor a la vez, después de un ciclo o repetir los pasos hasta que la absorbancia alcance un valor máximo o supere un valor umbral aceptable.
Una optimización de un factor a la vez es consistente con la noción de que para determinar la influencia de un factor debemos mantener constantes todos los demás factores. Este es un diseño experimental efectivo, aunque no necesariamente eficiente cuando los factores son independientes [Sharaf, M. A.; Illman, D. L.; Kowalski, B. R. Chemometrics, Wiley-Interscience: New York, 1986]. Dos factores son independientes cuando un cambio en el nivel de un factor no influye en el efecto de un cambio en el nivel del otro factor. Table 14.1.1 proporciona un ejemplo de dos factores independientes.
| factor A | factor B | respuesta |
|---|---|---|
| \(A_1\) | \(B_1\) | 40 |
| \(A_2\) | \(B_1\) | 80 |
| \(A_1\) | \(B_2\) | 60 |
| \(A_2\) | \(B_2\) | 100 |
Si mantenemos el factor B en el nivel B 1, cambiar el factor A del nivel A1 al nivel A2 aumenta la respuesta de 40 a 80, o un cambio en la respuesta,\(\Delta R\) de
\[R = 80 - 40 = 40 \nonumber\]
Si mantenemos el factor B en el nivel B 2, encontramos que tenemos el mismo cambio de respuesta cuando el nivel de factor A cambia de A1 a A2.
\[R = 100 - 60 = 40 \nonumber\]
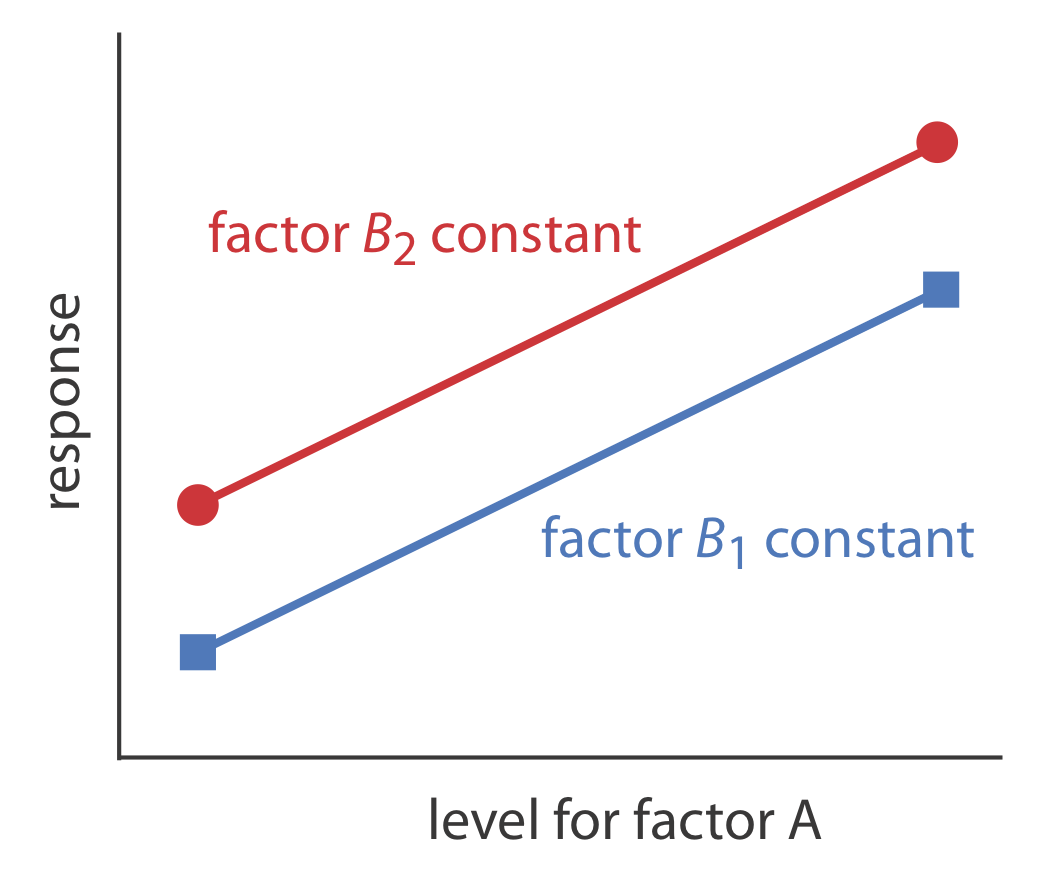
Podemos ver esta independencia visualmente si trazamos la respuesta en función del nivel del factor A' s, como se muestra en la Figura 14.1.6 . Las líneas paralelas muestran que el nivel de factor B no influye en el efecto del factor A' s sobre la respuesta.
Utilizando los datos de la Tabla 14.1.1 , mostrar que el efecto del factor B sobre la respuesta es independiente del factor A.
- Contestar
-
Si mantenemos el factor A en el nivel A1, cambiar el factor B del nivel B 1 al nivel B2 aumenta la respuesta de 40 a 60, o un cambio,\(\Delta R\), de
\[\Delta R = 60 - 40 = 20 \nonumber\]
Si mantenemos el factor A en el nivel A 2, encontramos que tenemos el mismo cambio en la respuesta cuando el nivel de factor B cambia de B 1 a B 2.
\[\Delta R = 100 - 80 = 20 \nonumber\]
Matemáticamente, dos factores son independientes si no aparecen en el mismo término en la ecuación que describe la superficie de respuesta. La ecuación 14.1.1 , por ejemplo, describe una superficie de respuesta con factores independientes porque ningún término en la ecuación incluye tanto el factor A como el factor B.
\[R = 2.0 + 0.12 A + 0.48 B - 0.03A^2 - 0.03 B^2 \label{14.1}\]
La Figura 14.1.7 muestra la superficie pseudo-tridimensional resultante y un mapa de contorno para la Ecuación\ ref {14.1}.
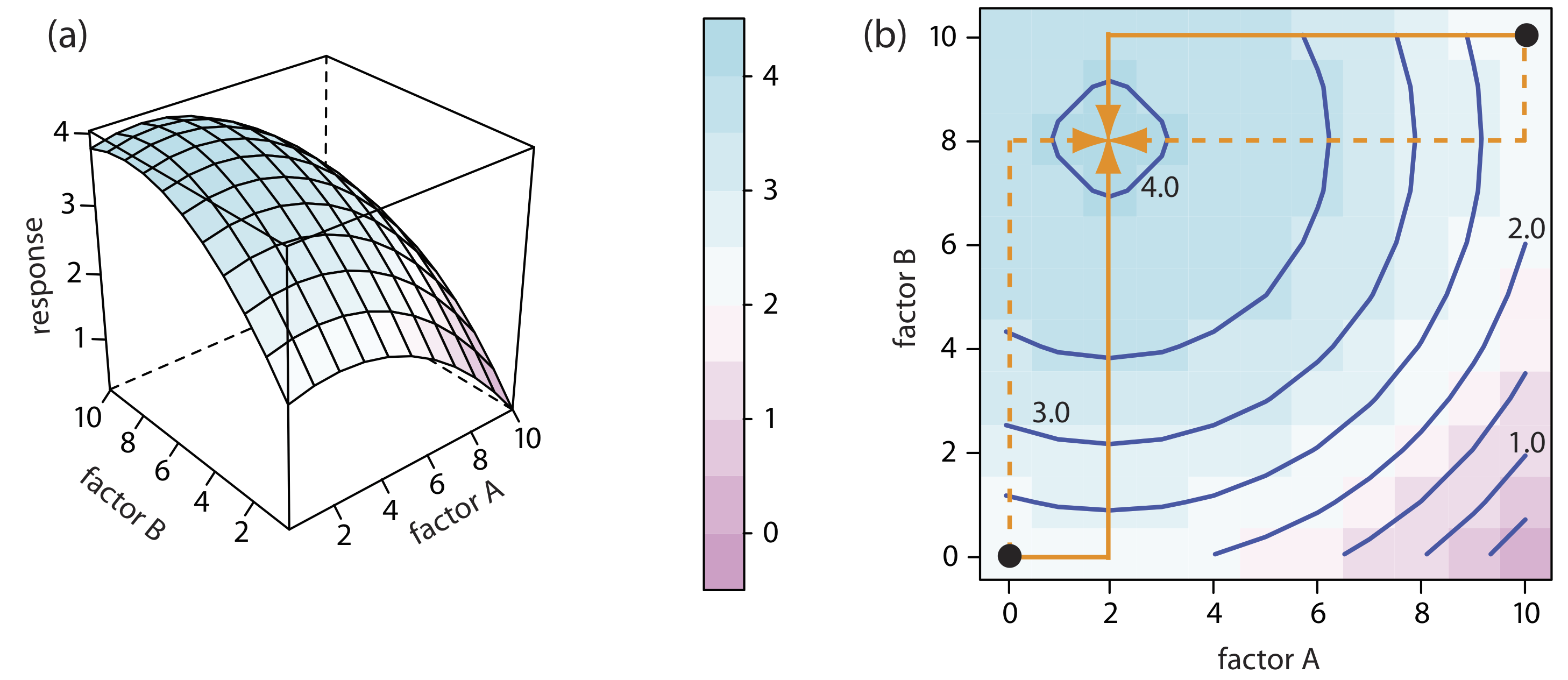
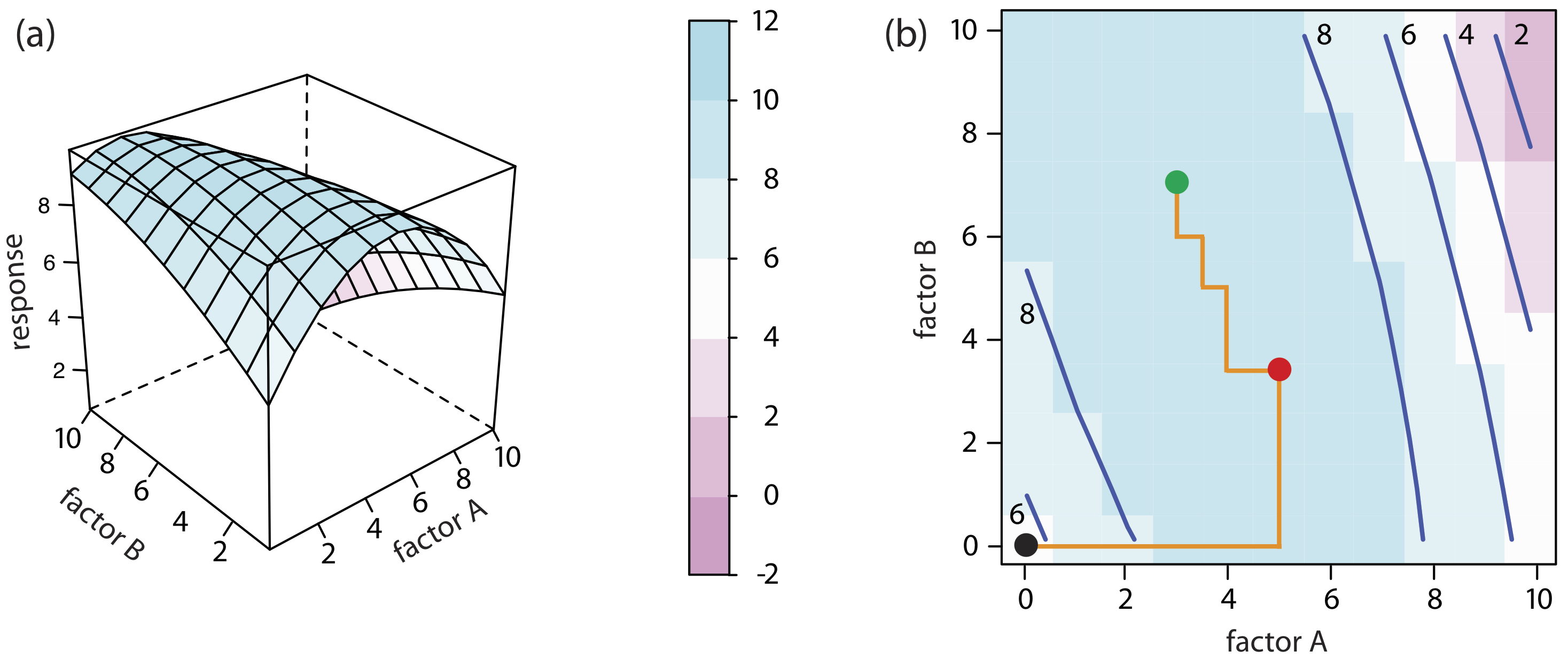
La forma más fácil de seguir el progreso de un algoritmo de búsqueda es mapear su ruta en una gráfica de contorno de la superficie de respuesta. Las posiciones en la superficie de respuesta se identifican como (a, b) donde a y b son los niveles para el factor A y para el factor B. La gráfica de contorno en la Figura 14.1.7 b, por ejemplo, muestra cuatro optimizaciones de un factor a la vez de la superficie de respuesta para la Ecuación\ ref {14.1}. La efectividad y eficiencia de este algoritmo a la hora de optimizar factores independientes es clara: cada ensayo alcanza la respuesta óptima en (2, 8) en un solo ciclo.
Desafortunadamente, los factores a menudo no son independientes. Considere, por ejemplo, los datos en la Tabla 14.1.2
| factor A | factor B | respuesta |
|---|---|---|
| \(A_1\) | \(B_1\) | 20 |
| \(A_2\) | \(B_1\) | 80 |
| \(A_1\) | \(B_2\) | 60 |
| \(A_2\) | \(B_2\) | 80 |
donde un cambio en el nivel de factor B del nivel B 1 al nivel B2 tiene un efecto significativo en la respuesta cuando el factor A está en el nivel A1
\[R = 60 - 20 = 40 \nonumber\]
pero ningún efecto cuando el factor A está en el nivel A 2.
\[R = 80 - 80 = 0 \nonumber\]
La figura 14.1.8 muestra esta relación dependiente entre los dos factores. Se dice que los factores que son dependientes interactúan y la ecuación para la superficie de respuesta' incluye un término de interacción que contiene tanto el factor A como el factor B. El término final en la ecuación 14.1.2 , por ejemplo, da cuenta de la interacción entre el factor A y el factor B.
\[R = 5.5 + 1.5 A + 0.6 B - 0.15 A^2 - 0.245 B^2 - 0.0857 AB \label{14.2}\]
La Figura 14.1.9 muestra la superficie pseudo-tridimensional resultante y un mapa de contorno para la Ecuación\ ref {14.2}.
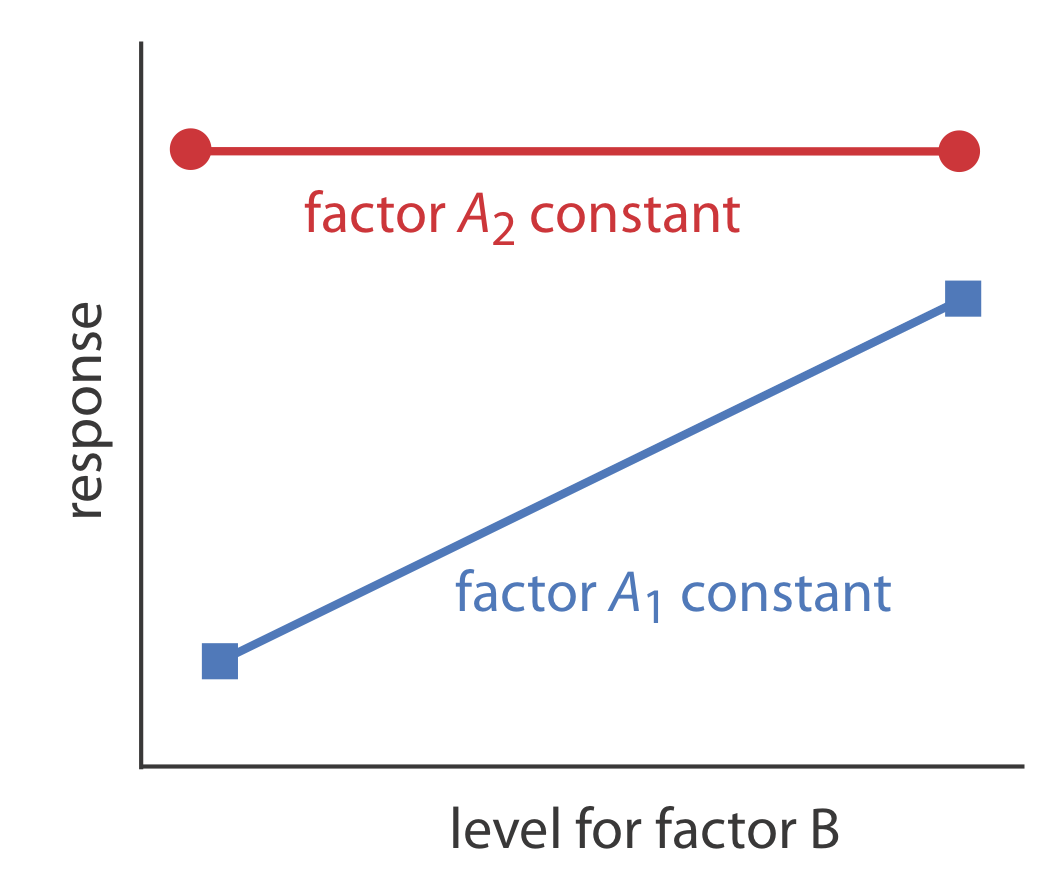
Usando los datos de la Tabla 14.1.2 , mostrar que el efecto del factor A sobre la respuesta depende del factor B.
- Contestar
-
Si mantenemos el factor B en el nivel B 1, cambiar el factor A del nivel A1 al nivel A2 aumenta la respuesta de 20 a 80, o un cambio,\(\Delta R\), de
\[\Delta R = 80 - 20 = 60 \nonumber\]
Si mantenemos el factor B en el nivel B 2, encontramos que el cambio en la respuesta cuando el nivel de factor A cambia de A1 a A2 es ahora 20.
\[\Delta R = 80 - 60 = 20 \nonumber\]
El progreso de una optimización de un factor a la vez para la Ecuación\ ref {14.2} se muestra en la Figura 14.1.9 b. Aunque la optimización para factores dependientes es efectiva, es menos eficiente que para factores independientes. En este caso se necesitan cuatro ciclos para alcanzar la respuesta óptima de (3, 7) si comenzamos en (0, 0).
Optimización Simplex
Una estrategia para mejorar la eficiencia de un algoritmo de búsqueda es cambiar más de un factor a la vez. Una manera conveniente de lograr esto cuando hay dos factores es comenzar con tres conjuntos de niveles de factores iniciales como los vértices de un triángulo. Después de medir la respuesta para cada conjunto de niveles de factores, identificamos la combinación que da la peor respuesta y la reemplazamos por un nuevo conjunto de niveles de factores usando un conjunto de reglas (Figura 14.1.10 ). Este proceso continúa hasta alcanzar el óptimo global o hasta que no sea posible una mayor optimización. El conjunto de niveles de factores se llama simplex. En general, para k factores un simplex es una figura geométrica\(k + 1\) dimensional [(a) Spendley, W.; Hext, G. R.; Himsworth, F. R. Technometrics 1962, 4, 441—461; (b) Deming, S. N.; Parker, L. R. CRC Crit. Rev. Anal. Chem. 1978 7 (3), 187—202].
Así, para dos factores el simplex es un triángulo. Por tres factores el simplex es un tetraedro.
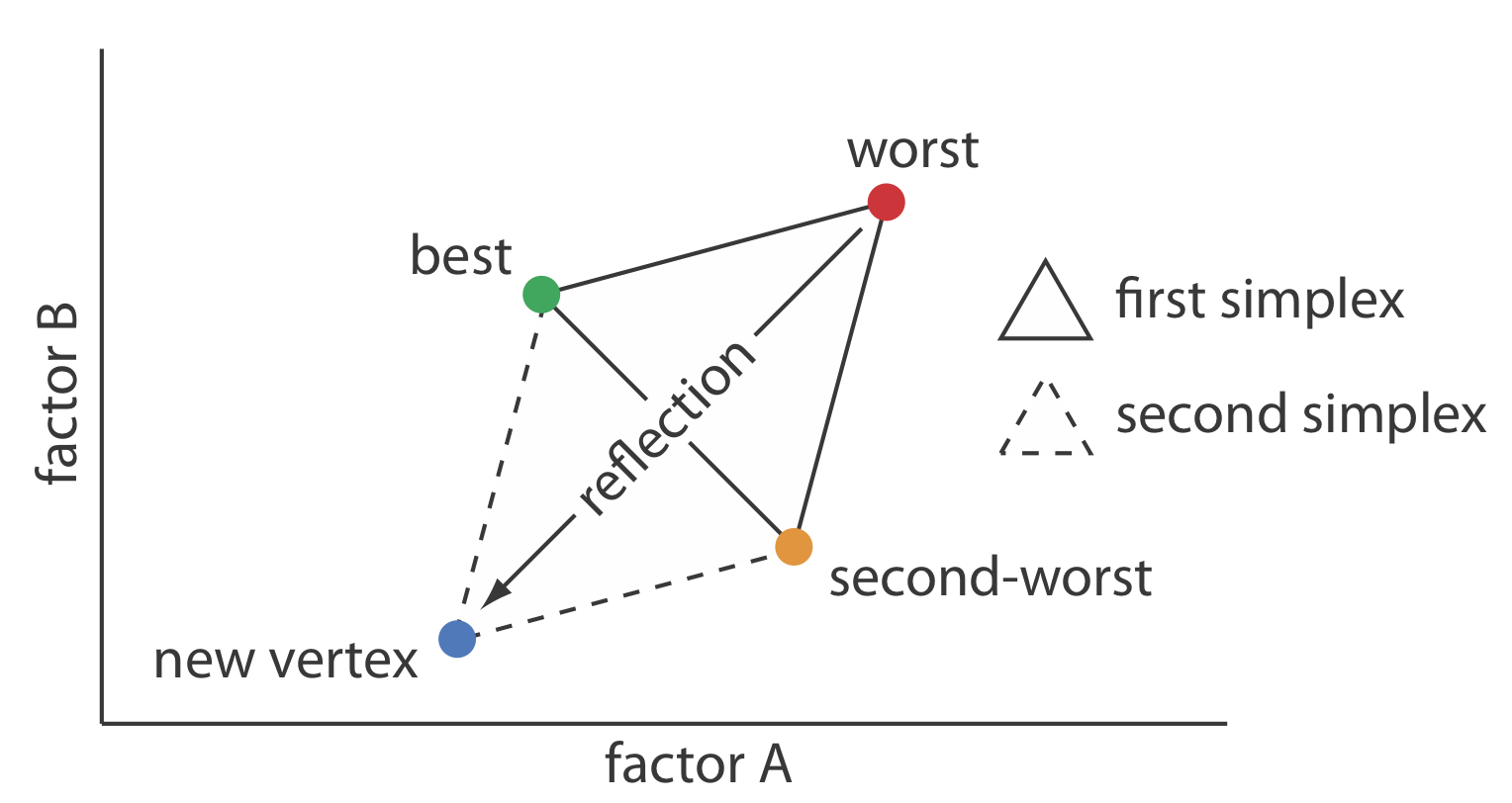
Para colocar el simplex inicial de dos factores en la superficie de respuesta, elegimos un punto de partida (a, b) para el primer vértice y colocamos los dos vértices restantes en (a + s a, b) y (a + 0. 5s a, b + 0. 87s b) donde s a y s b son tamaños de paso para el factor A y para el factor B [Largo, D. E. Anal. Chim. Acta 1969, 46, 193—206]. El siguiente conjunto de reglas mueve el simplex a través de la superficie de respuesta en busca de la respuesta óptima:
Regla 1. Clasificar los vértices de mejor (v b) a peor (v w).
Regla 2. Rechazar el peor vértice (v w) y reemplazarlo por un nuevo vértice (v n) reflejando el peor vértice a través del punto medio de los vértices restantes. Los niveles de factor del nuevo vértice son el doble de los niveles de factor promedio para los vértices retenidos menos los niveles de factor para el peor vértice. Para una optimización de dos factores, las ecuaciones se muestran aquí donde v s es el tercer vértice.
\[a_{v_n} = 2 \left( \frac {a_{v_b} + a_{v_s}} {2} \right) - a_{v_w} \label{14.3}\]
\[b_{v_n} = 2 \left( \frac {b_{v_b} + b_{v_s}} {2} \right) - b_{v_w} \label{14.4}\]
Regla 3. Si el nuevo vértice tiene la peor respuesta, entonces regresa al vértice anterior y rechaza el vértice con la segunda peor respuesta, (v s) calculando los niveles de factor del nuevo vértice usando la regla 2. Esta regla asegura que el simplex no regrese al simplex anterior.
Regla 4. Las condiciones de contorno son una forma útil de limitar el rango de posibles niveles de factores. Por ejemplo, puede ser necesario limitar la concentración de un factor por razones de solubilidad, o limitar la temperatura porque un reactivo es térmicamente inestable. Si el nuevo vértice excede una condición de límite, entonces asígnele la peor respuesta y siga la regla 3.
Las variables a y b en la Ecuación\ ref {14.3} y Ecuación\ ref {14.4} son los niveles de factor para el factor A y para el factor B, respectivamente. El problema 3 en los problemas de fin de capítulo le pide derivar estas ecuaciones.
Debido a que el tamaño del simplex permanece constante durante la búsqueda, este algoritmo se denomina optimización simplex de tamaño fijo. El ejemplo 14.1.1 ilustra la aplicación de estas reglas.
Encuentre el óptimo para la superficie de respuesta en la Figura 14.1.9 usando el algoritmo de búsqueda simplex de tamaño fijo. Use (0, 0) para los niveles de factor iniciales y establezca el tamaño de paso de cada factor en 1.00.
Solución
Dejando a = 0, b =0, s a = 1.00, y s b = 1.00 da los vértices para el simplex inicial como
\[\text{vertex 1:} (a, b) = (0, 0) \nonumber\]
\[\text{vertex 2:} (a + s_a, b) = (1.00, 0) \nonumber\]
\[\text{vertex 3:} (a + 0.5s_a, b + 0.87s_b) = (0.50, 0.87) \nonumber\]
Las respuestas, de la Ecuación\ ref {14.2}, para los tres vértices se muestran en la siguiente tabla
| vértice | a | b | respuesta |
|---|---|---|---|
| \(v_1\) | 0 | 0 | 5.50 |
| \(v_2\) | 1.00 | 0 | 6.85 |
| \(v_3\) | 0.50 | 0.87 | 6.68 |
con\(v_1\) dar la peor respuesta y\(v_3\) la mejor respuesta. Siguiendo la Regla 1, la rechazamos\(v_1\) y reemplazamos por un nuevo vértice usando la Ecuación\ ref {14.3} y la Ecuación\ ref {14.4}; así
\[a_{v_4} = 2 \left( \frac {1.00 + 0.50} {2} \right) - 0 = 1.50 \nonumber\]
\[b_{v_4} = 2 \left( \frac {0 + 0.87} {2} \right) - 0 = 0.87 \nonumber\]
La siguiente tabla da los vértices del segundo simplex.
| vértice | a | b | respuesta |
|---|---|---|---|
| \(v_2\) | 1.50 | 0 | 6.85 |
| \(v_3\) | 0.50 | 0.87 | 6.68 |
| \(v_4\) | 1.50 | 0.87 | 7.80 |
con\(v_3\) dar la peor respuesta y\(v_4\) la mejor respuesta. Siguiendo la Regla 1, la rechazamos\(v_3\) y reemplazamos por un nuevo vértice usando la Ecuación\ ref {14.3} y la Ecuación\ ref {14.4}; así
\[a_{v_5} = 2 \left( \frac {1.00 + 1.50} {2} \right) - 0.50 = 2.00 \nonumber\]
\[b_{v_5} = 2 \left( \frac {0 + 0.87} {2} \right) - 0.87 = 0 \nonumber\]
La siguiente tabla da los vértices del tercer simplex.
| vértice | a | b | respuesta |
|---|---|---|---|
| \(v_2\) | 1.50 | 0 | 6.85 |
| \(v_4\) | 1.50 | 0.87 | 780 |
| \(v_5\) | 2.00 | 0 | 7.90 |
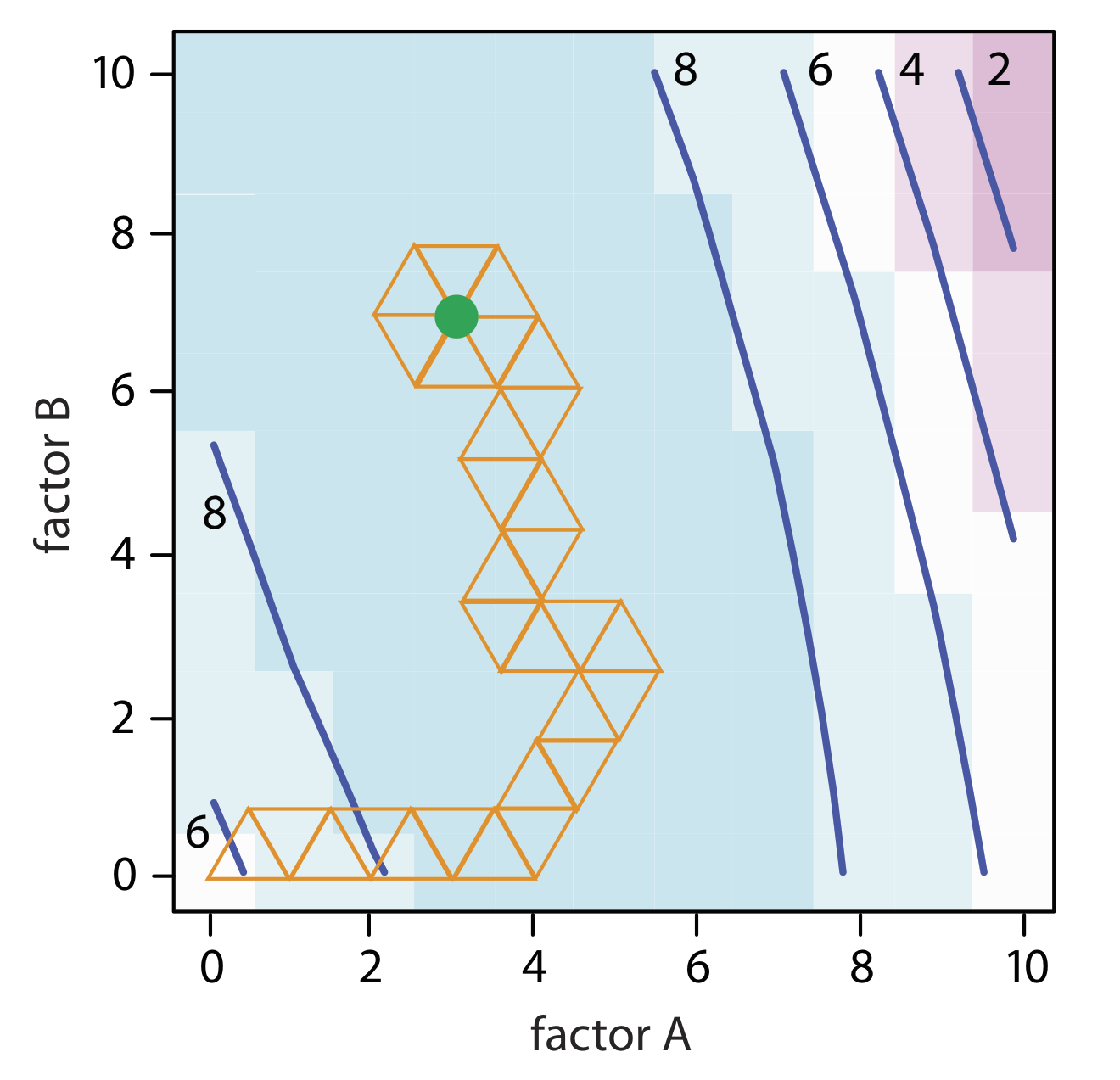
El cálculo de los vértices restantes se deja como ejercicio. La figura 14.1.11 muestra el progreso de la optimización completa. Después de 29 pasos el simplex comienza a repetirse, dando vueltas alrededor de la respuesta óptima de (3, 7).
El tamaño del simplex inicial finalmente limita la efectividad y la eficiencia de un algoritmo de búsqueda simplex de tamaño fijo. Podemos aumentar su eficiencia permitiendo que el tamaño del simplex se expanda o contraiga en respuesta a la tasa a la que nos acercamos al óptimo. Por ejemplo, si encontramos que un nuevo vértice es mejor que cualquiera de los vértices en el simplex anterior, entonces expandimos el simplex más en esta dirección asumiendo que nos estamos moviendo directamente hacia el óptimo. Otras condiciones podrían hacer que contratemos lo simple, para hacerlo más pequeño, para fomentar la optimización para avanzar en una dirección diferente. Llamamos a esto una optimización simplex de tamaño variable. Consulte los recursos adicionales de este capítulo para obtener más detalles sobre la optimización simplex de tamaño variable.
Modelos matemáticos de superficies de respuesta
Una superficie de respuesta se describe matemáticamente mediante una ecuación que relaciona la respuesta con sus factores. La ecuación\ ref {14.1} y la ecuación\ ref {14.2} proporcionan dos ejemplos de tales modelos matemáticos. Si medimos la respuesta para varias combinaciones de niveles factoriales, entonces podemos modelar la superficie de respuesta usando un análisis de regresión para ajustar una ecuación apropiada a los datos. Existen dos amplias categorías de modelos que podemos utilizar para un análisis de regresión: modelos teóricos y modelos empíricos.
Modelos teóricos de la superficie de respuesta
Un modelo teórico se deriva de las relaciones químicas y físicas conocidas entre la respuesta y sus factores. En espectrofotometría, por ejemplo, la ley de Beer es un modelo teórico que relaciona la absorbancia de un analito, A, con su concentración, C A
\[A = \epsilon b C_A \nonumber\]
donde\(\epsilon\) es la absortividad molar y b es la longitud de trayectoria de la radiación electromagnética que pasa a través de la muestra. Una curva de calibración de la ley de Beer, por lo tanto, es un modelo teórico de una superficie de respuesta.
Para una revisión de la ley de Beer, véase el Capítulo 10.2. La figura 14.1.1 de este capítulo es un ejemplo de una curva de calibración de la ley de Beer.
Modelos empíricos de la superficie de respuesta
En muchos casos se desconoce la relación teórica subyacente entre la respuesta y sus factores. Todavía podemos desarrollar un modelo de superficie de respuesta si hacemos algunas suposiciones razonables sobre la relación subyacente entre los factores y la respuesta. Por ejemplo, si creemos que los factores A y B son independientes y que cada uno solo tiene un efecto de primer orden en la respuesta, entonces la siguiente ecuación es un modelo adecuado.
\[R = \beta_0 + \beta_a A + \beta_b B \nonumber\]
donde R es la respuesta, A y B son los niveles de factores, y\(\beta_0\)\(\beta_a\), y\(\beta_b\) son parámetros ajustables cuyos valores están determinados por un análisis de regresión lineal. Otros ejemplos de ecuaciones incluyen aquellos para factores dependientes
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \nonumber\]
y aquellos con términos de orden superior.
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{aa} A^2 + \beta_{bb} B^2 \nonumber\]
Cada una de estas ecuaciones proporciona un modelo empírico de la superficie de respuesta porque no tiene base en una comprensión teórica de la relación entre la respuesta y sus factores. Aunque un modelo empírico puede proporcionar una excelente descripción de la superficie de respuesta en un rango limitado de niveles factoriales, no tiene base teórica y no podemos extenderla de manera confiable a partes inexploradas de la superficie de respuesta.
Los cálculos para una regresión lineal cuando el modelo es de primer orden en un factor (una línea recta) se describen en el Capítulo 5.4. Un tratamiento matemático completo de la regresión lineal para modelos que son de segundo orden en un factor o que contienen más de un factor está fuera del alcance de este texto. Los cálculos para algunos casos especiales, sin embargo, son sencillos y se consideran en esta sección. Un tratamiento más integral de la regresión lineal está disponible en varios de los recursos adicionales de este capítulo.
Diseños factoriales
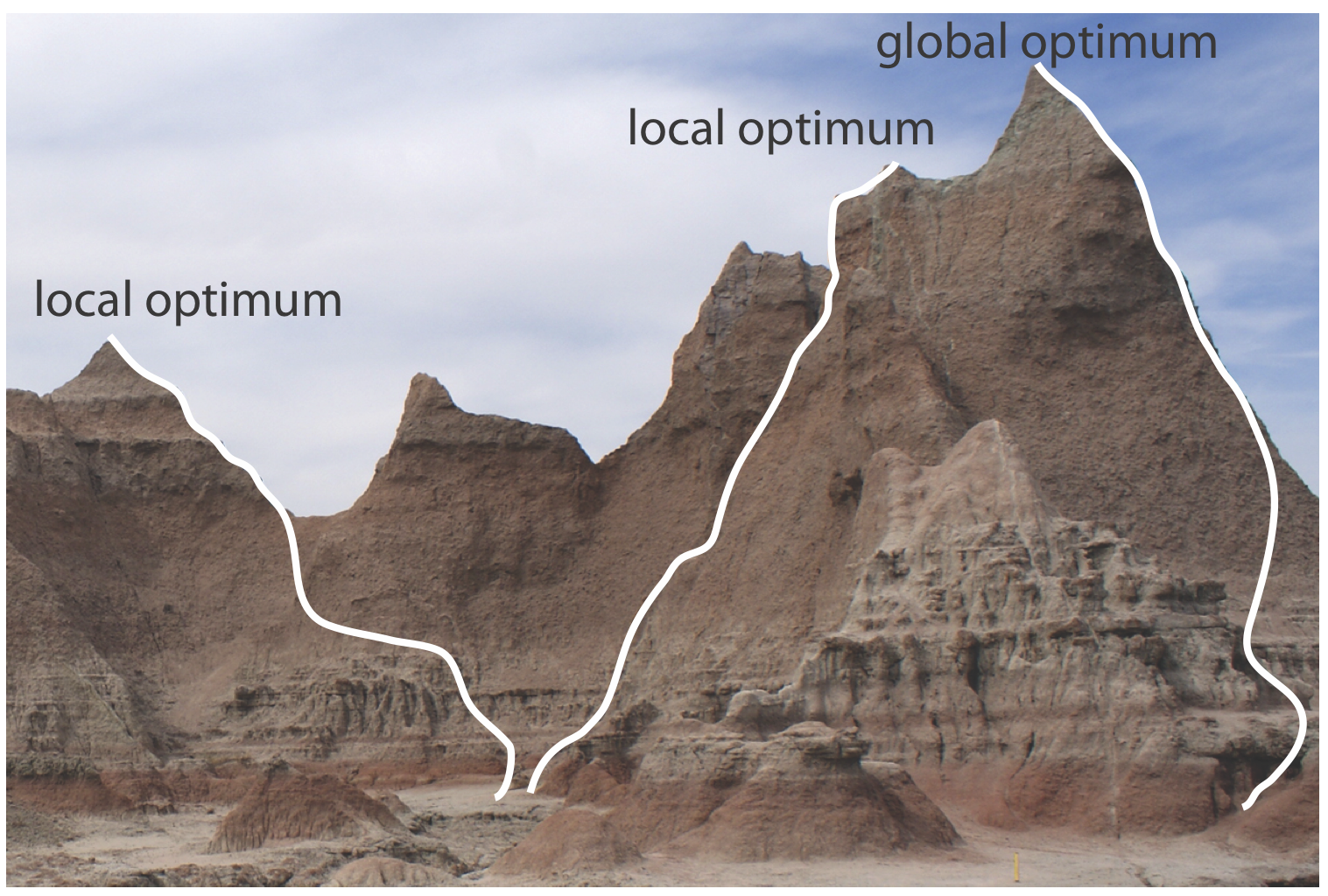
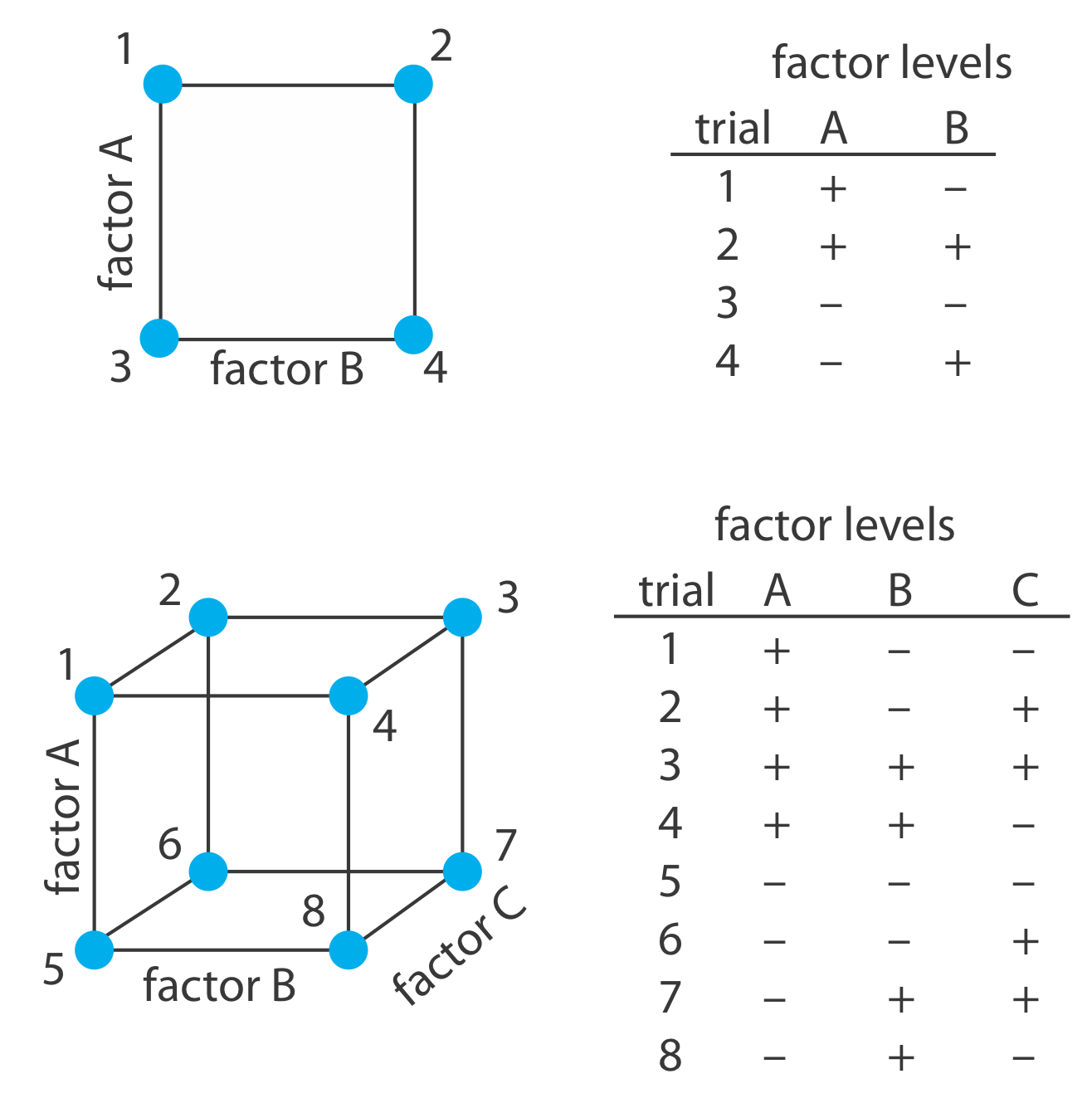
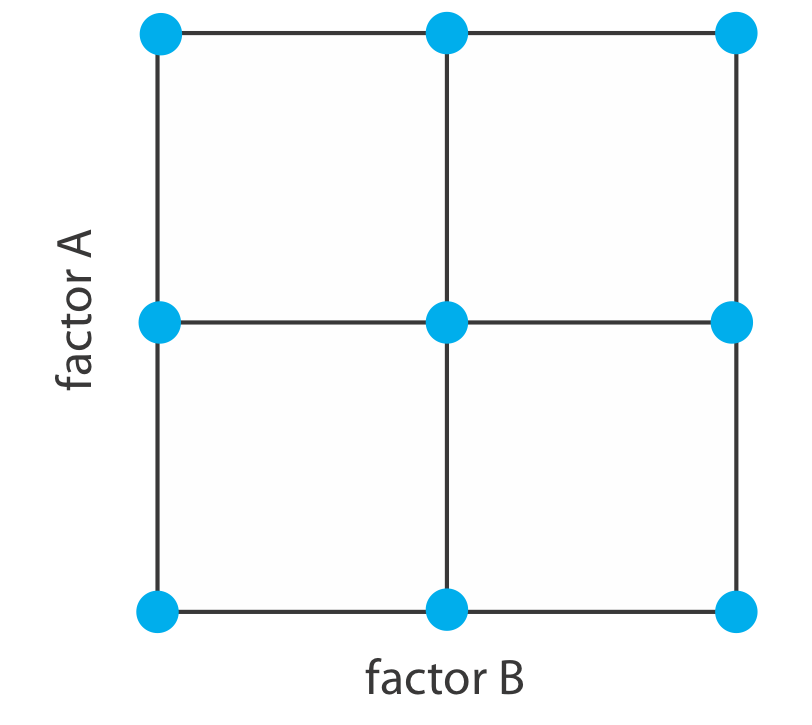
Para construir un modelo empírico medimos la respuesta para al menos dos niveles para cada factor. Por conveniencia etiquetamos estos niveles como alto, H f, y bajo, L f, donde f es el factor; así H A es el nivel alto para el factor A y L B es el nivel bajo para el factor B. Si nuestro modelo empírico contiene más de un factor, entonces el nivel alto de cada factor se empareja tanto con el nivel alto como con el nivel bajo para todos los demás factores. De la misma manera, el nivel bajo para cada factor se empareja con el nivel alto y el nivel bajo para todos los demás factores. Como se muestra en la Figura 14.1.12 , esto requiere 2 k experimentos donde k es el número de factores. Este diseño experimental se conoce como un diseño factorial de 2 k.
Otro sistema de notación es usar un signo más (+) para indicar el nivel alto de un factor y un signo menos (—) para indicar su nivel bajo. Usaremos H o L al escribir una ecuación y un signo más o un signo menos en tablas.
Niveles de Factor Codificado
Los cálculos para un diseño factorial de 2 k son sencillos y fáciles de completar con una calculadora o una hoja de cálculo. Para simplificar los cálculos, codificamos los niveles de factores usando\(+1\) para un nivel alto y\(-1\) para un nivel bajo. La codificación tiene dos ventajas adicionales: escalar los factores a la misma magnitud facilita la evaluación de la importancia relativa de cada factor, y coloca la intercepción del modelo\(\beta_0\), en el centro del diseño experimental. Como se muestra en el Ejemplo 14.1.2 , es fácil convertir entre niveles de factores codificados y no codificados.
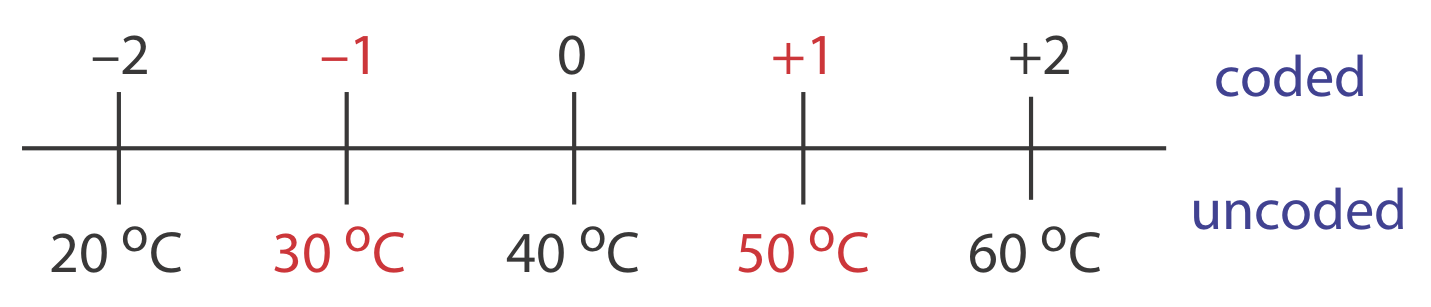
Para explorar el efecto de la temperatura en una reacción, asignamos 30 o C a un nivel de factor codificado\(-1\) y asignamos un nivel codificado\(+1\) a una temperatura de 50 o C. Qué temperatura corresponde a un nivel codificado de\(-0.5\) y cuál es el nivel codificado para una temperatura de 60 o C?
Solución
La diferencia entre\(-1\) y\(+1\) es 2, y la diferencia entre 30 o C y 50 o C es 20 o C; así, cada unidad en forma codificada es equivalente a 10 o C en forma no codificada. Con esta información, es fácil crear una escala simple entre los valores codificados y los no codificados, como se muestra en la Figura 14.1.13 . Una temperatura de 35 o C corresponde a un nivel codificado de\(-0.5\) y un nivel codificado de\(+2\) corresponde a una temperatura de 60 o C.
Determinar el modelo empírico
Comencemos considerando un ejemplo sencillo que involucra dos factores, A y B, y el siguiente modelo empírico.
\[R = \beta_0 + \beta_a A + \beta_b B + \beta_{ab} AB \label{14.5}\]
Un diseño factorial de 2 k con dos factores requiere cuatro corridas. La Tabla 14.1.3 proporciona los niveles no codificados (A y B), los niveles codificados (A * y B *) y las respuestas (R) para estos experimentos. Los términos\(\beta_0\),\(\beta_a\),\(\beta_b\), y\(\beta_{ab}\) en la Ecuación\ ref {14.5} explican, respectivamente, el efecto medio (que es la respuesta promedio), los efectos de primer orden debidos al factor A y al factor B, y la interacción entre los dos factores.
La ecuación\ ref {14.5} tiene cuatro desconocidas, los cuatro términos beta, y la Tabla 14.1.3 describe los cuatro experimentos. Tenemos la información suficiente para calcular los valores de\(\beta_0\),\(\beta_a\),\(\beta_b\), y\(\beta_{ab}\). Al trabajar con los niveles de factores codificados, los valores de estos parámetros son fáciles de calcular utilizando las siguientes ecuaciones, donde n es el número de corridas.
\[\beta_{0} \approx b_{0}=\frac{1}{n} \sum_{i=1}^{n} R_{i} \label{14.6}\]
\[\beta_{a} \approx b_{a}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} R_{i} \label{14.7}\]
\[\beta_{b} \approx b_{b}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} R_{i} \label{14.8}\]
\[\beta_{ab} \approx b_{ab}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} R_{i} \label{14.9}\]
Resolviendo para los parámetros estimados usando los datos de la Tabla 14.1.3
\[b_{0}=\frac{22.5+11.5+17.5+8.5}{4}=15.0 \nonumber\]
\[b_{a}=\frac{22.5+11.5-17.5-8.5}{4}=2.0 \nonumber\]
\[b_{b}=\frac{22.5-11.5+17.5-8.5}{4}=5.0 \nonumber\]
\[b_{ab}=\frac{22.5-11.5-17.5+8.5}{4}=0.5 \nonumber\]
nos deja con el modelo empírico codificado para la superficie de respuesta.
\[R = 15.0 + 2.0 A^* + 5.0 B^* + 0.05 A^* B^* \label{14.10}\]
Recordemos que introdujimos niveles de factores codificados con la promesa de que simplifican los cálculos. Aunque podemos convertir este modelo codificado a su forma no codificada, no hay necesidad de hacerlo. Si necesitamos conocer la respuesta para un nuevo conjunto de niveles de factores, simplemente los convertimos en forma codificada y calculamos la respuesta. Por ejemplo, si A es 10 y B es 15, entonces A * es 0 y B * es —0.5. Sustituir estos valores en la Ecuación\ ref {14.10} da una respuesta de 12.5.
Podemos extender este enfoque a cualquier número de factores. Para un sistema con tres factores —A, B y C — podemos utilizar un diseño factorial 2 3 para determinar los parámetros en el siguiente modelo empírico
donde A, B y C son los niveles de factores. Los términos\(\beta_0\),\(\beta_a\),\(\beta_b\), y\(\beta_{ab}\) se estiman usando la Ecuación\ ref {14.6}, Ecuación\ ref {14.7}, Ecuación\ ref {14.8} y Ecuación\ ref {14.9}, respectivamente. Para encontrar estimaciones para los parámetros restantes utilizamos las siguientes ecuaciones.
\[\beta_{c} \approx b_{c}=\frac{1}{n} \sum_{i=1}^{n} C^*_{i} R \label{14.12}\]
\[\beta_{ac} \approx b_{ac}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} C^*_{i} R \label{14.13}\]
\[\beta_{bc} \approx b_{bc}=\frac{1}{n} \sum_{i=1}^{n} B^*_{i} C^*_{i} R \label{14.14}\]
\[\beta_{abc} \approx b_{abc}=\frac{1}{n} \sum_{i=1}^{n} A^*_{i} B^*_{i} C^*_{i} R \label{14.15}\]
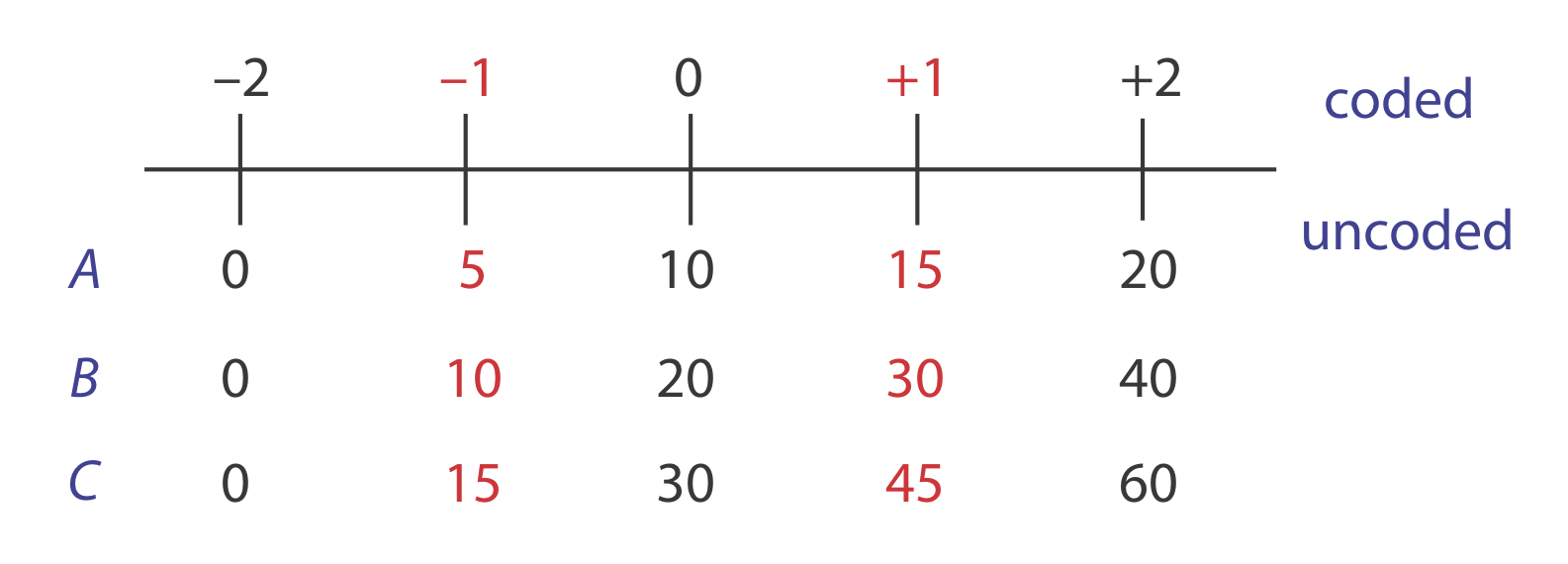
La tabla 14.1.4 enumera los niveles de factores no codificados, los niveles de factores codificados y las respuestas para un diseño factorial de 2 3. Determinar el modelo empírico codificado para la superficie de respuesta basado en la Ecuación\ ref {14.11}. ¿Cuál es la respuesta esperada cuando A es 10, B es 15 y C es 50?
Solución
La ecuación\ ref {14.11} tiene ocho desconocidas, los ocho términos beta, y la Tabla 14.1.4 describe ocho experimentos. Tenemos la información suficiente para calcular valores para\(\beta_0\),\(\beta_a\),\(\beta_b\),\(\beta_{ab}\),\(\beta_{ac}\)\(\beta_{bc}\), y\(\beta_{abc}\); estos valores son
\[b_{0}=\frac{1}{8} \times(137.25+54.75+73.75+30.25+61.75+30.25+41.25+18.75 )=56.0 \nonumber\]
\[b_{a}=\frac{1}{8} \times(137.25+54.75+73.75+30.25-61.75-30.25-41.25-18.75 )=18.0 \nonumber\]
\[b_{b}=\frac{1}{8} \times(137.25+54.75-73.75-30.25+61.75+30.25-41.25-18.75 )=15.0 \nonumber\]
\[b_{c}=\frac{1}{8} \times(137.25-54.75+73.75-30.25+61.75-30.25+41.25-18.75 )=22.5 \nonumber\]
\[b_{ab}=\frac{1}{8} \times(137.25+54.75-73.75-30.25-61.75-30.25+41.25+18.75 )=7.0 \nonumber\]
\[b_{ac}=\frac{1}{8} \times(137.25-54.75+73.75-30.25-61.75+30.25-41.25+18.75 )=9.0 \nonumber\]
\[b_{bc}=\frac{1}{8} \times(137.25-54.75-73.75+30.25+61.75-30.25-41.25+18.75 )=6.0 \nonumber\]
\[b_{abc}=\frac{1}{8} \times(137.25-54.75-73.75+30.25-61.75+30.25+41.25-18.75 )=3.75 \nonumber\]
El modelo empírico codificado, por lo tanto, es
\[R = 56.0 + 18.0 A^* + 15.0 B^* + 22.5 C^* + 7.0 A^* B^* + 9.0 A^* C^* + 6.0 B^* C^* + 3.75 A^* B^* C^* \nonumber\]
Para encontrar la respuesta cuando A es 10, B es 15 y C es 50, primero convertimos estos valores en su forma codificada. Figura 14.1.14 nos ayuda a realizar las conversiones adecuadas; así, A * es 0, B * es\(-0.5\) y C * es\(+1.33\). Sustituir de nuevo al modelo empírico da una respuesta de
\[R = 56.0 + 18.0 (0) + 15.0 (-0.5) + 22.5 (+1.33) + 7.0 (0) (-0.5) + 9.0 (0) (+1.33) + 6.0 (-0.5) (+1.33) + 3.75 (0) (-0.5) (+1.33) = 74.435 \approx 74.4 \nonumber\]
Un diseño factorial de 2 k solo puede modelar el efecto de primer orden de un factor, incluyendo interacciones de primer orden, sobre la respuesta. Un diseño factorial 2 2, por ejemplo, incluye el efecto de primer orden de cada factor (\(\beta_a\)y\(\beta_b\)) y una interacción de primer orden entre los factores (\(\beta_{ab}\)). Un diseño factorial de 2 k no puede modelar efectos de orden superior porque no hay suficiente información. Aquí hay un ejemplo sencillo que ilustra el problema. Supongamos que necesitamos modelar un sistema en el que la respuesta sea una función de un solo factor, A. La Figura 14.1.15 a muestra el resultado de un experimento utilizando un diseño factorial 2 1. El único modelo empírico que podemos ajustar a los datos es una línea recta.
\[R = \beta_0 + \beta_a A \nonumber\]
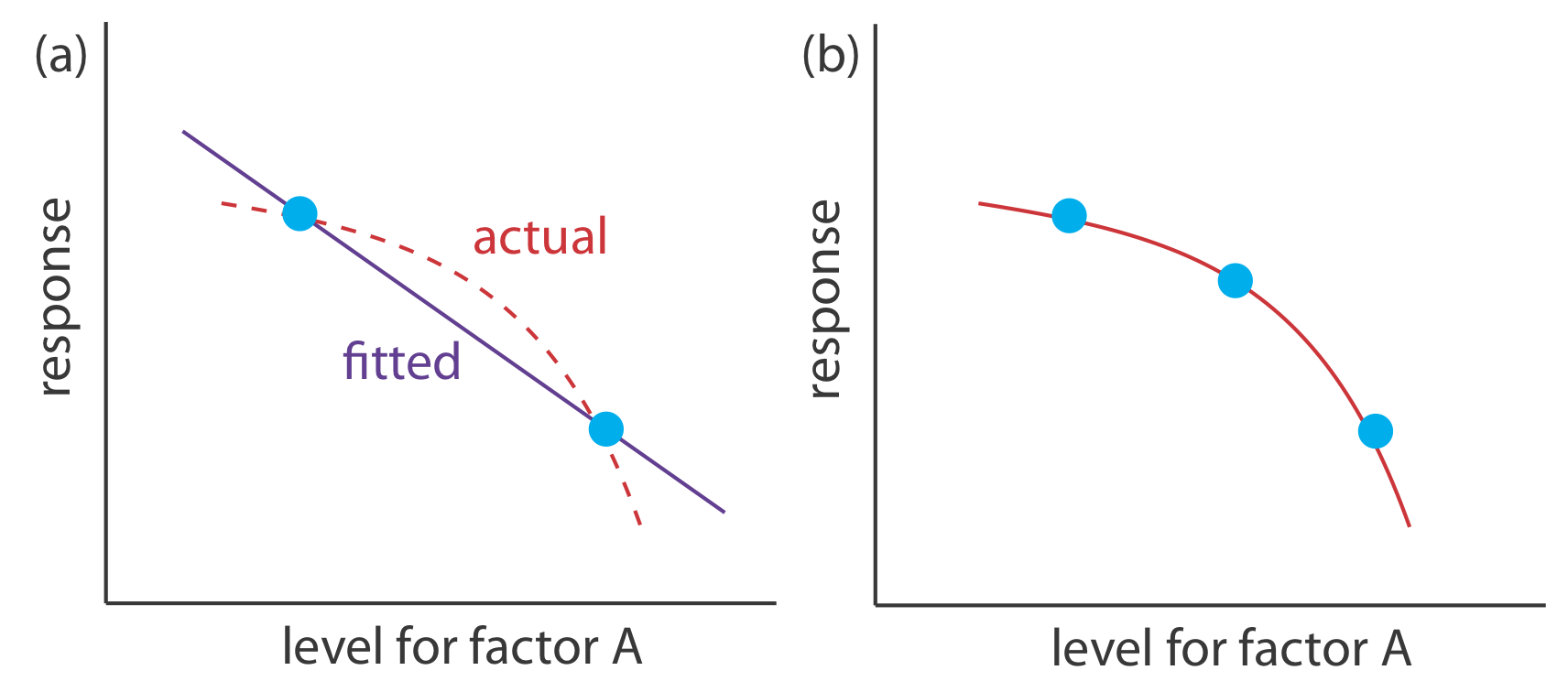
Si la respuesta real es una curva en lugar de una línea recta, entonces el modelo empírico está en error. Para ver evidencias de curvatura debemos medir la respuesta para al menos tres niveles por cada factor. Podemos ajustar el diseño factorial de 3 1 en la Figura 14.1.15 b a un modelo empírico que incluye efectos factoriales de segundo orden.
\[R = \beta_0 + \beta_a A + \beta_{aa} A^2 \nonumber\]
En general, un diseño factorial de nivel n puede modelar términos de factor único e interacción hasta el orden (n — 1) th.
Podemos juzgar la efectividad de un modelo empírico de primer orden midiendo la respuesta en el centro del diseño factorial. Si no hay efectos de orden superior, entonces la respuesta promedio de los ensayos en un diseño factorial de 2 k debe ser igual a la respuesta medida en el centro del diseño factorial. Para dar cuenta de la influencia de los errores aleatorios realizamos varias determinaciones de la respuesta en el centro del diseño factorial y establecemos un intervalo de confianza adecuado. Si la diferencia entre las dos respuestas es significativa, entonces un modelo empírico de primer orden probablemente sea inapropiado.
Una de las ventajas de trabajar con un modelo empírico codificado es que b 0 es la respuesta promedio de los ensayos de 2\(\times\) k en un diseño factorial de 2 k.
Un método para el análisis cuantitativo de vanadio es acidificar la solución añadiendo H 2 SO 4 y oxidando el vanadio con H 2 O 2 para formar un compuesto soluble rojizo marrón con la fórmula general (VO) 2 (SO 4) 3. Palasota y Deming estudiaron el efecto de las cantidades relativas de H 2 SO 4 y H 2 O 2 sobre la absorbancia de la solución, reportando los siguientes resultados para un diseño factorial 2 2 [Palasota, J. A.; Deming, S. N. J. Chem. Educ. 1992, 62, 560—563].
| H 2 SO 4 | H 2 O 2 | absorbancia |
|---|---|---|
| \(+1\) | \(+1\) | 0.330 |
| \(+1\) | \(-1\) | 0.359 |
| \(-1\) | \(+1\) | 0.293 |
| \(-1\) | \(-1\) | 0.420 |
Cuatro mediciones replicadas en el centro del diseño factorial dan absorbancias de 0.334, 0.336, 0.346 y 0.323. Determinar si un modelo empírico de primer orden es apropiado para este sistema. Utilice un intervalo de confianza del 90% cuando se tenga en cuenta el efecto del error aleatorio.
Solución
Comenzamos determinando el intervalo de confianza para la respuesta en el centro del diseño factorial. La respuesta media es de 0.335 con una desviación estándar de 0.0094, lo que da un intervalo de confianza del 90% de
\[\mu=\overline{X} \pm \frac{t s}{\sqrt{n}}=0.335 \pm \frac{(2.35)(0.0094)}{\sqrt{4}}=0.335 \pm 0.011 \nonumber\]
La respuesta promedio,\(\overline{R}\), desde el diseño factorial es
\[\overline{R}=\frac{0.330+0.359+0.293+0.420}{4}=0.350 \nonumber\]
Debido a que\(\overline{R}\) excede el límite superior del intervalo de confianza de 0.346, podemos suponer razonablemente que un diseño factorial de 2 2 y un modelo empírico de primer orden son inapropiados para este sistema en el nivel de confianza del 95%.
Diseños centrales de compuestos
Una limitación para un diseño factorial de 3 k es el número de ensayos que necesitamos ejecutar. Como se muestra en la Figura 14.1.16 , un diseño factorial 3 2 requiere 9 ensayos. Este número aumenta a 27 para tres factores y a 81 para 4 factores.
Un diseño experimental más eficiente para un sistema que contiene más de dos factores es un diseño compuesto central, dos ejemplos del cual se muestran en la Figura 14.1.17 . El diseño compuesto central consiste en un diseño factorial de 2 k, que proporciona datos para estimar el efecto de primer orden de cada factor y las interacciones entre los factores, y un diseño de estrella que tiene\(2^k + 1\) puntos, lo que proporciona datos para estimar efectos de segundo orden. Si bien un diseño compuesto central para dos factores requiere el mismo número de ensayos, nueve, como un diseño factorial 3 2, solo requiere 15 ensayos y 25 ensayos cuando se utilizan tres factores o cuatro factores. Consulte los recursos adicionales de este capítulo para obtener detalles sobre los diseños centrales de compuestos.