5.2: Modelos teóricos para la distribución de datos

Hay cuatro tipos importantes de distribuciones que consideraremos en este capítulo: la distribución uniforme, la distribución binomial, la distribución de Poisson y la distribución normal, o gaussiana. En el Capítulo 3 y Capítulo 4 se utilizó el análisis de bolsas de M&Ms para explorar formas de visualizar datos y resumir datos. Aquí utilizaremos el mismo conjunto de datos para explorar la distribución de los datos.

Distribución Uniforme

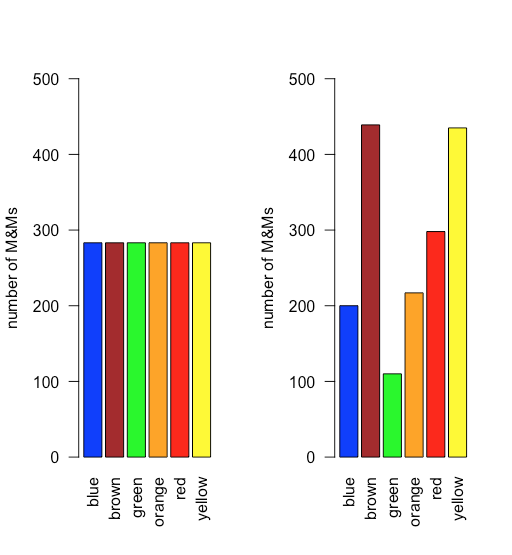
En una distribución uniforme, todos los resultados son igualmente probables. Supongamos que la población de M&Ms tiene una distribución uniforme. Si este es el caso, entonces, con seis colores, esperamos que cada color aparezca con una probabilidad de 1/6 o 16.7%. La figura\(\PageIndex{1}\) muestra una comparación de los resultados teóricos si dibujamos 1699 M&MS, el número total de M&Ms en nuestra muestra de 30 bolsas, de una población con una distribución uniforme (a la izquierda) a la distribución real de las 1699 M&M en nuestra muestra (a la derecha). ¡Parece poco probable que la población de M&Ms tenga una distribución uniforme de colores!

Figura\(\PageIndex{1}\): Comparación de (a la izquierda) una distribución uniforme de 1699 M&Ms con (a la derecha) la distribución real de la muestra en el Cuadro 3.1.1.

Distribución binomial

Una distribución binomial muestra la probabilidad de obtener un resultado particular en un número fijo de ensayos, donde se conocen las probabilidades de que ese resultado ocurra en un solo ensayo. Matemáticamente, una distribución binomial se define por la ecuación

\[P(X, N) = \frac {N!} {X! (N - X)!} \times p^{X} \times (1 - p)^{N - X} \nonumber\]

donde P (X, N) es la probabilidad de que el evento ocurra X veces en N ensayos, y donde p es la probabilidad de que el evento ocurra en un solo ensayo. La distribución binomial tiene una media teórica,\(\mu\), y una varianza teórica\(\sigma^2\), de

\[\mu = Np \quad \quad \quad \sigma^2 = Np(1 - p) \nonumber\]

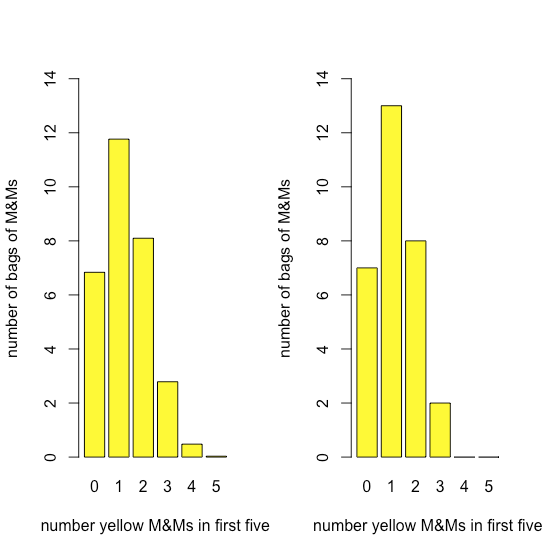
La figura\(\PageIndex{2}\) compara la distribución binomial esperada para el dibujo 0, 1, 2, 3, 4 o 5 M&M amarillos en los primeros cinco M&Ms —suponiendo que la probabilidad de dibujar un M&M amarillo es 435/1699, la relación entre el número de M&Ms amarillos y el número total de M&Ms— con la distribución real de resultados. La similitud entre los resultados teóricos y los reales parece evidente; en el Capítulo 6 consideraremos formas de probar esta afirmación.

Figura\(\PageIndex{2}\): Comparación de (a la izquierda) la distribución binomial teórica de M&Ms amarillas en los cinco primeros seleccionados de una bolsa de M&Ms y (a la derecha) la distribución real de M&Ms.

Distribución de Poisson

La distribución binomial es útil si queremos modelar la probabilidad de encontrar un número fijo de M&Ms amarillos en una muestra de M&Ms de tamaño fijo —como los primeros cinco M&Ms que extraemos de una bolsa— pero no la probabilidad de encontrar un número fijo de M&Ms amarillos en una sola bolsa porque hay cierta variabilidad en el número total de M&Ms por bolsa.

Una distribución de Poisson da la probabilidad de que un número dado de eventos ocurrirá en un intervalo fijo en el tiempo o el espacio si el evento tiene una tasa promedio conocida y si cada nuevo evento es independiente del evento anterior. Matemáticamente una distribución de Poisson se define por la ecuación

\[P(X, \lambda) = \frac {e^{-\lambda} \lambda^X} {X !} \nonumber\]

donde\(P(X, \lambda)\) es la probabilidad de que un evento ocurra X veces dada la tasa promedio del evento,\(\lambda\). La distribución de Poisson tiene una media teórica,\(\mu\), y una varianza teórica,\(\sigma^2\), que son cada una igual a\(\lambda\).

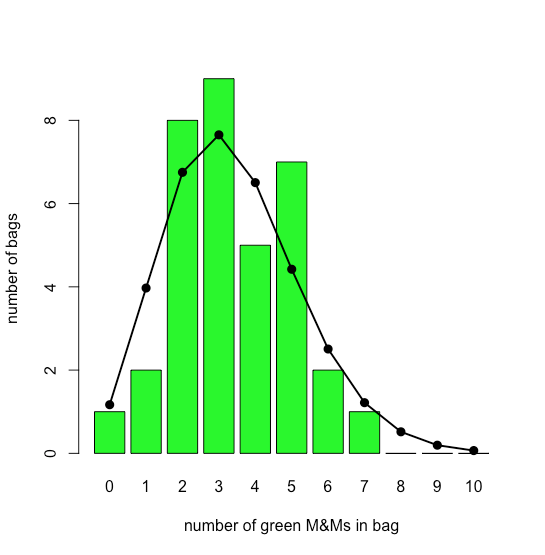
La gráfica de barras en la Figura\(\PageIndex{3}\) muestra la distribución real de M&Ms verdes en 35 bolsas pequeñas de M&Ms (según lo reportado por M. A. Xu-Friedman “Ilustrando conceptos de análisis cuántico con un modelo intuitivo de aula”, Adv. Physiol. Educ. 2013, 37, 112—116). Superpuesta a la parcela de barras se encuentra la distribución teórica de Poisson basada en su tasa promedio reportada de 3.4 M&Ms verdes por bolsa. La similitud entre los resultados teóricos y los reales parece evidente; en el Capítulo 6 consideraremos formas de probar esta afirmación.

Figura\(\PageIndex{3}\): Comparación de una distribución de Poisson para M&Ms verdes (puntos y línea) con resultados experimentales (barras). Los datos son de M. A. Xu-Friedman, “Ilustrando conceptos de análisis cuántico con un modelo intuitivo de aula”, Adv. Physiol. Educ. 2013, 37, 112—116.

Distribución Normal

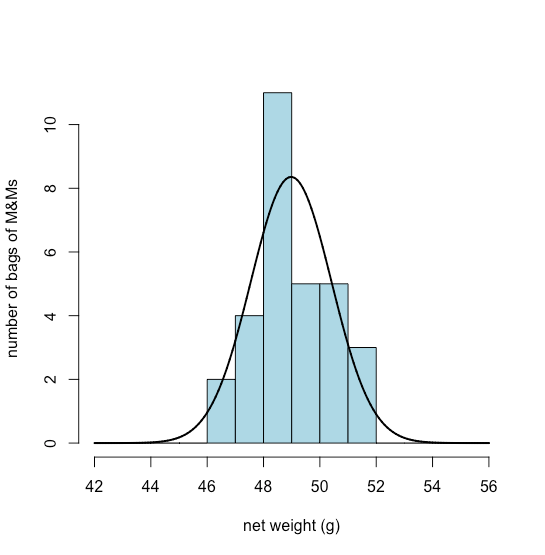
Una distribución uniforme, una distribución binomial y una distribución de Poisson predicen la probabilidad de un evento discreto, como la probabilidad de encontrar exactamente dos M&Ms verdes en la siguiente bolsa de M&Ms que abrimos. No todos los datos que recopilamos son discretos. Los pesos netos de las bolsas de M&Ms son un ejemplo de datos continuos ya que la masa de una bolsa individual no se restringe a un conjunto discreto de valores permitidos. En muchos casos podemos modelar datos continuos usando una distribución normal (o gaussiana), lo que da la probabilidad de obtener un resultado particular, P (x), de una población con una media conocida,\(\mu\), y una varianza conocida,\(\sigma^2\). Matemáticamente una distribución normal se define por la ecuación

\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber\]

La figura\(\PageIndex{4}\) muestra la distribución normal esperada para los pesos netos de nuestra muestra de 30 bolsas de M&Ms si asumimos que su media\(\overline{X}\),, de 48.98 g y desviación estándar, s, de 1.433 g son buenos predictores de la media de la población,\(\mu\), y desviación estándar, \(\sigma\). Dada la pequeña muestra de 30 bolsas, el acuerdo entre el modelo y los datos parece razonable.

Figura\(\PageIndex{4}\): Comparación de una distribución normal para los pesos netos de M&Ms (línea) con los resultados experimentales (barras).