5.3: El Teorema del Límite Central

Última actualización
Guardar como PDF

Page ID: 69289

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Supongamos que tenemos una población para la cual una de sus propiedades tiene una distribución uniforme donde cada resultado entre 0 y 1 es igualmente probable. Si analizamos 10,000 muestras no debemos sorprendernos al encontrar que la distribución de estos 10000 resultados se ve uniforme, como lo muestra el histograma del lado izquierdo de la Figura\(\PageIndex{1}\). Si recolectamos 1000 muestras agrupadas, cada una de las cuales consta de 10 muestras individuales para un total de 10,000 muestras individuales, y reportamos los resultados promedio para estas 1000 muestras agrupadas, vemos algo interesante ya que su distribución, como lo muestra el histograma de la derecha, se ve notablemente como una normal distribución. Cuando extraemos muestras individuales de una distribución uniforme, cada resultado posible es igualmente probable, por lo que vemos la distribución a la izquierda. Cuando dibujamos una muestra agrupada que consta de 10 muestras individuales, sin embargo, es más probable que los valores promedio estén cerca de la mitad del rango de la distribución, como vemos a la derecha, porque la muestra agrupada probablemente incluye valores extraídos tanto de la mitad inferior como de la mitad superior de la distribución uniforme .

Figura\(\PageIndex{1}\): Distribución de los resultados al analizar muestras de tamaño n = 1 (izquierda) y muestras de tamaño n = 10 (derecha) extraídas de una distribución uniforme.

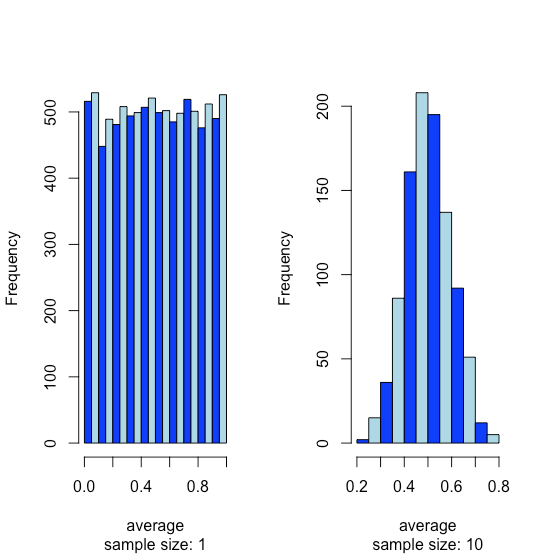
Esta tendencia a que surja una distribución normal cuando agrupamos muestras se conoce como el teorema del límite central. Como se muestra en la Figura\(\PageIndex{2}\), vemos un efecto similar con poblaciones que siguen una distribución binomial o una distribución de Poisson.

Figura\(\PageIndex{2}\): Distribución de los resultados al analizar muestras de tamaño\(n = 1\) (izquierda) y muestras de tamaño\(n = 10\) (derecha) extraídas de una distribución binomial con p = 0.167 (arriba) y una distribución de Poisson con\(\lambda = 4\) (abajo).

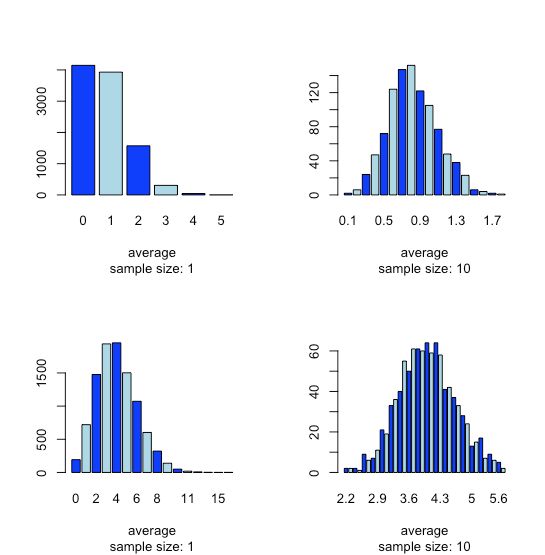
Podría preguntarse razonablemente si el teorema del límite central es importante ya que es poco probable que completemos 1000 análisis, cada uno de los cuales es el promedio de 10 ensayos individuales. Esto es engañoso. Cuando adquirimos una muestra de suelo, por ejemplo, consiste en muchas partículas individuales cada una de las cuales es una muestra individual del suelo. Nuestro análisis de esta muestra, por lo tanto, es la media para un gran número de partículas individuales de suelo. Debido a esto, el teorema del límite central es relevante.