6.1: Propiedades de una distribución normal

Última actualización
Guardar como PDF

Page ID: 69341

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

Matemáticamente una distribución normal se define por la ecuación

\[P(x) = \frac {1} {\sqrt{2 \pi \sigma^2}} e^{-(x - \mu)^2/(2 \sigma^2)} \nonumber\]

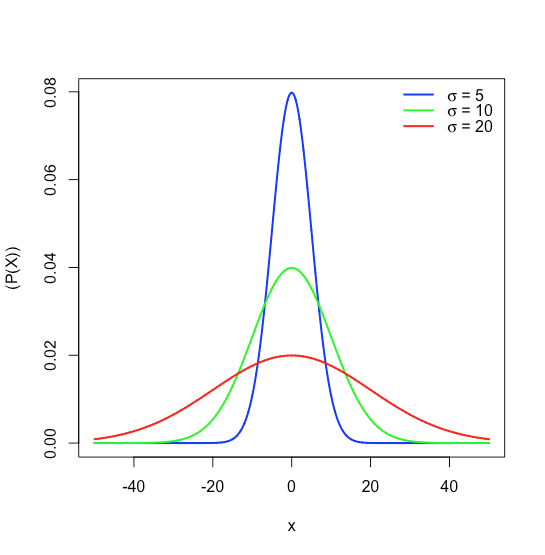
donde\(P(x)\) es la probabilidad de obtener un resultado,\(x\), de una población con una media conocida,\(\mu\), y una desviación estándar conocida,\(\sigma\). La figura\(\PageIndex{1}\) muestra las curvas de distribución normal para\(\mu = 0\) con desviaciones estándar de 5, 10 y 20.

Figura\(\PageIndex{1}\): Tres ejemplos de curvas de distribución normal. Aunque la altura y el ancho se ven afectados por\(\sigma\), el área bajo cada curva es la misma.

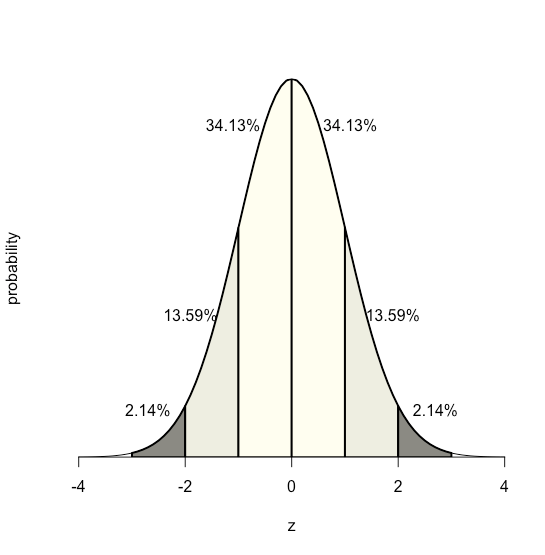
Debido a que la ecuación para una distribución normal depende únicamente de la media de la población\(\mu\), y de su desviación estándar\(\sigma\), la probabilidad de que una muestra extraída de una población tenga un valor entre dos límites arbitrarios cualesquiera es la misma para todas las poblaciones. Por ejemplo, la Figura\(\PageIndex{2}\) muestra que 68.26% de todas las muestras extraídas de una población normalmente distribuida tienen valores dentro del rango\(\mu \pm 1\sigma\), y sólo 0.14% tienen valores mayores que\(\mu + 3\sigma\).

Figura\(\PageIndex{2}\): Curva de distribución normal para\(\mu = 0\) y\(\sigma = 1\) mostrando área bajo la curva para diversos valores de\(z\) in\(\mu \pm z \sigma\).

Esta característica de una distribución normal, que el área bajo la curva es la misma para todos los valores de, nos\(\sigma\) permite crear una tabla de probabilidad (ver Apéndice 1) basada en la desviación relativa,\(z\), entre un límite, x, y la media,\(\mu\).

\[z = \frac {x - \mu} {\sigma} \nonumber\]

El valor de\(z\) da el área bajo la curva entre ese límite y la cola más cercana de la distribución, como se muestra en la Figura\(\PageIndex{3}\).

Figura\(\PageIndex{3}\): Curva de distribución normal para\(\mu = 0\) y\(\sigma = 1\) mostrando (a la izquierda) el área bajo la curva para\(z = −1.5\) y (a la derecha para\(z = +0.5\).

Ejemplo\(\PageIndex{1}\)

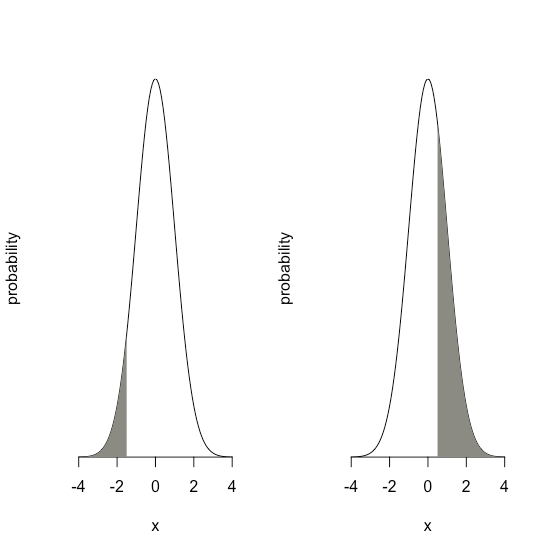
Supongamos que sabemos que\(\mu\) es 5.5833 ppb Pb y eso\(\sigma\) es 0.0558 ppb Pb para un material de referencia estándar particular (SRM). ¿Cuál es la probabilidad de que obtengamos un resultado mayor a 5.650 ppb si analizamos una sola muestra aleatoria extraída del SRM?

Solución

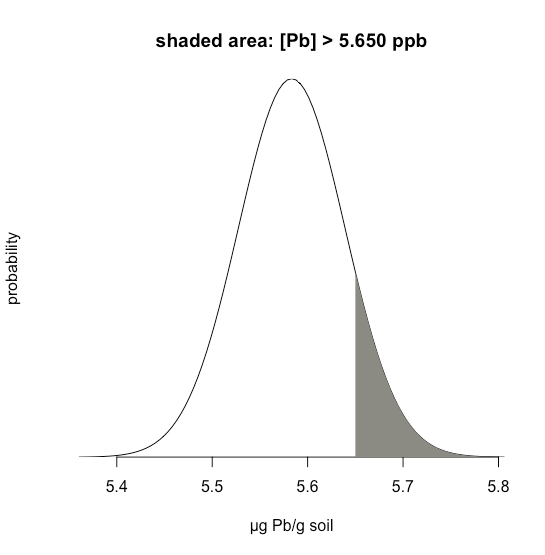
La figura\(\PageIndex{4}\) muestra la curva de distribución normal dada valores de 5.5833 ppb Pb para\(\mu\) y 0.0558 ppb Pb\(\sigma\). El área sombreada en las figuras es la probabilidad de obtener una muestra con una concentración de Pb mayor a 5.650 ppm. Para determinar la probabilidad, primero calculamos\(z\)

\[z = \frac {x - \mu} {\sigma} = \frac {5.650 - 5.5833} {0.0558} = 1.195 \nonumber\]

A continuación, buscamos la probabilidad en el Apéndice 1 para este valor de\(z\), que es el promedio de 0.1170 (para\(z = 1.19\)) y 0.1151 (para\(z = 1.20\)), o una probabilidad de 0.1160; así, esperamos que 11.60% de las muestras brinden un resultado mayor a 5.650 ppb Pb.

Figura\(\PageIndex{4}\): Curva de distribución normal para la cantidad de plomo en una referencia estándar con\(\mu = 5.5833\) ppb y\(\sigma = 0.0558\) ppb. El área sombreada muestra aquellos resultados para los cuales la concentración de plomo supera los 5.650 ppb.

Ejemplo\(\PageIndex{2}\)

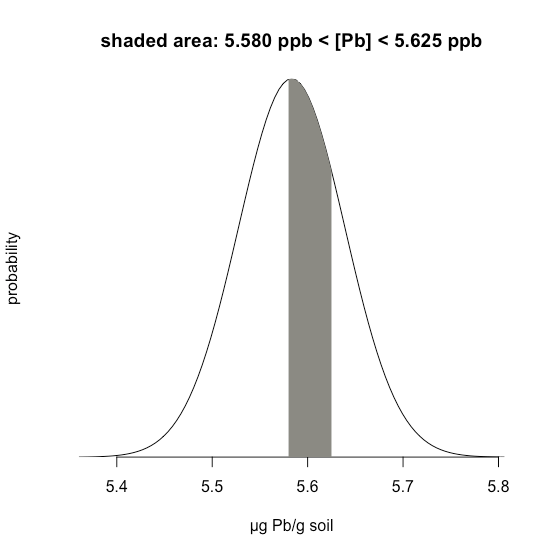
\(\PageIndex{1}\)El ejemplo considera un único límite: la probabilidad de que un resultado supere un solo valor. Pero, ¿y si queremos determinar la probabilidad de que una muestra tenga entre 5.580 g Pb y 5.625 g Pb?

Solución

En este caso nos interesa el área sombreada que se muestra en la Figura\(\PageIndex{5}\). Primero, calculamos\(z\) para el límite superior

\[z = \frac {5.625 - 5.5833} {0.0558} = 0.747 \nonumber\]

y luego calculamos\(z\) para el límite inferior

\[z = \frac {5.580 - 5.5833} {0.0558} = -0.059 \nonumber\]

Entonces, buscamos la probabilidad en el Apéndice 1 de que un resultado supere nuestro límite superior de 5.625, que es 0.2275, o 22.75%, y la probabilidad de que un resultado sea menor que nuestro límite inferior de 5.580, que es 0.4765, o 47.65%. El área total no sombreada es 71.4% del área total, por lo que el área sombreada corresponde a una probabilidad de

\[100.00 - 22.75 - 47.65 = 100.00 - 71.40 = 29.6 \% \nonumber\]

Figura\(\PageIndex{5}\): Curva de distribución normal para la cantidad de plomo en una referencia estándar con\(\mu = 5.5833\) ppb y\(\sigma = 0.0558\) ppb. El área sombreada muestra aquellos resultados para los cuales la concentración de plomo es superior a 5.580 ppb y menor a 5.625 ppb.