6.2: Intervalos de confianza

Última actualización
Guardar como PDF

Page ID: 69343

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \) \( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)\(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\) \(\newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\) \( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\) \( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\) \( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\) \( \newcommand{\Span}{\mathrm{span}}\)\(\newcommand{\AA}{\unicode[.8,0]{x212B}}\)

En la sección anterior, aprendimos a predecir la probabilidad de obtener un resultado particular si nuestros datos se distribuyen normalmente con un conocido\(\mu\) y uno conocido\(\sigma\). Por ejemplo, estimamos que 11.60% de las muestras extraídas al azar de un material de referencia estándar tendrán una concentración de Pb mayor a 5.650 ppb dada a\(\mu\) de 5.5833 ppb y a\(\sigma\) de 0.0558 ppb. En esencia, se determinó de cuántas desviaciones estándar es 5.650\(\mu\) y se utilizó esta para definir la probabilidad dada el área estándar bajo una curva de distribución normal.

Podemos verlo de otra manera haciendo la siguiente pregunta: Si recolectamos una sola muestra al azar de una población con un conocido\(\mu\) y otro conocido\(\sigma\), ¿dentro de qué rango de valores podríamos esperar razonablemente encontrar el resultado de la muestra 95% del tiempo? Reorganización de la ecuación

\[z = \frac {x - \mu} {\sigma} \nonumber\]

y resolviendo para\(x\) da

\[x = \mu \pm z \sigma = 5.5833 \pm (1.96)(0.0558) = 5.5833 \pm 0.1094 \nonumber\]

donde a\(z\) de 1.96 corresponde al 95% del área bajo la curva; llamamos a esto un intervalo de confianza del 95% para una sola muestra.

Por lo general, es una mala idea sacar una conclusión del resultado de un solo experimento; en cambio, solemos recolectar varias muestras y hacer la pregunta de esta manera: Si recolectamos muestras\(n\) aleatorias de una población con un conocido\(\mu\) y otro conocido\(\sigma\), dentro de qué rango de valores podríamos razonablemente esperar encontrar la media de estas muestras el 95% de las veces?

Podemos esperar razonablemente que la desviación estándar para la media de varias muestras sea menor que la desviación estándar para un conjunto de muestras individuales; de hecho lo es y se da como

\[\sigma_{\bar{x}} = \frac {\sigma} {\sqrt{n}} \nonumber\]

donde\(\frac {\sigma} {\sqrt{n}}\) se llama el error estándar de la media. Por ejemplo, si recolectamos tres muestras del material de referencia estándar descrito anteriormente, entonces esperamos que la media para estas tres muestras se encuentre dentro de un rango

\[\bar{x} = \mu \pm z \sigma_{\bar{X}} = \mu \pm \frac {z \sigma} {\sqrt{n}} = 5.5833 \pm \frac{(1.96)(0.0558)} {\sqrt{3}} = 5.5833 \pm 0.0631 \nonumber\]

es decir\(\pm 0.0631\) ppb alrededor\(\mu\), un rango que es menor que el de\(\pm 0.1094\) ppb cuando analizamos muestras individuales. Obsérvese que el valor relativo para nosotros de aumentar el tamaño de la muestra disminuye a\(n\) medida que aumenta debido al término raíz cuadrada, como se muestra en la Figura\(\PageIndex{1}\).

Figura\(\PageIndex{1}\): Gráfica que muestra cómo varía el error estándar de la media con el tamaño de la muestra. El valor para\(\sigma\) es 10.

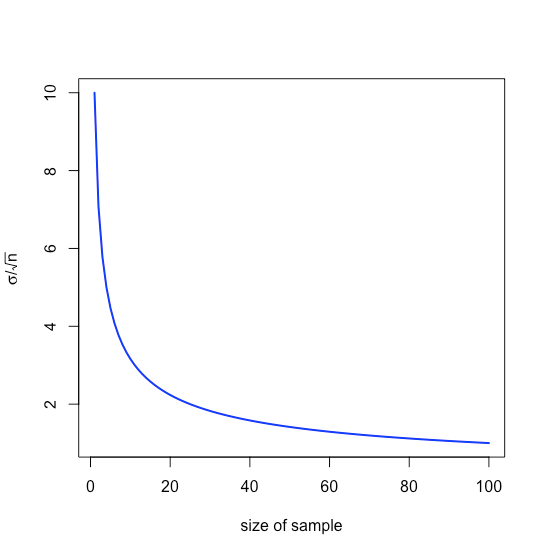
Nuestro tratamiento hasta ahora supone que conocemos\(\mu\) y\(\sigma\) para la población parental, pero rara vez conocemos estos valores; en cambio, examinamos muestras extraídas de la población parental y hacemos la siguiente pregunta: Dada la media de la muestra\(\bar{x}\),, y su desviación estándar,\(s\), cuál es nuestra mejor estimación de la media de la población\(\mu\), y su desviación estándar,\(\sigma\).

Para hacer esta estimación, reemplazamos la desviación estándar de la población,\(\sigma\), por la desviación estándar,\(s\), para nuestras muestras, reemplazamos la media de la población,\(\mu\), por la media,\(\bar{x}\), para nuestras muestras,\(z\) reemplazamos por\(t\), donde el valor de\(t\) depende de el número de muestras,\(n\)

\[\bar{x} = \mu \pm \frac{ts}{\sqrt{n}} \nonumber\]

y luego reorganizar la ecuación para resolver\(\mu\).

\[\mu = \bar{x} \pm \frac {ts} {\sqrt{n}} \nonumber\]

A esto lo llamamos intervalo de confianza. Los valores para\(t\) están disponibles en tablas (ver Apéndice 2) y dependen del nivel de probabilidad,\(\alpha\), donde\((1 − \alpha) \times 100\) está el nivel de confianza, y los grados de libertad,\(n − 1\); tenga en cuenta que para cualquier nivel de probabilidad,\(t \longrightarrow z\) como\(n \longrightarrow \infty\).

Debemos prestar especial atención a lo que significa este intervalo de confianza y a lo que no significa:

No significa que exista una probabilidad del 95% de que la media de la población esté en el rango\(\mu = \bar{x} \pm ts\) porque nuestras mediciones pueden estar sesgadas o la distribución normal puede ser inapropiada para nuestro sistema.
Proporciona nuestra mejor estimación de la media de la población,\(\mu\) dado nuestro análisis de\(n\) muestras extraídas al azar de la población parental; una muestra diferente, sin embargo, dará un intervalo de confianza diferente y, por lo tanto, una estimación diferente para\(\mu\).